2. 南卫理公会大学 电子工程系, 美国 达拉斯 德克萨斯州
2. Department of Electrical Engineering, Southern Methodist University Dallas, Texas, USA
低压差线性稳压器(low-dropout regulator, LDO)具有结构简单、低噪声、低功耗以及封装尺寸小等突出优点, 在便携式电子产品中作为电源转换电路得到广泛的应用.无片外电容LDO不需要外接特定的电容, 也不需增加额外引脚, 减小了芯片和印刷电路板(PCB)面积, 而成为近年来研究的热点.
为了提高电源转换效率, 需要降低LDO功耗.因此低静态电流成为LDO设计的重要指标.而减小静态电流不可避免会影响LDO的瞬态特性.因为LDO瞬态特性受环路带宽和功率管栅端摆率的影响, 这两者均随静态电流减小而减小[1].同时对于无片外电容LDO, 没有芯片输出端的负载电容, 会导致负载跳变时输出过冲电压增大, 影响LDO内部环路稳定.因此设计低功耗无片外电容型LDO的最大挑战是如何提高其瞬态特性和如何通过频率补偿保证环路稳定性.
由于LDO中的主环路由多级放大器级联而成, 使得在环路中存在多个极点, 主要包括放大器输出极点和LDO输出极点.对于无片外电容LDO, LDO负载电容下降3~4个数量级.无论有没有进行密勒补偿, LDO的输出极点都会被推高且随负载变化而变化[2].因此无片外电容LDO通常采用内部补偿.即将低频主极点设定在反馈内部而不在输出节点, 这与片外补偿相反.在内部补偿中, 密勒补偿是最常用也是最有用的补偿方式.
为使得LDO的压差降低并能输出大电流, 需要大尺寸的PMOS管作为功率器件.这时, PMOS管大的栅端电容产生一个低频极点, 可能会落入单位带宽内, 影响系统稳定性.同时, 低静态电流不可避免地减小了功率管栅端电压转换速率, 影响了系统的瞬态特性.目前有多种方法改善LDO的瞬态特性[3-8].对于带输出电容LDO, Lam等[3]增加动态偏置电路;Lee等[4]使用摆率增强电路;Man等[5]采用push-pull推挽电路.对于无片外电容LDO, Zhan等[6]增加动态偏置电路;Or P Y等使用电压峰值检测电路[7-8].上述方法需要复杂的转换电路或补偿电路, 系统的功耗和设计复杂度都难以降低.
鉴此,本文采用阻抗衰减缓冲器(buffer impedance attenuation, BIA)配合摆率增强电路作为驱动功率管的中间级.不仅可以减小第2级放大器的输出阻抗, 将功率管栅端极点推远, 保证在低压差大负载时该极点也在单位带宽之外, 也可以增强LDO大信号响应, 改善瞬态特性.同时采用嵌套式密勒补偿方式, 将主极点固定在第1级放大器输出点, 使得无论负载如何变化, 输出都能保持稳定, 并快速响应.
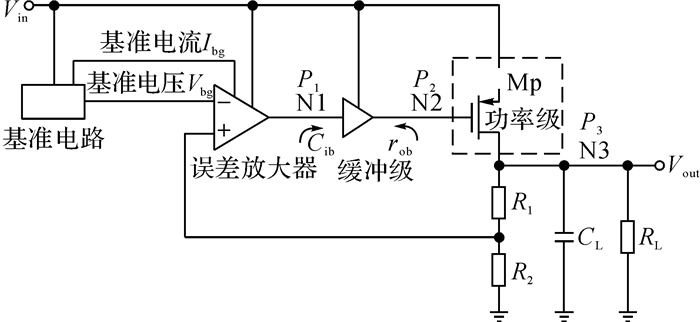
2 阻抗衰减缓冲器(BIA)如图 1所示为包含中间缓冲级的LDO结构.输入电压Vin经过功率管(power MOS)给负载供电, 通过负反馈和精确的参考电压Vbg保证输出电压为设定的稳定值.电路包含以下模块:基准电路、误差放大器、功率级、中间缓冲级以及其他辅助电路.存在3个极点:误差放大器输出极点(N1)、缓冲级输出极点(N2)、LDO输出极点(N3) 分别为
|
图 1 带有中间缓冲级的LDO传统结构 Fig. 1 Typical structure of low-dropout regulator with intermediate buffer stage |
| $ {P_{1\left| {{N_1}} \right.}} = 1/\left( {{r_{{\rm{ol}}}}{C_1}} \right), $ | (1) |
| $ {P_{2\left| {{N_2}} \right.}} = 1/\left( {{r_{{\rm{ob}}}}{C_2}} \right), $ | (2) |
| $ {P_{3\left| {{N_3}} \right.}} = 1/\left( {{R_{{\rm{oeq}}}}{C_{\rm{L}}}} \right). $ | (3) |
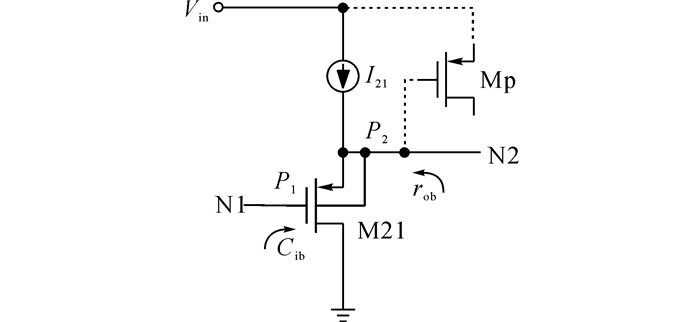
式中:ro1为误差放大器的输出电阻, C1为N1点的等效电容, 主要由缓冲级的输入电容Cib决定, rob为缓冲级的输出电阻, C2为N2点的等效电容, 主要由功率级的输入电容Cp决定, Roeq为LDO输出等效电阻, CL为LDO负载电容.为了使得缓冲级输出极点P2始终保持在单位带宽之外, rob应该很小.如图 2所示, 图中I2为电流源,采用PMOS源跟随器作为中间缓冲级, 输出阻抗rob=1/gm21, 可以增大M21管的跨导gm21来减小rob的值使得P2更加远离单位带宽.
|
图 2 采用源跟随器结构的中间缓冲级 Fig. 2 Source-follower implementation of intermediate buffer stage |
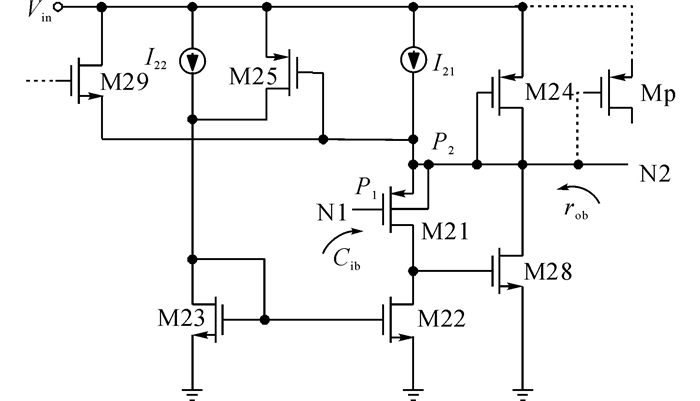
由于LDO的单位增益带宽是与负载电流相关的, 当负载电流增大时输出负载减小, 单位增益带宽变大, P2就需要被置于更高的频率上以致不会影响系统稳定性, 因此缓冲器的输出阻抗也需要减小, 如图 3所示通过增加2个PMOS管M24和M25, 来实现1种动态的补偿, 使系统在全负载变化的情况下都能维持稳定.电阻将第1级差分放大器2个支路电流变化量转换成电压后, 连接在M29的栅端, 由其产生摆率增强电路的输出电流.此时缓冲器的输出阻抗为
|
图 3 带有动态偏置并联反馈和摆率增强的中间缓冲器 Fig. 3 Buffer stage with dynamically-biased shunt feedback structure and slew rate enhancement circuit |
| $ \begin{array}{l} {r_{{\rm{ob}}}} = \frac{1}{{{g_{{\rm{m}}21}} + {g_{{\rm{m}}24}} + {g_{{\rm{m}}29}} + {g_{{\rm{m}}28}}\left( {{g_{{\rm{m}}21}} + M{g_{{\rm{m}}25}}} \right)\left( {\frac{{{r_{o21}}{r_{o22}}}}{{{r_{o21}} + {r_{o22}}}}} \right)}} \approx \\ \;\;\;\;\;\;\;\frac{1}{{{g_{{\rm{m}}21}}\left( {1 + \beta } \right) + {g_{{\rm{m}}24}} + {g_{{\rm{m}}29}}}}. \end{array} $ | (4) |
式中:
另外, 这种缓冲器的结构在负载变换时还能提高功率级栅端的摆率.当负载从空载到满载切换时, N1点电压降低, 导致大电流流过M21, 对M28的栅端充电.于是流经M28的电流加大, 对功率管栅端放电, N2电压以更高的速度降低.同理, 当负载从满载到空载切换时, N1点电压增大, M29栅端电位增高, M29提供额外的电流给功率管栅电容CGG, POW充电, 能够快速增加N2电压响应.
将极点P2、P3用输出电流IOUT表示为
| $ \begin{array}{l} {I_{{\rm{OUT,}}{P_2}}} = \frac{1}{{{r_{{\rm{ob}}}}{C_{{\rm{GG}},{\rm{POW}}}}}} \approx \\ \frac{{\left[ {\sqrt {\frac{{{W_{{{\rm{M}}_{21}}}}}}{{{L_{{{\rm{M}}_{21}}}}}}} \left( {1 + \beta } \right) + \sqrt {\frac{{{W_{{{\rm{M}}_{24}}}}}}{{{L_{{{\rm{M}}_{24}}}}}}} + \sqrt {\frac{{{W_{{{\rm{M}}_{29}}}}}}{{{L_{{{\rm{M}}_{29}}}}}}} } \right]\sqrt {2\mu {C_{{\rm{OX}}}}\left( {\alpha {I_{{\rm{OUT}}}}} \right)} }}{{{C_{{\rm{GG}},{\rm{POW}}}}}}, \end{array} $ | (5) |
| $ {I_{{\rm{OUT,}}{P_3}}} = \frac{1}{{\left[ {\frac{{\left( {{R_1} + {R_2}} \right){R_{\rm{L}}}}}{{{R_1} + {R_2} + {R_{\rm{L}}}}}} \right]{C_{\rm{L}}}}} \approx \frac{1}{{{R_{\rm{L}}}{C_{\rm{L}}}}} = \frac{{{I_{{\rm{OUT}}}}}}{{{V_{{\rm{OUT}}}}{C_{\rm{L}}}}}. $ | (6) |
式中:CGG, POW为功率管Mp的栅电容, WM21/LM21、WM24/LM24、WM29/LM29分别为M21、M24和M29的宽长比, μ为载流子的迁移率, COX为单位面积的栅氧化层电容, α为输出电流IOUT倍数, R1和R2为反馈电阻值, RL为负载电阻值, VOUT为输出电压.除了LDO输出电流IOUT外, 其余参数设计为常数, 可看作固定值.因此, 根据缓冲器的输出极点P2、LDO的输出极点P3与LDO输出电流IOUT的相对关系, 可以推导出缓冲器的输出极点P2和LDO的输出极点P3的关系式, 即
| $ {P_2} \propto \sqrt {{P_3}} . $ | (7) |
由式(7) 可知, 在图 3所示的缓冲器会形成极点-极点追踪效果.即缓冲器的输出极点P2会随着LDO的输出极点P3增大而增大.通过使用这种动态偏置的并联反馈, 减小了缓冲级的输出阻抗rob, 使得将环路次极点P2推至高频, 并且输出阻抗rob又能动态跟随负载电流的变化, 使电路能在全负载条件下都有很好的稳定性, 同时这种方法也提高了大尺寸功率级的摆率.
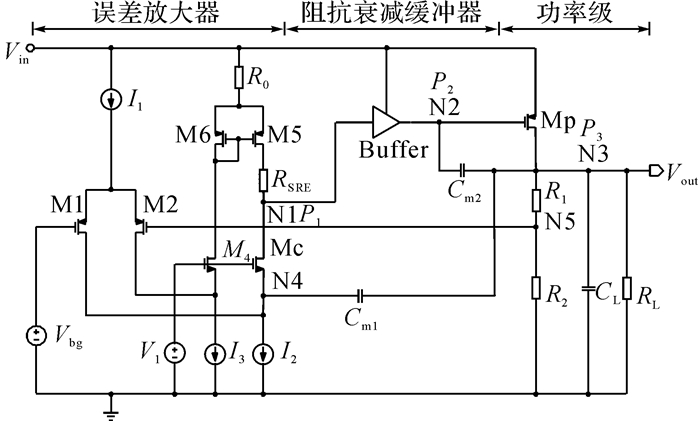
3 LDO电路设计由于低功耗的限制, 即使第2级放大器采用上述的阻抗衰减缓冲器结构, 其输出极点P2的最大值也受到限制.在这种情况下, 只能通过减小主极点P1的频率来减小单位增益带宽.LDO结构如图 4所示, 误差放大器第1级采用PMOS管输入PMOS管负载折叠运放结构, 由M1、M2、Mc、M4、M5、M6和R0、RSRE构成.本文提出的无片外负载电容LDO芯片中采用了嵌套式密勒电容补偿(nested Miller compensation, NMC)方案, 不同于以往嵌套式密勒补偿[9].将第1级密勒电容Cm1的左极板接到第1级放大器的折叠端而非第1级放大器的输出端.增大了输出极点P3, 与直接接入第1级放大器的输出端相比[10], 使得LDO输出端极点频率增大gmcro1倍.由于LDO的输出极点作为非主极点存在, 因此它的提高有助于环路的稳定性.采用上述的阻抗衰减缓冲器结构, 相比于PMOS源跟随器结构作为第2级[11], 主极点P1降低, P2被提被高, 且负载增大, 会随着LDO的输出极点P3增大而增大.同时, Cm2连接在功率管的栅端和漏端之间.可以改善LDO大信号响应, 利用电容两端电压不能跳变特性在LDO输出电压跳变的瞬间同时改变功率管的栅电容, 以抑制过冲电压.
|
图 4 采用嵌套式密勒补偿结构的LDO结构图 Fig. 4 Structure of proposed LDO using nested Miller compensation scheme |
1) 稳定性分析
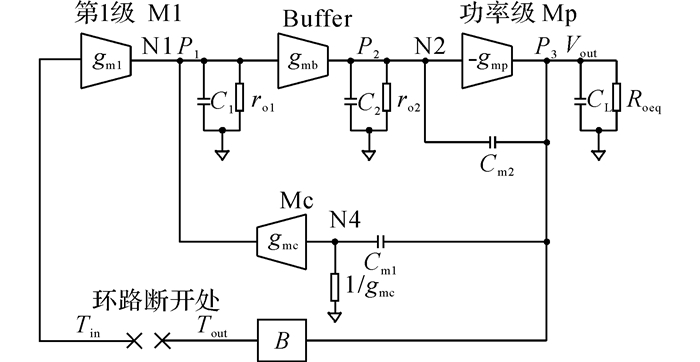
如图 5所示为图 4所示电路的小信号模型.利用其传递函数分析电路稳定性.其中gmL
|
图 5 采用嵌套式密勒补偿的LDO小信号模型 Fig. 5 Small-signal block diagram of proposed LDO with nested Miller compensation scheme |
| $ \begin{array}{*{20}{c}} {{A_{{\rm{open}}}}\left( s \right) = \frac{{B{g_{{\rm{ml}}}}{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{r_{{\rm{o1}}}}{r_{{\rm{ob}}}}{R_{{\rm{oeq}}}}\left( {1 - s\frac{{{C_{{\rm{m2}}}}}}{{{g_{{\rm{mp}}}}}} - {s^2}\frac{{{C_{{\rm{m1}}}}{C_{{\rm{m2}}}}}}{{{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}} \right)}}{{\left( {1 + s{C_{{\rm{m1}}}}{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{r_{{\rm{o1}}}}{r_{{\rm{ob}}}}{R_{{\rm{oeq}}}}} \right)\left[ {1 + s\frac{{{C_{{\rm{m2}}}}\left( {{g_{{\rm{mp}}}} - {g_{{\rm{mb}}}}} \right)}}{{{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}}} + {s^2}\frac{{{C_{\rm{L}}}{C_{{\rm{m2}}}}}}{{{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}} \right]}} \approx }\\ {\frac{{B{g_{{\rm{ml}}}}{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{r_{{\rm{o1}}}}{r_{{\rm{ob}}}}{R_{{\rm{oeq}}}}\left( {1 - s\frac{{{C_{{\rm{m2}}}}}}{{{g_{{\rm{mp}}}}}} - {s^2}\frac{{{C_{{\rm{m1}}}}{C_{{\rm{m2}}}}}}{{{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}} \right)}}{{\left( {1 + s{C_{{\rm{m1}}}}{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{r_{{\rm{o1}}}}{r_{{\rm{ob}}}}{R_{{\rm{oeq}}}}} \right)\left[ {1 + s\frac{{{C_{{\rm{m2}}}}}}{{{g_{{\rm{mb}}}}}} + {s^2}\frac{{{C_{\rm{L}}}{C_{{\rm{m2}}}}}}{{{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}} \right]}}.} \end{array} $ | (8) |
式中:B为反馈系数R2/(R1+R2), gm1为M1的跨导, gmb为buffer的输入跨导, gmc为Mc的跨导, gmp为Mp的跨导, Cm1为跨接在输出与第1级放大器折叠端之间的补偿电容值, Cm2为连接在功率管的栅端和漏端之间的补偿电容值.
根据式(8) 所给出的传递函数, 可以得到该LDO环路中包含3个极点和2个零点:
主极点P1的频率为
| $ {f_{{P_1}}} = \frac{1}{{{C_{{\rm{m1}}}}{g_{{\rm{mb}}}}{g_{{\rm{mp}}}}{r_{{\rm{o1}}}}{r_{{\rm{ob}}}}{R_{{\rm{oeq}}}}}}. $ | (9) |
缓冲级输出极点P2的频率为
| $ {f_{{P_2}}} = \frac{{{g_{{\rm{mb}}}}}}{{{C_{{\rm{m2}}}}}}. $ | (10) |
LDO的输出极点P3的频率为
| $ {f_{{P_3}}} = \frac{{{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}{{{C_{\rm{L}}}}}. $ | (11) |
另外存在2个零点的频率分别为
| $ {f_{{Z_1}}} = - \frac{{{g_{{\rm{mb}}}}}}{{{C_{{\rm{m2}}}}}}. $ | (12) |
| $ {f_{{Z_2}}} = \frac{{{g_{{\rm{mb}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}{{{C_{{\rm{ml}}}}}}. $ | (13) |
整个补偿电容Cm1的密勒效应决定了主极点的位置.为获得较好的相位裕度PM, 主极点P1应位于低频处而2个非主极点P2和P3分别置于高频位置.对于一个三阶的巴特沃斯响应, 采用极点分离方法, 增加输出级的跨导, 使非主极点P2和P3频率至少是增益带宽积(GBW)的2倍和4倍.即
| $ \frac{{{g_{{\rm{m1}}}}}}{{{C_{{\rm{m1}}}}}} \le \frac{1}{2}\frac{{{g_{{\rm{mb}}}}}}{{{C_{{\rm{m2}}}}}} \le \frac{1}{4}\frac{{{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}{{{C_{\rm{L}}}}}. $ | (14) |
通过式(14) 分析
| $ {\rm{GBW = }}\frac{{{g_{{\rm{m1}}}}}}{{{C_{{\rm{m1}}}}}} \le \frac{1}{4}\frac{{{g_{{\rm{mp}}}}{g_{{\rm{mc}}}}{r_{{\rm{o1}}}}}}{{{C_{\rm{L}}}}}. $ | (15) |
| $ {\rm{PM}} \ge {\rm{9}}{{\rm{0}}^ \circ } - {\tan ^{ - 1}}\left( {\frac{1}{2}} \right) - {\tan ^{ - 1}}\left( {\frac{1}{4}} \right) = {50^ \circ }. $ | (16) |
对于右半平面零点和高频处零点, 可以忽略它们对低频主极点的影响.假定gm1、gmb固定, Cm1和Cm2越大, 相位裕度越好.但带宽减小, 同时面积增大.因此Cm1、Cm2在满足上式中尽可能取比较小的值.但必须保证Cm1的值为第1级输出节点电容的3倍以上, Cm2为第2级输出节点电容的3倍以上, 否则输入噪声很大.
2) 电路设计
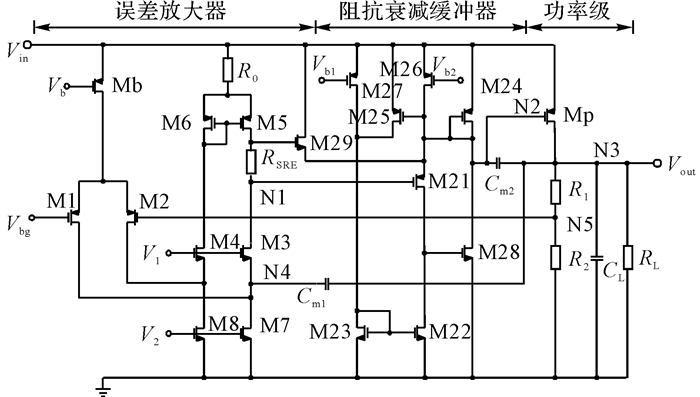
如图 6所示为该无片外电容LDO的主体电路, 其中包含了误差放大器、阻抗衰减缓冲器、功率级和密勒电容.基准模块产生1V的电压Vbg作为误差放大器的输入.
|
图 6 本文提出LDO的晶体管级电路图 Fig. 6 Transistor level schematic of proposed LDO |
在误差放大器中依然采用了两级放大器级联的形式, 并且第2级放大器采用了第2章提出的阻抗衰减缓冲器结构.阻抗缓冲器由源跟随器M21, NMOS管M28、M29, 2对电流镜(M24, M25), (M22, M23) 和2个电流源M26, M27构成.通过M21的电平转换可使得LDO工作在低电流模式.在空载情况下, M21将N1点电压提升Vgs来保证PMOS功率管Mp能够正常关断, 避免功率管栅端直接接N1点时导致M5进入线性区, 放大器失去增益.同时可以增加R1+R2的值来减小LDO的静态电流.这些可以改善LDO系统的大信号响应过程, 另外, 由于源跟随器的输出阻抗较小, 有利于提高第2级放大器输出极点P2的频率.通过添加密勒电容Cm1、Cm2, 减少误差放大器的单位增益带宽, 进而减少LDO环路的单位增益带宽, 能够有效地利用极点分裂效应将LDO的输出极点P3排除在单位增益带宽之外, 从而抑制了其对LDO稳定性的影响.
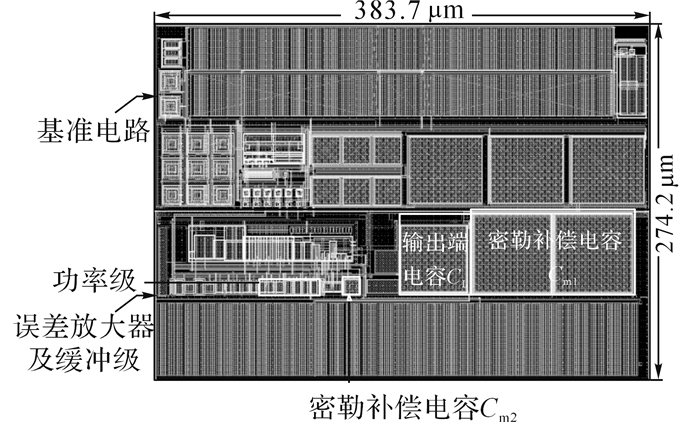
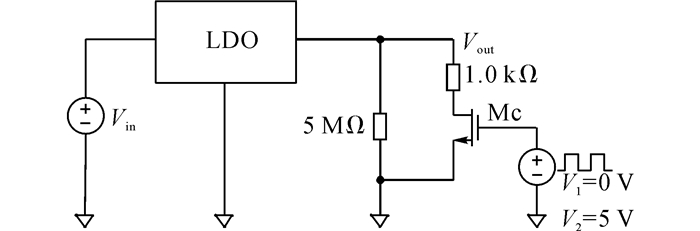
4 测试结果电路芯片采用GSMC公司的130 nm的CMOS混合信号工艺模型设计.芯片的面积为383.7×274.2 μm2, 作为超低功耗MCU的模拟IP一部分, 待机时工作, 为数字模块提供稳定电源.如图 7所示为该LDO芯片版图.其输入电压为1.6~4.0 V, 输出电压为1.5 V, 静态电流小于1 μA, 最大输出电流为1.5 mA.如图 8所示给出负载调整率和线性调整率的测试电路.开关管MC的开启电压为2.5 V.选择开关低电压为0 V, 高电压为5 V.当开关管打开时, 负载电流为1.5 mA, 关断时为0.3 μA.
|
图 7 LDO芯片版图 Fig. 7 Layout of proposed LDO |
|
图 8 LDO芯片的测试电路 Fig. 8 Testing circuits of LDO chip |
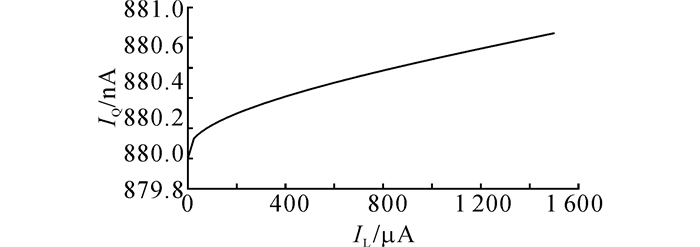
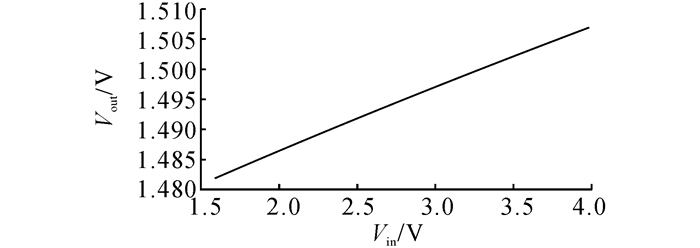
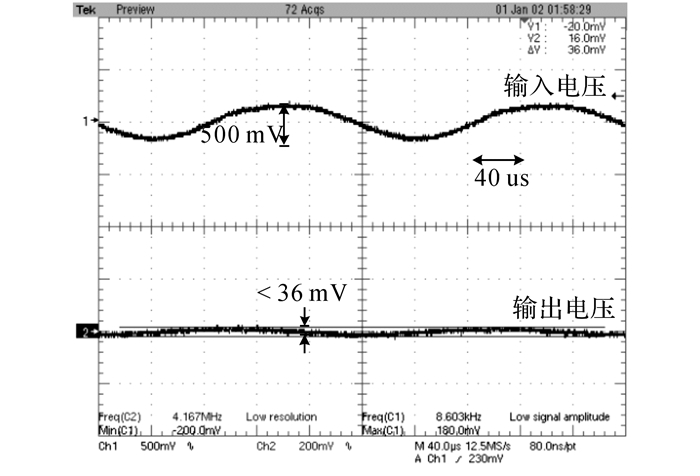
如图 9所示为LDO静态电流IQ随负载电流IL变化的曲线.在输入电压3.3 V时, 当负载电流从空载到重载逐渐增加时, 静态电流随之增大, 且在最大输出电流1.5 mA时不超过881 nA.如图 10所示为LDO输出电压Vout随IL变化的曲线, 测得LDO负载调整率为1.780 mV/mA;如图 11所示为LDO Vout随输入电压Vin变化的曲线, 测得LDO线性调整率为10.417 mV/V.图 12(a)给出LDO Vout在IL跳变时的瞬态响应, 跳变时间为100 ns.从图 12(b)可知, 100 ns内, 负载电流从1.5 mA跳变为0.3 μA (重载转轻载)时, 输出电压跳变小于95 mV;同样从图 12(c)可知, 100 ns内, 当负载电流从0.3 μA跳变为1.5 mA(轻载转重载)时, 输出电压跳变小于80 mV.恢复时间均在800 ns内.图 13给出输入电压Vin跳变时LDO线性瞬态响应, 当输入电压在0.5 V内波动时, 其输出电压跳变小于36 mV.从图 12、13中可以看出, 电路具有优异的稳定特性, 在各种瞬态响应时, 都不会发生震荡, 建立时间快, 输出电压跳变小.
|
图 9 不同负载电流情况下测量的静态电流值 Fig. 9 Measured quiescent current under different load currents |

|
图 10 LDO输出电压Vout随负载电流IL变化的曲线 Fig. 10 Output voltage of LDO during load regulation |
|
图 11 LDO输出电压Vout随输入电压Vin变化的曲线 Fig. 11 Output voltage of LDO during line regulation |

|
图 12 LDO负载瞬态响应 Fig. 12 Measured load transient response of proposedLDO |
|
图 13 LDO输出电压Vout在输入电压跳变时的瞬态响应 Fig. 13 Measured line transient response of proposedLDO |
如表 1所示是文献[12]~[14]中介绍的电路与本文设计的电路性能的比较.其中, L为工艺尺寸, A为芯片面积, ΔVOUT/ΔIOUT表示负载调整率(load regulation), 反应了负载电流对输出电压准确度的影响, ΔVOUT/ΔVIN表示线性调整率(line regulation), 反应了输入电压对输出电压准确度的影响.由表 1可见, 本文设计的LDO的功耗优于其他电路, 静态电流小于1 μA.并有较好的线性调整率与负载调整率.
| 表 1 本文设计的LDO与其他文献低功耗LDO的性能比较 Table 1 Comparison of properties among low-power LDO presented in present work and references |
本文设计的无片外电容LDO作为超低功耗MCU的模拟IP一部分, 为数字模块提供稳定电源.该LDO在MCU待机模式下工作, 减小了系统整体功耗.电路采用带有动态偏置并联反馈结构的缓冲器形成极点-极点追踪效果, 减小第2级放大器的输出阻抗, 将功率管栅端极点推远, 并改善其瞬态特性.同时采用嵌套式密勒电容补偿方式, 将主极点固定在第1级放大器输出点, 获得足够的相位裕度.测试结果表明, 在100 ns内负载由满载跳变至空载时, 输出电压的跳变量小于95 mV, 在电源电压0.5 V跳变时, 输出电压跳变量小于36 mV, 电路的静态电流小于881 nA.实现了在超低静态电流情况下输出稳定性要求.
| [1] | QU X, ZHOU Z, ZHANG B, et al. An ultralow-power fast-transient capacitor-free low-dropout regulator with assistant push-pull output stage[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2013, 60(2): 96–100. DOI:10.1109/TCSII.2012.2235732 |
| [2] | 王忆, 何乐年. CMOS低压差线性稳压器[M]. 北京: 科学出版社, 2012. |
| [3] | LAM Y H, KI W H. A 0.9V 0.35 μm adaptively biased CMOS LDO regulator with fast transient response[J]. IEEE, 2008, 51: 442–626. |
| [4] | LEE H, MOK P K T, LEUNG K N. Design of low-power analog drivers based on slew-rate enhancement circuits for CMOS low-dropout regulators[J]. Briefs IEEE Transactions on Circuits and Systems Ⅱ Express, 2005, 52(9): 563–567. DOI:10.1109/TCSII.2005.850781 |
| [5] | MAN T Y, MOK P K T, CHAN M. A high slew-rate push-pull output amplifier for low-quiescent current low-dropout regulators with transient-response improvement[J]. IEEE Transactions on Circuits and Systems Ⅱ Express Briefs, 2007, 54(9): 755–759. DOI:10.1109/TCSII.2007.900347 |
| [6] | ZHAN C, KI W H. An output-capacitor-free adaptively biased low-dropout regulator with sub-threshold undershoot-reduction for SoC[J]. IEEE Transactions on Circuits & Systems Ⅰ Regular Papers, 2012, 59(5): 45–48. |
| [7] | OR P Y, LEUNG K N. An output-capacitorless low-dropout regulator with direct voltage-spike detection[J]. IEEE Journal of Solid-State Circuits, 2010, 45(2): 458–466. DOI:10.1109/JSSC.2009.2034805 |
| [8] | GUO J P, LEUNG K N. A 6-μW Chip-area-efficient output-capacitorless LDO in 90-nm CMOS technology[J]. IEEE Journal of Solid-State Circuits, 2010, 45(9): 1896–1905. DOI:10.1109/JSSC.2010.2053859 |
| [9] | LEUNG K N, MOK P K T. Analysis of multistage amplifier-frequency compensation[J]. IEEE Transactions on Circuits and Systems Ⅰ Fundamental Theory & Applications, 2001, 48(9): 1041–1056. |
| [10] | CUI C R, GONG W C, WANG Y, et al. Low dropout linear regulator with no off-chip capacitor and low power consumption[J]. Journal of Zhejiang University, 2009, 43(11): 2006–2011. |
| [11] | WANG Y, CUI C R. CMOS low-dropout regulator with 3.3μA quiescent current without off-chip capacitor[J]. Journal of Southeast University:English Edition, 2009, 25(2): 441–445. |
| [12] | ZHENG C, MA D. Notice of violation of IEEE publication principles design of monolithic low dropout regulator for wireless powered brain cortical implants using a line ripple rejection technique[J]. IEEE Transactions on Circuits & Systems Ⅱ Express Briefs, 2010, 57(9): 686–690. |
| [13] | KEIKHOSRAVY K, MIRABBASI S. A 0.13-μm CMOS low-power capacitor-less ldo regulator using bulk-modulation technique[J]. IEEE Transactions on Circuits & Systems Ⅰ Regular Papers, 2014, 61(11): 3105–3114. |
| [14] | WANG J H, TSAI C H, LAI S W. A low-dropout regulator with tail current control for dpwm clock correction[J]. IEEE Transactions on Circuits and Systems Ⅱ Express Briefs, 2012, 59-Ⅱ(1): 45–49. |



