随着直流输配电技术的不断发展, 海上直流风电场已成为近年来的研究热点.相比于传统海上风电场, 直流风电场在系统损耗、建设成本、设备的体积和重量等方面具有明显优势[1].大容量、高增益的模块化隔离型DC/DC变换器(modular isolated DC/DC converter, MIDC)作为其中的关键设备, 利用中频变压器进行升压, 并实现低压侧与高压侧的电隔离.与工频变压器相比, 中频变压器的功率密度较高, 可以大幅减小变压器的体积和重量, 从而降低整个系统的工程造价.由于MIDC采用模块化结构, 子模块的输入输出端存在数百千伏的对地电压差, 因此中频变压器的原副边绝缘成为一个必须解决的问题.
目前实现变压器绕组之间高压绝缘的方法主要分为2种, 即填充绝缘材料和采用高压电缆.Bahmani等[2-6]提出在绕组之间填充绝缘材料的方法, 实现高压绝缘, 缺点是工艺制作较为复杂.Prasai等[7]采用高压电缆作为绕组, 设计匝数比为1:1的同轴变压器, 优点是克服传统同轴变压器绝缘电压较低的局限性, 易于解决变压器原副边绕组高压绝缘的问题.Yamanaka等[8]研究交联聚乙烯(Cross Linked Polyethylene, XLPE)高压电缆的电场分布, 进行寿命试验, 结果表明±500 kV XLPE高压直流电缆的绝缘厚度可减少至23 mm, 电缆的寿命可达43 a, 充分论证电缆绝缘的可靠性.因此, 通过高压电缆作为同轴变压器的高压侧绕组来实现变压器原副边高压绝缘的方案是可行的.
在上述方案论证的基础上, 本文改进了传统同轴变压器[9-11], 提出了一种采用高压电缆作为高压侧绕组的新型同轴变压器, 首先根据MIDC子模块的参数设置, 确定同轴变压器的设计目标, 然后对该变压器进行理论分析和参数设计, 提出了中频同轴变压器的优化设计流程, 最后以额定容量250 kV·A的中频变压器为例, 进行优化设计, 仿真结果验证设计方案的有效性.
1 LLC谐振变换器在海上直流风电场中, MIDC可以有效解决单个DC/DC变换器容量和增益有限的问题.LLC谐振变换器具有宽输入电压的特性, 可实现软开关技术, 并且在较宽的输入功率范围内都具有较高的效率, 因而特别适合作为MIDC的子模块应用于海上风电场中.如图 1所示为LLC谐振变换器的拓扑.

|
图 1 LLC谐振变换器拓扑 Fig. 1 Topology of LLC resonant converter |
本文中, MIDC和LLC谐振变换器的参数设置说明如下:一个MIDC的额定容量设为40 MW, MIDC连接中压直流母线和高压直流输电线路, 中压直流母线电压为±4 kV, 高压直流输电线路电压为±200 kV, 因此MIDC子模块的输入输出端的最大对地电压差为196 kV.一个MIDC包含20个子模块组, 子模块组的输入端并联、输出端串联, 子模块组包含8个子模块, 子模块的输入端串联、输出端串联.因此, LLC谐振变换器的额定容量为250 kV·A, 额定输入电压1 kV, 输出电压2.5 kV.为保证额定工作状态时, 二极管整流桥工作于电流断续模式, 以降低二极管反向恢复损耗, 需适当减小变压器的变比, 本文保留8%的裕量, 确定变压器的变比为2.3.对LLC参数进行设计:选取品质因数0.75和串联谐振频率6 kHz, 确定电路增益, 计算LLC电路的电感和电容参数值.结果为:串联电感Ls=76.2 μH, 并联电感Lp=381.1 μH, 串联电容Cs=9.232 μF.根据LLC谐振变换器的运行曲线, 额定工作频率约为5 165 Hz.需要指出的是, 在对LLC谐振变换器中的中频隔离变压器进行设计时, 可将谐振回路的并联电感集成至变压器中.由于同轴变压器的漏感数值较小, LLC电路中的串联电感不可能集成于变压器中, 故还需对谐振回路的串联电感进行单独设计.
因此, 中频同轴变压器的设计指标如表 1所示, 其中P为额定功率, f为工作频率, Vin为输入电压, Vout为输出电压, n为原副边匝数比, Lleak为同轴变压器的泄漏电感, Lmag为励磁电感, Vh为变压器高压侧对地绝缘电压, Vl为低压侧对地绝缘电压.
| 表 1 同轴变压器的设计指标 Table 1 Specifications for the coaxial transformer design |
本节提出适合作为MIDC子模块隔离变压器的中频同轴变压器结构, 并对其参数进行了详细设计及优化.在选定变压器的磁芯材料、绕组规格、绝缘材料后, 对其磁芯损耗和绕组损耗进行了计算.在此基础上, 采用粒子群算法对同轴变压器的参数进行了优化, 保证在稳定运行情况下, 温度处于合理范围内的同时, 变压器具有最小的体积和重量.
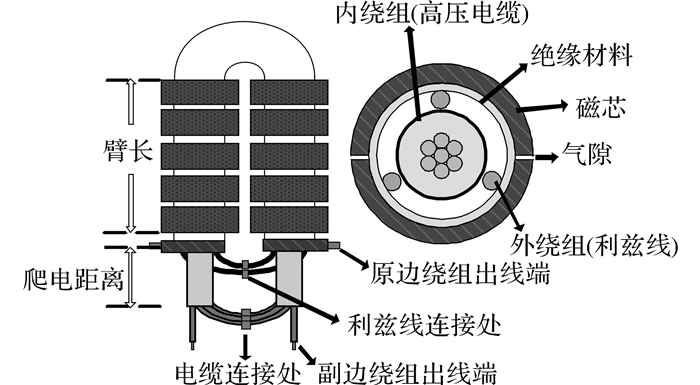
2.1 同轴变压器的结构设计本文提出的中频变压器结构如图 2所示, 根据绕组的相对位置, 同轴变压器的绕组可分为内绕组和外绕组.其中, 内绕组作为高压侧绕组, 由一根高压电缆构成, 有效地解决了变压器内外绕组之间高电压绝缘的问题.高压电缆位于同轴变压器的中心, 内含七股彼此间相互绝缘的载流导线.变压器的外绕组为低压侧绕组, 由3根利兹线构成, 利兹线互成120°对称放置于内绕组和磁芯之间.外绕组和磁芯之间为变压器的填充绝缘材料.
|
图 2 中频同轴变压器结构示意图 Fig. 2 Structure of proposed medium frequency coaxial transformer |
由于单个DC/DC变换器的传输功率明显低于高压电缆的传输功率, 本文所采用的高压电缆需要专门定制, 鉴于电缆制造技术已较为成熟, 故制作该高压电缆不存在工艺问题.满足设计要求的高压电缆结构为:内含7股彼此间相互绝缘的载流导线, 每股导线均为多股利兹线结构, 以减少中频变压器工作时由于电流的集肤效应和邻近效应导致的涡流损耗.高压电缆与低压侧绕组以及电缆与磁芯之间均需保证足够的爬电距离.在电缆的两端, 引出其内部的7股载流导线, 将前一股导线的末端和后一股导线的首端依次串联连接, 构成高压侧绕组.除此之外, 高压侧绕组的出线端和低压侧绕组的出线端之间也必须留有足够的爬电距离.由于变压器的低压侧绕组对地电压较低, 故采用填充绝缘材料的方法就可解决低压侧绕组和磁芯之间的绝缘问题.类似地, 低压侧绕组的出线端需要与磁芯保持一定的爬电距离, 然后引出3根利兹线, 将前一根利兹线的末端和后一根利兹线的首端依次串联连接.
2.2 磁芯、绕组及绝缘材料选择变压器的磁芯选择主要基于磁芯的饱和磁通密度和磁芯损耗, 两者均影响变压器的功率密度和效率.为了保证中频变压器正常工作时, 温升处于合理范围内, 必须选择损耗较低的磁芯材料, 包含非晶形合金、铁氧体、超微晶材料等, 如表 2所示为典型的中频变压器磁芯材料.表中μ为磁导率, Bs为饱和磁感应强度, Hc为矫顽力, ρ1为磁芯密度.
中频变压器多数采用铁氧体磁芯材料, 价格相对便宜.但由于铁氧体的饱和磁通密度低, 在海上风电场等场合中, 为了减小变压器的体积和重量, 需要采用超微晶等饱和磁通密度高且损耗低的磁芯材料, 缺点是价格相对较高.因此, 本文中变压器的磁芯材料需要满足损耗较低、饱和磁通密度较高、可连续工作温度较高的要求, 选择一种超微晶材料Vitroperm500F作为变压器的磁芯, 饱和磁感应强度为1.2 T, 磁芯损耗为0.07 kW/kg(20 kHz), 且具有良好的稳定性和耐蚀性, 比较适合作为中频变压器的磁芯材料.
变压器的绕组规格根据变压器的工作频率和额定电流选定.选择New England 1/0利兹线作为高压电缆内的载流导线, 半径为8 mm, 单股导线规格为AWG#30.选择New England 4/0利兹线作为低压侧绕组, 半径为12.46 mm, 单股导线规格为AWG#30.
选定绕组规格后, 需要选择变压器低压侧绕组与磁芯之间的绝缘填充材料.常见的变压器绝缘材料如表 3所示.其中λ为导热系数, Eins为抗电强度, 功率因数角的余角δ1为介质损耗角, tan δ1为介质损耗因数.
选择CoolPoly D5506作为绝缘材料, 低压侧绕组与磁芯之间的最小绝缘距离为
| $ {d_{{\rm{ins}}}} = \frac{{{V_{{\rm{ins}}}}}}{{\upsilon {E_{{\rm{ins}}}}}}. $ | (1) |
式中:Vins为绝缘电压, υ为绝缘裕量系数, 本文υ取0.2.
2.3 损耗计算同轴变压器的损耗主要包含磁芯损耗和绕组损耗.磁芯损耗可由B-P曲线估算单位质量的磁芯损耗(W/kg), 由变压器的参数尺寸, 计算变压器的磁芯质量, 便可计算磁芯损耗.变压器的绕组损耗为中频工况下, 电流的集肤效应和邻近效应导致的涡流损耗.变压器绕组损耗为
| $ {P_{\rm{w}}} = \sum\limits_{{\rm{n}} = 1}^\infty {{P_{{\rm{ac}},n}}} = \sum\limits_{{\rm{n}} = 1}^\infty {I_{{\rm{rms}},n}^2{R_{{\rm{ac}},n}}} . $ | (2) |
式中:Pac, n为n次基频谐波分量的功率损耗值, Irms, n为绕组电流经傅里叶分解后, 电流n倍频分量的有效值, Rac, n为n次谐波对应的交流电阻.
变压器的绕组损耗即为各整数倍频率时的绕组损耗之和, 因此, 必须要计算绕组在各整数倍频率时的交流电阻.根据Tourkhani等[15]提出的利兹线交流电阻的解析模型, 计算各整数倍频率时, 单位长度利兹线的交流电阻, 表达式如下.
| $ \begin{array}{l} {R_{{\rm{ac}},n}} = \frac{{\sqrt 2 N\rho }}{{{\rm{\pi }}{\delta _2}{N_{\rm{s}}}{d_{\rm{s}}}}}\left( {{\psi _1}\left( \varsigma \right) - \frac{{{{\rm{\pi }}^2}{N_{\rm{s}}}\beta }}{{24}} \times } \right.\\ \;\;\;\;\;\left. {\left( {16{m^2} - 1 + \frac{{24}}{{{{\rm{\pi }}^2}}}} \right){\psi _2}\left( \varsigma \right)} \right). \end{array} $ | (3) |
式中:N为利兹线的匝数, ρ为铜的电阻率, Ns为利兹线的股数, ds为单股导线直径, δ2为中频工况下电流的集肤深度, β为利兹线的填充系数, m为绕组的层数, m=1. ψ1(ς)和ψ2(ς)的泰勒级数展开式以及的定义如下.
| $ \left. \begin{array}{l} {\psi _1}\left( \varsigma \right) = 2\sqrt 2 \left( {\frac{1}{\varsigma } + \frac{1}{{{{32}^8}}}{\varsigma ^3} - \frac{1}{{{{32}^{14}}}}{\varsigma ^5} + \cdots } \right),\\ {\psi _2}\left( \varsigma \right) = \frac{1}{{\sqrt 2 }}\left( { - \frac{1}{{{2^5}}}{\varsigma ^3} + \frac{1}{{{2^{12}}}}{\varsigma ^7} + \cdots } \right),\\ \varsigma = \frac{{{d_{\rm{s}}}}}{{{\delta _2}}},\\ {\delta _2} = \frac{1}{{\sqrt {{\rm{\pi }}f{\mu _0}{\mu _{\rm{r}}}\sigma } }}. \end{array} \right\} $ | (4) |
式中:ς为单股导线直径与电流集肤深度的比值, μ0为真空磁导率, μr为铜的相对磁导率, σ为铜的电导率.由于利兹线单股导线的半径小于中频工况下电流的集肤深度, 也即ς<2, 因此可以忽略式(4) 中泰勒级数展开式的高阶项.
2.4 优化设计基于2.1~2.3的分析, 根据表 1中变压器的设计指标, 进行变压器的优化设计.选取变压器的尺寸参数作为自由变量和约束变量, 建立数学模型并采用粒子群算法对同轴变压器的参数进行优化.变压器的优化目标为:在保证变压器稳定运行时, 温升处于合理范围内的情况下, 变压器具有最小的体积和重量.通常, 变压器的体积较小时, 其重量也相对较低, 因此可以将变压器的体积作为优化目标.中频同轴变压器的设计流程如下:
1) 根据子模块的参数设计, 确定同轴变压器的额定输入输出电压、额定电流、绕组匝数以及漏感等参数要求.
2) 选择磁芯材料、绕组规格、绝缘填充材料, 并计算最小绝缘距离.
3) 建立数学模型, 以变压器的体积作为目标函数, 利用粒子群算法迭代寻优, 得出体积最小时对应的变压器尺寸参数的数值.
4) 改变变压器的某些尺寸参数, 获得不同参数下, 变压器的体积、功率密度、温度的变化趋势, 最后绘制变压器的工作特性图.
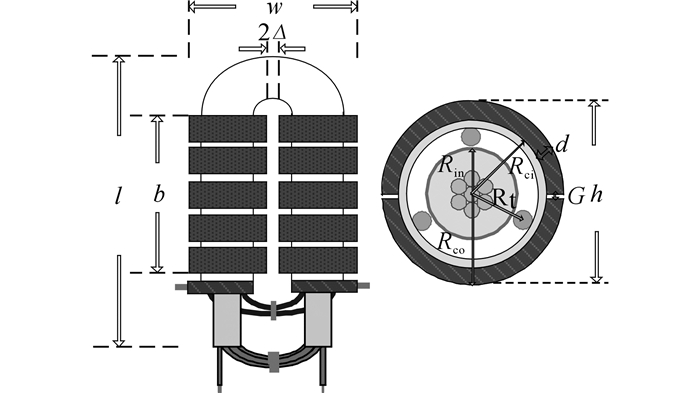
2.4.1 模型建立同轴变压器的参数表示如图 3所示.其中Rin为内绕组(高压电缆)的半径, Rt为外绕组(利兹线)的外径, Rci为磁芯内径, Rco为磁芯外径, b为磁芯臂长, lturn为单匝绕组的平均长度, dins为外绕组与磁芯之间的绝缘距离, d为磁芯厚度, G为磁芯气隙, Δ为U形管的中心线到磁芯的空气距离, l为变压器的长度, w为变压器的宽度, h为变压器的高度.本文中, 选取的自由变量为:Rci、b和Rt, 约束变量为:d、Rco、lturn和Δ.
|
图 3 中频同轴变压器的参数表示 Fig. 3 Parameters of designed medium frequency coaxial transformer |
建立以变压器的体积为目标函数的多约束条件的单目标优化数学模型.需要说明的是, 在优化计算时并未考虑变压器的励磁电感, 由于磁芯气隙较小, 可忽略不计气隙对变压器尺寸优化计算的影响.最后利用Maxwell进行励磁电感仿真, 改变磁芯气隙G, 使得变压器的励磁电感满足设计要求.
变压器优化计算的目标函数为
| $ \min V = 2{\rm{\pi }}R_{{\rm{co}}}^2b + \frac{{\rm{\pi }}}{2}R_{{\rm{ci}}}^2\left( {{l_{{\rm{turn}}}} - 2b} \right). $ | (5) |
约束条件为
| $ {R_{{\rm{ci}}}} - {R_{\rm{t}}} - {r_2} \ge {d_{{\rm{ins}}}}, $ | (6) |
| $ {R_{\rm{t}}} - {R_{{\rm{in}}}} \ge {r_2}, $ | (7) |
| $ \mathit{\Delta} = \frac{1}{{2{\rm{\pi }}}}\left( {{l_{{\rm{turn}}}} - 2b} \right) - {R_{{\rm{ci}}}} - d > 0, $ | (8) |
| $ \theta \le 100{\;^ \circ }{\rm{C}}{\rm{.}} $ | (9) |
其中:
| $ bd = \frac{{{V_{{\rm{rms}}}}}}{{16{N_1}B{f_{\rm{s}}}}}, $ | (10) |
| $ {R_{{\rm{co}}}} = {R_{{\rm{ci}}}} + d, $ | (11) |
| $ {R_{{\rm{in}}}} = {R_{{\rm{cable}}}} = 49.05\;{\rm{mm,}} $ | (12) |
| $ {d_{{\rm{ins}}}} = \frac{{{V_{{\rm{ins}}}}}}{{\upsilon {E_{{\rm{ins}}}}}} = 0.43\;{\rm{mm}},\upsilon = 0.2, $ | (13) |
| $ {l_{{\rm{turn}}}} = 2b + 2{\rm{\pi }}\left( {\mathit{\Delta} + {R_{{\rm{ci}}}} + d} \right). $ | (14) |
| $ {l_{{\rm{turn}}}} = \frac{{8{\rm{\pi }}{L_{{\rm{leak}}}}}}{{N_{\rm{w}}^2{\mu _0}\left[ {1 + 4\ln \left( {\frac{{{R_{\rm{t}}}}}{{{R_{{\rm{in}}}}}}} \right)} \right]}}, $ | (15) |
| $ \theta = {P_{{\rm{loss}}}}{R_{\rm{p}}} + {\theta _0},{\theta _0} = 40{\;℃}, $ | (16) |
| $ {P_{{\rm{loss}}}} = {P_{{\rm{core}}}} + {P_{\rm{w}}}, $ | (17) |
| $ {R_{\rm{p}}} = \frac{{{R_{{\rm{rad}}}}{R_{{\rm{conv}}}}}}{{{R_{{\rm{rad}}}} + {R_{{\rm{conv}}}}}}, $ | (18) |
| $ {r_2} = 12.46\;{\rm{mm}}. $ | (19) |
式中:Rcable为高压电缆的半径, r2为利兹线的半径.式(10) 为同轴变压器的磁芯面积公式, 其中N1为低压侧绕组匝数, Vrms为低压侧电压的有效值, fs为工作频率, 为避免磁芯饱和, B取为0.8Bsat, Bsat为磁芯的饱和磁感应强度.式(15) 为Hayt[16]提出的同轴变压器泄漏电感计算公式, 得出的单匝绕组平均长度计算公式.其中Nw为内绕组的匝数, θ为变压器的温度, Ploss为变压器损耗, θ0为环境温度, Rp为变压器热阻.式(17) 为变压器的损耗计算表达式, 本文主要考虑磁芯损耗和绕组损耗, 未考虑绝缘介质损耗, 其中Pcore为磁芯损耗.式(18) 为变压器热阻的计算公式, 其中Rrad为辐射热阻, Rconv为空气对流热阻.
分析变量的取值范围:
由式(7)、(12~19) 计算得Rt的最小值Rtmin=61.51 mm, 代入式(6) 计算得Rci的最小值Rcimin=74.4 mm.将Rtmin=61.51 mm代入式(15) 计算得lturn最大值lturnmax=1.328 m.结合式(10)、(14) 计算得b的最大值bmax=0.38 m, d的最小值dmin=12 mm.而
| $ \left. \begin{array}{l} {l_{{\rm{turn}}}} = 2b + 2{\rm{\pi }}\left( {\mathit{\Delta} + {R_{{\rm{ci}}}} + d} \right),\\ {l_{{\rm{turn}}}} > 2b + 2{\rm{\pi }}d + 2{\rm{\pi }}{R_{{\rm{ci}}}},\\ {l_{{\rm{turn}}}} \ge 2\sqrt {4{\rm{\pi }}bd} + 2{\rm{\pi }}{R_{{\rm{ci}}}}. \end{array} \right\} $ | (20) |
由式(10) 可知bd为一常数, 结合lturnmax=1.328 m和式(20) 可得Rcimax=0.157 4 m, 代入式(6) 得Rtmax=0.144 5 m.选取磁芯厚度最大值dmax=50 mm, 由式(10) 计算得bmin=0.1 m, 变量的取值范围如下:
| $ \left. \begin{array}{l} 0.074\;4 \le {R_{{\rm{ci}}}} \le 0.157\;4,\\ 0.1 \le b \le 0.38,\\ 0.061\;51 \le {R_{\rm{t}}} \le 0.144\;5. \end{array} \right\} $ | (21) |
粒子群算法(PSO)是一种智能优化算法, 有着收敛速度快、鲁棒性好的特点, 因此本文利用粒子群算法进行优化计算.
具体计算时选用粒子群算法的改进算法PSO-W算法, 其迭代公式为
| $ \begin{array}{*{20}{c}} {{v_{i{\rm{d}}}}\left( {{t_1} + 1} \right) = w{v_{i{\rm{d}}}}\left( {{t_1}} \right) + {c_1}{\rm{rand}}\left( {} \right)\left( {{p_{{\rm{best}}}}\left( {{t_1}} \right) - } \right.}\\ {\left. {{x_{i{\rm{d}}}}\left( {{t_1}} \right)} \right) + {c_2}{\rm{rand}}\left( {} \right)\left( {{g_{{\rm{best}}}}\left( {{t_1}} \right) - {x_{{\rm{id}}}}\left( {{t_1}} \right)} \right).} \end{array} $ | (22) |
| $ {x_{i{\rm{d}}}}\left( {{t_1} + 1} \right) = {x_{i{\rm{d}}}}\left( {{t_1}} \right) + {v_{{\rm{id}}}}\left( {{t_1} + 1} \right). $ | (23) |
式中:t1为迭代次数, c1、c2为加速系数, w为惯性权值, pbest、gbest分别为局部最优值和全局最优值,i为粒子编号rand为随机函数,取值为0~1,xid(t)为粒子位置.为了避免局部最优, 并且保证寻优速度, 对惯性权值做线性递减处理:
| $ w = \frac{{{i_{t\max }} - {i_t}}}{{{i_{t\max }}}}\left( {{w_{\max }} - {w_{\min }}} \right) + {w_{\min }}. $ | (24) |
式中:wmax与wmin分别为惯性权值的初始值与终止值, it为当前的迭代次数, itmax为迭代次数的最大值.
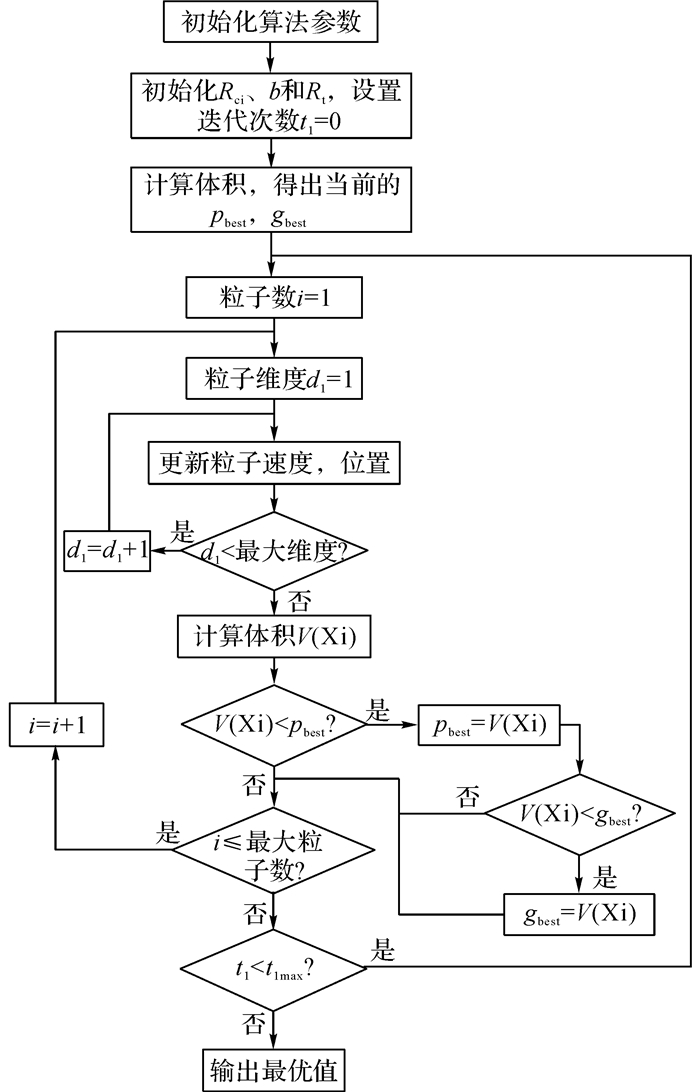
由于本文模型优化目标仅是变压器的体积, 粒子的维度即为1.其他参数的选择为:c1、c2取为2.0, wmax与wmin分别设为1.3和0.7, 最大迭代次数设置为100次, 粒子数设为50.粒子群算法寻优过程如图 4所示.
|
图 4 粒子群算法寻优过程图 Fig. 4 Design flowchart of particle swarm optimization |
根据上述同轴变压器的设计流程, 对变压器的参数进行详细设计和优化, 粒子群算法优化计算满足允许温升范围内变压器的最小体积, 最后绘制变压器的工作特性图.
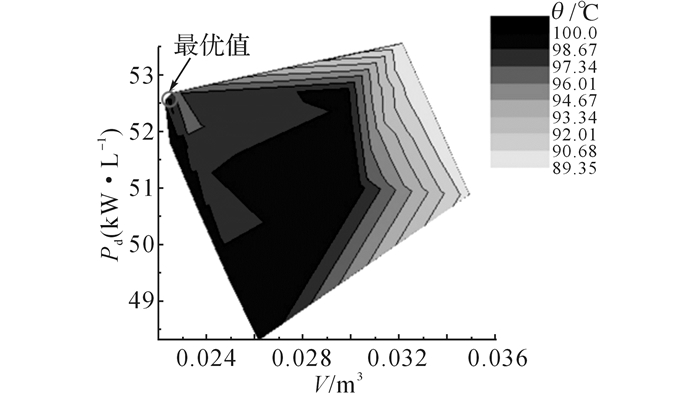
如图 5所示为正常运行温度在100 ℃范围内, 变压器体积V和功率密度Pd的分布图.其中, 变压器的体积范围为:0.022 3~0.035 0 m3, 功率密度范围为:47~54 kW/L.为满足变压器运行在允许温度范围内的同时, 具有最小体积, 变压器设计的最优值选在点(0.022 3, 52.55), 此时变压器的体积为最小值0.022 3 m3, 功率密度为52.55 kW/L, θ=98.5 ℃, 变压器的尺寸参数如表 4所示, 其中mcore为磁芯质量, mcable为电缆质量, mt为变压器质量, η为变压器的工作效率.
|
图 5 100 ℃范围内, 变压器的体积和功率密度分布图 Fig. 5 Transformer Volume and power density within temperature below 100 ℃ |
| 表 4 同轴变压器的尺寸规格 Table 4 Dimensions for the optimized coaxial transformer |
由于变压器采用低损耗磁芯和利兹线结构的绕组, 两者有效地降低了工作频率范围内的磁芯损耗和绕组损耗, 变压器的效率可达99.87%.在体积的最优解条件下, 为使励磁电感满足设计要求, 对变压器进行电磁场仿真, 求取磁芯的气隙大小, 然后对变压器的温度场分布进行仿真.
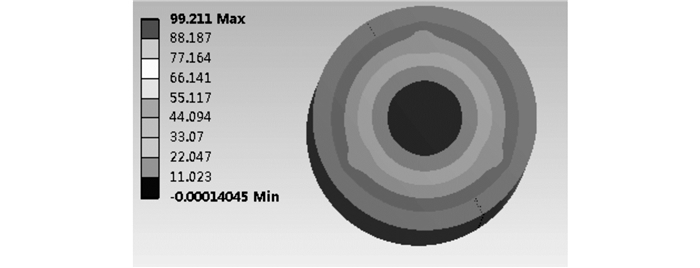
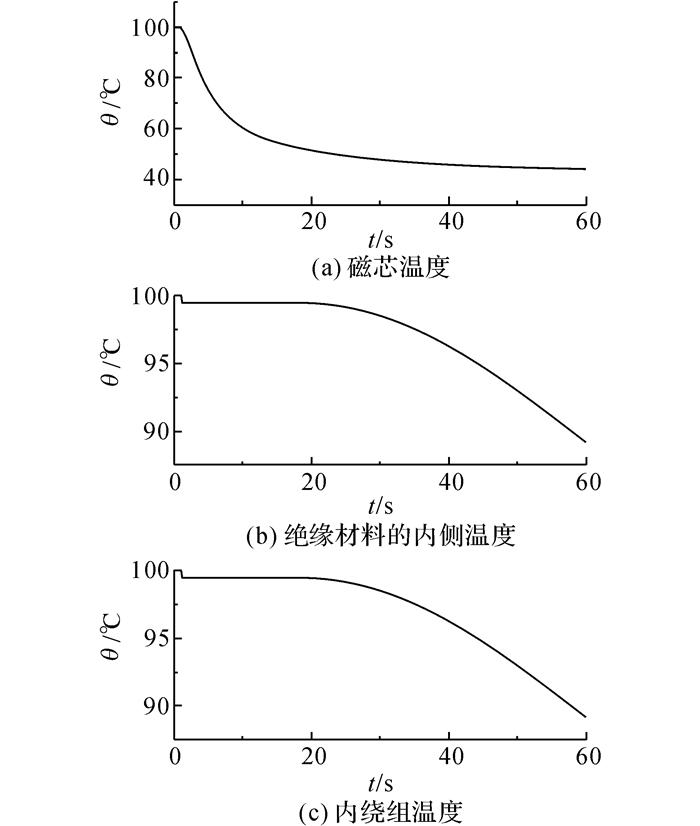
首先利用Maxwell软件仿真励磁和泄漏电感, 结果为:当气隙G=0.3 mm时, 变压器的励磁电感值为382.2 μH, 满足设计要求.然后进行泄漏电感仿真, 漏感值为2.2 μH.由于式(15) 为同轴变压器泄漏电感的估算公式, 漏感的设计值与实际值存在一定误差.然后利用Ansys软件进行变压器的温度场仿真, 设置环境温度θ0=40 ℃.如图 6所示为变压器的截面温度分布, 当变压器满载工作时, 温度最高点位于内绕组, 约为99.21 ℃.温度沿半径由内向外逐渐降低, 磁芯最外侧的温度最低, 约为44 ℃.然后进行瞬态场仿真, 仿真时间设为60 s.设定0~25 s, 变压器以额定工作状态运行, 25 s后变压器自然冷却, 温度变化曲线如图 7所示.t为仿真时间,结果表明:当满载运行时, 内绕组的温度约为99 ℃, 绝缘材料温度的最大值也即内绕组的温度.在60 s时, 磁芯内侧的温度约降至环境温度, 变压器的内绕组和绝缘材料的温度降至89 ℃.
|
图 6 瞬态场中变压器的截面温度分布 Fig. 6 Transient thermal simulation oftransformer |
|
图 7 变压器的磁芯、绝缘材料和内绕组的瞬态温度场仿真 Fig. 7 Transient thermal simulation of core, insulation material and inner winding of coaxial transformer |
在上述理论分析的基础上, 考虑到实际工程中电缆的最小弯曲半径要求, 且弯曲倍数由电缆厂商确定.本文最后对变压器的优化设计进行简要说明:根据电缆的弯曲倍数, 重新列出单匝绕组的平均长度表达式, 由于单匝绕组的平均长度增加, 变压器的泄漏电感值亦随之增加, 因此可设定新的漏感值.再根据上文提出的优化计算流程, 计算变压器尺寸参数的最优解.需要说明的是, 应用于大功率场合时, 为保证变压器和其他电力电子器件的正常稳定运行, 本文中变压器满载时允许的最高温度设定为100 ℃, 若温度超过设定值, 需要加散热器进行降温.
4 结语为解决MIDC子模块其中频变压器原副边高压绝缘的问题, 本文提出了一种将高压电缆作为高压侧绕组的新型同轴变压器设计方案;同时提出了此类变压器的设计流程, 仿真验证了变压器设计的可行性.在本文优化计算的基础上, 由于实际工程中电缆存在最小弯曲半径, 变压器的优化设计结果将随电缆的弯曲倍数而变化.本文为高电压大功率中频同轴变压器的理论设计及样机研制提供参考.
| [1] |
江道灼, 谷泓杰, 尹瑞, 等. 海上直流风电场研究现状及发展前景[J].
电网技术, 2015(9): 2424–2431.
JIANG Dao-zhuo, GU Hong-jie, YIN Rui, et al. Research status and developing prospect of offshore wind farm with pure DC systems[J]. Power System Technology, 2015(9): 2424–2431. |
| [2] | BAHMANI M A, THIRINGER T, KHAREZY M, et al.Design methodology and optimization of a medium frequency transformer for high power DC-DC applications[C]//Proceedings of Applied Power Electronics Conference and Exposition.Charlotte:APEC, 2015:2532-2539. http://ieeexplore.ieee.org/document/7104707/ |
| [3] | ORTIZ G, BIELA J, KOLAR J W.Optimized design of medium frequency transformers with high isolation requirements[C]//Proceedings of Industrial Electronics Society.Glendale:IECON, 2010:631-638. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5675240 |
| [4] | ORTIZ G, BIELA J, BORTIS D, et al.1 Megawatt, 20 kHz, isolated, bidirectional 12kV to 1.2kV DC-DC converter for renewable energy applications[C]//Proceedings of Power Electronics Conference.Sapporo:IPEC, 2010:3212-3219. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5542018 |
| [5] | ERNESTOL BARRIOS, ALFREDO URSUA, LUIS MARROYO, et al. Analytical design methodology for litz-wired high-frequency power transformer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2103–2113. DOI:10.1109/TIE.2014.2351786 |
| [6] | K SANO, M TAKASAKI. A boost conversion system consisting of multiple DC-DC converter modules for interfacing wind farms and HVDC transmission[C]//Proceedings of Energy Conversion Congress and Exposition.Denver:ECCE, 2013:2613-2618. http://ieeexplore.ieee.org/document/6647038/ |
| [7] | PRASAI A, YIM JUNG-SIK, et al. A new architecture for offshore wind farms[C]//Proceedings of PowerElectronics and Applications European Conference. Aalborg:EPE, 2007:1198-1204. http://ieeexplore.ieee.org/document/4495551/ |
| [8] | YAMANAKA T, MARUYAMA S, et al. The development of DC +/-500kV XLPE cable in consideration of the space charge accumulation[C]//Proceedings of the International Conference on Properties and Applications of Dielectric Materials.Nagoya:ICPADM, 2003:689-694. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1218511 |
| [9] | RAULS M S, NOVOTNY D W, et al. Design considerations for high-frequency coaxial winding power transformers[J]. IEEE Transactions on Industry Applications, 1993, 29(2): 375–381. DOI:10.1109/28.216547 |
| [10] | WALTRICH G, DUARTE JL, HENDRIX M.Design of symmetrical high-frequency coaxial wound transformer for multiport Converters[C]//Proceedings of Power Electronics Conference.Sapporo:IPEC, 2010:3151-3157. https://www.mysciencework.com/publication/show/design-of-symmetrical-high-frequency-coaxial-wound-transformer-for-multiport-converters |
| [11] | WATER W, LU J. Shielding analysis of high-frequency coaxial transformers used for electric vehicle on-board charging systems[J]. IEEE Transactions on Magnetics, 2013, 49(7): 4005–4008. DOI:10.1109/TMAG.2013.2239267 |
| [12] |
沙占友, 孟志永, 安国臣. 超微晶磁芯及其在开关电源中的应用[EB/OL]. [2016/4/10]. http://www.cediy.com/webHtml/Article/power/521520060506112600.html.
SHA Zhan-you, MENG Zhi-yong, AN Guo-chen. Ultra-fine crystalline core and its application in the switching power supply[EB/OL].[2016/4/10]. http://www.cediy.com/webHtml/Article/power/521520060506112600.html. |
| [13] | CELANESE. Datasheet of CoolPoly D thermally conductive polyphenylene sulfide (PPS)[EB/OL].[2016/4/10]. http://www.coolpolymers.com/. |
| [14] | KAYE G W C, LABY T H. Chapter 2 general physics[EB/OL].[2016/4/10]. http://www.kayelaby.npl.co.uk/general_physics/. |
| [15] | TOURKHANI F, VIAROUGE P. Accurate analytical model of winding losses in round litz wire windings[J]. IEEE Transactions on Magnetics, 2001, 37(1): 538–543. DOI:10.1109/20.914375 |
| [16] | HAYT W H. Engineering Electromagnetics[M]. Atlanta: Mcgraw-Hill Press, 1989: 387-389. |



