近几十年发展迅速的热声转换是一种基于热声效应的新型能源技术, 具有高效可靠、环保的特点[1-4].目前热声转换相对卡诺效率已达49%[5], 完全可同内燃机相媲美[6];另外, 热声起振温差可低至30 K[7], 热声系统输出功率有望突破10 kW[8], 在低品位能源回收领域发展潜力巨大.
热能经热声热机转换为工质振荡的声能, 再经声电换能器转化为电能.目前主要声电换能方式有:直线电机[9-14]、压电换能器[15]及扬声器[16]等.其中, 压电换能器和磁流体发电的方式存在效率较低、发电功率小的缺陷;大功率热声发电系统普遍采用直线电机, 直线电机虽效率高、机械部件少, 但受密封方式、支撑结构强度等因素影响, 单机功率规模的提升受到很大限制[8], 不利于热声发电技术应用发展.曲柄连杆可将直线运动与旋转运动相互转换, 结构简易, 与旋转电机广泛用于内燃机[6]、斯特林发动机[17]等动力机械中.曲柄连杆的机械效率可达85%以上[18], 旋转电机综合成本低、易实现大功率化.因此随着大功率热声技术的发展, 采用曲柄连杆式换能器与热声发动机匹配将是一种实现低成本、大功率热声发电工业应用的可行解决方案.
然而, 曲柄连杆用于热声热机发电的研究还非常缺乏.已有脉冲管发动机[19-20]、斯特林热滞后发动机[21-22]等研究中只关注活塞功或输出轴功的整机优化, 未考察换能器阻抗及与发动机的匹配特性, 而换能器工作特性对于行波热声发动机运行性能影响显著[23], 针对大功率行波热声系统尚没有此类研究.为此, 本文利用理论分析和数值模拟相结合的方法, 针对用于热声发电的曲柄连杆式换能器开展研究, 讨论了活塞质量、转动惯量、压力振幅及负载电阻对换能器性能的影响规律, 阐明了曲柄连杆式换能器中各力的矢量关系和阻抗特性, 为与大功率热声热机高效匹配的曲柄连杆式换能器应用提供了理论基础.
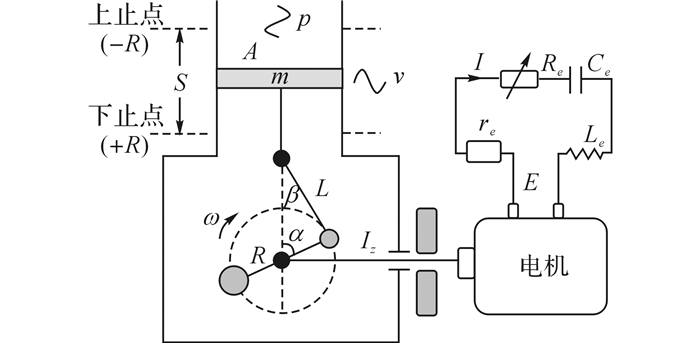
1 物理模型如图 1所示为曲柄连杆式换能器结构示意图, 由活塞、曲柄连杆、飞轮及旋转电机等组成.活塞面积为A, 质量为m, 连杆长为L, 曲轴偏心距为R, 转轴转动惯量(包括曲柄偏心质量、平衡块、飞轮及电机转子)为Iz, 电机内阻为re, 线圈电感为Le, 外接电容为Ce, 电路接有可调电阻Re.由热声发动机输入的压力波p推动活塞往复运动, 带动曲轴旋转驱动发电机工作, 由电路负载输出电功.
|
图 1 曲柄连杆式换能器原理示意图 Fig. 1 Schematic diagram of crank-rod transducer |
在此模型中, 假设:
1) 所有部件为刚性部件;
2) 所有运动部件的质量在分析中已集中到一点, 假定形心即为重心;
3) 活塞往复运动及曲轴转动的摩擦系数都为定值, 忽略其他接触摩擦;
4) 电机扭矩常数与电压常数为定值;
5) 输入压力波为定幅值、定频率的稳定正弦波.
1.1 运动学方程如图 1所示, 活塞运动存在上止点(TDC)和下止点(BDC), 行程为S(S=2R).设活塞位移为ξ, 速度为v, 曲轴转速为ω, 其运动关系可由式(1)~(4) 表示:
| $ \xi = L - R\cos \alpha - L\cos \beta , $ | (1) |
| $ \omega = \frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}, $ | (2) |
| $ v = \frac{{{\rm{d}}\xi }}{{{\rm{d}}t}}. $ | (3) |
| $ \lambda \sin \alpha = \sin \beta $ | (4) |
式中:λ为曲轴偏心距R与连杆长L的比值, 称为连杆比.α为曲轴转角, β为连杆摆动角, 曲轴转速ω以图 1中所示顺时针方向为正.
1.2 动力学方程忽略重力, 活塞受力方程为
| $ \left( {{p_{\rm{m}}} + p} \right)A - \left( {{p_{\rm{m}}} + {p_{\rm{b}}}} \right)A - {R_{\rm{m}}}v - {F_{\rm{L}}} = m\frac{{{\rm{d}}v}}{{{\rm{d}}t}}, $ | (5) |
| $ \frac{{{\rm{d}}{p_{\rm{b}}}}}{{{\rm{d}}t}} = \frac{{\gamma {p_{\rm{m}}}A}}{{{V_{\rm{b}}}}}v. $ | (6) |
式中:pm为充气压力, pb为背腔压力波动量, Rm为活塞与气缸间的摩擦系数, FL为连杆力, γ为工质压缩比, Vb为背腔体积.
连杆力FL在曲轴切线方向具有分力, 形成力矩驱动发电机工作, 与转子所受电磁力矩Te、摩擦力矩及转轴回转质量产生的惯性力矩平衡, 可表示为
| $ {F_{\rm{L}}}R\frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \beta }} - \left( {{X_{\rm{m}}}\omega + {T_{\rm{e}}}} \right) = {I_{\rm{z}}}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}. $ | (7) |
式中:Xm为转轴摩擦系数.
1.3 电机特性方程采用单相交流电机, 设电机运行稳定, 线圈感应电动势有效值为E, 电路电流有效值为I, 电压常数和扭矩常数分别为Ke、Kt, 控制方程可表示为
| $ E = {K_{\rm{e}}}\omega , $ | (8) |
| $ I = \frac{E}{{\sqrt {{{\left( {{R_{\rm{e}}} + {r_{\rm{e}}}} \right)}^2} + {{\left( {\omega {L_{\rm{e}}} - \frac{1}{{\omega {C_{\rm{e}}}}}} \right)}^2}} }}, $ | (9) |
| $ {T_{\rm{e}}} = {K_{\rm{t}}}I, $ | (10) |
设一个周期时长为τ, 活塞接收声功率为
| $ {W_{\rm{a}}} = \frac{A}{\tau }\int {pv{\rm{d}}t} . $ | (11) |
换能器输出电功率We及声电效率ηe分别为
| $ {W_{\rm{e}}} = {I^2}{R_{\rm{e}}}, $ | (12) |
| $ {\eta _{\rm{e}}} = \frac{{{W_{\rm{e}}}}}{{{W_{\rm{a}}}}} = \frac{{{W_{\rm{a}}} - {W_{\rm{s}}} - {W_{\rm{t}}} - {W_{\rm{r}}}}}{{{W_{\rm{a}}}}}. $ | (13) |
式中:Ws、Wt及Wr分别为活塞摩擦损失、转轴摩擦损失及线圈内阻损失.摩擦损失与活塞速度、转轴转速二次方成正比, 线圈内阻损失与电路负载有关.
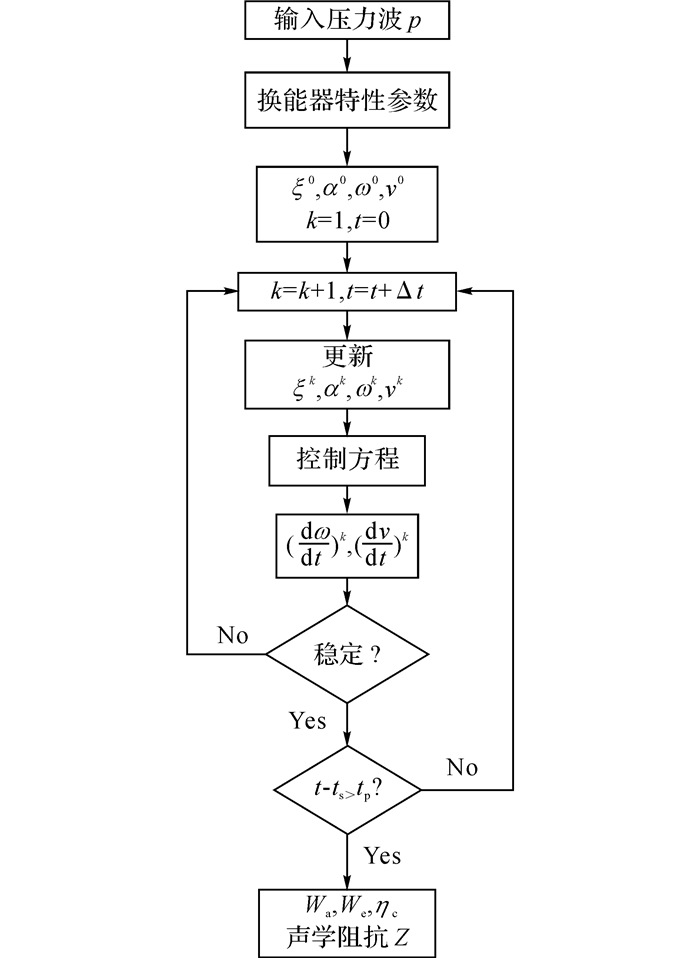
2 数值计算方法及参数设置根据输入压力波、换能器特性参数及初值, 可联立式(1)~(10) 求解各量, 本文采用数值计算的方法求解.如图 2所示给出了数值计算的流程示意图, 迭代时间为t, 步长为Δt, 迭代步数为k, 判定稳定的依据是连续10个曲轴转速的峰峰值之间的相对变化率不超过±5×10-6, 从开始迭代起到稳定之间的时长为ts, 之后继续观察的时长为tp, 最后计算出稳定时换能器的性能指标及声学阻抗值.
|
图 2 曲柄连杆式发电装置理论模型计算流程 Fig. 2 Flow chart of computation process |
根据已有文献, 选择气体谐振管结构的斯特林型行波热声发动机[25]作为驱动源, 其谐振频率主要由气体谐振管决定, 换能器扫气容积相比发动机容积来说较小, 因此能够保证输入稳定频率、振幅的压力波.工质为氦气, 充气压力为3 MPa, 驱动压力波振幅为0.2 MPa, 频率为65 Hz.表 1与2分别给出了换能器结构参数及电机特性参数, 其中电机额定功率为Pe, 额定电流Ie.设定步长Δt=1×10-6 s, 初始起动转速为400 rad/s, 已验证步长足够小到可使结算结果与时间步长无关.
| 表 1 换能器结构参数 Table 1 Structural parameters of crank-rod transducer |
| 表 2 电机特性参数 Table 2 Parameters of alternator |
如图 3所示给出了换能器曲轴转速曲线.图中, 约25 s后转轴转速稳定于一定范围内周期变化, 一个周期内有2个波峰, 其波动频率1/τ与驱动压力波频率基本一致.稳定时转速平均值为408.6 rad/s, 转速最大值为410.1 rad/s, 最小值为406.8 rad/s, 不均匀度(最大值和最小值之差与平均值的比)为0.81%, 满足连接旋转电机的曲柄连杆机构一般要求[6], 转速波动是由于驱动压力波周期变化及曲柄连杆结构特性所致.

|
图 3 换能器曲轴转速 Fig. 3 Speed of crankshaft |
由式(1)~(4) 可知活塞速度与曲轴转速关系由曲柄连杆结构参数决定:
| $ v = \omega R\left[ {\sin \left( {\omega t} \right) + \frac{{\lambda \sin \left( {2\omega t} \right)\omega }}{{2\sqrt {1 - {\lambda ^2}{{\sin }^2}\left( {\omega t} \right)} }}} \right]. $ | (14) |
为保证电机稳定运行, 要求转速ω稳定至电机转轴角速度ω0.将式(14) 通过牛顿二项式展开得
| $ \begin{array}{*{20}{c}} {v \approx {\omega _0}R\sin \left( {{\omega _0}t} \right) + \frac{{{\omega _0}R\lambda }}{2}\sin \left( {2{\omega _0}t} \right) + }\\ {\frac{{{\omega _0}R{\lambda ^3}}}{4}\sin \left( {2{\omega _0}t} \right){{\sin }^2}\left( {{\omega _0}t} \right) + \cdots .} \end{array} $ | (15) |
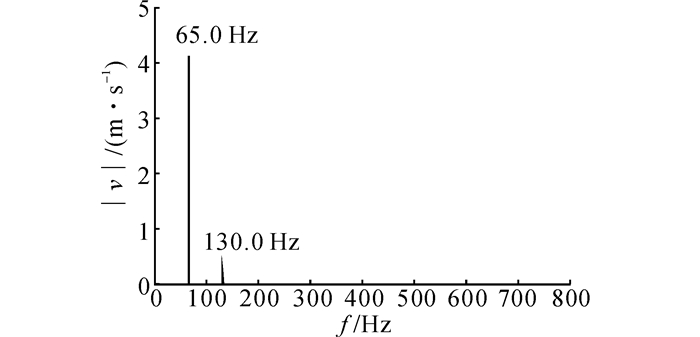
活塞速度必定存在高阶谐波成分, 这由曲柄连杆几何结构所决定, 不能消除.谐波呈λ2递减, 当λ=1/8时, 忽略二倍频以后小量的误差小于1%, 二倍频幅值为基频幅值的6.3%, 且当连杆比越小时, 占比越小.如图 4所示给出了对应图 3中35~40 s时段活塞速度FFT分析的频谱图, 其中f为频率, |v|为速度振幅.如图所示, 活塞速度主要分布于基频(约65.0 Hz)与二阶频(约130.0 Hz), 其他频率振幅较小可忽略不计.
|
图 4 35~40 s时段活塞速度FFT分析频谱图 Fig. 4 FFT analysis of piston speed in 35~40 s |
根据声学原理[26], 可将换能器等效为各力学元件.如表 3所示给出了稳定时段35~40 s活塞速度及活塞所受各力FFT分析的一阶、二阶振幅及相位数据, 其中Amp为振幅, θ为相位, 下标数字表示阶数.如表中数据所示, 与直线电机[23]相同, 曲柄连杆式换能器中摩擦力Rmv体现阻性(与速度同相);惯性力Mdv/dt体现感性(领先速度90°);背腔力pbA体现容性, 相当于气体弹簧(落后速度90°);而连杆力FL克服阻力矩做功, 相当于直线电机中的电磁力, 不同是的:直线电机中的电磁力与电流成正比, 其阻抗特性由电路负载决定, 而连杆力与电磁力矩及曲柄连杆几何结构有关.如表所示, 连杆力一阶相位落后于速度77.0°, 体现阻性和容性.
| 表 3 活塞速度与各力FFT分析的一阶、二阶幅值与相位 Table 3 First and second order FFT analysis of piston speed and forces |
由式(7)~(10) 可得连杆力的表达式:
| $ {F_L} = \frac{{\cos \beta }}{{R\sin \left( {\alpha + \beta } \right)}}\left[ {{I_{\rm{z}}}\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} + \left( {{X_m}\omega + {T_e}} \right)} \right]. $ | (16) |
式中:

|
图 5 活塞所受各力一阶矢量分析示意图 Fig. 5 First order vector analysis of forces on piston |
换能器声学阻抗可由速度一阶量估算:
| $ \left| Z \right| \approx \frac{{\left| p \right|}}{{\left| {\omega RA} \right|}}, $ | (17) |
| $ {\mathop{\rm Re}\nolimits} \left[ Z \right] \approx \left| Z \right|\cos {\theta _{v - p}}. $ | (18) |
| $ {\rm{Im}}\left[ Z \right] \approx - \left| Z \right|\sin {\theta _{v - p}}. $ | (19) |
式中:|p|为压力振幅, |Z|为声学阻抗幅值, Re[Z]和Im[Z]分别表示阻抗的实部值与虚部值.可知, 换能器阻抗幅值由压力振幅、压力波频率、活塞行程及面积决定, 与活塞质量、背腔体积、惯性动量及负载电阻等因素皆无关, 而相位角影响实部值与虚部值的相对大小.
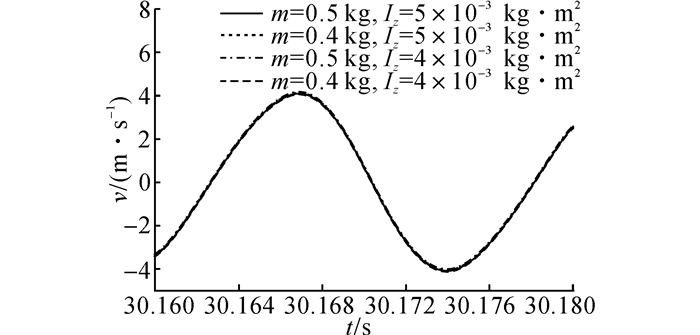
3.2.1 活塞质量和转动惯量对阻抗的影响如图 6所示给出了换能器稳定运行时段30.16 ~30.18 s不同活塞质量、转动惯量下的活塞速度曲线.如图所示, 各曲线重合, 表明活塞质量和转动惯量变化不影响对速度振幅及相位, 即换能器阻抗值不变.这是由于一个周期内活塞质量和转动惯量相互储存、释放能量, 使得换能器感、容性不变.
|
图 6 不同活塞质量、转动惯量下的活塞速度波动曲线 Fig. 6 Piston speed of different piston weight and rotational inertia |
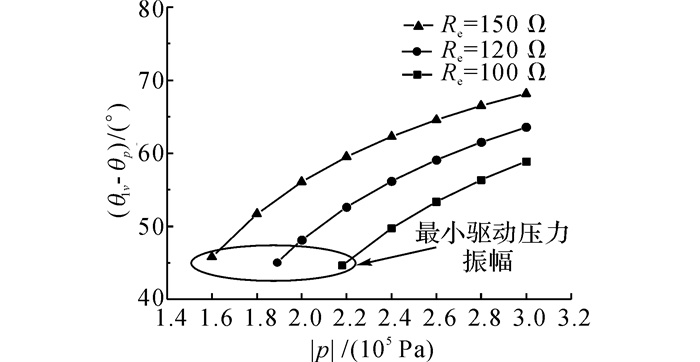
图 7给出了不同负载电阻对应速度与压力波的相位夹角随压力振幅变化的曲线.如图所示, pm=3 MPa, f=65 Hz, ω0=400 rad/s, 只有输入动力(压力振幅)大于负载阻力(电阻)时换能器才能稳定运行, 电阻越小时所需驱动压力振幅越大.当Re=150、120和100 Ω时, 最小驱动压力振幅分别为0.160、0.189及0.218 MPa, 其对应相位角分别为45.8°、45.1°及44.7°.此外, 电阻不变时相位角随着压力振幅增大而增大, 压力振幅不变时相位角随电阻增大而增大.如电阻为150 Ω时, 压力振幅0.18、0.20和0.22 MPa所对应相位角分别为51.7°、57.1°和59.5°;压力振幅为0.24 MPa时, 电阻100、120及150 Ω对应相位角分别为49.7°、56.2°和62.3°.根据图 5中各力矢量关系也可得到相同结论.
|
图 7 不同电阻对应速度压力相位角随压力振幅的变化规律 Fig. 7 Phase angle under different input pressure amplitude and load |
如图 8所示给出了不同电阻对应换能器声学阻抗的实部与虚部值.如图所示, 当压力振幅及频率固定时, 当|p|=0.2 MPa, f=65 Hz时,随着电阻增大, 换能器声学阻抗实部值减小, 而虚部值绝对值增大, 即阻性越小, 容性越大.当负载电阻Re=110、130及150 Ω时, 对应换能器的实部阻抗值分别为1.244×107、1.085×107和9.682×106 Pa·s/m3, 虚部分别为-1.209×107、-1.353×107和-1.439×107 Pa·s/m3.

|
图 8 不同电阻对应换能器声学阻抗的实部与虚部值 Fig. 8 Real and imaginary impendence of CRT under different load |
如图 9所示给出了不同电阻对应换能器接收声功率、输出电功率及声电效率.如图所示, 换能器接收声功和输出电功随电阻减小而增大, 当Re=110 Ω时, 换能器接收声功为827.8 W, 输出电功为680.1 W, 声电效率为82.2%.声功与电功之间差值为换能器运行过程中的能量损失(主要为摩擦损失), 由于固定频率声波驱动下活塞速度、转速基本保持不变, 摩擦分损失基本不变, 因此负载功率增大时, 换能器接收声功增大, 体现为速度压力相位角减小, 换能器实部阻抗值增大, 声电效率升高.

|
图 9 不同电阻对应换能器接收声功率、输出电功率及声电效率 Fig. 9 Received acoustic power, output electrical power and acoustic-electrical efficiency of CRT under different electrical load |
以上分析说明了曲柄连杆式换能器与直线电机的本质不同:直线电机是具有固有频率的机械振子, 行程不固定, 其阻抗与驱动压力无关, 电路负载不变时增大压力振幅可提高输入声功及输出电功;而曲柄连杆式换能器行程固定, 并非具有固有频率的机械振子, 阻抗随驱动压力变化而变化, 电路负载不变、固定频率压力波驱动下, 增大压力振幅不改变输入声功, 而是增大速度压力相位角.另外, 由于存在飞轮等调速结构, 换能器存在较大容性, 速度压力相位角越大时容性越大.与热声发动机耦合时应充分考虑这一特点, 确保发动机和换能器都能工作在性能最优点.
对于计算中采用的气体谐振管结构的斯特林型行波热声发动机[25], 由于谐振管接近纯阻性状态, 发动机在纯阻性负载下性能最佳, 因此需要在曲柄连杆式换能器和热声发动机件增加传输管进行调相, 平衡换能器的容性, 在保证换能器稳定压力波输入的情况下优化热声转化效率.
4 结论随着大功率高效热声发动机技术的发展, 针对目前热声系统声电换能高成本、功率受限的应用局限, 曲柄连杆式换能器将是热声发电系统提高功率、降低成本的一种可行的解决方案.本文针对应用于热声发电的曲柄连杆式换能器建立了物理模型, 采用数值求解方法, 探究稳定压力波驱动下活塞质量、转动惯量、压力振幅及负载电阻对其性能及阻抗特性的影响规律, 结论如下:
(1) 固定频率压力波驱动下, 活塞速度及转轴转速保持不变, 换能器接收的声功、输出电功及声电效率只与电路负载有关, 并都随负载电阻增大而减小.当输入振幅为0.2 MPa、频率为65 Hz的压力波, 负载电阻为110 Ω时, 输出电功为680.1 W, 声电效率为82.2%;
(2) 与直线电机不同, 曲柄连杆式换能器行程固定, 声学阻抗与输入压力有关.换能器阻抗幅值由压力振幅、频率、活塞面积及行程决定, 而相位角由输入动力(压力振幅)与负载阻力(电阻)决定, 电阻不变时相位角随着压力振幅增大而增大, 压力振幅不变时相位角随电阻增大而增大;
(3) 曲柄连杆式换能器中飞轮等调速结构体现较大容性, 速度压力相位角越大, 换能器的容性越大, 阻性越小.当电阻Re=110 Ω时, 对应换能器阻抗实部值为1.244×107 Pa·s/m3, 虚部值为-1.209×107 Pa·s/m3.
由于热声发动机对于声场分布要求苛刻, 负载阻抗显著影响热声转换效率及声功的输出, 因此耦合大功率热声系统时必须明确换能器的工作特性, 本文揭示了曲柄连杆式换能器与直线电机的工作特性差异, 在匹配热声发动机时应采用合理的调相手段以保证热-声-电高效转换.
| [1] | BACKHAUS S, SWIFT G W. A thermoacoustic Stirling heat engine[J]. Nature, 1999, 399(6734): 335–338. DOI:10.1038/20624 |
| [2] | SUN D M, WANG K, XU Y, et al. Thermoacoustic compression based on alternating to direct gas flow conversion[J]. Journal of Applied Physics, 2012, 111(9): 094905–094905-5. DOI:10.1063/1.3699360 |
| [3] | YU Z, JAWORSKI A J, BACKHAUS S. Travelling-wave thermoacoustic electricity generator using an ultra-compliant alternator for utilization of low-grade thermal energy[J]. Applied Energy, 2012, 99: 135–145. DOI:10.1016/j.apenergy.2012.04.046 |
| [4] | ZHAO Y, YANG Z, LUO E C, et al. Travelling-wave thermoacoustic hightemperature heat pump for industrial waste heat recovery[J]. Energy, 2014, 77: 397–402. DOI:10.1016/j.energy.2014.09.023 |
| [5] | TIJANI M E H, SPOELSTRA S. A high performance thermoacoustic engine[J]. Journal of Applied Physics, 2011, 110(9): 093519. DOI:10.1063/1.3658872 |
| [6] | 周龙保. 内燃机学[M]. 北京: 机械工业出版社, 2011: 28-32. |
| [7] | KEES D B. Novel 4-stage traveling wave thermoacoustic power generator [C]//ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels. Montreal: American Society of Mechanical Engineers, 2010: 73-79. |
| [8] | KEES D B, SYSTEMEN A T. Multi-stage traveling wave thermoacoustics in practice [C]//19th International Congress on Sound and Vibration, Vilnius: ICSV, 2012: 1573-1580. |
| [9] | WU Z H, MAN M, LUO E C, et al. Experimental investigation of a 500 W traveling-wave thermoacoustic electricity generator[J]. Chinese Science Bulletin, 2011, 56(19): 1975-7. DOI:10.1007/s11434-011-4504-1 |
| [10] | SUN D M, WANG K, ZHANG X J, et al. A traveling-wave thermoacoustic electric generator with a variable electric R-C load[J]. Applied Energy, 2013, 106: 377–82. DOI:10.1016/j.apenergy.2013.01.051 |
| [11] | WU Z, ZHANG L, DAI W, et al. Investigation on a 1kW traveling-wave thermoacoustic electrical generator[J]. Applied Energy, 2014, 124: 140–147. DOI:10.1016/j.apenergy.2014.02.063 |
| [12] | WANG K, SUN D, ZHANG J, et al. Operating characteristics and performance improvements of a 500W traveling-wave thermoacoustic electric generator[J]. Applied Energy, 2015, 160: 853–862. DOI:10.1016/j.apenergy.2015.03.085 |
| [13] | WANG K, SUN D, ZHANG N, et al. An acoustically matched traveling-wave thermoacoustic generator achieving 750 W electric power[J]. Energy, 2016, 103: 313–321. DOI:10.1016/j.energy.2016.03.001 |
| [14] | WANG Y, LI Z, LI Q. A novel method for improving the performance of thermoacoustic electric generator without resonator[J]. Energy Conversion and Management, 2016, 110: 135–141. DOI:10.1016/j.enconman.2015.11.065 |
| [15] | JENSEN C, RASPET R. Thermoacoustic power conversion using a piezoelectric transducer[J]. The Journal of the Acoustical Society of America, 2010, 128(1): 98–103. DOI:10.1121/1.3409370 |
| [16] | KANG H, CHENG P, YU Z, et al. A two-stage traveling-wave thermoacoustic electric generator with loudspeakers as alternators[J]. Applied Energy, 2015, 137: 9–17. DOI:10.1016/j.apenergy.2014.09.090 |
| [17] | 金东寒. 斯特林发动机技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2009: 30-38. |
| [18] | 邹降清. 斯特林发动机[M]. 长沙: 湖南大学出版社, 1985: 38-40. |
| [19] | MOLDENHAUER S, THESS A, HOLTMANN C, et al. Thermodynamic analysis of a pulse tube engine[J]. Energy Conversion and Management, 2013, 65: 810–818. DOI:10.1016/j.enconman.2012.03.013 |
| [20] | MOLDENHAUER S, HOLTMANN C, STARK T, et al. Theoretical and Experimental Investigations of the Pulse Tube Engine[J]. Journal of Thermophysics and Heat Transfer, 2013, 27(3): 534–541. DOI:10.2514/1.T4021 |
| [21] | CHENG C H, YANG H S, JHOU B Y, et al. Dynamic simulation of thermal-lag Stirling engines[J]. Applied Energy, 2013, 108: 466–476. DOI:10.1016/j.apenergy.2013.03.062 |
| [22] | CHENG C H, YANG H S. Theoretical model for predicting thermodynamic behavior of thermal-lag Stirling engine[J]. Energy, 2013, 49: 218–228. DOI:10.1016/j.energy.2012.10.031 |
| [23] |
孙大明, 赵益涛, 王凯, 等. 热声发电系统中直线发电机工作特性研究[J].
工程热物理学报, 2013, 34(7): 1225–1228.
SUN D M, ZHAO Y T, WANG K, et al. Study on the working characteristics of linear alternator in thermoacoustic power generation system[J]. Journal of Engineering Thermophysics, 2013, 34(7): 1225–1228. |
| [24] | WANG K, SUN D, ZHANG J, et al. Beating effect between a thermoacoustic source and its mechanical partner[J]. Journal of Applied Physics, 2015, 118(24): 244907. DOI:10.1063/1.4939291 |
| [25] |
王凯. 行波热声发电系统热-声-电耦合及转换机理研究[D]. 杭州: 浙江大学, 2014.
WANG K, Thermal-acoustic-electrical coupling and conversion mechanisms of a traveling-wave thermoacoustic power generation system [D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015539616.htm |
| [26] | 杜功焕. 声学基础[M]. 2版. 南京: 南京大学出版社, 2001: 116-162. |
| [27] | 奚碚华, 付中泽, 潘龙飞, 刘春和. 直流永磁电机的动态特性[J]. 中国惯性技术学报, 2006, 14(4): 59–66. |



