2. 北京航空材料研究院, 北京 100095
2. Beijing Institute of Aeronautical Materials, Beijing 100095, China
由于孔边的应力集中, 飞机结构中带孔元件在服役过程中容易产生疲劳裂纹, 降低结构件疲劳寿命.孔挤压强化是航空结构寿命增益的主要方法.该方法用一定过盈量的挤压棒连续、均匀地挤压孔, 使孔边产生残余压应力层[1].在疲劳载荷下, 残余压应力通常不会影响孔边的应力幅值, 但会显著降低孔边的平均应力, 进而提高结构件疲劳寿命[2-4].
目前关于孔挤压强化的研究主要是通过有限元模拟孔挤压强化过程获得孔边残余压应力场, 进一步对残余应力影响参数和分布规律进行定性分析.Nigrelli等[5]通过三维有限元模拟开缝衬套挤压过程, 分析了衬套开缝位置对残余应力场的影响;Houghton等[6]分别采用二维和三维有限元模型模拟了孔挤压强化过程, 得出了残余应力沿板厚的分布规律;何志明等[7]通过ABAQUS三维模型分析了300M钢耳片孔挤压后铰削量和孔边倒圆对疲劳寿命的影响, 并给出了最佳参数;刘晓龙等[8]使用ANSYS模拟了7050-T7451板三维孔挤压过程, 研究了板厚对残余应力场的影响;赵艳丽等[9]利用有限元建立了30CrMnSiNi2A超高强度的三维有限元模型, 分析了不同孔径、过盈量、厚度和孔边距对残余应力场的影响;葛恩德等[10]采用ABAQUS三维有限元模型分析了不同挤压量对孔边应力分布的影响, 得到钛合金TC4板孔的最优挤压量为4%;卢国鑫等[11]分析对比了不同芯棒尺寸对孔边残余应力场的影响;Mahendr等[12]采用了一种新的简化方法模拟了残余应力沿板厚方向的变化, 避免了复杂接触分析所需的大量计算资源;Liu等[13]采用芯棒加载及孔边位移加载的方式模拟了孔挤压过程, 比较了挤压量和2种加载方式对残余应力场的影响, 并分析比较了不同挤压量下LY12-CZ的疲劳增益效果和裂纹起源位置;欧阳小穗等[14]采用Marc模拟了7075铝合金板开缝衬套挤压过程, 并分析了残余应力对疲劳寿命的影响.综上可以看出:国内外对孔挤压有限元分析研究主要集中在不同参数对残余应力影响的定性分析上, 如挤压量、衬套开缝位置等, 而很少对孔挤压强化的缺口件进行疲劳寿命的定量预测, 对孔挤压强化的铰孔过程模拟和铰孔对残余应力的影响也研究甚少[7].事实上, 铰孔过程对孔边残余应力具有重要影响, 孔挤压强化带来的疲劳寿命增益的定量分析也一直是工程应用中关注的焦点.因此, 通过采用弹塑性有限元模拟孔挤压强化芯棒挤压和铰孔全过程, 获得可靠的孔边残余应力场, 建立定量分析和预测强化缺口试件的疲劳寿命模型, 并通过疲劳试验验证, 对孔挤压强化的定量分析与工艺优化具有重要意义.
为此, 本文采用ABAQUS有限元模拟了钛合金Ti-6Al-4V(简称TC4) 中心孔板衬套挤压和铰孔的全过程, 分析了铰孔模拟方式对残余应力场的影响.采用弹塑性有限元获得铰孔后中心孔板受疲劳载荷下的孔边应力分布, 结合临界距离法预测未强化和强化后中心孔板受疲劳载荷作用下的最危险位置和疲劳寿命, 预测结果和本文试验结果吻合良好.
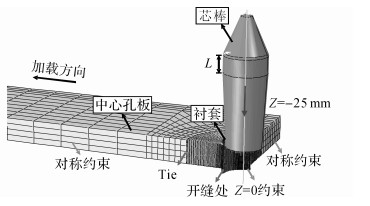
1 孔挤压强化过程有限元模拟 1.1 孔挤压有限元模型孔挤压强化工艺通常分为3步:1) 用先钻后铰的方式制作初孔, 并对铰孔后试样进行应力退火;2) 芯棒开缝衬套挤压, 采用FTI衬套, 开缝位置如图 1所示, 对于TC4钛合金, 挤压量通常选用4%[10];3) 孔边铰孔去掉凸台, 铰销后达到设计直径.
|
图 1 孔挤压有限元模型 Fig. 1 Finite element model for cold expansion |
孔挤压应力分析是一个复杂问题, 它涉及接触非线性和材料非线性.有限元法目前常用于获得孔挤压试样的残余应力场.本文将采用ABAQUS 6.14模拟钛合金TC4中心孔板芯棒衬套挤压和铰孔的全过程.
考虑到模型的对称性, 孔挤压有限元分析模型如图 1所示.
钛合金中心孔板长宽高尺寸为200 mm ×40 mm ×4 mm, 孔的初始直径为7.161 mm, 挤压铰销后直径为8.00 mm.试验测得钛合金TC4的工程应力应变曲线如图 2所示, 图中ε为应变, 为无量纲,σ为应力.在进行弹塑性有限元分析中, 将工程应力应变曲线转换为真实应力应变曲线, 并作为材料参数输入.钛合金板采用三维实体单元C3D8R, 在靠近孔边部分加密网格, 粗细网格邻接区采用ABAQUS中的Tie约束绑定在一起, 在确保精度的情况下减少计算量.

|
图 2 TC4的工程应力应变曲线 Fig. 2 Engineering stress-strain curve relation of TC4 |
衬套厚度为0.254 mm, 为避免孔边变形过大, 衬套相对中心孔板上下表面多出0.8 mm.衬套材料为Cr15Ni7Mo2AL.由于衬套刚度较大且厚度很小, 在挤压过程中的变形可忽略不计.为减小计算量, 衬套采用线弹性材料模拟, 弹性模量E=210 GPa, 有限元单元采用C3D8R三维实体单元.由于衬套开缝位置远离危险截面, 且衬套挤压后孔边还有铰孔过程, 是否开缝将对危险截面的残余应力场影响不大[6,15], 因此, 模型采用全衬套代替开缝衬套以减小计算量.
芯棒材料为V2合金钢, 采用解析刚体模拟以减小计算量.芯棒总长21 mm, 工作段长度L=3 mm, 工作段直径由孔挤压量4%确定, 为6.94 mm, 入、出口锥度分别为3°和23°.
有限元边界条件如图 1所示, 中心孔板和衬套底部z方向固定约束, 简化模型对称面施加对称约束.芯棒施加载荷位移Z=-25 mm, 从中心孔上表面(挤入端)挤入, 从下表面(挤出端)退出, 完成孔挤压过程.芯棒和衬套间无摩擦, 衬套和孔表面摩擦系数取0.1[16].
1.2 铰孔的有限元实现目前铰孔有限元模拟方法分为2种.一种是直接删除单元法, 模拟步骤如下:1) 通过有限元模拟中心孔衬套挤压过程, 确定挤压后孔径初始变形量后, 根据终孔直径大小确定后续铰孔的材料量;2) 提前规划好需要铰销的位置, 分别将铰销部分和未铰销的基体进行不同的单元划分;3) 在第1步的有限元模型孔挤压分析步后新增删除单元的分析步, 重新模拟孔挤压过程, 然后在孔边材料受芯棒挤压产生塑性变形的基础上, 通过删除铰销有限元单元的方式来模拟铰销过程.
直接删除单元法的不足之处在于需要重复模拟孔挤压过程, 大大增加了计算量.为了弥补这一不足, 另一种铰孔模拟方法是赋应力场法, 赋应力场法将直接删除单元法第1步中孔挤压模拟获得的残余应力场作为初始应力赋给未变形的中心孔板(本文铰孔前为直径7.161 mm的中心孔板), 然后在未变形材料上通过删除预先划分的铰销单元来模拟铰孔过程, 从而省略了直接删除单元法第3步中重复模拟孔挤压的过程, 大大地减小了计算量[7].但赋应力场法的不足之处是, 无法考虑孔挤压后孔边材料的塑性变形.这2种不同模拟铰孔方式的差异将在2.1节中介绍.
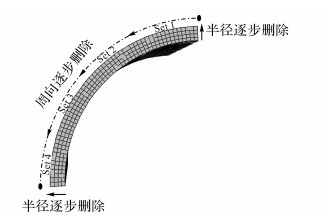
在铰孔有限元模拟方法确定之后, 铰销单元的删除方式也可能对模拟结果带来影响.本文研究了3种不同单元删除方式对残余应力场的影响, 如图 3所示:1) 一次全部删除:将所有铰销单元划分为一个组, 在一个分析步中删除;2) 半径逐层删除:将铰销单元沿半径方向依照不同层数分为4个组, 沿图示方向在4个分析步依次删除4个组;3) 周向逐步删除:将铰销单元沿周向方向分为4个组, 沿图示方向在4个分析步依次删除4个组.不同有限元单元删除方式的差异也将在2.2节中介绍.
|
图 3 不同单元删除方式示意图 Fig. 3 Schematic of different element deletion methods |
在芯棒衬套挤压过程中, 孔边材料将产生大的塑性变形.如果有限单元尺寸过大, 则难以准确反映孔边材料受芯棒挤压的真实状态;而尺寸过小, 则将大大增加计算量.因此, 在保证精度要求的前提下, 选取合适尺寸的有限元网格是有限元孔挤压残余应力分析的重要步骤.
本文对4种不同有限元网格进行分析, 这4种网格的参数如表 1所示.表中L×W×H表示孔边最小单元分别在半径、厚度和周向方向的尺寸, N为孔挤压模型有限元单元的总数.从表中可以看出:Mesh 2表示半径方向网格密度为Mesh 1的2倍;Mesh 3表示半径、厚度和周向3个方向网格密度均为Mesh 1的2倍;Mesh 4表示半径方向网格密度为Mesh 1的4倍.
| 表 1 4种不同网格划分参数 Table 1 Parameters for four different meshs |
采用1.1节中的有限元模型, 图 4给出了衬套挤压后尚未铰孔的孔边材料在x方向(长轴拉伸方向)典型的残余应力分布云图.受拉伸疲劳载荷作用的结构件, 对疲劳寿命影响最大的是拉伸方向最小截面(危险截面)上的残余应力, 因此, 本文将用危险截面上x方向的残余应力场表征孔挤压强化孔边的应力场分布.

|
图 4 铰孔前x方向残余应力分布云图 Fig. 4 Contour of residual stress in x direction, cold expansion without reaming |
在危险截面上建立如图 4所示y-z坐标系, 原点在铰孔前的挤入端孔边, y轴为沿半径方向远离铰孔前孔表面的距离(深度);z轴为沿厚度方向远离挤入端的距离.本文将统一用这个y-z坐标系描述危险截面的应力场分布.
采用表 1中的4种网格, 如图 5所示给出了不同网格密度获得沿厚度方向z(图 5(a))和厚度z=0和z=2 mm处沿深度方向y(图 5(b)), 铰孔后孔边残余应力σS分布.从图 5中可以看出:随着网格密度在3个方向不同程度的细化, 铰孔后孔边残余应力场在厚度和深度方向基本不变.这表明:利用Mesh 1的网格划分方法获得的结果是可靠的.为减小计算量, 本文将采用Mesh 1网格划分进行有限元分析.

|
图 5 4种不同网格密度铰孔后残余应力分布 Fig. 5 Residual stress distributions obtained from four different mesh density, after reaming |
采用1.1节的有限元模型和方法, 给出铰孔模拟方法及铰孔对残余应力的影响.
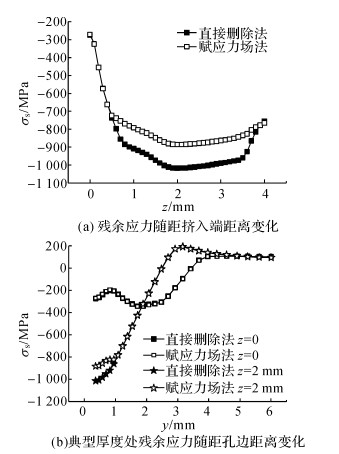
2.1 铰孔模拟方式对残余应力的影响在1.2节中介绍了直接删除单元法和赋应力场法2种不同模拟铰孔方式.采用这2种方法, 图 6给出了沿厚度方向(图 6(a))和厚度z=0和z=2 mm处沿深度方向(图 6(b)), 铰孔后孔边残余应力场的分布.从图中对比可以看出:1) 在挤入端附近, 2种模拟方法得到的残余压应力场几乎没有差别.2) 在距挤入端0.4~3.8 mm的厚度范围内, 赋应力场法得到的孔边残余压应力绝对值比直接删除法小, 在厚度中心处相差最大, 达130 MPa.由于直接删除法能够保留材料铰孔前的状态(比如材料进入弹塑性状态), 而赋应力场法不能, 因此导致了分析结果的差异.本文建议采用直接删除法.3) 由于挤入端孔边引入的残余压应力小, 是最有可能发生疲劳破坏的位置(这一点可以从3.4节看出), 因此采用这2种不同的模拟方式对之后的疲劳寿命预测结果没有影响.
|
图 6 不同模拟方法铰孔后残余应力分布 Fig. 6 Residual stress distributions obtained from two different simulation methods, after reaming |
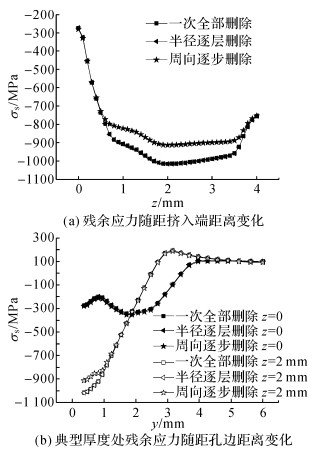
在1.2节中介绍了一次全部删除、半径逐层删除和周向逐步删除3种不同单元删除方式.通过2.1节中的直接删除法, 采用以上3种单元删除方式, 图 7给出了沿厚度方向(图 7(a))和厚度z=0和z=2 mm处沿深度方向(图 7(b)), 铰孔后孔边残余应力场的分布.从图中可以看出:1) 半径逐层删除方式与一次全部删除方式得到的孔边压应力场几乎没有差别.2) 周向逐步删除方式相对一次全部删除方式, 在挤入端附近的孔边压应力场相差很小;在厚度中点附近, 孔边0.7 mm深度范围内, 周向逐步删除方式得到的孔边残余压应力绝对值比一次全部删除小.由于周向逐步删除法能够反映真实的铰孔过程, 本文建议采用周向逐步删除法.3) 由于挤入端孔边是最有可能发生疲劳破坏的位置, 因此采用这3种不同的模拟方式对之后的疲劳寿命预测结果没有影响.
|
图 7 不同单元删除方式铰孔后残余应力分布 Fig. 7 Residual stress distributions obtained from three different element deletion methods, after reaming |
定量给出衬套挤压后铰孔对孔边残余应力分布的影响.铰孔模拟方式选取直接删除法, 单元删除方式选取周向逐步删除方式.
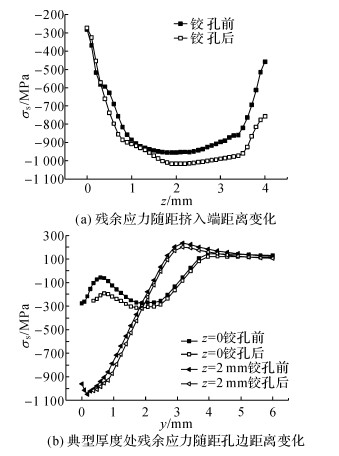
图 8给出了沿厚度方向(图 8(a))和厚度z=0和z=2 mm处沿深度方向(图 8(b)), 铰孔前和铰孔后的孔边残余应力分布.从图中可以看出:1) 铰孔前和铰孔后残余压应力绝对值沿厚度方向均先增大, 在厚度中点z=2 mm附近达到最大, 随后逐渐减小, 直至在挤出端附近开始迅速减小.在挤入端引入的残余压应力最小.2) 在厚度中点处, 铰孔前残余压应力绝对值在孔边深度方向较小距离内先增大, 在y=0.2 mm左右增加到最大值, 随后在远离孔边迅速减小为0, 并转变成拉应力继续增大, 拉应力在y=3 mm左右达到最大值, 随后在远端缓慢减小.考虑到残余压应力绝对值在孔边附近较小深度范围内有一个增大的过程, 铰孔铰销量不宜过大, 以避免铰掉残余压应力最大的位置.3) 在厚度中点附近, 铰孔会使深度方向的残余压应力绝对值略有增大.4) 铰孔后新的孔表面相对旧表面, 残余压应力绝对值均有显著地增大, 特别是在挤入端孔边附近, 深度方向0~2 mm范围内, 残余压应力绝对值增大明显.由于裂纹萌生大多源于有加工缺陷的孔表面, 且挤入端孔边是最容易发生疲劳破坏的位置, 适量的铰孔不仅能提高挤压后的孔表面质量, 而且能有效增加挤入端孔边引入的残余压应力, 这对疲劳寿命是有益的.因此, 在疲劳寿命预测时, 铰孔对孔边残余应力的影响需要认真考虑, 忽略铰孔的影响可能会引起较大的误差.
|
图 8 铰孔前后残余应力变化 Fig. 8 Residual stress distributions before and afterreaming |
本文对3种钛合金TC4板试样进行疲劳试验.3种试样分别为:1) 未开孔板;2) 未强化中心孔板;3) 强化中心孔板.未开孔板疲劳试验用于获得材料的疲劳寿命S-N曲线.未强化和强化中心孔板疲劳试验用于验证临界距离法是否可以可靠地预测中心孔板, 尤其是挤压强化后中心孔试样的疲劳寿命.
中心孔试样与4%挤压铰孔后试样尺寸一样.在室温条件下, 试样一端夹持固定, 另一端施加恒幅正弦波载荷, 交变频率在90~140 Hz.未开孔板疲劳载荷采用3种应力比, 分别为R=-1、0.06和0.5, 未强化和强化中心孔板应力比均为R=0.06.每一种应力比下选取3~4组应力水平, 每一级应力水平利用成组法得到恒幅疲劳中值寿命, 每组试样个数满足95%置信度要求.每一种应力比下, 利用升降法确定其疲劳极限.
通过对未开孔试样疲劳试验中值寿命和疲劳极限拟合得到的疲劳寿命S-N曲线如图 9所示.图中Nf为疲劳实验中值寿命次数, 采用对数坐标系, 最大应力σS, max.

|
图 9 TC4钛合金材料疲劳寿命曲线 Fig. 9 S-N curve of TC4 titanium alloy |
缺口试样的疲劳寿命评估是工程抗疲劳设计的关键.目前分析缺口试样疲劳寿命的方法主要包括有局部应力应变法、应力梯度法、名义应力法、应力场强法和临界距离法等[17].其中, 临界距离法是指将缺口附近最大主应力场的某一临界尺寸内的平均应力作为控制疲劳的特征应力, 进一步代入材料的S-N曲线中预测其疲劳寿命的方法.临界距离法充分考虑了局部区域应力的影响, 材料参数少, 计算简单, 且精度高, 因而得到广泛关注[17-18].
缺口试样危险截面孔边某一厚度处, 深度方向临界距离L0长度范围内的特征应力为
| $ {\sigma _{\rm{m}}} = \frac{1}{{{L_0}}}\int_0^{{L_0}} {{\sigma _y}{\rm{d}}{y}{\rm{.}}} $ | (1) |
式中: σy为不同深度y处的拉伸应力;临界距离L0为材料参数.
本文用临界距离法预测未强化和强化中心孔板疲劳寿命的步骤如下:1) 首先确定钛合金材料参数L0.采用一个应力水平下, 未强化中心孔板试验疲劳寿命反推得到材料参数L0, L0确定之后, 它将用于中心孔试样在其他疲劳载荷水平下的寿命预测以及强化试样的寿命预测.2) 对未强化和强化后试样, 通过弹塑性有限元模型, 在不同疲劳载荷作用下进行应力分析, 获得危险截面最容易产生疲劳破坏的位置, 在深度方向取L0长度范围内的平均应力作为控制疲劳的特征应力.3) 将特征应力代入图 9所示的材料S-N曲线中插值获得疲劳寿命.
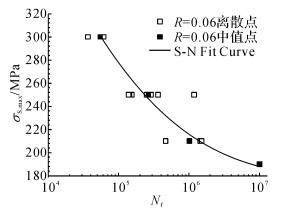
3.3 未强化中心孔板疲劳寿命预测为了更准确地得到TC4钛合金的临界距离L0, 本文将通过疲劳试验结果反推出L0值.如图 10所示, 未强化中心孔板在应力比R=0.06, σS, max=250 MPa时, 对应265 348个循环.在图 9中R=0.06应力比的材料S-N曲线中, 用对应的疲劳寿命可以插值得到对应材料的σS, max=660 MPa.根据临界距离法, 中心孔板在加载R=0.06, σS,max=250 MPa时, 孔边最危险位置(厚度中点)深度L0长度内的平均应力σ也应该为660 MPa.
|
图 10 钛合金中心孔板疲劳寿命曲线 Fig. 10 S-N curve of central hole plates |
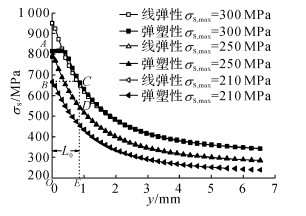
图 11给出了端部不同载荷水平加载时, 未强化中心孔板线弹性和弹塑性分析获得的在厚度中点处拉应力随深度变化的曲线.对σS, max=250 MPa应力水平对应的弹塑性曲线, 在σS=660 MPa处作一条水平线BC, 使得面积OADE和OBCE相等, 即孔边长度L0范围内的σm=660 MPa, 则推出L0=0.84 mm.
|
图 11 不同应力水平下厚度中点处x方向应力随深度变化 Fig. 11 X direction stress variation along distance from hole edge at mid thickness under different loads |
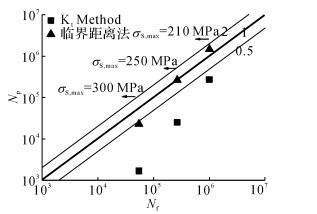
在得到临界距离L0之后, 进一步可对另外两级σS, max=210和300 MPa的疲劳寿命进行预测.如图 12所示;Kt Method是指用远端载荷乘以应力集中系数Kt作为特征应力的方法.图中Np为2种方法的预测值, 0.5~2表示预测值与试验值的比值, 从图中对比可以看出:1) 临界距离法预测的结果与试验结果的比值基本在0.5~2之间, 表明预测方法可行有效.2) Kt Method法在σS, max=300 MPa时, 预测结果严重偏小, 主要原因是Kt Method法无法考虑孔边材料塑形变形的影响.对比图 11中的300 MPa的线弹性和弹塑性曲线可知, 孔边塑性变形使得孔边应力大大降低, 远低于用应力集中系数Kt求出的孔边特征应力.3) 在σS, max=210和250 MPa时, 尽管孔边未产生塑形变形, Kt Method法预测结果依旧有较大误差, 说明疲劳寿命并非单一由孔边最大应力决定.
|
图 12 未强化中心孔板疲劳寿命预测 Fig. 12 Predicted fatigue life of unstrengthened center hole plate |
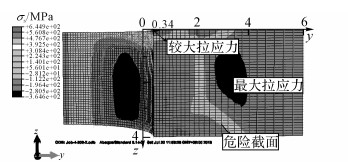
采用第1、2节的模型和方法, 图 13给出了挤压强化铰孔后中心孔板在端部施加300 MPa均布拉伸载荷的应力分布云图.从图 13可以看出:1) 挤入端的孔边附近存在明显的拉应力, 主要原因是孔挤压强化铰孔过程中挤入端附近引进的残余压应力较小, 而单轴加载时孔边的应力集中明显, 所以叠加后产生了较大拉应力.2) 在中层面稍上位置厚度z=1.5 mm, 深度y=3 mm附近产生了最大的拉应力, 主要原因是孔挤压强化后在深度方向y=3 mm位置会产生峰值拉应力(详见2.3节), 与单轴疲劳载荷叠加后拉应力进一步增大.
|
图 13 强化中心孔板端部加载x方向应力分布云图 Fig. 13 X direction stress contour of strengthened plate |
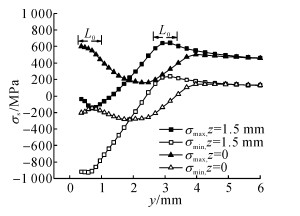
图 14给出了强化后试样端部加载应力比R=0.06, σS, max=300 MPa的疲劳载荷时, 危险厚度z=0和z=1.5 mm的位置处, 不同深度位置受载的最大应力σmax和最小应力αmin情况.从图中可以看出:1) 在挤入端, 孔边的最大应力和幅值在深度方向均为最大, 结合图 9中材料不同应力比下的S-N曲线可知, 孔边是深度方向最容易发生疲劳破坏的位置.2) 对于厚度z=1.5 mm处, 深度方向的最大应力在y=3 mm处.在接近孔边方向, 最大应力急剧减小, 虽然应力幅值有所增大, 但靠近孔边的应力载荷主要以负应力为主, 而疲劳裂纹萌生和扩展主要受拉应力影响, 所以深度方向最危险的位置为最大应力处.因此, 最容易产生疲劳破坏的位置为挤入端孔边和z=1.5 mm, y=3 mm处.
|
图 14 危险厚度处最大应力和最小应力随深度变化曲线 Fig. 14 Maximum stress and minimum stress variation along distance from hole edge at dangerous thickness |
对危险位置挤入端孔边和z=1.5 mm, y=3 mm处, 由于残余应力的叠加, 临界距离L0=0.84 mm范围内不同位置(z, y)载荷的应力比将是不断变化的, 需要通过平均的方法求出临界距离内的特征应力, 以端部加载300 MPa应力水平为例:1) 对于孔边挤入端, 如图 14所示, 自孔边取深度范围L0, 孔边的应力比R变化范围并不大, 在-0.5~-0.3之间, 对L0范围内的最大应力和应力比分别进行平均, 得到平均最大应力和平均应力比分别为499 MPa和-0.38, 进一步在图 9材料疲劳寿命S-N曲线中插值得到疲劳寿命.2) 对于z=1.5 mm, y=3 mm处, 应力比R在0.5左右, 取最大应力两侧L0范围内的平均应力预测其寿命.
图 15给出了强化中心孔板不同应力水平单轴加载时, 挤入端孔边和z=1.5 mm, y=3 mm两处的疲劳寿命预测值Np和试验值Nf的对比图, 其中挤入端孔边分别采用3种方法进行预测对比:1) 将铰孔后的孔边临界距离L0=0.84 mm内的平均应力作为特征应力的预测方法;2) 将铰孔后的挤入端孔壁处的最大应力作为特征应力的预测方法;3) 不考虑铰孔工艺, 将芯棒挤压强化后的挤入端孔边临界距离L0=0.84 mm内的平均应力作为特征应力的预测方法.危险位置z=1.5 mm, y=3 mm处采用铰孔后最大应力两侧L0范围内的平均应力预测其疲劳寿命.

|
图 15 强化中心孔板疲劳寿命预测 Fig. 15 Fatigue life prediction of strengthened center hole plate |
从图 15可以看出:1) 考虑铰孔的挤入端孔边临界距离法预测结果远小于z=1.5 mm, y=3 mm处, 说明最容易发生疲劳破坏的位置为挤入端的孔边, 这正好与试验结果吻合.2) 考虑铰孔的挤入端孔边临界距离法预测结果与试验值的比值在0.5~2之间, 说明考虑铰孔的临界距离法是可行和有效的.3) 将铰孔后挤入端孔壁处的最大应力作为特征应力的预测结果相对试验值和临界距离法预测结果都严重偏小, 说明疲劳寿命并非单一由孔边最大应力决定, 还与局部区域应力有关, 这与3.3节结论一致.4) 不考虑铰孔的临界距离法预测结果相对试验值和考虑铰孔的临界距离法预测结果都偏小, 这是因为铰孔后挤入端的残余压应力比不铰孔的明显增大, 这与2.3节的结论一致.综上, 在预测孔挤压强化缺口试件的疲劳寿命时, 应充分考虑铰孔过程对孔边残余应力的影响, 选取特征应力时也应充分考量孔边局部区域应力的影响.
4 结论本文研究了钛合金Ti-6Al-4V中心孔板衬套挤压和铰孔的有限元分析方法, 定量获得了衬套挤压铰孔对孔边残余应力场的影响.采用临界距离法对未强化和强化中心孔板的单轴加载疲劳寿命进行了预测, 得到如下结论:
(1) 芯棒衬套挤压能在孔边有效引入残余压应力, 适当铰孔能明显增大挤入端孔边残余压应力, 从而增强中心孔板的抗疲劳性能.
(2) 采用弹塑性有限元获得经孔挤压和铰孔Ti-6Al-4V中心孔板在疲劳载荷作用下的应力场, 结合临界距离法定量预测了挤压强化钛合金中心孔的疲劳寿命, 预测破坏位置与试验结果吻合, 预测寿命在0.5~2倍试验寿命之内, 相对不考虑铰孔过程和局部区域应力影响的传统预测方法, 预测精度显著提高.
研究为孔挤强化残余应力及寿命增益的定量分析与挤压、铰孔工艺优化提供了重要参考, 具有重要意义.
| [1] |
HB/Z 170-2005. 航空金属零件孔挤压强化工艺[S]. 北京: 中国航空综合技术研究所, 2005.
HB/Z 170-2005.Cold expansion process for hole of aircraft metal part [S].Beijing: China Aero-poly technology Establishment, 2005. http://industry.wanfangdata.com.cn/dl/Detail/Standard?id=Standard_HB%2FZ%20170-2005&type=Free |
| [2] | WU H. On the prediction of initiation life for fatigue crack emanating from small cold expanded holes[J]. Journal of Materials Processing Technology, 2012, 212(9): 1819–1824. DOI:10.1016/j.jmatprotec.2012.04.004 |
| [3] | LARUE J E, DANIEWICZ S R. Predicting the effect of residual stress on fatigue crack growth[J]. International Journal of Fatigue, 2007, 29(3): 508–515. DOI:10.1016/j.ijfatigue.2006.05.008 |
| [4] | CHAKHERLOU T N, VOGWELL J. The effect of cold expansion on improving the fatigue life of fastener hole[J]. Engineering Failure Analysis, 2003, 10(1): 13–24. DOI:10.1016/S1350-6307(02)00028-6 |
| [5] | NIGRELLI V, PASTA S. Finite-element simulation of residual stress induced by split-sleeve cold-expansion process of holes[J]. Journal of Materials Processing Technology, 2008, 205(1/3): 290–296. |
| [6] | HOUGHTON S J, CAMPBELL S K. Identifying the residual stress field developed by hole cold expansion using finite element analysis[J]. Fatigue & Fracture of Engineering Materials & Structures, 2012, 35(1): 74–83. |
| [7] |
何志明, 张晓晶, 刘天琦, 等. 300M钢耳片孔挤压强化全过程有限元模拟[J].
浙江大学学报:工学版, 2016, 50(4): 783–791.
HE Zhi-ming, ZHANG Xiao-jing, LIU Tian-qi, et al. Numerical simulation of the whole process of cold expansion in 300M steel lug[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(4): 783–791. |
| [8] |
刘晓龙, 高玉魁, 刘蕴韬, 等. 孔挤压强化残余应力场的三维有限元模拟和试验研究[J].
航空材料学报, 2011, 31(2): 24–27.
LIU Xiao-long, GAO Yu-kui, LIU Yun-tao, et al. 3D finite element simulation and experimental test on residual stress field by hole cold expansion[J]. Journal of Aeronautical Materials, 2011, 31(2): 24–27. |
| [9] |
赵艳丽, 高玉魁, 仲政. 30CrMnSiNi2A超高强度钢孔挤压强化残余应力场的模拟[J].
力学季刊, 2014(2): 243–252.
ZHAO Yan-li, GAO Yu-kui, ZHONG Zheng. Finite element simulation of the residual stress fields of 30CRMNSINI2A ultrahigh strength steel by hole cold expansion[J]. Chinese Quarterly of Mechanics, 2014(2): 243–252. |
| [10] |
葛恩德, 苏宏华, 程远庆, 等. TC4板孔冷挤压强化残余应力分布与疲劳寿命[J].
中国机械工程, 2015, 26(7): 971–976.
GUO En-de, SU Hong-hua, CHEN Yuan-qing, et al. Residual stress fields and fatigue life of cold expansion hole in Titanium alloy TC4[J]. China Mechanical Engineering, 2015, 26(7): 971–976. |
| [11] |
卢国鑫, 王强, 宋颖刚, 等. 芯棒规格对孔挤压强化效果的影响[J].
制造业自动化, 2014(17): 34–38+48.
LU Guo-xin, WANG Qiang, SONG Yi-gang, et al. Hole extrusion strengthening effect caused by mandrel specifications[J]. Journal of Manufacturing Automation, 2014(17): 34–38+48. DOI:10.3969/j.issn.1009-0134.2014.17.010 |
| [12] | MAHENDRA BABU N C, JAGADISH T, RAMACHANDRA K, et al. A simplified 3-D finite element simulation of cold expansion of a circular hole to capture through thickness variation of residual stresses[J]. Engineering Failure Analysis, 2008, 15(4): 339–348. DOI:10.1016/j.engfailanal.2007.02.003 |
| [13] | LIU Y S, SHAO X J, LIU J, et al. Finite element method and experimental investigation on the residual stress fields and fatigue performance of cold expansion hole[J]. Materials and Design, 2010, 31(3): 1208–1215. DOI:10.1016/j.matdes.2009.09.031 |
| [14] |
欧阳小穗, 张晓晶, 杨树勋. 孔挤压强化有限元分析及疲劳寿命估算[J].
科学技术与工程, 2011, 11(12): 2787–2790.
OUYANG Xiao-sui, ZHANG Xiao-jing, YANG Shu-xun. Finite element analysis and fatigue life prediction of cold expansion[J]. Science Technology and Engineering, 2011, 11(12): 2787–2790. DOI:10.3969/j.issn.1671-1815.2011.12.035 |
| [15] | ISMONOV S, DANIEWICZ S R, NEWMAN J C, et al. Three dimensional finite element analysis of a split-sleeve cold expansion process[J]. Journal of Engineering Materials and Technology, 2009, 131(3): 031007-1–031007-8. DOI:10.1115/1.3120392 |
| [16] | CHAKHERLOU T N, VOGWELL J. The effect of cold expansion on improving the fatigue life of fastener holes[J]. Engineering failure analysis, 2003, 10(1): 13–24. DOI:10.1016/S1350-6307(02)00028-6 |
| [17] |
张成成, 姚卫星. 典型缺口件疲劳寿命分析方法[J].
航空动力学报, 2013, 28(6): 1223–1230.
ZHANG Cheng-cheng, YAO Wei-xing. Typical fatigue life analysis approaches for notched components[J]. Journal of Aerospace Power, 2013, 28(6): 1223–1230. |
| [18] | TAYLOR D. Geometrical effects in fatigue: a unifying theoretical model[J]. International Journal of Fatigue, 1999, 21(5): 413–420. DOI:10.1016/S0142-1123(99)00007-9 |



