行星齿轮箱是直升机、车辆、机械等领域传动系统的重要组成部分, 对行星齿轮箱进行故障诊断研究对于提高设备运行的安全性和可维护性具有重要意义[1].
行星齿轮箱振动信号成分复杂, 不仅包含各个部件的旋转频率、齿轮副啮合频率及其倍频, 还含有设备被激起的固有频率、环境噪声等, 故障频率容易被淹没;此外, 调制现象显著, 除齿轮故障之外, 安装误差、制造误差、振动传递路径的变化、行星轮通过效应等同样会引起信号的幅值或频率调制[2].上述2个特点使得行星齿轮箱振动信号分析存在困难.
基于行星齿轮箱振动信号多成分和调制的特点, 可以先将振动信号分解为一组单分量信号, 再运用传统解调方法对单分量信号进行幅值解调和频率解调分析, 既避免了传统解调分析方法只在单分量调制信号的分析中效果较好[3-6]的弊端, 又能降低诊断难度.当前, 基于多分量分解的解调分析方法成为研究的热点.冯志鹏等[7]运用经验模式分解将行星齿轮箱信号分解成一组本征模函数, 再利用局部相位微分方法对本征模函数进行频率解调分析.白亚红等[8]将经验模式分解和支持向量机这2种分析方法结合起来, 准确识别出风电齿轮箱齿轮早期磨损故障.雷亚国等[9]将提出一种新的自适应总体平均模式分解方法应用于行星轮故障特征识别, 获得了成功, 并降低了模式混淆问题对分析结果的干扰.
迭代Hilbert变换(iterated hilbert transform, IHT)是由Gianfelici等[10-11]提出的一种新的多分量调幅-调频信号分解方法.IHT充分利用Hilbert变换(Hilbert transform, HT)的解调功能从待分析信号中分离出幅值信号, 再利用滤波器从幅值信号中分离出单分量成分, 通过对HT和滤波器的迭代使用, 可以从待分析信号中提取出任意多个调幅-调频单分量成分.迭代Hilbert变换方法具有完备的数学理论基础;不受信号长度、单分量个数以及分解精度的限制;根据信号自身包含的信息逐步提取单分量成分, 无需先验信息, 具有高度自适应性;算法简单, 收敛速度快.当前, 国内Qin等[12-13]对IHT方法进行改进, 提出采用一种平滑瞬时频率估计算法, 并应用于定轴齿轮箱故障诊断, 分别提取了轴承外圈和齿轮断齿的特征频率.邓等将[14]IHT与共振解调技术结合起来, 用于识别轴承故障信息, 并与Hilbert-Huang变换对比, 发现基于IHT的共振解调法精度更高.基于IHT的良好分解效果, 本文将IHT与FT结合引入到行星齿轮箱振动信号分析中, 提取出故障信息, 实现对行星齿轮箱的准确诊断.
1 迭代Hilbert变换Gianfelici等学者在迭代Hilbert变换的理论阐述中, 构建了调幅-调频多分量信号数学模型, 证明了算法的收敛性质, 给出了收敛情况下的滤波器设置条件.
1.1 调幅-调频信号模型调幅-调频单分量信号模型可表示为
| $ x\left( t \right) = a\left( t \right)\cos \left[ {\phi \left( t \right)} \right]. $ | (1) |
式中:a(t)和φ(t)分别为单分量信号的瞬时幅值和瞬时相位.
任意调幅-调频多分量信号x(t)数学模型为
| $ x\left( t \right) = \sum\limits_i^n {{x_i}\left( t \right)} = \sum\limits_{i = 1}^n {{a_i}\left( t \right)\cos \left( {{w_i}t + {\varphi _i}\left( t \right)} \right)} . $ | (2) |
式中:n为单分量个数, xi(t)为第i个调幅-调频单分量, ai(t)、wit+φi(t)、wi、φi分别为第i个单分量的瞬时幅值、瞬时相位、基频、调制相位.
1.2 迭代Hilbert变换推导 1.2.1 迭代计算定义j为第j次迭代, aj(t)、αj(t)分别为第j次迭代后经HT得到的幅值和相位.当j=0时, 对原始信号x(t)进行HT可得
| $ x\left( t \right) = R\left[ {z\left( t \right)} \right] = {a_0}\left( t \right)\cos \left[ {{\alpha _0}\left( t \right)} \right]. $ | (3) |
式中:z(t)为x(t)的解析信号, R[·]表示取实部, a0(t)、α0(t)分别为原始信号的幅值和相位.
由于aj(t)总是非负, 且具有振荡性质, 无法直接进行下一次HT处理, 为此, 需要通过滤波处理分离出aj(t)的趋势成分aj(t)和交变成分
| $ {a_j}\left( t \right) = {{\bar a}_j}\left( t \right) + {{\tilde a}_j}\left( t \right). $ | (4) |
式中:趋势成分aj(t)为所要提取的单分量成分的瞬时幅值, 交变成分
将式(4) 代入式(3) 可得
| $ x\left( t \right) = \left[ {{{\bar a}_0}\left( t \right) + {{\tilde a}_0}\left( t \right)} \right]\cos \left[ {\varphi _0^1\left( t \right)} \right]. $ | (5) |
式中:φ01(t)=α0(t).
交变成分
| $ {z_{j + 1}}\left( t \right) = {{\tilde a}_j}\left( t \right) + iH\left[ {{{\tilde a}_j}\left( t \right)} \right]. $ | (6) |
式中:H[·]表示对信号做Hilbert变换.
根据HT原理,
| $ \begin{array}{l} {{\tilde a}_j}\left( t \right) = \left| {{z_{j + 1}}\left( t \right)} \right|\cos \left[ {\arg \left( {{z_{j + 1}}\left( t \right)} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;{a_{j + 1}}\cos \left[ {{\alpha _{j + 1}}\left( t \right)} \right]. \end{array} $ | (7) |
将式(7) 代入式(5) 可得
| $ \begin{array}{l} x\left( t \right) = {{\bar a}_0}\left( t \right)\cos \left[ {\varphi _0^1\left( t \right)} \right] + \\ \;\;\;\;\;\;\;\;\;{a_1}\left( t \right)\left\{ {\cos \left[ {{\alpha _1}\left( t \right)} \right]\cos \cdots \left[ {\varphi _0^1\left( t \right)} \right]} \right\}. \end{array} $ | (8) |
根据Werner三角公式, 公式(8) 可化为
| $ x\left( t \right) = {{\bar a}_0}\left( t \right)\cos \left[ {\varphi _0^1\left( t \right)} \right] + \frac{{{a_1}\left( t \right)}}{2}\sum\limits_{k = 1}^{{2^1}} {\cos \left[ {\varphi _1^k\left( t \right)} \right]} . $ | (9) |
式中:φ11(t)=α1(t)-φ01(t), φ12(t)=α1(t)+φ01(t).由此, 经一次迭代后, 得到了第一个调幅-调频单分量成分a0(t)cos [φ01(t)], 其瞬时幅值和瞬时相位都已知.
根据公式(4) 对a1(t)继续转化, 并重复上述步骤, 经j次迭代计算以后, 解调出N个单分量信号, 此时有
| $ \begin{array}{l} x\left( t \right) = \sum\limits_{j = 0}^N {\frac{{{{\bar a}_j}\left( t \right)}}{{{2^j}}}} \sum\limits_k^{{2^j}} {\cos \left[ {\varphi _j^k\left( t \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{{{\tilde a}_N}\left( t \right)}}{{{2^N}}}\sum\limits_{k = 1}^{{2^N}} {\cos \left[ {\varphi _N^k\left( t \right)} \right]} . \end{array} $ | (10) |
式中:相位φjk(t)按下式计算
| $ \varphi _j^{2l - 1}\left( t \right) = {\alpha _j}\left( t \right) - \varphi _{j - 1}^l\left( t \right). $ | (11) |
| $ \varphi _j^{2l}\left( t \right) = {\alpha _j}\left( t \right) + \varphi _{j - 1}^l\left( t \right). $ | (12) |
其中, l=1, …, 2j-1, j=1, …, N.
根据式(10), 定义信号IHT分解的余量为
| $ {r_N}\left( t \right) = \frac{{{{\tilde a}_N}\left( t \right)}}{{{2^N}}}\sum\limits_{k = 1}^{{2^N}} {\cos \left[ {\varphi _N^k\left( t \right)} \right]} . $ | (13) |
文献[14]中已经证明, 当N→∞时, rN→0, 即IHT分解算法是收敛的.于是, 式(10) 可以写成
| $ \begin{array}{l} x\left( t \right) \approx \sum\limits_{j = 0}^N {\frac{{{{\bar a}_j}\left( t \right)}}{{{2^j}}}} \sum\limits_k^{{2^j}} {\cos \left[ {\varphi _j^k\left( t \right)} \right]} = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{{2^{N + 1}} - 1} {{{\bar A}_i}\left( t \right)\cos \left[ {{{\Phi }_i}\left( t \right)} \right]} . \end{array} $ | (14) |
式中:
| $ {{\bar A}_i}\left( t \right) = \frac{{{{\bar a}_j}\left( t \right)}}{{{2^j}}},i = {2^j} - 1 + k; $ | (15) |
| $ {{\Phi }_i}\left( t \right) = \varphi _j^k\left( t \right),{2^j} - 1 < i < {2^{j + 1}} - 1. $ | (16) |
滤波器分离趋势成分aj(t)和交变成分
1)
2) 为了保证IHT分解的收敛性, 即滤波所得交变成分
假设高通滤波器传递函数为G(w), aj(t)经滤波得到
| $ {{\tilde A}_j}\left( w \right) = {A_j}\left( w \right)G\left( w \right). $ | (17) |
式中:
滤波过程中损失的能量系数κ定义为
| $ \kappa = \frac{{{{\left\| {{A_j}\left( w \right)G\left( w \right)} \right\|}^2}}}{{{{\left\| {{A_j}\left( w \right)} \right\|}^2}}}. $ | (18) |
其中
| $ {\left\| {{A_j}\left( w \right)} \right\|^2} = \frac{1}{{2{\rm{\pi }}}}\int_{ - \infty }^{ + \infty } {{{\left| {{A_j}\left( w \right)} \right|}^2}{\rm{d}}w} . $ | (19) |
| $ {\left\| {{A_j}\left( w \right)G\left( w \right)} \right\|^2} = \frac{1}{{2{\rm{\pi }}}}\int_{ - \infty }^{ + \infty } {{{\left| {{A_j}\left( w \right)G\left( w \right)} \right|}^2}{\rm{d}}w} . $ | (20) |
将式(19) 和(20) 代入式(18) 得到
| $ \kappa = \frac{{\int_{ - \infty }^{ + \infty } {{{\left| {{A_j}\left( w \right)G\left( w \right)} \right|}^2}{\rm{d}}w} }}{{\int_{ - \infty }^{ + \infty } {{{\left| {{A_j}\left( w \right)} \right|}^2}{\rm{d}}w} }}. $ | (21) |
在分解过程中, 滤波器截止频率可先设置一个较小值f0, 然后判断滤波结果是否同时满足

|
图 1 滤波流程框图 Fig. 1 Flow chart of filtering |
由式(14) 可知信号x(t)的幅-相调制模型为
| $ x\left( t \right) = \sum\limits_{i = 1}^{{2^{N + 1}} - 1} {{{\bar A}_i}\left( t \right)\cos \left[ {{{\Phi }_i}\left( t \right)} \right]} . $ | (22) |
为了估算IF, 对相位Φi(t)进行如下转化
| $ {{\Phi }_i}\left( t \right) = {{{\bar \Phi }}_i}\left( t \right) + {{{\tilde \Phi }}_i}\left( t \right). $ | (23) |
| $ {{{\bar \Phi }}_i}\left( t \right) = \int\limits_0^t {{{\bar w}_i}\left( \tau \right){\rm{d}}\tau } . $ | (24) |
式中:Φi(t)、
Gianfelici等[15]提出了一种自适应细分算法来估算IF, 虽然该方法可以弱化噪声的干扰, 但其更适用于具有分段线性性质的相位信号.而行星齿轮箱振动的相位信号通常为正弦调制形式, 用该方法求解精度低.且其中涉及线性回归计算, 大大增加了计算量, 降低了计算效率.故本文采用对瞬时相位求导来估算IF, 具体公式为
| $ f\left( t \right) = \frac{1}{{2{\rm{\pi }}}}\left| {{{\bar w}_i}\left( t \right)} \right| = \frac{1}{{2{\rm{\pi }}}}\left| {\frac{{{\rm{d}}{{{\bar \Phi }}_i}\left( t \right)}}{{{\rm{d}}t}}} \right|. $ | (25) |
由第1节分析可知, 信号分解的过程, 就是利用HT分离出调幅-调频单分量成分瞬时幅值和瞬时相位的过程.IHT应用于行星齿轮箱解调分析的具体过程为:
(1) IHT分解:采用IHT方法分解振动信号, 获得n个单分量成分的瞬时幅值和瞬时相位.根据IHT的理论推导, 在满足滤波器设计的2个条件的前提下, 单分量个数n可以取任意值.然而, 在实际分析中, 单分量成分按能量递减顺序排列, 随着n的增大, 后续单分量成分包含的故障信息越弱, 因此, 在满足分析要求前提下, n可取较小值;
2) 求解IF:将各个单分量成分的瞬时相位对时间求导后取绝对值, 得到相应的IF;
3) 选取敏感分量:选取最先分解得到的且IF以啮合频率或其倍频为波动中心的单分量成分作为敏感分量.这是因为单分量成分按照瞬时幅值能量递减顺序分解出来, 能量越大特征频率幅值越明显;并且行星齿轮箱信号中的调幅和调频频率对应着故障特征频率, 载波频率对应着啮合频率或其倍频, 所以说, IF波动中心正好与啮合频率或其倍频相等的单分量成分含有大量故障信息, 适合做进一步分析;
4) 解调分析:对敏感分量的瞬时幅值和IF分别做Fourier频谱分析, 解调出特征频率.
3 基于仿真信号的优势对比 3.1 仿真信号分析行星架旋转的调制作用在任何情况下都存在, 因此, 在对行星齿轮箱进行故障判断时并没有影响.基于这个原因, 本文的行星齿·轮箱振动仿真信号只考虑了故障引起的振动成分, 而不考虑正常和故障情况下均存在的行星架旋转所引起的调制成分.
假设行星齿轮箱中太阳轮轮齿发生了局部损伤故障, 建立相应的振动模型如下:
| $ \begin{array}{l} x\left( t \right) = \left[ {1 - \cos \left( {2{\rm{\pi }}{f_{{\rm{sr}}}}t} \right)} \right]\left[ {1 + C\cos \left( {2{\rm{\pi }}{f_{\rm{s}}}t} \right)} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\cos \left[ {2{\rm{\pi }}{f_{\rm{m}}}t + D\sin \left( {2{\rm{\pi }}{f_{\rm{s}}}t} \right) + \phi } \right] + n\left( t \right). \end{array} $ | (26) |
式中:太阳轮绝对转频fsr=18 Hz, 太阳轮故障频率fs=47 Hz, 啮合频率fm=300 Hz, 调幅系数C=1, 调频系数D=1.2, 初始相位φ=0.在仿真信号中加入信噪比为1 dB的Gauss白噪声n(t).采样频率为3 000 Hz, 采样时间为10 s.
仿真信号的分析结果如图 2所示, 图中,t为时间, A为幅值, f为频率,fA为幅值频率.图 2(a)是仿真信号的时域波形, 从图 2(b)、(c)分别展示了IHT分解得到的前5个单分量成分的瞬时幅值和IF.选取IF围绕啮合频率2倍频波动的第1个单分量作为敏感分量, 如图 2(d)所示.从图 2(e)和(f)中可以看到, 无论是在幅值解调还是频率解调的结果中, fsr、太阳轮故障频率fs及组合频率fs±fsr幅值非常突出, 可以判断太阳轮发生了故障.分析结果与模型特征吻合, 初步验证了所提方法的有效性.

|
图 2 仿真信号分析结果 Fig. 2 Analysis result of simulation signal |
在此需要说明, 仿真信号中的频率成分只含有啮合频率, 没有啮合频率倍频, 之所以第1个单分量的IF波动中心为2倍频啮合频率, 是由于加入的噪声干扰引起的偏差.如果仿真信号中不加入噪声, 第1个单分量的IF波动中心频率正好等于1倍啮合频率.如果逐渐提高信号的信噪比, 第1个单分量的IF波动中心频率会逐渐向1倍啮合频率靠拢.当信噪比达到60 dB时, 第1个单分量的IF波动中心频率大约为317 Hz, 与1倍啮合频率非常接近.然而, 经验证噪声对敏感分量的选取无影响.
3.2 对比分析Hilbert振动分解(hilbert vibration decomposition, HVD)是由学者Feldman提出一种多分量信号分解方法.通过HT、平滑滤波以及同步检测的迭代运用, 能将多分量信号分解为一组能量依次递减的单分量.HVD与IHT类似, 2种方法都以Hilbert变换为基础, 都运用了迭代计算, 分解速度都较快.且与经验模式分解(empirical mode decomposition, EMD)相比, HVD具有不存在模态混叠现象、计算简单易实现、分解效率高的优点[16-17].因此, 本文将IHT与HVD进行比较, 以展示IHT方法的先进性.
为了保证IHT和HVD对比结果的可靠性, 除分解算法以外, 其他步骤, 如敏感分量选取、解调分析、分解单分量个数等, 2种方法都保持一致.且根据公式(26) 设计3组仿真信号:x1(t)不加噪声、x2(t)加入信噪比为10 dB的Gauss白噪声、x3(t)加入信噪比为1 dB的Gauss白噪声, 从分解速度、分解结果信噪比以及特征频率提取效果3个方面进行比较.仿真信号采样频率为3 000 Hz, 采样时间为10 s.
分解速度是以完成分解所需时间长短衡量.在3组信号x1(t)、x2(t)、x3(t)中, IHT分解所用时间分别为3.811、3.825、3.818 s, HVD分解所用时间依次为6.457、6.463、6.832 s.3组信号分解中, IHT的分解速度都远远快于HVD.
分解结果信噪比能从一定程度上反映分解方法对噪声的抑制效果.参考文献[15], 定义分解结果的信噪比如下:
| $ {\rm{snr}} = 10{\rm{lg}}\left[ {\frac{{{敏感分量幅值^2}}}{{{{\left( {敏感分量幅值 - 原始信号幅值} \right)}^2}}}} \right]. $ | (27) |
对3组信号x1(t)、x2(t)、x3(t)进行分解, 根据选取原则, IHT和HVD 2种方法都选取第1个单分量成分作为敏感分量.按照式(27) 求得IHT的3组分解结果信噪比分别为80.355 7、13.754 3、4.212 6 dB, HVD的分解结果信噪比依次为10.439 7、5.370 4、-2.178 1 dB.由此可见, IHT的分解结果信噪比都大于HVD, IHT分解在抑制噪声上表现更好.
特征频率提取效果通过比较2种方法的幅值和瞬时频率的解调频谱中特征频率的幅值大小来判断.具体结果如表 1和2所示.表 2中:“-”表示解调频谱中, 该频率成分幅值小, 无法识别.在幅值解调频谱中, HVD除了0.511、0.736和0.457分别大于IHT的0.500、0.654、0.407以外, 其他特征频率的幅值都小于IHT.在瞬时频率解调频谱中, 除了信号x1(t)中的fsrHVD幅值高于IHT, 其他情况下, 基于IHT的解调频谱中的特征频率成分幅值都高于HVD, 且在信号x2(t)、x3(t)解调中, fs-fsr、fs+fsr这2个特征频率成分无法识别.综上分析, IHT特征频率提取效果同样优于HVD.
| 表 1 幅值解调频谱特征频率处的幅值对比 Table 1 Values comparison of amplitude demoducation spectirum in characteristic frequency |
| 表 2 瞬时频率解调频谱特征频率处的幅值对比 Table 2 Volues comparison of IF demodulation spectrum in characteristic freguency |
综上所述, 较之HVD, IHT在分解速度、噪声抑制以及特征频率提取3个方面都有更好的表现, 体现了IHT方法的先进性.
4 实验信号分析 4.1 实验说明所用实验系统为NGW21型一级减速机行星齿轮箱系统, 行星齿轮箱的构成为:1个齿数为13的太阳轮, 3个单个齿数为38的行星轮, 1个齿数为92的齿圈(固定).当采集信号时, 磁粉制动器加载的恒定载荷为31.25 N·m, 系统输入轴转频(即太阳轮转频)为24.98 Hz, 采样频率为20 480 Hz, 时间为60 s.计算得到各个齿轮故障的特征频率见表 3.其中, fpr、fc分别为行星轮、行星架的绝对旋转频率, fp、fr分别为行星轮、齿圈的局部故障特征频率.
| 表 3 行星齿轮箱特征频率 Table 3 Characteristic frequencies of planetary gearboxHz |
需要说明一点, 本文的分析是建立在齿轮发生明显故障的前提下的.在实验中, 加工的齿轮局部故障较大, 如图 3所示.

|
图 3 齿轮局部损伤 Fig. 3 Gear localized damage |
如图 4所示为正常行星齿轮箱的分析结果.图 4(a)为信号时域波形, 图 4 (b)、(c)是IHT的分解结果.图中,aA为幅值是加速度,图 4(d)中, 第1个单分量的瞬时频率围绕啮合频率11倍频波动, 根据敏感分量选取方法, 对其做进一步解调分析.敏感分量解调分析结果如图 4(e)、(f)所示.其中齿轮安装误差、制造误差对振动信号的调制引起的行星架转频fc及其倍频幅值很大.行星架对振动信号的调制产生的频率3fc幅值也较突出[18], 但是其倍频没有出现, 说明齿轮安装误差、制造误差引起的调制程度比行星架调制程度更大.分析结果符合实际情况.

|
图 4 正常齿轮信号分析结果 Fig. 4 Analysis result of normal gear signal |
与前面的分析方法相同, 选取了IF围绕12倍啮合频率波动的第1个单分量作为敏感分量.观察敏感分量的瞬时幅值Fourier频谱图 5(b)可以发现, fs及其倍频nfs、fsr及其倍频2fsr、正常状态下的主导频率成分nfc以及它们的组合频率幅值很大.在频率解调结果图 5(c)中, 依然能观察到故障频率fs、2fs及其与太阳轮转频fsr的组合频率幅值非常突出.此外, 由于故障信号强, 频率成分nfc幅值并不突出, 在后续的行星轮故障和齿圈故障信号分析中, 存在同样现象.基于以上分析可以判定太阳轮发生了故障, 与实际情况相符.

|
图 5 太阳轮故障信号分析结果 Fig. 5 Analysis result of faulty sun gear signal |
同样地, 将基于IHT的解调分析方法应用于行星轮和齿圈故障信号分析中, 结果依然准确.
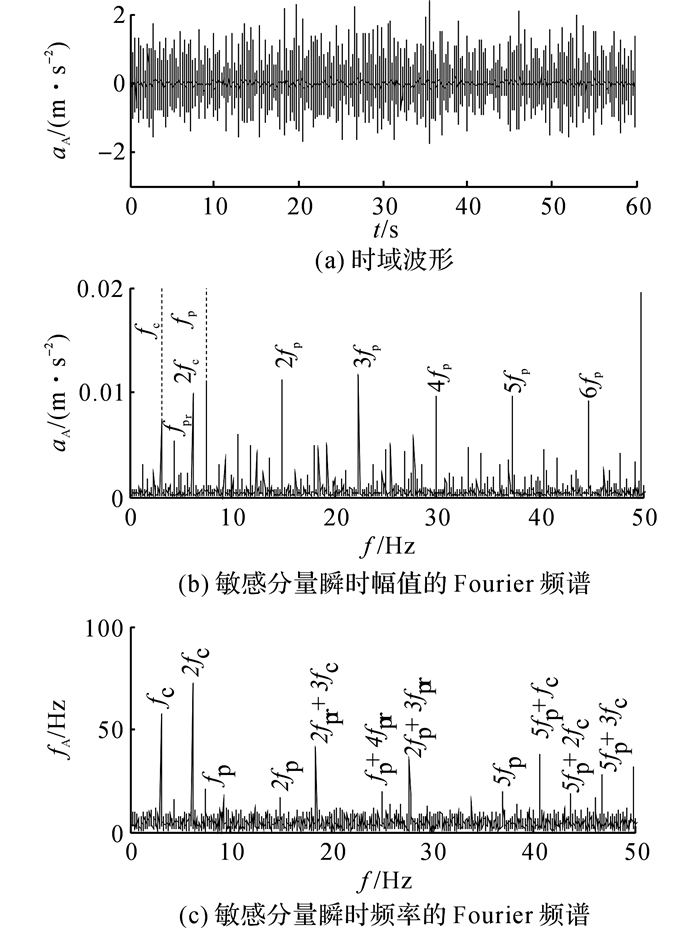
与正常状态的分析结果不同, 行星轮故障信号分析结果图 6(b)、(c)中行星轮故障特征频率fp及其倍频nfp成分占主导地位, 与行星轮发生了故障的事实一致.
|
图 6 行星轮故障信号分析结果 Fig. 6 Analysis result of faulty planet gear signal |
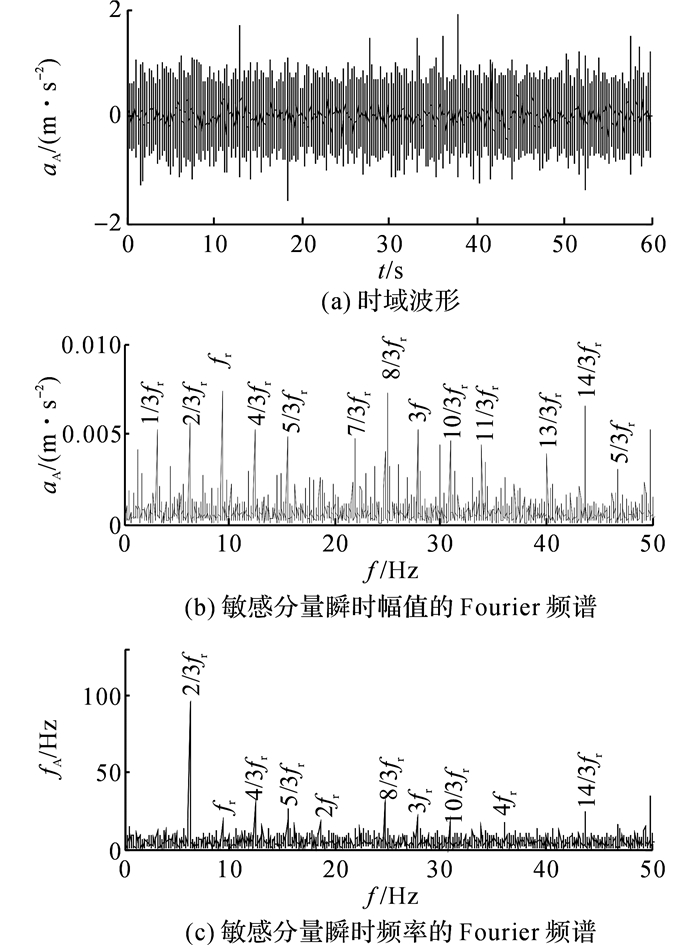
在实际运行中, 齿圈同时与3个行星轮啮合, 各个行星轮之间必然存在差异性, 因此, 在齿圈故障频率分析中, 应当关注1/3fr及其倍频n/3fr.齿圈信号分析结果图 7(b)、(c)中, 可以观察到n/3fr频率成分显著, 与上述分析的齿圈频率特点完全一致.
|
图 7 齿圈故障信号分析结果 Fig. 7 Analysis result of faulty ring gear signal |
IHT能从复杂的调幅-调频多分量信号中按照能量递减的顺序依次分离出任意多个调幅-调频单分量成分的瞬时幅值和瞬时相位.将IHT与FT结合起来用于行星齿轮箱局部故障的仿真和实验信号的解调分析:(1) 在低信噪比情况下, 从复杂信号中有效分离出包含故障信息的单分量, 单分量信号的信噪比较原始信号得到提高, 改善了瞬时频率频谱的效果, 准确提取了特征频率, 诊断了齿轮故障, 验证了所提方法的有效性, 同时也展示了IHT提取信号成分并抑制噪声干扰的能力;(2) 基于仿真信号, 通过IHT与HVD分析结果的对比, 突出了HVD在分解速度、抑制噪声以及特征频率提取中的优势, 表明了所提方法的先进性.
| [1] | 冯志鹏, 褚福磊, 左明健. 行星齿轮箱振动故障诊断方法[M]. 北京: 科学出版社, 2015: 1-3. |
| [2] |
冯志鹏, 褚福磊. 行星齿轮箱齿轮分布式故障振动频谱特征[J].
中国电机工程学报, 2013, 33(2): 118–125.
FENG Zhi-peng, CHU Fu-lei. Vibration spectral characteristics of distributed gear fault of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(2): 118–125. |
| [3] | KAISER J F. On a simple algorithm to calculate the energy of a signal [C]// 1990 International Conference on Acoustics, Speech, and Signal Processing. Albuquerque: IEEE, 1990: 381-384. |
| [4] | MARAGOS P, KAISER J F, QUATIERI T F. On amplitude and frequency demodulation using energy operators[J]. Signal Processing Transactions on IEEE, 1993, 41(4): 1532–1550. DOI:10.1109/78.212729 |
| [5] | FELEMAN M. Hilbert transform in vibration analysis[J]. Mechanical Systems & Signal Processing, 2011, 25(3): 735–802. |
| [6] |
丁康, 米林, 王志杰. 解调分析在故障诊断中应用的局限性问题[J].
振动工程学报, 1997, 10(1): 13–20.
DING Kang, MI Lin, WANG Zhi-jie. Investigation on limitations for demodulation analysis application in failure diagnosis[J]. Journal of Vibration Engineering, 1997, 10(1): 13–20. |
| [7] |
冯志鹏, 褚福磊. 行星齿轮箱故障诊断的频率解调分析方法[J].
中国电机工程学报, 2013, 33(11): 112–117.
FENG Zhi-peng, CHU Fu-lei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(11): 112–117. |
| [8] |
白亚红, 王奉涛. EMD分解和支持向量机技术在风电齿轮箱早期齿轮磨损故障诊断中的应用[J].
工业控制计算机, 2010, 23(2): 70–71.
BAI Ya-hong, WANG Feng-tao. Early recognition based on EMD and support vector machine for wind power gear box failure[J]. Industrial Control Computer., 2010, 23(2): 70–71. |
| [9] |
雷亚国, 孔德同, 李乃鹏, 等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].
机械工程学报, 2014, 50(3): 64–70.
LEI Ya-guo, KONG De-tong, LI Nai-peng, et al. Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering, 2014, 50(3): 64–70. |
| [10] | GIANFELICI F, BIAGETTI G, CRIPPA P, et al. AM-FM decomposition of speech signals: an asymptotically exact approach based on the iterated Hilbert transform [C]// 2005 IEEE/SP 13th Workshop on Statistical Signal Processing. Novosibirsk: IEEE, 2005: 333-338. |
| [11] | GIANFELICI F, TURCHETTI C, CRIPPA P. Multicomponent AM-FM demodulation: The state of the art after the development of the iterated hilbert transform [C]//2007 IEEE International Conference on Signal Processing and Communications. Dubai: IEEE, 2007: 1471-1474. |
| [12] | QIN Y, QIN S, MAO Y. Research on iterated Hilbert transform and its application in mechanical fault diagnosis[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1967. DOI:10.1016/j.ymssp.2008.01.014 |
| [13] |
秦毅, 王家序, 汤宝平. 基于迭代Hilbert变换的多分量信号解调方法研究及应用[J].
机械工程学报, 2009, 45(8): 37–44.
QIN Yi, WANG Jia-xu, TANG Bao-ping. Multicomponent demodulation based on iterated Hilbert transform and its application[J]. Journal of Mechanical Engineering, 2009, 45(8): 37–44. |
| [14] |
邓四二, 王勇, 王恒迪. 基于IHT的共振解调技术的滚动轴承故障诊断方法[J].
航空动力学报, 2012, 27(1): 69–74.
DENG Si-er, WANG Yong, WANG Heng-di. Resonance demodulation technique based on IHT for rolling bearings fault diagnosis[J]. Journal of Aerospace Power, 2012, 27(1): 69–74. |
| [15] | GIANFELICI F, BIAGETTI G, CRIPPA P, et al. Multicomponent AM-FM representations: an asymptotically exact approach[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(3): 823–837. DOI:10.1109/TASL.2006.889744 |
| [16] | FELDMAN M. Theoretical analysis and comparison of the Hilbert transform decomposition methods[J]. Mechanical Systems and Signal Processing, 2008, 22: 509–519. DOI:10.1016/j.ymssp.2007.09.013 |
| [17] | BRAUN S, FELDMAN M. Decomposition of non-stationary signals into varying time scale: Some aspects of the EMD and HVD methods[J]. Mechanical Systems and Signal Processing, 2011, 25: 2608–2630. DOI:10.1016/j.ymssp.2011.04.005 |
| [18] |
黄奕宏, 丁康, 何国林. 行星传动系统振动信号数学模型及特征频率分析[J].
机械工程学报, 2016, 52(7): 46–53.
HUANG Yi-hong, DING Kang, HE Guo-lin. Mathematical model of planetary gear sets' vibration signal and characteristic frequency analysis[J]. Journal of Mechanical Engineering, 2016, 52(7): 46–53. |



