磁流变阻尼器具有阻尼力连续可控、响应速度快、能耗小、稳定性好等优点, 结合了被动控制与主动控制的优势, 成为土木工程结构减振的智能半主动控制装置^[1-3].在实际应用中, 采用磁流变阻尼器的半主动控制系统需要测量结构的响应和外激励信息, 由系统控制律确定符合减振目标的期望控制力, 再通过一定的力跟踪控制算法确定控制电压使磁流变阻尼器的输出阻尼力尽量逼近期望控制力.基于Heaviside阶跃函数的力跟踪算法^[4]是较为常用的方法, 它需要测量阻尼力作为反馈信息, 操作简单, 但忽略了磁流变阻尼器的非线性动力学.另一类方法是基于磁流变阻尼器的逆向动力模型确定控制电压.参数化逆向动力模型通过简化参数化正向模型, 忽略非线性滞回效应求逆得到^[5-6], 或者通过反馈进行滞回补偿^[6-7].非参数化逆向模型采用神经网络^[8-10]、模糊逻辑^[12-13]、神经模糊推理^[14-15]等技术能够直接充分考虑磁流变阻尼器的非线性动力特性, 因此获得广泛使用.

为提高控制系统的可靠性, 采用Chen等^[10]提出的自传感磁流变阻尼器(self-sensing magnetorheological damper, SMRD), 实现传感器和阻尼器同位式配置的控制方案.针对SMRD的非线性滞回特性, 本文利用试验数据, 建立基于贝叶斯推理的非线性自回归(nonlinear autoregressive with exogenous inputs, NARX)网络模型以描述SMRD的正向和逆向动力学行为, 并融入线性二次高斯(linear-quadratic-Gaussian, LQG)控制系统回路中, 通过试验评价基于逆向动力学的SMRD阻尼力实时跟踪控制性能, 并与基于Heaviside函数的LQG控制策略进行比较研究.

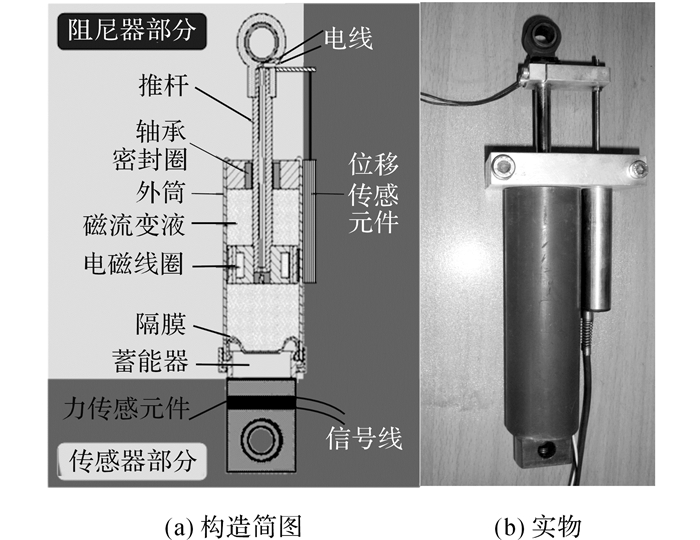
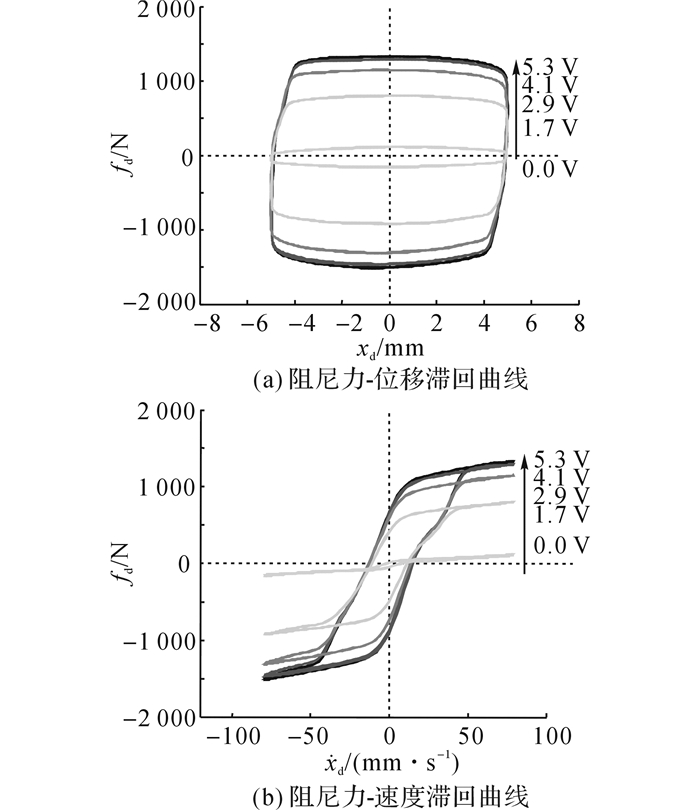
1 自传感磁流变阻尼器

如图 1所示为自传感磁流变阻尼器, 它由阻尼器和传感器2部分构成, 通过将力及位移传感功能与MR阻尼器的阻尼调谐能力高度集成, 形成兼具传感和可控阻尼双重功能的一体化控制装置^[10-11].因此, 在实际应用中, SMRD能够实时量测阻尼器产生的阻尼力和结构在阻尼器安装位置的位移响应(即阻尼器推杆的位移), 由阻尼力和位移测量值的乘积实际上反映了结构和控制系统之间的能量交换, 这些实测信息将反馈到控制系统以确定半主动控制律, 实现同位式的半主动结构控制.图 2显示了SMRD在2.5 Hz、5.0 mm正弦位移激励以及不同输入电压下的阻尼力-位移(f_d-x_d)和阻尼力-速度(f_d- ${{{\dot x}_d}}$)滞回曲线.可见, 当无输入电压时, SMRD表现出黏性阻尼的特征；随着电压增大, 阻尼力幅值和滞回区域非线性递增, 表明SMRD的可控耗能能力, 且当电压趋于最大值时呈现饱和现象.

2 SMRD动力学模型 2.1 贝叶斯NARX网络

由于SMRD的强非线性特征, 建立能够准确表征其动力学行为、控制应用导向的模型具有一定挑战性.本文采用基于贝叶斯推理的NARX网络建模方法^[10-11], 从网络结构和学习算法优化相结合的角度来确定SMRD的正向和逆向动力模型.

NARX网络模型可表示为

$ \hat y\left( k \right) = \phi \left( {\mathit{\boldsymbol{x}}\left( k \right);\mathit{\boldsymbol{w}}} \right). $

(1)

式中：x(k)=[y(k-1), …, y(k-n_y), u(k), u(k-1), …, u(k-n_u)]为网络模型的输入向量；${\hat y}\left( k \right)$为网络模型的预测输出；u和y分别为系统输入和输出；n_u和n_y分别为系统输入和输出的时延阶数；φ(·)为反映输入输出映射关系的神经网络, 可表示为

$ \begin{array}{l} \phi \left( {\mathit{\boldsymbol{x}}\left( k \right);\mathit{\boldsymbol{w}}} \right) = \\ \;\;\;\;\;\;{g_2}\left( {\sum\limits_{j = 1}^{{n_{\rm{h}}}} {w_j^0{g_1}} \left( {\sum\limits_{i = 1}^{{n_{\rm{i}}}} {w_{ji}^{\rm{h}}{x_{i\left( k \right)}} + b_j^{\rm{h}}} } \right) + {b^{\rm{o}}}} \right). \end{array} $

(2)

式中：n_i(=n_y+n_u+1) 和n_h分别为输入层和隐层的神经元数目；w=[w_ji^h,w_j^o,b_j^h，b^o]^T为神经元连接权和阈值组成的网络参数向量；g₁(·)和g₂(·)分别为隐层和输出层的激励函数.NARX网络的参数寻优采用贝叶斯正则化算法求解, 在贝叶斯分析框架下, 通过修正网络的训练性能函数式(3) 来降低网络训练误差, 同时自适应控制网络结构的复杂性, 以增强模型的泛化能力.

$ \mathit{S}\left( \mathit{\boldsymbol{w}} \right) = \beta {E_\mathit{D}} + \alpha {E_\mathit{w}}. $

(3)

式中：${E_{D}} = \frac{1}{2}\sum\limits_{k = 1}^{{n_D}} {{{\left( {\hat y\left( k \right) - {y_k}} \right)}^2}} $反映模型预测性能；${E_w} = \frac{1}{2}\sum\limits_{i = 1}^{{n_w}} {w_i^2} $反映网络结构的复杂性；α和β为正则化参数, 控制着E_w在目标函数中的参与程度；n_D和n_w分别为数据样本和网络参数的个数.

在贝叶斯分析框架下, 将网络参数w视为随机变量, 对训练数据D和w的先验分布分别为P(D|w, β)和P(w|α)进行假设, 得到网络参数的后验概率分布式(4) 以确定最优网络参数：

$ \begin{array}{l} P\left( {\mathit{\boldsymbol{w}}|\mathit{D}, \alpha, \beta } \right) = \frac{{P\left( {\mathit{D}|\mathit{\boldsymbol{w}}, \beta } \right)P\left( {\mathit{\boldsymbol{w}}|\alpha } \right)}}{{P\left( {\mathit{D|}\alpha, \beta } \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\exp \left( { - S\left( \mathit{\boldsymbol{w}} \right)} \right)}}{{\int {\exp \left( { - S\left( \mathit{\boldsymbol{w}} \right)} \right){\rm{d}}\mathit{\boldsymbol{w}}} }}. \end{array} $

(4)

贝叶斯推理学习算法的另一个优势是网络训练过程中可以同步优化正则化参数α和β.通过求取正则化参数的最大后验概率分布为

$ P\left( {\alpha, \beta |\mathit{D}} \right) = \frac{{P\left( {\mathit{D}|\alpha, \beta } \right)P\left( {\alpha, \beta } \right)}}{{P\left( \mathit{D} \right)}}. $

(5)

获得最优的正则化参数为

$ {\alpha ^{{\rm{MP}}}} = \frac{{{\gamma _{{\rm{eff}}}}}}{{2E_w^{{\rm{MP}}}}}, {\beta ^{{\rm{MP}}}} = \frac{{{n_{D - }}{\gamma _{{\rm{eff}}}}}}{{2E_D^{{\rm{MP}}}}}. $

(6)

式中：$ {\gamma _{{\rm{eff}}}} = {n_w} - 2{\alpha ^{{\rm{MP}}}}{\rm{trace}}\left( {{{\left( {\nabla \nabla S\left( {{\mathit{\boldsymbol{w}}^{{\rm{MP}}}}} \right)} \right)}^{ - 1}}} \right) $为实际参与正则化学习的网络参数的数量，E_w^MP、E_D^MP分别为以最优网络参数w^MP计算的E_w值和E_D值.

2.2 模型训练和验证数据

为使训练样本能够基本覆盖SMRD的工作范围, 保证其动力学模型在控制应用中的有效性, 将SMRD安装到置于振动台上的钢框架结构上, 由振动台产生有限带宽的白噪声基础振动加速度信号, 使SMRD在随机振动状态下工作, 同时对其施加带限白噪声的随机电压, 以获取丰富的动态响应信息.如图 3所示为用于模型学习训练的随机样本, 为在8.0 m·s^-2峰峰幅值(a_pp)、0.8~10 Hz频率(ω_a)范围的基础加速度激励以及输入电压幅值(V₀)为0~5 V、频率(ω_v)为0~10 Hz的试验工况下所获取的SMRD推杆位移x_d、速度 ${{{\dot x}_d}}$、电压V和阻尼力f_d时程.如表 1所示为试验采集的与训练数据不同输入工况的3组验证样本, 表中f_d(RMS)为阻尼力均方根(RMS)，以检验经训练后模型的泛化性能, 其评价指标取为实际值与模型预测值的均方根误差, 即

$ {\delta _{{\rm{RMS}}}} = \sqrt {\frac{1}{{{n_D}}}\sum\limits_{k = 1}^{{n_D}} {{{\left[{y\left( k \right)-\hat y\left( k \right)} \right]}^2}} } . $

(7)

2.3 SMRD正向动力学模型

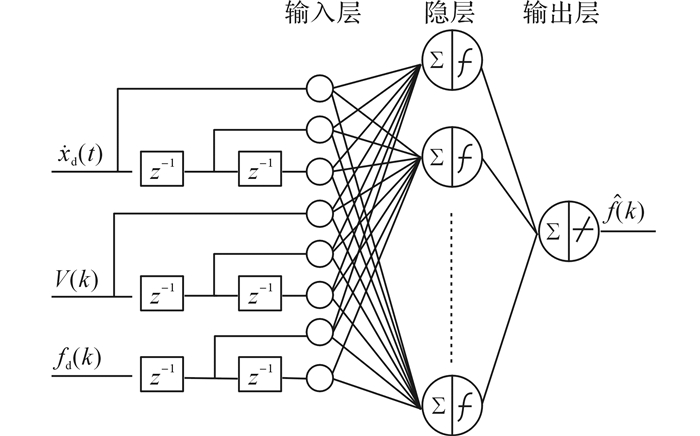
描述SMRD正向动力学行为的NARX网络模型选用3层前馈神经网络, 包括1个输入层、1个隐含层和1个输出层, 隐含层和输出层的传递函数分别选为双曲正切S型函数和线性函数.通过模型误差综合分析, 最终确定输入层神经元为8个, 输入变量由阻尼器速度 ${{\dot x}_{\rm{d}}}$、电压V和过去时刻的阻尼力f_d组成, 各个输入变量的时延阶数为 ${n_{\dot x}} = {n_V} = {n_f} = 2$；隐含层神经元为18个；输出层只有1个神经元, 输出变量为当前时刻的阻尼力；网络结构如图 4所示.根据式(1), SMRD正模型可表示为

$ \begin{array}{l} {{\hat f}_d}\left( k \right) = {\phi _{{\rm{fwd}}}}\left( {{{\dot x}_{\rm{d}}}\left( k \right), {{\dot x}_{\rm{d}}}\left( {k - 1} \right), {{\dot x}_{\rm{d}}}\left( {k - 2} \right)} \right., \\ \left. {V\left( k \right), V\left( {k - 1} \right), V\left( {k - 2} \right), {f_{\rm{d}}}\left( {k - 1} \right), {f_{\rm{d}}}\left( {k - 2} \right)} \right). \end{array} $

(8)

式中：φ_fwd(·)为建立输入输出映射关系的单隐含层 NARX 网络.式(8) 包含了SMRD输入输出的多阶时延信息, 因此可以反映其动态行为.

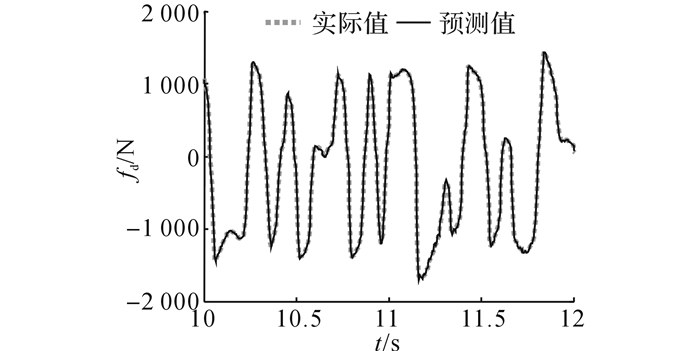
利用图 3中的实测随机数据对NARX网络采用贝叶斯正则化算法进行训练, 并采用表 1中的验证数据进行泛化性能检验.对数据样本3的检验结果如图 5所示, 可见SMRD正模型预测的阻尼力和实测值吻合得很好.正模型对3组验证数据样本的均方根预测误差δ_RMS分别为17.49、23.94和23.01 N, 误差值均小于对应的实测阻尼力RMS值的5%, 表明NARX网络模型对SMRD正向动力学的准确表征能力.

2.4 SMRD逆向动力学模型

当实际控制实施时, 需要调节电压来控制SMRD的输出阻尼力以准确跟踪实现期望控制力.运用贝叶斯NARX网络来建立SMRD的逆向动力学模型, 该模型将与系统控制算法结合实现控制电压的连续可调, 以充分发挥SMRD的智能阻尼特性.

类似于SMRD正模型, 逆模型也采用单隐含层前馈网络, 隐含层和输出层的传递函数分别为双曲正切S型函数和线性函数.经优化设计, 网络输入层神经元为8个, 包含阻尼器速度、阻尼力和过去时刻的电压, 各输入变量的时延阶数为 ${n_{\dot x}} = {n_V} = {n_f} = 2$；隐含层神经元为18个；输出层有1个神经元, 为当前时刻的控制电压；网络结构如图 6所示.

根据式(1) 和(8), SMRD逆向动力学的NARX网络模型可写成

$ \begin{array}{l} \mathit{\hat V}\left( k \right) = {\phi _{{\rm{inv}}}}\left( {{{\dot x}_{\rm{d}}}\left( k \right), {{\dot x}_{\rm{d}}}\left( {k - 1} \right), {{\dot x}_{\rm{d}}}\left( {k - 2} \right)} \right., \\ {f_{\rm{d}}}\left( k \right), {f_{\rm{d}}}\left( {k - 1} \right), {f_{\rm{d}}}\left( {k - 2} \right), V\left( {k - 1} \right), V\left( {k - 2} \right). \end{array} $

(9)

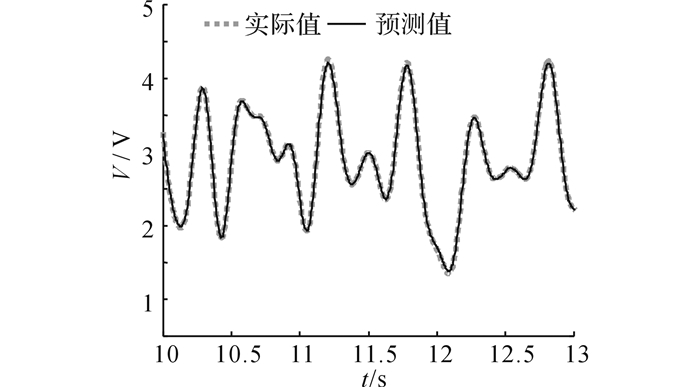
式中：φ_inv(·)为SMRD的逆向动态网络模型函数, 网络参数基于图 3所示的随机试验数据采用贝叶斯正则化算法进行优化.优化后的逆模型采用表 1中的检测数据进行泛化性检验.图 7显示了对数据样本3的预测结果, 可见SMRD逆模型可以准确地预测电压值.SMRD逆模型对3组验证数据样本的预测误差RMS值δ_RMS分别为0.004、0.042和0.020 V, 均小于目标实测值的3%, 验证了NARX网络模型能够准确表征SMRD的逆向动力学行为.

3 磁流变阻尼力跟踪控制试验

为了验证SMRD逆向动力模型在实际控制实施时的预测和泛化能力, 开展基于SMRD的斜拉索半主动控制试验, 将逆向模型与LQG控制结合形成闭环半主动控制, 评价基于SMRD逆向动力学的实时阻尼力跟踪能力和控制系统性能.

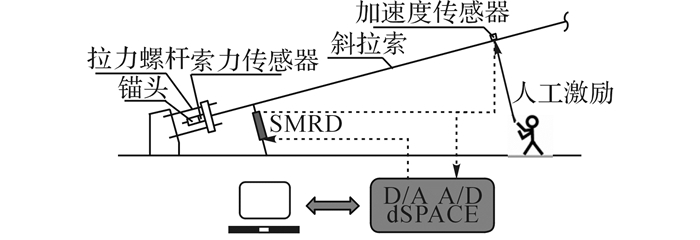
3.1 试验装置

试验装置如图 8所示, 其中钢绞线斜拉索的基本物理参数：长度L = 24.2 m、倾角θ = 14.2°、截面积A = 1.39×10^-4 m²、单位长度质量m=11.1 kg·m^-1、静态索力F_t = 43.5 kN、轴向刚度EA=2.57×10⁷ N, 索的前四阶固有频率经试验测得分别为1.39、2.55、3.84和5.11 Hz, 相应的阻尼比各为0.11%、0.12%、0.13%和0.11%.SMRD安装于距索底部锚固端0.4 m(0.016L)处.在距索底部1/4L处安装加速度传感器以观测索的面内振动响应并评价控制效果.斜拉索控制试验通过dSPACE控制平台执行.

3.2 控制策略

斜拉索在模态坐标下的横向运动微分方程为

$ \mathit{\boldsymbol{M\ddot z}}\left( t \right) + \mathit{\boldsymbol{C\dot z}}\left( t \right) + \mathit{\boldsymbol{Kz}}\left( t \right) = \mathit{\boldsymbol{D}}{f_{\rm{d}}}\left( t \right) + {\mathit{\boldsymbol{f}}_{\rm{e}}}\left( t \right). $

(10)

式中：z为模态位移向量, M、C和K分别为质量、阻尼和刚度矩阵, D为阻尼力位置矩阵, f_e为外激励.式(10) 写成状态方程为

$ \mathit{\boldsymbol{\dot Z}}\left( t \right) = \mathit{\boldsymbol{AZ}}\left( t \right) + {\mathit{\boldsymbol{B}}_1}{f_{\rm{d}}}\left( t \right) + {\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{f}}_{\rm{e}}}\left( t \right). $

(11)

式中：$\mathit{\boldsymbol{Z = }}\left[\begin{array}{l} \mathit{\boldsymbol{z}}\\ {\mathit{\boldsymbol{\dot z}}} \end{array} \right]$, $\mathit{\boldsymbol{A}} = \left[\begin{array}{l} \;\;\;\;\;\;\;{\bf{0}}\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{I}}\\ -{\mathit{\boldsymbol{M}}^{-1}}\mathit{\boldsymbol{K}}\;\;\;\;-{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{C}} \end{array} \right]$, ${\mathit{\boldsymbol{B}}_1} = \left[\begin{array}{l} \;\;\;\;{\bf{0}}\\ {\mathit{\boldsymbol{M}}^{-1}}\mathit{\boldsymbol{D}} \end{array} \right]$, ${\mathit{\boldsymbol{B}}_2} = \left[\begin{array}{l} \;\;{\bf{0}}\\ {\mathit{\boldsymbol{M}}^{-1}} \end{array} \right]$.

采用LQG控制算法, 通过最小化系统的最优控制性能指标

$ {J_t} = \int_0^\infty {\left[{\mathit{\boldsymbol{Z}}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{QZ}}\left( t \right) + Rf_{\rm{d}}^2\left( t \right)} \right]{\rm{d}}t} . $

(12)

式中：R为控制力权参数.

确定最优主动控制律为

$ \mathit{f}\;_{\rm{d}}^{{\rm{ac}}}\left( t \right) = - {\mathit{\boldsymbol{G}}_{\rm{d}}}\mathit{\boldsymbol{\hat Z}}\left( t \right). $

(13)

式中：G_d为控制增益, ${\mathit{\boldsymbol{\hat Z}}}$为采用Kalman滤波算法基于SMRD的实测位移进行重构的系统估计状态.由于斜拉索具有极低的结构阻尼, 将式(12) 中的状态权矩阵取为

$ \mathit{\boldsymbol{Q}} = \frac{1}{2}\left[\begin{array}{l} \mathit{\boldsymbol{K}}\;\;\;{\bf{0}}\\ {\bf{0}}\;\;\;\mathit{\boldsymbol{M}} \end{array} \right]. $

(14)

使得耗散拉索的振动能量(近似为变形能和动能之和)成为控制目标.R由试验比较选定.

考虑SMRD的耗散性和出力有界性, 对式(13) 进行约束确定实际的最优半主动控制律为

$ \left\{ \begin{array}{l} - {\mathop{\rm sgn}} \;\;\left( {{{\dot x}_d}} \right)\left| {{f_{\max }}\left( t \right)} \right|, 若\mathit{f}\;_{\rm{d}}^{{\rm{ac}}}\left( t \right){{\dot x}_d}\left( t \right) < 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;及\left| {\mathit{f}\;_{\rm{d}}^{{\rm{ac}}}\left( t \right)} \right| > \left| {{f_{\max }}\left( t \right)} \right|;\\ - {\mathop{\rm sgn}} \;\;\left( {{{\dot x}_d}} \right)\left| {\mathit{f}\;_{\rm{d}}^{{\rm{ac}}}\left( t \right)} \right|, 若\mathit{f}_{\rm{d}}^{{\rm{ac}}}\left( t \right){{\dot x}_d}\left( t \right) < 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;及\left| {{f_{\min }}\left( t \right)} \right| \le \left| {\mathit{f}\;_{\rm{d}}^{{\rm{ac}}}\left( t \right)} \right| \le \left| {{f_{\max }}\left( t \right)} \right|, \\ - {\mathop{\rm sgn}} \;\;\left( {{{\dot x}_d}} \right)\left| {{f_{\min }}\left( t \right)} \right|, 其他\mathit{.} \end{array} \right. $

(15)

式中：${{{\dot x}_d}}$为阻尼器的作动速度, sgn (·)为符号函数, f_min(t)和f_max(t)分别为在即时速度 ${{\dot x}_d}\left( t \right)$下由式(8) 计算的SMRD的最小(零电压输入时)和最大(最大电压输入V_max时)阻尼力.

为形成闭环控制回路, 需要串联力跟踪控制器来调节电流驱动器的控制电压, 以使SMRD输出的阻尼力跟踪期望的半主动控制力f_d^sa.本文考虑2种力跟踪控制算法以做比较.1) 基于Heaviside阶跃函数的控制算法^[4], 该算法(16) 根据期望控制力f_d^sa和实测阻尼力f_d来决定控制电压在最小值(0 V)和最大值(V_max)上开关式地切换.

$ {\mathit{V}_{\rm{d}}} = {V_{\max }}H\left[{\left( {f_{\rm{d}}^{{\rm{sa}}}-{f_{\rm{d}}}} \right){f_{\rm{d}}}} \right]. $

(16)

这种开关式双态控制方法缺乏考虑SMRD的非线性动力特征, 无法充分发挥SMRD在各种电压下的工作性能, 而且电压开关处的跃变可能造成阻尼器工作状态的不连续, 导致控制能量溢出到结构的高阶振动模态^[16], 降低系统控制性能和稳定性.2) 基于SMRD逆向动力学的控制算法, 该算法考虑了SMRD的非线性动力学, 与系统控制器相结合, 利用逆向动力模型(9) 预测连续变化的电压以期改善实时阻尼力跟踪性能, 提高系统控制效果.

3.3 试验结果与分析

在斜拉索1/4L处以第1阶固有频率人工施加激励起振后释放, 使拉索进入自由振动状态.SMRD分别采用基于Heaviside函数和基于SMRD逆向动力学的半主动LQG控制算法(H-LQG和i-LQG)进行控制.

在H-LQG控制下, SMRD的实时阻尼力跟踪控制结果如图 9所示.由图 9(a)可见, 阻尼力幅值随受控拉索的自由振动衰减响应而减小.图 9(b)放大比较了3 s时间窗内的SMRD阻尼力时程.可见, 由Heaviside函数确定的SMRD控制电压为幅度0~5 V、时变宽度的脉冲信号(图 9(c)), 频繁快速的电压切换使得SMRD的实际输出阻尼力f_d不能准确地跟踪期望半主动控制力f_d^sa(图 9(b)), 跟踪误差主要在于：

1) SMRD在0 V电压下存在一定的摩擦阻尼力, 在该零电压阻尼力范围内, SMRD近似处于被动状态, 很难通过电压进行控制.因此, 在前屈服区内存在较大的阻尼力跟踪误差, 甚至实测值f_d与期望值f_d^sa反向, 如图 9(b)、(d)及 (e)所示.

2) 在后屈服区, 为使SMRD产生尽量逼近期望值的阻尼力, 控制电压由0 V快速跳跃至5 V, 导致了实际阻尼力超出期望值约15%~30%, 该跟踪误差由图 9(d)和9(e)中的SMRD滞回曲线明显可见.

采用i-LQG控制时, SMRD输出阻尼力与输入电压时程分别如图 10(a)、(b)和(c)所示, 图 10(b)是对3 s时间窗内的SMRD阻尼力时程的放大比较, 图 10(d)和(e)分别展示了相应的SMRD位移、速度与阻尼力的滞回曲线.由图 10(a)和(b)可见, SMRD阻尼力幅值同样随受控拉索的自由振动衰减响应而减小.图 10(c)显示了SMRD逆向动力学模型确定的控制电压在0~3 V区间连续变化, 最大控制电压值小于最大允许工作电压5 V.在此连续输入电压下, SMRD能够连续作动, 输出的阻尼力准确地逼近期望半主动控制力(图 10(b)), 也避免了H-LQG控制对SMRD内线圈的频繁电流加载和卸载.由图 10(d)和(e)可见, 在前屈服区域, 由于残余摩擦阻尼力的不可控, 仍存在一定的阻尼力跟踪误差, 但其值小于H-LQG控制下的跟踪误差值.在后屈服区, SMRD阻尼力跟踪误差为7%~13%, 约为H-LQG控制时的50%, 在合理范围之内, 由此验证了SMRD逆向动力模型的实际在线预测能力和泛化性能, 同时表明了将SMRD逆向动力学融入LQG控制算法中能够实现对SMRD强非线性的有效补偿.

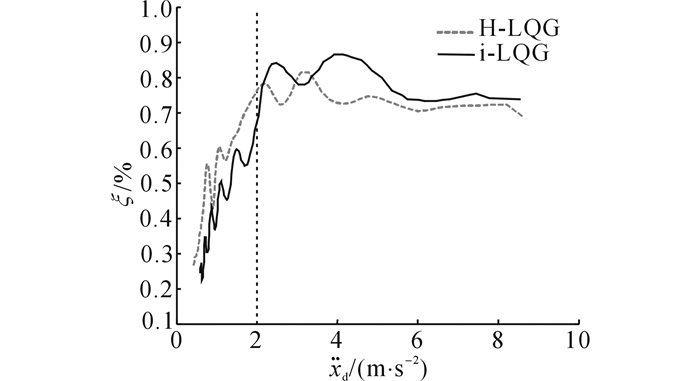
根据斜拉索1/4L处自由衰减的加速度响应${{\mathit{\ddot x}}_{\rm{d}}}$, 评价不同控制算法下拉索-SMRD系统的阻尼比ξ.如图 11所示为SMRD在H-LQG和i-LQG控制下, 拉索系统阻尼比ξ随加速度幅值${{\mathit{\ddot x}}_{\rm{d}}}$的变化.当加速度小于2 m·s^-2时, 期望阻尼力小于零电压时的摩擦阻尼力, SMRD无法跟踪期望阻尼力, 导致系统阻尼比的降低.当加速度大于2 m·s^-2时, i-LQG控制下的阻尼比总体上高于H-LQG控制下的阻尼比；计算比较阻尼比的平均值, i-LQG控制比H-LQG控制提高了11%, 表明i-LQG控制由于考虑了SMRD非线性动力学、改善了实时阻尼力跟踪能力而具有更高效的控制性能.

4 结论

采用磁流变阻尼器的半主动结构控制系统需要力跟踪控制算法以使磁流变阻尼器的输出阻尼力尽量逼近期望控制力.为提高控制的可靠性和阻尼力跟踪性能, 采用贝叶斯NARX网络技术建立准确表征SMRD非线性动力学且控制导向的模型, 并融入LQG控制系统以充分考虑SMRD动力学.控制试验研究表明, (1) 在H-LQG控制确定的脉冲电压下, SMRD在前屈服区由于零电压摩擦阻尼力的约束、以及在后屈服区由于电压的频繁突变至最大值, 阻尼力跟踪误差较大, 超出期望值15%~30%.(2) 在i-LQG控制下输出幅值小于最大工作限值的连续变化电压信号, 使得SMRD在后屈服区的阻尼力跟踪误差减小为7%~15%, 从而验证了SMRD逆向动力学模型的良好在线预测能力、及其在控制中对SMRD强非线性的有效补偿.(3) 由于i-LQG控制下实时阻尼力跟踪能力的改善, 使得受控结构阻尼比相比于H-LQG控制时提高了11%.因此, 基于SMRD逆向动力学的实时阻尼力跟踪控制能够实现更高效的半主动结构控制性能.