大型桥梁综合技术状况评估是一个复杂的系统工程, 由于评估过程中判断的主观性、统计的局限性和某些因素的不可定量性, 使得桥梁评估存在极大的模糊性和不确定性[1].层次分析法(analytic hierarchy process, AHP)具有实用性、系统性和简捷性等优点[2], 已被广泛应用于桥梁评估的研究中.采用层次分析法对桥梁评估进行研究可以分为5个步骤, 分别为:1) 评估指标选取;2) 评估体系建立;3) 指标权重确定;4) 评估方法研究;5) 评估标准划分.其中, 评估方法研究是桥梁评估工作中的核心内容.
近年来, 桥梁评估研究人员积极引入系统工程的有关理念, 形成了一系列桥梁结构的评估方法, 如模糊综合评估方法、变权综合评估方法, 以及基于神经网络的评估方法等[3-6].然而, 上述评估方法仍存在一定的局限性:模糊综合评估方法中如何选择模糊运算法则、如何合理确定隶属函数等问题似没有得到根本的解决;变权综合评估方法中没有对如何选取符合桥梁劣化规律的变权模式进行讨论;神经网络算法需要大量样本, 若积累的资料少, 评估结果的准确性难以保证.
为解决以上问题, 本文以层次分析法为基础, 尝试将局部变权原理和云理论应用于大跨径悬索桥综合技术状况评估研究中.首先分析了桥梁评估研究中各阶段权重的变化特点, 确定局部变权模式中惩罚水平p和变权幅度c等参数取值, 使得变权效果能够与桥梁劣化规律相适应.然后, 根据现行行业规范确定正态云模型的有效论域, 根据有效论域分别计算云模型的期望值Ex、熵En和超熵He这3个参数, 采用前向云发生器生成正态云图.最后, 以某悬索桥为例进行综合技术状况评定, 论证了方法的可行性和适用性.
1 局部变权原理局部变权原理是在变权原理的基础上发展起来的.相比于传统的变权原理, 局部变权具有较好的可控性和灵活性.汪培庄[7]在1985年首先提出了变权的思想, 强调指标权重应随指标状态值的变化而变化, 以弥补常权决策带来的偏差.随后, 李洪兴[8]给出了变权原理的公理化体系.而局部变权的公理化体系由姚炳学等[9]最早给出.随后, 局部变权原理被广泛应用于智能电网无线传感网络综合性能评估和煤层地质脆弱性评估等研究领域中[10-11].在桥梁评估理论中, 局部变权的应用相对较少.
定义1[9]:给定映射W:[0, 1]m→(0, 1]m, 如果满足条件:
1)
2) 对任意的j∈{1, 2, …, m}, 均存在Tj, Uj∈(0, 1), 且Tj≤Uj, 使得Wj(X)关于xj在[0, Tj]上单调递减, 而在[Uj, 1]上单调递增;
则称向量W(X)为一个m维局部变权向量.
定义2[9]:给定映射S:[0, 1]m→(0, +∞)m, 如果对任意的j∈{1, 2, …, m}, 存在Tj, Uj∈(0, 1), Tj≤Uj, 满足条件:
1)
2) xk≤xi≤Tk∧Ti⇒Sk(X)≥Si(X), Uk∨Ui≤xk≤xi⇒Sk(X)≤Si(X);
则称向量S(X)=(S1(X), S2(X), …, Sm(X))为一个m维局部状态变权向量.
2 云理论简介 2.1 云理论的基本概念自然现象和事物的随机性和模糊性一直是自然科学研究的热点和重点.研究随机现象的主要手段是概率理论, 概率论有坚实的理论基础, 能够很好地表示和处理随机不确定性.模糊集合理论是处理模糊不确定性问题的主要工具, 在理论和应用中取得了诸多成就.云理论是在以上2种理论进行交叉渗透的基础上, 通过特定的算法, 形成定性概念与其定量表示之间的转换模型, 并揭示随机性和模糊性的内在关系.李德毅等[12]最早提出了云理论的概念.随后, 国内外学者[13-14]对柯西、岭形和正态等多种云模型进行分析, 论证了正态云模型的普适性.
设U为一个论域, C是U上的模糊集合, 对于任意的元素x对C的隶属度是有稳定倾向的随机数μ(x), 则隶属度在U上的分布称为隶属云, 记为云C(x), (x, μ(x))称为云滴.
云的数字特征由期望值Ex、熵En和超熵He这3个参数表示.其中, 期望值Ex表示云滴在论域空间分布的期望值;熵En是模糊度的量度;超熵He反映云滴的凝聚程度[15].
2.2 正态云模型正态分布是最重要的概率分布之一, 与其对应的正态云模型具有普遍适用性[13], 本文拟采用正态云模型进行研究.
对于给定的有效论域Ci=[cimin, cimax], cimin和cimax分别为有效论域的下限值和上限值.云模型的期望值为
| ${E_x}_i = {c_{i{\rm{min}}}} + {\theta _i}\left( {{c_{i{\rm{max}}}} - {c_{i{\rm{min}}}}} \right).$ | (1) |
式中:θi为参数, 一般取0.5.对于任意的云滴(x, μ(x)), 由于xi服从正态分布N(Ex, Eni′2), 因此Eni′的取值应满足3σ准则,
| $3{\varepsilon _1}E_{{n_i}}^\prime = {\rm{max}}\left( {{c_{i{\rm{max}}}} - {E_{{x_i}}},{E_{{x_i}}} - {c_{i{\rm{min}}}}} \right).$ | (2) |
式中:ε1≥1.Eni可以看作是其对应云与相邻云Eni′的平均值.又由Eni′服从正态分布N(En, Hei2), 因此Hei的取值也应满足3σ准则,
| $3{\varepsilon _2}{H_{{e_i}}} = {\rm{max}}\left( {E_{{n_i}}^\prime - {E_{{n_i}}},{E_{{n_i}}} - E_{{n_i}}^\prime } \right).$ | (3) |
式中:ε2≥1.为避免状态云过早重叠, 本文中暂取ε1=1, ε2=2.
通过以上分析可知, 只要给定有效论域Ci=[cimin, cimax], 则能够求出云模型的3个参数Ex、En和He.根据期望值Ex、熵En、超熵He和云滴数N, 采用前向云发生器方法(forward cloud transformation, FCT)可以生成正态云图[16], 具体流程框图如图 1所示.
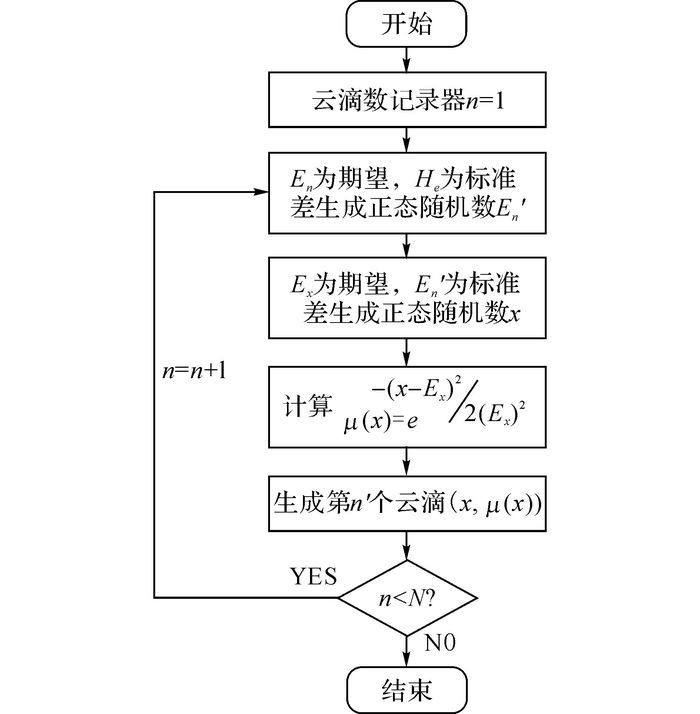
|
图 1 FCT生成正态云图的流程框图 Fig. 1 Flow chart for normal cloud model generation by FCT |
《公路桥涵养护规范》(JTG H11-2004) 和《公路桥梁技术状况评定标准》(JTG/T H21-2011) 为了满足评估对象的普遍适用性, 将桥梁结构划分为上部结构、下部结构和桥面系.但是, 大跨径悬索桥结构形式复杂, 规范的结构划分层次适用性不强, 需要更加精细的层次划分.本文根据大跨径悬索桥的结构层次特点, 综合考虑安全性、耐久性和适用性, 以全面性、简捷性、独立性、客观性和可检性为指标选取原则, 融合人工检查、健康监测和无损检测数据, 建立基于多源数据的综合技术状况评估模型.该评估模型以主缆系统、吊索系统、加劲梁、索塔、锚碇、下部结构和附属设施为一级指标;选择主缆索股索力、主缆线形和主缆索体等31个元素为二级指标.大跨悬索桥综合技术状况评估模型中的具体指标如图 2所示.
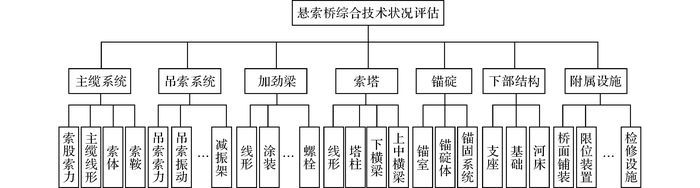
|
图 2 悬索桥综合技术状况评估模型 Fig. 2 Comprehensive technical condition assessment model for suspension bridges |
以上述评估模型指标为基础, 开展专家调查问卷和群组决策分析, 应用遗传算法、PSO-K-MEANS聚类算法和对等共识模型计算各层指标权重, 并与《公路桥梁技术状况评定标准》(JTG/T H21-2011) 中悬索桥的评估指标权重进行比较, 对比结果如表 1所示.
| 表 1 指标权重分配结果对比表 Table 1 Contrast table of index weight distribution |
规范中规定的主缆系统、吊索系统、锚碇和下部结构的权重与本文选取的权重几乎一致.主塔是悬索桥的主要受力构件之一, 规范中的主塔权重仅为0.081, 与主塔的重要性地位相比, 这一权重值似偏小.规范中附属设施的权重值达到了0.204, 但是附属设施并非悬索桥主要受力构件, 规范中给出的权重值与其重要性似不相符.因此可认为, 相对于规范而言, 本文提出的主塔和附属设施权重似更趋合理.
3.2 确定局部变权模式在实际桥梁结构中, 当某个构件出现严重缺陷时, 可能会引起桥梁结构可靠性的急剧下降.本文在指标权重设定上引入惩罚性局部变权方法来体现这一特点.
指数型状态变权向量的特点是决策要求明显、参数设置灵活、模型扩展能力强[17], 故本文拟采用指数型局部变权模式, 其对应的状态变权向量S(X)=(S1(X), S2(X), …, Sm(X))中任意元素Sj(X)的表达式为
| ${S_j}\left( X \right) = \left\{ {\begin{array}{*{20}{l}} {{\rm{exp}}({p_1}\left( {100 - {x_j}} \right)) + c - 1,{\rm{ }}} & {x \in \left[ {{U_1},100} \right];}\\ {{\rm{exp}}({p_2}\left( {{U_1} - {x_j}} \right)) + {\rm{exp}}({p_1}\left( {100 - {U_1}} \right)) + c - 2,} & {x \in \left[ {{U_2},\left. {{U_1}} \right)} \right.;}\\ {{\rm{exp}}({p_3}\left( {{U_2} - {x_j}} \right)) + {\rm{exp}}({p_2}\left( {{U_1} - {U_2}} \right)) + {\rm{exp}}({p_1}\left( {100 - {U_1}} \right)) + c - 3,} & {x \in \left[ {{U_3},\left. {{U_2}} \right)} \right.;}\\ {{\rm{exp}}({p_4}\left( {{U_3} - {x_j}} \right)) + {\rm{exp}}({p_3}\left( {{U_2} - {U_3}} \right)) + } & {}\\ {{\rm{exp}}({p_2}\left( {{U_1} - {U_2}} \right)) + {\rm{exp}}({p_1}\left( {100 - {U_1}} \right)) + c - 4,} & {x \in \left[ {{U_4},\left. {{U_3}} \right)} \right.;}\\ {{\rm{exp}}({p_5}\left( {{U_4} - {x_j}} \right)) + {\rm{exp}}({p_4}\left( {{U_3} - {U_4}} \right)) + {\rm{exp}}({p_3}\left( {{U_2} - {U_3}} \right)) + } & {}\\ {\quad \quad {\rm{exp}}({p_2}\left( {{U_1} - {U_2}} \right)) + {\rm{exp}}({p_1}\left( {100 - {U_1}} \right)) + c - 5,} & {x \in \left[ {0,\left. {{U_4}} \right).} \right.} \end{array}} \right.$ | (4) |
式中:p称为惩罚水平, p值越大, 惩罚效果越明显, 即权重变化速率越快;U是分段区间的上下限值;c为变权幅度, 其值越大, 变权幅度越小, 反之亦然, 本文中暂取c=0.1进行计算.
按照现行行业规范《公路技术状况评定标准》(JTG/T H21-2011), 将指标评分值[0, 100]分为5个区间, 区间限值(U1, U2, U3, U4)分别为(95, 80, 60, 40).当指标评分值x∈[95, 100]时, 惩罚水平较低, 随着评分值的降低, 惩罚水平不断提升, 最后当评分值x∈[0, 40]时, 此时技术状况等级已经达到5类, 且权重达到了较高的水平, 惩罚水平有所降低.本文中暂时取惩罚水平(p1, p2, p3, p4, p5)=(0.003, 0.01, 0.03, 0.07, 0.03) 进行计算.
3.3 局部变权模型参数验证《公路桥涵养护规范》(JTG H11-2004) 中规定, 桥梁评估结果可以用于指导养护维修策略的制定, 具体对应关系如表 2所示.
| 表 2 评估结果与养护策略对应关系 Table 2 Assessment results matchup with maintenancestrategy |
表 2中Dj为技术状况等级, Dr为技术状况评分, S为养护策略.《公路养护技术规范》(JTG H10-2009) 对桥梁养护策略进行了具体的定义.本文设计评估算例, 应用局部变权模型进行评估, 计算各算例中桥梁的技术状况等级, 通过该技术状况等级对应的理论维修策略与《公路养护技术规范》(JTG H10-2009) 中的实际维修策略是否一致来验证局部变权模型中惩罚水平p和变权幅度c取值的合理性, 比较结果如表 3所示.
| 表 3 理论维修策略与实际维修策略对比表 Table 3 Contrast table of theory and actual maintenancestrategy |
通过表 3可知, 根据本文中局部变权模型惩罚水平p和变权幅度c的取值, 计算得到的桥梁评估结果对应的维修策略与规范中规定的维修策略一致, 论证了局部变权模型中参数取值的合理性.
3.4 确定正态云模型参数根据《公路桥梁技术状况评定标准》(JTG/T H21-2011) 的规定, 可以将桥梁状态(包括子指标)划分为5个等级, 可表示为D=(D1, D2, D3, D4, D5).其中(D1, D2, D3, D4, D5)的取值范围分别为[95, 100], [80, 95), [60, 80), [40, 60), [0, 40).有效论域Ci和正态云模型的3个参数取值如表 4所示.根据表 4中的参数, 采用前向云发生器生成1 000个云滴, 形成的正态云模型如图 3所示, 图中A为隶属度.
| 表 4 正态云模型参数取值 Table 4 Parameter value of normal cloud model |
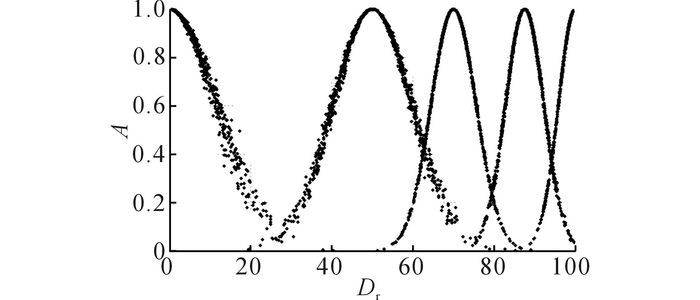
|
图 3 正态云模型 Fig. 3 Normal cloud model |
按照上述局部变权原理和正态云模型理论, 对某悬索桥进行评估计算, 评定结果如表 5所示.表 5中聚合云中的3个参数分别对应于期望值Ex、熵En和超熵He.
| 表 5 某悬索桥评估结果 Table 5 Assessment result of a certain suspension bridge |
从表 5中可知, 该悬索桥综合技术状况评估结果为(53.82, 8.72, 0.44), 即该悬索桥总体综合技术状况评分结果为53.82, 聚合云的熵En=8.72表示该评估结果的模糊程度, 超熵He=0.44表示评估结果的随机程度.根据现行行业规范《公路桥梁技术状况评定标准》(JTG/T H21-2011) 的规定, 桥梁总体综合技术状况评分值53.82对应的桥梁等级为4, 属于4类桥, 对应的维修对策是大修.该悬索桥最严重的病害是某根吊索存在严重的护套破损, 吊索钢丝、锚头和索夹发生普遍锈蚀, 需要对该吊索进行更换.根据《公路养护技术规范》(JTG H10-2009) 的规定, 悬索桥更换吊索属于大修工程, 与本文计算得到的评估结果对应的维修对策一致.
4 结论(1) 提出了适用于悬索桥评估的局部变权模式.本文选择指数型状态变权向量对应的变权模式作为研究对象, 根据现行行业规范《公路桥梁技术状况评定标准》(JTG/T H21-2011) 将指标评分值分为5个部分, 根据试算分别确定了5个部分的惩罚水平(p1, p2, p3, p4, p5)和变权幅度c等参数的取值, 使得各阶段变权效果和桥梁劣化规律相一致.
(2) 建立了适用于桥梁评估研究的正态云模型.本文根据现行行业规范确定了云模型的有效论域, 并根据有效论域确定了云模型中3个参数Ex、En和He的取值, 利用前向云发生器建立了正态云模型.云理论有效地解决了模糊评估方法中隶属度函数难以确定的问题, 将对象的模糊性和随机性进行了有效融合.
(3) 通过算例分析验证了本文提出方法的可行性和适用性.采用本文提出的评估方法对某悬索桥进行评估计算, 对评估结果进行分析发现, 本文提出的评估方法得到的评估结果与实际维修对策相符, 且评估结果能够体现模糊性和随机性.
| [1] | HUANG Q, REN Y, LIN Y. Application of uncertain type of AHP to condition assessment of cable-stayed bridges[J]. Journal of Southeast University:English Edition, 2007, 23(4): 599–603. |
| [2] | SAATY T. Analytic hierarchy process[M]//Wiley StatsRef:Statistics Reference Online. John Wiley & Sons, Ltd, 2014:15-45. |
| [3] | JIAO Y, LIU H, CHENG Y, et al. Fuzzy neural network-based damage assessment of bridge under temperature effect[J]. Mathematical Problems in Engineering, 2014, 2014(1): 1–9. |
| [4] |
兰海, 史家钧. 灰色关联分析与变权综合法在桥梁评估中的应用[J].
同济大学学报:自然科学版, 2001, 29(1): 50–54.
LAN Hai, SHI Jia-jun. Degree of grey incidence and variable weight synthesizing applied in bridge assessment[J]. Journal of Tongji University:Natural Science Edition, 2001, 29(1): 50–54. |
| [5] | SASMAL S, RAMANJANEYULU K. Condition evaluation of existing reinforced concrete bridges using fuzzy based analytic hierarchy approach[J]. Expert Systems with Applications, 2008, 35(3): 1430–1443. DOI:10.1016/j.eswa.2007.08.017 |
| [6] |
任远. 大跨度斜拉桥养护管理系统的数字化研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
REN Yuan. Digitization research on maintenance and management system of long-span cable-stayed bridges[D]. Harbin:Harbin Institute of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10213-2009223796.htm |
| [7] | 汪培庄. 模糊集与随机集落影[M]. 北京: 北京师范大学出版社, 1985: 10-13. |
| [8] |
李洪兴. 因素空间理论与知识表示的数学框架(Ⅷ):变权综合原理[J].
模糊系统与数学, 1995(3): 1–9.
LI Hong-xing. Factor spaces and mathematical frame of knowledge representation(Ⅷ):varied weight principle[J]. Fuzzy Systems and Mathematics, 1995(3): 1–9. |
| [9] |
姚炳学, 李洪兴. 局部变权的公理体系[J].
系统工程理论与实践, 2000, 20(1): 106–109.
YAO B, LI H. Axiomatic system of local variable weight[J]. System Engineering Theory & Practice, 2000, 20(1): 106–109. |
| [10] | WU Q, LI B, CHEN Y. Vulnerability assessment of groundwater inrush from underlying aquifers based on variable weight model and its application[J]. Water Resources Management, 2016, 30(10): 3331–3345. DOI:10.1007/s11269-016-1352-4 |
| [11] | CHEN Z, ZHANG H, HAN D. Research on comprehensive performance assessment for wsn based on anp with equilibrium variable weight and cloud gravity center[J]. China Communications, 2015(S2): 1–9. |
| [12] |
李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J].
计算机研究与发展, 1995, 32(6): 15–20.
LI Di-yi, MENG Hai-jun, SHI Xue-mei. Membership clouds and membership cloud cenerators[J]. Journal of Computer Research and Development, 1995, 32(6): 15–20. |
| [13] |
李德毅, 刘常昱. 论正态云模型的普适性[J].
中国工程科学, 2004, 6(8): 28–34.
LI De-yi, LIU Chang-. yu Study on the university of the noamal cloud model[J]. Chinese Engineering Science, 2004, 6(8): 28–34. |
| [14] | WANG G, XU C, LI D. Generic normal cloud model[J]. Information Sciences, 2014, 280(280): 1–15. |
| [15] | DONG W, ZENG D, SINGH V P, et al. A cloud model-based approach for water quality assessment[J]. Environmental Research, 2016(149): 113–121. |
| [16] | YANG J, LIU H, YU X, et al. Entropy-cloud model of heavy metals pollution assessment in farmland soils of mining areas[J]. Polish Journal of Environmental Studies, 2016, 25(3): 1315–1322. DOI:10.15244/pjoes/61883 |
| [17] |
杨宝臣, 陈跃. 基于变权和TOPSIS方法的灰色关联决策模型[J].
系统工程, 2011(6): 106–112.
YANG Bo-chen, CHEN Yue. Grey relational decision-making model based on variable weight and TOPSIS method[J]. System Engineering, 2011(6): 106–112. |



