开孔板连接件(德文:Perfobond Leiste[1], PBL), 主要是依靠开孔板内的混凝土和横向贯穿钢筋(或仅有混凝土)共同抵抗钢与混凝土之间的作用力.它在承载力和抗疲劳性等方面均优于栓钉连接件, 因而近年来已在混合梁、混合塔、组合拱肋等大跨径桥梁组合结构中得到了较为广泛的应用[2-4].
近年来, 国内外较多学者对PBL连接件的各项力学性能展开了一系列研究, 研究内容主要包括:PBL连接件的极限承载力[5-6]、抗剪刚度[7]、黏结滑移性能[8-9]、抗疲劳性能[10-12]等.然而, 对PBL连接件在承受一定循环次数疲劳荷载后的剩余承载力的研究相对较少, 目前尚没有一个适用的理论模型可用于计算疲劳后PBL连接件的剩余承载力.
根据疲劳累积损伤理论, 结构的每一次加载都会对结构造成不可逆的损伤[13].肖林等[14]在对PBL连接件进行疲劳试验时发现, 在既定循环次数下没有发生疲劳破坏的试件, 实际承载力发生了一定程度的下降.汪炳等进行9个PBL推出试件的试验结果同样表明, PBL连接件的承载力随疲劳循环次数呈非线性下降趋势.
鉴此, 本文基于标准推出试件中带贯穿钢筋的PBL连接件的受力模式, 建立一种PBL连接件在疲劳荷载作用后剩余承载力的计算方法.采用弹性地基梁法分析了PBL连接件在线弹性阶段的受力特征, 推导出在给定疲劳荷载幅值的情况下贯穿钢筋和孔内混凝土的应力幅值.同时基于疲劳累积损伤准则, 计入贯穿钢筋和混凝土在疲劳后的损伤, 进而推导出PBL连接件在一定疲劳次数后的剩余承载力计算模型.最后通过笔者的试验结果对该计算模型进行了验证.
1 基于弹性地基梁法的PBL连接件受力分析有贯穿钢筋的PBL连接件一般由开孔钢板、混凝土、贯穿钢筋共同组成.在实际受力过程中, 其内部受力包括开孔钢板、混凝土和贯穿钢筋之间的摩擦、黏结、挤压、剪切等作用, 受力情况极为复杂.
本文基于标准推出试件, 分析PBL连接件在外荷载作用下的受力特征, 为便于分析, 采用以下假定:1) 不计PBL连接件底部承压的影响;2) 不计开孔钢板与混凝土之间的摩擦;3) 假设PBL连接件在疲劳过程中钢筋和混凝土均处于线弹性范围.
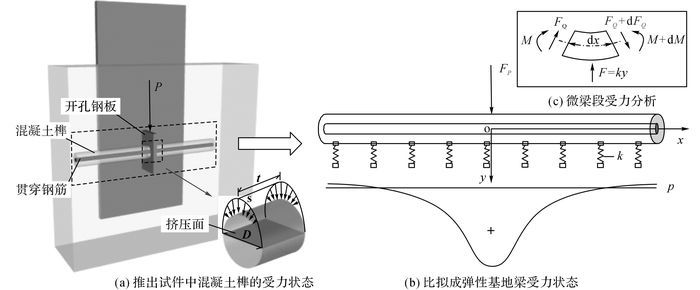
设有横向贯穿钢筋的PBL连接件的受力模式可以简化为开孔钢板将外力传递给中间包裹着钢筋的混凝土榫, 由这个混凝土榫承担水平及竖向剪力, 混凝土榫的直径为开孔板的孔径.这个混凝土榫是一个无穷多次超静定结构, 在实际受力中不仅需考虑到自身变形, 还需考虑底下支撑混凝土的变形状况, 该种受力模式及边界条件与弹性地基梁极为类似, 因而, 在钢与混凝土弹性受力阶段, 该混凝土榫的受力模式可以比拟成弹性地基梁的受力状态, 如图 1(a)所示.
|
图 1 PBL连接件的力学模型 Fig. 1 Mechanical model of PBL connector |
由图 1(b)可知, 单个PBL连接件中带贯穿钢筋的混凝土榫可看成是放置在弹性地基上的无限长梁, 根据文克尔假定[15], 弹性地基梁的地基反力与沉降成正比, 即
| $ F = ky. $ | (1) |
式中:F为地基反力;k为基地弹性系数, 其中k=Ec,Ec为混凝土弹性模量;y为梁的变形.
在如图 1(b)所示的坐标系下, 现取作用力FP右侧其中一无穷小的梁单元, 其长度为dx, 微梁段的受力情况如图 1(c)所示.考虑单元的平衡, 垂直力总和应为零, 其中FQ为竖向剪力, 即
| $ {F_Q} - \left( {{F_Q} + {\rm{d}}{F_Q}} \right) + F{\rm{d}}x = 0, $ | (2) |
则
| $ \frac{{{\rm{d}}{F_Q}}}{{{\rm{d}}x}} = F. $ | (3) |
由于FQ=dM/dx, M为弹性地基梁截面弯矩, 于是式(3) 可以写成
| $ F = \frac{{{{\rm{d}}^2}M}}{{{\rm{d}}{x^2}}}. $ | (4) |
假设混凝土榫和贯穿钢筋处于线弹性阶段, 并满足平截面假定, 则弯矩与曲率成正比, 即
| $ M = - K\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}.}} $ | (5) |
式中:K为混凝土榫和贯穿钢筋组合截面等效抗弯刚度, 可表示为
| $ K = {E_{\rm{c}}}\frac{{\rm{\pi }}}{{64}}\left( {{D^4} - d_s^4} \right) + {E_{\rm{s}}}\frac{{\rm{\pi }}}{{64}}d_{\rm{S}}^4. $ | (6) |
式中:Es为钢筋弹性模量, D为开孔板直径, ds为钢筋直径.
将式(1)、(5) 代入式(4), 整理得到
| $ \frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}} + \frac{k}{K}y = 0, $ | (7) |
引入特征系数β, 并令
| $ \frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}} + 4{\beta ^4}y = 0. $ | (8) |
式(8) 为一四阶常系数线性齐次微分方程, 其通解为
| $ \begin{array}{l} y = \exp \left( {\beta x} \right)\left( {A\cos \beta x + B\sin \beta x} \right) + \\ \;\;\;\;\;\;\exp \left( { - \beta x} \right)\left( {C\cos \beta x + D\sin \beta x} \right). \end{array} $ | (9) |
式中:A, B, C, D为待定常数.
由边界条件分析可知, 当x→∞时, y(x)→0.同时, 由于当x→∞时, exp (βx)→∞, exp (-βx)→∞, 所以
| $ \infty \cdot \left( {A\cos \beta x + B\sin \beta x} \right) \to 0. $ | (10) |
当且仅当A=B=0时, 式(9) 成立, 则式(8) 可简化为
| $ y = \exp \left( { - \beta x} \right)\left( {C\cos \beta x + D\sin \beta x} \right). $ | (11) |
由原点处的对称性可知, 当x=0时, 转角θ=0, 剪力FQ=-FP/2.
由于
| $ \left. {\begin{array}{*{20}{c}} { - C + D = 0,}\\ { - \frac{k}{{2\beta }}\left( {C + D} \right) = - \frac{{{F_{\rm{P}}}}}{2}.} \end{array}} \right\} $ | (12) |
得到
| $ C = D = \frac{{{F_{\rm{P}}}\beta }}{{2k}}. $ | (13) |
进而可求得
| $ y = \frac{{{F_{\rm{P}}}\beta }}{{2k}}\exp \left( { - \beta x} \right)\left( {\cos \beta x + \sin \beta x} \right), $ | (14) |
| $ {F_{\rm{p}}} = \frac{{{F_{\rm{P}}}\beta }}{2}\exp \left( { - \beta x} \right)\left( {\cos \beta x + \sin \beta x} \right), $ | (15) |
| $ {F_Q} = - \frac{{{F_{\rm{P}}}}}{2}\exp \left( { - \beta x} \right)\cos \beta x. $ | (16) |
在第1节中得到了带贯穿钢筋的混凝土榫的受力分布, 本节在给定疲劳幅值(ΔFP)的情况下, 孔内混凝土和钢筋所受的应力幅、对应的疲劳寿命及疲劳损伤.设在常幅疲劳荷载作用下, 单个PBL连接件所受的疲劳荷载上限值为FP, max, 疲劳荷载下限值为FP, min.
2.1 孔洞内混凝土应力幅孔洞内混凝土处于三向受力状态, 荷载作用方向为混凝土主要受压方向, 考虑开孔钢板厚度(t)范围内混凝土的压力, 可由式(15) 反算得到
当荷载上限值时:
| $ \begin{array}{l} 2\int\limits_0^{t/2} {\frac{{{F_{{\rm{P,max}}}}\beta }}{2}\exp \left( { - \beta x} \right)\left( {\cos \beta x + \sin \beta x} \right){\rm{d}}x} = \\ \;\;\;\;{F_{{\rm{P,max}}}}\left( {1 - \frac{1}{2}\exp \left( { - \frac{{t\beta }}{2}} \right)\cos \frac{{t\beta }}{2}} \right). \end{array} $ |
当荷载下限值时:
| $ \begin{array}{l} 2\int\limits_0^{t/2} {\frac{{{F_{{\rm{P,min}}}}\beta }}{2}\exp \left( { - \beta x} \right)\left( {\cos \beta x + \sin \beta x} \right){\rm{d}}x} = \\ \;\;\;\;{F_{{\rm{P,min}}}}\left( {1 - \frac{1}{2}\exp \left( { - \frac{{t\beta }}{2}} \right)\cos \frac{{t\beta }}{2}} \right). \end{array} $ |
由材料力学可知, 处于挤压状态的结构, 其挤压应力应为外力与投影的挤压面之比, 于是
| $ \sigma _{\max }^{\rm{c}} = {F_{{\rm{P,max}}}}\left( {1 - \frac{1}{2}\exp \left( { - \frac{{t\beta }}{2}} \right)\cos \frac{{t\beta }}{2}} \right)/\left( {Dt} \right), $ | (17) |
| $ \sigma _{\min }^{\rm{c}} = {F_{{\rm{P,min}}}}\left( {1 - \frac{1}{2}\exp \left( { - \frac{{t\beta }}{2}} \right)\cos \frac{{t\beta }}{2}} \right)/\left( {Dt} \right), $ | (18) |
| $ \Delta {\sigma ^{\rm{c}}} = \sigma _{\max }^{\rm{c}} - \sigma _{\min }^{\rm{c}}. $ | (19) |
式中:Δσ为疲劳荷载作用下的混凝土应力幅值, σmax、σmin分别为疲劳荷载作用下混凝土最大应力和最小应力.
2.2 贯穿钢筋应力幅孔洞内的贯穿钢筋是以剪为主的受力状态, 由式(16) 可知, 带钢筋的混凝土榫的受剪面的剪力幅值为
| $ \Delta {F_Q} = \frac{1}{2}\exp \left( { - \frac{{t\beta }}{2}} \right)\cos \frac{{t\beta }}{2}\left( {{F_{{\rm{P,max}}}} - {F_{{\rm{P,min}}}}} \right). $ | (20) |
根据假设, 贯穿钢筋和混凝土榫处于线弹性受力阶段, 所以贯穿钢筋和混凝土榫的竖向位移是协调一致的, 即两者具有相同的竖向应变, 因而其剪力分配可按其剪切刚度分配, 则钢筋的应力幅值为
| $ \Delta {\tau _{\rm{s}}} = \Delta {F_Q} \cdot \left( {\frac{{{G_{\rm{s}}}{A_{\rm{s}}}}}{{{G_{\rm{c}}}{A_{\rm{c}}} + {G_{\rm{s}}}{A_{\rm{s}}}}}} \right)/{A_{\rm{s}}}. $ | (21) |
式中:Gs为钢筋剪切模量, As为钢筋面积, Gc为混凝土剪切模量, Ac为混凝土面积.
在钢筋与混凝土剪切模量未知的情况下, 则可下式换算得到
| $ G = \frac{E}{{2\left( {1 + \mu } \right)}}. $ | (22) |
式中:E为钢筋或混凝土弹性模量, μ为钢筋或混凝土泊松比.
2.3 混凝土与钢筋的疲劳寿命关于混凝土的疲劳性能, 已有很多学者做过研究, 本文采用Aas-Jakobsen提出的混凝土抗压疲劳强度计算公式, 该公式应用范围广泛, 被工程界普遍采用[16]:
| $ {S_{\max }} = 1 - \alpha \left( {1 - R} \right)\lg {N_{\rm{c}}}. $ | (23) |
式中:Smax=σmax/fc, fc为混凝土圆柱体抗压强度, 本文考虑到PBL连接件开孔板内的混凝土处于三轴受力状态, 故对fc乘了1.2的提高系数[17];R=σmin/σmax;α为材料常数, 文献[18]根据疲劳试验结果得出, 当疲劳应力比R<0.8时, α可取0.068 5, Nc为混凝土的疲劳寿命.
贯穿钢筋在剪切应力作用下的疲劳计算模型可以参考《公路钢结构桥梁设计规范》(JTG D64-2015) 中提出的剪应力幅疲劳强度曲线[19], 其计算公式为
| $ \left. {\begin{array}{*{20}{c}} {\Delta \tau _{\rm{R}}^5{N_{\rm{s}}} = 2 \times {{10}^6}\Delta \tau _C^5,} & {{N_{\rm{s}}} \le {{10}^8};}\\ {\Delta {\tau _{\rm{R}}} = 0.457\Delta {\tau _{\rm{C}}},} & {{N_{\rm{s}}} > {{10}^8}.} \end{array}} \right\} $ | (24) |
式中:ΔτR为实际构件的剪切应力幅值;Ns为在剪应力幅为ΔτR情况下构件(本文为贯穿钢筋)的疲劳循环次数;ΔτC为疲劳细节类别, 即2.0×106次循环疲劳强度的参考值.
在单剪或双剪的情况下, 对应的疲劳细节类别为100, 即ΔτC=100 MPa.
根据2.1和2.2节计算得到的混凝土和钢筋应力幅, 然后利用式(23) 和(24) 分别可以计算出在给定疲劳幅值的情况下, PBL连接件内的混凝土榫和贯穿钢筋的疲劳寿命.基于Miner疲劳累积损伤理论, 可计算出在等幅荷载作用下, 混凝土和钢筋的损伤累积情况.
| $ {D_{\rm{c}}} = \frac{n}{{{N_{\rm{c}}}}}, $ | (25) |
| $ {D_{\rm{s}}} = \frac{n}{{{N_{\rm{s}}}}}. $ | (26) |
式中:Dc和Ds分别为混凝土和钢筋的疲劳损伤度;n为实际疲劳加载循环次数.
2.4 剩余承载力计算模型PBL连接件疲劳后的剩余承载力计算模型, 主要用来计算在一定疲劳荷载循环次数后, PBL连接件在没有发生疲劳破坏的情况下, 其所剩余的静力承载力, 这里用Fr表示.
PBL连接件的承载力主要由钢筋和混凝土榫共同承担, 在现有规范和学者提出的承载力计算公式中, 通常采用如下的公式形式:
| $ {F_{\rm{v}}} = a{A_{\rm{c}}}{f_{\rm{c}}} + a{A_{\rm{s}}}{f_{\rm{s}}}. $ | (27) |
式中:a和b为拟合系数, fs为贯穿钢筋屈服强度.
式(27) 中, 第1项为孔内混凝土对承载力的贡献, 第2项为贯穿钢筋对承载力的贡献.由此可根据混凝土榫和钢筋各自承担的比例得到在一定疲劳荷载循环次数后, 考虑疲劳累积损伤的PBL连接件剩余承载力计算模型:
| $ \begin{array}{l} {F_{\rm{r}}} = {F_{\rm{u}}} \cdot \left( {\frac{{a{A_{\rm{c}}}{f_{\rm{c}}}}}{{a{A_{\rm{c}}}{f_{\rm{c}}} + b{A_{\rm{s}}}{f_{\rm{s}}}}}} \right) \cdot \left( {1 - {D_{\rm{c}}}} \right) + {F_{\rm{u}}} \cdot \\ \;\;\;\;\;\;\;\left( {\frac{{a{A_{\rm{s}}}{f_{\rm{y}}}}}{{a{A_{\rm{c}}}{f_{\rm{c}}} + b{A_{\rm{s}}}{f_{\rm{s}}}}}} \right) \cdot \left( {1 - {D_{\rm{s}}}} \right) \end{array} $ | (28) |
式中:Fu为PBL静力极限承载.
为得到a和b的取值, 本文参考公路钢结构桥梁规范[19]中的PBL连接件承载力计算公式, 将其除以π/4后, 改写成式(27) 的形式:
| $ {F_{\rm{v}}} = 1.78{A_{\rm{c}}}{f_{\rm{c}}} + 1.53{A_{\rm{s}}}{f_{\rm{s}}}. $ | (29) |
于是得到, a=1.78, b=1.53.
将式(25)、(26) 代入(28), 即可得到与疲劳加载次数n相关的PBL连接件剩余承载力计算公式:
| $ \begin{array}{l} {F_{\rm{r}}}\left( n \right) = {F_{\rm{u}}}\left[ {\left( {\frac{{a{A_{\rm{c}}}{f_{\rm{c}}}}}{{a{A_{\rm{c}}}{f_{\rm{c}}} + b{A_{\rm{s}}}{f_{\rm{s}}}}}} \right)\left( {1 - \frac{n}{{{N_{\rm{c}}}}}} \right) + } \right.\\ \left. {\left( {\frac{{a{A_{\rm{s}}}{f_{\rm{s}}}}}{{a{A_{\rm{c}}}{f_{\rm{c}}} + b{A_{\rm{s}}}{f_{\rm{s}}}}}} \right) \cdot \left( {1 - \frac{n}{{{N_{\rm{s}}}}}} \right)} \right],n < {N_{\rm{c}}},n < {N_{\rm{s}}}. \end{array} $ | (30) |
式中:a=1.78, b=1.53.
可见, 通过公式(30) 可以计算钢筋和混凝土达到疲劳寿命前任意疲劳加载次数下PBL连接件的承载力.当疲劳加载次数大于PBL连接件内部混凝土或钢筋的疲劳寿命时, 该公式将不再适用.图 2给出了PBL连接件剩余承载力的计算流程图.

|
图 2 剩余承载力计算步骤流程图 Fig. 2 Flow chart of calculation steps of residual bearing capacity |
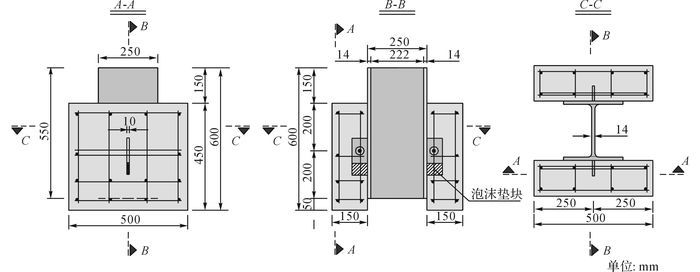
本次推出试件设计主要参考了欧洲规范4中推荐的尺寸及配筋, 如图 3所示, 选用的混凝土强度等级为C50, 构造筋采用φ10 mm的HPB300级热轧钢筋, 钢板选用Q345钢材.PBL连接件设置个数为2个, 开孔钢板的长宽为105 mm×65 mm, 厚度为10 mm, 开孔孔径为35 mm, 孔中贯穿钢筋采用直径为φ12 mm的HPB300级热轧钢筋, 开孔板下方垫有50 mm高的立方体泡沫块以避免混凝土局部承压.在试件混凝土浇筑前, 在钢梁与混凝土接触表面刷油, 以减少钢板与混凝土黏结对试验结果的影响.材料试验测得混凝土的立方体强度平均值为59.7 MPa, 换算成圆柱体强度为49.7 MPa, 弹性模量平均值为3.59×104 MPa.贯穿钢筋的弹性模量为2.06×105 MPa, 屈服强度为365 MPa, 极限强度为508 MPa.
|
图 3 推出试件尺寸及构造 Fig. 3 Dimension and structure of push-out specimen |
推出试验在双通道微机控制电液伺服动静态加载试验系统(JAW-500K)上完成.该系统配有量程为500 kN的低摩擦球铰的电液伺服加载作动器, 可用于静力加载和动力加载.
试验共分2组, 第1组为静载破坏试验, 共包括3个试件, 编号为SPP-1~SPP-3.第2组为剩余承载力试验, 即在经历一定疲劳荷载循环次数后进行静力破坏试验, 试件编号为FPP-1~FPP-3及SFPP-1~SFPP-3.其中疲劳加载方式为往复加载, 疲劳控制波形为正弦波, 加载频率为4 Hz.在此主要考察疲劳荷载比和疲劳循环次数这2个疲劳加载参数对PBL连接件的影响, 具体见表 1.表中,Fs为PBL剩余承载力.由表 1可知, 单个PBL连接件的静力极限承载力均值为133 kN.由试件FPP-1~FPP-3结果可知, 在相同疲劳荷载幅, 相同疲劳循环次数下, 疲劳荷载比越高, 连接件的承载力下降越多;由试件SFPP-1~SFPP-3结果可知, 在相同疲劳幅值, 相同疲劳荷载比的情况下, 连接件的承载力随疲劳循环次数的增加而下降.如图 4所示为PBL推出试件试验加载过程.
| 表 1 单个PBL连接件试验结果 Table 1 Test results for a single PBL connector |

|
图 4 PBL推出试件试验加载过程 Fig. 4 Loading process of the PBL push-out specimen |
值得注意的是, 由于我国公路钢结构桥梁设计规范[19]中并未给出与PBL连接件相关的疲劳细节类别的描述, 这里参照栓钉连接件抗疲劳设计的相关规定:用于组合梁的焊接栓钉对应的疲劳细节类别为90, 即栓钉循环200万次的疲劳强度参考值为90 MPa.由此可知, 栓钉循环200万次对应的疲劳强度设计值占栓钉抗剪承载力设计值的比例为ΔτR·As/Vsu=0.25.在本次试验中, 根据实测PBL连接件的抗剪承载力确定疲劳荷载幅值, 其对应比值参照栓钉的比例0.25.
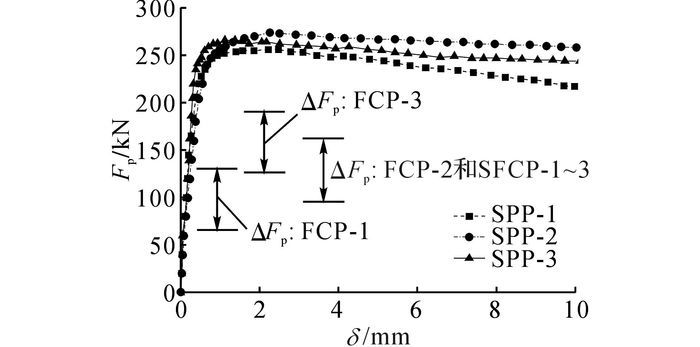
3.2 试验结果图 5给出了试件SPP-1~SPP-3静载试验中的荷载-滑移曲线.图中δ为滑移量, 由图可知, 试件FCP-1~FCP-3及SFCP-1~SFCP-3所设置的疲劳幅值范围(ΔFP)均在试件的线弹性阶段, 因而适用于本文建立的PBL连接件剩余承载力计算模型.
|
图 5 SPP-1~SPP-3的荷载-滑移曲线 Fig. 5 Load-slip curves of SPP-1~SPP-3 specimens |
为验证本文建立的PBL连接件剩余承载力计算模型的正确性, 现以该试验为例, 计算在该试验条件下, PBL连接件在疲劳后的剩余承载力, 并与试验值进行对比.按照图 2的计算流程, 计算求得各PBL连接件的剩余承载力, 其与实际试验值的对比情况如表 2所示.
| 表 2 PBL连接件剩余承载力试验值与计算值对比 Table 2 Comparison of calculated and tested values of residual bearing capacity for PBL connector |
由表 2可知, 试件FPP-1~FPP-3为在相同疲劳循环次数, 不同疲劳荷载比下, PBL连接件的剩余承载力结果, 模型计算值与试验值吻合良好, 且计算值与试验值之比在0.97~0.99之间, 说明计算较实际情况偏于安全.这里需要说明的是, FPP-3在计算混凝土疲劳寿命(式23) 时发现Nc<300万次, 超过了本文公式(30) 的适用范围, 因而未给出计算结果.可见, 在高疲劳荷载比(0.7) 和高循环次数(300万)共同作用下, 易超出本文公式的适用范围.
试件SFPP-1~SFPP-3为在相同疲劳荷载比, 不同疲劳循环次数下的PBL连接件的剩余承载力结果, 其计算值与试验值同样吻合良好.
同时, 对表 2中公式的计算值与试验值的比值进一步统计分析, 得到其均值为0.976, 方差为0.009, 离散系数为0.009.可见, 本文所建立的PBL连接件剩余承载力计算模型的计算结果不仅误差较小, 稳定性好, 且偏于安全.
4 结论本文基于标准推出试件中带贯穿钢筋的PBL连接件的受力模式, 建立一种PBL连接件在疲劳荷载作用后剩余承载力的计算方法.通过理论分析和试验验证, 可得到以下几点结论:
(1) 有贯穿钢筋的PBL连接件内部受力复杂, 本文在合理假定的基础上, 将带贯穿钢筋的混凝土榫比拟成放置在弹性地基上的无限长梁, 利用弹性地基梁法得到其在线弹性阶段的受力分布, 该方法物理意义明确, 具有一定的适用性.
(2) 基于疲劳累积损伤准则, 计入贯穿钢筋和混凝土在疲劳后的损伤, 并根据两者对承载力的贡献比例, 得到了一个与加载次数有关的PBL连接件剩余承载力计算模型, 该模型可计算钢筋和混凝土达到疲劳寿命前任意加载次数下PBL连接件的承载力.
(3) 通过与疲劳后PBL连接件剩余承载力的推出试验结果对比, 表明本文建立的模型计算值与试验值吻合良好, 且偏于安全.
| [1] | VIANNA J D C, COSTA-NEVES L F, VELLASCO P C G D S, et al. Structural behaviour of T-Perfobond shear connectors in composite girders:An experimental approach[J]. Engineering Structures, 2008, 30(9): 2381–2391. DOI:10.1016/j.engstruct.2008.01.015 |
| [2] |
张清华, 李乔, 唐亮. 桥塔钢-混凝土结合段剪力键破坏机理及极限承载力[J].
中国公路学报, 2007, 20(1): 85–90.
ZHANG Qing-hua, LI Qiao, TANG Liang. Fracture mechanism and ultimate carrying capacity of shear connectors applied for steel-concrete joint segment of bridge pylon[J]. Zhongguo Gonglu Xuebao/china Journal of Highway & Transport, 2007, 20(1): 85–90. |
| [3] |
卫星, 李小珍, 李俊, 等. 钢-混凝土混合结构在大跨度连续刚构桥中的应用[J].
中国铁道科学, 2007, 28(5): 43–46.
WEI Xing, LI Xiao-zhen, LI Jun, et al. Using steel-concrete hybrid structure in long-span continuous rigid frame bridge[J]. China Railway Science, 2007, 28(5): 43–46. |
| [4] |
刘荣, 余俊林, 刘玉擎, 等. 鄂东长江大桥混合梁结合段受力分析[J].
桥梁建设, 2010(3): 33–35.
LIU Rong, YU Jun-lin, LIU Yu-qing, et al. Mechanical analysis of joint section of hybrid girder of Edong Changjiang River Bridge[J]. Bridge Construction, 2010(3): 33–35. |
| [5] |
薛伟辰, 代燕, 周良, 等. 开孔板连接件受剪性能试验研究[J].
建筑结构学报, 2009, 30(5): 103–111.
XUE Wei-chen, DAI Yan, ZHOU Ling, et al. Experimental studies on shear behavior of perfobond connectors[J]. Journal of Building Structures, 2009, 30(5): 103–111. |
| [6] |
赵晨, 刘玉擎. 开孔板连接件抗剪承载力试验研究[J].
工程力学, 2012, 29(12): 349–354.
ZHAO Chen, LIU Yu-qing. Experimental study of shear capacity of perfobond connector[J]. Engineering Mechanics, 2012, 29(12): 349–354. DOI:10.6052/j.issn.1000-4750.2011.09.0604 |
| [7] |
郑双杰, 刘玉擎. 开孔板连接件初期抗剪刚度试验[J].
中国公路学报, 2014, 27(11): 69–75.
ZHENG Shuang-jie, LIU Yu-qing. Experiment of initial shear stiffness of perfobond connector[J]. Zhongguo Gonglu Xuebao/china Journal of Highway & Transport, 2014, 27(11): 69–75. |
| [8] | JEONG Y J, KIM H Y, KOO H B. Longitudinal shear resistance of steel-concrete composite slabs with perfobond shear connectors[J]. Journal of Constructional Steel Research, 2009, 65(1): 81–88. DOI:10.1016/j.jcsr.2008.01.031 |
| [9] | CNDIDO-MARTINS J P S, COSTA-NEVES L F, VELLASCO P C G D S. Experimental evaluation of the structural response of Perfobond shear connectors[J]. Engineering Structures, 2010, 32(8): 1976–1985. DOI:10.1016/j.engstruct.2010.02.031 |
| [10] |
张宁, 刘永健, 刘士林. 单孔PBL剪力连接件疲劳性能试验研究[J].
建筑结构学报, 2014, 35(3): 186–192.
ZHANG Ning, LIU Yong-jian, LIU Shi-lin. Experimental study on fatigue behavior of single PBL shear connector[J]. Journal of Building Structures, 2014, 35(3): 186–192. |
| [11] |
欧阳雯欣, 王清远, 石宵爽, 等. PBL剪力连接件的疲劳试验与分析[J].
浙江大学学报:工学版, 2012, 46(6): 1090–1096.
OUYANG Wen-xin, WANG Qing-yuan, SHI Xiao-shuang, et al. Fatigue test and analysis of PBL shear connectors[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(6): 1090–1096. |
| [12] | AHN J H, JEONG Y J, KIM S H. Shear behaviour of perfobond rib shear connector under static and cyclic loadings[J]. Magazine of Concrete Research, 2008, 60(5): 347–357. DOI:10.1680/macr.2007.00046 |
| [13] |
汪炳, 黄侨, 刘小玲. 疲劳荷载作用下栓钉连接件的抗剪承载力退化规律[J].
哈尔滨工业大学学报, 2016, 48(9): 76–82.
WANG Bing, HUANG Qiao, LIU Xiao-ling. Shear capacity degradation law of stud connectors under fatigue loading[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 76–82. DOI:10.11918/j.issn.0367-6234.2016.09.014 |
| [14] |
肖林, 李小珍, 卫星, 等. PBL剪力键的疲劳性能试验研究[J].
土木工程学报, 2015, 48(7): 93–101.
XIAO Lin, LI Xiao-zhen, WEI Xing, et al. Experimental study on fatigue performance of PBL shear connectors[J]. Tumu Gongcheng Xuebao/china Civil Engineering Journal, 2015, 48(7): 93–101. |
| [15] | 龙驭球. 弹性地基梁的计算[M]. 北京: 高等教育出版社, 1981: 15-78. |
| [16] |
李少骏. 中小跨径混凝土桥梁疲劳荷载模型及疲劳性能研究[D]. 杭州: 浙江大学, 2015.
LI Shao-jun. Fatigue load model and fatigue behavior of medium & short span concrete bridges[D]. Zhejiang University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015592064.htm |
| [17] | 中华人民共和国住房和城乡建设部组织. 混凝土结构设计规范[M]. 北京: 中国建筑工业出版社, 2014. |
| [18] | TEPFERS R, KUTTI T. Fatigue strength of plain, ordinary, and lightweight concrete[J]. ACI Journal, 1979, 76(5): 635–652. |
| [19] |
JTG D64-2015. 公路钢结构桥梁设计规范[S]. 北京: 人民交通出版社, 2015. 10: 56-64.
JTG D64-2015. Specifications for design of highway steel bridge[S]. Beijing:China Communications Press, 2015.10:56-64. |



