2. 同济大学 绿色建筑与新能源研究中心, 上海 200092
2. Green Building and New Energy Research Center, Tongji University, Shanghai 200092, China
高校是社会用能大户.随着国家可再生能源政策的支持, 近年来太阳能热水系统在高校浴室得到大力推广应用.高校浴室太阳能系统的主要特点为用水时间集中于傍晚和夜间使用, 用水需求量大;一般采用定时用水、热水增压、恒温供水;夏季热水负荷需求相对较小, 太阳保证率高, 冬季太阳辐射强度减小, 但寒假学生离校, 热水需求也相应下降.因此, 太阳能热水系统在高校中应用具有优势.但不同地区的高校太阳能热水系统的能效不相同, 即使是同一地方, 由于系统参数不同, 也会导致高校浴室太阳能热水系统的能效差别.加之各地的能源价格、太阳能热水系统辅助热源的形式也不一样, 因此对各地高校浴室太阳能热水系统应用的能效、经济和环境效益进行综合评价显得非常重要.
在适应性评价方面, 卢素珍[1]以高层住宅建筑为对象, 分析了在热水负荷动态变化情况下太阳能集热器布置方式、集热面积、水箱容量、辅助热源方式与用户用水方式对太阳能热水系统全年性能影响, 结合天津市某工程案例, 对高层建筑规模化应用太阳能热水系统的经济和环境效益进行了综合分析.罗奎等[2]采用实验测试的方法从集热效率、得热量、太阳能保证率方面对重庆地区太阳能热水适宜性进行了实测研究.王贤君[3]从建筑全寿命周期角度出发, 建立太阳能热水系统经济、环境、社会效益以及综合效益评价模型, 对陕西省太阳能热水系统应用做出了评价.王利珍等[4]依据多属性决策分析方法, 建立了基于能效、经济、社会环保评价因子的居住建筑太阳能光热系统适应性评价模型.国外Cassard等[5]分析全美地区太阳能热水器的节能效益及经济性能, Raisul等[6]研究不同类型太阳能热水系统的经济性.综合分析已有研究发现, 当前研究主要针对居住建筑进行评价, 对高校浴室太阳能热水系统应用适应性评价的研究非常少.评价主要以某个城市进行分析, 缺乏对全国各区域的综合分析.从评价模型来看, 多数综合评价模型中的评价因子权重采用专家咨询法获得, 主观性较强.因此, 本文以高校浴室太阳能热水系统为对象, 引入能效、环境、经济3方面评价指标, 提出基于数量化理论Ⅲ的综合评价模型, 以客观数据为基础进行权重计算, 利用该模型对我国33个省会城市进行评价, 以期为太阳能热水系统在高校浴室中的应用提供理论依据.
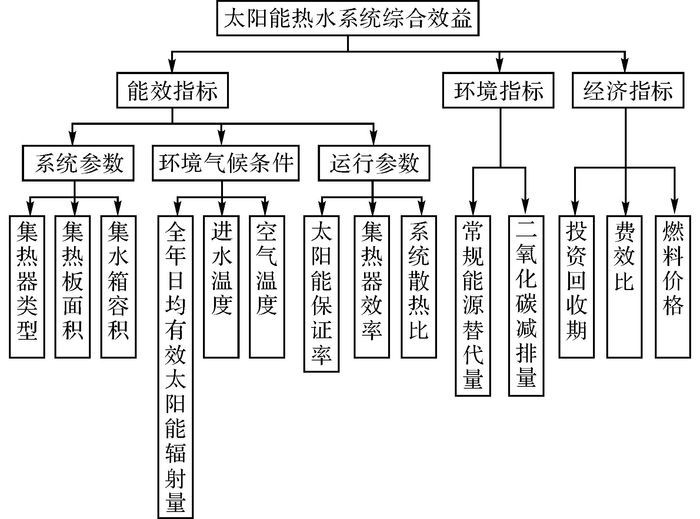
1 太阳能热水系统适应性综合评价指标体系的建立太阳能热水系统适应性综合评价指标体系从能效指标、环境效益、经济效益3个方面建立.能效指标主要用来评估系统运行性能及其性能影响因素, 这与系统节能效益直接相关.环境效益用来评价太阳能热水系统对生态环境影响的积极作用, 是政府推动太阳能热水系统应用的重要驱动因素.经济效益评价反映太阳能热水系统投资前景, 是投资方最为关心的问题.在获得上述3类评价指标的数值后, 对各指标设置相应的权重系数, 最终得到“太阳能热水系统综合效益”评价指标值, 用以整体评价太阳能热水系统应用的适应性情况.如图 1所示列出了太阳能热水系统适用性综合评价指标体系.
|
图 1 太阳能热水系统适应性综合评价指标体系 Fig. 1 Comprehensive evaluation index system for solar water heating system |
从已有研究可知, 环境气候条件、系统参数、运行参数是影响和反映太阳能热水系统运行效率及能效的重要参数, 因此从这3个方面建立能效评价指标[2-4].其中, 环境气候条件指标选取全年日均有效太阳能辐射量、进口水温、空气温度3个参数, 主要因为这3个参数是直接影响太阳能系统效率以及热水负荷的重要气候资源参数[4].系统参数选取集热器类型、集热板面积和水箱容积3个参数, 太阳能集热器类型不同, 系统设计不同, 系统能效也不一样[6, 7].太阳能保证率和集热器效率是直接影响太阳能热水系统运行效率的2个重要指标, 而因系统中热水储备和循环过程中存在热量损失, 因此系统散热比也是系统运行参数.
建筑热水负荷由式(1) 计算, 太阳能保证率由式(2) 计算, 其中全年太阳能集热系统得热量由式(3) 计算, 集热器效率由式(4) 计算[7].
| $ {Q_{\rm{z}}} = {10^{ - 6}}m{c_p}\Delta t. $ | (1) |
式中:Qz为建筑热水负荷(MJ);m为热水消耗量(kg);cp为水的比定压热容(J/kg·℃);Δt为供水水温和进口水温之差(℃).
| $ f = \frac{{{Q_{\rm{j}}}}}{{{Q_{\rm{z}}}}} \times 100. $ | (2) |
式中:f为太阳能保证率(%);Qj为太阳能集热系统得热量(MJ).
| $ {Q_{\rm{j}}} = AH\eta . $ | (3) |
式中:A为集热系统的集热器总面积(m2);H为全年太阳总辐射量(MJ/m2);η为集热器工作效率(%).
| $ \eta = {\eta _0} - U\left( {{t_{\rm{i}}} - {t_{\rm{a}}}} \right)/G. $ | (4) |
式中:η0为测试得出的集热器特性参数, 当ti=ta时的集热器工作效率, 无量纲;U为测试得出的集热器特性参数, 集热器热损系数(W/(m2·℃));ti为集热器工质进口温度(℃);ta为环境空气平均温度(℃);G为太阳辐照度(W/m2).
1.2 环境效益指标对太阳能热水系统的环境效益和经济效益进行评价, 必须设定基准方案.基准方案由常规能源供热水, 如电或燃气.提议方案中由太阳能加辅助热源供热水, 太阳能系统不足供应的部分由辅助热源(燃气辅助加热)等补充.
环境指标通常用常规能源替代量和二氧化碳减排量来体现[2-4, 8].常规能源替代量由公式(5) 计算[7]:
| $ {Q_{{\rm{tr}}}} = \frac{{{Q_{\rm{j}}}}}{{q{\eta _{\rm{t}}}}}. $ | (5) |
式中:Qtr为太阳能热水系统的标准煤常规能源替代量(kg);q为标准煤热值(MJ/kg), 取值为29.307 MJ/kg;ηt为以传统能源为热源时的运行效率, 当传统能源为电时, ηt取0.31, 当传统能源为天然气时, ηt取0.84.
太阳能热水系统的二氧化碳减排量[8]为
| $ {Q_{{\rm{rc}}{{\rm{o}}_2}}} = {Q_{{\rm{tr}}}}{V_{{\rm{c}}{{\rm{o}}_2}}}. $ | (6) |
式中:Qrco2为太阳能热水系统的二氧化碳减排量(kg);Vco2为标准煤的二氧化碳排放因子(kg/kg), 取值为2.47 kg/kg.
1.3 经济效益指标投资回收期、费效比作为常用的经济参数能直接反映项目的投资应用价值, 而地区燃料价格能够在一定程度上代表地区的经济发展水平, 间接影响决策者对太阳能热水器这类替代能源的选择, 因此, 采用投资回收期、费效比、地区燃料价格作为经济效益参数[7].
投资回收期指太阳能热水系统运行N年后节省的总资金与系统增加的初始投资相等时对应的年限, 系统初始投资包括集热器、热水箱等成本.投资回收期采用式(7) 计算[8]:
| $ {N_{\rm{h}}} = \frac{{{c_{{\rm{gz}}}}}}{{{c_{{\rm{sr}}}}}}. $ | (7) |
式中:Nh为太阳能热水系统的静态投资回收年限;czr为太阳能热水系统的初始投资(元);csr为太阳能热水系统的年节约费用(元).
太阳能热水系统的费效比是指太阳能热水系统的增量成本和系统寿命年限内的产热量的比值, 由公式(8) 计算[7]:
| $ {\rm{CB}}{{\rm{R}}_{\rm{r}}} = \frac{{3.6{c_{{\rm{zr}}}}}}{{{Q_{{\rm{tr}}}}}}. $ | (8) |
式中:CBRr为太阳能热水系统的费效比(元/(kW·h)).
2 基于数量化理论Ⅲ的高校宿舍太阳能热水系统综合评价模型数量化理论Ⅲ和因子分析、主成分分析等方法类似, 都是用于分析样品和自变量中起支配作用的主要因素或成分, 并据以实现对样品或变量的分类.所不同的是因子分析和主成分分析通常采用定量变量, 而数量化理论Ⅲ不仅可以包含定量变量, 还可以包含定性变量.它能根据定性数据的实际情况,
用0和1标记反应值, 运用多元分析的原理和方法通过计算将定性数据量化, 从而不需要专家来主观量化定性数据.此外, 该方法同样不需要专家打分来确定各指标值的权重系数, 而是通过样本数据计算得到, 克服了评分法的不足.
数理化理论Ⅲ的基本原理是:1) 每个样本(变量)赋予合适的值, 即样本(变量)的得分.得分相近的样本(变量)可分为一组;2) 同一组内的样本(变量)在某些方面具有相似特性;3) 绝对值较大的变量是作为解释样本分类的重要因素.
在数理化理论Ⅲ中, 假定n个样本数, 其具有相互独立的s个定量变量和m个定性变量:
| $ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} {{\delta _1}\left( 1 \right)}&{ \cdots {\delta _1}\left( m \right)}&{{U_{11}}}& \cdots &{{U_{1s}}}&{}\\ {{\delta _2}\left( 1 \right)}&{ \cdots {\delta _2}\left( m \right)}&{{U_{21}}}& \cdots &{{U_{2s}}}&{}\\ \vdots &{}& \vdots & \vdots &{}& \vdots \\ {{\delta _n}\left( 1 \right)}&{ \cdots {\delta _n}\left( m \right)}&{{U_{n1}}}& \cdots &{{U_{ns}}}&{} \end{array}} \right]. $ | (9) |
式中:X为样本的反应矩阵;δn(m)是定性变量m在样本n中的值, Uns为定量变量在样本n中数值0~1标准化后的值.数理化理论Ⅲ的目的是计算m+s个变量的得分.
| $ \mathit{\boldsymbol{b = }}{\left[ {{b_1},{b_2}, \cdots ,{b_m},{a_1}, \cdots ,{a_s}} \right]^{\rm{T}}}. $ | (10) |
式中:b为m+s个变量的得分向量,b1,b2, bm为m个定性变量得分,a1, a2, as为s个定量变量的得分.
对于每个样本来说:
| $ \mathit{\boldsymbol{Y = }}{\left[ {{Y_1},{Y_2}, \cdots ,{Y_n}} \right]^{\rm{T}}} = \frac{1}{{\left( {m + s} \right)}}\mathit{\boldsymbol{Xb}}. $ | (11) |
式中:Y为样本得分向量.
根据变量的得分b和样本的得分Yn可以对变量和样本进行分类.变量(样本)的得分可被用来表示不同变量(样本)之间的关系.
每个样本是变量得分的集合, 根据组间方差相关比最大原则确定变量得分, 每组的平均得分确定为样本得分, 根据这些原则可以使得分最大程度地反映样本之间的差异.所以数理化理论Ⅲ最关键的问题就是求得向量b和Yn.具体计算方法见文献[8-11].
以太阳能热水系统综合评价指标体系中的各指标为变量, 各省会城市为样本, 变量得分实为各变量的权重, 样本得分可反映各城市中高校宿舍太阳能热水系统的综合效益.根据数量化理论Ⅲ的模型, 可对太阳能热水系统在不同城省会城市高校学生宿舍的应用适应性做出综合评价.模型中变量得分和样本得分利用MATLAB编程求解.
3 太阳能热水系统在高校学生宿舍的应用案例分析 3.1 案例概况选取上海市某综合型高校某一校区的集中浴室为对象进行研究.该校区近8 000名学生, 其中集中浴室每天开放的学生数为3 500人.该案例以太阳能热水系统为集中浴室供热水, 采取集中集热、集中蓄热的方式.此外, 相对于燃煤锅炉而言, 天然气锅炉因其优质高效、环保节能、热源稳定等特点在当前很多实际工程作为辅助热源得以广泛应用[12], 因此案例分析中选取天然气锅炉为辅助热源.案例系统应用原理图如图 2所示, 系统技术参数设置如表 1所示, 考虑到实际铺设条件限制, 太阳能集热器铺满整个建筑屋面的可利用面积.

|
图 2 太阳能热水系统案例应用原理图 Fig. 2 Principle photo of application case of solar water heating system |
| 表 1 集中浴室系统参数 Table 1 System parameter of central bathroom |
根据各省会城市的气象条件和天然气价格、以及系统技术参数, 按照上述综合评价指标体系及各指标计算方法, 获取各省会城市高校浴室太阳能热水系统评价指标值, 以揭示太阳能热水系统应用在各城市高校学生浴室的能效、环境效益、经济效益等方面的情况.指标计算所涉及的各城市环境气候条件, 包括各地的太阳能辐射资源、进水温度和空气温度, 均来自加拿大自然资源机构(natural resources canada)的地面监测站数据和美国国家航空航天局(NASA)的卫星气象资料, 为1983年~2003年的平均值[13].各城市的天然气价格来源于中华人民共和国国家发展和改革委员会网站发布的2014年天然气价格信息[14].
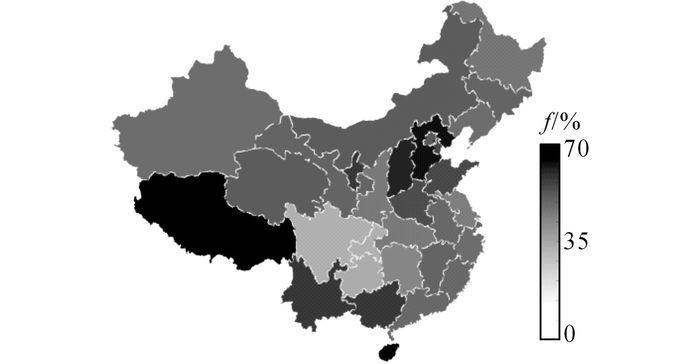
3.2.1 能效指标区域性特征分析各省会城市的太阳能资源存在明显的地域差别, 西部太阳能资源普遍丰富, 华北、东北城市次之, 长江中下游地区太阳能资源一般, 西南部如重庆、成都地区太阳能资源较为匮乏.各城市自来水水温从南往北逐渐降低.各地的太阳能集热系统效率相差不大(各地年均效率在0.26~0.4之间, 标准差仅为0.03), 而太阳能保证率却有较大差别(数值为0.38~0.80, 标准差为0.1), 如图 3所示:海口和拉萨两城市太阳能保证率最高, 分别达到80%和79%, 华北地区、以及香港、澳门、南宁等南方城市的太阳能保证率均在60%以上;其次为长江中下游地区以及东北地区, 如南昌、上海、长春、福州等城市的太阳能保证率为50%~60%;中部地区较低, 其中成都达到最低值, 仅为38%.
|
图 3 能效指标—太阳能保证率 Fig. 3 Energy efficiency index-solar assurance rate |
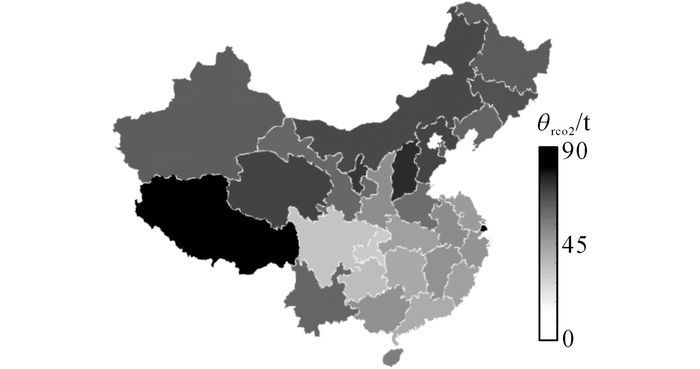
对于各城市的二氧化碳减排量, 西部地区和华北地区的全年二氧化碳减排量较高, 东部地区次之, 长江中下游以及西南部的二氧化碳减排量相对较低, 如图 4所示.而各城市常规能源替代量的变化趋势和二氧化碳减排量一致.
|
图 4 环境指标-全年二氧化碳减排量 Fig. 4 Environmental index-annual emission reduction amount of carbon dioxide |
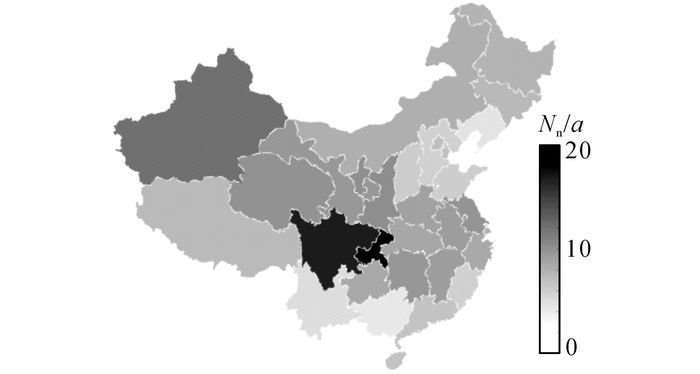
如图 5所示反映了各城市高校太阳能热水系统的投资回收期.总体而言, 南方和华北地区的城市, 太阳能热水系统的投资回收期较短, 大部分城市在8 a以内可收回成本.长江流域、北方城市、以及部分西部地区城市的太阳能热水系统投资回收期次之, 在8~12 a之间.进一步分析可知, 拉萨、银川和乌鲁木齐虽然太阳能资源在所有城市中最为丰富, 但因燃气价格很低, 其投资回收期并不短, 反而处于中等水平.成都和重庆两城市, 因太阳能资源较为缺乏, 燃气价格又非常低, 两城市的投资回收期分别达到了20和23 a, 均达到甚至超过了系统寿命期, 没有投资前景.适当调整辅助热源的燃料价格, 对推广太阳能热水系统有重要影响.
|
图 5 经济指标-静态投资回收年限 Fig. 5 Economic index-Payback period of static investment |
从上述分析发现, 由于我国地域辽阔, 不同区域的高校宿舍太阳能热水系统应用的能效、环境效益、经济效益都存在较大差异.系统能效较好的城市, 应用太阳能热水系统的环境效益也相对优异, 而经济效益则没有表现出和能效、环境效益相似的变化趋势.即因此单一的指标并不能反映太阳能热水系统的应用适应性, 需要对各类指标进行综合考虑.
对于图 1中的综合评价指标, 因各城市案例的集热器类型、集热板面积和集热水箱容积3个指标在各城市的案例中均相同, 同时因案例中的太阳能热水系统为集中集热、集中蓄热型, 且集中浴室的热水管道相对较短, 模型假设水箱和热水管道的保温性能好, 因此各城市案例中太阳能热水系统的系统散热比较小, 且各城市的数值差别非常小, 因此综合评价模型中不考虑上述4个指标.将日均有效太阳能辐射量、温度、气温、集热器效率、太阳能保证率、常规能源替代量、二氧化碳减排量、投资回收期和费效比这10个指标因子属性值作为评价参数, 按照数量化Ⅲ的综合评价模型, 对各省会城市高校集中浴室太阳能热水系统适应性进行综合评价.
根据数量化理论Ⅲ的原理, 变量得分b实为模型特征根所对应的特征向量, 类似于主成分分析中得出的主因子, 可以代表所有变量的贡献度.当取一个特征向量所反映的变量贡献度不高时, 可以取2个或多个特征向量.模型计算所得的特征根中选取最大的2个特征根λ1和λ2时, 其对应的贡献度总和已达到85.2%, 认为其能够代表 80%以上的评价因子的信息, 因此, 选取特征根λ1、λ2和对应的变量得分向量b进行分析, b向量中的每个变量得分值代表各评价指标的权重, 计算结果如表 2所示.
| 表 2 太阳能热水系统各评价指标权重 Table 2 Evaluation index weight of solar water heatingsystem |
各评价指标权重的绝对值越大, 对判定热水系统适应性等级的影响就越大.根据中评价指标的权重值, 确定对综合效益等级判定有重要影响的评价因子有:日均有效太阳能辐射量、费效比、二氧化碳减排量、太阳能保证率、常规能源替代量.同理, 根据中评价指标的权重值, 确定对综合效益等级判定有重要影响的评价因子有:进水温度、气温、集热器效率、燃料价格.
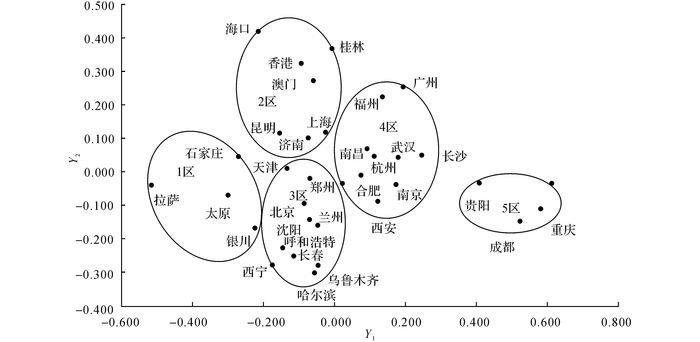
由于和呈线性相关, 根据特征向量的取值(即为各评价指标的权重), 以及各指标在各城市中的取值, 可以得到各样本的得分(即太阳能热水系统在各城市高校学生宿舍中应用的综合效益得分), 如图 6所示.根据各样本得分和, 可将样本划分为5类:
|
图 6 太阳能热水系统在各城市高校学生宿舍中应用的综合效益得分 Fig. 6 Comprehensive benefits scoring of solar water heating system in college student dormitory in each city |
第1类:拉萨、太原、石家庄、银川.这4个城市太阳能资源丰富(日均太阳能辐射量为15.8~21 MJ/(m2·天));进水水温较低导致集热器效率在所有城市中相对较高;太阳能保证率也较高(66%~80 %);全年CO2减排量高(64~83 t), 全年标准煤常规能源替代量高(38×103~48×103 kg);但城市天然气价格低(分别为1.5、2.1、2.4、1.4元/m3), 导致系统投资回收期在各省会城市中略偏长(7~12 a回收).太阳能热水系统在这4个城市的高校学生宿舍中应用的综合效益最好.
第2类:海口、香港、南宁、澳门、昆明、济南、上海.这7个城市的太阳能资源也较丰富(各城市日均太阳能辐射量高于14 MJ/(m2·d));系统进水水温偏高导致集热器效率相对较低;但因太阳能资源丰富, 太阳能保证率较高(60%~75%), 全年CO2减排量比较高(40~60 t), 全年标准煤常规能源替代量(28×103-40×103 kg)仍较高;同时这些城市的天然气价格较高(2.2~3.1元/m3), 导致系统投资回收期比1类城市略短(5~10 a回收).综合而言, 太阳能热水系统在这4个城市的高校学生宿舍中应用的综合效益也较高, 适合应用.
第3类:天津、郑州、沈阳、北京、兰州、呼和浩特、西宁、长春、乌鲁木齐、哈尔滨.这10个城市的太阳能资源略低于2类城市, 但集热器效率在所有城市中最高;太阳能保证率、全年常规能源替代量和全年CO2减排量比上述2类城市略低;各城市天然气燃料价格有高有低, 其系统投资回收期在5~12 a之间.综合而言, 将太阳能热水系统用于这些城市的高校学生宿舍, 有一定的综合效益和应用前景.
第4类:福州、广州、南昌、杭州、武汉、长沙、合肥、南京、西安.这9个城市的日照辐射量基本在11.3~12.6 MJ/(m2·d)之间;集热效率相对较低;太阳能保证率在46%~56%之间;全年CO2减排量基本在30~45 t之间, 全年标准常规能源的替代量基本在20×103-30×103 kg之间;投资回收期在7~12 a之间.太阳能热水系统可以应用于这些城市的高校学生宿舍.
第5类:贵阳、成都、重庆.这3个城市日均辐射量较低, 集热器效率也低, 太阳能保证率、全年常规能源替代量和全年CO2减排量也均较低;重庆和成都两城市的天然气价格也很低(仅为1.7元/m3和1.9元/m3), 投资回收期在20 a以上.有上述分析可知, 该3个城市在高校学生宿舍中不适合应用太阳能热水系统.
4 结语近年来, 随着可再生能源的大力推广, 太阳能热水系统在热水需求量大的建筑中逐渐普及, 各城市高校也纷纷为学生浴室安装太阳能热水系统, 而其应用效益却缺乏综合评估.本研究从能效、环境效益和经济效益3方面建立了太阳能热水系统综合效益评价指标体系, 在此基础上, 利用数量化理论Ⅲ, 建立以天然气为辅助热源的高校学生浴室太阳能热水系统适应性评价模型, 并对我国33个省会城市的高校学生集中浴室太阳能热水系统适应性进行综合评价.从评价结合可知, 前4类城市均可将太阳能热水系统应用于高校学生集中宿舍, 其中第1类和第2类城市综合应用效益较高, 第3类城市有一定的应用前景;而第5类城市不合适应用太阳能热水系统.大部分城市的适应性综合评价值和当地太阳能资源丰富程度和太阳能利用率相对应, 当太阳能资源适中时, 环境及经济效益成为决定综合评价等级的重要依据.考虑到辅助加热设备的自身安全性、节能环保效益等因素, 越来越多的太阳能热水工程开始选用空气源热泵、地源热泵、工业余热等作为辅助热源, 因此在未来市场上, 以天然气为辅助热源的应用市场份额将有所降低, 辅助热源形式将多样化.而该模型能较好地反馈能源价格、太阳能资源、系统形式及性能等各种因素的影响, 也能为其他辅助热源的应用分析提供方法支持.
| [1] |
卢素贞. 高层建筑规模化应用太阳能热水系统研究[D]. 天津: 天津大学2008: 54-65.
LU Su-zhen. Research on large-scale solar water heating system applied on the High building[D]. Tianjin:Tianjin University School of Mechanical Engineering, 2008:54-65. http://cdmd.cnki.com.cn/Article/CDMD-10056-2009071539.htm |
| [2] |
罗奎, 丁勇, 叶强. 重庆地区太阳能热水应用适宜性分析[J].
重庆建筑, 2014(6): 60–62.
LUO Kui, DING Yong, YE Qiang. Suitability analysis of solar water heating in Chongqing[J]. Chongqing Architecture, 2014(6): 60–62. |
| [3] |
王贤君. 太阳能热水系统在建筑全寿命期的综合效益评价研究[D]. 西安: 西安建筑科技大学, 2013: 21-51.
WANG Xian-jun. Comprehensive benefit evaluation research of solar water heating system in building's whole life period[D]. Xi'an:Xi'an university of architectural science and technology, 2013:21-51. http://cdmd.cnki.com.cn/Article/CDMD-10703-1014010755.htm |
| [4] |
王利珍, 谭洪卫, 庄智, 等. 基于MADM方法的太阳能光热系统区域适应性评价[J].
太阳能学报, 2014, 35(4): 649–655.
WANG Li-zhen, TAN Hong-wei, ZHUANG Zhi, et al. Regional adaptability evaluation of solar thermal system based on multiple attribute decision making method[J]. Acta Energiae Solaris Sinica, 2014, 35(4): 649–655. |
| [5] | CASSARD H, DENHOLM P, ONG S. Technical and economic performance of residential solar water heating in the United States[J]. Renewable and Sustainable Energy Reviews, 2011(15): 3789–3800. |
| [6] | RAISUL M I, SUMATHY K, SAMEE U K. Solar water heating systems and their market trends[J]. Renewable and Sustainable Energy Reviews, 2013(17): 1–25. |
| [7] |
GB/T50801-2013. 再生能源建筑应用工程评价标准[S]. 北京: 中国建筑工业出版社, 2013
GB/T50801-2013. Renewable energy construction and application engineering evaluation standard[S]. Beijing:China Architecture & Building Press, 2003 |
| [8] | 董文泉, 周光亚, 夏立显. 数量化理论及其应用[M]. 长春: 吉林人民出版社, 1979: 1-136. |
| [9] |
罗晓明, 俞科群. 数量化理论在马瑙山矿突水危险性评价中的应用[J].
采矿技术, 2004, 4(3): 26–28.
LUO Xiao-ming, YU Ke-qun. Quantification theory used in water inrush risk assessment of the manao mine mountain[J]. Mining Technology, 2004, 4(3): 26–28. |
| [10] |
王道林. 河流污染状况分类的数学模型[J].
山东矿业学院学报:自然科学版, 1999, 18(2): 116–119.
WANG Dao-lin. The mathematical model of river pollution status classification[J]. Journal of Shandong University of Science and Technology:Natural Science, 1999, 18(2): 116–119. |
| [11] |
吴财芳, 秦勇, 张许良. 数量化理论Ⅲ在瓦斯突出预测敏感地质指标筛选中的应用[J].
工程地质学报, 2005, 13(2): 263–268.
WU Cai-fang, QIN Yong, ZHANG Xu-liang. Quantification theory Ⅲ used in the sensitive geological index screening for gas outburst prediction[J]. Journal of engineering geology, 2005, 13(2): 263–268. |
| [12] |
刘品, 何雪冰. 关于燃气锅炉应用的几点探讨[J].
山西建筑, 2010, 36(29): 162–163.
LIU Pin, HE Xue-bing. Discussion on the operation of gas-fired boiler[J]. Shanxi Architecture, 2010, 36(29): 162–163. DOI:10.3969/j.issn.1009-6825.2010.29.100 |
| [13] | Natural Resources Canada. Clean Energy Project Analysis RETScreen Engineering & Cases Textbook-solar water heating project analysis charpter (Third Edition).[EB/OL].(2003-6-16)[2017-6-26].http://publications.gc.ca/collections/collection_2007/nrcan-rncan/M39-101-2003E.pdf http://publications.gc.ca/collections/collection_2007/nrcanrncan/M154-13-2005E.pdf |
| [14] |
国家发展改革委. 国家发展改革委关于调整天然气价格的通知发改价格[2013] 1246号[EB/OL]. (2013-06-28)[2017-06-26]. http://jgs.ndrc.gov.cn/zcfg/201306/t20130628_748124.html
National Development and Reform Commission Notice about Adjusting Gas Price Issued by National Development and Reform Commission[2013] 1246.[EB/OL]. (2013-06-28)[2017-06-26]. http://jgs.ndrc.gov.cn/zcfg/201306/t20130628_748124.html |


