2. 杭州地铁集团有限责任公司, 浙江 杭州 310020;
3. 上海建工集团股份有限公司, 上海 201114;
4. 浙江省交通规划设计研究院, 浙江 杭州 310002;
5. 温州市交通投资集团有限公司, 浙江 温州 325000
2. Hangzhou Metro Group Limited Company Co., Ltd., Hangzhou 310020, China;
3. Shanghai Construction Group Limited Compamy., Ltd., Shanghai 201114, China;
4. Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou 310002, China;
5. Wenzhou Communication Investment Group Limited Company, Wenzhou 325000, China
我国越来越多的城市开始修建地铁以缓解城市的交通压力.而地铁的开通则带动了沿线房地产市场的发展, 很多高大的建筑群修筑在地铁隧道沿线或甚至位于上方.建筑基坑开挖出的土体经常违规堆载在地铁隧道上方的地面上.大面积的堆载会对已有的盾构隧道结构产生影响, 严重时会使得隧道的管片开裂, 接头防水失效.杭州市地铁1号线某区间隧道管片因为上方大面积的堆载而产生了大量裂缝, 同时由堆载引起的沿纵向不均匀沉降也对隧道的安全构成了极大的威胁.因此对堆载作用下隧道管片以及接头的受力变形进行分析是极为必要的.
在研究地面堆载对隧道结构的影响上, 前人工作主要集中在以下2个方面.1) 在堆载作用下隧道的纵向变形, 主要是基于弹性地基梁的理论, 将盾构隧道简化为无限长的弹性地基梁, 然后利用解析的方法推导出隧道在均布荷载或地面堆载下的纵向变形曲线[1-4].2) 将堆载以及隧道简化为平面应变的问题, 然后采用弹性理论, 得到隧道结构在横断面上的受力以及变形[5-6].
盾构隧道是一个由螺栓连接各管片组成的三维拼装结构, 无论是弹性地基梁法还是平面应变方法都不能真实反映出盾构隧道接头处的响应, 尤其是隧道纵向的响应.随着计算机的发展, 管片间及与接头间的相互作用可以通过引入三维有限元接触界面实现, 同时对隧道管片间接头的模拟也更为细致.Blom等[7], 张海波等[8], 陈俊生等[9], Mo等[10], Shi等[11], 王立忠等[12-14], 采用考虑各管片间、接头间相互作用的三维隧道模型对隧道结构的响应进行研究, 并取得了一定的成果.王立忠课题组的主要做法是将每环拼装结构等效为均质圆环, 环与环之间采用螺栓连接, 然后三维分析.这样既减少了计算工作量, 又反映了盾构隧道主要纵向特性.
本文建立了地面堆载对下方隧道管片及环缝接头影响的三维数值分析方法, 并将该方法应用于杭州地铁1号线某区间隧道受堆载作用影响的工程实例分析中, 研究得到了隧道管片及接头在堆载作用下的三维响应, 揭示了隧道接头和管片的变形以及受力规律, 并通过与现场监测结果对比, 验证了三维数值分析方法的合理性.本文成果可以为地铁保护提供一定依据.
1 地面堆载对隧道结构影响分析模型 1.1 隧道结构计算模型地面堆载对下方隧道管片及环缝接头影响的三维隧道计算模型如图 1所示, 为了较为精细地模拟隧道环缝接头以及管片的力学行为, 在数值分析计算中采用荷载-结构的计算模型.该隧道模型沿环向通过引入环向等效刚度系数η将隧道简化为均质环, 沿纵向环与环则通过纵向螺栓加以连接.隧道计算长度L, 外半径R, 内半径r以及环宽d均根据具体工程进行相应取值.
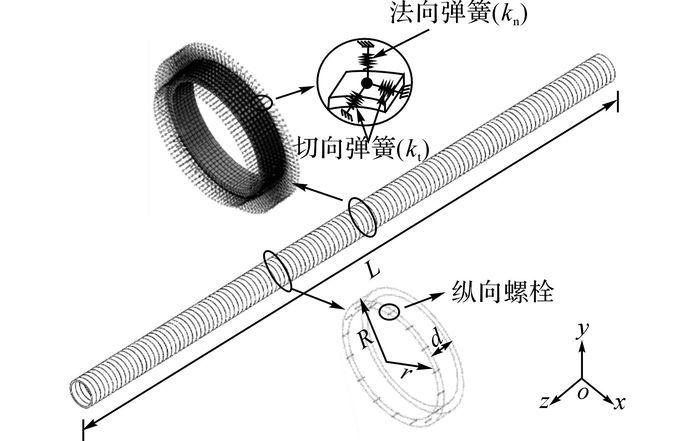
|
图 1 隧道结构计算模型 Fig. 1 Calculation model of tunnel structure |
模型中管片和纵向螺栓均采用实体单元进行模拟.管片间的连接通过将纵向螺栓嵌入2个相邻的管片中来模拟.管片间设置接触面, 接触面间的相互作用关系为面与面之间能够传递压力和剪力, 但不能传递拉力, 当面与面之间压力为0时, 2个面分开.
隧道与土之间的相互作用通过引入地层弹簧k来实现, 地层弹簧采用只受压不受拉的非线性三向(包括一个法向弹簧kn、2个切向弹簧kt)全周模式, 即土体与隧道接触压力为0时弹簧不提供约束.地层弹簧具体表述形式见图 2.其中其中F为弹簧受力, u为弹簧变形, 在弹簧拉伸阶段, 弹簧刚度为0, 在弹簧压缩阶段, 弹簧刚度为一定值.

|
图 2 非线性地层弹簧 Fig. 2 Nonlinear ground spring |
在堆载前, 土体对隧道的压力如图 3(a)所示, 图中pv1为上覆土压力, py1为隧道底部的土压力, 由静力平衡得到.土层的水平压力px认为是随着深度线性变化的, 通过竖向土压力乘以水平土压力系数λ得到.

|
图 3 堆载前后隧道受荷模型 Fig. 3 Load-tunnel model before and after surface surcharge |
在堆载后, 地面荷载将通过土体传递到隧道结构上, 作用在隧道上的压力将会发生变化, 通过引入应力调整系数α和β, 建立起堆载作用下的隧道受荷模型, 如图 3(b)所示.其中隧道底部附加反力由土弹簧单元提供, 因此底部荷载py1维持不变.系数α和β的计算, 通过建立隧道土体的三维有限元模型(此时隧道采用均质连续模型), 计算在堆载前后隧道上所受土压力的变化, 得到系数α和β沿隧道纵向的分布, 然后再将荷载施加到1.1节中的隧道结构计算模型上进行精细化分析.
1.3 α和β计算方法及验证为了介绍α和β的计算方法以及对影响α和β的参数进行分析, 特给定一个算例.算例参数如下:如图 4所示, 模型长120 m, 宽100 m, 高50 m.假定地面堆载p=60 kPa, 荷载沿隧道纵向长度为b, 沿隧道横向长度为a, 为计算简便, 假设荷载作用在地铁隧道正上方.地铁隧道外径D=6.2 m, 内径d=5.5 m, 管片采用C50混凝土.隧道上覆土厚度h=10 m.为简化计算分析, 计算采用单一土层进行.计算选取杭州市区典型砂质粉土层, 即隧道所处土层, 土体采用摩尔-库伦本构模型, 其具体物理力学参数如表 1所示, 其中ρ、μ、E、c、φ分别为土体密度、泊松比、弹性模量、黏聚力和内摩擦角.

|
图 4 算例模型示意图 Fig. 4 Numerical model for example |
| 表 1 土层物理力学参数 Table 1 Physical and mechanics parameters of soil |
隧道考虑为连续介质模型, 采用弹性本构, 根据Blom等[7]、Liao等[15]、吴庆等[16]研究成果, 盾构隧道环向等效刚度系数取为0.7, 纵向等效刚度折减系数取为0.01.将衬砌的本构模型取为线弹性的横观各向同性, 即隧道在横向的弹性模量一致E1=E3=2.415×1010 Pa, 沿纵向弹性模量E2=3.45×108 Pa.模型中考虑隧道与土体之间的接触关系, 隧道与土体在法向采用硬接触, 在切向采用库伦摩擦接触.计算采用三维弹塑性分析, 土体与隧道均采用三维实体单元.
模型上部模拟地表的自由边界, 下部边界施加法向和切向的约束, 前、后、左、右边界施加法向约束.
1.3.1 α和β计算方法简介对于系数α的计算方法, 如图 5所示, 当开挖完成后, 提取隧道上方竖向土压力值P1~P13, 然后在施加地面堆载后, 再次提取隧道上方土压力值P1′~P13′, α通过下式进行计算:

|
图 5 α提取技术示意图 Fig. 5 Schematic diagram of α extraction |
| $\alpha = \frac{{\left( {P1\prime - P1} \right) + \left( {P2\prime - P2} \right) + \cdots \left( {P13\prime - P13} \right)}}{{13p}}.$ | (1) |
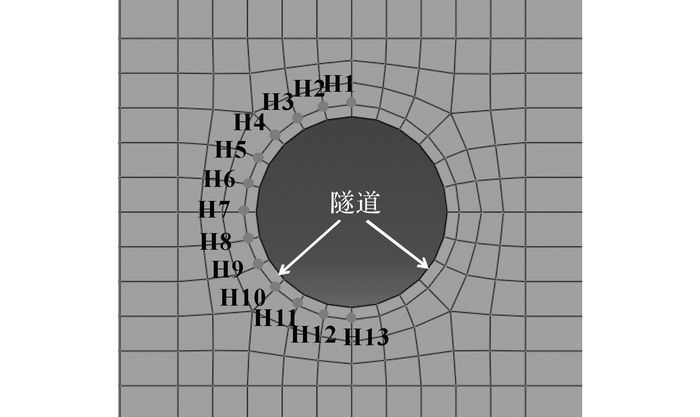
由于侧向附加应力沿深度变化不均, 因此对于β的计算方法则与α的计算方法稍有不同, 如图 6所示.首先是在隧道开挖完成后提取隧道侧方土压力值H1~H13, 然后在施加地面堆载后, 再次提取隧道侧方土压力值H1′~H13′, β则通过下式进行计算:
| $\beta = \left( {\frac{{H1\prime }}{{H1}} + \frac{{H2\prime }}{{H2}} + \cdots + \frac{{H13\prime }}{{H13}}} \right)/13 - 1.$ | (2) |
|
图 6 β提取技术示意图 Fig. 6 Schematic diagram of β extraction |
α和β的计算方法以及大小决定着隧道结构在地面堆载作用下的受力形态及性能.为了验证α和β计算方法以及取值的合理性, 选取算例中隧道中间环, 比较其在荷载-结构和地层-结构方法下的弯矩和轴力.
假定隧道埋深h=10 m, 堆载宽度a=4h=40 m.根据1.3.1节的计算方法, 可以得到隧道中心环α和β分别为0.58和0.10.将α和β代入到堆载作用下隧道荷载-结构模型中(其中地层弹簧系数k根据隧道所处地层以及《地基与基础》[17]取为10 000 kN/m3), 计算隧道的弯矩和轴力, 并与地层-结构方法下隧道中间环的弯矩和轴力进行对比.其中隧道中心环(三维实体单元)的弯矩和轴力是基于ABAQUS后处理里的free body cut功能, 选中相应的截面, 直接提取数据得到的.free body cut功能的基本原理就是对目标截面中每个三维实体单元内高斯积分点上的应力作积分, 得到相应的弯矩和轴力.
图 7给出了地层-结构方法下隧道中心环在堆载前后弯矩(M)和轴力(F)对比图, 其中θ为角度, 从隧道拱顶逆时针开始, 弯矩以内部受拉为正值.从图中可以看出, 在堆载前, 隧道顶部以及底部都为正弯矩, 而负弯矩发生在腰部, 说明隧道在堆载前处于横椭圆变形状态.而在堆载后, 隧道顶部、腰部以及底部的弯矩都有一个较大的增长, 说明隧道在堆载作用下横椭圆化变形加剧.由此可以得到因地面堆载引起的土体竖向附加应力要远大于侧向附加应力.
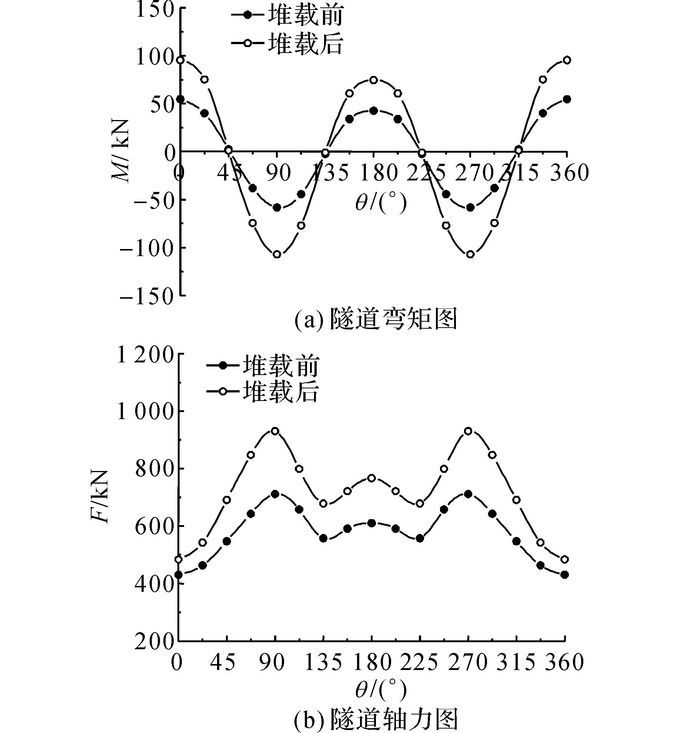
|
图 7 地层-结构方法下隧道堆载前后弯矩以及轴力分布图 Fig. 7 Bending moment and axial force of tunnel before and after surface surcharge based on stratum structure method |
图 8给出了地面堆载后, 隧道中心环在荷载-结构法和地层-结构法下弯矩和轴力对比图, 从隧道拱顶逆时针开始, 弯矩以内部受拉为正值.从图中可以看出, 荷载-结构法计算得到的弯矩和轴力分布与地层-结构法计算所得到的在趋势和大小上有着很好的吻合.荷载-结构法所得到的结果稍大于地层-位移法, 但是两者间的误差基本在10%以内, 因此在一定程度上可以证明1.3.1节α和β计算取值的可行性和合理性, 为后续分析奠定了基础.
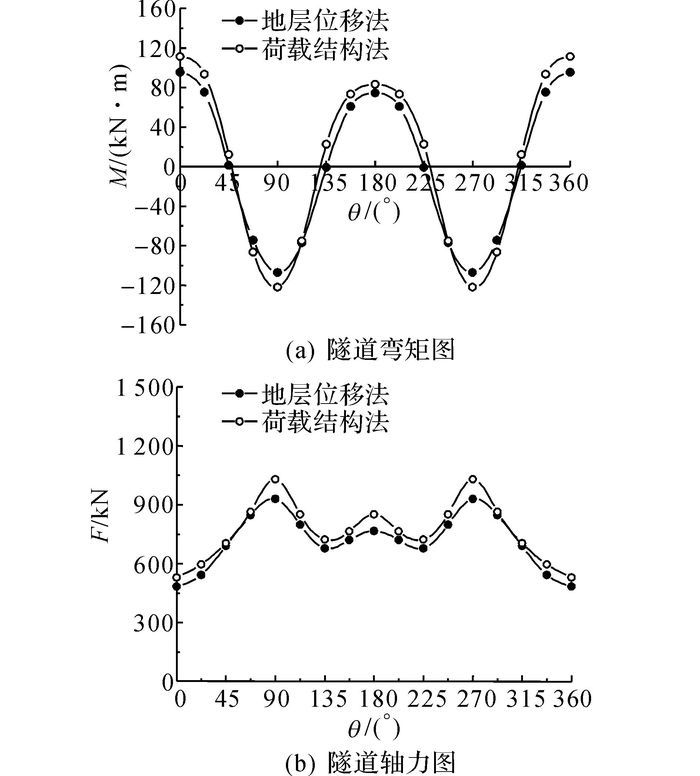
|
图 8 荷载-结构法与地层-结构法弯矩及轴力分布对比 Fig. 8 Comparison of bending moment and axial force between load-structure method and stratum structure method |
杭州地铁1号线是浙江省首条地铁线路, 为连接中心城核心区与江南、临平、下沙副城中心区的骨干线.运营监测单位于2012年在1号线某区间上方待开发地块上发现了大面积的堆土.图 9(a)和(b)分别给出了隧道与地面堆土在纵断面和横断面上的位置关系示意图.从图中可以看出堆土面积在1 600 m2左右, 堆土最大高度则达到了6 m左右.

|
图 9 隧道与地面堆载关系位置示意图 Fig. 9 Schematic diagram of relationship between tunnel and surface load |
该区间地铁隧道埋深为7.5 m, 主要处于③ 层砂质粉土中, 其中隧道管片采用C50混凝土, 内径为5.5 m, 外径为6.2 m, 管片厚0.35 m, 宽1.2 m.隧道在环向由6块管片组成, 沿纵向采用错缝拼装的模式.在环向和纵向分别采用12个和16个M30螺栓进行连接.
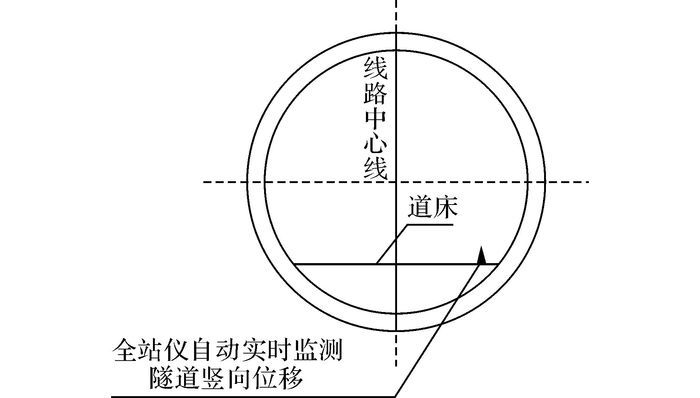
由于堆土的影响, 监测人员进入隧道对管片内侧进行了观测, 在局部隧道内侧顶部发现了沿隧道纵向的裂缝, 如图 10所示, 同时为了保证隧道的安全, 运营监测部门对于堆载下隧道的纵向沉降进行了监测, 监测范围共150 m(也就是125环), 每5环布置一个监测断面, 总共26个监测断面.监测断面示意图如图 11所示, 沉降监测采用全站仪自动实时监测, 监测点布置在隧道下部道床上.

|
图 10 现场管片顶部裂缝 Fig. 10 Crack on top of segment |
|
图 11 监测断面示意图 Fig. 11 Cross-section diagram of monitoring |
隧道结构选取如图 1所示的的计算模型, 根据工程实际和现场监测实际情况, 隧道计算模型长度L取为150 m, 管片外径R取为3.10 m, 内径r取为2.75 m, 宽度d=1.2 m.隧道环向等效刚度系数η取为0.7, 将每环拼装结构等效为均质圆环.地层弹簧系数k根据隧道所处地层以及《地基与基础》[17]对于基床系数k的取值, 在本模型中取为10 000 kN/m3.模型中管片及螺栓均采用弹性本构, 详细物理力学参数如表 2所示.
| 表 2 管片、螺栓参数取值 Table 2 Parameters of segment and bolt |
在堆载前, 土体对隧道的压力通过总应力法来计算.本文中水平土压力系数λ根据《隧道标准规范(盾构篇)及解说》[18]取为0.65.计算中的其他参数如下:pv1=141.5 kN/m2, py1=154.1 kN/m2, px1=91.9 kN/m2, px2=166.9 kN/m2.
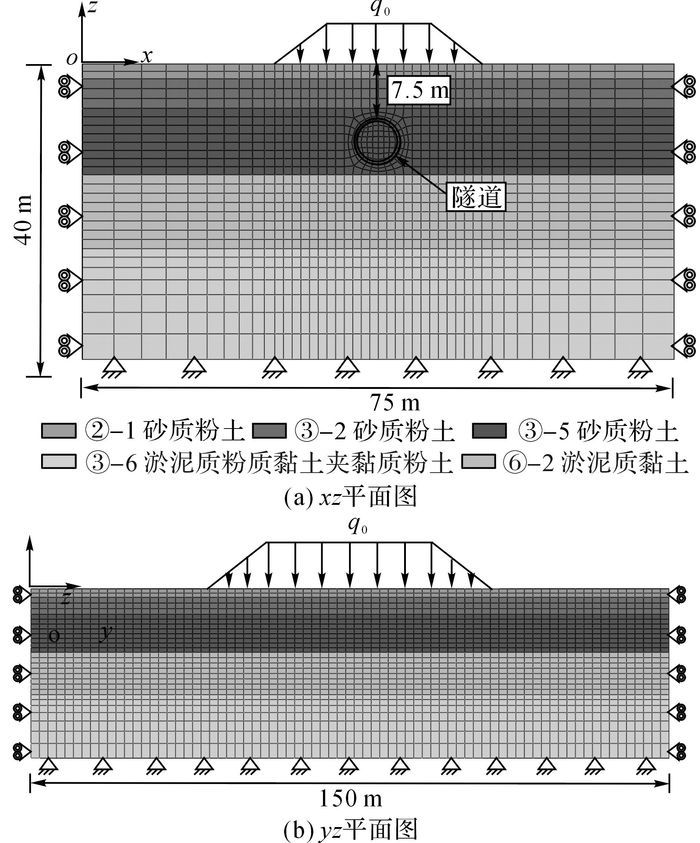
根据1.2节应力调整系数α和β需要通过建立隧道土体的三维有限元模型(此时隧道采用均质连续模型)来得到, 因此在本工程中计算应力调整系数α和β的三维模型如图 12所示.考虑到地面堆载的分布以及隧道开挖的影响范围, 因此模型长度、宽度和高度分别取为150、80和40.模型边界条件同1.3节.
|
图 12 计算α和β的FEM模型示意图 Fig. 12 FEM model for calculating α and β |
模型中隧道与土体之间的接触关系以及隧道的本构模型参数均同1.3节.地面堆载根据现场实际可以简化为如图 9(a)和(b)所示的梯形荷载施加在地表上, 根据堆载土体的重度, 可以计算出简化等效后的p约为110 kPa.模型计算所需要的土体材料参数如表 3所示, 土体采用摩尔库伦模型.
| 表 3 土层物理力学参数 Table 3 Physical and mechanics parameters of soils |
图 13给出了经过三维计算得到的应力调整系数α、β沿隧道纵向的分布曲线, 其中L为沿隧道纵向的距离.从图中可以看出, α在堆载中心区域内接近于1, 这是由于在本工程中, 隧道埋深较浅, 而堆载范围较长的缘故.同时可以看到地面堆载对隧道结构的侧向受力也有一定的影响, β值最大为0.15左右.将计算得到的应力调整系数α和β带入到隧道结构计算模型中, 得到隧道在堆载作用下的结构响应.

|
图 13 应力调整系数沿隧道纵向分布曲线 Fig. 13 Distribution curve of additional stress coefficients along tunnel longitudinal direction |
考虑到计算结果的对称性, 取隧道结构的一半进行分析.图 14(a)给出了隧道竖向位移的数值计算云图.从图中可以看到隧道整体变形大体可以分为2个区域, 分别为远离堆载基本不受堆载影响的区域(Ⅰ)和受堆载影响的变形区域(Ⅱ).隧道在区域(Ⅱ)中产生了接近高斯曲线形态的不均匀沉降, 因而导致隧道管片间产生了错台和张开, 其中以接头的环缝错台占主导.沉降曲线反弯点位置大约在离隧道端部40 m处.图 14(b)则给出了隧道纵向沉降s的计算值和监测值.从图中可以看出, 隧道底部计算值和道床处监测值在趋势上有着很好的吻合, 同时从图中可以看出, 由于隧道顶部离地面堆载更为接近, 因此隧道顶部的沉降要大于底部的沉降, 顶部最大沉降值约为25 mm, 约为底部沉降的2倍.而这个值也已经超过了《上海地铁保护技术标准》中所规定的隧道最大容许沉降值20 mm, 在图中未超过规范值和超过规范值部分用浅色和深色区域加以区分.

|
图 14 隧道竖向变形结果 Fig. 14 Results of tunnel vertical displacement |
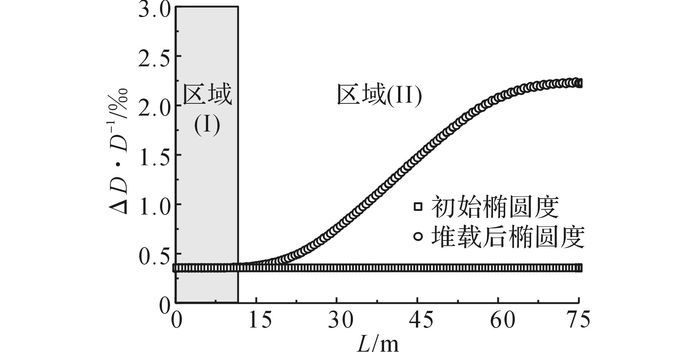
图 15给出了隧道每一环椭圆度(ΔD/D)沿纵向的变化趋势.从图中可以看出隧道在区域(Ⅰ)内基本不受到堆载的影响, 因此椭圆度基本没有变化;当进入到变形区域(Ⅱ), 隧道椭圆化变形开始增大, 椭圆度沿纵向呈高斯分布, 在隧道中心位置隧道的椭圆度达到最大.从图中可以看出, 中心位置的椭圆度由初始的0.35‰增加到了2.22‰.由于受到椭圆化变形的影响, 该环的管片应力会发生较大的变化, 因此对堆载中心位置正下方的隧道中心环进行管片受力分析就显得尤为必要.
|
图 15 隧道椭圆度沿纵向的分布曲线 Fig. 15 Distribution curve of tunnel ellipticity along longitudinal direction |
通过对隧道整体变形的分析, 可以看出在堆载作用下, 隧道会在区域(Ⅱ)内发生较大的接头错开和张开, 而在隧道的中心位置会产生较大管片应力.因此接下来将对区域(Ⅱ)内的接头变形以及受力和隧道中心位置的管片受力进行分析.
2.3.2 接头受力以及变形分析从前面对隧道的整体分析中, 可以看出隧道在变形区域(Ⅱ)内发生比较明显的错台和较小的张开, 由于这一区域错台相对于张开更为明显, 因此在分析中主要考虑错台的影响.图 16(a)给出了隧道竖向错台(Dv)沿隧道纵向的分布曲线.从图中可以看到, 在区域(Ⅰ)中, 由于隧道基本不受到堆载的影响, 因此隧道的错台量很小, 基本为0.在区域(Ⅱ)中, 隧道竖向错台沿隧道纵向呈高斯分布, 最大错台则发生在距离隧道端部约40 m的位置, 也就是隧道沉降曲线的反弯点处, 达到了1 mm.然而由于堆载会引起隧道的椭圆化变形, 因此隧道的腰部接头在侧向也会产生一定的错台, 图 16(b)给出了隧道腰部侧向错台(Dw)沿隧道纵向的分布, 可以看出侧向错台的分布规律与竖向错台相似, 同样是在隧道沉降曲线的反弯点位置达到最大, 约为0.78 mm.相比于顶部接头单一的竖向错台, 腰部接头则要在竖向和侧向2个方向发生错台, 错台量分别为0.75和0.78 mm, 此时腰部的总错台量约为1.08 mm, 与顶部接头的错台量基本一样, 因此腰部接头和顶部接头为反弯点断面中变形最大的, 同为影响隧道防水失效的重要因素.

|
图 16 隧道错台沿纵向分布曲线 Fig. 16 Distribution curve of tunnel dislocation along longitudinal direction |
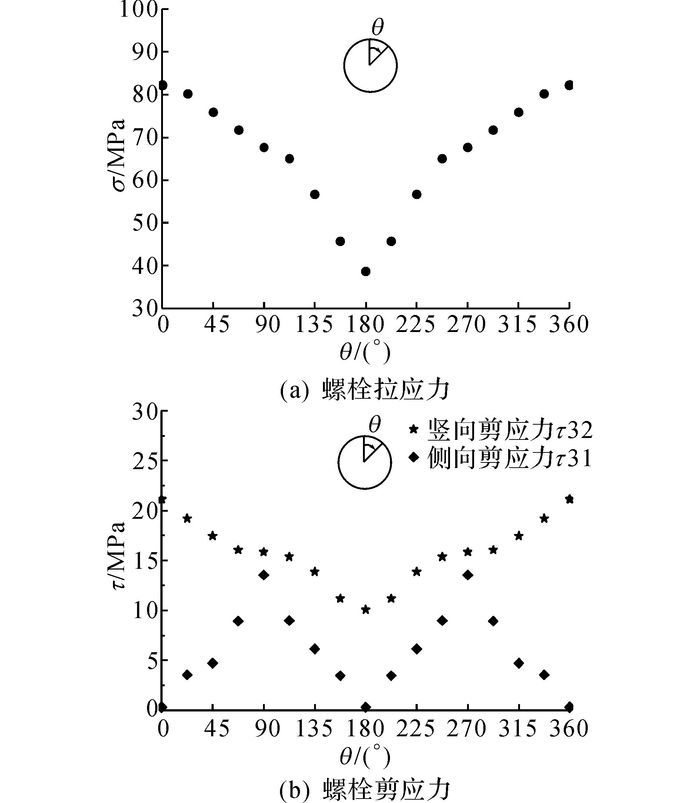
图 17给出了反弯点位置断面的16个纵向螺栓拉应力σ及剪应力τ的分布.从图中可以看出从隧道顶部到底部, 螺栓的拉应力在逐渐减小, 螺栓最大拉应力约为82 MPa.对于剪应力, τ32为螺栓沿竖向的剪应力, τ31为沿侧向的剪应力.从图中可以看出最大竖向剪应力约为21 MPa发生在隧道顶部的螺栓, 而此处螺栓在侧向基本不受剪应力.对于侧向剪应力最大则发生在腰部的螺栓, 大小约为14 MPa, 顶部和底部螺栓的侧向剪应力基本为0.同时可以看到腰部螺栓除受最大的侧向剪应力外, 还受较大的竖向剪应力约为16 MPa, 此时腰部螺栓总的剪应力约为21.3 MPa, 其值与顶部螺栓的剪应力基本相同, 因此腰部螺栓和顶部螺栓同为影响隧道安全的重要因素.基于对螺栓拉应力和剪应力的分析, 可以得到在堆载作用下, 隧道顶部的纵向螺栓是在反弯点位置断面中受力最不利的一个.
|
图 17 反弯点位置纵向螺栓拉应力和剪应力沿环向分布 Fig. 17 Distribution of longitudinal bolts' tensile and shear stress along circumferential direction in cross-section of inflection point |
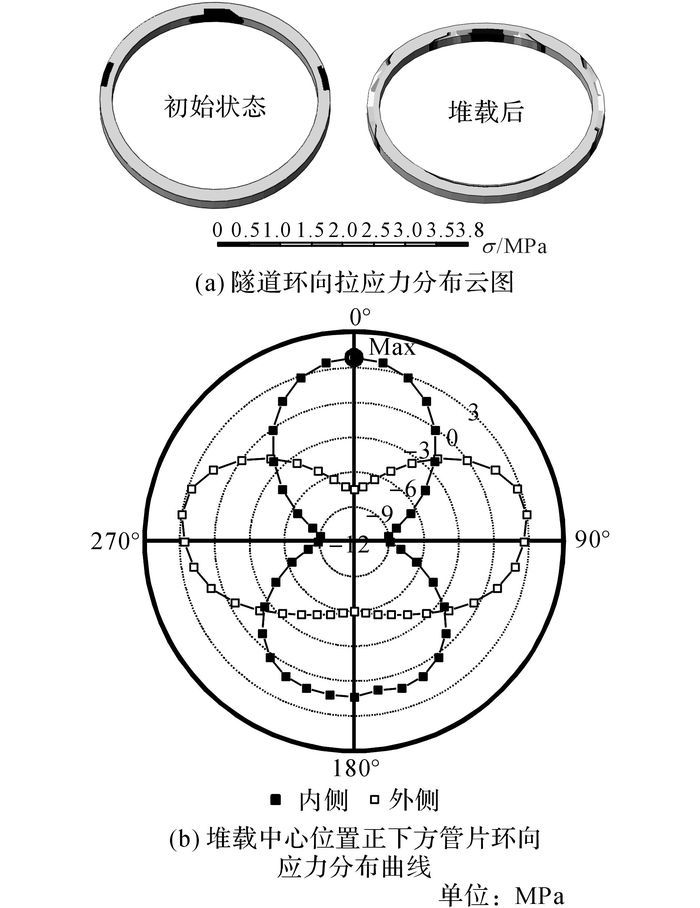
图 18(a)和(b)分别给出了堆载正下方隧道环的环向拉应力分布云图和环向应力分布曲线图.从图 18(a)中可以看出, 在初始状态下, 隧道在腰部外侧以及顶部内侧受到较小的环向拉应力, 最大值约为0.5 MPa位于隧道顶部内侧.而在堆载作用下, 隧道的环向应力发生了较大的增长, 隧道在堆载作用下底部内侧也产生了拉应力.结合图 18(b)中可以看出隧道最大环向拉应力达到了3.80 MPa, 出现在隧道顶部内侧的位置.根据《混凝土结构设计规范》[19]C50混凝土的抗拉强度设计值为1.89 MPa, 因此隧道顶部的环向拉应力已经超过了规范的设计值, 在隧道顶部极易出现裂缝, 这与在现场观测到管片12点钟方向有裂缝是极为吻合的, 如图 10所示.
|
图 18 堆载中心位置正下方管片环向压力分布 Fig. 18 Circumferential tensile stress distribution of tunnel under center of surface surcharge |
本文基于荷载-结构模型建立了地面堆载对下方隧道管片及环缝接头影响的三维数值分析方法.该方法首先采用连续体有限元模型分析堆载引起的附加应力, 并提取应力调整系数.然后将盾构隧道每环拼装结构等效为均质圆环、环与环之间采用螺栓连接, 进行应力叠加三维荷载-结构分析.这样既减少了计算工作量, 又反映了盾构隧道主要纵向特性.后将该方法应用到杭州地铁1号线某区间隧道管片和环缝接头在堆载作用下响应的数值分析中, 并与现场实测的结果进行了对比, 同时通过该方法补充分析得到了一些现场无法监测到的结果.
(1) 建立了地面堆载对下方隧道管片及环缝接头影响的三维数值分析模型, 提出了模型中较为重要的荷载系数α和β的计算方法并进行了验证.为后续工程设计人员在运用该模型分析堆载作用下隧道结构响应提供了一定的基础.
(2) 将该模型应用到具体的工程实例分析中, 通过对隧道沉降现场监测结果的对比分析, 验证了该分析模型的合理性.同时发现该模型可以很好的预测堆载影响范围, 揭示隧道管片和环缝接头响应规律.
(3) 通过对隧道变形的有限元和现场监测结果的对比分析, 发现在隧道沉降曲线上两者有着较好的吻合.可以将隧道沉降变形分为2个区域, 分别为基本不受堆载影响的区域(Ⅰ)和变形区域(Ⅱ).其中在变形区域(Ⅱ)内, 隧道的环缝接头会发生以错开为主的张开和错开变形, 在隧道中心位置, 隧道的椭圆化变形则是最大的.
(4) 受隧道不均匀沉降的影响, 隧道环缝接头的变形和受力在沉降曲线反弯点位置处达到最大, 在反弯点断面上的16个环缝接头中, 受力以及变形最不利的为顶部和腰部接头.
(5) 数值结果表明, 隧道由于受到椭圆化变形的影响, 管片的环向拉应力发生了较大增长, 其中最大环向拉应力发生在隧道内侧的顶部, 这与在现场观测到管片12点钟方向有裂缝是极为吻合的.
| [1] | KLAR A, VORSTER T E B, SOGA K, et a1. Soil-pipe interaction due to tunneling:comparison between Winkler and elastic continuum solutions[J]. Geotechnique, 2005, 55(6): 461–466. DOI:10.1680/geot.2005.55.6.461 |
| [2] |
王涛, 李浩, 徐日庆. 上方大面积加(卸)载引起盾构隧道的变形分析[J].
现代交通技术, 2005, 5(3): 29–31.
WANG Tao, LI Hao, XU Ri-qing. Analysis of deformation of shield tunnel when vertical loading and unloading[J]. Modern Transportation Technology, 2005, 5(3): 29–31. |
| [3] |
戴宏伟, 陈仁朋, 陈云敏. 地面新施工荷载对临近地铁隧道纵向变形的影响分析研究[J].
岩土工程学报, 2006, 28(3): 313–317.
DAI Hong-wei, CHEN Ren-peng, CHEN Yun-min. Study on effect of construction loads on longitudinal deformation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 313–317. |
| [4] |
李春良, 王国强, 赵凯军, 等.地面荷载作用盾构隧道纵向力学行为[J].吉林大学学报:工学报, 2011, 41(s2):180-184.
LI Chun-liang, WANG Guo-qiang, ZHAO Kai-jun, ZHU Chun-feng. Vertical mechanical behavior on shield tunnel under loads on ground surface[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(s2):180-184. http://www.cnki.com.cn/Article/CJFDTOTAL-JLGY2011S2037.htm |
| [5] |
房营光, 孙钧. 地面堆载下浅埋隧道围岩的粘弹性应力和变形分析[J].
岩石力学与工程学报, 1998, 17(3): 239–247.
FANG Ying-guang, SUN Jun. Analysis of visco-elastic stress and deformation of surrounding rocks for shallow tunnel under ground load[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(3): 239–247. |
| [6] |
陆文超. 地面荷载下浅埋隧道围岩应力的复变函数解法[J].
江南大学学报, 2002, 1(4): 409–412.
LU Wen-chao. The complex variable method on analysising the stress of surrounding rocks for shallow tunnel under ground load[J]. Journal of Southern Yangtze University(Natural Science Edition), 2002, 1(4): 409–412. |
| [7] | BLOM C B M, VAN DER HORST E J, JOVANOVIC P S. Three-dimensional structural analyses of the shield-driven "Green Heart" tunnel of the high-speed line South[J]. Tunnelling and Underground Space Technology, 1999, 14(2): 217–224. DOI:10.1016/S0886-7798(99)00035-8 |
| [8] |
张海波, 殷宗泽, 朱俊高, 等. 盾构法隧道衬砌施工阶段受力特性的三维有限元模拟[J].
岩土力学, 2005, 26(6): 990–994.
ZHANG Hai-bo, YIN Zong-ze, ZHU Jun-gao, et al. Three-dimensional FEM simulation of shield-driven tunnel lining during construction stage[J]. Rock and Soil Mechanics, 2005, 26(6): 990–994. |
| [9] |
陈俊生, 莫海鸿. 盾构隧道管片施工阶段力学行为的三维有限元分析[J].
岩石力学与工程学报, 2006, 25(s2): 3482–3489.
CHEN Jun-sheng, MO Hai-hong. Three dimensional finite element analysis of mechanical behaviors of shield tunnel segment during construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(s2): 3482–3489. |
| [10] | MO H H, CHEN J S. Study on inner force and dislocation of segments caused[J]. Tunneling and Underground Space Technology, 2007, 23: 281–291. |
| [11] | SHI C H, CAO C Y, LEI M F, et al. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints[J]. Tunneling and Underground Space Technology, 2016, 51(1): 175–188. |
| [12] | WANG L Z, WANG Z, Li L L, et al. Construction behavior simulation of a hydraulic tunnel during standpipe lifting[J]. Tunneling and Underground Space Technology, 2011, 26(6): 675–685. |
| [13] |
钟润辉, 王立忠, 王湛, 等. 海底取水盾构隧道管片力学性状的数值研究[J].
浙江大学学报:工学版, 2012, 46(4): 672–680.
ZHONG Run-hui, WANG Li-zhong, WANG Zhan, et al. Numerical analysis of mechanical behaviors of segments of subsea shield tunnel for water intake[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(4): 672–680. |
| [14] | WANG Z, WANG L Z, Li L L, et al. Failure mechanism of shield tunnel segmental lining joints and bolts with uneven longitudinal ground settlement[J]. Tunnelling and Underground Space Technology, 2014, 40(1): 300–308. |
| [15] | LIAO S M, PENG F, SHEN S L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction[J]. Tunnelling and Underground Space Technology, 2008, 23(4): 421–430. DOI:10.1016/j.tust.2007.07.001 |
| [16] |
吴庆. 地面堆载对既有盾构隧道结构的影响研究[D]. 上海: 上海交通大学, 2012.
WU Qing. Research on influence of shield tunnel structure on ground heaped load[D]. Shanghai:Shanghai Jiao Tong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10248-1012017908.htm |
| [17] | 顾晓鲁. 地基与基础(第3版)[M]. 北京: 中国建筑工业出版社, 2003. |
| [18] | 日土木协会. 隧道标准规范(盾构篇)及解说[M]. 朱伟译, 北京: 中国建筑工业出版社, 2006. |
| [19] |
GB50010-2002. 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
GB50010-2002. Code for design of concrete structures[S]. Beijing:China Architecture & Building Pr. |




