2. 广东省中科化灌工程与材料院士工作站, 广东 广州 510650;
3. 浙江省水利河口研究院, 浙江 杭州 310020;
4. 浙江省水利防灾减灾重点实验室, 浙江 杭州 310020
2. Guangdong Provincial Department of Chemical Engineering and Materials Irrigation Academician Workstation, Guangzhou 510650, China;
3. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China;
4. Key Laboratory of Hydraulics Disaster Prevention and Mitigation of Zhejiang Province, Hangzhou 310020, China
在我国的水利和海洋工程建设过程中, 每年都会产生大量的疏浚淤泥.这些疏浚淤泥工程性质差, 往往富含有机质或其他污染物.采用堆场或外海抛弃的方式进行处理不仅占用土地资源, 还会对周边环境造成恶劣的影响[1].同时, 大量围海、堤防以及道路工程的兴建导致优质工程填料严重短缺.因此, 疏浚淤泥土的无害化和工程资源化处理成为一个热门的研究问题.掺入水泥类胶凝材料对疏浚淤泥固化处理是目前国内外常用的方法[1-3], 固化处理的本质是通过水泥与淤泥反应的水化硅酸钙(CSH)产物对土颗粒包裹胶结并形成骨架结构来改善淤泥的力学性能.由于疏浚淤泥的工程处理规模往往巨大, 初始含水量较高, 在固化处理时会耗费大量的水泥, 而且加固效果不甚理想, 所以一般需要进行脱水减量的预处理.Azadegan等[4]通过一系列的抗压试验发现, 经减量处理再掺入适量水泥固化的疏浚淤泥, 强度一般能够满足工程的要求, 但会呈现出脆性破坏的缺点.这与朱伟等[1]、陈萍等[5]得到的试验结论吻合.Bahar等[6-7]则指出, 掺入水泥后, 疏浚淤泥的强度虽然有所提高, 但仍存在失水收缩开裂、泡水软化崩解的缺陷.而疏浚淤泥固化土一旦发生脆性开裂或产生收缩裂缝, 强度会迅速降低甚至消失, 难以满足复杂应力环境(如洪涝浸泡、受拉)下长期的变形和稳定性要求, 严重的还可能成为二次污染源, 释放出有机物或重金属.
近年来, 聚合物短纤维作为一种新的加筋材料, 常在土木水利工程中联合水泥或石灰一起补强软弱土质.Tang等[8-9]将聚合物纤维掺入水泥固化软土中, 通过大量的试验研究指出, 掺入纤维不但提高了水泥土的强度, 而且将脆性破坏形式转变为塑性破坏;蔡奕等[10]首次对纤维加筋石灰土的工程性质进行研究, 发现掺纤维可以降低固化土的脆性并延缓土体开裂.受这些成果启发, 对纤维加筋疏浚淤泥固化土的研究工作也陆续展开.高术森等[11]通过无侧限抗压和直剪试验研究, 得出淤泥固化土抗压强度和黏聚力均随纤维掺入比增加而增大的结论;Carruth等[12]通过对比掺纤维前后疏浚淤泥固化土的力学性质发现, 掺入纤维在提高土体弹性模量的同时, 还增加了土体的延性;Khattak等[13]通过一系列的劈裂和耐久性试验研究发现, 掺入纤维改善了淤泥固化土的抗拉强度, 减少了土体的收缩开裂.这些研究主要集中在考虑纤维掺入比影响的淤泥固化土的力学特性方面, 而有关纤维淤泥固化土本构模型的研究据笔者所知目前还一片空白.掌握材料在工程结构中的工作状态离不开解析和数值分析.这需要根据实际情况恰当选用材料的本构模型[14].由于邓肯-张本构模型[15-16]能较好地反映土体的非线性性态, 概念清楚, 易于理解, 所以在水利和岩土工程的解析和数值分析工作中得到广泛应用[17-18].
鉴此, 本文以纤维加筋疏浚淤泥固化土为研究对象, 在不同的纤维掺入比条件下进行20组排水三轴试验.考虑不同纤维掺入比(结构效应)的影响, 建立纤维加筋淤泥固化土的邓肯-张本构模型, 提出受纤维掺入比影响的模型参数经验公式, 供相关工程参考.
1 试验方案 1.1 试验材料淤泥取自浙江省台州临海港区航道疏浚淤泥堆场, 其初始水的质量分数高达100%~120%, 取样时已在堆场内排水晾晒了近10个月, 表面形成薄硬壳层和龟裂.取样淤泥在硬壳层下20 cm左右, 其水的质量分数wB为55%~70%.设γ为土体重度, ωL为液限, Ip为液性指数, wc为有机质质量分数, 具体的物理性质如表 1所示, 其中液塑限采用76 g锥式液塑限联合测定仪测定, 有机质质量分数采用重铬酸钾氧化法测定, 颗粒组成采用MAF5000激光粒度分析仪测定.为了减少水泥消耗量, 提高加固效率, 本文取水的质量分数为60%的疏浚淤泥作为试验用土.试验用的水泥为钱潮牌的P.C.32.5复合硅酸盐水泥, 产自杭州.试验用的纤维为长12 mm的聚乙烯醇(PVA)短纤维, 具有强度高、耐酸碱性优、分散性好等特点, 能方便地掺入土体之中, 且能很好地与水泥类的碱性胶凝材料协同工作[19].设ρfR为纤维线密度, D为直径, pt为抗拉强度, Ef为杨氏模量, δt为干断裂拉深度, 其物理力学性质见表 2.
| 表 1 台州地区疏浚淤泥的物理性质 Table 1 Physical properties of dredged sludge in Taizhou area |
| 表 2 聚乙烯醇纤维的物理力学性质 Table 2 Physical and mechanical properties of Polyvinylalcohol fiber |
| $ {w_{\rm{f}}} = \frac{{{m_{\rm{f}}}}}{m}, $ | (1) |
| $ {w_{\rm{c}}} = \frac{{{m_{\rm{c}}}}}{m}. $ | (2) |
式中:mf为纤维的质量, m为试验疏浚淤泥的质量, mc为水泥的质量.
根据陈萍等[5]研究成果, 掺入4%的水泥可以使wB=50%~70%的疏浚淤泥满足作为填土材料使用时的强度要求.所以综合考虑到加固效果和消耗量的问题, 本文中wc=4%.参考Tang等[8]以及高术森等[11]加固软土时有效的纤维掺入比范围, 本文的wf控制为0、0.05%、0.125%、0.20%、0.25%.
按上述配比制备纤维加筋淤泥固化土试样共20组, 每组包括3个平行试样, 具体分组情况如表 3所示.表中,σ3为围压,当制样时, 先将聚乙烯醇短纤维和疏浚淤泥通过人工搅拌的方式混合均匀, 再添加水泥充分搅拌, 最后装入内径为39.1 mm、高为80 mm的铜制试模内制成三轴试样.由于搅拌均匀后的混合物具有一定的流动性, 所以须采用质量控制的成型方法, 分3层装入试模中并适当振捣以排除其中的气泡.装样后用塑料薄膜多层密封置于室内养护, 经24 h后脱模.试样脱模后用塑料薄膜多层包裹密封并放入恒温(20±2 ℃)的水浴中养护7 d, 试验前一天再装入饱和器, 置于真空饱和缸中进行抽气预饱和.纤维加筋淤泥固化土的制样方法参考文献[3, 5, 12], 具体的制样和试验方法则参照《水泥土配合比设计规程(JGJ/T 233-2011)》[21]和《土工试验方法标准(GB/T 50123-1999)》[22].
| 表 3 制备试样和三轴试验的控制参数 Table 3 Parameters of sample preparation and triaxial test |
纤维加筋淤泥固化土的固结排水三轴试验(CID试验)是在GDS标准应力路径三轴仪上进行的.试验开始后, 先将试样装入GDS压力室中.余下的试验过程完全采用GDSLAB软件进行控制和数据采集.先对试样进行反压饱和, 待饱和度达到95%以上, 设定围压进行固结.待固结完成后, 设定0.01%/min的速率, 开始对试样进行排水剪切.当剪切至预先设定的20%最大轴向应变时, 试验自动停止.
2 试验结果整理与分析 2.1 纤维加筋淤泥固化土的破坏形态如图 1所示为σ3=100 kPa围压下, wf=0、0.05%、0.125%、0.20%、0.25%的疏浚淤泥固化土试样的破坏形态.从图中可以看出:当wf=0和0.05%时, 剪切后的试样存在一个与水平方向约成60°的破裂面, 破坏形式为局部剪切破坏;随着纤维掺量的增加, 试样没有出现明显的剪切破裂面, 其外形对称, 呈腰鼓状, 破坏形式为侧向鼓胀破坏.这表明, 掺入纤维改变了淤泥固化土的破坏形态.其破坏机理可能是, 纤维抗拉性能的有效发挥延缓了土体中潜在的破裂面的产生.

|
图 1 不同纤维掺入比的试样在100 kPa围压下的破坏形态 Fig. 1 Failure shape of samples with different fiber mixing ratio when confining pressure is 100 kPa |
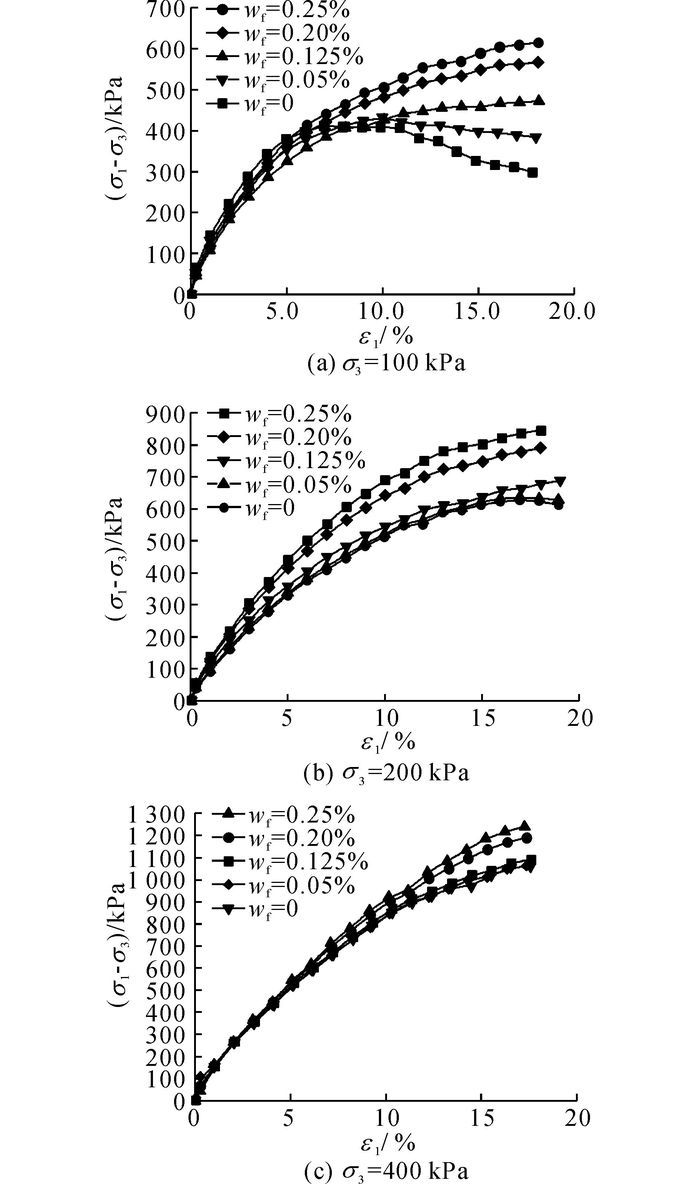
图 2给出了σ3=100、200、400 kPa时纤维加筋淤泥固化土的应力-应变关系曲线.从图 2(a)可以看出, 在σ3=100 kPa时, 对于wf=0和0.05%的试样, 主应力差(σ1-σ3)随轴向应变ε1的增加先增大, 达到峰值后逐渐减小, 但并未消失, 其应力-应变曲线表现为软化型.从图 2还看出, 随着围压和纤维掺入比继续增加, 试样的应力-应变曲线变化趋势相似, 均表现为应变硬化型, 呈现出双曲线变化特征.施利国等[20]在研究聚丙烯灰土的三轴强度特性时, 其应力-应变曲线也呈现出类似的规律.
|
图 2 不同围压σ3下纤维淤泥固化土的应力-应变曲线 Fig. 2 Stress-strain curves of fiber reinforced solidified sludge under different confining pressure σ3 |
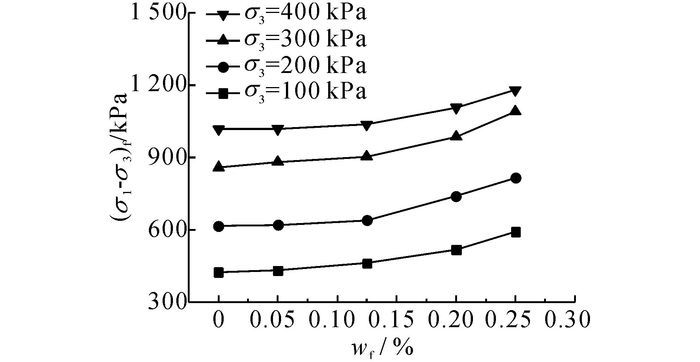
通过抗剪强度及相应的指标衡量掺入纤维对淤泥固化土强度的影响.当试样的主应力差无峰值时选取ε1=15%时的主应力差为破坏应力(σ1-σ3)f, 即抗剪强度;当其主应力差出现峰值时选取峰值作为抗剪强度.如图 3所示为淤泥固化土试样的抗剪强度随纤维掺入比变化的曲线.当σ3=100 kPa, wf=0时淤泥固化土的抗剪强度为424.4 kPa;当掺入wf=0.125%的纤维后, 抗剪强度为462.2 kPa, 增长了8.9%;当掺入wf=0.25%纤维后, 抗剪强度达到592.2 kPa, 相比未掺纤维时增长了40%.可见, 淤泥固化土的抗剪强度随纤维掺入比的增加得到显著的提高.
|
图 3 抗剪强度随纤维掺入比变化的曲线 Fig. 3 Variation curves of shear strength with fiber mixing ratio |
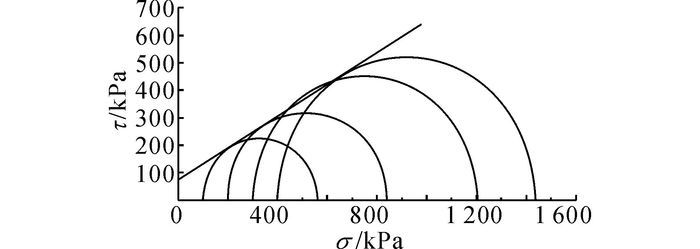
根据排水三轴剪切试验结果, 在τ-σ应力平面上绘制试样破坏时的应力摩尔圆和强度包线[22], 得到土体的抗剪强度指标, 在本文中用黏聚力c和内摩擦角φ表示.设τ为剪应力,σ为正应力.图 4给出了当wf=0.125%时试样的应力摩尔圆和相应的强度包线.
|
图 4 纤维掺入比为0.125%试样的应力摩尔圆和强度包线 Fig. 4 Mohr's stress circle and strength envelop of samples when fiber mixing ratio is 0.125% |
用同一方法获得其他纤维掺入比试样的黏聚力c和内摩擦角, 如表 4所示.从表 4中可以看出, 内摩擦角φ受纤维掺入比的影响很小, 基本保持不变, 其平均值为30.28°.当wf从0增加到0.25%的过程中, 淤泥固化土的黏聚力c从63.9增加到114.4 kPa, 增幅随着纤维掺入比的增加而逐渐提高.基于上述规律获得纤维淤泥固化土黏聚力的幂函数型经验公式为
| 表 4 不同纤维掺入比的淤泥固化土的抗剪强度指标 Table 4 Shear strength parameters of samples with different fiber mixing ratio |
| $ c = {c_0} + 1120.4{\left( {100{w_{\rm{f}}}} \right)^{2.242}}. $ | (3) |
式中:常数项c0为当wf=0时的c值, 等于64.37 kPa, 相关系数R2值为0.988.
综上可知, 纤维加筋淤泥固化土的抗剪强度以及相应的指标(尤其是黏聚力)随纤维掺入比的增加而增长, 与前人[8-9]的结论具有较好地一致性.这主要是因为分散的短纤维在土中形成一张三维受力网, 将土颗粒及水化产物牢牢锁住, 一旦土体受到剪切, 纤维网会随之产生拉应力, 抑制试样的破坏趋势.
3 纤维加筋淤泥固化土的邓肯-张模型及其参数 3.1 纤维加筋淤泥固化土的邓肯-张模型图 2中试样的应力-应变特征大致符合邓肯-张本构模型[15-16]的双曲线假设, 因此采用该模型来模拟纤维加筋淤泥固化土的应力-应变关系, 获得纤维掺入比和围压对邓肯-张模型参数的影响规律.
根据Kondner等[15]的建议, 将土体的应力-应变关系用双曲线模型表示为
| $ {\sigma _1} - {\sigma _3} = \frac{{{\varepsilon _1}}}{{a + b{\varepsilon _1}}}. $ | (4) |
式中:σ1为轴向应力,a, b为试验参数.
对式(4) 求导消去ε1可得某一围压下的切线弹性模量Et:
| $ {E_{\rm{t}}} = \frac{1}{a}{\left[ {1 - b\left( {{\sigma _1} - {\sigma _3}} \right)} \right]^2} = {E_{\rm{i}}}{\left[ {1 - \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}}}}}} \right]^2}. $ | (5) |
式中:Ei为初始切线弹性模量, (σ1-σ3)ult为轴向应变ε1趋于无穷大时主应力差的极限值.
令Rf为破坏应力(σ1-σ3)f与主应力差极限值(σ1-σ3)ult的比值(破坏比[15]).根据摩尔-库伦强度理论[15]确定破坏应力得到
| $ {R_{\rm{f}}} = \frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{\rm{f}}}}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}}}}} = \frac{{2\left( {c\cos \varphi + {\sigma _3}\sin \varphi } \right)}}{{\left( {1 - \sin \varphi } \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}}}}}. $ | (6) |
将式(6) 代入(5) 可得
| $ {E_{\rm{t}}} = {E_{\rm{i}}}{\left[ {1 - \frac{{{R_{\rm{f}}}\left( {1 - \sin \varphi } \right)\left( {{\sigma _1} - {\sigma _3}} \right)}}{{2\left( {c\cos \varphi + {\sigma _3}\sin \varphi } \right)}}} \right]^2}. $ | (7) |
在常规排水三轴剪切的试验条件下, 有Δσ2=Δσ3=0, Δσ1=(σ1-σ3).故体积模量为[16]
| $ {B_{\rm{t}}} = \frac{1}{3}\frac{{\Delta \left( {{\sigma _1} + 2{\sigma _3}} \right)}}{{\Delta \theta }} = \frac{1}{3}\frac{{\left( {{\sigma _1} - {\sigma _3}} \right)}}{{\Delta \theta }}, $ | (8) |
式中:Bt为某一围压下的体积模量;θ为体积应变.
3.2 纤维加筋淤泥固化土邓肯-张模型的参数分析将式(4) 改写得到
| $ \frac{{{\varepsilon _1}}}{{{\sigma _1} - {\sigma _3}}} = a + b{\varepsilon _1}. $ | (9) |
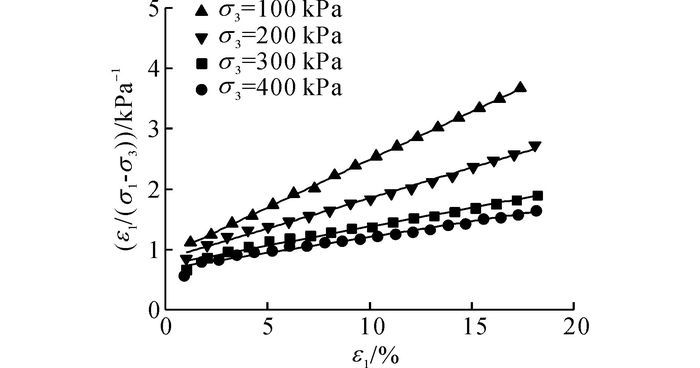
本文根据式(9) 变换坐标系, 并重绘纤维加筋淤泥固化土试样的应力-应变曲线.当纤维的wF=0.125%时, 得到的应力-应变曲线如图 5所示.从图 5中发现, ε1/(σ1-σ3)与ε1间大致成一阶线性关系, 说明纤维加筋淤泥固化土的应力-应变曲线基本符合双曲线关系.用相同的方法拟合得到其他试样的ε1/(σ1-σ3)-ε1关系直线, 确定其截距a和斜率b, 由此得到初始切线模量Ei, 极限主应力差(σ1-σ3)ult以及破坏比Rf等模型变量.本文给出了5种纤维掺入比的试样在400 kPa围压下的E-B模型变量数据, 如表 5所示, 表中S为应力水平.
|
图 5 当纤维掺入比为0.125%时试样的应力-应变曲线 Fig. 5 Replotted stress-strain curves of samples when fiber mixing ratio is 0.125% |
| 表 5 400 kPa围压下纤维加筋淤泥固化土的邓肯-张E-B模型变量 Table 5 Variables of Duncan-Chang E-B model for fiber reinforced solidified sludge when confining pressure is 400 kPa |
根据Janbu的建议, 土体的初始切线弹性模量Ei可以表示为围压的函数[15]:
| $ {E_{\rm{i}}} = K{p_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\rm{a}}}}}} \right)^n}. $ | (10) |
式中:K, n为初始切线模量参数;pa为单位大气压(103.30 kPa).
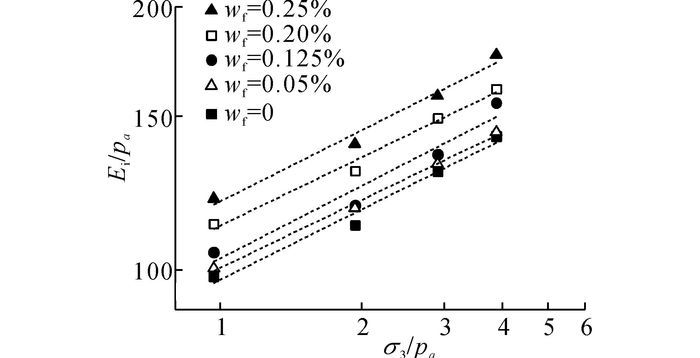
根据模型变量数据和式(10), 在双对数坐标系下绘制不同纤维掺入比的试样的(Ei/pa)-(σ3/pa)关系曲线, 并对其进行线性拟合, 拟合结果如图 6所示.
|
图 6 试样的初始切线弹性模量与周围压力的关系曲线 Fig. 6 Relationship curves of initial tangent modulus and confining pressure for samples |
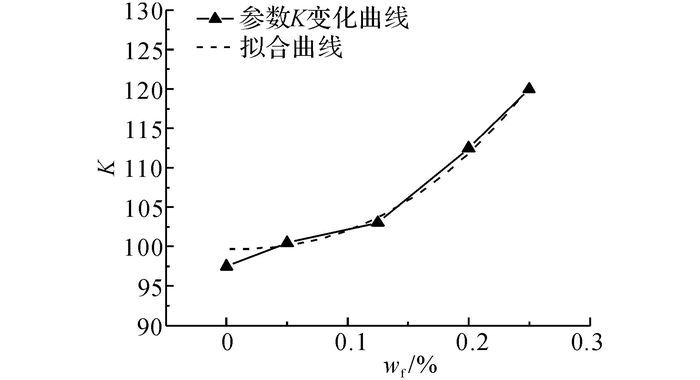
从图 6中发现, 初始切线模量不仅随着围压的增加而增大, 还随纤维掺入比的增加而增大.当wf=0时, K=97.50, n=0.267;当wf= 0.05%时, K=100.46, n=0.258;当wf=0.125%时, K=103.04, n=0.275;当wf=0.20%时, K=112.46, n=0.260;当wf=0.25%时, K=119.95, n=0.270.在0~0.25%的纤维掺入比范围内, 初始切线模量参数n受纤维掺入比的影响较小, 可取为常数(0.27).而初始切线模量参数K随wf的增加而增大, 呈现幂函数型的增长规律.本文利用Origin软件中的幂函数工具对其进行非线性拟合, 得到如图 7所示的结果.拟合得到的初始切线模量参数K的经验公式为
|
图 7 初始切线弹性模量参数K与纤维掺入比的关系曲线 Fig. 7 Relationship curves of initial tangent modulus parameter K and fiber mixing ratio |
| $ K = {K_0} + 528.58{\left( {100{\rho _{\rm{f}}}} \right)^{2.344}}. $ | (11) |
式中:常数项K0为令wf=0时K值, 等于99.68,相关系数R2=0.987.
结合式(10), 得到考虑纤维掺入影响的淤泥固化土的初始切线弹性模量为
| $ {E_{\rm{i}}} = \left[ {{K_0} + 528.58{{\left( {100{w_{\rm{f}}}} \right)}^{2.344}}} \right]{p_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\rm{a}}}}}} \right)^n}. $ | (12) |
结合式(6), 得到考虑纤维掺入影响的淤泥固化土的极限主应力差为
| $ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\rm{ult}}}} = \frac{{2\left( {c\cos \varphi + {\sigma _3}\sin \varphi } \right)}}{{{R_{\rm{f}}}\left( {1 - \sin \varphi } \right)}}. $ | (13) |
式中:Rf取所有破坏比的平均值, 为0.614;黏聚力按式(3) 取值, 内摩擦角取表 4中的平均值.
定义应力水平为
| $ S = \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{\rm{f}}}}}. $ | (14) |
邓肯等[16]认为, 体积应变θ与轴向应变ε1成双曲线关系, 在任一围压σ3下, 体积模量应近似为一常量.所以由式(8) 计算体积模量时, 根据他们的建议按70%的应力水平时的体积模量来取值.邓肯等[16]将体积模量Bt表示成围压的函数:
| $ {B_{\rm{t}}} = {K_{\rm{b}}}{p_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\rm{a}}}}}} \right)^r}. $ | (15) |
式中:Kb, r为体积模量参数.
受式(15) 的启发, 本文根据模型变量数据在双对数坐标系下绘制不同纤维掺入比的纤维加筋淤泥固化土试样的(Bt/pa)-(σ3/pa)关系曲线, 并对曲线进行线性拟合, 拟合的结果如图 8所示.

|
图 8 试样的体积模量与周围压力的关系曲线 Fig. 8 Relationship curves of bulk modulus and confining pressure for samples |
从图 8中可以看出, 体积模量随纤维掺入比的增加而增加.当wf =0时, Kb=24.60, r=0.195;当wf =0.05%时, Kb=25.12, r=0.206;当wf=0.125%时, Kb=26.79, r=0.200;当wf=0.20%时, Kb=29.79, r=0.203;当wf =0.25%时, Kb=33.04, m=0.215, 在0~0.25%的纤维掺入比范围内, 体积模量参数r受纤维掺入比的影响较小, 可取为常数(0.20).而体积模量参数Kb随wf的增加而增大.本文对体积模量参数Kb进行非线性拟合, 得到如图 9所示的结果, 图中R2=0.987.

|
图 9 体积模量参数Kb与纤维掺入比的关系曲线 Fig. 9 Relationship curves of bulk modulus parameter Kb and fiber mixing ratio |
拟合得到体积模量参数Kb的经验公式可表示为
| $ {K_{\rm{b}}} = {K_{{\rm{b}}0}} + 167.74{\left( {100{w_{\rm{f}}}} \right)^{2.188}}. $ | (16) |
式中:常数项Kb0为令wf=0时Kb值, 等于24.92.
结合式(15), 得到考虑纤维掺入比影响的淤泥固化土的体积模量为
| $ {B_{\rm{t}}} = \left[ {{K_{{\rm{b0}}}} + 167.74{{\left( {100{\rho _{\rm{f}}}} \right)}^{2.188}}} \right]{p_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\rm{a}}}}}} \right)^m}. $ | (17) |
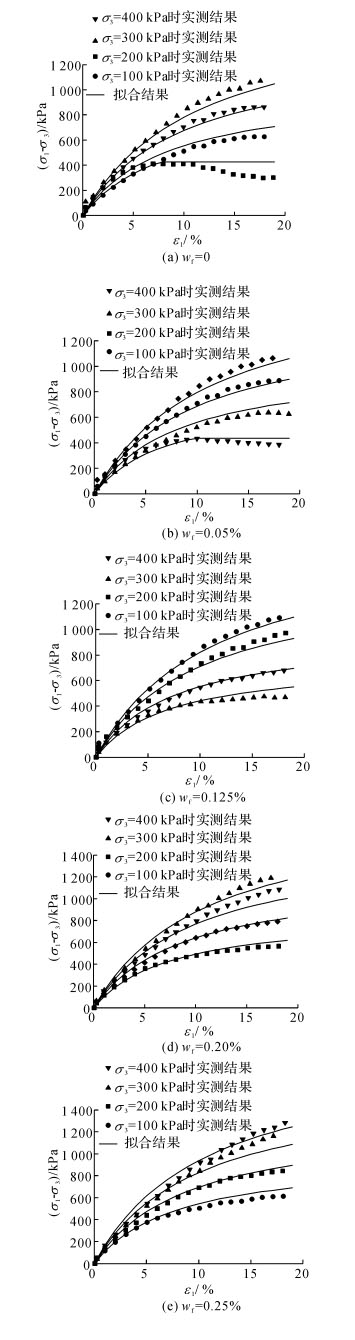
为了验证邓肯-张E-G模型参数经验公式的综合拟合效果, 本文利用式(5)、(12) 和(13) 计算出双曲线参数a和b, 代入式(4) 计算出应力-应变曲线, 与实测试验数据拟合比较, 结果如图 10所示.
|
图 10 不同纤维掺入比试样的应力-应变曲线的实测结果与拟合结果 Fig. 10 Experimental and fitting results of stress-strain curves for samples with different fiber mixingratio |
需要说明的是, 对于呈现出软化特性的应力-应变曲线, 邓肯等[15]建议分段进行处理:前半段从零开始增加到主应力差的峰值点结束, 为模型拟合的双曲线段;后半段为一条从主应力差峰值点出发的水平延伸直线.在图 10中沿用这一方法对100 kPa围压下未掺纤维试样和掺0.05%纤维试样的应力-应变曲线进行处理.从图 10中可知, 基于式(5) 以及经验式(12) 和(13) 获得的邓肯-张模型拟合应力-应变曲线与实测试验曲线具有较好的一致性.这表明用邓肯-张模型来模拟纤维加筋疏浚淤泥固化土的应力-应变关系是合理的, 采用掺入比来反映纤维对土体邓肯-张模型的初始切线模量参数K以及体积模量参数Kb的影响是有效的.
4 结论本文将聚乙烯醇短纤维和水泥一起掺入疏浚淤泥中, 通过排水三轴试验, 分别对纤维加筋淤泥固化土的工程特性和邓肯-张本构模型进行试验和研究, 并对其本构模型参数进行分析, 得到以下结论.
(1) 掺入短纤维后, 疏浚淤泥固化土的破坏形态发生了改变, 从局部剪切破坏转变为外形对称的侧向鼓胀破坏.
(2) 随着纤维掺入比的增加, 疏浚淤泥固化土的黏聚力呈幂函数型增长, 而内摩擦角几乎不变.
(3) 掺入纤维后, 淤泥固化土的应力-应变曲线表现为加工硬化型, 形状呈双曲线, 符合邓肯-张模型的假设.通过建立邓肯-张E-B本构模型, 获得了其初始切线弹性模量参数K与体积模量参数Kb随纤维掺入比增加而增长的规律.
上述结论表明, 将聚乙烯醇纤维掺入到疏浚淤泥固化土中, 能有效改善其工程力学性质(对增加黏聚力的贡献尤其明显);以纤维掺入比为影响因子获得的邓肯-张土体初始切线模量和体积模量经验公式可以作为合理设计纤维加筋疏浚淤泥固化土构筑物的指导依据.
| [1] |
朱伟, 张春雷, 高玉峰, 等. 海洋疏浚泥固化处理土基本力学性质研究[J].
浙江大学学报:工学版, 2005, 39(10): 1561–1565.
ZHU Wei, ZHANG Chun-lei, GAO Yu-feng, et al. Fundamental mechanical properties of solidified dredged marine sediment[J]. Journal of Zhejiang University:Engineering Science, 2005, 39(10): 1561–1565. |
| [2] | TANG Yi-xin, MIYAZAKI Y, TSUCHIDA T. Practices of reused dredgings by cement treatment[J]. Soils and Foundations, 2001, 41(5): 129–143. DOI:10.3208/sandf.41.5_129 |
| [3] |
孟庆山, 杨超, 雷学文, 等. 武汉东湖淤泥早强固化试验研究[J].
岩土力学, 2010, 31(3): 707–712.
MENG Qing-shan, YANG Chao, LEI Xue-wen, et al. Experimental study of early solidification of sludge in East Lake, Wuhan[J]. Rock and Soil Mechanics, 2010, 31(3): 707–712. |
| [4] | AZADEGAN O, JAFARI S H, LI J. Compaction characteristics and mechanical properties of lime/cement treated granular soils[J]. Electronic Journal of Geotechnical Engineering, 2012, 17: 2275–2284. |
| [5] |
陈萍, 高炎旭, 马美玲. 疏浚淤泥与焚烧底灰混合固化方法的试验研究[J].
水利学报, 2015, 46(6): 749–756.
CHEN Ping, GAO Yan-xu, MA Mei-ling. Experimental study on solidification method for dredged mud mixed with MSWI[J]. Journal of Hydraulic Engineering, 2015, 46(6): 749–756. |
| [6] | BAHAR R, BENAZZOUG M, KENAI S. Performance of compacted cement-stabilised soil[J]. Cement and concrete composites, 2004, 26(7): 811–820. DOI:10.1016/j.cemconcomp.2004.01.003 |
| [7] |
张俊峰, 戴小松, 邹维列, 等. 水泥改性固化脱水淤泥路用性能试验[J].
浙江大学学报:工学版, 2015, 49(11): 2165–2171.
ZHANG Jun-feng, DAI Xiao-song, ZOU Wei-lie, et al. Experiments on pavement performance of solidified sediment modified with cement[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(11): 2165–2171. |
| [8] | TANG C, SHI B, GAO W, et al. Strength and mechanical behavior of short polypropylene fiber reinforced and cement stabilized clayey soil[J]. Geotextilesand Geomembranes, 2007, 25(3): 194–202. DOI:10.1016/j.geotexmem.2006.11.002 |
| [9] | ESTABRAGH A R, NAMDAR P, JAVADI A A. Behavior of cement-stabilized clay reinforced with nylon fiber[J]. Geosynthetics International, 2012, 19(1): 85–92. DOI:10.1680/gein.2012.19.1.85 |
| [10] |
蔡奕, 施斌, 高玮, 等. 纤维石灰土工程性质的试验研究[J].
岩土工程学报, 2006, 28(10): 1283–1287.
CAI Yi, SHI Bin, GAO Wei, et al. Experimental study on engineering properties of fibre-lime treated soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1283–1287. DOI:10.3321/j.issn:1000-4548.2006.10.020 |
| [11] |
高术森. 聚丙烯纤维对固化海涂淤泥物理力学性能的影响研究[D]. 杭州: 浙江大学, 2012.
GAO Shu-sen. Research on the effect of polypropylene fiber on mechanical properties of solidified tideland sludge[D]. Hangzhou:Zhejiang University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10335-1012310656.htm |
| [12] | CARRUTH W D, HOWARD I L. Use of portland cement and polymer fibers to stabilize very high moisture content fine-grained soils[J]. Advances in Civil Engineering Materials, 2013, 2(1): 1–24. |
| [13] | KHATTAK M J, ALRASHIDI M. Durability and mechanistic characteristics of fiber reinforced soil-cement mixtures[J]. The International Journal of Pavement Engineering, 2006, 7(1): 53–62. DOI:10.1080/10298430500489207 |
| [14] | HUANG B, BATHURST R J, HATAMI K. Numerical study of reinforced soil segmental walls using three different constitutive soil models[J]. Journal of Geotechnical and Geoenvironmental engineering, 2009, 135(10): 1486–1498. DOI:10.1061/(ASCE)GT.1943-5606.0000092 |
| [15] | DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1970, 96(5): 1629–1653. |
| [16] | DUNCAN J M, WONGKS, MABRYP. Strength, stress-strain and bulk modulus parameters for finite element analyses of stresses and movements in soil masses//Geotechnical engineering[M]. California: University of California, Berkeley, 1980: 75. |
| [17] | XIONG J H, KOU X Y, LIU F, et al. Applicability of Duncan-Chang model and its modified versions to methane hydrate-bearing sands[C]//Advanced Materials Research. Switzerland:Trans Tech Publications, 2012, 347:3384-3387. |
| [18] | MIYAZAKI K, TENMA N, AOKI K, et al. A nonlinear elastic model for triaxial compressive properties of artificial methane-hydrate-bearing sediment samples[J]. Energies, 2012, 5(10): 4057–4075. |
| [19] | PARK S S. Unconfined compressive strength and ductility of fiber-reinforced cemented sand[J]. Construction and building materials, 2011, 25(2): 1134–1138. DOI:10.1016/j.conbuildmat.2010.07.017 |
| [20] |
施利国, 张孟喜, 曹鹏. 聚丙烯纤维加筋灰土的三轴强度特性[J].
岩土力学, 2011, 32(9): 2721–2728.
SHI Li-guo, ZHANG Meng-xi, CAO Peng. Triaxial shear strength characteristics of lime-soil reinforced with polypropylene fiber inclusions[J]. Rock and Soil Mechanics, 2011, 32(9): 2721–2728. |
| [21] |
JGJ/T 233-2011. 水泥土配合比设计规程[S]. 北京: 中国建筑工业出版社, 2011.
JGJ/T 233-2011. Specification for mix proportion design of cement soi l[S]. Beijing:China Architecture & Building Press, 2011. |
| [22] |
GB/T50123-1999. 土工试验方法标准[S]. 北京: 中国计划出版社, 1999.
GB/T50123-1999. Standard for soil test method[S]. Beijing:China Planning Press, 1999. |


