2. 复杂系统建模与仿真教育部重点实验室, 浙江 杭州 310018
2. Key Laboratory of Complex Systems Modeling and Simulation of Ministry of Education, Hangzhou 310018, China
近些年来, 面向服务的计算作为一种新的计算模式无论是在学术界还是工业界都吸引了许多的关注.随着服务技术的飞速发展, 越来越多的企业将自身业务以服务的方式发布, 使得用户可以随意选择符合需求的Web服务.然而面对众多具有相同或相近功能的Web服务, Web服务的非功能属性成为用户选择服务的重要条件.Web服务的非功能属性使用服务质量(quality of service, QoS)描述, 常见Web服务的QoS属性包括:响应时间、吞吐量及代价等.在真实环境中, 通常某一用户不可能调用过每一个服务, 所以QoS数据往往存在部分缺失的情况, 这使得根据已知的QoS数据预测出缺失的QoS成为服务推荐过程中的重要问题[1-2].
目前, 使用混合协同过滤方法进行服务QoS预测得到广泛的研究和应用, 并取得较好的效果.常用的协同过滤算法分为2类:基于用户的协同过滤算法和基于服务的协同过滤算法[3-7].然而, 这2种协同过滤方法都需要根据历史QoS信息筛选相似邻居以及基于相似邻居进行QoS预测.在这2个步骤中, 一方面, 在数据稀疏情况下, 用户之间有共同调用记录的服务十分有限, 基于有限的记录筛选相似邻居会影响预测的准确率;另一方面, 由于网络环境具有突发性、不确定性等特点, Web服务的QoS值不可避免地受到用户和服务所处网络环境的影响, 那么在用户调用服务时, QoS值会展现出一定的随机性, 产生一些QoS噪声数据, 而这些噪声数据往往不能反映正常状态下的QoS水平.重要的是,噪声数据不仅可能降低相似邻居的相似性, 也会存在将某些用户或者服务因为偶然取得相近的QoS而判定为相似邻居的情况, 噪声数据也必将对协同过滤方法的预测精度造成影响.如何发现并识别噪声数据, 减少噪声数据对预测精度的影响是服务QoS预测中的一个关键问题.
针对这一问题, 本文提出基于贝叶斯分类的Web服务QoS预测方法.
1) 针对噪声数据影响相似邻居计算的问题, 提出一种基于朴素贝叶斯概率分类器的相似邻居过滤机制.该机制可以对通过相似度计算得到的相似邻居进行筛选, 得到更加准确的相似邻居.
2) 为进一步提高预测精度, 通过改进目前的混合协同过滤方法, 在进行预测QoS时, 将使用贝叶斯分类器得到的分类概率作为权值, 进行缺失QoS值的计算.
3) 基于一个广泛使用的真实数据集进行实验, 结果显示,本文所提出的QoS预测算法具有较好的预测精度.
1 相关工作基于QoS的Web服务推荐技术可根据服务的非功能属性为用户推荐最合适的服务, 已成为服务计算领域的研究热点[1-2].服务QoS预测是解决服务推荐问题的关键.目前, 服务计算领域广泛采用协同过滤方法[3-7]来解决QoS预测问题[8-10].协同过滤方法包括基于近邻的方法以及基于模型的方法.基于近邻的方法以计算用户和项目之间的关系为中心[11-12].基于近邻的方法又可以划分成3个子方法, 包括基于用户的方法[13-14]、基于项目的方法[15-16]以及混合方法[17].Shao等[18]提出了一种典型的基于用户的协同过滤方法预测缺省的QoS, 该方法认为相似用户对相似服务会有相近的QoS值, 并使用PCC计算相似度.Zheng等[19]公布了大规模的真实QoS数据集, 并提出了一种混合的协同过滤算法WSRec[17], 通过调节基于用户与基于服务这2种方法的计算结果比例得到最终的预测结果, 该方法在一定程度上缓解了数据稀疏性问题.基于模型的方法是根据QoS历史数据训练出一个预测模型, 大量的实验已验证了该方法在推荐系统中的有效性[20-22].Lo等[23]提出了基于矩阵分解模型EMF的QoS预测方法.EMF模型使用正则化项将用户和服务的QoS进行结合预测.另外, 考虑在真实的服务调用场景中, 服务QoS的值受到用户和服务的双重影响, 比如网络带宽和连接速度.许多结合了用户、服务上下文信息的Web服务推荐算法应运而生[24].He等[24]结合服务位置属性, 利用用户和服务的相对位置信息对服务QoS进行预测并提高预测精度.部分研究工作注意到用户的地理位置对于QoS属性值的影响[25-26], 当位于网络环境优劣与地理区域存在差异的用户调用相同的Web服务时, Web服务并非总能展现出相同的QoS.例如基于距离越近的用户具有越相似的QoS值这一假设, Chen等[27]提出了基于区域的方法, 将相似IP的小区域聚合成为大区域, 用以计算缺失的QoS值.然而这些方法都没有考虑由于网络突发情况, 而产生的噪声QoS数据的情况, 在QoS值预测中不对这些噪声数据进行处理势必影响预测精确度.
2 Web服务的服务质量预测系统框架Web服务的服务质量预测系统, 简称Web服务的QoS预测系统,其目标是为服务推荐作支撑, 服务推荐系统是为目标用户推荐服务质量最优或者较优的候选服务.Web服务的QoS预测的流程框架如图 1所示.
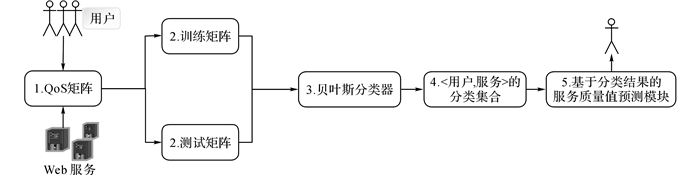
|
图 1 Web服务的服务质量(QoS)预测系统框架 Fig. 1 Frame of Web service QoS prediction system |
1) 服务质量矩阵.服务质量矩阵存储了所有历史调用服务质量值, 其中缺失值标记为空;
2) 训练矩阵和测试矩阵.从服务质量矩阵中随机抽样生成训练矩阵和测试矩阵.训练矩阵用于训练预测模型, 测试矩阵用于评估模型的预测精度;
3) 贝叶斯分类器.利用训练矩阵学习得到贝叶斯概率分类器.该分类器以贝叶斯统计和用户、服务个性特征为基础;
4)〈用户, 服务〉对的分类集合.使用步骤3) 得到的分类器预测训练矩阵的分类标签及其分类标签概率, 输出概率最大的K个分类标签及其分类标签概率;
5) 基于分类结果的服务质量值预测模块.利用分类结果提高筛选相似邻居的准确率.
3 基于贝叶斯分类的QoS预测方法传统协同过滤算法主要包括相似邻居集选择以及基于相似邻居集历史信息进行缺失服务质量值预测2个步骤.然而, 协同过滤算法在数据稀疏情况下存在相似邻居筛选不准确的问题.为了解决这个问题,一方面,在传统相似邻居选择过程中,引入了基于朴素贝叶斯概率分类器的噪声数据过滤机制,以提高相似邻居的筛选准确度.另一方面,在进行缺失值预测时,本文通过使用〈用户,服务〉对的分类概率作为预测QoS值的权重,改进了传统协同过滤方法,进一步提高预测精确度.
3.1 朴素贝叶斯概率分类器朴素贝叶斯是一种基于贝叶斯定理和特征独立性假设的分类方法.本文将〈用户, 服务〉对的外部信息转化为〈用户, 服务〉对的特性向量, 从而成功地将朴素贝叶斯分类方法用于〈用户, 服务〉对的分类.
3.1.1 特征提取本文所使用的数据集附带〈用户, 服务〉对的外部信息, 从中选择5个字段作为算法使用的特征向量:用户IP、用户经度、用户维度、服务提供商和服务所在国家.将该5个特征值映射为浮点数值形成反映〈用户,服务〉对的个性化属性向量,通过对这些个性化属性建模得到分类预测器.
3.1.2 类别划分本文采用的数据集为连续数值且其分布为[-1, 20], 考虑到朴素贝叶斯需要离散型标签, 通过对连续数值向下取整处理得到离散分类标签, 即得到[-1, 0, 1, …, 19]共21个分类标签.
3.1.3 朴素贝叶斯概率分类器朴素贝叶斯是基于贝叶斯定理、特征独立性假设的分类方法.对于一个给定待预测的〈用户, 服务〉对, 假设其特征向量为X, 那么其可能得到的分类标签y的条件概率为
| $ P(y|{x_1}, \ldots {x_n}) = \frac{{P\left( y \right) \bullet P({x_1}, \ldots ,{x_n}|y)}}{{P({x_1}, \ldots ,{x_n})}}. $ | (1) |
对于贝叶斯分类器来说, 输出的分类结果就是选择条件概率最高的分类标签.由于上述条件概率求解较为困难, 朴素贝叶斯基于下面2个假设简化了条件概率的求解:
1) 条件独立性假设, 在类确定的条件下, 用于分类的特征都是条件独立的;
2) 特征同等重要, 朴素贝叶斯认为反映样本属性的每个特征基于同等重要的地位.
因此, 式(1) 可以简化为
| $ P(y|{x_1}, \ldots, {x_n}) = \frac{{P\left( y \right)\cdot\Pi _{_{i = 1}}^nP({x_i}|y)}}{{P\left( {y|{x_1}, \ldots, {x_n}} \right)}}. $ | (2) |
式(2) 的分母对于任意一个特定的输入都是等值常量, 因此式(2) 可以进一步简化为
| $ P(y|{x_1}, \ldots, {x_n}) \approx P\left( y \right)\Pi _{_{i = 1}}^nP({x_i}|y). $ | (3) |
朴素分类的输出结果就是满足下式的分类标签:
| $ \bar y = {\rm{arg}}\;\mathop {{\rm{max}}}\limits_y P\left( y \right)\mathop \Pi \limits_{i = 1}^n P({x_i}|y). $ | (4) |
基于不同方法计算条件概率P(Xi|y)可以得到不同的朴素贝叶斯模型, 本文使用朴素贝叶斯, 假设条件概率P(Xi|y)符合下列分布:
| $ P({x_i}|y) = \frac{1}{{\sqrt {2\pi {\sigma ^2}_y} }}{\rm{exp}}( - \frac{{{{\left( {{x_i} - {\mu _y}} \right)}^2}}}{{2{\sigma ^2}_y}}). $ | (5) |
上述参数使用极大似然估计求解.分类器最终输出条件概率最大的标签.
3.1.4 分类器的输出通过3.1.3节的分类器, 可以得到任意指定特征向量在21个分类标签上的条件概率, 即分类结果的可能性.本文使用Top-K算法,得到分类器输出的概率最高的K个分类结果及其概率,并基于分类结果,改进传统协同过滤算法来预测缺失QoS值,其目的在于利用分类结果提高相似邻居的筛选准确度,利用各分类的概率提高预测精确度.
算法GNBC Creating:贝叶斯分类器生成算法
输入:训练数据集D, 测试数据集T
输出:预测结果R
1) 对训练数据集D和测试数据集T进行预处理, 生成〈用户, 服务〉对特征向量, 〈用户, 服务〉对分类标签;
2) 基于贝叶斯假设, 使用训练数据计算分布, 即可求得条件概率P(Xi|y);
3) 基于上述的分布结果, 计算测试数据分类标签的条件概率P(y|X1, X2, X3, … Xn);
4) 输出上述测试数据分类标签概率最高的K个分类标签及其分类结果, 作为测试数据的预测结果R.
3.2 基于概率分类器的可能性预测在进行服务推荐时首要步骤是为用户预测出其缺失的QoS值.对于待预测的QoS, 首先将其转化为4.1.1节中给出的〈用户, 服务〉特征向量.其次, 朴素贝叶斯概率分类器预测〈用户, 服务〉对的分类结果及其分类概率.最后, 输出K个概率最高的分类标签及分类标签概率值.下述的协同过滤算法将基于此输出结果, 同时综合考虑用户和服务所在的地理位置信息, 改进基于近邻的协同过滤算法, 进一步提高了预测精度.
3.3 基于分类概率的混合协同过滤算法混合协同过滤算法被广泛用于服务质量值的预测, 并且具有较好的预测精度.然而, 协同过滤算法在数据稀疏情况下存在相似邻居筛选不准确的问题.通过利用3.2节的分类预测结果以及〈用户, 服务〉对的地理位置信息, 本文通过过滤噪声数据, 有助于提高相似邻居的筛选准确度.
3.3.1 协同过滤算法传统的协同过滤算法可以分为基于用户的协同过滤算法和基于服务的协同过滤算法.
基于用户的协同过滤算法, 首先采用Top-K算法为目标用户u选择最为相似的K个用户邻居的集合, 记为N(u).其中, 相似度计算使用基于平均欧式距离的相似度计算方法, 平均欧式距离越小表示用户间越相似.然后基于相似邻居集合对目标服务i的历史行为预测目标用户对目标服务的行为.基于用户的协同过滤算法公式如下所示:
| $ {{\bar q}_{u, i}} = \frac{{\sum\limits_{v \in N\left( u \right)} {({s_{u, v}}{q_{v, i}})} }}{{\sum\limits_{v \in N\left( u \right)} {{s_{u, v}}} }}. $ | (6) |
式中:
基于服务的协同过滤算法, 首先为目标服务i选择最为相似的K个服务邻居的集合, 记为N(i).其中, 相似度计算使用基于平均欧式距离的相似度计算方法, 平均欧式距离越小表示服务间越相似.然后基于目标用户对相似邻居集合的历史行为预测目标用户对目标服务的行为, 基于服务的协同过滤算法公式如下所示:
| $ {{\bar q}_{u, i}} = \frac{{\sum\limits_{j \in N\left( i \right)} {({s_{i, j}}{q_{u, j}})} }}{{\sum\limits_{j \in N\left( i \right)} {{s_{i, j}}} }}. $ | (7) |
式中:
本文将3.2节得到的概率分类器作为噪声过滤器, 为目标用户和目标服务过滤那些因为偶然因素而成为相似邻居的“假”邻居, 这有助于提高相似邻居的筛选准确度.对于特定〈用户, 服务〉对经过贝叶斯分类器分类后得到的K个概率最高的分类标签的集合, 记为l, 即l规定了该〈用户, 服务〉对的待预测服务质量值的可能分类标签集合, 若其相似邻居对应的服务质量值不在这个分类标签集合内, 则将该相似邻居排除以提高筛选准确度.因此, 筛选目标用户u的相似邻居, 可使用如下公式:
| $ \overline {N\left( u \right)} = \{ v|v \in N\left( u \right), \left\lfloor {{q_{v, i}}} \right\rfloor \in l\} . $ | (8) |
式中:⌊qv, i⌋为其相似邻居向下取整后的服务质量值,
通过式(8), 可以在使用基于常用的相似度计算方法得到的相似邻居的基础上, 排除那些对目标服务实际表现与期望不符合的相似邻居.同时, 本文进一步考虑了不同预测结果标签的概率大小对最终预测结果的影响, 为概率大的标签所对应的相似邻居分配更大的权重.
利用贝叶斯分类结果的基于用户的协同过滤算法, 公式如下:
| $ {{\bar q}_{u, i}} = \frac{{\sum\limits_{v \in \overline {N\left( u \right)} } {({s_{u, v}}{\rho _{v, i}}{q_{v, i}})} }}{{\sum\limits_{v \in \overline {N\left( u \right)} } {({s_{u, v}}{\rho _{v, i}})} }}. $ | (9) |
式中:ρv, i为用户v调用目标服务i的QoS值所对应的分类标签的概率, 该概率越大则对应的历史QoS值qv, i在最终的预测结果中所占的权重越大, 表示该相似用户对目标用户有更大的影响力.
与相似用户邻居的更新类似, 更新目标服务i的相似邻居为
| $ \overline {N\left( i \right)} = \{ j|j \in N\left( i \right), \left\lfloor {{q_{u, j}}} \right\rfloor \in l\} . $ | (10) |
式中:⌊qu, j⌋为其相似邻居向下取整后的服务质量值,
考虑贝叶斯分类结果的基于服务的协同过滤算法的形式化表示如下:
| $ {{\bar q}_{u, i}} = \frac{{\sum\limits_{j \in \overline {N\left( i \right)} } {({s_{i, j}}{\rho _{u, j}}{q_{u, j}})} }}{{\sum\limits_{j \in \overline {N\left( i \right)} } {({s_{i, j}}{\rho _{u, j}})} }}. $ | (11) |
式中:ρu, j为目标用户u调用服务j的QoS值所对应的分类标签的概率, 该概率越大则对应的用户u对服务j的历史QoS值qu, j在最终的预测结果中所占的权重越大, 表示该相似服务对目标服务有更大的影响力.
3.3.3 聚合算法预测用户u对服务i的QoS值时, 本文不仅考虑基于用户的近邻方法, 也考虑基于服务的近邻方法, 并将2种方法预测的QoS值进行聚合, 公式为
| $ {{\bar q}_{u, i}} = \alpha {u_{u, i}} + \left( {1 - \alpha } \right){w_{u, i}}. $ | (12) |
式中:
实验采用WSDream公开数据集[17].该数据集包括5 825个服务和339个用户, 包括2个服务质量属性:响应时间和吞吐量.本文使用响应时间数据集, 该数据集被广泛用于服务QoS值预测精度评估, 因此基于该数据集的实验是可信且可靠的.
4.2 评估标准实验采用的度量标准是平均绝对误差(mean absolute error, MAE), MAE通过计算预测值与实际值的平均误差大小度量系统的推荐质量, MAE越小, 预测的准确率越高.MAE的计算公式如下:
| $ {\rm{MAE}} = \frac{1}{N}\sum\limits_{\left( {u, i} \right) \in {M_t}} {|{{\bar q}_{u, i}} - {q_{u, i}}|} . $ | (13) |
同时使用规一化平均绝对误差(normalized mean absolute error, NMAE)来进一步衡量算法的预测精度:
| $ {\rm{NMAE}} = \frac{{{\rm{MAE}}}}{{\left( {\sum\limits_{\left( {u, i} \right) \in {M_{\rm{t}}}} {{q_{u, i}}} } \right)/N}}. $ | (14) |
式中:Mt为测试集, N是测试集中待预测服务质量的个数, (u, i)为测试集中待预测服务质量的(用户, 服务)对.
由式(13)、(14) 可知,平均绝对误差和规一化平均绝对误差越小, 预测精度越高.
4.3 实验设置真实环境下, 用户服务矩阵是非常稀疏的, 用户通常只调用少部分服务, 不同用户之间重合的服务调用更是稀少.为了模拟真实环境, 本文从原始WSDream数据集中抽取部分数据作为训练集, 其余则为测试集.本文选取4个不同稀疏度的训练集进行实验, 稀疏度d分别为5%、10%、15%、20%, 其余全部作为测试集, 对4个不同稀疏度的训练集进行10次实验并取平均结果作为最终结果.
4.4 性能比较为了更好地评估所提出算法的性能, 本文实现了下述几个常见的服务质量值预测算法, 并在该实验集上进行大量比较实验:
1) UMEAN:通过求每个用户的平均QoS值对缺失值进行预测.
2) IMEAN:通过求每个Web服务的平均QoS值对缺失值进行预测.
3) UPCC:基于用户协同过滤算法, 使用皮尔逊相似度计算用户间的相似度.
4) IPCC:采用基于物品的协同过滤算法, 使用皮尔逊相似度计算物品间的相似度.
5) WSRec[17]:一种线性聚合协同过滤算法, 使用一个参数平衡UPCC和IPCC的预测结果在最终结果中的比重.
6) SVD[28]:采用矩阵因子分解算法, 挖掘历史数据的潜在信息寻找一个属性空间, 目标用户调用目标服务的服务质量值由用户和服务在此属性空间的点积求得.
7) LBR2[23]:使用用户信息中的经度、纬度来计算用户间的相似度、然后取离当前用户位置近的邻居集加入到矩阵因子分解的正则项中进行预测.
如表 1所示为不同训练矩阵密度情况下不同模型的预则性能比较.表中, MAE为平均绝对误差, NMAE为规一化平均绝对误差, d为训练矩阵的稀疏度.可以发现, 本文提出的预测方法BBCF在预测精度上高于其他的方法, 预测精度平均提升了超过10%.另外, 在不同的数据稀疏度情况下, 算法的性能差异不明显, 特别是在高数据稀疏度情况下, BBCF模型的预测精度仍旧较高, 这说明BBCF能较好地应对数据稀疏性问题.
| 表 1 不同训练矩阵密度情况下不同模型的预测性能比较 Table 1 Prediction performance comparison of different models on different training matrix densities |
贝叶斯分类器的分类预测精度结果如图 2所示.图中, topKLabels为概率最高的K个可能的分类标签, r为分类准确率, d为稀疏度, 如topKLabels=3, r=0.901 7, 说明真实标签落在概率最高的3个可能标签集合中的概率为90.17%.图 2给出了稀疏度d为5%和15%的实验结果, 随着topKLabels的逐渐增大, 分类准确率一开始迅速的增大, 当增大到一定程度后, 分类准确度开始收敛, 逐渐平稳.这说明分类器如果输出一个适当大小的结果区间能够得到较高的分类准确度.同时, 5%和15%的分类准确度相近, 说明该贝叶斯分类器对数据稀疏不敏感, 在数据稀疏的情况下, 可以保持模型的预测性能.

|
图 2 不同训练矩阵密度下贝叶斯分类器分类准确率随topKLabels变化 Fig. 2 Change of accuracy rate of Bayes classification when topKLabels increase on different training matrix density |
如图 3所示为在不同稀疏度(d=5%, 10%, 15%, 20%)情况下, 参数α取不同值时预测精度的实验结果.实验结果使用MAE进行评估, 较小的MAE表示较高的预测精度.从图中可以看出, 随着稀疏度的提高, MAE呈现下降趋势, 这是因为随着稀疏度的提高, 训练模型可以使用的历史数据随之增多, 模型能够从历史数据中挖掘出更多的有用信息来训练、修正模型参数.同时, 协同过滤算法为用户和服务筛选相似邻居时, 相似度计算由于拥有更多数据的支撑变得更加可靠和准确, 提高了协同过滤算法的预测精度.因此, 鼓励用户调用更多的服务可以提高推荐系统个性化推荐的效果.
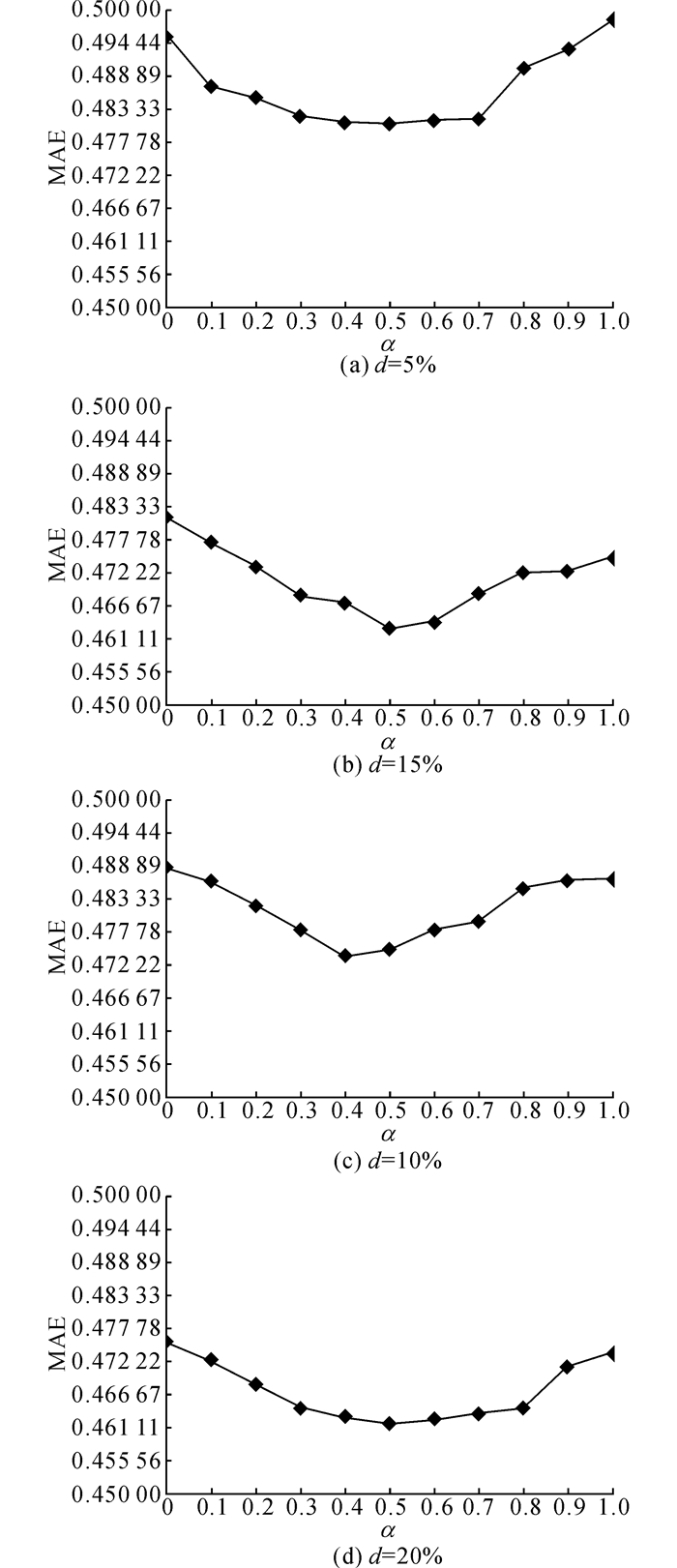
|
图 3 不同训练矩阵密度下预测精度随参数α变化 Fig. 3 Change of accuracy rate when α increase under different training matrix densities |
参数α作为一个平衡常数,调节了基于用户的协同过滤算法的预测结果和基于服务的协同过滤算法的预测结果在最终预测结果中所占的比例.如果α=0,则聚合算法将退化为基于用户的算法;α=1,则聚合算法退化为基于服务的算法.本文通过大量的实验确定参数的合理取值.从图中可以看出, 当α=0.4时,模型取得最佳预测性能,这是由于α取该值时模型既能够充分地利用用户相关属性的信息,同时兼顾了服务属性的相关信息,通过综合用户和服务个性信息,提高了预测精度.因此参数α最终取值为0.4.从图中可以看到,当α取值较小或者较大时,模型的预测性能明显快速下降,MAE迅速升高.这说明当只使用用户或者只使用服务的相关信息时,模型由于可用的信息不够而性能不佳.
4.7 参数topKUser的敏感性分析如图 4所示为不同稀疏度情况下, 参数topKUser的不同取值对预测精度的影响.较低的稀疏度意味着更少的可用信息.参数topKUser表示协同过滤算法中基于相似度为用户选择的相似邻居的大小, 其中相似度基于历史数据使用平均欧式距离计算.平均欧式距离越大, 表示用户之间的相似度越小.

|
图 4 不同训练矩阵密度下预测精度随参数topKUser变化 Fig. 4 Chang of accuracy rate when topKUser increase on different training matrix densities |
从图 4中可以看出,随着topKUser的逐渐增大, MAE一开始快速减小.这是由于随着为目标用户选择更多的近邻数, 目标用户真正的相似用户被选中的可能性变大, 同时由于本文使用贝叶斯分类器对上述筛选出相似邻居集合进行过滤, 会排除那些因为偶然原因成为相似用户的“假”相似用户.这些“假”相似用户和目标用户仅有少量的共用调用记录, 同时该调用记录由于偶然因素表现出强的相似性.相似邻居的可靠性得到增强.从这里可以看出, 通过进一步使用贝叶斯分类器进行过滤, 可以提高模型的预测精度.
当topKUser增大到一定程度后, MAE趋向于平缓, 这是由于参数取较大值后, 相似的定义变得宽松, 很多相似性不强的用户也被筛选出作为目标用户的相似用户, 这影响了预测精度的进一步提高.
4.8 参数topKWs的敏感性分析如图 5所示为不同稀疏度情况下, 参数topKWs取不同值时对预测精度的影响.参数topKWs表示协同过滤算法中为目标服务筛选相似邻居的大小.
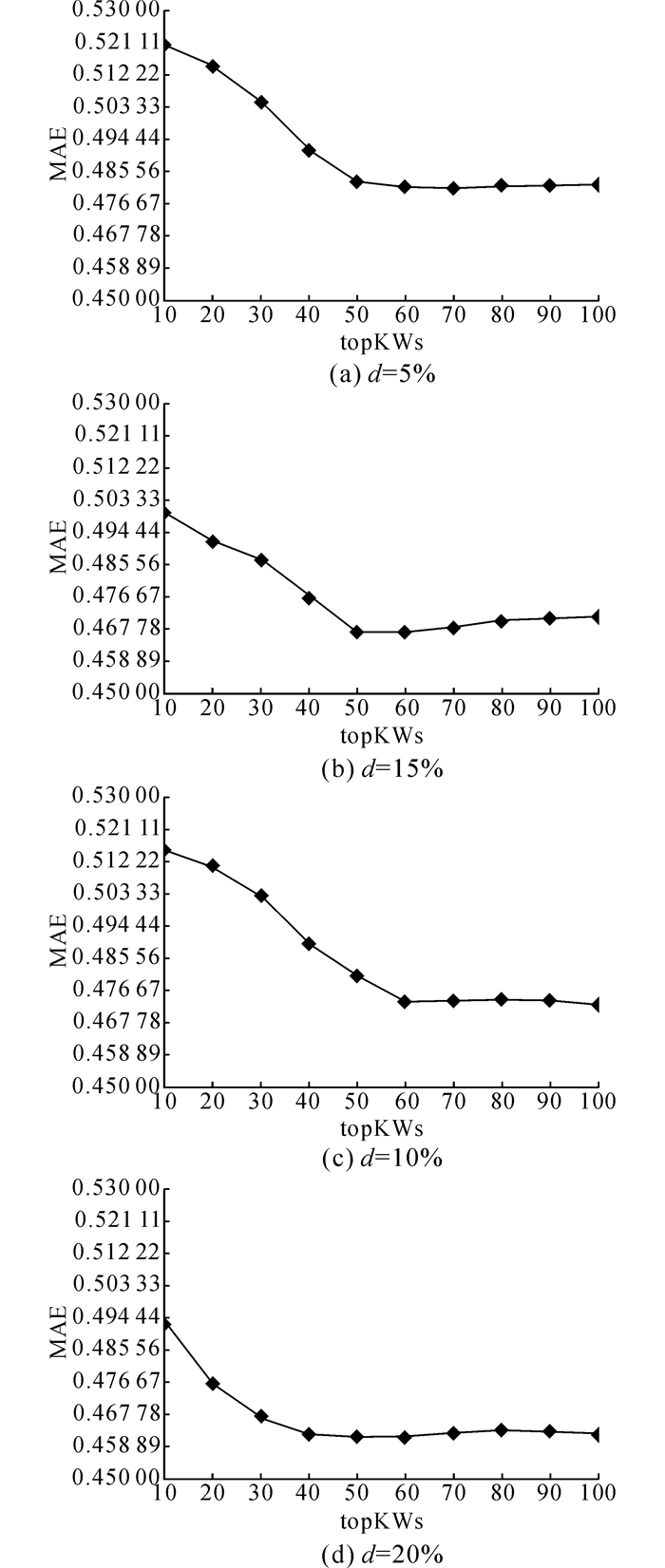
|
图 5 不同训练矩阵密度下预测精度随参数topKWs变化 Fig. 5 Change of accuracy rate when topKWs increases under different training matrix densities |
当参数topKWs取较小值时, 相似邻居的筛选标准趋于严格, 只有历史行为趋势十分一致的服务才会被选为相似邻居.此时筛选出的相似邻居数量较少, 如果此相似邻居是该目标服务真正的相似服务, 则该情况下模型的预测精度较高.相反地, 此时筛选出的相似服务如果仅仅是由于偶然因素而被选为相似邻居, 则此时预测精度较低.虽然, 出现由于偶然因素成为相似邻居的情况较少, 但此时相似邻居集合较小, 因此一旦出现该情况则会严重影响最终的预测精度.从图中可以看出,当topKWs取较小值时MAE较大, 而随着topKWs的逐渐增大, MAE逐渐减小.这样,当topKWs取值较大时, 即使出现上述误选择的情况, 也不会明显影响最终的预测结果.
5 结语本文提出了一种基于贝叶斯分类的混合协同过滤Web服务质量预测方法.实验结果表明, 通过对相似邻居的过滤, 能够有效降低服务质量噪声数据对服务质量预测的影响.与其他服务质量预测方法相比, 本文所提BBCF方法均表现出较高的预测精确度, 特别是在数据稀疏度较高的情况下, BBCF方法仍能保持较高的预测精度仍能保持较高水平.
下一步的改进方向包括基于其他联合概率分布计算朴素贝叶斯的后验概率, 期待更好地符合服务质量数据集的分布, 提高分类准确率.此外,可尝试进一步挖掘用户和服务的地理位置信息以及时间信息以进一步提高预测精度.
| [1] | SHAO L, ZHANG J, Wei Y, et al. Personalized QoS prediction for Web services via collaborative filtering[C] // 2007 IEEE International Conference on Web Services. Salt Lake City: IEEE, 2007: 439-446. |
| [2] | ZHENG Z, MA H, LYU M R, et al. QoS-aware Web service recommendation by collaborative filtering[J]. IEEE Transactions on Services Computing, 2011, 4(2): 140–152. DOI:10.1109/TSC.2010.52 |
| [3] | KONSTAN J A, MILLER B N, MALTZ D, et al. GroupLens: applying collaborative filtering to Usenet news[J]. Communications of the ACM, 1997, 40(3): 77–87. DOI:10.1145/245108.245126 |
| [4] | RESNICK P, IACOVOU N, SUCHAK M, et al. GroupLens: an open architecture for collaborative filtering of netnews[C] // Proceedings of the 1994 ACM Conference on Computer Supported Cooperative Work. New York: ACM, 1994: 175-186. |
| [5] | LINDEN G, SMITH B, YORK J. Amazon. com recommendations: item-to-item collaborative filtering[J]. IEEE Internet computing, 2003, 7(1): 76–80. DOI:10.1109/MIC.2003.1167344 |
| [6] | HILL W, STEAD L, ROSENSTEIN M, et al. Recommending and evaluating choices in a virtual community of use[C] // Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. New York: ACM, 1995: 194-201. |
| [7] | DESHPANDE M, KARYPIS G. Item-based top-n recommendation algorithms[J]. ACM Transactions on Information Systems (TOIS), 2004, 22(1): 143–177. DOI:10.1145/963770 |
| [8] | BALABANOVI M, SHOHAM Y. Fab: content-based, collaborative recommendation[J]. Communications of the ACM, 1997, 40(3): 66–72. DOI:10.1145/245108.245124 |
| [9] | STOJANOVA D, CECI M, APPICE A, et al. Network regression with predictive clustering trees[J]. Data Mining and Knowledge Discovery, 2012, 25(2): 378–413. DOI:10.1007/s10618-012-0278-6 |
| [10] | MILLER B N, ALBERT I, LAM S K, et al. MovieLens unplugged: experiences with an occasionally connected recommender system[C] // Proceedings of the 8th International Conference on Intelligent User Interfaces. Florida: ACM, 2003: 263-266. |
| [11] | SU X, KHOSHGOFTAAR T M. A survey of collaborative filtering techniques[J]. Advances in Artificial Intelligence, 2009, 2009(4): 1–19. |
| [12] | ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(6): 734–749. DOI:10.1109/TKDE.2005.99 |
| [13] | BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C] // Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence. Madison: Morgan Kaufmann Publishers Inc, 1998: 43-52. |
| [14] | CARDELLINI V, CASALICCHIO E, GRASSI V, et al. Flow-based service selection for Web service composition supporting multiple QoS classes[C]//2007 IEEE International Conference on Web Services. Salt Lake City: IEEE, 2007: 743-750. |
| [15] | JIA Z, YANG Y, GAO W, et al. User-based collaborative filtering for tourist attraction recommendations[C]//Computational Intelligence and Communication Technology (CICT). Paris: IEEE, 2015: 22-25. |
| [16] | SARWAR B, KARYPIS G, KONSTAN J, et al.Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. Hong Kong: ACM, 2001: 285-295. |
| [17] | ZHENG Z, MA H, LYU M R, et al. Wsrec: a collaborative filtering based web service recommender system[C] // 2009 IEEE International Conference on Web Services. Los Angeles: IEEE, 2009: 437-444. |
| [18] | SHAO L, ZHANG J, WEI Y, et al. Personalized QoS prediction for Web services via collaborative filtering[C] // 2007 IEEE International Conference on Web Services. Salt Lake City: IEEE, 2007: 439-446. |
| [19] | ZHENG Z, ZHANG Y, LYU M R. Distributed QoS evaluation for real-world Web services[C] // 2010 IEEE International Conference on Web Services. Miami: IEEE, 2010: 83-90. |
| [20] | RENNIE J D M, SREBRO N. Fast maximum margin matrix factorization for collaborative prediction[C] //Proceedings of the 22nd International Conference on Machine Learning. Bonn: ACM, 2005: 713-719. |
| [21] | SALAKHUTDINOV R, MNIH A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo[C] // Proceedings of the 25th International Conference on Machine Learning. Helsinki: ACM, 2008: 880-88. |
| [22] | SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization[J]. Advances in Neural Information Processing Systems, 2007, 49(8): 1257–1264. |
| [23] | LO W, YIN J, DENG S, et al. Collaborative Web service QoS prediction with location-based regularization[C] // 2012 IEEE 19th International Conference on Web Services. Honolulu: IEEE, 2012: 464-471. |
| [24] | HE P, ZHU J, ZHENG Z, et al. Location-based hierarchical matrix factorization for Web service recommendation[C] // 2014 IEEE International Conference on Web Services. Anchorage: IEEE, 2014: 297-304. |
| [25] | XU Y, YIN J, LO W, et al. Personalized location-aware QoS prediction for Web services using probabilistic matrix factorization[C] // 14th International Conference on Web Information Systems Engineering. Nanjing: WISE, 2013: 229-242. |
| [26] | CHEN X, ZHENG Z, LIU X, et al. Personalized QoS-aware web service recommendation and visualization[J]. IEEE Transactions on Services Computing, 2013, 6(1): 35–47. DOI:10.1109/TSC.2011.35 |
| [27] | CHEN X, LIU X, HUANG Z, et al. Regionknn: a scalable hybrid collaborative filtering algorithm for personalized Web service recommendation[C] // IEEE International Conference on Web Services. Miami: IEEE, 2010: 9-16. |
| [28] | KOREN Y. Collaborative filtering with temporaldynamics[J]. Communications of the ACM, 2010, 53(4): 89–97. DOI:10.1145/1721654 |



