大数据试验场是支撑用户开展试错性在线研究和试验, 完成基于大数据样本数据组织、分析、利用及其系统架构方面试验的公共平台, 其目的是提高数据的利用能力, 降低大数据应用开发和利用的门槛.试验场将为应用企业、个人和科研机构提供大数据处理的模拟环境, 以支撑用户从平台、数据、数据分析方法等方面对大数据的处理、应用和系统的分析进行拓展试验.大数据试验场是用于开展大数据技术研究和人才培养、具有科技与工程创新的开放性、领先性的重大基础设施, 将成为国家大数据战略的重要组成部分[1-2].
大数据试验场拟支持4类试验:探索类试验、证明类试验、体系结构类试验和模拟类试验.探索类试验要求数据已知, 但目标和方法不限定, 如应根据几组数据找出其关联性或者一组数据中可以提取出多少信息.证明类试验数据和目标都已知, 仅需要验证结果与所要求证的是否相符.体系结构类试验的研究领域及目标都没有约束, 需要根据已有数据去探索发现其中一些未知的关系.模拟类试验是以已知的数据和方法作为模拟试验达到之前未知的目标.
本文根据已有的基准测试程序集, 给其分配不同类型及数量的资源, 经过一系列方法的处理, 资源分配方法得到优化, 实现资源利用率的提升.以大数据试验场的样本数据为基础, 采用本文提出的两段式优化资源方法, 计算出多个用户各自可申请的最大任务数, 故本文实验属于大数据试验场应用中的体系结构类试验.
1 背景介绍大数据试验场以云平台为基础, 用户向云平台申请资源, 申请的资源数量是需要关注的问题.申请资源的数量不当会导致资源无法充分利用, 称之为无效资源.假如多个用户同时向云平台申请资源, 无效的资源配置方案会导致资源利用率较低, 从而资源分配将无法实现全局最优.总之, 资源分配不当将诱发以下不良影响:1) 资源浪费, 对同一类应用, 当提供等量资源而无法获得同样收益的情况下, 再投入的资源将造成浪费,称之为无效资源;2) 无效开销, 对无效资源的支付增大了应用的开销;3) 资源配置低效, 对于给定的平台, 系统总资源是一定的, 无效的资源分配对同一平台上的其他类应用的运行造成影响, 这种非优的资源配置将造成系统性能的劣化;4) 环境影响, 运算资源的利用需要耗用自然资源, 例如耗电、碳排放等.无效资源分配和配置有悖于绿色计算的趋势.
为了避免上述由于资源分配不当而引起的不良影响, 用户在申请资源时需要确定单个任务需要投入的最合适资源数量, 而当多个用户同时申请资源时, 就需要有效的资源配置方案来实现全局最优.
YARN作为资源调度与分配的平台化工具[3],提高了资源利用率, 但还是存在资源浪费的情况.因每个应用程序在向YARN申请资源时都需要提供指定的CPU和内存数量, 而管理员往往并不能明确地知道每个应用程序实际需要的资源量, 这就使应用程序在申请资源时会申请比实际需求数量更多的资源, 致使不必要的资源浪费.针对资源浪费问题, 文献[3]里提出了Yadoop解决方案, 对资源进行动态管理.为了让YARN中容器内的资源量可以根据容器内进程的实际使用情况动态变化, 既不影响容器内任务的正常运行, 又能将容器资源量调整到一个合适的位置, 减少资源浪费.Yadoop解决方案中容器的部署和启动显得较为麻烦, 并且在进行与YARN的对比实验时, 测试单个任务CPU和内存利用率时选择的最佳CPU数量不当, 导致对比实验没有在同一基准情况下进行,虽然得到以下结果:Yadop比YAPN在任务运行时对系统资源的平均资源利用率高,但实际上此结果不具备充分的说服力.
针对如何提高资源利用率的问题, 本文提出两段式资源优化分配方法.第一阶段:对单类任务上的资源分配进行优化, 即确定每类任务应该分配的最优资源数量.当为单类任务分配资源时, 其性能的提升幅度与所分配的资源数量并非呈线性关系, 随着单位资源的等量投入,性能并不会等量提升, 需要通过合理的资源分配, 让资源的利用率更高.这就要求在资源-性能关系图上找到Trade-off Point (以下称为饱和点).在饱和点之前, 多分配一个单位的资源会让性能有更好的提升;而在饱和点之后, 多分配一个单位的资源提升性能的幅度很小.饱和点代表了应给任务投入的最佳资源, 找到了饱和点, 就实现了单个任务的最优化.为了简单说明问题, 本文将任务的运行时间作为性能的参考指标.第二阶段是在第一阶段完成的基础上, 利用占优资源公平分享算法(dominant resource fairness, DRF)算法[4]进行系统级的资源配置, 确立每类任务可启动的任务数, 达到全局最优的目标.DRF算法是Mesos中使用的资源调度算法, 支持在多种资源类型上的公平分配, 每个类型的作业根据各自对资源的需求, 在自己最需要的资源类型上获得公平分配, 以此来保证公平性和资源的最大使用效率.DRF具备了4条特性[4]:1) 资源共享:集群中的每个用户共享资源比独占资源有更好的使用效率; 2) 杜绝欺诈:用户谎报自己的实际需求并不能获取更多的资源; 3) 公平最优:一个用户不会愿意用自己已经获得的资源去交换另外一个用户的资源, 因为交换后并不会运行更多的任务; 4) 帕累托均衡[5-7]:每个用户都不可能在不减少其他用户资源份额的情况下增加自己的资源份额.这4条特性体现了DRF算法的公平共享特性.通过运用DRF算法可以制定出有效的系统级资源配置方案, 从而确定每类任务可启动的最大任务数, 进而达到全局最优的目的.
本文在提出两段式优化方法之前进行了大量试验, 验证了两段式优化方法的正确性及可靠性.实验样本采用Cilk+的基准程序测试集[8], 其中包括计算密集型和内存密集型(也可称为I/O密集型)程序, 这2种程序的运行时间分别受CPU和内存所分配的数量影响.另外, 本文采用Docker容器技术将程序封装成Docker镜像, 方便通过Docker命令进行资源分配.Docker容器的优势在于:1) 启动、停止或部署迅速, 几秒之内即可完成;2) 可以在运行时动态分配资源, 方便未来解决更复杂的资源分配问题.3) Docker容器可以独立部署和扩展, 完成某个特定的功能, 实现松耦合, 在出现问题时也容易定位[9-13].
2 相关工作在资源分配优化方面已有较多研究.Le等[14]提出了单个资源多任务之间的公平分配, 但无法应对多种资源之间的分配, Ghodsi等[4]将Max-min fairness扩展到了多种资源上, 使多任务多类型资源之间的公平分配得以实现. Joe等[15-16]对多种类型资源间的分配如何均衡作出改进, 在公平和效率之间进行了权衡.
YARN社区的Joe等[15]指出, 目前YARN的资源分配都是以容器为单位, 而容器资源量一旦分配后便不能再改变, 如果用户需要更改某些容器的资源量, 唯一的方法便是先释放容器再重新申请新的资源.Joe等[15]认为对容器的资源量要有可调节性, 提出了在命令行增加动态调节资源的命令接口, 使用户可以在合适的时候调节特定容器的资源, 然而这需要用户密切关注应用程序运行动态.赵颖[3]提出Yadoop资源解决方案, 为了让一个容器中运行多个进程, 可以动态地控制容器的资源, 采用的方法是不对CPU进行隔离, 即多任务共享CPU, 然而在内存资源方面, 无法做到不隔离.
本文利用Docker容器技术将程序封装成Docker镜像, 由于Docker容器是轻量级的, 无论是启动、停止或者删除, 都方便且迅速, 而且可以在任务运行过程中动态改变任务的资源, 不需要先释放容器再重新申请.另外, Docker容器之间相互隔离, 任务运行完毕后自动释放资源, 故Docker容器测出来的数据较合理, 从而在对单类任务寻找饱和点时效果甚佳.在第一阶段找出每个任务的饱和点后, 第二阶段利用DRF算法就可以构建出有效的资源配置方案, 确定每类任务可以同时启动的任务数, 资源利用率得以提升, 从而实现资源分配的全局最优.
3 技术路线 3.1 生成任务实例创立Dockerfile文件夹, 通过写Dockerfile指令将程序复制到Dockerfile文件夹, 然后运行Docker build命令建立Docker镜像, 通过Docker run命令生成Docker容器, 运行时可以动态调整所分配资源, 至此生成了一个任务实例.
3.2 两段式优化方法本文针对提高资源利用率的问题, 提出两段式资源优化分配方法.假设有M个用户, 每个用户共有N类任务.第一阶段:对于每类任务, 通过Docker容器技术封装成任务实例, 分别计算出每类任务的饱和点, 实现单个任务最优.第二阶段:在每类任务的饱和点已找出的基础上, 利用DRF算法实现多类任务的全局最优, 确定每类任务可启动的最大任务数.技术路线如图 1所示.
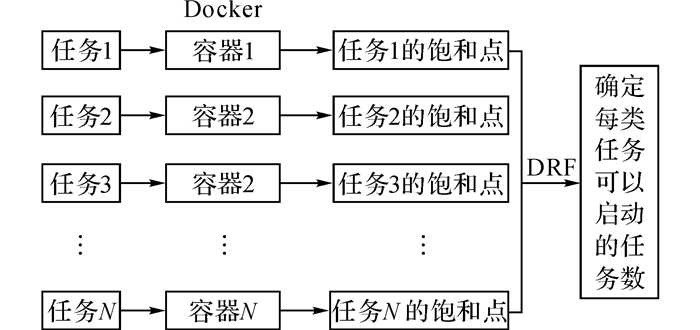
|
图 1 两段式资源优化分配方法框图 Fig. 1 Block diagram of two-phase optimizationmethod for resources allocation |
对单个任务来说, 通常随着所分配资源数量的增加, 其运行时间会越来越短, 但其关系并不是线性的, 故实现单个任务资源的最优化实际上就是找到资源-时间图上的饱和点.对于如何找到饱和点, 试验采取了3种方法并进行了比较.
观察对某计算密集型程序进行测试并绘出CPU-时间图, 如图 2所示. Jacob提出的方法为计算曲线各点到原点的距离[17], 取距离最近的点作为饱和点, 对于此程序所测的数据来说看似可行, 饱和点所对应的横坐标为3核, 即代表 3个CPU是应为此任务申请的最优计算资源.但是这种方法仅仅满足某些特例, 设想曲线斜率的绝对值若不是一直由大变小的, 如是从小变大, 那么此方法所计算出的最近的点就未必是其饱和点.
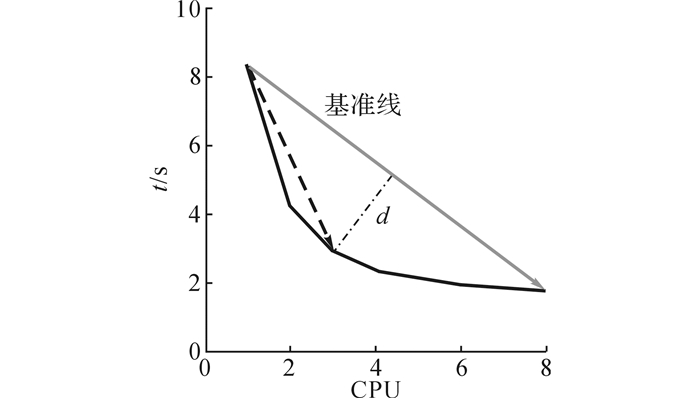
|
图 2 某计算密集型程序不同CPU数量下的运行时间变化 Fig. 2 Runtime variations of compute-intensive program in different numbers of CPU |
Jonas提出的方法为将图上的第一点到最后一点连起来[17], 称这条线为基准线, 如图 2所示.计算图上所有的点到基准线的距离, 距离最远的点作为饱和点.方法思想:第一个点是给该任务分配1个CPU时运行的时间, 最后一个点是8个CPU运行的时间, 基准线是把分配1个CPU到8个CPU时任务运行的时间假设成线性下降.刚开始资源分配数量从1个CPU提升到2个CPU时, 可观察到运行时间下降的非常快, 两点间直线斜率的绝对值远大于基准线斜率的绝对值, 意味着在此点多分配一个单位资源所带来的运行时间的缩短即性能提升是有利的.当资源数量从7个CPU提升到8个CPU时, 发现斜率已经趋于水平, 运行时间几乎没有减少, 就表示这里再多分配一个单位的资源完全没有必要, 而可将这一单位资源分配给其他任务.距离基准线最远的点就可以当作斜率刚好和基准线相等或者最接近(斜率绝对值大于基准线)时, 再多分配一个单位的资源, 运行时间相应的并没有等量的减少, 从而可以将距离基准线最远的点当作饱和点.
本文提出的方法是画一条y=-x的线作为基准线, 计算图中点到基准线的距离, 距离最近的点作为饱和点.取y=-x作为基准线是因为其斜率绝对值为1, 其意义是分配一个单位的资源刚好可以带来一个单位时间的下降, 即一个单位性能的提升.
在资源-时间图上每个点的斜率k的绝对值的几何意义为增加一单位的资源, 时间下降了k个单位, 如果|k|>1, 就表示增加一单位资源可以带来多于1个单位时间的性能提升;如果|k|≤1, 就表示增加一单位资源并不能带来同样的性能提升.综上, 取边界k=-1(因为运行时间是随着所分配资源的增加而下降的), 画出基准线——y=-x.可以将y=-x这条线不断向上平移, 第一个与资源-时间图相交的点就是所求的饱和点, 可以转化为求点到直线的距离, 即图上的点到y=-x这条基准线距离, 距离最近的点即为所求饱和点.
其中单个资源类型情况下计算图中点与基准线的距离公式为
| $ v=\min \left( \frac{\left( {{x}_{i}}+{{y}_{i}} \right)}{\sqrt{2}} \right). $ |
式中:xi和yi代表比例化后各点的x值和y值.计算出的v是线上点到基准线的最短距离, 而最初的第i个值对应的即为饱和点.寻找饱和点的算法如算法1.
算法1 FindTradeOffPoint (R, T)
输入:R[1…n]:资源数量
T[1…n]:运行时间
输出:最合适申请的资源数R[i]
1. scaling (R, T) //比例化
2. distance ← calc_distance (R, T) //计算点到基准线的距离
3. min_index = min (distance) //取距离基准线最小值的点
4. return R[min_index] //返回最合适的资源数
4.2 寻找饱和点的方法比较Jacob提出的方法[17]没有理论依据, 仅仅是某些特例的简化式计算方法, 当情况并不是如图 2所示的逐渐下降的趋势, 就可能出现错误的结果.
Jonas提出的方法[17]只能处理静态图, 即对于给定的数据和图来说, 求出的饱和点是正确的, 但是该方法仅适用于部分情况.如图 2所示, 由于是将第一点和最后一点连起来, 基准线的斜率会随着所测CPU数量的多少发生变化, 变化后的饱和点可能与之前的不一样.图 2是测1个CPU到8个CPU的资源-时间图, 基准线是从第1个点连到第8个点.如果是测1个CPU到16个或者是32个CPU的时候, 基准线斜率将会变化.由于此方法是计算图上的点到基准线的距离, 结果也会受到影响,求出的饱和点可能并不准确.
本文提出的方法弥补了上述方法的不足, 由于y=-x这条基准线是不随着所测数据的不同发生变化, 其几何意义也非常明确, 就是观察多分配一个单位的资源能否带来更好的性能提升.如果可以, 那么再多分配一个单位的资源, 直到不能带来更好的性能提升为止.所以综合来看, 本文提出的方法更合理.
4.3 基于DRF的多任务最优化配置第一阶段结束后, 每个用户的任务都已经获得自己的需求, 即获得应该向系统申请的资源数量, 为了制定有效的系统级资源配置方案, 本文利用Ghodsi等[4]提出的DRF算法.单个资源类型多用户之间的资源分配用的最多的方法就是Max-min fairness算法[18-20], 而DRF作为改进的Max-min fairness算法就可以适用于多资源类型的资源分配.
DRF方法满足于多种资源类型的公平分配, 并且满足帕累托最优[4].在一个用户申请资源的时候, 假设现在资源类型为CPU和内存2种, 即需求向量里是有CPU和内存的,计算其占服务端总CPU和内存的比重, 比重较大的为占优资源, 其比重称作占优比.例如, 用户A运行的任务占CPU比重较大, 用户B运行的任务占内存比重较大, 那么用户A的占优资源就是CPU, 其占优比即A的CPU占总资源中CPU的比重, 而用户B的占优资源即为内存.DRF算法是想最终让2个用户的占优比相等, 即A的CPU占总资源的比重与B的内存占总资源的比重相等, 这是为了让用户根据自己对资源的需求, 在自己最需要的资源类型上获得公平分配.
赵颖提出了Yadoop的解决方案[3], 在针对多任务多种类型资源的调度方面采用的也是DRF算法.因为DRF会同时考虑CPU和内存的分配情况, 但是在使用容器方面, Yadoop使用的容器启动与部署方面都比较复杂.本文利用Docker容器轻松解决这个问题, Docker容器能够非常快捷方便的启动、停止与释放.Yadoop与YARN的对比实验结果表明, Yadoop仅仅在CPU利用率上比YARN高出不少, 在内存利用率上几乎没有改进.在CPU利用率的对比实验中, 如图 3所示, 取6个CPU作为对比时的虚拟CPU个数不具有很强的说服力.尽管6个CPU是Yadoop利用率最高的一点, 却是YARN CPU利用率的最低点, 以6个CPU来做实验的话结果Yadoop比YARN利用率高不足为奇.
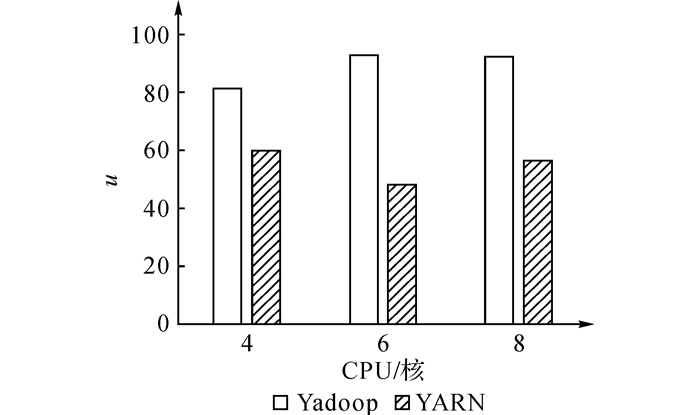
|
图 3 Yadoop与YARN在不同CPU数量下CPU利用率的变化 Fig. 3 CPU utilization rate viriations in different numbers of CPU between Yadoop and YARN |
本文以Docker容器承载应用程序, 方便快捷的进行启动部署及停止释放资源.在测出单个任务最优的资源需求向量后, 针对多个任务的情况利用DRF算法计算每类任务可以同时启动的实例个数.在不超过资源总数的情况下, 每个类型的作业根据各自对资源的需求, 在自己最需要的资源类型即占优资源上获得公平分配, 从而保证公平性, 并实现了资源使用效率的最大化.
本文假设单个用户的所有任务具有相同的需求向量, 利用DRF算法处理多个用户同时申请资源时需要建立的系统级资源配置方案.
DRF (D,R,C,U,s)
输入:D[1…n][1…m]: D[i]为用户i的任务需求
R[1…m]: R[i]总资源数量
C[1…m]: C[i]已消耗的资源数量
U[1…n][1…m]: U[i][j]用户i已得到的资源数量
s[1…n]: s[i]为用户i的占优比
输出:每个用户可启动的任务数T[1…n]
1. WHILE true
2. i ← min (s) //取最小的占优比, 先分配资源
3. IF C + D[i] ≤ R THEN
4. C ← C + D[i]
5. U[i] ← U[i] + D[i]
6. T[i] ← T[i] +1
7. s[i] ←maxjm=1{U[i][j]/R[j]}
8. ELSE
9. BREAK
10. END IF
11. END WHILE
12. RETURN T
DRF算法每轮先寻找具有最低占优资源的用户, 如果资源数足够, 则先分配给该用户相应的资源, 更新资源总消耗量和用户所占有的资源及任务数, 直到资源不足, 循环结束.设每个用户需要运行m个任务, 总共有n个用户, 每轮寻找最小的占优比需要遍历1次数组s, 为n次, 故时间复杂度为O(mn2).
5 案例分析本节介绍DRF的分配方法, 并对实验结果进行了验证和分析.本实验环境是在(8核, 8 GB)的单台机器上进行的, 实验样本采取Cilk+的基准测试程序集, 因为Cilk语言为C/C++语言增加了细粒度任务支持, 使其可以充分发掘多处理器的能力.Cilk+是针对多处理器即多核能力, 在需要改变所分配的核数时不需要修改代码, 通过Cilk+程序提供参数接口, 可直接在运行时修改参数.Cilk+是在将程序集各自封装成Docker镜像, 运行生成Docker容器, 在Docker层面可以控制内存的分配.这样可以通过容器的方法可以更好的操作, 如启动、停止操作在几s内就可以完成, 快捷方便, 还可在任务运作过程中动态控制资源.为了保证实验结果的真实性及可靠性, 每组实验重复测量5次,取其平均值.
5.1 实验结果及评估如图 4所示为几个不同类型基准测试程序的资源-时间图.通过本文提出的寻找饱和点的方法, 计算出每个任务的饱和点.圈出的点代表该任务最适合投入的资源数量.图 4(a)表明, 在3个CPU之前每多增加一个CPU, 运行时间下降很多.例如给其分配1 CPU的时候, 该任务的运行时间是20 s, 增加到2 CPU时就降为10 s, 3个CPU时为5 s;而在3个CPU之后, 从图中可知,运行时间随着资源的等量分配下降得越来越慢, 曲线渐渐平缓, 最后几乎不变.由此可确定3个CPU为找出的饱和点, 即该任务应向系统申请的资源数量.图 4(b)为一个任务的内存数量与运行时间的关系, 在给其分配10 MB内存的时候, 该任务的运行时间为4 s.当增加至15 MB内存时, 运行时间骤降到1.75 s左右, 而给其分配20 MB内存时, 该任务还是以同样的速度下降至低于0.5 s;之后无论分配多少内存, 时间几乎都没有下降.因此,20 MB就是该任务的饱和点, 该任务应向系统申请20 MB内存.同理, 从图 4(c)不难发现1 530 MB处为其饱和点.
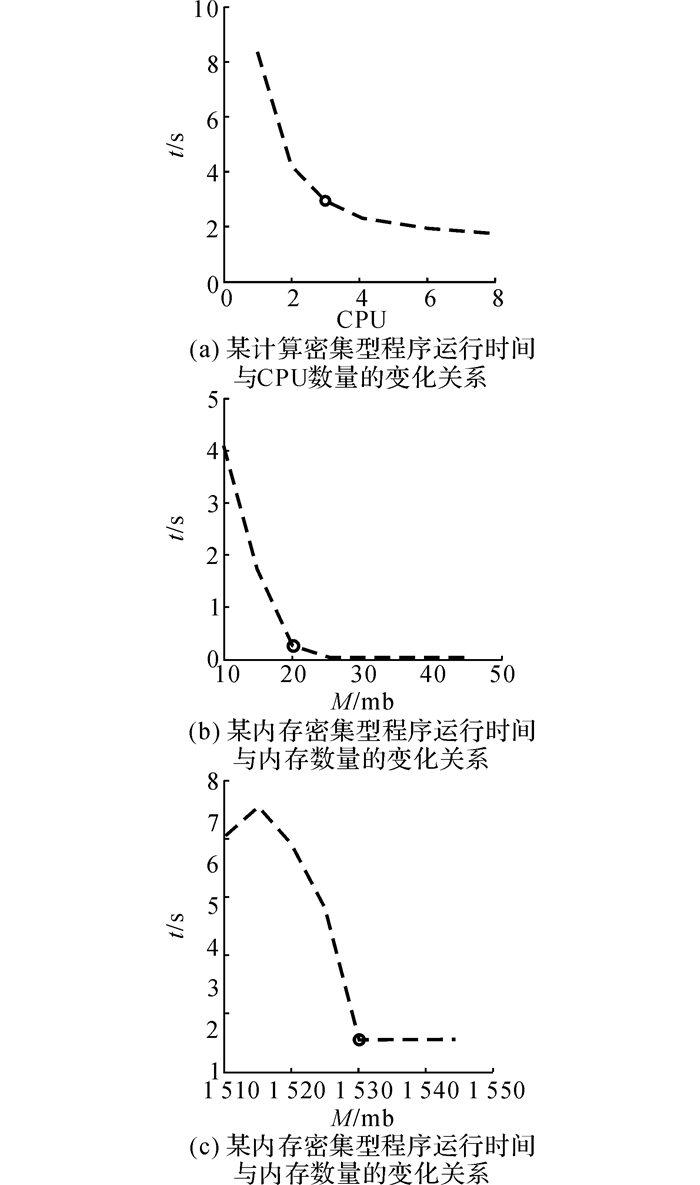
|
图 4 程序不同类型的运行时间与资源数量的变化关系 Fig. 4 Runtime of different program types variations in different numbers of resource |
通过以上的3个案例验证了本文提出的方法, 但很重要的一点是:在计算时, 首先必须将横纵坐标的单位间隔比例化,使之相同, 再将比例化后的坐标归一化, 这样确保了x轴的单位资源对应y轴的单位时间, 且能看出资源的等量投入是否会带来时间的等量下降, 从而观测出何时资源达到饱和, 保证结果的正确性.在一个任务受CPU和内存影响都比较大的情况下, 就需要对CPU和内存同时分配不同的数量进行测试, 根据测试的结果画出三维图形, 其中x轴是CPU, y轴是内存, z轴是运行时间.与二维图形中取直线y=-x作为基准线同理, 取平面x+y+z=0作为三维图形中的基准平面, 找出图中距离此平面最近的点, 即为饱和点.对于多变量指标的情况, 需要做定比运算, 以保持各个变量对目标(这里是运行时间)的影响一致.
针对上述Jacob提出的计算图中各点到原点的距离的方法[17], 以及Jonas提出的计算各点到由首尾点相连构成的基准线距离的方法[17], 也进行了大量实验.由于实验数据比较合理, 与本文提出的方法在单个自变量对运行时间的影响上差别不大, 但是Jacob和Jonas提出的方法无法针对多个自变量(如CPU和内存)对运行时间同时产生影响时准确地找出饱和点.实验对Cilk+的基准测试程序集都进行了实验验证, 实验结果都比较理想, 结论正确.
5.2 DRF的分配方法经过对单个任务进行优化, 已测出每类任务的饱和点.接下来将介绍DRF是如何对资源分配进行优化.
例如, 1个系统〈8 CPU, 16 GB〉和2个用户, 用户A运行的任务需求向量为〈1 CPU, 6 GB〉, 用户B运行的任务需求向量为〈3 CPU, 1 GB〉.不难发现用户A的每个任务需要消耗1/8 CPU和3/8内存, 所以A的占优资源为内存, 而用户B的每个任务消耗了3/8 CPU和1/16的内存, 所以B的占优资源为CPU.当用户A运行2个任务, 用户B运行2个任务时, A占了3/4的内存, B占了3/4的CPU, 达到了占优比相等的状态, 恰好CPU资源已分配完, 分配完成.
用户A和B能同时运行的最大任务数为max (x, y), 受到以下3个条件的约束:
| $ \begin{align} &x+3y\le 8, \\ &6x+y\le 16, \\ &{6}/{16x={3}/{8y.}\;}\; \\ \end{align} $ |
分配方法如下:设用户A运行x个任务, 用户B运行y个任务, 用户A将会占有〈x CPU, 6x GB〉, 占优比为3x/8, 用户B占有〈3y CPU, y GB〉, 占优比为3y/8, 则A和B共占有〈(x+3y) CPU, (6x+y) GB〉.在不超过总资源的前提下, 令3x/8 = 3y/8, 可得x=y=2.最终分配给用户A的资源为〈2 CPU, 12 GB〉, 分配给用户B的资源为〈6 CPU, 2 GB〉.此时, CPU资源刚好分配完, 用户A的占优资源即内存占了系统总资源中内存的3/4, 用户B的占优资源即CPU同样占了系统总资源中CPU的3/4.
当然, DRF算法也适用于多个用户间的资源分配, 而且总体上满足帕累托均衡, 因此可利用DRF算法实现多类任务间资源的最优配置, 从而使多类任务间的资源分配达到最优.
6 结语在大数据试验场的环境下, 本文提出了一种基于大数据试验场应用的两阶段资源优化分配方法.对于单类任务先通过标定资源饱和点, 之后对于多类任务分配资源, 本文基于DRF的最优资源配置, 确定给每类任务可启动的最大应用实例个数, 并利用试错法完成大数据试验, 以具有代表性的Cilk+的基准测试程序集进行实验, 检验了方法的有效性.
未来将会利用大数据试验场的样本数据开展进一步的实验, 根据试验应用类型以及特定应用的实例个数, 在有限的平台资源条件进行有效的优化资源配置.目前实验环境是在单台机器上进行的, 用Docker模拟多CPU的伪分布式情况.基于当前的实验结果, 以后会针对真正的分布式诉求环境, 在多台机器上进行真正的分布式实验, 进一步对结论进行验证.而时间弹性和用户动态改变资源需求将成为大数据试验场样本数据面临的挑战.
| [1] | 李吉萍. 复旦大学稳步推进大数据试验场建设[EB/OL]. [2016-08-29]. http://news.fudan.edu.cn/2016/0829/42127.html. |
| [2] | 上海数据科学重点实验室. 发展农业大数据产业的关键[R]. [2016-07-09]. http://wenku.baidu.com/view/4de92d88783e0912a3162aa9.html. |
| [3] |
赵颖. Hadoop环境下的动态资源管理研究与实现[D]. 上海交通大学, 2015.
ZHAO Ying. Research and implementation of dynamic resource management on Hadoop[D]. Shanghai: JiaoTong University, 2015. |
| [4] | GHODSI A, ZAHARIA M, HINDMAN B, et al. Dominant resource fairness: fair allocation of multiple resource types[C] // NSDI 2011. Boston:[s. n.], 2011: 24. |
| [5] | KANBUR R. Pareto's revenge[M]. New York: Cornell University, 2005: 2-8. |
| [6] | TOMOIAGA B, CHINDRIS M, SUMPER A, et al. Pareto optimal reconfiguration of power distribution systems using a genetic algorithm based on NSGA-Ⅱ[J]. Energies, 2013, 6(3): 1439–1455. DOI:10.3390/en6031439 |
| [7] | VIJAY K. How well do we know Pareto optimality?[J]. The Journal of Economic Education, 1991, 22(2): 172–178. DOI:10.1080/00220485.1991.10844705 |
| [8] | Cilk+的基准测试程序集[CP/DK]. Charles E. Leiserson: MIT CSAIL Supertech Research Group, 2010. |
| [9] | BALALAIE A, HEVDARNOORI A, JAMSHIDI P. Microservices architecture enables DevOps: migration to a cloud-native architecture[J]. IEEE Software, 2016, 33(3): 42–52. DOI:10.1109/MS.2016.64 |
| [10] | ALPERS S, BECKER C, OBERWEIS A, et al. Microservice based tool support for business process modelling[C] // Enterprise Distributed Object Computing Workshop. Adelaide: IEEE, 2015: 71-78. |
| [11] | NADAREISHVILI I, MITRA R, MCLARTY M, et al. Microservice architecture: aligning principles, practices, and culture[M]. O'Reilly Media, Inc, 2016. http://shop.oreilly.com/product/0636920050308.do |
| [12] | RICHARDSON C. Introduction to microservices[EB/OL]. [2015-05-19]. https://www.nginx.com/blog/introduction-to-microservices. |
| [13] | DRAGONI N, GIALLORENZO S, LAFUENTE A L, et al. Microservices: yesterday, today, and tomorrow[J/OL]. arXiv preprint arXiv: 1606.04036. 2016: 1-17. https://arxiv.org/abs/1606.04036. |
| [14] | LE B, JEAN Y. Rate adaptation, congestion control and fairness: a tutorial[EB/OL]. (2012-08-23)[2016-11-21]. http://ica1www.epfl.ch/PS_files/LEB3132.pdf. |
| [15] | JOE W, SEN S, LAN T, et al. Multiresource allocation: fairness-efficiency tradeoffs in a unifying framework[J]. IEEE/ACM Transactions on Networking, 2013, 21(6): 1785–1798. DOI:10.1109/TNET.2012.2233213 |
| [16] | PARKES D, PROCACCIA A, SHAH N. Beyond dominant resource fairness: extensions, limitations, and indivisibilities[J]. ACM Transactions on Economics and Computation, 2015, 3(1): 1–18. |
| [17] | BRIAN T. Finding the best trade-off point on a curve[EB/OL]. (2010-01-07)[2016-11-21]. http://stackoverflow.com/questions/2018178/finding-the-best-trade-off-point-on-a-curve. |
| [18] | SUH C, MO J. Resource allocation for multicast services in multicarrier wireless communications[J]. IEEE Transactions on Wireless Communications, 2008, 7(1): 27–31. DOI:10.1109/TWC.2008.060467 |
| [19] | HAHNE E. Round-robin scheduling for max-min fairness in data networks[J]. IEEE Journal on Selected Areas in Communications, 1991, 9(7): 1024–1039. DOI:10.1109/49.103550 |
| [20] | LAN T, KAO D, CHIANG M, et al. An axiomatic theory of fairness in network resource allocation[M]. [S.l]: IEEE, 2010: 1-17. |



