基于混合学习策略的教与学优化算法

引用本文 [复制中英文]

毕晓君, 王佳荟. 基于混合学习策略的教与学优化算法[J]. 浙江大学学报(工学版), 2017, 51(5): 1024-1031.
dx.doi.org/10.3785/j.issn.1008-973X.2017.05.024

BI Xiao-jun, WANG Jia-hu. Teaching-learning-based optimization algorithm with hybrid learning strategy[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(5): 1024-1031.
dx.doi.org/10.3785/j.issn.1008-973X.2017.05.024

[复制英文]

基金项目

国家自然科学基金资助项目(61175126)

作者简介

毕晓君(1966—), 女, 教授, 从事信息智能处理技术、智能优化算法、数字图像处理等研究.
orcid.org/0000-0002-5382-1000.
E-mail: bixiaojun@hrbeu.edu.cn

文章历史

收稿日期：2016-12-15

Contents Abstract Full text Figures/Tables PDF

基于混合学习策略的教与学优化算法

毕晓君 , 王佳荟

哈尔滨工程大学信息与通信工程学院, 黑龙江哈尔滨 150001

收稿日期：2016-12-15

基金项目：国家自然科学基金资助项目(61175126)

作者简介：毕晓君(1966—), 女, 教授, 从事信息智能处理技术、智能优化算法、数字图像处理等研究.
orcid.org/0000-0002-5382-1000.
E-mail: bixiaojun@hrbeu.edu.cn

摘要: 为了提高教与学优化算法(TLBO)的搜索能力, 解决算法易陷入局部最优的问题, 提出基于混合学习策略和扰动的教与学优化算法.在教与学算法的学阶段融合差分进化算法变异策略, 提出混合学习策略, 使学员在学习后期具有更好的学习能力, 提高算法的收敛性能；在算法后期提出新的扰动策略, 减小学员在算法后期陷入局部最优的可能, 保证算法全局最优性.基于标准测试函数的实验结果表明, 相比于目前性能优异的同类4种算法, 改进算法可有效提高算法的收敛速度和收敛精度, 优化性能明显提高.

关键词: 教与学优化算法差分变异扰动策略混合策略全局最优

Teaching-learning-based optimization algorithm with hybrid learning strategy

BI Xiao-jun , WANG Jia-hu

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China

Abstract: An improved teaching-learning-based optimization (TLBO) algorithm based on hybrid learning strategies and disturbance was proposed to improve the searching functions of the algorithm and solve the problem of being easy to fall into local optima. The mutation strategy of differential evolution algorithm was merged into the learning part of the algorithm, and a hybrid learning strategy was propased to improve the learning ability of students in the later learning as well as the convergence performance of the algorithm. A new disturbance strategy was constructed in the late stage to reduce the possibility of trapping into local optima and ensure global optimality. Experimental results based on the standard test function demonstrate that the proposed algorithm can effectively increase the convergence speed and accuracy and significantly advance the optimization compared with the current similar four kinds of algorithms with excellent performance.

Key words: teaching-learning-based optimization (TLBO) differential mutation disturbance strategy hybrid strategy global optimality

教与学优化算法(teaching-learning based optimization, TLBO)是2011年印度学者Rao等^[1]提出的一种新的群智能优化算法, 该方法通过模拟班级中老师的教学与学生的学习过程达到寻优目的.与粒子群算法、遗传算法等现有优化算法相比, 教与学优化算法具有收敛性能更优、需要的初始参数少、结构简单等优点, 特别在参数复杂的优化问题中效果更为明显^[2].但是TLBO算法在收敛精度和收敛速度上还有一定的提升空间^[3], 为此, 国内外学者在近几年相继提出多种改进的TLBO算法.利用粒子群优化算法具的有较好局部搜索能力^[4], Zou等^[5]将粒子群优化算法的粒子更新策略应用在TLBO的学习阶段, 提高了算法的搜索能力, 但易出现陷入局部最优的问题.高立群等^[6]提出了一种带差分算法交叉部分的TLBO算法(CTLBO), 在一定程度上提高了收敛精度, 但是增加的交叉部分使算法计算复杂度大大提高, 运算时间很长.李会荣等^[7]在2016年将差分进化算法(DE)变异策略融入TLBO算法, 提出一种融合差分变异的教与学优化算法(DMTLBO)来增强算法的收敛速度, 但是容易在迭代过程中陷入局部最优.这些改进算法都是以TLBO算法为基础, 提高了算法的收敛性能, 但是对于算法来说, 收敛性能还有一定的提升空间, 改进算法容易导致算法复杂度过高或种群多样性下降, 从而使得算法易陷入局部最优或早熟收敛.

鉴此, 本文提出一种基于混合学习策略和扰动策略的教与学优化算法(DSTLBO).在学习阶段, 融合差分变异策略, 同时控制变异策略在学习过程中的权重来形成一种混合学习策略, 使算法前期具有全局搜索能力, 而在后期增强局部搜索能力, 加快收敛速度.并且, 为了防止种群多样性下降而导致算法陷入局部最优, 加入扰动策略, 提升种群多样性, 使算法具有跳出局部极值的能力.通过仿真实验表明, 同4种目前优化性能最好的教与学优化算法相比, 本文在保证种群多样性的情况下在收敛速度和收敛精度2方面均有明显改善.

1 教与学优化算法

基本的教与学优化算法以班级为单位进行教学和学习.每个班级就是搜索空间中的每个种群, 班级里的人数就是种群的规模, 学生学习的科目就是决策空间的维度, 学习水平代表优化算法中的适应度, 老师是种群适应度值最好的个体^[8].教与学优化算法主要分为2个阶段, 教师对学生的教学阶段和学生之间相互学习阶段^[9].

1.1 初始化班级同学

为保证个体在决策空间中的多样性, 群智能优化算法中的初始种群一般按式(1) 生成^[10].TLBO算法中根据式(1), 在解空间中随机生成班级中的n个成员.

$ {\mathit{\boldsymbol{x}}^i} = {\mathit{\boldsymbol{x}}^{{\rm{min}}}} + {\rm{rand}}\left( {0, 1} \right)\left( {{\mathit{\boldsymbol{x}}^{{\rm{max}}}} - {\mathit{\boldsymbol{x}}^{{\rm{min}}}}} \right). $

(1)

式中:i=1, 2, …, n, {x₁, x₂, x₃…x_n}∈x, x^max和x^min分别为解空间中x能取到的最大值和最小值, rand (0, 1) 表示[0, 1]之间的随机数.

1.2 教学阶段

在TLBO的教学阶段, 选取适应度值最好的学员充当教师来提高班级学员的学习水平, 从而班级的平均水平不断提高, 向最优解方向移动.

班级同学的平均水平(种群均值)与老师之间的差距如式(2) 所示.

$ {D_{{\rm{difference}}}} = {\rm{rand}}\left( {0, 1} \right)\left( {{\mathit{\boldsymbol{x}}_{{\rm{teacher}}}} - {T_f}{\mathit{\boldsymbol{x}}_{{\rm{mean}}}}} \right). $

(2)

式中:x_teacher为当前种群适应度值最优的个体, x_mean为班级同学的平均个体, $ {{\mathit{\boldsymbol{x}}}_{\rm{mean}}}={\sum\limits_{i=1}^{n}{{{\mathit{\boldsymbol{x}}}^{i}}}}/{n}\; $, T_f为教学因子, 由式(3) 产生.

$ {{T}_{\rm{f}}}=\rm{round}\left( 1+\rm{rand}\left( 0,1 \right) \right). $

(3)

式中:round表示四舍五入取整.

在教学阶段班级中第i个学习者根据式(4) 产生新个体.

$ \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = \mathit{\boldsymbol{x}}_{{\rm{old}}}^i + {D_{{\rm{difference}}}}. $

(4)

用f(xⁱ)表示每个学员的适应度值, 它是寻优的判定准则, 如果f(x_newⁱ)大于f(x_oldⁱ), 则更新x_oldⁱ.反之, 则保留x_oldⁱ, 不进行更新.

1.3 学阶段

在实际教学过程中, 老师的教学是一个启发式的过程^[1], 学生不一定能根据老师的教学有效提高自己, 在课下不断向其他同学学习可以更有效的提高能力, 这就是TLBO算法的学阶段.

在学阶段, 学员从经过教学后的班级中随机选取一个个体x_r按照式(5) 进行学习, r∈(1, n).

$ \begin{array}{l} \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = \\ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}_{{\rm{old}}}^i + {\rm{rand}}\left( {0, 1} \right)\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i - {\mathit{\boldsymbol{x}}_r}} \right), f\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i} \right) > f\left( {{\mathit{\boldsymbol{x}}_r}} \right);\\ \mathit{\boldsymbol{x}}_{{\rm{old}}}^i + {\rm{rand}}\left( {0, 1} \right)\left( {{\mathit{\boldsymbol{x}}_r} - \mathit{\boldsymbol{x}}_{{\rm{old}}}^i} \right., \;\;f\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i} \right) < f\left( {{\mathit{\boldsymbol{x}}_r}} \right). \end{array} \right. \end{array} $

(5)

也就是说, 学生不仅通过教学阶段老师的教学提高自己的能力, 在学阶段也向班级中的其他同学学习, 通过比较自己和其他同学的差异进行自我学习^[11].教与学优化算法模拟教学过程进行成绩的提高, 在实际应用中解决最小化类型问题.

2 基于混合学习策略和扰动的教与学优化算法

现有教与学优化算法通过改进式(5) 在一定程度上提高了算法的收敛速度和精度, 但每个阶段都使用这个公式不能很好的满足不同迭代时期对算法的需求, 前期收敛过强就会使算法过早陷入局部最优, 后期增加其种群多样性就会降低局部搜索能力.为此, 在TLBO学习阶段融入DE算法变异策略并进行改进, 采用一种混合策略控制基本算法和差分变异学习算法的权重, 使算法前期进行有效全局搜索, 后期加大局部搜索能力以提高收敛速度.同时, 为了防止算法在搜索过程中出现陷入局部最优的问题, 在算法后期加入扰动策略, 保证种群的多样性, 从而实现TLBO算法整体求解性能的提升.

2.1 混合学习策略 2.1.1 改进的差分变异策略

差分进化算法(DE)在求解连续变量的全局优化问题方面有较强的收敛性能和鲁棒性^[12].作为DE算法的关键步骤, 其变异阶段利用从种群中随机选取的2个个体的差向量(差分矢量)作为第3个个体的变化源, 既保证了种群的多样性又能使算法具有很好的收敛性能.

在各种变异策略中, 目前收敛性能较好的变异策略^[13]如式(6) 所示.

$ \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = {\mathit{\boldsymbol{x}}_{{\rm{best}}}} + F(\mathit{\boldsymbol{x}}_{{\rm{old}}}^i - \mathit{\boldsymbol{x}}_{{\rm{old}}}^j). $

(6)

式中:i, j∈{1, 2, …, n}.(x_oldⁱ-x_old^j)为2个变量i, j构成的差向量.F∈[0, 2]称为变异因子, 是控制DE算法变异部分的主要参数, 通过控制其大小来控制差向量的缩放幅度, 也就是对基向量的影响程度.x_best表示将基向量选取为当前种群中的最优个体.式(6) 利用最优解个体引导搜索方向, 变异个体受其制约并围绕最优解展开, 因而可以使收敛速度大大增加, 趋向最优解的能力大大提高.

由式(5) 可以看出, 在TLBO算法学习阶段, 学生随机挑选一个同学x_r, 根据自己(x_oldⁱ)和他的差异向其学习提高自己.由于式中第1项始终是x_oldⁱ, 也就是围绕x_oldⁱ进行学习, 学习水平的提高具有局限性, 不具有向着最优解进行快速收敛的能力, 局部搜索能力有待提高.所以结合式(6) 差分变异策略可以使算法收敛速度增加、趋向最优解能力提高的优点, 提出式(7) 如下所示.

$ \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = {\mathit{\boldsymbol{x}}_{{\rm{teacher}}}} + {\rm{rand}}\left( {0, 1} \right)\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i - \mathit{\boldsymbol{x}}_{{\rm{old}}}^r} \right). $

(7)

并且, 只随机选取一个同学, 并不一定保证“择优”, 如果选取的同学为最差生或较差生将会影响学习的效果.因此, 对式(7) 进一步改进, 同时向2个同学学习, 避免只选取一个同学的局限性, 如式(8) 所示.

$ \begin{gathered} \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = {\mathit{\boldsymbol{x}}_{{\rm{teacher}}}} + {\rm{rand}}\left( {0, 1} \right)\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i - \mathit{\boldsymbol{x}}_{{\rm{old}}}^j} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;{\rm{rand}}\left( {0, 1} \right)\left( {\mathit{\boldsymbol{x}}_{{\rm{old}}}^i - \mathit{\boldsymbol{x}}_{{\rm{old}}}^k} \right). \hfill \\ \end{gathered} $

(8)

式中：第1项为老师, 以老师的能力作为主要引导者, 使学生始终以最优解为目标提高自己的学习水平, 跳出原有算法围绕x_oldⁱ带来的局限性, 解决TLBO算法局部搜索能力较差的问题, 达到快速收敛效果.同时使用2个差向量(x_oldⁱ-x_old^j)、(x_oldⁱ-x_old^k)代表学习者随机选取2个不同的同学, 根据自己与他们的差距进行学习, 降低了最差生带来的影响.为了保持TLBO算法参数简单的特点, 使用rand函数代替DE算法变异因子F.

2.1.2 混合学习策略的提出

式(8) 以老师x_teacher作为第1项学习引导者, 使学习方向快速向着最优解进行, 带来的问题就是收敛速度的大大提高会使算法在初期就陷入局部最优.所以迭代前期应保持算法的全局搜索性, 提出的式(8) 应在算法迭代的后期起主要作用, 才能达到目的.因此, 本文将提出的融合差分策略的学习阶段和基本教与学算法的学习阶段相结合, 采用一种混合学习策略, 提出的学习方法如式(9) 所示.

$ \mathit{\boldsymbol{x}}_{{\rm{new3}}}^i = \left( {1 - \frac{t}{{{T_{{\rm{max}}}}}}} \right)\mathit{\boldsymbol{x}}_{{\rm{new1}}}^i + \left( {\frac{t}{{T{\rm{max}}}}} \right)\mathit{\boldsymbol{x}}_{{\rm{new2}}}^i. $

(9)

式中：t为算法当前迭代次数, T_max为算法最大迭代次数, x_new1ⁱ, x_new2ⁱ分别由式(5) 和(8) 求得.

通过式(9) 可以看出, 在算法初期, t较小, x_new1ⁱ前的系数(1-t/T_max)较大, 即基本TLBO算法所占比重较大, x_new1ⁱ以学生自己引导优化过程, 利用TLBO算法的特点, 更注重算法的全局搜索性, 方便根据班级整体水平进行寻优, 避免算法早熟收敛陷入局部最优.随着算法的推进, t逐渐增大, x_new2ⁱ前的系数(t/T_max)越来越趋近1, 相比x_new1ⁱ比重增多, 即融合差分变异策略的学习方法起到主导作用, 利用差分变异的特点, 使算法局部搜索能力增强, 更有效的趋向最优解.混合学习策略融合了基本TLBO学习方法和加入变异策略的改进方法, 使算法在不同迭代时期侧重的目的不同, 初期侧重全局搜索性, 后期侧重局部搜索性, 有效解决式(8) 带来的算法初期陷入局部最优的问题, 提高了收敛性能.

2.2 扰动策略的提出

TLBO算法与其他智能优化算法一样都存在一个问题, 随着算法的收敛, 种群多样性也会逐渐减少, 使算法出现易陷入局部最优的缺陷.虽然式(9) 解决了算法前期种群多样性下降易于陷入局部最优的问题, 但当t=(T_max/2) 临近的一段时间里, x_new1ⁱ、x_new2ⁱ2种算法系数相差不大, 仍然可能造成种群多样性下降, 从而导致陷入局部最优问题.所以在算法后半段t≥(T_max/2) 时, 加入扰动策略, 保证x_new2ⁱ收敛性能的同时, 兼顾对搜索空间的探索能力, 使个体跳出当前位置, 避免局部最优的停止限制.为此, 本文提出一种扰动策略, 如式(10) 所示.

$ \begin{gathered} \mathit{\boldsymbol{x}}_{{\rm{new}}}^i = \mathit{\boldsymbol{x}}_{{\rm{new3}}}^i + \left( {{\rm{rand}}\left( {0, 2} \right) - 1} \right){\rm{exp}}\left( { - {{\left( {\frac{t}{{{T_{{\rm{max}}}}}}} \right)}^2}} \right) \times \hfill \\ \left( {{\mathit{\boldsymbol{x}}_{{\rm{teacher}}}} - \mathit{\boldsymbol{x}}_{{\rm{new3}}}^i} \right).{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;t \geqslant {T_{{\rm{max}}}}/2. \hfill \\ \end{gathered} $

(10)

式中：x_new3ⁱ由式(9) 得到.(rand (0, 2)-1) 产生(-1, +1) 随机数, 代表方向的随机性.

扰动以x_new3ⁱ为出发点, 向随机方向扩大搜索范围.扰动的大小由一个e指数exp (-(t/T_max)²)控制.由于e指数的控制, 扰动的权重严格控制在(0, 1) 内, 并且可以看出在加入扰动的初期也就是t=T_max/2附近, 扰动因子的权重较大, 越接近最大迭代次数扰动对学习者的影响接近为0.这是因为扰动策略主要是减小t=T_max/2之后一段时间x_new2ⁱ易陷入局部最优的缺点, 算法接近最大迭代次数时不需要考虑陷入局部最优的问题, 因为优化算法的最终目的是寻找最优解, 并且后期是主要利用x_new2ⁱ的强收敛能力, 所以在算法最后就尽量减小扰动以达到寻优的目的.通过方向和大小的控制, 扰动策略使算法保证原有寻优方向的同时, 适当扩大个体的搜索范围, 提高种群多样性, 从而能够有效改善算法易陷入局部最优的缺陷.

2.3 DSTLBO算法实现流程

综上所述, 本文提出的基于混合学习策略和扰动的教与学优化算法(DSTLBO)的具体步骤如下.

步骤1 设置班级人数n, 学习的科目即种群的维度d, 算法最大迭代次数T_max, 当前迭代次数t初始化为1.并按式(1) 初始化班级成员.

步骤2 寻找班级中最优的个体(老师), 并计算班级同学平均水平x_mean.

步骤3 教学阶段, 按照式(2)、(3)、(4) 产生新个体, 并计算适应度值, 如果新个体适应度值优于旧个体, 则更新新个体, 反之保留旧个体.

步骤4 学习阶段, 学习者首先按照式(5) 进行学习, 得到新解x_new1ⁱ.然后按照式(8) 进行学习, 得到新解x_new2ⁱ.最后根据式(9) 产生动态自适应学习后的新个体x_new3ⁱ

步骤5 t＜T_max/2, 进入步骤6.t≥T_max/2, 按照式(10) 加入扰动策略.

步骤6 计算新产生的个体适应度值, 若新个体适应度值优于旧个体, 则更新新个体.

步骤7 对班级中的每个个体都进行上述教与学的过程.

步骤8 置t=t+1, 若t＜T_max, 则返回步骤3.若t≥T_max则算法结束, 输出当前最优个体.

DSTLBO算法流程图如图 1所示.

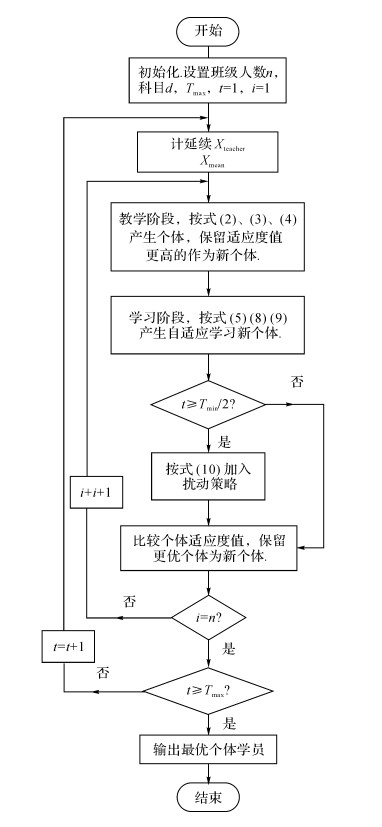
图 1 DSTLBO算法流程图 Fig. 1 Flow char of DSTLBO

3 仿真实验与结果分析

为验证本文提出DSTLBO算法的有效性和先进性, 选取通用的标准Benchmark函数^[14]和CEC2005^[15]测试函数中的部分函数作为适应度函数进行了一系列仿真实验, 该组测试函数包含不同特点的单峰和多峰函数, 在实际生活中具有普遍性.所有仿真实验都在Intel(R) Celeron(R) CPU G260@2.80GHz、4.00G内存、2.80GHz主频的计算机上进行, 软件运行环境为Matlab 2014a.

3.1 测试函数及评价标准

选取12个典型测试函数对算法进行测试, 其表达式如表 1所示.根据函数的性质分为单峰函数和多峰函数, 其中函数f₁~f₅是连续型单峰函数, f₆~f₁₂是连续型非线性多峰函数, 具有多个局部极值点, 可以用来测试算法的全局搜索性能和避免早熟的能力.

表 1 标准测试函数 Table 1 Benchmark functions

函数名称	搜索空间
$ {f_1}\left( x \right) = \sum\limits_{i = 1}^D {x_i^2} $	[-100, 100]
$ {f_2}\left( x \right) = \sum\limits_{i = 1}^D {{{\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)}^2}} $	[-100, 100]
$ {f_3}\left( x \right) = \sum\limits_{i = 1}^D {\left( {{{10}^6}} \right)\frac{{j - 1}}{{D - 1}}x_i^2} $	[-100, 100]
$ {f_4}\left( x \right) = \left( {\sum\limits_{i = 1}^D {{{\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)}^2}} } \right)\left( {1 + 0.4\left\| {{\rm{rand}}\left( {0, 1} \right)} \right\|} \right) $	[-100, 100]
$ {f_5}\left( x \right) = \sum\limits_{i = 1}^D {\left\| {{x_i}} \right\| + \Pi _{i = 1}^D\left\| {{x_i}} \right\|} $	[-10, 10]
$ {f_6}\left( x \right) = \sum\limits_{i = 1}^D {\left( {100{{\left( {x_i^2 - {x_{i + 1}}} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right)} $	[-100, 100]
$ \begin{array}{l} {f_7}\left( x \right) = - 20{\rm{exp}}\left( { - \frac{1}{5}\sqrt {\frac{1}{D}\sum\limits_{i = 1}^D {x_i^2} } } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;{\rm{exp}}\left( {\frac{1}{D}\sum\limits_{i = 1}^D {\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} {\rm{ }}} \right) + 20 + e \end{array} $	[-32, 32]
$ {f_8}\left( x \right) = \sum\limits_{j = 1}^D {\frac{{x_i^2}}{{4000}} - \Pi _{i = 1}^n{\rm{cos}}\left( {\frac{{{x_i}}}{{\sqrt i }}} \right) + 1} $	[-600, 600]
$ {f_9}\left( x \right) = \sum\limits_{j = 1}^D {\left( {x_i^2 - 10{\rm{cos}}\left( {2{\rm{ \mathsf{ π} }}{x_i}} \right) + 10} \right)} $	[-5.12, 5.12]
$ {f_{10}}\left( x \right) = \sum\limits_{j = 1}^D {x_i^2} + {\left( {\sum\limits_{i = 1}^D {0.5i{x_i}} } \right)^2} + {\left( {\sum\limits_{i = 1}^D {0.5i{x_i}} } \right)^4} $	[-10, 10]
$ \begin{array}{l} {f_{11}}\left( x \right) = \sum\limits_{j = 1}^D {\left( {\sum\limits_{k = 0}^{k{\rm{max}}} {\left[{{a^k}{\rm{cos}}\left( {2{\rm{ \mathsf{ π} }}{b^k}\left( {{x_i} + 0.5} \right)} \right)} \right]} } \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;D\sum\limits_{k = 0}^{k{\rm{max}}} {\left[{{a^k}{\rm{cos}}\left( {2{\rm{ \mathsf{ π} }}{b^k}0.5} \right)} \right]}, \\ \;\;\;\;\;\;\;\;\;\;\;\;a{\rm{ }} = 0.5, b = 3, {k_{{\rm{max}}}} = 20 \end{array} $	[-0.5, 0.5]
f₁₂(x)=f₈f₆=f₈(f₆(x₁, x₂))+ f₈(f₆(x₂, x₃))+…+ f₈(f₆(x_D-1, x_D))+f₈(f₆(x_D, x₁))	[-3, 1]

表 1 标准测试函数 Table 1 Benchmark functions

为了定量评价算法性能, 采用如下2种通用的评价指标^[16].

1) 收敛精度：达到最大迭代次数时的种群适应度值, 并且通过种群适应度的方差来判断算法的稳定性.

2) 收敛速度：采用进化过程曲线直观观察算法的收敛速度和精度的变化.

3.2 DSTLBO算法性能分析

为验证本文算法的先进性, 将其与TLBO算法^[1], 改进效果较好的CTLBO算法^[6]、TLBO-PSO算法^[5]、DMTLBO算法^[7]进行对比.为保证公平性, 综合参考群智能优化算法的相关文献, 所有算法的参数取值均为：算法初始种群规模n=50, 变量维度d=30, 最大迭代次数T_max=1 000.避免单次运行给算法评价带来的偶然现象, 各算法在每个测试函数上均运行30次.算法中还需要特殊设置的参数有：CTLBO算法中的交叉概率因子CR=0.95；DMTLBO算法中小组成员数量m=5, 动态分组频率p=5.

计算出30次运算的种群适应度的均值, 以此评价算法的收敛精度, 函数f₁~f₁₂的理想最优值均为0, 所以均值越接近0, 其收敛精度越高.每次运算得到的结果和均值比较得到的方差来评价算法的稳定性, 方差越小, 运算结果的浮动范围越小, 说明算法越稳定.实验数据如表 2所示.其中A_average为均值, V_variance为方差, t_second为程序的运行时间单位：s.

表 2 收敛精度结果对比 Table 2 Comparing the results of convergence precision

函数	算法	A_average	V_variance	t_second
f₁	TLBO	5.227×10^-188	6.451×10^-188	15.01
	CTLBO	3.256×10^-193	4.343×10^-193	41.00
	DMTLBO	6.512×10^-101	8.430 6×10^-101	17.02
	TLBO-PSO	0.000	0.000	14.82
	DSTLBO	0.000	0.000	18.66
f₂	TLBO	6.261×10^-61	9.242×10^-61	46.78
	CTLBO	3.582×10^-134	1.398×10^-134	610.54
	DMTLBO	1.073×10^-65	1.868×10^-65	50.26
	TLBO-PSO	9.952×10^-58	1.994×10^-57	41.45
	DSTLBO	2.501×10^-89	4.836×10^-89	38.98
f₃	TLBO	2.678×10^-182	3.489×10^-182	23.73
	CTLBO	9.323×10^-174	8.230×10^-174	403.54
	DMTLBO	5.871×10^-94	8.297 5×10^-94	30.34
	TLBO-PSO	0.000	0.000	34.45
	DSTLBO	0.000	0.000	28.48
f₄	TLBO	2.928×10^-172	3.159×10^-172	20.09
	CTLBO	6.687×10^-161	7.541×10^-161	185.54
	DMTLBO	2.740×10^-128	2.312×10^-128	32.69
	TLBO-PSO	0.000	0.000	18.51
	DSTLBO	0.000	0.000	27.95
f₅	TLBO	9.013×10^-32	1.509×10^-91	15.74
	CTLBO	3.242×10^-80	2.976×10^-80	170.44
	DMTLBO	1.224×10^-49	2.048×10^-49	13.14
	TLBO-PSO	8.907×10^-283	0.000	18.45
	DSTLBO	0.000	0.000	16.78
f₆	TLBO	2.384×10^-5	3.453×10^-5	16.25
	CTLBO	1.500×10^-9	1.932×10^-10	198.51
	DMTLBO	7.371	0.676	11.74
	TLBO-PSO	7.133	0.662	18.75
	DSTLBO	1.222	1.066	16.52
f₇	TLBO	3.553×10^-15	0.000	12.04
	CTLBO	3.989×10^-15	4.001×10^-15	180.4
	DMTLBO	3.553×10^-15	0.000	10.72
	TLBO-PSO	7.105×10^-16	1.423×10^-15	15.46
	DSTLBO	7.105×10^-16	1.423×10^-15	14.28
f₈	TLBO	0.028	0.0561	15.63
	CTLBO	4.292×10^-28	3.893×10^-28	186.69
	DMTLBO	4.761×10^-10	9.523×10^-10	12.41
	TLBO-PSO	0.000	0.000	15.18
	DSTLBO	0.000	0.000	15.19
f₉	TLBO	2.690	2.348	18.26
	CTLBO	6.383×10^-16	4.857×10^-17	195.54
	DMTLBO	2.364	4.728	22.96
	TLBO-PSO	3.980	4.874	19.46
	DSTLBO	0.000	0.000	18.24
f₁₀	TLBO	2.348×10^-167	0.000	40.54
	CTLBO	4.838×10^-188	9.382×10^-188	650.32
	DMTLBO	5.015×10^-94	4.809×10^-94	36.87
	TLBO-PSO	2.145×10^-283	0.000	87.35
	DSTLBO	7.26×10^-181	1.452×10^-181	66.65
f₁₁	TLBO	5.298×10^-188	6.873×10^-188	20.12
	CTLBO	9.253×10^-192	7.386×10^-192	458.13
	DMTLBO	3.744×10^-18	3.327×10^-18	29.14
	TLBO-PSO	0.000	0.000	22.83
	DSTLBO	0.000	0.000	25.18
f₁₂	TLBO	1.437×10^-64	2.543×10^-65	68.45
	CTLBO	9.287×10^-116	9.237×10^-116	715.24
	DMTLBO	4.935×10^-29	5.630×10^-29	84.16
	TLBO-PSO	8.235×10^-137	7.823×10^-137	64.28
	DSTLBO	9.234×10^-158	9.862×10^-158	68.85

表 2 收敛精度结果对比 Table 2 Comparing the results of convergence precision

从表 2中可以看出：对比TLBO算法、CTLBO算法、DMTLBO算法、TLBO-PSO算法, 本文提出的DSTLBO算法在12个测试函数中的9个函数优于其他算法, 其中f₁、f₃、f₄、f₅、f₈、f₉、f₁₁均能达到理论最优值.4个对比算法中, TLBO-PSO数据在大多函数上数据最优, 说明其在对比算法中效果最好.在函数f₁、f₃、f₄、f₈、f₁₁上DSTLBO和TLBO-PSO取得结果相同均能达到最优值, 在f₅、f₉、f₁₂上本文提出的DSTLBO要优于对比算法中最好的TLBO-PSO算法, 进一步说明本文算法在大部分测试函数上收敛精度均最优.对于f₂、f₆、f₁₀, 本文算法效果并不是最优, 通过观察函数图像发现, 这几个函数在最优值附近变化非常缓慢, 最优解周围的解相差很小, 其中单峰函数f₂加入扰动策略增大了向最优值的收敛速度, 但因解的范围集中所以扰动策略的效果影响较小；多峰函数f₆、f₁₀因为其各个局部最优值相差很小, 扰动策略的加入使其跳出极值的可能增大, 但辨别收缩方向需要更多时间, 因而并未搜索到最优解.所以本文算法针对极值附近变化缓慢、方向很难辨别的函数, 性能在几种对比算法中不能达到最优, 但相比基本TLBO算法性能还是有一定程度的提高.对于其他类型函数, DSTLBO算法在均值和方差上均明显优于其他算法, 且能够达到理想最优值.多峰函数由于其自身特性容易陷入局部最优导致算法停滞, 本文算法通过对多峰函数f₆~f₁₂的测试可以看出其具有跳出局部极值的能力, 拥有很好的收敛精度.所以可以看出, 在4种对比算法中, 本文提出的DSTLBO算法收敛精度较好, 稳定能力较强.

为了更直观地观察算法的性能, 列出几种算法在12个测试函数上的进化曲线以方便观察, 如图 2所示.图中t为迭代次数, 纵坐标F为适应度函数值, 为方便观察将其取log值.

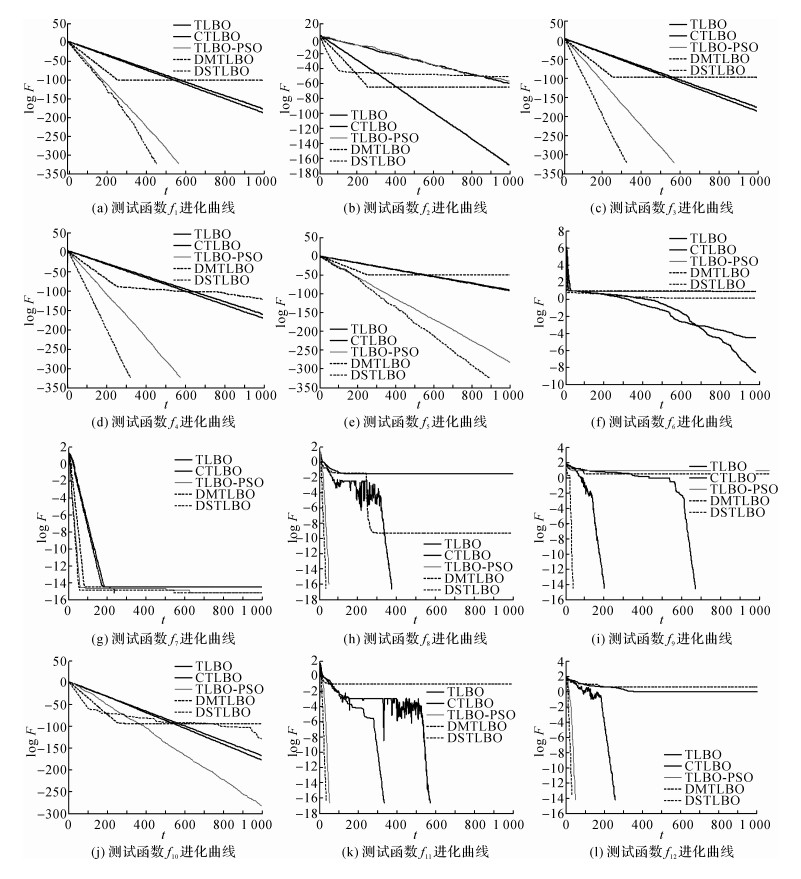
图 2 各个算法的收敛曲线 Fig. 2 The convergence curves of each algorithm

在12个测试函数中, f₁~f₅为单峰函数, f₆~f₁₂为多峰函数, 具有多个局部极值.通过图像可以更直观的看出, 对于大多数测试函数, 相比其他几种算法本文算法在进化代数相同的情况下达到的精度更优, 曲线的斜率更大, 说明算法的收敛速度更快.并且根据曲线的终点值可以看出本文算法达到的收敛值更优, 收敛精度更好.并且结合表 2中的运行时间, 该时间为算法运行30次平均每次的运行时间, 由于算法是在基本TLBO算法基础上进行的改进, 针对问题对求解过程有一定增加, 所以相对TLBO算法的运行时间本文算法稍长, 但是相对于其他改进的优化算法, 本文算法在运行时间上并未相差过多, 反而CTLBO算法由于交叉操作的引入使得程序运行时间过长.

通过观察f₁、f₉、f₁₁、f₁₂的几个图像看出, 同样加入差分变异的DMTLBO虽然在算法初期提高了收敛速度, 但是随着迭代的进行种群多样性下降, 收敛精度较差, 这是因为DMTLBO算法在学阶段一直使用快速收敛的方法, 没有考虑种群多样性的问题, 使其容易陷入局部最优停止收敛.对比算法中效果最好的TLBO-PSO算法, 在图 2中也可看出其相对其他对比算法的优越性, 但本文算法在大多测试函数上收敛性能要优于该算法.结合表 2得到的数据分析, 函数f₂、f₆、f₁₀由于其自身特点, 最优值附近函数值变化非常缓慢, 在搜索空间内大部分函数值和最优值接近, 局部最优值相差较小, 函数极值不明显, 在图中看出算法开始快速收敛后搜索方向的辨别难度增大使其不能更好的找到极值.所以进一步验证了本文算法对极值不明显、于其他类型的单峰函数和多峰函数, 本文算法具有较好的收敛性能.

通过对多峰函数的测试数据看出, 在多个局部极值的情况下, 本文算法仍然能具有较快的收敛速度, 同时保证了收敛精度的提高, 说明本文算法可以保证种群多样性, 有效避免迭代过程陷入局部最优.

综上所述, 本文提出的DSTLBO算法与其他算法相比, 具有较好的收敛精度、收敛速度和鲁棒性, 说明算法具有全局搜索能力和跳出局部最优的能力, 具有一定的应用价值.

4 结语

本文提出一种基于混合学习策略和扰动策略的教与学优化算法(DSTLBO).首先在教与学优化算法的学阶段融入差分变异策略, 并使用混合学习策略使学习前期进行全局搜索而后期利用差分进化算法的收敛性寻找最优解.其次, 在算法后期加入扰动策略, 使算法在寻找最优解的同时保证种群多样性, 避免过早陷入局部最优.在典型标准测试函数上进行仿真结果表明, 本文算法无论在单峰函数还是多峰函数上均具有很好的收敛性能, 下一步工作将验证DSTLBO在实际优化问题上的有效性.

参考文献

[1]	RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-aid Design, 2011, 43(3): 303–315. DOI:10.1016/j.cad.2010.12.015
[2]	RAO R V, PATEL V. Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm[J]. Applied Mathematical Modelling, 2013, 37(3): 1147–1162. DOI:10.1016/j.apm.2012.03.043
[3]	ZOU F, WANG L, HEI X H, et al. Teaching-learning-based optimization with dynamic group strategy for global optimization[J]. Information Sciences, 2014, 273: 112–131. DOI:10.1016/j.ins.2014.03.038
[4]	俞欢军, 张丽平, 陈德钊, 等. 基于反馈策略的自适应粒子群优化算法[J]. 浙江大学学报:工学版, 2005, 39(9): 1286–1291. YU Huan-jun, ZHANG Li-ping, CHEN De-zhao, et al. Adaptive particle swarm optimization algorithm based on feedback mechanism[J]. Journal of Zhejiang University: Engineering Science, 2005, 39(9): 1286–1291.
[5]	ZOU F, CHEN D, WANG J T. An improved teaching-learning-based optimization with the social character of pso for global optimization[J]. Computational Intelligence & Neuroscience, 2016, 2016(2): 1–10.
[6]	高立群, 欧阳海滨, 孔祥勇, 等. 带有交叉操作的教-学优化算法[J]. 东北大学学报:自然科学版, 2014, 35(3): 323–327. GAO Li-qun, OUYANG Hai-bin, KONG Xiang-yong, et al. Teaching-learning based optimization algorithm with crossover operation[J]. Journal of Northeastern University :Natural Science, 2014, 35(3): 323–327.
[7]	李会荣, 乔希民, 赵鹏军. 融合差分变异的教-学优化算法[J]. 计算机工程与应用, 2016, 52(5): 36–40. LI Hui-rong, QIAO Xi-min, ZHAO Peng-jun. Teaching-learning-based optimization algorithm by using differential mutation[J]. Computer Engineering and Applications, 2016, 52(5): 36–40.
[8]	CHEN D B, ZOU F, LI Z, et al. An improved teaching-learning-based optimization algorithm for solving global optimization problem[J]. Information Sciences, 2015, 297: 171–190. DOI:10.1016/j.ins.2014.11.001
[9]	刘前进, 许慧铭, 施超, 等. 改进教与学方法在电力系统无功优化中的应用研究[J]. 电力系统保护与控制, 2015, 43(9): 82–88. LIU Qian-jin, XU Hui-ming, SHI Chao, et al. Research on modified teaching-learning algorithm for reactive power optimization[J]. Power System Protection and Control, 2015, 43(9): 82–88. DOI:10.7667/j.issn.1674-3415.2015.09.013
[10]	匡芳君. 群智能混合优化算法及其应用研究[D]. 南京: 南京理工大学, 2014. KUANG Fang-jun. Hybridized optimization algorithms of swarm intelligence and their application [D]. Nanjing : Nanjing University, 2014.
[11]	CHEN D B, ZOU F, WANG J T, et al. A teaching-learning-based optimization algorithm with producer-scrounger model for global optimization[J]. Soft Computing, 2015, 19(3): 745–762. DOI:10.1007/s00500-014-1298-5
[12]	PRINCE K, STORN R M, LAMPINEN J A. Differential evolution: a practical approach to global optimization :natural computing series[J]. Natural Computing, 2005, 141(2): 1–24.
[13]	DAS S, SUGANTHAN P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4–31. DOI:10.1109/TEVC.2010.2059031
[14]	YAO X, LIU Y, LIN G M. Evolutionary programming made faster[J]. IEEE Trans on Evolutionary Computation, 1999, 3(2): 82–102. DOI:10.1109/4235.771163
[15]	SUGANTHAN P N, HANSEN N, LIANG J J, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R]. Singapore: NanyangTechnological University, 2005.
[16]	韩俊英, 刘成忠, 王联国. 动态双子群协同进化果蝇优化算法[J]. 模式识别与人工智能, 2013, 26(11): 1057–1067. HAN Ying-jun, LIU Cheng-zhong, WANG Lian-guo. Dynamic double subgroups cooperative fruit fly optimizationg algorithm[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(11): 1057–1067. DOI:10.3969/j.issn.1003-6059.2013.11.009