翼伞是一种伞衣完全充气展开后呈翼型的降落伞, 主要特点是具有可控性, 能够通过操纵单侧伞绳实现转弯动作, 控制翼伞的飞行方向, 通过下拉双侧伞绳减速实现雀降, 完成负载的平稳着陆.随着科学技术的发展和军事战略思想的转变, 精确空投和“定点无损”着陆在军事、航空航天等领域的应用越来越广泛[1].翼伞弥补了传统空投技术准确性、安全性不足的缺点, 能够通过操纵控制和雀降技术实现精确空投和平稳降落, 保证负载以较小的速度着陆, 减轻冲击和震荡[2-3].
动力翼伞系统不仅继承了翼伞的所有特点, 而且能够弥补空投高度不足带来的着陆误差, 实现远距离的精确空投.小型动力翼伞具有更广泛的用途, 例如在巡航应用中, 动力翼伞系统与固定翼无人机、四旋翼等飞行器相比具有速度低、性价比高、安全性高、续航时间长和抗干扰能力强的优势, 具有更广阔的应用前景[4].
在翼伞系统的轨迹跟踪控制中, 熊菁[5]针对传统比例-积分-微分控制(proportional-integral-differential, PID)和模糊PID控制以及混合型PID控制进行分析和研究, 李永新[6]提出了一种基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制方法, Benjamin[7]将L1自适应控制方法应用在大型翼伞的归航控制中, 以上研究均取得了较好的控制效果.但动力翼伞系统与无动力翼伞系统不同, 水平轨迹控制和垂直高度控制之间存在耦合效应, 控制难度较大.目前还没有关于翼伞下偏量和推力之间耦合关系的定量研究, 因此解耦控制方法尚不适用.Slegers[8]将模型预测控制方法应用于动力翼伞系统的轨迹跟踪控制, 利用简化的六自由度动力翼伞系统模型进行求解, 而简化模型不能完全反映动力翼伞系统的动态过程, 而且文献[8]只给出了动力翼伞系统的水平轨迹跟踪效果, 并未对高度控制进行仿真和实验分析.
为克服动力翼伞系统自身的非线性特性和外部风场干扰对轨迹跟踪控制的影响, 本文设计了一种基于自抗扰控制技术(active disturbance rejection control, ADRC)的轨迹跟踪控制器.自抗扰控制技术具有扰动估计和补偿能力, 所以动力翼伞系统的轨迹跟踪问题可以分为水平轨迹控制和垂直高度控制分别设计控制器, 将水平轨迹和垂直高度的耦合作用作为扰动进行实时估计和补偿, 实现了水平轨迹和垂直高度控制器的分离设计和独立工作.同时, 由于动力翼伞系统的GPS模块采样频率为1到10 Hz, 采样频率较低, 在设计ADRC控制器时采用零阶保持器法对扩张状态观测器(extended state observer, ESO)进行离散化可以取得更好的状态估计能力.此外, 本文通过改进水平轨迹控制通道的误差计算方法, 提高了动力翼伞系统的轨迹跟踪效果.
1 动力翼伞系统建模
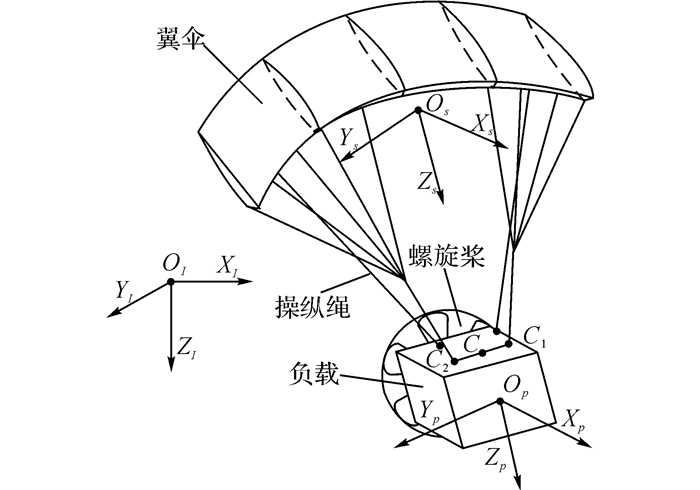
|
图 1 动力翼伞系统结构示意图 Fig. 1 Schematic diagram of powered parafoil system |
在对翼伞系统进行建模分析时一般只需建立6自由度动力学模型, 但在对动力翼伞系统进行分析时, 考虑到推力作用产生的负载与翼伞的相对偏航角和相对俯仰角, 需要建立8自由度动力学模型.
如图 1所示, 建立动力翼伞系统的8自由度模型时用到3个坐标系, 大地坐标系、翼伞坐标系和负载坐标系.大地坐标系OIxIyIzI的zI轴垂直指向大地, xI轴指向翼伞的前方, yI与xI轴和zI轴垂直, 组成右手坐标系.翼伞坐标系Osxsyszs选择翼伞的气动中心Os作为原点, xs轴的方向指向翼伞前方, zs轴由Os指向负载的质心Op, ys轴与xs轴和zs轴组成右手坐标系.负载坐标系Opxpypzp是以负载质心Op为原点建立的右手坐标系, 在负载与翼伞的相对偏航角和相对俯仰角为零时, 坐标系的xp轴、yp轴和zp轴与Osxsyszs坐标系的xs轴、ys轴和zs轴平行.
动力翼伞系统的8自由度动力学模型中的独立变量包括翼伞质心在大地坐标系中的坐标, 俯仰角、滚转角和偏航角3个欧拉角, 以及负载与翼伞的相对偏航角和相对俯仰角.利用动量定理和动量矩定理分别对负载和翼伞受力进行分析, 得
| $ \frac{{\partial {\mathit{\boldsymbol{P}}_{\rm{p}}}}}{{\partial t}} + {\mathit{\boldsymbol{W}}_{\rm{p}}} \times {\mathit{\boldsymbol{P}}_{\rm{p}}} = {\mathit{\boldsymbol{F}}_{\rm{p}}}^{{\rm{aero}}} + {\mathit{\boldsymbol{F}}_{\rm{p}}}^t + {\mathit{\boldsymbol{F}}_{\rm{p}}}^G + {\mathit{\boldsymbol{F}}_{\rm{p}}}^{{\rm{th}}}, $ | (1) |
| $ \frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{p}}}}}{{\partial t}} + {\mathit{\boldsymbol{W}}_{\rm{p}}} \times {\mathit{\boldsymbol{H}}_{\rm{p}}} = {\mathit{\boldsymbol{M}}_{\rm{p}}}^{{\rm{aero}}} + {\mathit{\boldsymbol{M}}_{\rm{p}}}^f + {\mathit{\boldsymbol{M}}_{\rm{p}}}^t, $ | (2) |
| $ \frac{{\partial {\mathit{\boldsymbol{P}}_{\rm{s}}}}}{{\partial t}} + {\mathit{\boldsymbol{W}}_{\rm{s}}} \times {\mathit{\boldsymbol{P}}_{\rm{s}}} = {\mathit{\boldsymbol{F}}_{\rm{s}}}^{{\rm{aero}}} + {\mathit{\boldsymbol{F}}_{\rm{s}}}^G + {\mathit{\boldsymbol{F}}_{\rm{s}}}^t, $ | (3) |
| $ \frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{s}}}}}{{\partial t}} + {\mathit{\boldsymbol{W}}_{\rm{s}}} \times {\mathit{\boldsymbol{H}}_{\rm{s}}} + {\mathit{\boldsymbol{V}}_{\rm{s}}} \times {\mathit{\boldsymbol{P}}_{\rm{s}}} = {\mathit{\boldsymbol{M}}_{\rm{s}}}^{{\rm{aero}}} + {\mathit{\boldsymbol{M}}_{\rm{s}}}^f + {\rm{ }}{\mathit{\boldsymbol{M}}_{\rm{s}}}^G + {\mathit{\boldsymbol{M}}_{\rm{s}}}^t. $ | (4) |
式中:下标p为对负载的受力分析, s为对翼伞的受力分析.上标aero、f、t、G和th分别为气动力、阻力、吊绳拉力、重力和推力的作用, F**和M**分别为力和力矩;Pp和Ps分别为负载和翼伞的动量, Hp和Hs分别为负载和翼伞的动量矩;Vs=[us, vs, ws]和Ws=[ωps, ωqs, ωrs]分别为翼伞的速度和角速度, Vp=[up, vp, wp]和Wp=[ωpp, ωqp, ωrp]分别为负载的速度和角速度.负载与翼伞的动量和动量矩表示为
| $ {\mathit{\boldsymbol{P}}_{\rm{p}}} = {m_{\rm{p}}}{\mathit{\boldsymbol{V}}_{\rm{p}}}, {\rm{ }}{\mathit{\boldsymbol{H}}_{\rm{p}}} = {\mathit{\boldsymbol{J}}_{\rm{p}}}{\mathit{\boldsymbol{W}}_{\rm{p}}}, $ | (5) |
| $ \left[\begin{array}{l} {\mathit{\boldsymbol{P}}_{\rm{s}}}\\ {\mathit{\boldsymbol{H}}_{\rm{s}}} \end{array} \right] = \left[{{\mathit{\boldsymbol{m}}_{\rm{ \mathsf{ α} }}} + {\mathit{\boldsymbol{m}}_{\rm{r}}}} \right]\left[\begin{array}{l} {\mathit{\boldsymbol{V}}_{\rm{s}}}\\ {\mathit{\boldsymbol{W}}_{\rm{s}}} \end{array} \right]. $ | (6) |
式中:mα为附加质量矩阵[9], mr为翼伞真实质量矩阵, mp为负载质量, Jp为负载的转动惯量矩阵.
翼伞和负载通过绳索连接, 两者的相对运动状态存在如下的约束关系:
| $ {\mathit{\boldsymbol{V}}_{\rm{p}}} + {\mathit{\boldsymbol{W}}_{\rm{p}}} \times {\mathit{\boldsymbol{L}}_{{\rm{p - c}}}} = {\mathit{\boldsymbol{V}}_{\rm{s}}} + {\mathit{\boldsymbol{W}}_{\rm{s}}} \times {\mathit{\boldsymbol{L}}_{{\rm{s - c}}}}, $ | (7) |
| $ {\mathit{\boldsymbol{W}}_{\rm{p}}} = {\mathit{\boldsymbol{W}}_{\rm{s}}} + {\mathit{\boldsymbol{\tau }}_{\rm{s}}} + {\mathit{\boldsymbol{\kappa }}_{\rm{p}}}. $ | (8) |
式中:τs=[0, 0, ψr], κp=[0, θr, 0], ψr、θr分别为翼伞和负载的相对偏航角和相对俯仰角. Lp-c和Ls-c分别为负载质心和翼伞质心到C点的距离. C点为负载上悬挂绳的中心点, 如图 1所示.
联立式(1)~(8) 即可建立动力翼伞系统的8自由度模型.详细的建模过程参考项目组关于动力翼伞系统8自由度建模的工作成果[4].
2 自抗扰控制技术及其离散化应用自抗扰控制技术是韩京清[10]提出的一种面向工程应用的控制算法, 其抗干扰能力和解决不确定性问题的能力已经在许多实验系统和实际工程中得到了检验[11-14], 从而受到了研究人员的广泛重视.
自抗扰控制技术包括跟踪微分器、扩张状态观测器和非线性误差反馈控制律(nonlinear state error feedback, NLSEF)3部分[15], 其中扩张状态观测器是自抗扰控制技术的核心部分.扩张状态观测器能对系统的内部扰动、外部扰动以及未建模和非线性变化进行估计和补偿, 将被控对象等效成“积分器串联型”的线性系统进行控制[10].
2.1 自抗扰控制技术考虑一类单输入单输出的系统, 数学描述为
| $ {y^{(n)}} = f\left( {{y^{(n - 1)}}, {y^{(n - 2)}}, \ldots, y, w} \right) + bu. $ | (9) |
式中:y为系统的输出, u为系统输入, w为系统的外界干扰, b为非零的输入增益, f(y(n-1), y(n-2), …, y, w)为对系统的动态描述, 可以是线性或者非线性的.
对与系统(9) 构建连续形式的扩张状态观测器:
| $ \begin{array}{l} \\ \left. \begin{array}{l} e = {z_1} - y, \\ {{\dot z}_1} = {z_2} - {\beta _{01}}{g_1}\left( e \right), \\ {{\dot z}_2} = {z_3} - {\beta _{02}}{g_2}\left( e \right), \\ \vdots \\ {{\dot z}_n} = {z_{n + 1}} + bu - {\beta _n}{g_2}\left( e \right), \\ {{\dot z}_{n + 1}} = - {\beta _{n + 1}}{g_{n + 1}}\left( e \right). \end{array} \right\} \end{array} $ | (10) |
式中:β01, β02, …, βn+1为系统的状态误差反馈增益, zi为观测状态, e为系统输出y的观测误差, gi(e)是关于e的非线性函数, 且egi(e)≥0.如果取gi(e)=e的线性形式, 则扩张状态观测器变为线性的, 称为线性扩张状态观测器(Linear ESO, LESO).
为了简化LESO的参数调整过程, Gao 16]提出将LESO的极点配置在-ωo, 其中ωo为观测器带宽.
取ωo > 0, LESO的误差反馈增益可表示为
| $ {\beta _i} = \frac{{\left( {n + 1} \right)!{\omega _o}^i}}{{i!\left( {n + 1 - i} \right)!}}, {\rm{ }}\left( {i = 1, 2, \ldots, n + 1} \right). $ |
适当设置LESO的参数可以实现对系统状态的准确估计, 包括系统内部和外部的扰动.此时有
| $ {z_{n + 1}} \approx f. $ |
取:
| $ u = \frac{{{u_0} - {z_{n + 1}}}}{b}. $ | (11) |
式中:u0为误差反馈控制律计算的输出控制量, 将式(11) 作为系统输入, 代入式(9), 得
| $ {y^{(n)}} = {u_0}. $ | (12) |
即将系统变为简单的串联积分形式.
2.2 扩张状态观测器的离散化应用在数字控制器中应用自抗扰控制算法, 需要对核心部分的扩张状态观测器进行离散化.目前常用的离散化方法有欧拉法和零阶保持器法2种[17].
2.2.1 欧拉法应用欧拉法对控制算法进行离散化, 即用2次采样值的差与采样周期的比值近似代替系统状态的导数.以二阶系统为例进行分析, 忽略h, 则二阶系统的扩张状态离散空间表达式为
| $ \left. \begin{array}{l} \mathit{\boldsymbol{X}}\left( {k + 1} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}u\left( k \right), \\ y\left( k \right) = \mathit{\boldsymbol{CX}}\left( k \right). \end{array} \right\} $ | (13) |
式中:X(k)=[x1(k), x2(k), x3(k)]T为列向量, u(k)为系统输入u离散比以后的表达式, 是标量,c为离散系统输出矩阵,c=[1, 0, 0].用T为采样周期, 则式(13) 中Φ和Γ表达式为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[\begin{array}{l} 1\;\;\;T\;\;\;0\\ 0\;\;\;1\;\;\;T\\ 0\;\;\;0\;\;\;1 \end{array} \right], {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[\begin{array}{l} 0\\ bT\\ 0 \end{array} \right]. $ |
建立对应的线性扩张状态观测器为
| $ \left. \begin{array}{l} e\left( k \right) = {z_1}\left( k \right) - y\left( k \right)\\ \mathit{\boldsymbol{Z}}\left( {k + 1} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}Z\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}u\left( k \right) - T\mathit{\boldsymbol{L}}e\left( k \right) \end{array} \right\}. $ | (14) |
式中:Z(k)=[z1(k), z2(k), z3(k)]T为二阶系统的状态观测值和扰动观测值, L为误差反馈系数矩阵.L=[β1, β2, β3].
2.2.2 零阶保持器法零阶保持器法离散化后的二阶系统的扩张状态离散空间表达式(14) 中的Φ和Γ表达式变为
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[\begin{array}{l} 1\;\;\;T\;\;\;\frac{{{T^2}}}{2}\\ 0\;\;\;1\;\;\;T\\ 0\;\;\;0\;\;\;1 \end{array} \right], \\ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[\begin{array}{l} \frac{{{bT^2}}}{2}\\ bT\\ \;\;0 \end{array} \right]. \end{array} $ |
对应离散扩张状态观测器表达式为
| $ \left. \begin{array}{l} e\left( k \right) = {z_1}\left( k \right) - y\left( k \right), \\ \mathit{\boldsymbol{Z}}\left( {k + 1} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} Z}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}u\left( k \right) - {\mathit{\boldsymbol{L}}_p}e\left( k \right). \end{array} \right\} $ | (15) |
取Lp=ΦLc, 将式(15) 改写为
| $ \left. \begin{array}{l} e\left( k \right) = {z_1}\left( k \right) - y\left( k \right), \\ \mathit{\boldsymbol{Z}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{L}}_c}\mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{Z}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}u\left( k \right) + {\mathit{\boldsymbol{L}}_p}y\left( k \right). \end{array} \right\} $ | (16) |
为了简化参数, 将离散系统(Φ-ΦLcC)的特征根配置在β处, 即
| $ |z\mathit{\boldsymbol{I}} - \left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{L}}_c}\mathit{\boldsymbol{C}}} \right)| = {\left( {z - \beta } \right)^3}. $ | (17) |
式中:离散系统配置的特征跟β与连续系统配置的特征根-ωo的关系为
| $ \beta = {\rm{exp}}\left( { - {\omega _o}T} \right). $ |
对式(17) 进行求解, 得
| $ {\mathit{\boldsymbol{L}}_c} = \left[\begin{array}{l} \;\;\;\;\;\;\;1-{\beta ^3}\\ \left( {2-3\beta + {\beta ^3}} \right)\frac{3}{{2T}}\\ \;\;\;\;{\left( {1-\beta } \right)^3}\frac{1}{{{T^2}}} \end{array} \right]. $ | (18) |
2种离散化方法在系统采样周期较短时扩张状态观测器的观测效果接近, 但在系统的采样周期较长时扩张状态观观测器的估计能力表现出较大差异, 零阶保持器法离散化的扩张状态观测器具有更高的估计精度和跟踪速度.
3 动力翼伞系统轨迹跟踪控制器动力翼伞系统共有2个输入操纵量, 翼伞的下偏量用以控制动力翼伞系统的飞行方向, 加在负载的推力用以控制动力翼伞系统的飞行高度.根据动力翼伞系统的动力学特性和自抗扰控制算法的特点, 将动力翼伞系统轨迹跟踪控制分为水平轨迹跟踪和垂直高度跟踪2个控制通道, 独立设计控制器.
3.1 水平轨迹控制器设计动力翼伞系统的水平轨迹控制器通过控制动力翼伞系统的飞行方向实现轨迹控制, 即控制偏航角ψ, 因此选择三阶扩张状态观测器对动力翼伞系统的偏航角、偏航角速度和总扰动进行估计.三阶线性扩张状态观测器表达式为
| $ \left. \begin{array}{l} {e_1} = {z_{11}} - \psi, \\ {{\dot z}_{11}} = {z_{12}} - {\beta _1}{e_1}, \\ {{\dot z}_{12}} = {z_{13}} + {b_1}\delta - {\beta _2}{e_1}, \\ {{\dot z}_{13}} = - {\beta _3}{e_1}. \end{array} \right\} $ | (19) |
式中:z11为偏航角ψ的观测值, δ为控制器的输出, 即翼伞的后缘下偏量,e1为偏航角的观测误差,b1为下偏量δ的输入增益.
水平轨迹控制的误差计算方法一般采用横向轨迹误差法与视差法相结合的方法, 即动力翼伞系统飞行方向与设定参考方向的角度差和动力翼伞系统所在位置与参考轨迹的水平距离的和.计算原理如图 2所示.
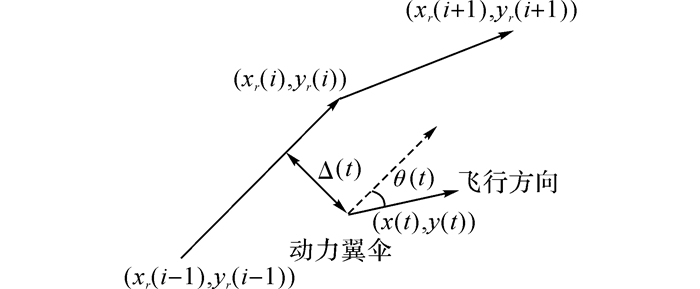
|
图 2 水平轨迹误差计算原理图 Fig. 2 Computation principle diagram of horizontal trackingerror |
图 2中(xr(i-1), yr(i-1))、(xr(i), yr(i))和(xr(i+1), yr(i+1))分别为给定参考轨迹上点在水平投影的坐标.(x(t), y(t))为动力翼伞所在位置在水平面上投影的坐标.θ(t)为动力翼伞飞行方向与参考轨迹方向的水平夹角, Δ(t)为动力翼伞到参考轨迹的水平距离.
根据之前的研究方法[6], 由图 2可得水平轨迹控制的误差计算表达式为
| $ {e_h}\left( t \right) = \theta \left( t \right) + {k_\Delta }\Delta \left( t \right). $ | (20) |
式中:kΔ为水平距离误差的加权系数.
但在实际应用中, 式(20) 形式的误差计算方法可能因为动力翼伞系统与参考轨迹距离过大而使飞行方向的误差不起作用, 对误差计算方法进行改进, 选择:
| $ {e_{\rm{h}}}\left( t \right) = \theta \left( t \right) + {\rm{ta}}{{\rm{n}}^{ - 1}}(\frac{{\Delta \left( t \right)}}{{{k_{\rm{e}}}}}). $ | (21) |
式中:ke为水平距离误差的调整系数.
改进后的误差计算方法使得距离误差在计算中有界, 可以保证动力翼伞在距离参考轨迹较远时能够快速减小距离误差而不会出现反向调节.
水平轨迹控制通道的误差反馈控制律采用PD控制, 得
| $ \delta = \frac{{{u_{{\rm{0h}}}} - {z_{13}}}}{{{b_1}}}, {\rm{ }}{u_{{\rm{0h}}}} = {k_{{\rm{p1}}}}{e_{\rm{h}}} + {k_{{\rm{d1}}}}{\dot e_{\rm{h}}}. $ |
式中:u0h为线性PD输出的控制量.
本文仿真实验中水平轨迹控制器参数选择kp1=0.045, kd1=0.44.
3.2 垂直高度控制器设计动力翼伞系统的垂直高度控制器用以跟踪参考轨迹在垂直方向的分量, 即参考高度.高度控制通道的自抗扰控制器选择三阶扩张状态观测器进行系统总扰动的估计和补偿.高度控制通道的扩张状态观测器表达式为
| $ \left. \begin{array}{l} {e_2} = {z_{21}} - {h_v}, \\ {{\dot z}_{21}} = {z_{22}} - {\beta _1}{e_2}, \\ {{\dot z}_{22}} = {z_{23}} + {b_2}{F_{{\rm{th}}}} - {\beta _2}{e_2}, \\ {{\dot z}_{23}} = - {\beta _3}{e_2}. \end{array} \right\} $ | (22) |
式中:hv为动力翼伞系统所处的海拔高度, z21为hv的观测值, Fth为推力, e2为动力翼伞系统的高度观察误差,b2为Fth的输入增益.
高度误差的计算相对于水平误差的计算较为简单, 计算方法为
| $ {e_v}\left( t \right) = r - {h_v}. $ | (23) |
式中:r为参考轨迹的高度分量.
同样对高度控制通道的误差反馈控制律选择PD控制, 推力计算表达式为
| $ {F_{{\rm{th}}}} = \frac{{{u_{0v}} - {z_{23}}}}{{{b_2}}}, {u_{0v}} = {k_{p2}}{e_v} + {k_{d2}}{\dot e_v}. $ |
本文仿真实验中垂直高度控制器参数选择kp2=0.013, kd2=0.24.
4 仿真结果与分析动力翼伞系统依靠伞翼充气后产生升力飞行, 而伞翼质量较轻, 在飞行过程中容易受到风场的干扰, 因此在设计动力翼伞系统的轨迹跟踪控制器时需要考虑其对风场的抗干扰能力.为了说明自抗扰控制器的控制效果和抗干扰性能, 本文在仿真实验结果中加入了广义预测控制算法(generalized predictive control, GPC)进行对比[6, 18]. GPC控制算法在项目组之前的翼伞归航控制中取得了比较理想的控制效果.
用于建模和仿真的动力翼伞系统参数如表 1所示.
| 表 1 动力翼伞系统参数 |
研究中GPS位置采样频率设置为4 Hz, 在该采样频率下, 对欧拉法和零阶保持器法离散化的线性扩张状态观测器对动力翼伞偏航角的估计能力进行对比, 结果如图 3所示, 图中Δe为偏航角的观测误差.从图 3中可以看出, 2种离散线性扩张状态观测器最终均可以实现对动力翼伞偏航角的无差估计, 但零阶保持器法离散化的线性扩张状态观测器具有更好的动态性能.在初始阶段, 欧拉法离散线性扩张状态观测器最大误差达到0.004 rad, 而零阶保持器法离散线性扩张状态观测器最大误差为0.002 5 rad.图 3中5~40 s的动态过程和100 s时控制量发生变化的对比图也显示零阶保持器法离散线性扩张状态观测器估计误差的收敛速度更快, 过程误差更小.
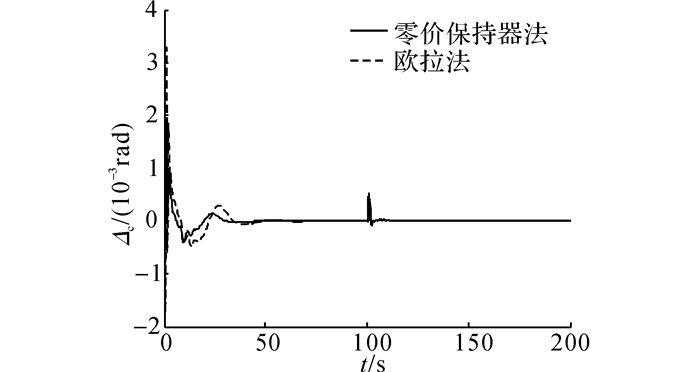
|
图 3 线性扩张状态观测器离散化方法比较 Fig. 3 Comparison between discretization methods of LESO |
式(20) 中将动力翼伞与参考轨迹的水平距离误差加权后与飞行角度误差相加计算得到水平误差, 优点是计算简单, 但当动力翼伞与参考轨迹位置较远时, 距离误差在水平总误差中比重过大, 可能造成反向调节而使动力翼伞不能到达参考轨迹.
如图 4和5所示为2种误差计算方法对动力翼伞水平轨迹控制的影响以及对应的下偏控制量, 图 4中横轴坐标x为大地坐标系的x轴, 纵轴坐标y为大地坐标系的y轴, 图 5中纵轴坐标δ为控制量, 用百分比形式表示.误差法1为采用式(21) 计算水平距离误差, 误差法2为采用式(20) 计算水平距离误差.式(20) 中k的取值影响系统的动态性能, k取值过大增大了距离误差在总水平误差中的权重, 造成下偏控制量的振动, k取值过小则会减慢水平距离误差的收敛速度.经过实验比较, 计算时取k=0.01, 式(21) 中ke取k的倒数, 即ke=100.从图 4中可以看出, 当采用误差法1计算水平轨迹误差时, 动力翼伞系统直接飞向参考轨迹, 而且在到达参考轨迹后的超调量较小, 为3.6 m.当采用误差法2计算水平轨迹误差时, 因为距离误差较大, 动力翼伞系统先向下偏转而后飞向参考轨迹, 而且超调量较大, 达到了6.2 m.

|
图 4 水平误差方法对比 Fig. 4 Comparison between computation methods of horizontal error |

|
图 5 水平误差计算方法的控制量对比 Fig. 5 Control output of different horizontal error computation methods |
图 5显示自抗扰控制器采用误差法1时控制量一直为正, 而采用误差法2时控制器的初始输出为负值, 即出现反向调节.如果动力翼伞系统的初始位置与参考轨迹的距离继续加大, 采用误差法2计算水平误差可能使动力翼伞系统的水平轨迹跟踪控制器失效.
4.3 轨迹跟踪控制本节的实验分析中, 在系统中加入沿x轴正方向的3 m/s的稳定风叠加y轴方向的2 m/s的NASA阵风模型作为外部风场扰动[19].仿真结果如图 6~9所示.
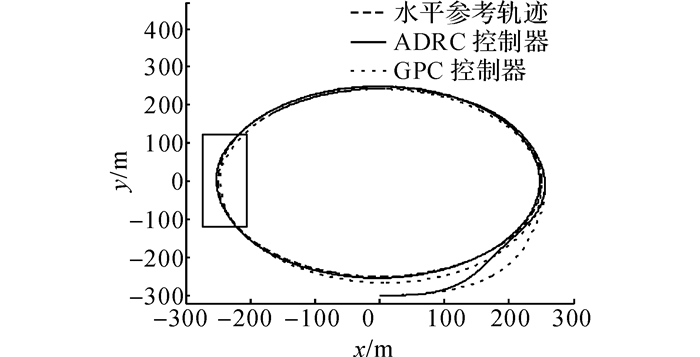
|
图 6 水平轨迹跟踪控制曲线 Fig. 6 Controlled horizontal trajectory of powered parafoil system |

|
图 7 水平轨迹控制器下偏量控制信号输出 Fig. 7 Deflection output of horizontal controllers |
|
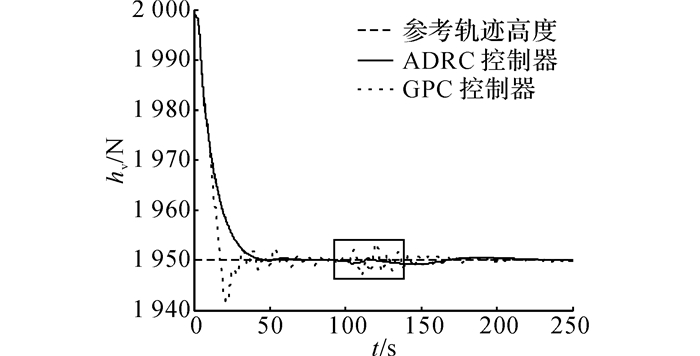
图 8 垂直高度控制曲线 Fig. 8 Controlled altitude of powered parafoil |

|
图 9 推力控制信号输出 Fig. 9 Thrust output of vertical controllers |
图 6中的方框内动力翼伞的轨迹表示突风对动力翼伞系统的动态影响, 自抗扰控制器的水平控制轨迹能够很好地跟踪参考轨迹, GPC控制器的水平控制轨迹虽能跟踪参考轨迹, 但是因为稳定风扰的存在, 跟踪效果比自抗扰控制器差, 最大误差达到17.8 m.在初始阶段, 自抗扰控制器能够控制动力翼伞系统快速无超调的跟踪参考轨迹, GPC控制器则响应较慢, 距离误差收敛速度比自抗扰控制器低.在突风扰动作用时, 自抗扰控制器和GPC控制器均能快速克服突风对动力翼伞系统的影响, 保证动力翼伞系统的水平轨迹跟踪精度.
但通过图 7中的对比可以得出结论, 自抗扰控制器在干扰过后能够快速稳定动力翼伞系统, 实现控制量的平稳输出, 下偏控制量的变化仅受到稳定风扰的影响而呈周期性变化.GPC控制器在受到突风扰动时, 产生长时间的震荡, 下偏控制量与高度控制的推力在动力翼伞系统中产生耦合无法消除.自抗扰控制器能通过线性扩张状态观测器将耦合作用当作外部扰动进行估计和补偿, 降低了两通道之间的干扰影响, 取得了更好的控制效果.
图 8所示为动力翼伞系统高度控制结果, 图中方框区域为动力翼伞系统受突风影响时的高度变化.图 8显示, 自抗扰控制器能够控制动力翼伞系统准确跟随给定高度, 从2 000 m降落到1 950 m时无超调和震荡. GPC控制器在控制动力翼伞系统时有8.1 m的超调, 跟踪误差呈震荡收敛.在加入突风时, 自抗扰控制器对风扰影响进行实时估计和补偿, 使动力翼伞系统的高度变化较小, 而且实现了快速稳定.GPC控制器作用下的动力翼伞系统高度则震荡收敛.从图 9中控制器的推力输出比较中可以看出, 自抗扰控制器的推力输出较为平滑, 在受到突风干扰时变化范围小, 而且经过37 s的调整后实现了系统稳定.GPC控制器则一直处于波动调整中, 在动力翼伞系统受到突风干扰时推力变化剧烈, 随后呈震荡收敛状态, 稳定过程较长.图 9中Fth为动力翼伞的推力.
仿真实验和比较验证了自抗扰控制器对动力翼伞系统轨迹跟踪控制的有效性.仿真实验证明, 自抗扰控制器在水平轨迹和垂直高度控制中具有响应速度快和调整时间短和的特点, 在动力翼伞系统受到稳定风和突变风作用时能够克服干扰, 高精度地跟踪参考轨迹, 表现出较强的鲁棒性.自抗扰控制在轨迹跟踪控制中与GPC算法相比更具优势.
5 结论自抗扰控制技术可以将复杂的非线性系统补偿成简单的“积分器串联型”进行控制, 达到了很好的控制效果.自抗扰技术在动力翼伞系统轨迹跟踪控制中应用的仿真结果表明:
(1) 动力翼伞系统中水平轨迹和垂直高度2个控制通道的耦合以及动力翼伞系统受到的外部风场影响均可以通过自抗扰控制器进行估计和补偿, 因此动力翼伞系统可以通过自抗扰控制器实现对参考轨迹的准确跟踪, 跟踪效果优于GPC控制器.
(2) 在动力翼伞系统的轨迹跟踪控制中, 零阶保持器法离散化的线性扩张状态观测器具有更好的状态估计能力, 跟踪速度快且动态误差小.
(3) 在水平轨迹控制通道的误差计算中, 对距离误差进行反正切处理可以增加控制器的适用范围, 提高轨迹跟踪性能.
| [1] |
韩雅慧, 杨春信, 肖华军, 等. 翼伞精确空投系统关键技术和发展趋势[J].
兵工自动化, 2012, 31(7): 1–7.
HAN Ya-hui, YANG Chun-xin, XIAO Hua-jun, et al. Review on key technology and development of parafoil precise airdrop systems[J]. Ordnance Industry Automation, 2012, 31(7): 1–7. |
| [2] |
赵秋艳. 翼伞雀降技术[J].
航天返回与遥感, 1999, 20(2): 5–9.
ZHAO Qiu-yan. Flare maneuver of ram-air parachute[J]. Spacecraft Recovery & Remote Sensing, 1999, 20(2): 5–9. |
| [3] |
张兴会, 朱二琳. 翼伞系统雀降性能及控制研究[J].
航天控制, 2012, 30(1): 29–33.
ZHANG Xing-hui, ZHU Er-lin. The study of the flare-landing performance and control of parafoil system[J]. Aerospace Control, 2012, 30(1): 29–33. |
| [4] | ZHU E L, SUN Q L, TAN P L, et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear Dynamics, 2015, 79(1): 617–629. DOI:10.1007/s11071-014-1690-9 |
| [5] |
熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科技大学, 2005.
XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005. http://cdmd.cnki.com.cn/Article/CDMD-90002-2006127563.htm |
| [6] |
李永新, 陈增强, 孙青林. 基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制[J].
智能系统学报, 2012, 7(6): 481–488.
LI Yong-xin, CHEN Zeng-qiang, SUN Qing-lin. Flight path tracking of a parafoil system based on the switching between fuzzy control and predictive control[J]. CAAI Transactions on Intelligent Systems, 2012, 7(6): 481–488. |
| [7] | BENJAMIN S C. Adaptive control of a 10K parafoil system[C]// 23rd AIAA Aerodynamic Decelerator Systems Technology Conference. Daytona Beach, FL:[s. n.], 2015, 1-27. |
| [8] | SLEGERS N, COSTELLO M. Model predictive control of a parafoil and payload system[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(4): 816–821. DOI:10.2514/1.12251 |
| [9] |
熊菁, 秦小波, 程文科. 降落伞系统附加质量的研究[J].
中国空间科学技术, 2002, 22(4): 32–39.
XIONG Jing, QIN Xiao-bo, CHENG Wen-ke. The added mass research in parachute system[J]. Chinese Space Science and Technology, 2002, 22(4): 32–39. |
| [10] |
韩京清. 自抗扰控制器及其应用[J].
控制与决策, 1998, 13(1): 19–23.
HAN Jing-qing. Auto disturbance rejection control and it's application[J]. Control and Decision, 1998, 13(1): 19–23. |
| [11] |
盖江涛, 黄庆, 黄守道, 等. 基于模型补偿的永磁同步电机自抗扰控制[J].
浙江大学学报:工学版, 2014, 48(4): 581–588.
GAI Jiang-tao, HUANG Qing, HUANG Shou-dao, et al. Active-disturbance rejection controller for permanent magnet synchronous motor based on model compensation[J]. Journal of Zhejiang University :Engineering Edition, 2014, 48(4): 581–588. |
| [12] |
李毅, 陈增强, 刘忠信. 自抗扰技术在四旋翼飞行姿态控制中的应用[J].
哈尔滨工业大学学报, 2014, 46(3): 115–119.
LI Yi, CHEN Zeng-qiang, LIU Zhong-xin. Attitude control of a quad-rotor robot based on ADRC[J]. Journal of Harbin Institute of Technology, 2014, 46(3): 115–119. DOI:10.11918/hitxb20140320 |
| [13] |
刘一莎, 杨晟萱, 王伟. 四旋翼飞行器的自抗扰飞行控制方法[J].
控制理论与应用, 2015, 32(10): 1–10.
LIU Yi-sha, YANG Sheng-xuan, WANG Wei. An active disturbance-rejection flight control method forquad-rotor unmanned aerial vehicles[J]. Control Theory and Application, 2015, 32(10): 1–10. |
| [14] | FENG G, LIU Y F, HUANG L P. A new robust algorithm to improve the dynamic performance on the speed control of induction motor drive[J]. IEEE Transactions on Power Electronics, 2004, 19(6): 1614–1627. DOI:10.1109/TPEL.2004.836619 |
| [15] | HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900–906. DOI:10.1109/TIE.2008.2011621 |
| [16] | GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the American Control Conference. Denver. Colorado:[s. n.] 2003: 4989-4996. |
| [17] | ZHENG Q, DONG L L, LEE D H, et al. Active disturbance rejection control for MEMS gyroscopes[J]. IEEE Transactions on Control Systems Technology, 2009, 17(6): 1432–1438. DOI:10.1109/TCST.2008.2008638 |
| [18] |
焦亮. 基于翼伞空投机器人系统的自主归航研究[D]. 南开大学, 2011.
JIAO Liang. Research on autonomous homing based on parafoil and air-dropped robot system[D]. Tianjin: Nankai University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10055-1011111449.htm |
| [19] |
熊菁, 秦子增, 程文科. 回收过程中高空风场的特点及描述[J].
航天返回与遥感, 2003, 24(3): 9–14.
XIONG Jing, QIN Zi-zeng, CHENG Wen-ke. The characteristics and description of mid-high altitude wind in recovery[J]. Spacecraft Recovery and Remote Sensing, 2003, 24(3): 9–14. |



