水辅成型(water-assisted injection molding, WAIM)自气辅成型(gas-assisted injection molding, GAIM)发展而来[1-2], 具有成型周期短、制品质量高、材料成本低等优点[3-4], 近些年来越来越受到人们的关注[5].水辅成型在汽车工业、家用电器、办公设备等领域具有广泛的应用前景.其中, 浮动芯注射法[6]是一种新型的水辅成型方法.普通的水辅成型是将高压水直接注射到充满高温塑料熔体的模具型腔内, 高压水推动高温熔体前进, 从而形成中空塑料制品[7].相比直接注射法, 浮动芯注射法采用一个子弹状的浮动芯放置在注水口前端, 高压水注射时推动浮动芯在高温熔体中前进, 最终形成品质更佳的中空塑料制品.
国内外研究人员针对水辅成型的研究主要集中在设备研制、试验研究和仿真研究3个方面[8], 试图找出影响成型效果的因素.其中, 残余壁厚是衡量成型效果的一项重要指标.Pudpong等[9-13]研究了熔体温度、延迟时间、保压压力、模具壁面温度等工艺参数对制品残余壁厚以及充模流动的影响.Sannen等[14]研究了材料特性与残余壁厚之间的关系.周华等[15]发现制品截面圆率大小影响残余壁厚水平.Yang等[16-17]研究了管状制品的形状与残余壁厚的关系.Zhang等[18-20]分析了残余壁厚形成过程中的一次穿透和二次穿透行为.Polynkin等[21-23]研究了残余壁面上空洞缺陷及界面穿透行为.Liu等[24]研究了工艺参数对壁面“水指”缺陷的影响.
本文结合试验和数值模拟, 对比分析了水辅成型浮动芯注射法与直接注射法在制品残余壁厚性能方面的表现差异, 以及研究了延迟时间对2种注射法的影响, 发现浮动芯注射法在壁厚控制方面具有较大的优越性.
1 数学模型 1.1 基本假设水辅成型是高温塑料熔体与高压水相互作用的两相流动过程, 其中涉及到高温熔体的非牛顿特性、高压水的高雷诺数湍流特性以及两相界面间的不稳定性, 其成型机理是极其复杂的, 难以建立精确的数学模型.为简化两者相互作用的流动过程, 现作出以下假设:1) 初始环境下, 高温熔体在模具腔内均匀布满, 温度处处相等; 2) 流体视为不可压缩的; 3) 注射成型过程中, 高温熔体的定压比热容、热传导率视为常数.4) 浮动芯注射时, 假设浮动芯与塑料熔体之间不发生热交换.
1.2 基本方程连续性方程
不可压缩流体的连续性方程为
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0. $ | (1) |
式中:ui为xi方向上的流体速度.
动量方程
工程计算中直接求解N-S方程非常困难, 通常对其进行雷诺平均处理, 首先将满足动力学方程的湍流瞬时运动分解为平均运动和脉动运动2部分, 然后把脉动运动部分对平均运动的贡献通过雷诺应力项来模化.雷诺平均N-S方程为
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_l}}}{{\partial {x_l}}}} \right] - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}} - \rho \overline {u{' _i}u{' _j}} . $ | (2) |
式中:ρ, μ, p分别为流体的密度、动力黏度、压力, ul, uj为xl, xj方向上的流体速度, δij为克罗内克函数,
由于式(2) 考虑了雷诺应力项
| $ - \rho \overline {u{' _i}u{' _j}} = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\left( {\rho k + {\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right){\delta _{ij}}. $ | (3) |
式中:μt为湍流黏度, k为湍流动能.
能量方程
| $ \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left( {{u_i}\left( {\rho E + p} \right)} \right) = \frac{\partial }{{\partial {x_i}}}\left( {{\lambda _{{\rm{eff}}}}\frac{{\partial T}}{{\partial {x_i}}} + {u_i}{{({\tau _{ij}})}_{{\rm{eff}}}}} \right). $ | (4) |
式中:E为流体的总能量, λeff为有效热传导系数, (τij)eff为偏应力张量.
浮动芯运动方程
浮动芯是在高压水和塑料熔体共同作用下运动的, 其运动轨迹无法用方程准确描述, 故采用6自由度动网格求解模型.该模型根据压力场对面的积分计算出作用在浮动芯上的力Fc和力矩Mc, 从而计算出浮动芯的运动轨迹.浮动芯的运动分解为平动和转动, 运动方程为
| $ \left. \begin{array}{l} \frac{{{\rm{d}}{\boldsymbol{v}_c}}}{{{\rm{d}}t}} = \frac{{{\boldsymbol{F}_c}}}{m},\\ \frac{{{\rm{d}}{\boldsymbol{\omega }_c}}}{{{\rm{d}}t}} = \frac{{{\boldsymbol{M}_c}}}{J}. \end{array} \right\} $ | (5) |
式中:vc、ωc分别为浮动芯的平动速度和转动速度.m、J分别为浮动芯质量和转动惯量.
1.3 湍流模型引入Boussinesq假设后, 湍流模型的计算主要归结为湍流黏性系数的计算.根据计算中使用的变量数目和方程数目的不同, 湍流模型主要分为零方程模型、一方程模型和二方程模型.在注射成型系统中, 常用的是二方程k-ε和k-ω模型.张增猛等[25]通过对比计算发现, k-ω模型对水辅成型制品残余壁厚的预测更准确.k-ω模型又分为标准k-ω模型和剪切应力输运k-ω模型.在计算过程中发现, 前者对两相流动的热传导过程预测不准确, 出现了流场温度升高的现象, 与实际冷却过程不符.因此采用剪切应力输运k-ω模型.
剪切应力输运k-ω模型, 简称SSTk-ω模型.该模型引入湍流动能k和耗散系数ω, 它们的输运方程为
| $ \left. \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = - \frac{\partial }{{\partial {x_j}}}\left( {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k},\\ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = - \frac{\partial }{{\partial {x_j}}}\left( {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega }. \end{array} \right\} $ | (6) |
式中:Gk, Gω为湍流动能项, Yk, Yω为湍流耗散项, σk, σω为湍流普朗特数, Dω为湍流正交耗散项.
k-ω模型中湍流黏度为
| $ {\mu _t} = {\alpha ^*}\frac{{\rho k}}{\omega }. $ | (7) |
式中:α*为低雷诺数修正系数.α*的计算公式如式(8) 所示.
| $ {a^*} = a_\infty ^*\left( {\frac{{a_0^* + R{e_{\rm{t}}}/{R_k}}}{{1 + R{e_{\rm{t}}}/{R_k}}}} \right). $ | (8) |
式中:Ret为湍流雷诺数,Rk为模型常数,
高温熔体在模具腔内充模流动时, 其最重要的性能是它的非牛顿黏性流动.通常采用Cross模型描述熔体非牛顿黏性性质.由于水辅成型过程中伴有明显的熔体冷却效应, 通常采用温度适用范围更广的Cross-WLF模型, 它能更好地描述熔体的冷却固化现象.Cross-WLF模型表达式为
| $ \left. \begin{array}{l} \eta \left( {\gamma ,T,p} \right) = \frac{{{\eta _0}\left( {T,p} \right)}}{{1 + {{({\eta _0}\gamma /{\tau ^*})}^{1 - n}}}},\\ {\eta _0}\left( {T,p} \right) = {D_1}\exp \left[ {\frac{{ - {A_1}(T - ({D_2} + {D_3}p))}}{{{A_2} + T - {D_2}}}} \right]. \end{array} \right\} $ | (9) |
式中:η, η0分别为高温熔体的黏度、零剪切黏度,γ, T分别为高温熔体的剪切速率、温度.τ*为材料常数, n为非牛顿指数.A1, A2为与温度相关的量.D1, D2为与材料的玻璃化温度Tg相关的量, 通常取D2=Tg.D3为模型系数, D3非常小, 通常取D3=0.
数值模拟采用的Cross-WLF模型参数[26]取值分别为:n=0.236, τ*=46 114.3 Pa, Tg=263 K, D1=9.9×1019 Pa·s, A1=45.56, A2=30.68.
1.5 制品模型制品整体外形为弯管形, 截面直径40 mm, 制品总长500 mm, 其中直线段长度为230 mm, 其余部分为弯管形, 弯曲半径128 mm, 三维模型如图 1所示.

|
图 1 弯管形制品的三维模型 Fig. 1 3D model of bent pipe part |
根据制品模型以及水辅成型实际环境条件, 利用Fluent软件建立水辅成型浮动芯注射和直接注射2种模型, 研究制品残余壁厚分布情况.模型采用PISO算法求解压力速度耦合方程, 采用PRESTO!格式离散压力项, 一阶迎风格式离散动量项、能量项、湍流动能项和耗散系数项.同时采用VOF两相流模型模拟高压水和塑料熔体的耦合流动.
利用弹性光顺法(Smoothing)和局部网格重划法(Remeshing)划分6自由度动网格.浮动芯边界设置为刚性体(Rigid Body)类型, 不考虑浮动芯的变形运动.模具壁面的边界条件设置为壁面(Wall)类型, 塑料熔体与模具壁面之间的热边界条件设置为温度(Temperature)类型.高压水注射口边界条件设置为压力入口(Pressure-inlet)类型, 压力值变化规律如式(10) 所示.溢料口边界条件设置为压力出口(Pressure-outlet)类型, 出口压力设为恒定值.利用Fluent建立的CFD模型为
| $ {p_{{\rm{in}}}} = \left\{ \begin{array}{l} \frac{{{p_{\rm{b}}}}}{{{t_{\rm{s}}}}}t,\;0 \le t < {t_{\rm{s}}};\\ {p_{\rm{b}}}.{\rm{ }}\;t \ge {t_{\rm{s}}}. \end{array} \right. $ | (10) |
式中:pin为注射水压力值, pb为保压压力, ts为水压上升时间.
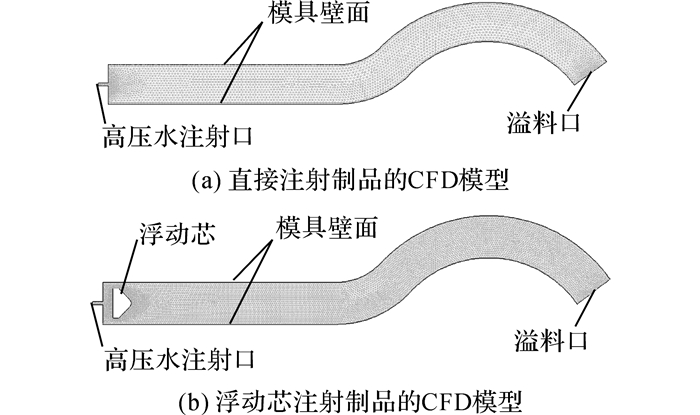
|
图 2 弯管形制品的CFD模型 Fig. 2 CFD model of bent pipe part |
试验采用的材料为等规聚丙烯, 型号为PP-T20, 生产单位是台州市飞宏塑料有限公司.该材料与水辅成型相关的基本热性质参数如表 1所示, Tm表示熔点, MFR为熔融指数, cp为比定压热容, λ为热传导率, MS为成型收缩率.
| 表 1 聚丙烯PP-T20的热性质参数 Table 1 Thermal properties parameters of polypropylene (PP-T20) |
高压水注射设备
该设备是浙江大学流体动力与机电系统国家重点实验室自主研发的水辅成型高压水注射设备, 如图 3所示.该设备采用油水混合系统, 充分利用了油压与水压的优势.其中, 油压系统主要由油箱、过滤器、单向阀、比例溢流阀、安全阀、冷却器、三位四通换向阀等组成.水压系统主要由水箱、加热器、过滤器、单向阀、电磁开关阀等组成, 对顶缸连接油压与水压系统.该系统最大注水压力25 MPa, 一次最大注水量2 L.

|
图 3 水辅成型高压水注射设备 Fig. 3 High-pressure water injection equipment of WAIM |
浮动芯
试验中要求制品的中空截面为圆形, 因此浮动芯尾部设计成圆柱形.为了减小浮动芯在高温熔体中运动的阻力, 浮动芯头部做成圆锥形.试验前将浮动芯放置在注水口前端, 开始注射时浮动芯随高压水一起射出.与直接注射相比, 浮动芯可以有效避免浇注高温熔体时, 熔体通过注水口回流进入注射水管.试验为了对比不同外径的浮动芯对制品残余壁厚的影响, 分别设计了外径Φ1=34 mm和Φ2=28 mm这2种不同规格的浮动芯, 取名分别为1号浮动芯和2号浮动芯, 如图 4所示.

|
图 4 水辅成型浮动芯注射法的浮动芯 Fig. 4 Floating core of floating core injection of WAIM |
试验采用的注塑机由广东东华机械有限公司生产, 额定注射量1 kg, 锁模力550 t.试验采用满射法, 并在模具型腔制品末端处添加一个溢料腔, 用于存放因高压水穿透溢出的塑料熔体.影响水辅成型制品残余壁厚的工艺参数主要有延迟时间、水压上升时间、保压压力、塑料熔体温度和模具壁面温度等.分别取不同的延迟时间, 研究其对制品残余壁厚的影响.其余参数设置成一个合理的固定值, 并使仿真和试验参数保持一致, 如表 2所示, Tw为模具壁面温度.
| 表 2 水辅成型试验参数 Table 2 Experimental parameters of WAIM |
残余壁厚作为试验的主要数据指标, 其测量方法如下:沿高压水流动方向取8个位置, 记为Pi(i=1, 2…8), 然后分别测量每个位置截面上的残余壁厚.Pi处的残余壁厚记为bi(i=1, 2…8), 如图 5所示.为了综合反应每个位置截面上的残余壁厚, 采用不同方位多次测量取平均值的方式.

|
图 5 水辅成型制品残余壁厚测量示意图 Fig. 5 Schematic diagram of parts residual wall thickness measurement of WAIM |
为了更好地比较不同注射方法对残余壁厚的影响, 选取相同延迟时间注射的试验及仿真结果分析, 本节的延迟时间均为4 s.如图 6所示为2种不同注射法水与高温塑料熔体共存的相分布图.从图中可以直观地发现, 直接注射与浮动芯注射的残余壁厚有显著差异, 并且不同外径浮动芯注射的残余壁厚也存在差异.图 6(a)显示直接注射时距离注水口较近的P1和P2处内壁比较粗糙.这是因为距离注水口较近处高压水的湍流强度较大, 导致内壁不光滑.对比图 6(b)和(c), 浮动芯注射可以减缓因距离注水口较近的高压水湍流强度过大引起的内壁不均匀缺陷.

|
图 6 直接注射和浮动芯注射的水与高温塑料熔体相分布 Fig. 6 Phase distribution of water and high-temperature plastic melt with direct injection and floating core injection |
如图 7所示为用不同方法注射时P3处的纵截面仿真与试验结果.从图中可以直观发现, 仿真与试验结果基本吻合, 并且仿真与试验结果都表明注射方法对制品残余壁厚的影响较大.下面将进一步通过定量方法研究不同注射方法的残余壁厚差异性.

|
图 7 直接注射和浮动芯注射P3处纵截面仿真与试验结果 Fig. 7 Simulative and experimental results of longitudinal section in P3 with direct injection and floating core injection |
如图 8所示为直接注射和1号、2号浮动芯注射的残余壁厚值.由图 8可知, 直接注射时试验结果和仿真结果差异较大, 试验残余壁厚明显小于仿真残余壁厚.这是因为试验过程中高压水穿透熔体后还需保压一段时间, 保压时高压水会沿垂直壁面方向产生二次挤压行为, 导致残余壁厚减小.而仿真假设流体不可压缩, 因此残余壁厚较大.另外, 试验残余壁厚沿水流注射方向逐渐增大, 而仿真除P1和P2处外, 残余壁厚分布比较均匀.这是由于试验中熔体温度沿水流注射方向逐渐降低, 相应的黏度逐渐上升, 高压水流动时不易带走黏度较大的熔体, 因此试验残余壁厚逐渐增大.而仿真假设初始状态下熔体温度处处相等, 因此仿真无法模拟这一现象.熔体温度沿水流注射方向逐渐降低的原因有2个:1) 熔体浇注过程中距离注水口远的地方的熔体先从浇注口射出(熔体浇注口距离注水口较近), 冷却时间更长; 2) 高压水注射过程中, 距离注水口远的地方的熔体后被高压水贯穿, 冷却时间再次加长.
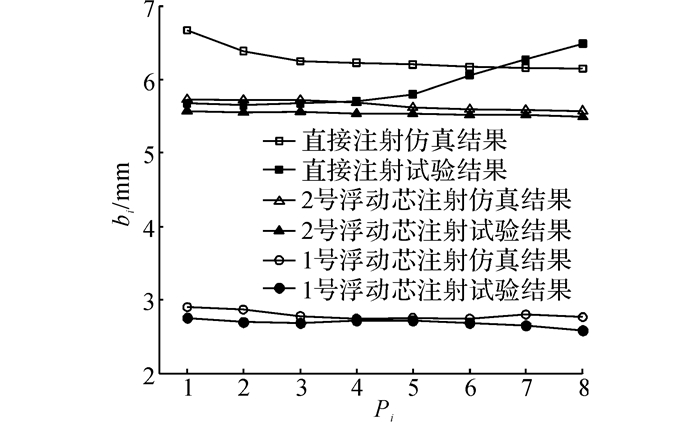
|
图 8 直接注射和浮动芯注射的制品残余壁厚对比 Fig. 8 Residual wall thickness of parts comparison between direct injection and floating core injection |
采用1号和2号浮动芯注射时, 仿真和试验结果比较吻合.图 8显示1号和2号浮动芯注射的残余壁厚分别在2.75和5.6 mm左右.对比制品外径(40 mm)、1号浮动芯外径(34 mm)和2号浮动芯外径(28 mm), 可以发现1号和2号浮动芯注射的理想残余壁厚分别是3和6 mm, 结果初步证明, 在一定误差范围内, 浮动芯注射法能够控制制品的残余壁厚.并且试验和仿真结果都显示, 残余壁厚沿水流注射方向分布比较均匀.这是因为浮动芯在运动过程中会带走前端所有的熔体, 而受熔体黏度分布不均匀影响较小, 因此浮动芯注射的残余壁厚分布比较均匀.
为了进一步验证浮动芯注射法能够控制制品的残余壁厚, 添加3号浮动芯(外径24 mm)和4号浮动芯(外径22 mm)进行仿真研究.如图 9所示分别采用1号、2号、3号和4号浮动芯注射时P3处的纵截面图.从图中可以直观看出, 随着浮动芯外径的减小, 残余壁厚呈明显的上升趋势, 表明浮动芯外径对残余壁厚有较大影响.

|
图 9 不同外径浮动芯注射的P3处纵截面仿真结果 Fig. 9 Simulative results of longitudinal section in P3 with different outer diameter floating core injection |
表 3列出了不同外径的浮动芯注射时理想残余壁厚与仿真残余壁厚值.其中, Φ为浮动芯外径, bid为理想残余壁厚, bsi为仿真残余壁厚, Eerr为bid与bsi之间的误差.工业用和民用的塑料制品对残余壁厚的精度要求不是非常高, 10%以内的残余壁厚控制误差是可以接受的.从表中数据看出, 在误差范围内, 仿真残余壁厚与理想残余壁厚是相符的, 因此可以进一步证明浮动芯注射法能够控制制品的残余壁厚.
| 表 3 不同外径浮动芯注射的制品残余壁厚仿真结果对比 Table 3 Simulative residual wall thickness of parts comparison with different outer diameter floating core injection |
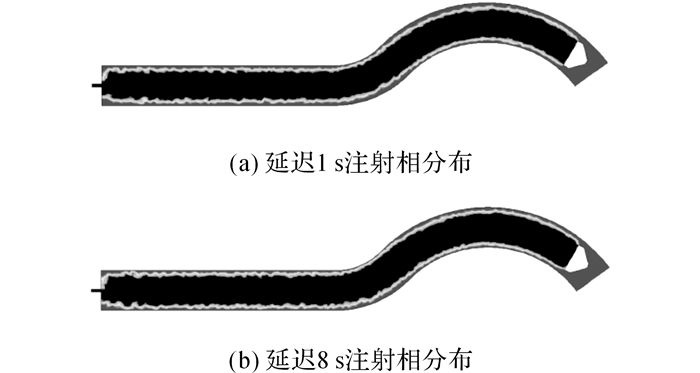
延迟时间对水辅成型制品残余壁厚有较大的影响.分别取延迟时间为1、2、4、6、8 s进行对比试验和仿真.如图 10~12所示分别列出了直接注射、1号和2号浮动芯注射延迟1和8 s的相分布图.从图中可以直观发现, 直接注射时延迟1和8 s的残余壁厚差异较大, 而1号和2号浮动芯注射时, 延迟1和8 s的残余壁厚差异相对较小.
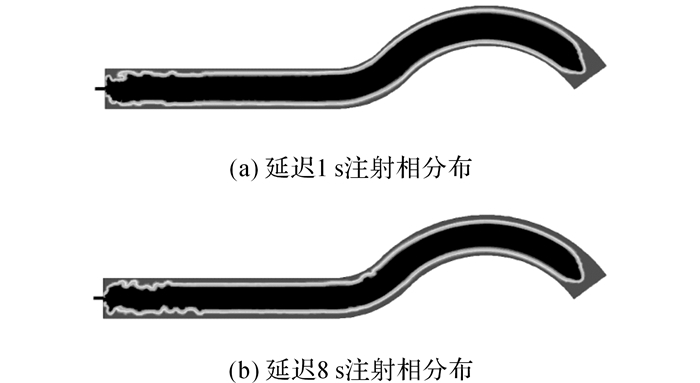
|
图 10 不同延迟时间下直接注射的水与高温塑料熔体相分布 Fig. 10 Phase distribution of water and high-temperature plastic melt with direct injection at different delay time |
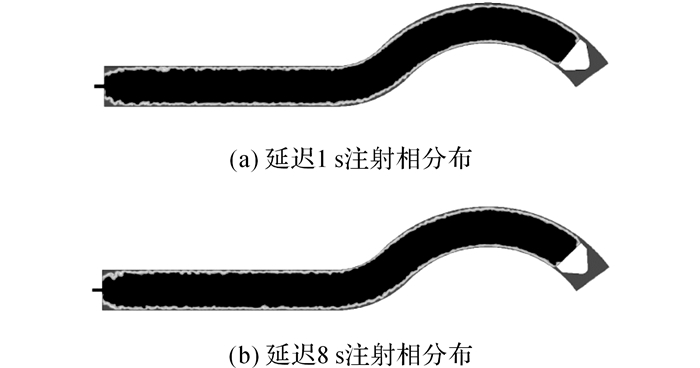
|
图 11 不同延迟时间下1号浮动芯注射的水与高温塑料熔体相分布 Fig. 11 Phase distribution of water and high-temperature plastic melt with No.1 floating core injection at different delay time |
|
图 12 不同延迟时间下2号浮动芯注射的水与高温塑料熔体相分布 Fig. 12 Phase distribution of water and high-temperature plastic melt with No.2 floating core injection at different delay time |
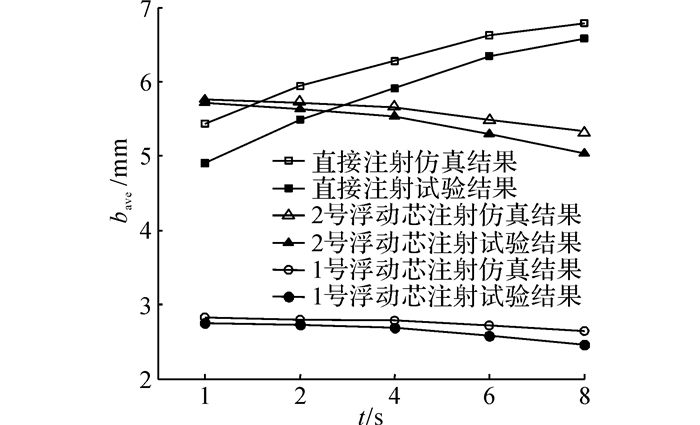
取P1~P8处残余壁厚的平均值, 记为bave.如图 13所示为平均残余壁厚随延迟时间变化的关系.由图 13可知, 试验和仿真结果都表明直接注射的残余壁厚随延迟时间增长呈上升趋势.这是由于延迟时间越长, 熔体冷却越充分, 相应黏度越大, 高压水注射时不易带走黏度较大的熔体, 导致残余壁厚增大.但是浮动芯注射的残余壁厚随延迟时间增长呈缓慢下降趋势, 与直接注射的趋势恰恰相反.分析原因, 延迟时间越长, 塑料熔体黏度越大, 浮动芯在运动过程中更易带走黏度较大的熔体.因此延迟时间越长反而残余壁厚越小.
|
图 13 制品残余壁厚随延迟时间的变化关系 Fig. 13 Residual wall thickness of parts variations at different delay time |
延迟1和8 s注射的平均残余壁厚分别记为b1ave和b8ave.表 4列出了直接注射与浮动芯注射时b8ave相对b1ave的变化率Δ.对比3种注射方法的变化率, 试验和仿真结果都显示直接注射的残余壁厚变化率明显大于浮动芯注射.因此可以说明浮动芯注射的残余壁厚变化受延迟时间影响较小.并且浮动芯注射时延迟时间越短, 残余壁厚越接近理想残余壁厚.越短的延迟时间就能得到越接近理想的残余壁厚, 意味着提高制品质量的同时提高了生产效率, 这是浮动芯注射的一大优点.
| 表 4 延迟时间引起的制品残余壁厚变化比较 Table 4 Residual wall thickness of parts variations comparison at different delay time |
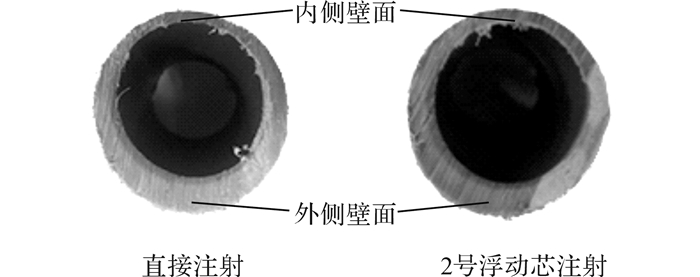
试验过程中发现制品转弯P5~P8处内外侧壁厚分布不均匀, 内侧壁厚明显小于外侧壁厚, 如图 14所示.对于薄壁制品, 这种偏差会严重影响其力学性能.仿真结果同样反映了这一问题, 如图 6所示.高压水或者浮动芯在高温熔体中会朝着流阻较小的方向运动.转弯处由于外侧壁面的阻挡作用, 外侧壁面附近的流阻会大于内侧壁面.因此高压水或者浮动芯会优先选择贴近内侧壁面方向运动, 从而导致内侧壁厚较小.
|
图 14 直接注射和2号浮动芯注射的P5处横截面 Fig. 14 Cross section in P5 with direct injection and No.2 floating core injection |
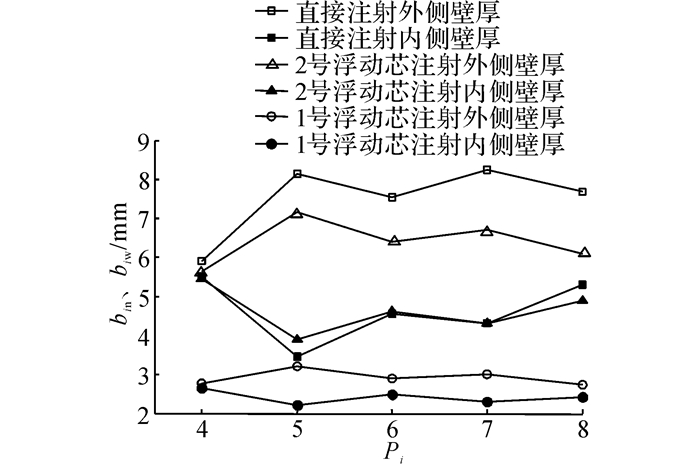
选取延迟4 s的试验结果分析这一现象.如图 15所示为不同注射方法制品转弯处的内外侧壁厚关系曲线.从图中曲线可以看出, P5处的内外侧壁厚差最大, P6、P7、P8处次之, P4处最小.观察制品形状, 发现P5处的转弯曲率最大, P6、P7、P8处曲率次之, P4处的曲率为零.这说明转弯曲率越大的位置, 内外侧壁厚差越大.曲率越大的位置内外侧壁面附近熔体流阻差异越大, 从而导致壁厚差越大.
|
图 15 制品转弯处内外侧壁厚关系 Fig. 15 Relationship between internal and external wall thickness in curve parts |
引入内外侧壁厚差相对值, Pi处的内外侧壁厚差相对值记为Δbi(i=1, 2…8), 计算公式如式(11) 所示.Δbi的大小反映了制品转弯处内外侧壁厚分布不均匀的程度.
| $ \Delta {b_i} = \frac{{{b_{{\rm{iw}}}} - {b_{{\rm{in}}}}}}{{{b_{{\rm{iw}}}} + {b_{{\rm{in}}}}}}. $ | (11) |
式中:bin和biw分别为Pi处内侧和外侧壁厚.
表 5列出了不同注射方法不同位置处的内外侧壁厚差相对值.对比不同注射方法各位置处的内外侧壁厚差相对值, 发现浮动芯注射的明显小于直接注射.对比图 14中P5处横截面照片, 可以发现直接注射和2号浮动芯注射的P5处残余壁厚较为接近, 但后者的内外侧壁厚差要小于前者的内外侧壁厚差.这是因为浮动芯在转弯处运动时, 外侧壁面附近的熔体与浮动芯之间有一个相互挤压力, 提供浮动芯运动的向心力, 这个挤压力使得内外侧壁厚差减小.因此, 相比直接注射, 采用浮动芯注射制品转弯处的内外侧壁厚分布更均匀.
| 表 5 制品转弯处内外侧壁厚差相对值比较 Table 5 Comparison of relative difference in internal and external wall thickness in curve parts |
(1) 在一定的误差范围内, 浮动芯注射法能够控制制品的残余壁厚.通过控制浮动芯外径与制品外径的大小关系, 就能得到接近理想控制值的残余壁厚, 并且残余壁厚沿水流注射方向分布较为均匀.
(2) 相比于直接注射, 浮动芯注射的残余壁厚受延迟时间的影响较小.而且, 延迟时间越短, 得到的残余壁厚越接近理想控制值, 使得制品质量与生产效率同时得到了提升.
(3) 无论是直接注射还是浮动芯注射, 制品转弯处都会出现外侧壁厚大于内侧壁厚的现象.但浮动芯的存在使得内外侧壁厚差值减小很多, 有利于提高制品转弯处力学性能.
本文采用试验与数值模拟相结合的方法, 研究了水辅成型浮动芯注射法制品的残余壁厚, 发现了浮动芯注射法在残余壁厚控制方面的诸多优点.浮动芯的结构对残余壁厚分布均匀性、内壁粗糙度等性能具有一定的影响, 本文在这一方面未进行深入的探究.浮动芯结构的影响有待进一步研究, 使得浮动芯注射法的壁厚控制性能更佳.本文的研究结论对进一步的研究奠定了一定基础, 以及对浮动芯注射法的推广应用具有一定的指导作用.
| [1] | LIANG J C, LI Y, ZHOU D H, et al. Analysis of diffusion mechanism between gas and melt in gas-assisted injection molding[J]. Journal of Materials Processing Technology, 2007, 187: 685–689. |
| [2] |
辛勇, 阮雪榆, 何成宏, 等. 气体辅助注射成形充模流动数值模拟的研究[J].
机械工程学报, 2003, 39(4): 112–115.
XIN Yong, RUAN Xue-yu, HE Cheng-hong, et al. Study on numerical simulation of cavity filling in gas-assisted injection molding[J]. Chinese Journal of Mechanical Engineering, 2003, 39(4): 112–115. |
| [3] |
杨建根, 王冉, 周雄辉. 水辅助注射成型技术研究[J].
工程塑料应用, 2012, 40(2): 43–47.
YANG Jian-gen, WANG Ran, ZHOU Xiong-hui. Research of water assisted injection molding technology[J]. Engineering Plastics Application, 2012, 40(2): 43–47. |
| [4] |
杨建根, 周雄辉. 水辅助注塑成型制品质量及工艺优化研究[J].
塑料工业, 2015, 43(11): 1–3.
YANG Jian-gen, ZHOU Xiong-hui. Study of optimization of product quality and processing in water-assisted injection molding[J]. China Plastics Industry, 2015, 43(11): 1–3. DOI:10.3969/j.issn.1005-5770.2015.11.001 |
| [5] | HUANG H X, ZHOU R H, YANG C. Fiber orientation propelled by high-pressure water penetration in water-assisted injection molded fiber-reinforced thermoplastics part[J]. Journal of Composite Materials, 2013, 47(2): 183–190. DOI:10.1177/0021998312438083 |
| [6] |
孔虎子. 水辅成型PP制品注射工艺及性能试验研究[D]. 杭州: 浙江大学, 2013.
KONG Hu-zi. Experimental Investigation on Injection Process and Performance of PP Samples by WAIM [D]. Hangzhou: Zhejiang University, 2013. |
| [7] |
贾振华, 郑国强, 郝晓琼. 水辅注射成型技术的特点及研究进展[J].
现代塑料加工应用, 2009(5): 60–63.
JIA Zhen-hua, ZHENG Guo-qiang, HAO Xiao-qiong. Characteristics and research development of Water-Assisted Injection Molding technology[J]. Modern Plastics Processing and Application, 2009(5): 60–63. |
| [8] | PROTTE R, BANGERT H, COOPER C, et al. Water-assist injection molding-an innovative process technology for productivity improvement: developments in processing, equipment and materials[C]//Proceedings of the 61st Annual Technical Conference SPE ANTEC. Nashville:TN, US, 2003: 404-408. |
| [9] | PUDPONG T, BUAHOM P, AREERAT S, et al. The effects of processing parameters on the residual wall thickness distribution at the sharp angle corner of water assisted injection molded parts[J]. International Polymer Processing, 2013, 28(5): 528–540. DOI:10.3139/217.2792 |
| [10] | AHMADZAI A Z, BEHRAVESH A H. Effect of processing parameters on water penetration in water assisted injection molding of ABS[J]. Polimery, 2011, 56(3): 232–239. |
| [11] |
邓志武, 黄汉雄, 曲杰, 等. 水辅助注塑制品水穿透长度和残留壁厚的研究[J].
中国塑料, 2006, 20(8): 55–59.
DENG Zhi-wu, HUANG Han-xiong, QU Jie, et al. a1.Study on water penetration length and residual wall thickness of Water-assisted Injection Molding[J]. China Plastics, 2006, 20(8): 55–59. |
| [12] | LIU S, CHEN Y. Water-assisted injection molding of thermoplastic materials: Effects of processing parameters[J]. Polymer Engineering & Science, 2003, 43(11): 1806–1817. |
| [13] |
周国发, 江先念, 巢芳超. 模壁温差对水辅共注成型不平衡充填流动的影响[J].
工程塑料应用, 2015, 43(7): 40–45.
Zhou Guo-fa, Jiang Xian-nian, Chao Fang-chao. Influence of die wall temperature difference on unbalanced filling flow in Water-assisted Co-injection Molding process[J]. Engineering Plastics Application, 2015, 43(7): 40–45. |
| [14] | SANNEN S, MUNCK M D, PUYVELDE P V, et al. Water penetration behavior in water-assisted injection molding (WAIM): A study of product quality for different process and material parameters[J]. International Polymer Processing, 2012, 27(5): 602–616. DOI:10.3139/217.2622 |
| [15] |
周华, 陈英龙, 张增猛, 等. 水辅成型非圆截面制件残余壁厚的仿真与试验研究[J].
机械工程学报, 2010, 46(18): 169–176.
ZHOU Hua, CHEN Ying-long, ZHANG Zeng-meng, et al. Simulation and experimental analysis on non-circular cross-section parts residual wall thickness of Water-assisted Injection Molding[J]. Journal of Mechanical Engineering, 2010, 46(18): 169–176. |
| [16] | YANG J G, ZHOU X H. Numerical simulation on residual wall thickness of tubes with dimensional transitions and curved sections in water-assisted injection molding[J]. Journal of Applied Polymer Science, 2012, 128(3): 1987–1994. |
| [17] | LIU S J, LIN C H. An experimental study of water-assisted injection molding of plastic tubes with dimensional transitions[J]. Journal of Reinforced Plastics and Composites, 2007, 26(14): 1441–1454. DOI:10.1177/0731684407079756 |
| [18] | ZHANG S, CAO W, ZHENG G, et al. Model and numerical simulation for the second penetration in water-assisted injection molding[J]. International Polymer Processing, 2011, 26(5): 560–568. DOI:10.3139/217.2491 |
| [19] | LI Q, CAO W, ZHANG S, et al. Model and numerical simulation for the evolution of residual wall thickness in water-assisted injection molding [C]// IOP Conference Series: Materials Science and Engineering. [S.l.] IOP Publishing, 2010: 012140. |
| [20] |
匡唐清, 余春丛, 邓洋, 等. 水辅助注塑气泡与二次穿透的分析[J].
高分子材料科学与工程, 2014(11): 112–116.
KUANG Tang-qing, YU Chun-cong, DENG Yang, et al. Analysis of air bubble and secondary penetration of water in water assisted injection molding process[J]. Polymer Materials Science and Engineering, 2014(11): 112–116. |
| [21] | POLYNKIN A, BAI L, PITTMAN J F T, et al. Water assisted injection molding: development of insights and predictive capabilities through experiments on instrumented process in parallel with computer simulations[J]. Plastics, Rubber and Composites, 2008, 372(4): 131–141. |
| [22] | KUANG T Q, YU C C, XU B P, et al. Experimental study of penetration interfaces in the overflow fluid-assisted co-injection molding process[J]. Journal of Polymer Engineering, 2016, 36(2): 139–148. |
| [23] | KUANG T Q, ZHOU K, WU L X, et al. Experimental study on the penetration interfaces of pipes with different cross-sections in overflow water-assisted co-injection molding[J]. Journal of Applied Polymer Science, 2016, 133(1): 914–918. |
| [24] | LIU S J, LIN S P. Factors affecting the formation of fingering in water-assisted injection-molded thermoplastics[J]. Advances in Polymer Technology, 2006, 25(2): 98–108. DOI:10.1002/(ISSN)1098-2329 |
| [25] |
张增猛, 周华, 高院安, 等. 水辅助注射成型充模流动的仿真与分析[J].
机械工程学报, 2010, 46(8): 140–146.
ZHANG Zeng-meng, ZHOU Hua, GAO Yuan-an, et al. Simulation and analysis on cavity filling process in Water-assisted Injection Molding[J]. Journal of Mechanical Engineering, 2010, 46(8): 140–146. |
| [26] |
陶俏, 王敏杰, 徐斌. 基于Pareto遗传算法的聚合物黏度模型参数拟合[J].
塑料, 2010, 39(2): 7–9.
TAO Qiao, WANG Min-jie, XU Bin. Viscosity model parameter fitting of polymer based on Pareto genetic algorithm[J]. Plastics, 2010, 39(2): 7–9. |



