2. 广西岩土力学与工程重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Rock-soil Mechanics and Engineering, Guilin 541004, China
活性粉末混凝土(reactive powder concrete, RPC)是法国Bouygues试验室在上世纪九十年代研制出的一种具有超高强度、高韧性、高耐久性的新型水泥基复合材料.近年来RPC在核工程、防爆工程、高铁工程等特种大型工程中的应用越来越广, 国内外学者在RPC材料自身的强度、韧性、抗冲击性、抗渗性[1-4]等有较多研究, 但对配筋RPC梁的研究较少, 尤其在抗剪方面更少.在该领域, 澳大利亚学者Vool[5-6]等进行了一系列的预应力RPC无腹筋梁抗剪试验研究, 总结了预应力变化、钢纤维种类及掺量对梁的初始剪切开裂荷载和极限荷载影响.北京交通大学季文玉等[7]通过12根T型截面普通钢筋RPC简支梁的抗剪试验, 总结出影响RPC梁破坏形态和抗剪承载能力的主要因素是剪跨比、配箍率和配筋率[7].北京工业大学邓宗才等[8]通过6根T形梁的抗剪试验, 并结合压力场理论, 探讨了该理论应用于RPC梁抗剪分析和承载力计算存在的问题.
现行《混凝土结构设计规范》[9]已经把HRB500级钢筋列入混凝土构件的主导受力钢筋, 近年来, 科研人员对配置该级别钢筋混凝土构件的力学性能进行了大量研究[10-14].结果表明:由于HRB500级钢筋强度较高, 与普通混凝土共同工作时, 裂缝较大, 常无法充分利用其高强性能, 同时HRB500级钢筋的延性性能也较现行常见的HRB400级钢筋略有降低, 从而会影响到构件的延性性能.
本文通过对14根HRB500级纵筋RPC梁的抗剪试验研究, 分别考虑了剪跨比、钢纤维体积率、配箍率、配筋率以及纵筋强度的影响, 通过观察构件斜裂缝开展情况、破坏形态, 并分析混凝土应变和剪力-位移曲线等试验数据, 得出这些因素对试验梁的开裂荷载、抗剪承载力与剪切延性的影响规律, 并探讨RPC梁的抗剪机理和承载力, 以及2种材料在抗剪方面共同工作的匹配性.
1 试验概况 1.1 试件原材料及其力学性能RPC原材料:1) 水泥:海螺牌52.5普通硅酸盐水泥;2) 石英砂:粒径为0.4~0.6 mm;3) 微硅粉成份为二氧化硅(SiO2), 平均粒径为0.1 μm, 表面积为15 000~20 000 m2/kg;4) 硅微粉:粒径2 μm以下, 平均粒径约为0.31 μm;5) 石英粉:粒径小于4 μm;6) 钢纤维:采用镀铜光面平直钢纤维, 长度约为13 mm, 直径约为0.15~0.2 mm.本次试验用到不同钢纤维体积率的RPC, 其配合比见表 1, 表中,ρm为质量密度,小组分为不便公开的专利产品.RPC力学性能测试结果见表 2, 表中φB为钢纤维体积分数, fcu为尺寸100×100×100 mm的立方体抗压强度, fc为尺寸100×100×300 mm的棱柱体抗压强度, fcf为抗折强度, fts为劈裂强度, Ec为RPC弹性模量, 从表中可以看出当钢纤维体积率由0增加到2%, 其各项力学指标增强效果明显, 当由2%增加到3%时, 效果已不是很明显.试验梁底部纵筋主要选用HRB500级钢筋;箍筋及架立筋选用HRB400级钢筋, 其力学性能测试结果见表 3, 表中,fy为屈服强度, fst为极限抗拉强度, Es为钢筋弹性模量.
| 表 1 RPC配合比 Table 1 Mix proportion of RPC |
| 表 2 RPC力学性能 Table 2 Mechanical properties of RPC |
| 表 3 钢筋力学性能 Table 3 Mechanical properties of reinforcement |
本次试验的目的是研究构件的抗剪性能, 故试验梁的设计首先要考虑到在加载过程中, 首先应发生剪切破坏, 而不是弯曲破坏, 故构件的截面设计应根据文献[15-16]中给出的相关公式、适用条件进行预估算, 以满足此条件.14根试验梁截面尺寸均为150 mm(宽)×250 mm(高), 跨度为2 200 mm, 计算跨度为1 800 mm, 其弯剪段配有2根HRB400级直径为8的架立筋, 构件设计及编号见表 4, 其中:a为加载点到支座距离, λ为剪跨比, ρsv为配箍率, ρ为配筋率, 
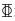
| 表 4 试件参数 Table 4 Parameters of specimens |
|
图 1 试验方案及加载图 Fig. 1 Test scheme and loading |
如图 2所示, 试验梁的裂缝发展规律基本都是跨中纯弯段先出现竖向微裂缝, 而后在弯剪段出现斜裂缝, 由于试验梁底部纵筋配置较多, 跨中竖向裂缝发展较为缓慢, 但弯剪段斜裂缝发展较快, 最终破坏时, 在梁的破坏端基本都能形成一条具有最大宽度的主斜裂缝, 走向大体沿支座到加载点之间.具体到各个不同参数, 剪跨比对斜裂缝的倾角和破坏形态影响较大, 随着剪跨比的增加, 斜裂缝与水平向的夹角逐渐减小, 破坏形态由“趋向斜压型”转为“剪压型”, 再转为“趋向斜拉型”, 同时梁的跨中竖向裂缝也变得更加密集, 长度也有所增加;配箍率则对弯剪段斜裂缝的分布形态影响较大, 在试验梁的弯剪段配置箍筋对其剪切延性的影响较明显, 在试验现象上则表现为随着配箍率的增加, 试验梁弯剪段斜裂缝的分布规律由少而集中变得多而发散, 裂缝变得更细更密, 至LB-4(ρsv=0.75%)时, 已无明显的主斜裂缝;钢纤维体积率则对试验梁的整体延性影响较明显, 随着钢纤维体积率的增加, 不管是试验梁的跨中纯弯段的竖向裂缝, 还是支座弯剪段的斜裂缝都明显变得更密;纵筋率与纵筋强度对试验梁破坏形态与斜裂缝的影响最不明显.

|
图 2 试件破坏形态和裂缝分布 Fig. 2 Failure mode and crack distribution |
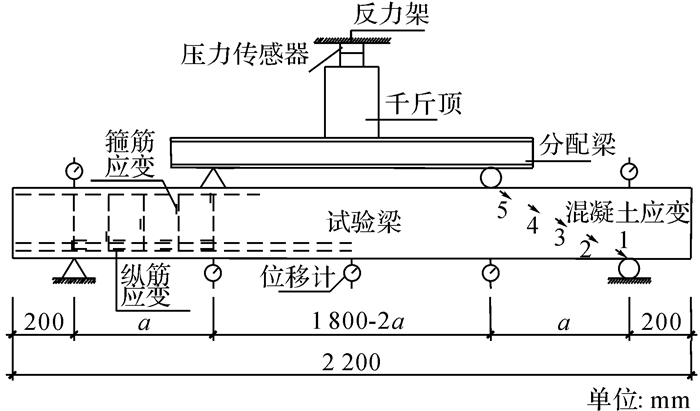
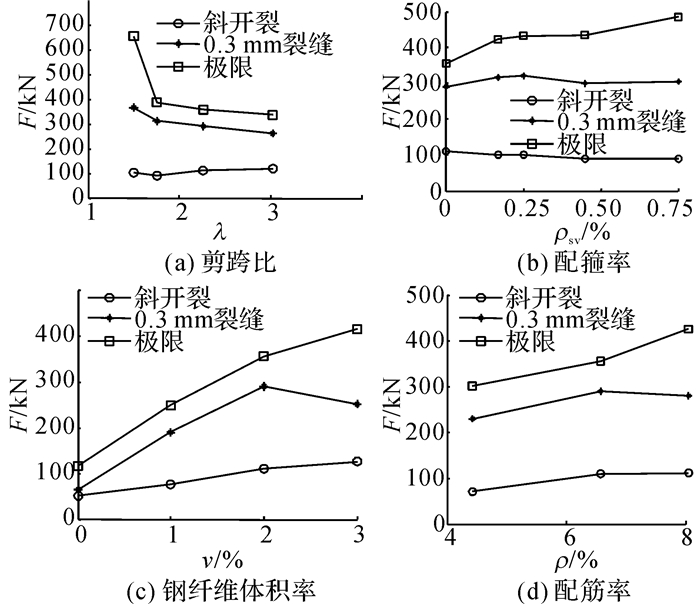
如图 3所示为不同的影响因素对各阶段梁端剪力值F的影响, 从图 3中可以看出:1) 极限荷载:剪跨比对试验梁的极限承载力最为明显, 大致呈反比例关系, 且当剪跨比由1.5增加到2左右时, 抗剪承载力减弱明显.同时随配箍率、钢纤维体积率、配筋率的增大而增大, 而配箍率对极限荷载的影响相对较小.2) 斜向开裂荷载:钢纤维体积率对试验梁开裂荷载影响明显, 说明钢纤维对抑制斜裂缝的开展起到了良好的作用, 体积率由0增加至2%时, 其提高程度较明显, 但由2%增加至3%时, 其提高程度有所减弱.而其他条件则对试验梁的开裂荷载影响不明显.3) 斜裂缝宽为0.3 mm时的梁端剪力:剪跨比和钢纤维体积率对该荷载值影响较大, 剪跨比的不同导致试验梁弯剪段RPC材料的二维应力状态的改变, 钢纤维在RPC中的锚固与拉扯, 可以有效地阻止裂缝的开展, 但当体积率由2%增加至3%时, 该荷载值反而降低, 说明当钢纤维体积率过高时, 由于拌制振捣等因素, 纤维材料容易结团, 不利于浇筑, 反而会影响到RPC材料性能, 这点可以从表 2中得到印证.4) 带裂缝工作能力:由极限荷载与开裂荷载的差值可以反映该能力的大小, 其值随着剪跨比的增大而减小, 随着配箍率、钢纤维体积率、配筋率的增大而增大, 其中不含钢纤维的试验梁该能力最差, 开裂荷载、极限荷载均最小, 结合LC-1的裂缝图可以看出构件表面裂缝分布较少, 只有主斜裂缝, 故出现“一裂就坏”的脆性破坏现象.
|
图 3 各参数对不同阶段荷载的影响 Fig. 3 Each stage load in different factors |
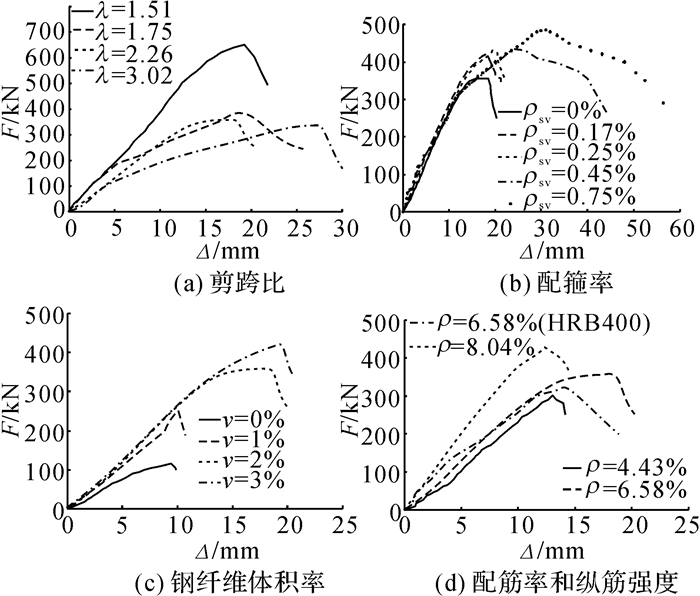
如图 4所示为剪力挠度曲线,图中Δ为挠度, 试验梁的剪力挠度曲线形态均大致呈现出“弹性-弹塑性-破坏-回落”4个阶段, 不同因素对该曲线形态的影响各不相同.剪跨比对构件的破坏形态影响最明显, 随着剪跨比的增大, 其破坏形态由“趋向斜压型”逐渐向“趋向斜拉型”过度, 在曲线形态上则表现为, 随着剪跨比的增大, 构件极限承载力下降明显, 但其所对应的挠度值有所增加, 说明RPC中的钢纤维提高了材料的抗拉强度, 对其延性有所改善, 并没有出现普通混凝土梁在“斜拉破坏”时的脆性现象;同时剪跨比还决定了RPC材料微元体的应力模型, 随着剪跨比增大, RPC微元体以拉应力为主, 故斜裂缝的发展更为迅速, 构件刚度下降更快, 在曲线形态上则表现为随着荷载的增加, 曲线斜率下降更快.配箍率对构件延性影响最为明显, 在曲线形态上则表现为极限荷载峰值点所对应的挠度值随配箍率的增大而明显增大, 同时曲线下降段斜率变小, 挠度回落速度变缓;相对于延性, 配箍率对构件抗剪承载力的影响相对较小.由表 2可知, 钢纤维体积率的不同直接影响到RPC的各项力学指标, 当RPC中不掺钢纤维或者钢纤维体积率较低时, 其与强度与配筋率均较高的HRB500级纵筋共同作用时, 产生了不匹配现象, 不仅使得构件的抗剪承载力急剧下降, 其下降程度高于材料强度的下降程度, 同时极限荷载对应的挠度值也急剧下降, 说明构件延性也较差, 此现象在钢纤维体积率由0到2%尤为明显, 但由2%提高到3%则变化不明显, 说明最优钢纤维体积率就在2%到3%之间.纵筋率对构件的刚度影响较大, 这可以从曲线上升段的斜率看出, 同时也对其抗剪承载力有一定影响, 但纵筋强度对构件的力学性能影响不大.
|
图 4 剪力挠度曲线 Fig. 4 Shear load-deflection responses |
本文引用剪切延性系数μv来描述试验梁的剪切延性[17], 即
| $ {\mu _{\rm{v}}} = {\mathit{\Delta }_{\rm{u}}}/{\mathit{\Delta }_{\rm{y}}}. $ | (1) |
式中:Δu为荷载-挠度曲线下降段上对应0.85Fmax的位移, Δy为梁的屈服点所对应的位移.由于本次试验梁大部分为无腹筋梁, 其抗剪破坏都具有明显的脆性特征, 且本次试验梁的梁底纵筋都未达到屈服强度, 故本文采用等能量法将构件的剪力-挠度曲线进行折线化处理, 即曲线OAB包含的面积与曲线BYM包含的面积相等, 见图 5, 计算出各试验梁的剪切延性系数, 见表 5.

|
图 5 剪切延性系数线 Fig. 5 Shear ductility indexes |
| 表 5 试件剪切延性指数表 Table 5 Shear ductility index of specimens |
由表 5可以看出, 影响构件延性性能的主要因素为配箍率和钢纤维体积率.LB-3(ρsv=0.45%)、LB-4(ρsv=0.75%)的剪切延性要远远大于其他试验梁, 说明适当的提高构件弯剪段配箍率, 可有效提高构件受剪破坏时的延性性能, 同时也应当看出当配箍率过小时, 构件延性性能改善并不明显, 但过高时其改善效果又有限, 所以存在一个范围值, 使得箍筋对其改善的效果最为明显, 即普通钢筋混凝土构件中所提到的最小配箍率的限定条件和最小截面尺寸的限定条件;LC-2的剪切延性最小, 且明显小于其他试验梁, 其主要原因是由于该构件钢纤维体积率较低, 由表 2知其抗拉和抗折强度均较低, 当构件接近破坏时, 其脆性性能十分明显, LC-1的钢纤维体积率虽然最小, 但由于其极限荷载远小于LC-2, 故在构件破坏时, 其瞬间释放的能量也较小, 体现在延性性能上则略好于LC-2, 但较低钢纤维体积率的试验梁无论从承载力还是延性性能上都表现出了不匹配的特性;剪跨比、配筋率、纵筋强度则对构件剪切延性的影响不是很明显, 因为这些构件均为无腹筋梁, 构件的延性性能主要取决于RPC材料的塑性性能, 故这些因素对剪切延性的影响不是很明显.
3 试验结果机理分析RPC梁的抗剪工作机理与普通混凝土梁相似, 所不同的是RPC不含粗骨料, 而普通混凝土不含钢纤维, 这使得当构件开裂后, 普通混凝土界面上的骨料咬合力被RPC中钢纤维的拉拔阻力所取代, 同时对纵筋的销栓作用也带来一定影响.构件开裂前处于弹性工作状态, 弯剪段内的二维应力状态符合材料力学规律, 且基本上都由RPC承担, 纵筋和箍筋的应变值都很低.当截面出现弯剪斜裂缝时, RPC中钢纤维的拉拔阻力和纵筋的销栓力参与抗剪.当斜裂缝继续发展穿越箍筋时, 箍筋参与抗剪, 且承担的剪力逐渐增大, 并有效地约束斜裂缝继续开展.当荷载继续加大, 箍筋屈服, 此时斜裂缝较宽, 开裂截面内的大部分钢纤维被拔出或拉断, 最终斜裂缝上端未开裂混凝土达到极限强度, 纵筋的销栓力撕脱梁端混凝土的保护层.同时应当看出, 无腹筋试验梁的剪力—挠度曲线也较为平滑, 这是由于RPC中钢纤维分布在这些裂缝尖端处, 由于钢纤维强度远高于RPC基体中水泥的胶凝力, 且尺寸远大于裂缝尖端, 故钢纤维可以起到桥接和销栓的作用, 阻碍裂缝开展, 并使得其开裂后的RPC还可以继续承担部分应力, 刚度没有发生突变的原因.
如图 6所示, 试验梁弯剪段内承载力的主要成分是:斜裂缝上端、靠梁顶部未开裂RPC的抗剪承载力(Fc)、沿斜裂缝RPC中钢纤维的牵引力的竖向分量(Fi)、纵筋的销栓力(Fd)以及箍筋的抗剪承载力(Fs)等.这4种抗剪成分在试件最终抗剪承载力所占的比重和很多因素有关, 主要包括RPC的强度、箍筋和纵筋的数量和布置等因素有关, 同时还和剪跨比以及裂缝开展形态有关, 裂缝穿越的箍筋数量越多, 箍筋所承担的剪力就越大.当构件达到极限抗剪承载力力(Fu)时, 应为上述各抗剪分量总和, 即

|
图 6 抗剪计算模型 Fig. 6 Shear model for calculating |
| $ {F_{\rm{u}}} = {F_{\rm{c}}} + {F_{\rm{i}}} + {F_{\rm{d}}} + {F_{\rm{s}}}. $ | (2) |
普通钢筋混凝土构件的抗剪本身就是一个非常复杂的问题, 影响因素众多, 研究至今提出过很多理论与计算公式, 但大多都存在一定的局限性, 本试验中构件的主要材料为RPC而不是普通混凝土, 所以需要合适的力学模型同时针对RPC材料自身特点来合理解释破坏机理, 从而推导出承载力公式.本文拟从现有规范和塑性理论所给出的公式进行分析探讨.
4.1 现有规范分析鉴于目前尚无RPC梁抗剪承载力规范, 本文选取《混凝土结构设计规范》[9]、《高强混凝土结构技术规程》[18]、《纤维混凝土结构技术规程》[19]和美国ACI规范[20]的抗剪承载力进行计算, 结果见表 6, 表中材料强度指标取实测值;Fex为实测值;Fcu为计算值.
| 表 6 抗剪承载力试验值与规范计算值比较 Table 6 Comparison of test results with values calculated by codes |
由表 6可以看出, 各规范均较保守, 且计算结果离散性也较大.《混凝土结构设计规范》的抗剪承载力公式以大量普通钢筋混凝土梁试验数据为依据, 进行回归分析, 得出其上下限曲线的近似计算式, 同时又考虑到受剪破坏的突然性和试验数据的离散性, 以及设计原则上安全性, 规范采用了比下限值更低的抗剪承载力计算公式, 故该公式适用于强度较低且不含钢纤维的普通钢筋混凝土梁, 同时公式没有考虑RPC高强高韧性的材料特点, 对RPC中钢纤维的牵引力考虑不足, 也忽略了纵筋销栓力的贡献.《高强混凝土结构技术规程》是以《混凝土结构设计规范》为基础, 考虑到高强混凝土的延性更差, 破坏时脆性更加明显, 故更加降低了混凝土材料对抗剪承载力的影响, 故该规范的结果最低.美国ACI规范是分别对腹剪裂缝和弯剪裂缝进行计算, 通过裂缝控制进行计算, 同时并未考虑剪跨比的影响, 这不仅使得计算结果偏低, 同时稳定性最差.相比之下《纤维混凝土结构技术规程》考虑了混凝土材料中钢纤维的影响, 计算结果与实测值最为接近, 同时变异系数最小, 其结果的稳定性最好, 只是钢纤维混凝土与RPC从材料组成上还有很大不同, 钢纤维混凝土的强度较低(一般低于C80) 且含粗骨料, 但还是可以看出《纤维混凝土结构技术规程》的抗剪承载力公式推导思路对于RPC梁来讲是可以借鉴的.
4.2 塑性剪切理论由于RPC中钢纤维的掺入, 其变形能力得到显著提高, 当RPC梁开裂后, 钢纤维有桥接和阻裂作用, 使得斜截面裂缝扩展缓慢, 塑性变形能力增加.塑性理论是把钢筋和混凝土转化为理想刚塑性材料, 设定某一屈服准则, 用塑性理论上下限定理来求解, 从而得到抗剪极限承载力的上限解和下限解.上限解是指结构破坏时形成的机动体系是由若干个刚性区所组成, 各刚性区之间由塑性区相衔接, 结构的内功全部消耗在塑性区上, 然后利用虚功原理求出最低上限解(机动解);下限解是依据结构的受力状态假定一个静定的应力场, 然后利用几何条件和平衡条件求出下限解(静力解).如果上、下限解相同, 即为精确解[21].
4.2.1 塑性极限分析赵军等[21]根据钢纤维混凝土的应力应变关系特点, 确定了钢筋和钢纤维混凝土的屈服条件, 建立了钢纤维混凝土梁斜截面破坏模型.本文运用塑性分析方法推导出斜截面受剪承载力计算公式的塑性解, 最终公式为
| $ {F_u} = 0.5{\mu _{\rm{f}}}{f_{\rm{c}}}b{h_0}(\sqrt {1 + {\lambda ^2}} - \lambda ) + 0.5(1 - {\mu _{\rm{f}}}){f_{\rm{t}}}b{h_0}(\sqrt {1 + {\lambda ^2}} + \lambda ) + {\rm{ }}{f_{{\rm{yv}}}}{A_{{\rm{sv}}}}a/s. $ | (3) |
式中:b为梁截面宽度, h0为梁截面的有效高度, fyv为箍筋抗拉强度, Asv为箍筋面积, s为箍筋间距.ft为RPC轴心抗拉强度, 由文献[22]可知:ft=0.75fts, μf为塑性系数, 反映了极限状态时平面主拉应力和主压应力状态关系, 由二元线型回归方法得到, 由于RPC的试验数据缺乏, 本文采用钢纤维钢筋混凝土梁的计算方法.
| $ {\mu _{\rm{f}}} = 1 - 0.009{f_{{\rm{cu}}}} + 15.5\rho . $ | (4) |
Voo等[6]基于塑性上限理论, 在裂缝滑移模型的基础上, 考虑了钢纤维对RPC的增韧, 提出了无腹筋RPC梁抗剪承载力计算公式:
| $ {F_u} = 0.5f_{\rm{c}}^*bh(\sqrt {1 + {{\left( {x/h} \right)}^2}} - x/h). $ | (5) |
式中:fc*为塑性抗压强度, h为梁截面高度, x为弯剪段主斜裂缝的水平投影长度.
| $ f_{\rm{c}}^* = {\nu _{\rm{c}}}{f_{\rm{c}}}. $ | (6) |
式中:νc为抗压有效系数, 取0.8.为使该公式更加便于计算, 同时便于和公式(3) 进行对比, 令x=a, 即主斜裂缝的水平投影长度即为加载点到支座的水平距离(由图 2可以看出), 同时模型中不考虑受拉区混凝土保护层参与抗剪, 即用h0替换h, 同时借鉴式(3) 中箍筋提供抗剪承载力的表达式, 则得最终表达式为
| $ {F_u} = 0.5f_{\rm{c}}^*b{h_0}(\sqrt {1 + {\lambda ^2}} - \lambda ) + {f_{{\rm{yv}}}}{A_{{\rm{sv}}}}a/s. $ | (7) |
将塑性理论计算结果与实测值进行比较, 见表 7.其中Fcu3为式(3) 计算的结果, Fcu7为式(7) 计算的结果.
| 表 7 抗剪承载力试验值与塑性理论计算值比较 Table 7 Comparison between test values and calculated values by plastic theory |
由表 7可以看出, 用基于塑性理论所计算的结果更加接近实测值, 且离散性也不是很大, 说明该理论模型在RPC梁的抗剪承载力公式推导上的可行性, 只是鉴于目前试验数据较少, 公式中的某些由回归方法求得的系数, 还需进一步研究确定.
5 结论(1) 在一定范围内, 构件抗剪承载力随钢纤维体积率、配箍率、配筋率以及纵筋强度的提高而增大, 随剪跨比的增加而降低, 其中钢纤维体积率和剪跨比的影响最为明显.当钢纤维体积率由0提高到2%时, 构件的抗剪承载力提高明显, 由2%提高到3%, 提高程度降低, 剪跨比由1.5增加到2左右时, 抗剪承载力减弱明显, 由2增加到3时, 减弱不明显.
(2) RPC中钢纤维的掺入, 使得其变形能力得到显著提高.当RPC梁开裂后, 钢纤维有桥接和阻裂作用, 使得斜面裂缝扩展缓慢, 塑性变形能力增加, 剪跨比对构件裂缝的倾角以及最终破坏形态有一定影响, 配箍率对斜裂缝的分布与发展有较大影响, 且对剪切延性影响最大, 当配箍率由0.25%提高到0.45%, 剪切延性增加明显, 说明当抵抗由集中荷载为主所产生的剪应力时, 钢纤维不能替代箍筋的作用.
(3) 当RPC中不含钢纤维或体积率较低时, RPC材料本身各项力学性能指标较低, 当梁底配有强度较高的HRB500级纵筋且配筋率也较高时, 构件的破坏形态脆性明显, 抗剪承载力的下降程度远大于材料抗拉、抗压等力学指标的下降程度, 从而说明钢纤维体积率较低的RPC与HRB500级纵筋在抗剪性能上相互不匹配, 材料特性没有充分发挥, 同时说明钢纤维体积率为2%的RPC与HRB500级纵筋的抗剪共同工作的匹配性较好.
(4) 在RPC梁受剪承载力模型理论及公式方面, 现有规范中的CECS 38-2004考虑了混凝土材料中钢纤维的影响, 计算结果与实测值最为接近, 同时变异系数最小, 其抗剪承载力公式推导思路对于RPC梁来讲是可以借鉴的.用基于塑性理论所计算的结果更加接近实测值, 且离散性也不是很大, 说明该理论模型在RPC梁的抗剪承载力公式推导上是可行的.
| [1] | RICHARD P, CHEYREZY M. Composition of reactive powder concretes[J]. Cement and Concrete Research, 1995, 25(7): 1501–1511. DOI:10.1016/0008-8846(95)00144-2 |
| [2] | DUGAT J, ROUX N, BEMIER G. Mechanical properties of reactive powder concretes[J]. Materials and Structures, 1996, 29(5): 233–240. |
| [3] |
鞠彦忠, 王德弘, 康孟新. 不同钢纤维体积率活性粉末混凝土力学性能的试验研究[J].
应用基础与工程科学学报, 2013, 21(2): 299–306.
JU Yan-zhong, WANG De-hong, KANG Meng-xin. Mechanical properties of RPC with different steel fiber contents[J]. Journal of Basic Science and Engineering, 2013, 21(2): 299–306. |
| [4] |
王晓飞, 王阳平. 钢纤维活性粉末混凝土力学特性[J].
建筑材料学报, 2015, 18(6): 941–945.
WANG Xia-ofei, WANG Yang-ping. Mechanical properties of RPC with different steel fiber Volume contents[J]. Journal of Building Materials, 2015, 18(6): 941–945. |
| [5] | VOO Y L, FOSTER S J, GILBERT R I. Shear strength of fiber reinforced reactive powder concrete girders without stirrups [D]. Australia: The University of New South Wales, 2003. |
| [6] | VOO Y L, FOSTER S J, GILBERT R I. Shear strength of fiber reinforced reactive powder concrete prestressed girders without stirrups[J]. ACI Structural Journal, 2006, 4(1): 123–132. |
| [7] |
季文玉, 丁波, 安明喆. 活性粉末混凝土T形梁抗剪试验研[J].
中国铁道科学, 2011, 32(5): 38–41.
JI Wen-yu, DING Bo, AN Ming-zhe. Experimental study on the shear capacity of reactive powder concrete T-beams[J]. China Railway Science, 2011, 32(5): 38–41. |
| [8] |
邓宗才, 周冬至, 程舒锴. 配筋活性粉末混凝土梁抗剪承载力[J].
哈尔滨工程大学学报, 2014, 35(12): 1512–1578.
DENG Zong-cai, ZHOU Dong-zhi, CHENG Shu-kai. The shear bear capacity of reactive powder concrete beam with high strength stirrup[J]. Journal of Harbin Engineering University, 2014, 35(12): 1512–1578. |
| [9] |
GB50010—2010. 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010
GB 50010—2010. Code for design of concrete structures[S]. Beijing: China Architecture and Building Press, 2010. |
| [10] |
王晓锋, 傅剑平, 朱爱萍, 等. 配置HRB500级钢筋混凝土柱抗震性能模拟分析[J].
建筑结构学报, 2011, 32(8): 99–105.
WANG Xiao-feng, FU Jian-ping, ZHU Ai-ping, et al. Numerical simulation of seismic behavior of RC columns reinforced with HRB500 steel bars[J]. Journal of Building Structures, 2011, 32(8): 99–105. |
| [11] |
金伟良, 陆春华, 王海龙, 等. 500级高强钢筋混凝土梁裂缝宽度试验及计算方法探讨[J].
土木工程学报, 2011, 44(3): 16–22.
JIN Wei-liang, LU Chun-hua, WANG Hai-long, et al. Experiment and calculation of crack width of reinforced concrete beams with 500MPa steel bars[J]. China Civil Engineering Journal, 2011, 44(3): 16–22. |
| [12] |
易伟建, 潘柏荣, 吕艳梅. HRB500级钢筋配箍的混凝土梁受剪性能试验研究[J].
土木工程学报, 2012, 45(4): 56–42.
YI Wei-jian, PAN Bai-rong, LV Yan-mei. Experimental study on the shear failure of reinforced concrete beams with grade HRB500 steel stirrups[J]. China Civil Engineering Journal, 2012, 45(4): 56–42. |
| [13] |
蒋遨宇, 陈驹, 金伟良. HRB500级钢筋混凝土梁受弯性能分析[J].
浙江大学学报:工学版, 2013, 47(9): 1566–1572/1671.
JIANG Ao-yu, CHEN Ju, JIN Wei-liang. Flexural behaviour analysis of HRB500 reinforced concrete beams[J]. Journal of Zhejiang University :Engineering science, 2013, 47(9): 1566–1572/1671. |
| [14] |
邓宗才, 袁常兴. 高强钢筋与活性粉末混凝土黏结性能的试验研究[J].
土木工程学报, 2014, 47(3): 69–78.
DENG Zong-cai, YUAN Chang-xing. Experimental study on bond capability between high strength rebar and reactive powder concrete[J]. China Civil Engineering Journal, 2014, 47(3): 69–78. |
| [15] |
李莉. 活性粉末混凝土梁受力性能及设计方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
LI Li. Mechanical behavior and design method for reactive powder concrete beams [D].Harbin: Harbin Institute of Technology, 2010. |
| [16] |
陈彬. 预应力RPC梁抗剪性能研究[D]. 长沙: 湖南大学, 2007.
CHEN Bin. Study on the shear strength of prestressed RPC girders [D]. Changsha: Hunan University, 2007. |
| [17] | PAULAY T, PRIESTLEY M J N. Seismic design of reinforced concrete and masonry buildings[M]. New York: John Wiley & Sons, Inc., 1992. |
| [18] |
CECS 104: 99. 高强混凝土结构技术规程[S]. 北京: 中国建筑工业出版社, 1999.
CECS 104: 99. Technical specification for high-strength concrete structures [S].Beijing: China Architecture & Building Press, 1999. |
| [19] |
CECS 38—2004. 纤维混凝土结构技术规程[S]. 北京: 中国计划出版社, 2004.
CECS 38—2004. Technical specification for fiber reinforced concrete structures [S]. Beijing: China Planning Press, 2004. |
| [20] | ACI318-05. Building code requirements for structural concrete (ACI318-05) and Commentary (ACI318R-05) [S]. Farmington Hills: American Concrete Institute, 2005. |
| [21] |
赵军, 高丹盈, 朱海堂. 钢纤维增强钢筋混凝土梁斜截面受剪承载力塑性极限分析[J].
力学季刊, 2005, 26(2): 235–240.
ZHAO Jun, GAO Dan-ying, ZHU Hai-tang. Shear capacity plastic analysis of steel fiber reinforced concrete beams with reinforcement[J]. Chinese Quarterly of Mechanics, 2005, 26(2): 235–240. |
| [22] | GRAYBEAL B A. Characterization of the behavior of Ultra-High performance concrete [D]. American: The University of Maryland, 2005. |


