2. 浙江财经大学 东方学院, 浙江 杭州 310012;
3. 杭州国际城市学研究中心, 浙江 杭州 310002
2. Dongfang College, Zhejiang University of Finance and Economics, Hangzhou 310012, China;
3. Hangzhou International Urban Research Center, Hangzhou 310002, China
随着社会经济的快速发展以及城市化进程的加速推进, 城市交通拥堵加剧、交通网络可靠性降低、交通能耗增加等问题日益凸显.《国家新型城镇化规划(2014—2020年)》提出, 到2020年我国常住人口城镇化率将达到60%左右, 比2015年的56.1%提高3.9%.届时, 城市交通压力将进一步增强, 而交通系统是城市生活品质的关键、宜居城市的基础.各地政府相继出台了各项交通政策, 力图缓解交通形势的恶化, 但效果欠佳, 北京、上海等各大城市交通拥堵频频告急.主要原因是对居民的出行规律把握不够, 这主要是:1) 传统的公交客流调查方式, 不能全面准确的把握居民的出行需求, 缺少对出行活动特征和出行分布的整体全面判断;2) 未能考虑到居民出行的空间自相关的特征.
手机信令数据为居民出行影响因素研究提供了丰富可靠的数据支持.Gonzalez等[2]分析十万人连续6个月的手机信令数据、以及206人持续一周的每次穿越小区或超过2个小时即更新位置信息的手机信令数据, 研究居民出行行为.Ren等[3]基于大规模手机数据, 提取小汽车出行信息, 估计动态交通需求, 建立“道路使用网络”, 分析发现不同交通小区的“拥堵贡献”存在很大差异, 导致拥堵的大部分车流仅出自少量交通小区, 为优化交通组织方案、缓解交通拥堵提供了重要科学依据.Çolak等[4]利用手机数据分析各城市出行距离与出行时间的关系, 以此来分析城市的拥堵状况.
Bhat等[5]提出交通需求本质具有空间依赖性(spatial dependency)和空间异质性(spatial heterogeneity), 也就是空间中各变量之间存在相互影响, 同时, 各变量由于其所处的区位位置不同而存在着差异性.现有的统计分析、计量经济学、结构方程模型(SEM)和模拟仿真等研究方法忽略了地理空间邻近所带来的数据空间相关性和空间异质性[6-9], 由此导致计量估计方法和检验结果的失效或偏差.
本文基于杭州市手机信令数据, 借助地理分析工具ArcGIS和空间计量经济学方法, 构建居民出行OD的空间计量模型, 定量化量度各因素的变化对居民出行的影响, 并分析相应的政策含义, 为交通需求预测、公交线路规划、城市土地规划等奠定基础.
1 数据来源与描述本文研究的数据来源主要有3个部分:
1) 来自某运营商的杭州市手机信令数据.数据采集区域覆盖杭州主要城区, 包括上城区、下城区、江干区、拱墅区、西湖区、滨江区、以及萧山区和余杭区与杭州联系较密的区域, 如萧山机场和临平2大板块, 共计55 372个基站.萧山区和余杭区的剩余区域以及富阳区、桐庐县、淳安县、建德市和临安市等辖区, 因与主城区联系相对较少, 故不列入本文的研究范围.
手机信令可以由以下5种方式产生:接打电话、收发短信、开关机、用户在基站大区之间切换和周期性的位置更新(例如大于2 h基站设备就会自动与手机通信一次).每条信令记录包含用户的匿名ID、基站ID、基站经纬度、信令时间戳、停留时间、与上一通讯基站间的距离.
对于某一匿名用户i, 其第k条手机信令记录为Ri(k), 包含的位置信息为pi(k), 时间戳为ti(k).根据手机信令产生的时间序列, 其连续的记录为{Ri(1), Ri(2), …, Ri(n)}.本研究将一次出行定义为, 当一串手机信令记录{Ri(q), Ri(q+1), …, Ri(z)}, 1≤q≤z≤n, 满足2个条件:1)ti(z)-ti(q)>ΔT, 即第z条记录与第q条记录的时间差大于某个阈值(本研究取为30 min);2)
数据采集时间为2015年9月7日(星期一)至9月13日(星期日), 历时一周, 每天数据包含8:00~11:00和16:00~19:00这2个时段, 共14个时间段.Qs, Qp分别表示出行人数非零的基站OD数量和出行次数, 如表 1所示.平均每天早、晚高峰的基站OD数量约分别为213.2万个OD对和213.9万个OD对.平均每天早、晚高峰的出行次数分别约为411.2万人次和400.5万人次.
| 表 1 手机基站间出行OD对及出行人数统计表 Table 1 OD trips and number of travels between cellular base stations |
本文提出以下算法将某一网络运营商的手机信令数据OD转化为全人口出行OD.
| $ \rm{O}{{\rm{D}}_{\rm{people}}}=\frac{\rm{O}{{\rm{D}}_{\rm{mobile}}}}{{{\alpha }_{1}}{{\alpha }_{2}}{{\alpha }_{3}}{{\alpha }_{4}}}. $ | (1) |
式中:ODpeople为常住人口的OD分布;ODmobile为某一运营商利用手机信令数据得出来的OD分布;杭州人均手机数α1=1.077;手机用户比例α2 =min{客户数/常住人口, 1}=1;某运营商的市场占有率α3=69.56%;手机被检测到的概率α4=0.84.
2) 来自杭州市交通建设与管理部门的路网数据, 根据路网特征, 整个杭州市被划分为589个交通小区, 其属性数据主要包括:总人口数、常住人口数、暂住人口数、住宅面积、工厂面积、商业面积、医院面积等.
3) 基于百度地图, 查找和统计的杭州市三甲医院、高等级商业、交通枢纽、公交站和地铁站数量.由于589个交通小区相对于三甲医院、高等级商业等分布密度分的过细, 为便于分析, 本文将589个交通小区合并为51个交通中区.
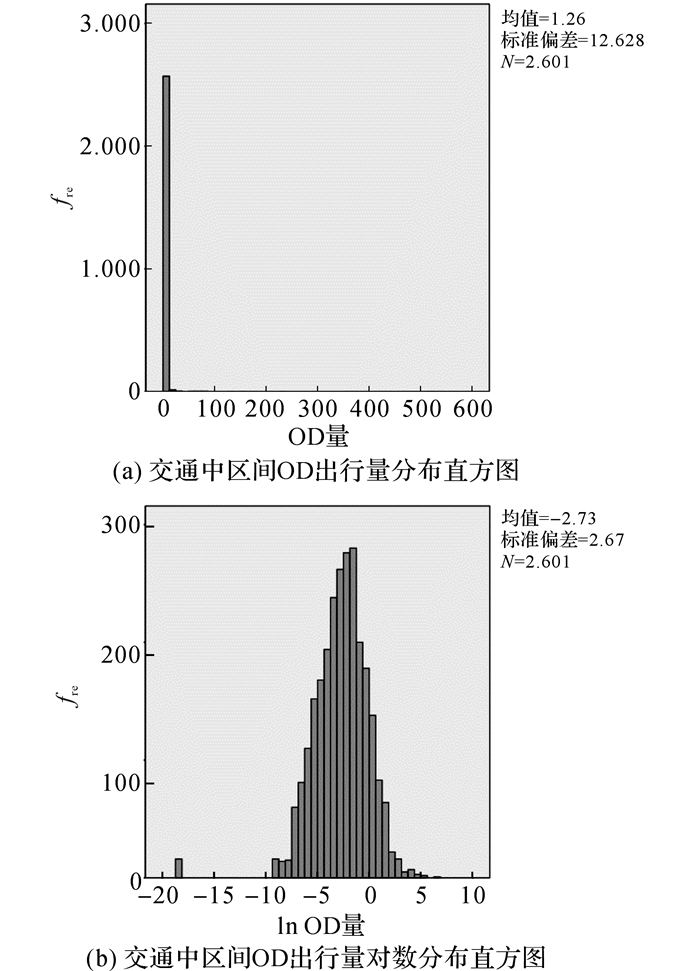
1.1 因变量分析由运营商所提供的数据主要包括55 372基站的经纬度和基站之间的14个时间段的OD出行量.根据基站的经纬度将各基站映射到51个交通中区, 可计算51个交通中区间14个时间段的出行量.由于早晚高峰流量多为对称流量, 为了研究交通中区之间流量的影响因素, 按51个交通中区的7天早高峰时段的平均OD出行量整理, 可获得2 601(51×51) 个OD对的居民出行量, 其中, 最大值为510 507人次, 最小值为0人次, 平均值为1 239人次.经过对交通中区间OD出行量做对数转化, 取对数后的OD出行量的频数分布更符合正态分布规律, 如图 1所示, 其中, fre表示交通中区间出行量的频率.因此, 选择51个交通中区起讫点(OD)之间14个时间段的平均出行量的对数作为因变量.
|
图 1 交通中区间OD出行量和出行量对数分布直方图 Fig. 1 Histograms of OD trips distribution and logarithmic OD trips distribution between TAZs |
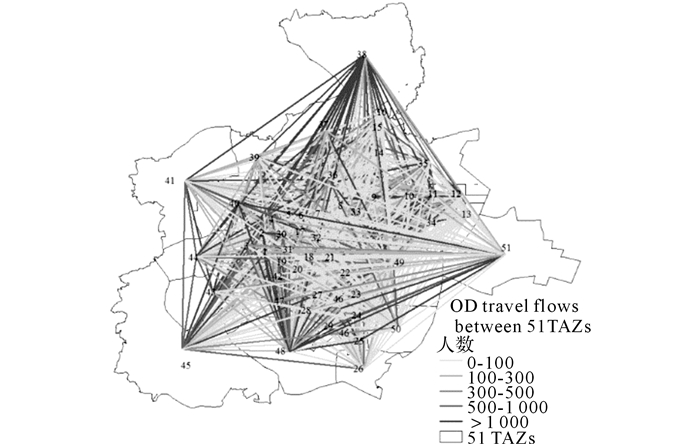
借助ArcGIS, 对51个TAZ之间的OD出行流进行分层分析, 如图 2所示, 西面的TAZ基本与北面、南面、东面多个TAZ都有较高的出行量, 最北边TAZ与西边、西南、南面的多个TAZ都有较高的出行量, 南面的TAZ与西面、东面和北面的部分TAZ都有较高的出行量, 东面的TAZ主要与西面的一个TAZ和南面的多个TAZ有较高的出行量.
|
图 2 51个交通中区OD出行量分布图 Fig. 2 Distribution of OD travel flows between 51 TAZs |
人口是影响区域间出行量的重要因素, 一般来说, 出行量随人口的增加而增加.总人口和常住人口的相关分析显示两者具有非常高的相关性.将总人口和常住人口与出行量之间进行Pearson相关性分析, 确定常住人口为其中一项影响因素.
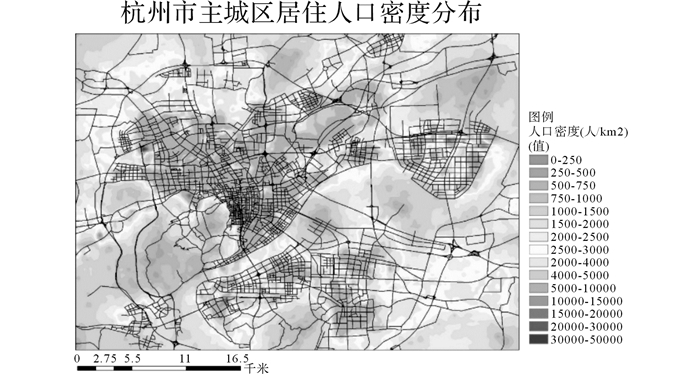
杭州市常住人口主要集中在主城区的西部、北部以及临平地区, 而下沙、滨江的常住人口相对较少, 如图 3所示.这与51个交通中区间OD出行量分布基本吻合, 主城区西部人口最集中, 与其他TAZ的出行活动联系度也最高, 东面下沙地区其常住人口最少, 主要与西面和南面的几个TAZ出行活动联系度较高, 而与其他TAZ的出行活动联系较低.由于各交通中区间人口数变动范围较大, 最大值为737 725, 最小值为655, 均值为57 319, 因此, 将其取对数处理.
|
图 3 杭州市主城区居住人口密度分布 Fig. 3 Distribution of residential population density in Hangzhou |
商场和医院都是出行吸引的重要设施, 特别是高等级商业区和高等级医院.王德, 张晋庆(2001)、仵宗卿, 柴彦威等(2001)、周素红, 林耿等(2008) 分析了商业空间业态对居民出行的影响.GUAGLIARDO(2004) 研究了商业、医院以及交通等服务点的规模和距离对居民出行的影响, 指出在相同距离下, 居民更倾向于前往规模大、等级高的服务点, 而当服务点的规模和等级差不多时, 则倾向于到访距离近的服务点.随着生活水平的提高, 购物、休闲会友的出行日渐增多, 越来越多的居民选择在环境良好的高等级商业中心从事购物、会友等休闲活动, 有较多居民都习惯放弃身边的社区医院, 转而去高等级医院就医.商业、医疗和教育配套设施越来越成为居民选择居住地所考虑的重要因素.相较而言, 教育单位都要求就近入学, 学校对居民交通中区间出行量的影响相对较少.
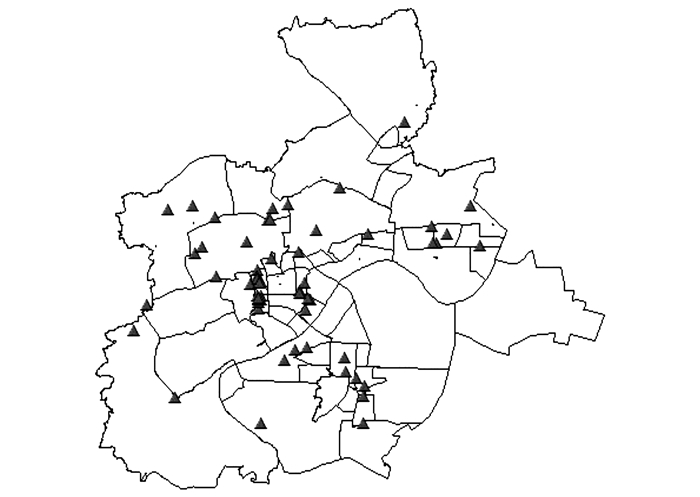
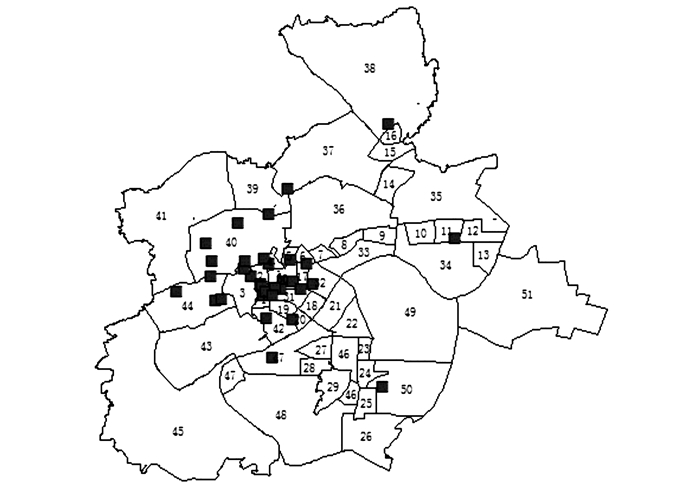
因此, 本文主要选择交通中区内高等级商业和高等级医院的数量来表示.其中, 高等级商业主要指居民熟悉, 规模较大的大型商场;高等级医院主要指三甲医院, 三甲医院的分院则作为单独一家医院计算.经统计, 杭州市共有55个高等级商业中心, 38家高等级医院, 具体分布如图 4、5所示.由图可知, 杭州市高等级商业和医院分布与人口密度分布相吻合, 最密集的地区都集中在市中心位置, 西北方向次之, 东南面和西南面最少.
|
图 4 高等级商业分布图 Fig. 4 Distribution of high-grade commercial centers |
|
图 5 高等级医院分布图 Fig. 5 Distribution of high-grade hospitals |
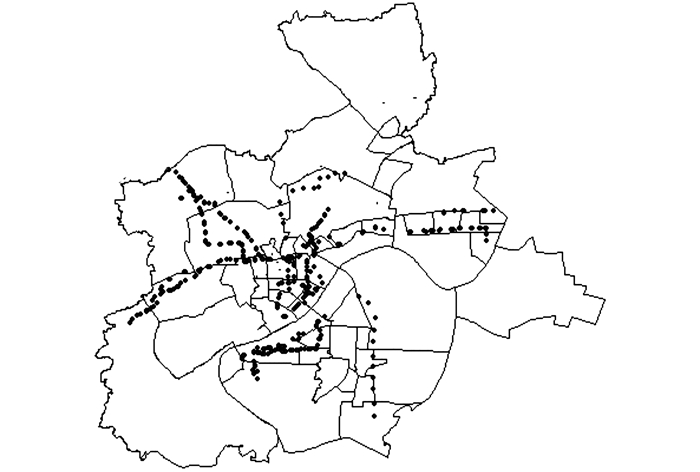
便利的交通将促使居民更多的选择出行, 杭州住房与城市建设委员会(2012) 指出出行便利性是居民选择居住场所的重要考量指标.交通便利指数主要指城市路网的通畅性、公交通达性和轨道交通的便利性.城市路网的通畅性在下一个变量居民感知距离有所体现.由于杭州市的轨道交通建设还没形成完整的路网结构, 对大部分城市居民的出行影响还不显著, 因此, 本文重点考察地面公交通达性的影响, 包括常规公交和快速公交.公交通达性用起点和终点交通中区内的公交站台数乘以通过线路数来表示, 也就是如果某一个公交站台经过有10辆公交车, 则公交站数计数为10.经过网络爬虫程序在百度地图上抓取, 整个研究区域内共有公交站数13 813个, 快速公交站数650个, 具体分布如图 6、7所示.

|
图 6 公交站点分布 Fig. 6 Distribution of bus stations |
|
图 7 快速公交站点分布 Fig. 7 Distribution of rapid bus stations |
从图 6、7可知, 杭州市公交站点在市中心、西北部、南部以及东边均比较密集, 东南面和最北面的密度最低, 西南面次之, 且随着与市中心距离的增加, 公交站密度下降.杭州快速公交已经横贯东西和南北, 具有一定的规模, 但离网状结构还有一定距离.
1.2.4 距离变量一般来说, 居民出行量随着出行距离的增加而减少, 但是随着快速主干道、轨道交通等设施的修建, 有时两点之间虽然实际距离较远, 但通行总时间却较少.因此, 本文用TAZ间通行总时间替代实际距离来反映居民感知的距离.该数据通过在百度地图中输入起点质心和终点质心, 获得公交车出行和自驾车出行耗费的时间, 然后根据式(2) 获得居民的感知距离, 即
| $ {{\mathit{t}}_{\mathit{Lij}}}=\frac{{{\mathit{b}}_{1}}\mathit{t}_{i\mathit{j}}^{1}+{{\mathit{b}}_{2}}\mathit{t}_{\mathit{ij}}^{2}}{{{\mathit{b}}_{1}}+{{\mathit{b}}_{2}}}. $ | (2) |
式中:tLij为从交通中区i到交通中区j的感知距离;b1, b2分别为城市公交车出行和自驾车出行的比例, 根据发布的《2011杭州市年度交通发展报告》可知, 杭州市的公交出行和自驾车出行比例分别占17%和16%;tij1, tij2分别为从交通中区质心i到交通中区质心j的公交车出行和自驾车出行耗费的时间, 分别通过在百度地图上统一输入出行时间(早上8:30与手机信令数据获取时间一致)和OD交通中区的质心坐标, 选择公交和自驾2种出行方式后获得.对于交通中区内部的出行, 则将半径作为出行距离, 除以杭州市一周早晚高峰地面主次干道平均速度的均值22.3 km/h[15], 作为交通中区内出行的居民感知距离.
为分析居民出行的空间效应, 本文将排除距离变量外的所有自变量分为起点变量和终点变量, 以上变量的统计情况见表 2.将所有变量与因变量建立回归方程, 其共线性统计量VIF均小于2, 说明变量之间的相关性可以接受.
| 表 2 各变量统计表 Table 2 Descriptive statistics of variables |
居民出行具有很强的空间自相关性, 也就是, 各交通中区的变量之间存在相互影响.其中, 空间自相关可以分为起点空间自相关、终点空间自相关和OD空间自相关.起点空间自相关就是指某OD出行流受到起点的相邻区域出发至同终点的出行流的影响.如图 8所示, 从交通中区A到Z的出行流受到由交通中区A的相邻区域B和C出发到终点Z的出行流的影响.终点空间自相关就是指某OD出行流受到由同起点出发至终点的相邻区域的出行流的影响, 例如, 从交通中区A到Z的出行流受到由交通中区A出发到终点X和Y的出行流的影响.OD空间自相关是指某OD出行流受到由起点相邻区域出发至终点相邻区域的出行流的影响, 如从交通中区A到Z的出行流受到由B至X或Y, C至X或Y的出行流的影响.

|
图 8 出行流空间自相关 Fig. 8 Spatial autocorrelation of travel flows |
根据LeSage和Pace(2008), 居民出行自相关模型的具体表达式如下:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{y}} = {\rho _{\rm{o}}}{\mathit{\boldsymbol{W}}_{\rm{o}}}\mathit{\boldsymbol{y}} + {\rho _{\rm{d}}}{\mathit{\boldsymbol{W}}_{\rm{d}}}\mathit{\boldsymbol{y}} + {\rho _{\rm{w}}}{\mathit{\boldsymbol{W}}_{\rm{w}}}\mathit{\boldsymbol{y}} + }\\ {\;\;\;\;\;{\mathit{\boldsymbol{X}}_{\rm{o}}}{\beta _{\rm{o}}} + {\mathit{\boldsymbol{X}}_{\rm{d}}}{\beta _{\rm{d}}} + \alpha {\mathit{\boldsymbol{l}}_\mathit{\boldsymbol{N}}} + \mathit{\boldsymbol{\gamma }}{\mathit{\boldsymbol{t}}_L} + \varepsilon .} \end{array} $ | (3) |
式中:y为N×1维向量, N=n2, 代表n个交通中区间的出行量, 即
| $ \mathit{\boldsymbol{y}}=({{\mathit{y}}_{11}}, {{\mathit{y}}_{12}}, \ldots, {{y}_{1n}}, {{y}_{21}}, {{y}_{22}}, \ldots {{y}_{2n}}, \ldots, {{y}_{n1}}, {{y}_{n2}}, \ldots, {{y}_{nn}})\prime $ |
yij表示从起点i至终点j的出行流.Wo, Wd, Ww为N×N的空间权重矩阵, 分别表示起点空间自相关, 终点空间自相关和OD空间自相关.假设W=[wij]n×n表示所有51个交通中区之间空间影响程度的矩阵, 一般来说, 距离越远, 空间影响越小, 因此, 本文采用任意2个TAZ之间的感知距离的倒数来表示, 并对行作归一化处理.由于其自身不受自身的空间影响, 因此, W的对角线元素均设为0.In是n×n的单位矩阵.所以, Wo, Wd和Ww的具体计算公式如下:
模型采用极大似然估计法进行估计, 并用极大似然比来检验空间自相关模型相较于不考虑空间效应的标准现行模型的优越性, 具体的形式如下:
| $ \begin{align} & \rm{ln}\ \mathit{L}({{\mathit{\rho }}_{\rm{o}}}, {{\mathit{\rho }}_{\rm{d}}}\rm{, }{{\mathit{\rho }}_{\rm{w}}}\rm{)=}\mathit{C+}\rm{ln}\mathit{|}{{\mathit{\boldsymbol{l}}}_{\mathit{\boldsymbol{N}}}}\mathit{-}{{\mathit{\rho }}_{\rm{o}}}{{\mathit{\boldsymbol{W}}}_{\rm{o}}}\mathit{-}{{\mathit{\rho }}_{\rm{d}}}{{\mathit{\boldsymbol{W}}}_{\rm{d}}}\mathit{-}{{\mathit{\rho }}_{\rm{w}}}{{\mathit{\boldsymbol{W}}}_{\rm{w}}}\mathit{|-} \\ & \begin{array}{*{35}{l}} \ \ \ \ \ \frac{\mathit{N}}{2}\rm{ln}~\left( \mathit{S}\left( {{\mathit{\rho }}_{\rm{o}}}, {{\mathit{\rho }}_{\rm{d}}}, {{\mathit{\rho }}_{\rm{w}}} \right) \right). \\ {} \\ \end{array} \\ \end{align} $ | (4) |
式中:C为常数项, S(ρo, ρd, ρw)为误差平方和.
3 边际效应分析在非空间自相关模型中, TAZ内某一属性的变化只影响与这个TAZ相关的出行流.但是, 在空间自相关模型中, 其周边TAZ的相关出行流也将受到该TAZ内部某一属性变化的影响.记TE为某一TAZ内某一变量对整个网络出行流的影响, OE为对该TAZ流出的出行量的影响, DE为该TAZ流入的出行量的影响, IE为TAZ内部出行量的影响, NE为对其他TAZ之间的出行量的影响, 且
| $ \rm{TE=OE+DE+IE+NE}\rm{.} $ | (5) |
根据LeSage和Pace(2015), TE、OE、DE、IE的计算公式如下:
| $ \rm{TE=(}{{\mathit{\boldsymbol{I}}}_{\rm{N}}}\rm{-}{{\mathit{\rho }}_{\rm{d}}}{{\mathit{\boldsymbol{W}}}_{\rm{d}}}\rm{-}{{\mathit{\rho }}_{\rm{o}}}{{\mathit{\boldsymbol{W}}}_{\rm{o}}}\rm{-}{{\mathit{\rho }}_{\rm{w}}}{{\mathit{\boldsymbol{W}}}_{\rm{w}}}{{)}^{\rm{-1}}}\left( \begin{align} & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{d}}}_{\rm{1}}}\mathit{\beta }_{\rm{d}}^{\mathit{r}}\rm{+}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{o}}}_{\rm{1}}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{d}}}_{\rm{2}}}\mathit{\beta }_{\rm{d}}^{\mathit{r}}\rm{+}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{o}}}_{\rm{2}}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \ \ \ \ \ \ \ \ \ \ \vdots \\ & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{d}}}_{\mathit{n}}}\mathit{\beta }_{\rm{d}}^{\mathit{r}}\rm{+}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{o}}}_{\mathit{n}}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ \end{align} \right). $ |
式中:Jdi为第i列为ιnβd, 其余元素为0的n×n矩阵, Joi为第i行为ι′nβo, 其余元素0的n×n矩阵.
| $ \rm{OE}=\left( \begin{align} & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{o}}}_{1}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{o}}}_{2}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \ \ \ \ \ \vdots \\ & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{o}}}_{\mathit{n}}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ \end{align} \right). $ |
式中:
| $ \rm{OE}=\left( \begin{align} & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{d}}}_{1}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{d}}}_{2}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ & \ \ \ \ \ \vdots \\ & \mathit{\boldsymbol{\tilde{J}}}{{\mathit{\boldsymbol{d}}}_{\mathit{n}}}\mathit{\beta }_{\rm{o}}^{\mathit{r}} \\ \end{align} \right). $ |
式中:
| $ \rm{IE}=\left( \begin{align} & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{i}}}_{1}}\rm{(}\mathit{\beta }_{\mathit{d}}^{\mathit{r}}\mathit{+\beta }_{\rm{o}}^{\mathit{r}}) \\ & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{i}}}_{2}}\rm{(}\mathit{\beta }_{\mathit{d}}^{\mathit{r}}\mathit{+\beta }_{\rm{o}}^{\mathit{r}}) \\ & \ \ \ \ \ \vdots \\ & \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{i}}}_{\mathit{n}}}\rm{(}\mathit{\beta }_{\mathit{d}}^{\mathit{r}}\mathit{+\beta }_{\rm{o}}^{\mathit{r}}) \\ \end{align} \right). $ |
式中:Jii为第i行i列为1, 其余元素为0的n×n矩阵.
由于因变量为出行量的对数形式, 因此, 假如自变量也采用对数形式, 那么边际效应就可以解释为弹性, 否则边际效应就是指自变量单位变化对应于因变量的增长率.
4 结果讨论空间自相关模型(spatial autocorrelation model, SAM)和标准线性模型(standard linear model, SLM)的计算结果如表 3所示, 其中, **表示0.05置信水平下统计显著;*.表示0.1置信水平下统计显著;NA表示不适用.极大似然比检验结果显示SAM优于SLM, 且除了距离变量外, SAM的系数均小于SLM的系数;空间自相关模型的结果显示, 起点、终点和OD空间自相关系数都具有统计上的显著性, 表明考虑起点、终点和OD空间自相关都是非常有必要的.
| 表 3 空间自相关模型和标准线性模型结果汇总表 Table 3 Results comparison between SAM and SLM |
由表 3可知, 起点和终点的常住人口数量对居民OD出行量都有统计上的显著的正相关.边际效应分析结果显示, 人口对整个网络的出行流的影响为4.097, 也就是说某TAZ的起点人口增加1%, 整个网络的出行流增加4.097%, 如表 4所示.表中, 该TAZ人口的增加值对其他TAZ的出行量的增加影响最大, 占3.321%, 其次为从该TAZ流出的出行流, 占0.626%, 流入该TAZ的出行流占0.136%, 最低的是该TAZ内部增加的流量, 仅0.014%.
| 表 4 空间自相关模型的边际效应分析 Table 4 Marginal Effects of SAM |
配套设施方面, 起点和终点的高等级商业数量对居民OD出行量呈正相关影响, 虽然起点的高等级商业数量的影响在统计上是不显著的.根据边际效应分析, 某TAZ内的高等级商业数量每增加1个, 整个网络的出行量估计会增加1.119%, 其中, 由该TAZ流出的出行量预计增加0.131%, 流入的出行量预计增加0.044%, TAZ内的流量预计增加0.003%, 对周边TAZ的出行量影响最大, 预计增加0.941%.起点高等级医院数量对居民OD出行量具有统计上的显著负相关性, 这主要是由于某TAZ内高等级设施数量的增加一定程度降低了该区域的居住密度, 从而导致由该TAZ产生的出行流的减少.而终点的高等级医院数量则在统计上影响不显著.从边际效应上看, 高等级医院的建设使得某TAZ生成的出行量下降, 而吸引的出行量略有增加, 但总体对整个网络出行的影响为负.
交通便利度对居民OD出行量同样也有显著的正相关.提高起点和终点交通中区的出行便利程度, 都将显著的提高居民OD出行量.如表 4所示, 从边际效应分析来看, 某TAZ的公交站点数每增加100个, 预计整个网络的居民OD出行量将增加1.377%, 其中, 该TAZ自身生成、该TAZ吸引的、该TAZ内部的以及周边TAZ增加的出行量预计将分别增加0.181%, 0.05%, 0.004%和1.142%.
空间变量方面, 居民出行感知距离一定程度代表了居民出行的成本.一般来说, 随着感知距离的增加, 居民出行量减少.由表 3可知, 距离对居民OD出行量具有显著的负相关, 居民对两地之间的出行时间预计多增加1 min, OD出行量预计下降0.01%.除了距离以外, 起点、终点和OD空间自相关系数都为显著正相关, 且起点自相关系数ρo和终点空间自相关系数ρd的值基本相等, 说明起点空间自相关和终点空间自相关的重要程度基本相同.其中, 起点自相关系数ρo=0.84, 表明起点交通中区和它的相邻区域具有显著的正相关关系, 也就是, 随着某一OD间出行量增加, 则由该起点的相邻区域到该终点的出行量也会增加.因此, 一个交通中区内的常住人口的增加、高等级商业和医院等配套设施的改善以及交通便利程度的提高不仅促使自身出行流的增加, 也刺激了周边区域出行流的增加.终点空间自相关系数ρd=0.85, 表明终点交通中区和它的相邻区域具有显著的正相关关系, 同理, 随着某一OD间出行量的增加, 由该起点到该终点相邻区域的出行量也会相应增加.同样的, OD空间自相关系数ρw=0.74, 不等于-ρoρd=0.71, 该结果表明随着某一OD间出行量的增加, 由该起点相邻区域出发到该终点相邻区域的出行量也会相应增加.因此, 某一区域的人口增加、配套设施和交通的改善不仅增加自身出行量的吸引量, 同时也刺激了相邻区域出行量的产生和吸引量.
5 结语本文基于手机信令数据, 通过建立空间计量模型, 分析了人口、商业和医院等配套设施、交通便利度以及距离对居民出行的影响.研究发现, 常住人口、高等级商业、交通便利程度等都与出行量有显著的正相关关系, 而感知距离对出行量有显著的负相关影响.所有的空间自相关系数包括起点空间自相关、终点空间自相关和OD空间自相关参数都具有统计上和实际上的显著影响, 因此, 如果忽略空间自相关的影响, 将会错误估计人口、配套和交通等因素对出行量影响的重要程度.
| [1] | ASAKURA Y, HATO E. Tracking survey for individual travel behavior using mobile communication instruments[J]. Transportation Research Part C: Emerging Technologies, 2004, 12(3): 273–291. |
| [2] | GONZALEZ M C, HIDALGO C A, BARABASI A L. Understanding individual human mobility patterns[J]. Nature, 2008, 453(7196): 779–782. DOI:10.1038/nature06958 |
| [3] | REN Y, ERCSEY-RAVASZ M, WANG P, et al. Predicting commuter flows in spatial networks using a radiation model based on temporal ranges[J]. Nature Communications, 2014, 5: 5347. DOI:10.1038/ncomms6347 |
| [4] | ÇOLAK S, LIMA A, GONZÁLEZ M C. Understanding congested travel in urban areas[J]. Nature Communications, 2016, 7: 10793. DOI:10.1038/ncomms10793 |
| [5] | BHAT C, ZHAO H. The spatial analysis of activity stop generation[J]. Transportation Research Part B: Methodological, 2002, 36(6): 557–575. DOI:10.1016/S0191-2615(01)00019-4 |
| [6] | WANG X, KOCKELMAN K M. Application of the dynamic spatial ordered probit model: patterns of land development change in austin, texas[J]. Regional Science, 2009, 88(2): 345–365. DOI:10.1111/pirs.2009.88.issue-2 |
| [7] | ZHANG L, HONG J H, NASRI A, et al. How built environment affects travel behavior: A comparative analysis of the connections between land use and vehicle miles traveled in US cities[J]. Journal of Transport and Land Use, 2012, 5(3): 40–52. |
| [8] | HONG J, SHEN Q. Residential density and transportation emissions: Examining the connection by addressing spatial autocorrelation and self-selection[J]. Transportation Research Part D: Transport and Environment, 2013, 22: 75–79. DOI:10.1016/j.trd.2013.03.006 |
| [9] |
丁川. 考虑空间异质性的城市建成环境对交通出行的影响研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
CHUAN Ding. Resesrch on impacts of urban built environment on travle accounting for spatial hiterogeneity [D]. Harbin: Doctoral Dissertation of Harbin Institute of Technology, 2014. |
| [10] |
王德, 张晋庆. 上海市消费者出行特征与商业空间结构分析[J].
城市规划, 2001, 25(10): 6–14.
WANG De, ZHANG Jin-qing. The analysis of consumer trip characteristics and spatial structure of commerical facilities in Shanghai[J]. Planning Studies, 2001, 25(10): 6–14. DOI:10.3321/j.issn:1002-1329.2001.10.002 |
| [11] |
仵宗卿, 柴彦威, 戴学珍, 等. 购物出行空间的等级结构研究—以天津市为例[J].
地理研究, 2001, 20(4): 379–488.
WU Zong-qing, CHAI Yan-wei, DAI Xue-zhen, et al. On hierarchy of shopping trip for urban residents-A case study of Tianjing city[J]. Geographical Research, 2001, 20(4): 379–488. |
| [12] |
周素红, 林耿, 闫小培. 广州市消费者行为与商业业态空间及居住空间分析[J].
地理学报, 2008, 63(4): 395–404.
ZHOU Su-hong, LIN Geng, YAN Xiao-pei. The relationship among consumer's travel behavior, urabn commerical and residential spatial structure in Guangzhou, China[J]. Acta Geographicl Sinica, 2008, 63(4): 395–404. DOI:10.11821/xb200804004 |
| [13] | GUAGLIARDO M F. Spatial accessibility of primary care: Concepts, methods and challenges[J]. International Journal of Health Geography, 2004, 3(1): 1–13. DOI:10.1186/1476-072X-3-1 |
| [14] |
杭州住房与城市建设委员会. 2011杭州市交通发展年度报告[R]. 杭州: 住房与城市建设委员会, 2012.
Hangzhou Manicipal Commission of Housing and Urban-Rural Development. The 2011 transprotation development annclal report of Hangzhou [R]. Hangzhou: Hangzhou Municipal commission of Housing and Urban-Rural Development, 2012. |
| [15] |
杭州市综合交通研究中心. 杭州交通拥堵指数实时监测平台[ EB/0L]. [2016-09-12]. http://www.hzjtydzs.com/web/current.aspx.
Hangzhou city comprehensive transportation research center. Hang zhou traffic congestion index red-time monitoring platform [2016-09-12]. htpp://www.hzjtydzs.com/web/current.aspx. |
| [16] | LESAGE J P, PACE R K. Spatial enonometric modeling of origin-destination flows[J]. Journal of Regional Science, 2008, 48(5): 941–967. DOI:10.1111/jors.2008.48.issue-5 |
| [17] | LESAGE J P, THOMAS-AGNAN C. Interpreting spatial econometric origin-destiantion flow models[J]. Journal of Regional Science, 2015, 55(2): 188–208. DOI:10.1111/jors.2015.55.issue-2 |



