2. 中国电建集团华东勘测设计研究院, 浙江 杭州 310014;
3. 浙江大学 防灾工程研究所, 浙江 杭州 310058;
4. 苏州大学 城市轨道交通学院, 江苏 苏州 215131
2. Power China Huadong Engineering Corporation, Hangzhou, 310014, China;
3. Institute of Disaster Prevention Engineering, Zhejiang University, Hangzhou, 310058, China;
4. School of Urban Rail Transportation, Soochow University Suzhou, 215131, China
近年来, 盾构隧道施工中往往面临着更为复杂的地质条件, 相应的风险和事故也不断增多[1], 其中开挖面的稳定性控制仍然是一个亟待解决的难题[2].由于支护力过小导致的开挖面失稳事故在地铁盾构施工中时有发生.合理选取支护力是保证盾构开挖面稳定的关键.
已有众多学者对开挖面稳定性进行了理论分析、数值分析和试验研究.Leca等[3]建立机动场模型得到了支护力的上下限解.在此基础上, Mollon等[4]、Huang等[5]、吕玺琳等[6]分别对机动场进行改进使其得到更广泛的应用.Horn[7]率先提出了楔形体筒仓模型, Broere[8]、Anagnostou等[9]分别考虑成层地层和渗流得到了改进的楔形体筒仓模型.朱伟等[10-12]采用有限差分软件FLAC3D对开挖面稳定性进行了数值模拟研究.Chambon等[13]开展了一系列离心模型试验, 分析了支护力变化规律, 得出了不同埋深比下最终破坏示意图.Mair等[14]在文献综述的基础上给出了开挖面破坏更为一般的概念解释图.周小文等[15-16]采用模型试验研究了支护力、地表沉降的变化规律.陈仁朋等[17-18]利用直径1 m的盾构模型, 研究了干砂地层中开挖面支护力、地表沉降随开挖面位移的变化规律及开挖面前方土拱效应.上述模型试验多关注支护力、地表沉降或开挖面前方应力状态的变化规律, 得到的多为最终破坏模式, 缺少对开挖面前方土体失稳发展全过程的直接观测与分析.借助数字图形技术, Kirsch[19]和Idinger等[20]分别采用小比尺模型试验和离心机试验, 对盾构开挖面前方失稳进行了图像观测分析, 但未将失稳区域剪切带变化与支护力变化联系起来分析其发展过程.
本文利用对称性, 采用半隧道模型, 开展了不同支护板后退速率下盾构隧道开挖面失稳发展过程的模型试验研究.研究了不同支护板后退速率下开挖面支护力、地层变形规律, 并借助颗粒图像测速技术(PIV)分析了不同支护板后退速率下开挖面失稳区域位移增量场、剪应变增量场.以此为基础, 结合支护力变化过程对开挖面失稳发展过程进行了详细分析, 并将试验得到的失稳破坏过程与已有的理论模型进行了对比分析.
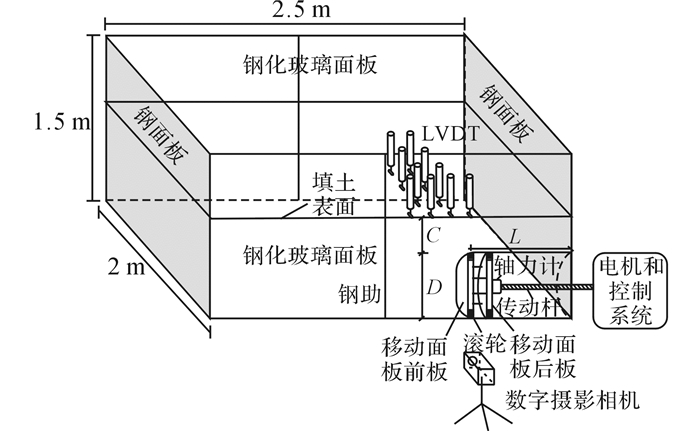
1 模型试验 1.1 模型设备本文模型试验在2.5 m×2 m×1.5 m(长×宽×高)的模型槽中进行, 如图 1所示.模型槽底部和侧面均采用钢板整体焊接而成, 前后面板采用钢化玻璃进行围护.试验过程中可以实时观测邻近玻璃面板的土体颗粒的运动.试验采用轴对称的隧道模型, 前玻璃面板为对称面.半圆筒盾壳采用不锈钢材料, 盾壳内径D=0.6 m, 长度L=0.8 m.开挖面由一个支护板代替.支护板由钢柱连接的2个半圆形钢面板组成, 借助安装在边缘的滑轮, 可以在隧道内前后移动.支护板边缘粘贴有橡胶密封条, 防止土样进入隧道内.支护板连接到传动杆上, 传动杆与电机连接, 电机通过控制传动杆的转动来控制支护板的运动.
|
图 1 模型试验装置图 Fig. 1 Setup of tunnel model |
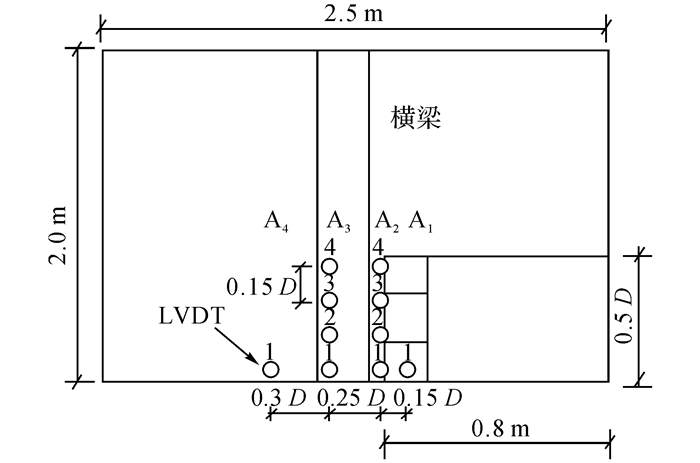
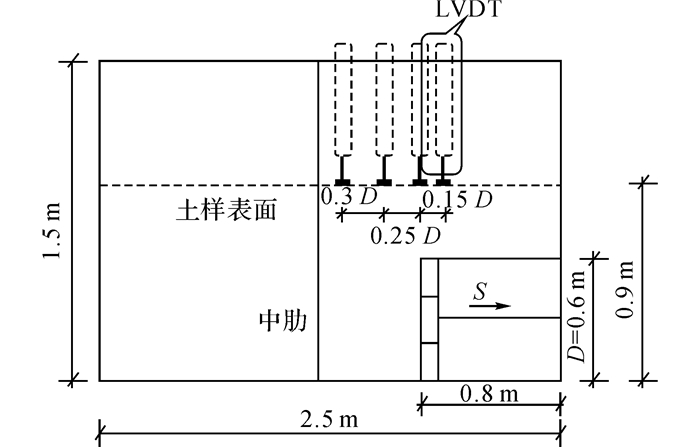
10个位移传感器(LVDT)固定在模型槽的横梁上(如图 2、3所示), 用来监测地表沉降量d.轴力计固定在支护板和传动杆之间, 用来监测开挖面轴力F.
|
图 2 LVDT布置俯视图 Fig. 2 Top view of layout of LVDT |
|
图 3 LVDT布置正视图 Fig. 3 Front view of layout of LVDT |
颗粒图像测速技术(PIV)是七十年代末发展起来的一种瞬态、多点、无接触式的激光流体力学测速方法.自2000年以来, 数码相机的发展和计算机硬件性能的提高, 图像采集技术的成熟, PIV由于能准确测量大量颗粒的运用而开始大量应用于岩土变形测量和土体基本力学性质实验中[21-22].本文开挖面前方土体的变形的监测分析采用颗粒图像测速技术.图像采集采用数字摄影相机, 数字摄影相机安放在模型槽前方(如图 1), 对焦位置为支护板正前方土体颗粒处, 用于记录试验过程中开挖面前方土颗粒的运动情况.图像后处理采用Thielicke等[23]编写的PIVlab1.35.
1.3 试验土样试验土样为京杭大运河河砂, 采用室内烘干的方法获得干砂.土样制备采用落雨法, 将干砂分层填充到模型槽中.参照Chen[18]中干砂相对密实度与落高之间的关系, 保持沙箱高度以确保相对密实度Dr=60%.制样中用标定盒验证砂样的相对密实度和均匀性.试样填充高度为0.9 m, 隧道埋深C=0.3 m.如表 1所示为制备砂样的基本物理指标.
| 表 1 试验砂物理指标 Table 1 Parameters of sand in tests |
试验方案如表 2所示.表中C为隧道埋深, D为模型隧道直径, smax为支护板最大后退距离, v为支护板后退速率, fs为LVDT采集频率, ft为轴力和数字图像采集频率.当试验开始时, 首先用4组试验速率启动电机, 支护板匀速后退, 同时开始LVDT、轴力计及数字图像的采集.支护板后退位移为smax时, 停止电机和监测系统, 保存监测数据.
| 表 2 模型试验方案设计 Table 2 Design of model test scheme |
采用1/2隧道模型, 需要考虑砂土与钢化玻璃间的摩擦对试验的影响.钢化玻璃与干砂间的摩擦主要通过紧贴的薄层砂土发挥, 摩阻力较小, 通过增加钢化玻璃的光滑性也进一步减小了该摩阻力, 所以对支护力的影响并不大.另外, 本文关注不同支护板后退速率下沉降规律的差异性, 对沉降测量的绝对精度并没有过高要求.对于PIV云图, 文献Kirsch[19]中曾指出, 砂土与钢化玻璃之间的摩擦对位移及剪切增量的影响也基本可以忽略.
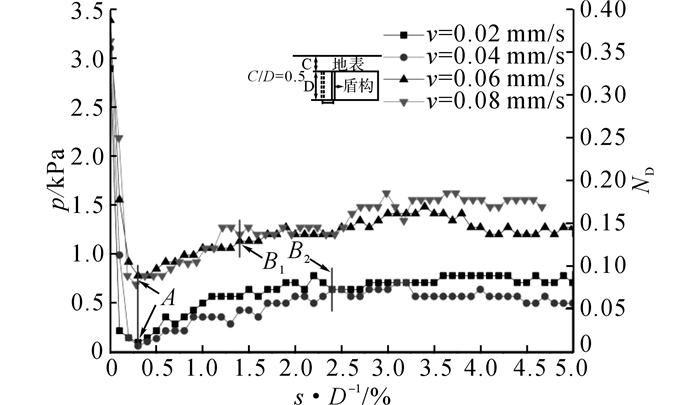
2 试验结果及分析 2.1 开挖面支护力如图 4所示为4组速度条件下开挖面支护力随开挖面位移的变化规律, 图中,p为支护力,ND(p/(γD))为无量纲化支护力, s/D为无量纲化开挖面位移.开挖面支护力p=8F/(πD2).其中, F为开挖面轴力, γ为试验干砂容重.
|
图 4 开挖面支护力变化规律 Fig. 4 Support pressure-displacement curve of tunnel face |
从图中可以看出, 在v=0.02和0.04 mm/s速率下2组试验结果比较接近, 而v=0.06和0.08 mm/s速率下2组结果相似.当零开挖面位移时, 4组试验的支护力初值在2.8~3.5 kPa之间, 此时的土压力系数在0.32~0.40之间, 这与砂土的静止土压力系数K0=1-sin φ=0.45相符.开挖面产生后退位移时, 开挖面前方土体进入主动土压力状态, 支护压力快速下降至最小值(A点).当开挖面继续后退, 从A点到B点, 支护压力逐渐增大.B点之后, 开挖面支护力出现稳定值psta.可以发现, 支护板后退速率并不影响支护力的变化规律.
如表 3所示为支护力和对应的开挖面位移总结.其中, pmin为最小支护压力, δmin=smin/D为最小支护力对应的无量纲化开挖面位移, psta为稳定支护压力, δsta=ssta/D为稳定支护力对应的无量纲化开挖面位移.可以发现, 本试验0.06和0.08 mm/s速率下得到的支护力指标与Chen等[18-19]得到的结果基本一致, 而与Chambon等[13]的结果有一定的偏差, 这可能与本文、Chen[18-19]开挖面采用位移控制而Chambon等[13]采用压力控制有关.本试验在v=0.02和0.04 mm/s速率下的支护力比v=0.06和0.08 mm/s速率及Chen等[18-19]得到的结果偏小, 说明进行开挖面稳定性试验研究时, 支护板后退速率在一定程度上影响支护力的数值.
| 表 3 支护压力的总结 Table 3 Summary on support pressure |
由2.1节的分析可知, 当v=0.02和0.04 mm/s速率下相同支护板位移下开挖面支护力相近;类似的,当v=0.06和0.08 mm/s速率下开挖面支护力相近.本节选取v=0.04和0.08 mm/s速率来进行分析.
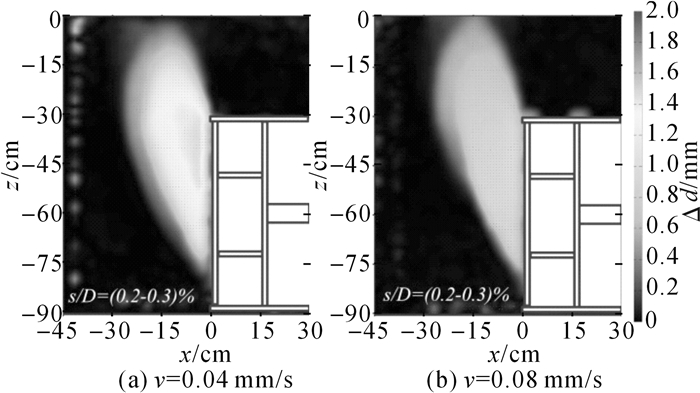
如图 5所示为最小支护力时(图 4中A点处)地层位移增量场.图中,x为距掌子面距离,z为距地表竖向高度,Δs为位移增量.从图中可以看出, 此时位移增量出现在开挖面前方和隧顶上方, 2种速率下地层位移影响区形状相似, 均由开挖面前方倒三角区域和上部弧形拱区域组成.2种速率下变形区域内位移增量均出现“分层”现象, 即内部位移增量一致, 外部位移增量一致但内部增量值大于外部增量值.2种速率下地层位移沿隧道纵向延伸最远处均在隧顶高度处, 距离开挖面约为0.5D.在竖直方向, 在v=0.08 mm/s速率下地层位移已延伸至地表, 而v=0.04 mm/s速率下地层位移还未延伸至地表.另外, 地表距离开挖面0.25D处最先出现沉降, 所以此处是最大沉降位置, 这与Chen等[18]和Idinger等[20]的观测规律一致.
|
图 5 最小支护力时(图 4中A点处)地层位移增量 Fig. 5 Ground displacement at minimum support pressure state (A point at the figure 4) |
如图 6所示为开挖面支护力稳定时(图 4中B点处)地层位移增量场.此时, 2种速率下地层位移增量均已发展至地表, 且在地表出现明显沉降区.地层位移增量场的形状为开挖面前方的倒三角形区域和上部扩展至地表的矩形区域组成.此时地层位移云图“分层”现象消失, 整个云图内位移增量基本相同.

|
图 6 支护力稳定时(图 4中B点位处)地层位移增量 Fig. 6 Ground displacement at stable support pressure state (B point at the figure 4) |
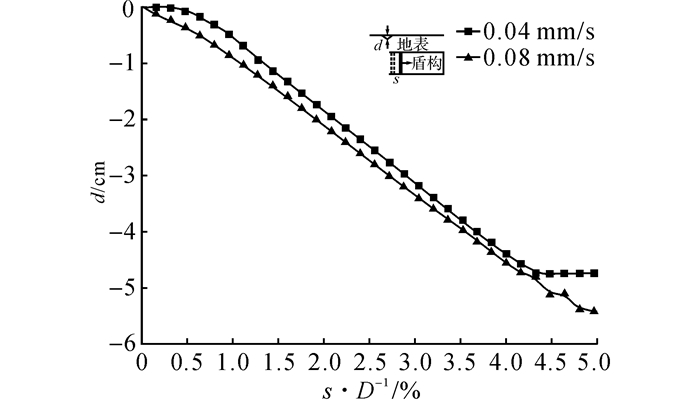
如图 7所示为最大沉降点位A31(距离开挖面0.25D)沉降曲线.最小支护力时(s/D=0.3%), v=0.04 mm/s速率下地表几乎没有沉降, 而v=0.08 mm/s速率下地表已开始出现明显沉降, 这与图 5位移增量云图中观测结果相一致.达到稳定沉降时, 两种速率下沉降增量基本相同.相对于v=0.04 mm/s速率, v=0.08 mm/s速率下地表沉降更加敏感, 更早出现明显沉降.
|
图 7 最大沉降点位A31沉降曲线 Fig. 7 Relationship between face displacement and maximum subsidence on ground surface |
综合图 5、6和7的观测结果可以发现, 支护板后退速率影响地层位移的发展, 高速率下地层位移更快发展到地表, 相应的地表更早出现明显沉降.支护板在相同位置处, 较大的支护板后退速率下, 对应的失稳地层位移增量较小.最小支护力时和支护力稳定时位移增量云图中内部的位移增量一致, 说明开挖面失稳是以块体滑动形式出现, 验证了开挖面支护力理论计算中假定失稳块体方法的合理性.
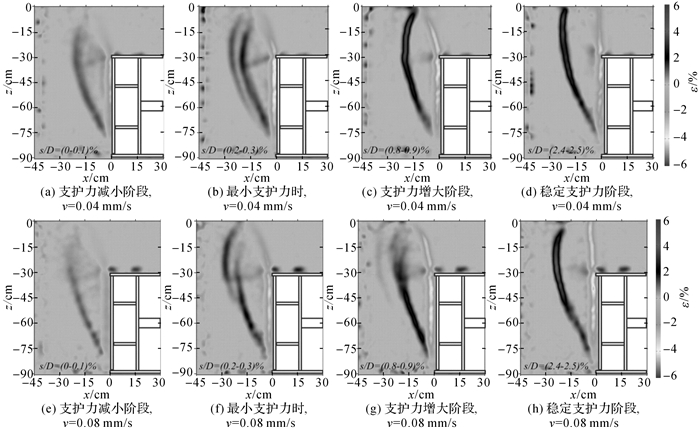
2.3 开挖面失稳发展过程现选取v=0.04和v=0.08 mm/s速率下的数字图像进行PIV分析.图 8给出了剪应变增量Δε场随支护板位移的变化模式.从图中可以发现, 不同支护板后退速率下, 剪切带的发展规律大体相同.随支护板后退位移的增大, 开挖面前方经历局部剪切带的形成(如图 8(a), 8(e));变形区域出现二次剪切带(如图 8(b), 8(f)), 这与上节出现的位移增量“分层”现象相一致;剪切带逐渐汇聚成一个闭合的剪切环(如图 8(c), 8(g));最后剪切环在地表处展开成竖直剪切带(如图 8(d), 8(h)).结合上节对位移增量场的分析可以发现浅埋隧道在失稳破坏的规律大致分为局部剪切带、闭合剪切带、贯穿剪切带3个阶段.
|
图 8 不同后退速率下剪应变增量随开挖面位移变化模式 Fig. 8 Shear strain increment for different face displacement and different moving speed |
当s/D<0.3%(图 4中A点之前)时, 开挖面支护力处于快速减小阶段, 开挖面失稳发展处于局部剪切带阶段.开挖面前方土体在模型隧道顶部和底部分别以近似相同的破坏角(45°+φ/2) 开始剪切发展, 接着顶部和底部剪切带向上分别以逆时针和顺时针旋转剪切形成弧形剪切带, 但此阶段2个弧形剪切带并未闭合(如图 8(a), 8(e)).
当0.3%≤s/D≤1.4%(图 4中B1)/2.4%(图 4中B2)时, 开挖面支护力处于增大阶段, 此时开挖面失稳发展处于闭合剪切带阶段.此阶段开始时, 即开挖面支护力达到最小支护力时, 剪切带已经闭合成环, 此时变形区域中还存在二次剪切带(如图 8(b), 8(f),), 随着开挖面位移继续增大, 变形区域内二次剪切带汇合为一条主剪切带, 剪切环更加明显(如图 8(c), 8(g),).此时剪切环最大宽度在隧顶高度处, 大约为0.5D.
当s/D≥1.4%(图 4中B1)/2.4%(图 4中B2)时, 开挖面支护力处于稳定阶段, 开挖面失稳发展处于贯穿剪切带阶段.剪切环上部的弧形段已经逐渐展开成竖直的剪切带, 此时2条竖直剪切带在地表的间距稳定, 约为开挖面前方0.4D左右(如图 8(d), 8(h)).
2.4 开挖面失稳过程与理论模型的对比现将本文观察和分析得到的失稳发展过程与理论模型进行了比较.
如图 9所示为试验中最小支护力和稳定支护力时剪切破坏模式与理论模型的对比.从图 9中可以看出, 当最小支护力时, 隧道直径范围内, 剪切带与Leca等[3]的双块机动场模型边界基本重合, 在隧顶上部剪切带高度大于理论模型边界.而稳定支护力时, 剪切带与Horn[7]的楔形体筒仓模型边界几乎完全重合.同时, 将Leca等[3]的机动场模型和Broere[8]的楔形体模型得到的支护力与本试验中最小支护力和稳定支护力进行了对比, 见表 4.表 4中的计算采用本试验中土体参数如下:隧道直径D=0.6 m;土体容重γ=14.95 kN/m3;黏聚力c=0.2 kPa;摩擦角φ=33°.

|
图 9 试验和理论破坏模式的对比 Fig. 9 Comparison of the failure modes between tests and theory |
| 表 4 最小支护压力对比 Table 4 Comparison of the minimum support pressure |
表 4与理论值对比发现, Leca等[3]的上限解略小于本试验中v=0.06和0.08 mm/s速率下最小支护力, 这与图 9(a)中理论破坏模式高度比试验观测到的高度较低相一致.Broere[8]的楔形体筒仓模型得到的最小支护力大于v=0.06和0.08 mm/s速率下得到的最小支护力而比较接近试验中的稳定支护力, 这与图 9(b)中其破坏模式与试验中稳定支护力时重合相一致.
综合图 9剪切带和表 4支护力与理论模型的对比分析, 可以推测, 基于上限解的机动场模型处于闭合剪切带阶段, 得到的支护力更接近于最小支护力;而楔形体筒仓模型处于贯穿剪切带阶段, 得到的支护力更接近于隧道完全破坏时的稳定支护力.
3 结论通过模型试验中不同支护板后退速率下开挖面支护力、地层变形规律、土体破坏发展过程随开挖面位移的变化规律进行对比分析, 可以得到以下结论:
(1) 开挖面前方土体失稳发展过程中开挖面支护力先快速下降到最小支护力, 再缓慢增大, 最后稳定.对应于支护力变化阶段, 开挖面前方土体依次经历局部剪切带、闭合剪切带、贯穿剪切带3个阶段.开挖面支护力快速下降阶段, 开挖面失稳处于局部剪切, 此时隧道顶部和底部分别以近似相同的破坏角(45°+φ/2) 开始剪切发展.开挖面支护力上升阶段, 开挖面失稳处于剪切连通, 剪切带上部弧形段闭合成环.开挖面支护力稳定阶段, 开挖面失稳处于剪切贯穿, 剪切环上部的弧形段已经逐渐展开成竖直的剪切带.
(2) 试验中剪切带发展与理论模型的对比发现, 基于上限解的机动场模型处于闭合剪切带阶段, 得到的支护力更接近于最小支护力;而楔形体筒仓模型处于贯穿剪切带阶段, 得到的支护力更接近于隧道完全破坏时的稳定支护力.
(3) 支护板后退速率影响最小支护力和支护力稳定值, 但并不影响支护力的发展规律.支护板后退速率越大, 地表沉降越敏感.支护板在相同位置处, 较大的支护板后退速率下, 对应的失稳地层位移增量较小.
(4) 位移增量云图和剪切增量云图表明, 最小支护力时, 沿隧道纵向影响区域最远的位置为隧顶高度处, 约为0.5D.地表最大沉降点位于开挖面前方0.25D附近.
| [1] | 竺维彬, 鞠世健. 地铁盾构施工风险源及典型事故的研究[M]. 广州: 暨南大学出版社, 2009. |
| [2] | MAID L B, HERRENKNECHT M, ANHEUSER L. Mechanised shield tunnelling[M]. Berlin: ERNST & Sohn, 1996. |
| [3] | LECA E, DORMIEUX L. Upper and lower bound solutions for the stability of shallow circular tunnels in frictional material[J]. Géotechnique, 1990, 40(4): 581–606. DOI:10.1680/geot.1990.40.4.581 |
| [4] | MOLLON G, DIAS D, SOUBRA A. Face stability analysis of circular tunnels driven by a pressurized shield[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1): 215–229. DOI:10.1061/(ASCE)GT.1943-5606.0000194 |
| [5] | HUANG M S, SONG C X. Upper bound stability analysis of plane strain tunnel in non-homogeneous clay[J]. Tunnelling and Underground Space Technology, 2013, 38: 213–223. DOI:10.1016/j.tust.2013.07.012 |
| [6] |
吕玺林, 王浩然, 黄茂松. 盾构隧道开挖面稳定性极限理论分析[J].
岩土工程学报, 2011, 33(1): 57–62.
LV Xi-lin, WANG Hao-ran, HANG Mao-song. Limit theoretical study on face stability of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 57–62. |
| [7] | HORN N. Horizontaler erddruck auf senkrechte abschlussflchen von tunnelr?hren[C]/ /Landeskonferenz der Ungarischen Tiefbauindustrie. German: [s. n.], 1961: 7-16. |
| [8] | BROERE W. Tunnel face stability and new CPT applications [D]. PhD Thesis, Technical University of Delft, 2001. |
| [9] | ANAGNOSTOU G, KOVARI K. The face stability of slurry-shield-driven tunnels[J]. Tunnelling and Underground Space Technology, 1994, 9(2): 165–174. DOI:10.1016/0886-7798(94)90028-0 |
| [10] |
朱伟, 秦建设, 卢廷浩. 砂土中盾构开挖面变形与破坏数值模拟研究[J].
岩土工程学报, 2005, 27(8): 897–902.
ZHU Wei, QIN Jian-she, LU Ting-hao. Numerical study on face movement and collapse around shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(8): 897–902. |
| [11] |
秦建设, 虞兴福, 钟小春, 等. 黏土中盾构开挖面变形与破坏数值模拟研究[J].
岩土力学, 2007, 28(S1): 511–515.
QIN Jian-she, YU Xing-fu, ZHONG Xiao-chun, et al. Numerical research on face movement and collapse of shield tunneling in silt ground[J]. Rock and Soil Mechanics, 2007, 28(S1): 511–515. |
| [12] |
黄正荣, 朱伟, 梁精华, 等. 浅埋砂土中盾构法隧道开挖面极限支护力压力及稳定研究[J].
岩土工程学报, 2006, 28(11): 2005–2009.
HUANG Zheng-rong, ZHU Wei, LIANG Jing-hua, et al. Study on limit supporting pressure and stabilization of excavation face for shallow shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 2005–2009. DOI:10.3321/j.issn:1000-4548.2006.11.016 |
| [13] | CHAMBON P, CORT'E J F. Shallow tunnels in cohesionless soil: Stability of tunnel face[J]. Journal of Geotechnical Engineering, 1994, 120(7): 1148–1165. DOI:10.1061/(ASCE)0733-9410(1994)120:7(1148) |
| [14] | MAIR R J, TAYLOR R N. Theme lecture: bored tunneling in the urban environment[C]// Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering. Berlin: Springer, 1997:2353-2385. |
| [15] |
周小文, 濮家骝. 砂土中隧洞开挖引起的地面沉降试验研究[J].
岩土力学, 2002, 23(5): 1074–1079.
ZHOU Xiao-wen, PU Jia-liu. Centrifuge model test on ground settlement induced by tunneling in sandy soil[J]. Rock and Soil Mechanics, 2002, 23(5): 1074–1079. |
| [16] |
李昀, 张子新, 张冠军. 泥水平衡盾构开挖面稳定模型试验研究[J].
岩土工程学报, 2007, 29(7): 1074–1079.
LI Yun, ZHANG Zi-xin, ZHANG Guan-jun. Laboratory study on face stability mechanism of slurry shields[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(7): 1074–1079. |
| [17] |
陈仁朋, 李君, 陈云敏, 等. 干砂盾构开挖面稳定性模型试验研究[J].
岩土工程学报, 2011, 33(1): 117–122.
CHEN Ren-peng, LI Jun, CHEN Yun-min, et al. Large-scale tests on face stability of shield tunneling in dry cohesionless soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 117–122. |
| [18] | CHEN R P, LI J, CHEN YM, et al. Experimental study on face instability of shield tunnel in sand[J]. Tunneling and Underground Space Technology, 2013, 33(1): 12–21. |
| [19] | KIRSCH A. Experimental investigation of the face stability of shallow tunnels in sand[J]. Acta Geotechnica, 2010, 5(1): 43–62. DOI:10.1007/s11440-010-0110-7 |
| [20] | IDINGER G, AKLIK P, Wu W, et al. Centrifuge model test on the face stability of shallow tunnel[J]. Acta Geotechnica, 2011, 6(2): 105–117. DOI:10.1007/s11440-011-0139-2 |
| [21] | WHITE D J, TAKE W A, BOLTON M D. Soil deformation using particle image velocimetry (PIV) and photogrammetry[J]. Géotechnique, 2003, 53(7): 619–631. DOI:10.1680/geot.2003.53.7.619 |
| [22] | NÜBEL K, WEITBRECHT V. Visualization of localization in grain skeletons with particle image velocimetry[J]. ASTM Journal of Testing and Evaluation, 2002, 30(4): 322–329. DOI:10.1520/JTE12322J |
| [23] | THIELICKEW, STAMHUIS E J. PIVlab-Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB[J]. Journal of Open Research Software, 2014, 2(1): (e30): 1–10. |



