2. 浙江大学 软弱土与环境土工教育部重点实验室, 浙江 杭州 310058
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education, Zhejiang University, Hangzhou 310058, China
填埋场覆盖系统是垃圾填埋场的重要组成部分, 主要作用是防止雨水入渗, 从而减少渗滤液产量和垃圾体失稳风险[1].垃圾填埋场中填埋体降解过程中极易产生局部沉陷等情况[2], 在覆盖层下方形成空洞.现场调查发现[3], 局部沉陷导致的覆盖层破坏为水分入渗形成优势通道, 显著降低覆盖层的防渗性能.因此, 深入认识局部沉陷诱发覆盖层破坏模式对指导填埋场覆盖层设计具有重要价值.
土质覆盖层是近年发展起来的一种新型填埋场覆盖系统, 主要由适合植物生长的细粒土组成, 如粉土、粉质黏土等.细粒土层的设计厚度一般介于50~150 cm[4].该类型覆盖层具有就地取材、造价低廉、耐久性好等优点, 在我国西北地区有广阔应用前景[5].土质覆盖层工作原理与海绵类似, 降雨时吸收和储存水分, 非降雨时通过腾发作用释放水分.覆盖层土体含水率随内外环境不断变化, 具有显著的非饱和特性, 因此, 覆盖层物理和力学性能受土体含水率的显著影响.
对于非饱和浅土层塌陷问题, 吴子树等[6-7]开展现场调查和原型试验[8]观测;蔺港[9]则针对土质覆盖层开展离心模型试验, 研究局部沉陷诱发的土层破坏模式.上述研究发现, 上覆土层存在内部和整体塌陷2种破坏模式.土层在沉陷区上方形成拱形剪切面, 仅剪切面下方土体发生塌落, 称为内部塌陷模式;土层产生起于沉陷区边缘的竖直破坏面, 沉陷区范围内土层整体塌落, 称为整体塌陷模式.一般内部塌陷先于整体塌陷产生.蔺港[9]的试验还发现:含水率10%粉土土层仅产生内部塌陷;而含水率16.3%和18%的土层先后出现内部塌陷和整体塌陷2种塌陷模式.说明含水率对覆盖层塌陷模式有显著影响.
已有不少学者提出了基于土拱效应的土层塌陷分析模型[6~16], 但针对非饱和土层塌陷问题的研究工作仍十分有限.Villard[7]推导了内部塌陷的力学模型, 但仅能分析土层厚度的影响;贺可强[8]建立了内部塌陷和整体塌陷模型, 并考虑了两者级联关系, 然而其内部塌陷模型仍采用经验参数, 难以与土体强度指标建立联系.由于分析模型的局限性, 上述学者均未讨论如含水率、基质吸力等非饱和土参数变化对破坏模式的影响.蔺港[16]首次将非饱和土强度理论应用到Terzaghi极限平衡分析模型中, 但其模型与后期的离心试验观察存在一定差异.
鉴于土质覆盖层水分储存-释放的工作原理, 含水率是影响土质覆盖层破坏模式的关键因素.因此需要建立能够考虑含水率变化的非饱和土层塌陷分析模型, 认识含水率对土层不同塌陷模式的影响规律, 为土质覆盖层设计提供技术支持.本文基于结构拱假定和Terzaghi极限平衡法, 通过引入非饱和土抗剪强度指标与含水率关系式, 建立基于土拱效应理论的土质覆盖层内部塌陷和整体塌陷力学模型;为验证所提理论模型的合理性, 采用土工离心机开展了非饱和黄土的trapdoor离心模型试验;最后, 结合试验数据, 讨论含水率对土质覆盖层塌陷模式的影响规律.
1 非饱和土质覆盖层塌陷分析模型已有学者指出[7, 10], 土拱效应的不同作用形式是局部沉陷条件下上覆土层产生多种破坏模式的内在原因.当局部沉陷产生时, 沉陷区土体相对于周边土体产生位移, 土体应力重分布, 屈服土体的应力转移向临近的非屈服土体, 即产生土拱效应[11].内部塌陷和整体塌陷2种破坏模式分别对应了2种土拱效应作用形式.一种是假设土体“楔紧”形成类似结构拱的土拱, 支撑拱体以上土体自重, 研究者一般采用结构拱模型研究内部塌陷模式[7-8, 10, 12~14];另一种则将土拱简化成一条过梁, 梁上土体自重通过边缘竖直滑动面上的剪应力传递至周边土体, 研究者一般基于Terzaghi极限平衡法建立整体塌陷模型[6-7, 10, 15~16].下面推导中同样采用上述假定的土拱形式分别建立内部塌陷和整体塌陷模型.
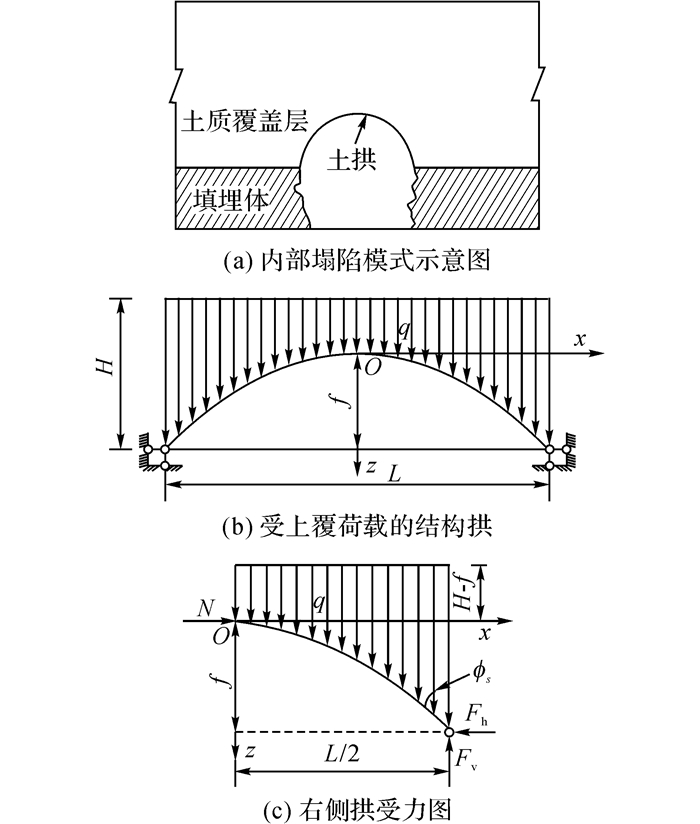
1.1 内部塌陷模型对于如图 1(a)所示内部塌陷问题, 本分析也采用结构拱假定, 结构拱模型示意图如图 1(b)所示, 与刘丹珠等[12]模型相似, 该模型能考虑拱轴上不同位置处竖向荷载随深度的变化.以拱顶O为原点建立如图 1(b)所示的直角坐标系, x轴水平指向右, 在z轴指向下.设拱形高度为f, 跨度为L, 上覆土层厚度为H, q为结构拱上方土体自重产生的竖向荷载q=γ(H-f)+γz, 式中:γ为土体容重.贾海莉等[17]研究指出, 土体中自发形成的土拱应为最合理拱轴线, 其受力特点为拱体单元剪力和弯矩处处为零, 只受轴力作用.图 1(c)给出该拱体右半部分的受力分析图, 拱顶O只存在水平反力N.
|
图 1 内部塌陷力学模型 Fig. 1 Mechanical modeling of internal failure |
在竖向荷载作用下, 结构拱上各点的弯矩M由竖向荷载产生的弯矩M0和Ny叠加而成.如前所诉拱轴线上弯矩等于零(M=0), 有z=M0/N, 刘丹珠等[12]将此式两边对x求二阶导数得
| $ \frac{{{{\rm{d}}^{\rm{2}}}\mathit{z}}}{{{\rm{d}}{\mathit{x}^{\rm{2}}}}}{\rm{ = }}\frac{{\rm{1}}}{\mathit{N}}\frac{{{{\rm{d}}^{\rm{2}}}{\mathit{M}^{\rm{0}}}}}{{{\rm{d}}{\mathit{x}^{\rm{2}}}}}{\rm{ = }}\frac{{\rm{1}}}{\mathit{N}}\mathit{q}{\rm{(}}\mathit{x}{\rm{)}}{\rm{.}} $ | (1) |
根据拱顶和拱脚的边界条件x=0, z=0; x=0, dz/dx=0, 并令
| $ z{\rm{ = }}(H{\rm{ - }}f)({\rm{cosh}}\;(mx){\rm{ - 1}}). $ | (2) |
式中:cosh(mx)是关于x的双曲余弦函数.
方程(2) 表明最合理拱轴线为一条悬链线.将x=L/2, z=f代入式(2) 得拱形高度的方程:
| $ f{\rm{ = }}H({\rm{1 - 1/cosh}}\;(mL{\rm{/2}})). $ | (3) |
根据图 1(c)中拱体水平向和竖向平衡条件并将式(2) 和(3) 代入得拱脚水平反力Fh和竖直反力Fv分别为
| $ {\mathit{F}_{\rm{h}}}{\rm{ = }}\mathit{N}{\rm{ = }}\frac{\gamma }{{{\mathit{m}^2}}}. $ | (4) |
| $ {F_{\rm{v}}}{\rm{ = }}\frac{{\gamma H}}{m}{\rm{tanh}}\;(mL{\rm{/2}}). $ | (5) |
式中:tanh(mL/2) 为双曲正切函数.
普氏[18]提出, 为保证拱体在水平方向拱脚处的稳定性, 水平反力Fh应小于拱脚处地层的最大摩擦力即
| $ {\mathit{F}_{\rm{h}}} \le {\mathit{F}_{\rm{v}}}{\rm{tan}}\;{\phi _{\rm{s}}} $ | (6) |
式中:ϕs为土体的等效内摩擦角, 其取值与土体总黏聚力c和内摩擦角ϕ有关.蔡美峰[18]认为对于松散无黏性的土体, ϕs等于ϕ;对于有黏聚力的黏性土体, ϕs也会受c的影响.而Villard等[8]理论分析表明, f(或ϕs)与c无关, 仅与ϕ有关;最近, Yamamoto等[19]和Abbo等[20]分别针对有黏聚力的黏性土(c和ϕ均不为零)和不排水饱和黏性土(ϕ=0) 两土质情况开展数值分析工作, 计算结果验证了Villard等[8]的结论.
Bierbaumer[13]、Iglesia[10, 21]通过无黏性土试验和理论分析得到拱脚与竖直面夹角为ϕ.故不等式(6) 宜取极限状态条件:
| $ {\mathit{F}_{\rm{h}}} = {\mathit{F}_{\rm{v}}}{\rm{tan}}\;{\phi _{\rm{s}}} $ | (7) |
式(7) 表明拱轴线在拱脚处和竖直方向的夹角即为土体等效内摩擦角ϕs(如图 1(c)).土质覆盖层采用土体一般具有黏性故参考Villard等[8]、Yamamoto等[19]和Abbo等[20]研究成果, 式(7) 中的ϕs取ϕ.有研究表明[22-23], 非饱和土体中含水率对ϕ有较大影响, 其随含水率的增大而减小.考虑到含水率对ϕ的影响, 将式(4) 和(5) 代入式(7) 后, 并将ϕ表示为含水率w的函数:
| $ m\mathit{H}{\rm{tanh}}\;(mL{\rm{/2}}){\rm{ - cot}}\;\phi (w){\rm{ = 0}}. $ | (8) |
式中:ϕ(w)是一个总应力抗剪强度指标.对于非饱和土, 总应力强度指标可以采用常规直剪试验获得, 因此便于室内测定和工程应用.龚壁卫[24]曾提出非饱和土总应力抗剪强度公式:
| $ \tau {\rm{ = }}\mathit{c}{\rm{(}}\mathit{w}{\rm{) + }}\sigma {\rm{tan}}\;\phi {\rm{(}}\mathit{w}{\rm{)}}{\rm{.}} $ | (9) |
需要说明的是, 式(9) 中2个强度参数c(w)和ϕ(w)随含水率变化规律受非饱和土中基质吸力随含水率变化规律的影响, 因此与土的种类和含水率范围密切相关[23].考虑到土质覆盖层通常采用的土壤类型及含水率范围, 并参考本研究中采用土体的试验数据(见后), 选用申春妮等[22]推荐的经验公式:
| $ \mathit{c}{\rm{(}}\mathit{w}{\rm{) = }}{\mathit{c}_{\rm{0}}}{\rm{ + }}\mathit{wk}_\mathit{w}^\mathit{c}{\rm{.}} $ | (10) |
| $ \phi {\rm{(}}\mathit{w}{\rm{) = }}{\phi _{\rm{0}}}{\rm{ + }}\mathit{wk}_\mathit{w}^\phi {\rm{.}} $ | (11) |
式中:c0和ϕ0均为试验参数;kwc和kwϕ分别为c(w)和ϕ(w)随含水率增加线性减小的倾角.将式(11) 代入(8) 得
| $ \mathit{mH}{\rm{tanh(}}\mathit{mL}{\rm{/2) - cot}}\;\;({\phi _0} + \mathit{wk}_\mathit{w}^\phi ) = 0. $ | (12) |
式(12) 中等式左端是一个关于参数m的隐函数, 当含水率一定时, m有多种近似求解方法[12], 本文采用二分法通过迭代方式得到近似解.当m值确定后, 代入式(3) 即可得到拱形破坏面高度.
当发生内部塌陷时, 土拱承受拱形上方土体的自重, 塌落区域土体与上部土体脱离, 脱离土体自重表示为
| $ \begin{array}{l} \mathit{W} = \\ 2\gamma \int_0^{\frac{L}{2}} {(f - z){\rm{d}}x} = \gamma (LH - \frac{{2H\tanh \;\;(mL/2)}}{m}). \end{array} $ | (13) |
将W除以沉陷区宽度可以得到沉陷区上覆土压力, 蔺港[9]试验结果表明, 此时得到土压力值为松动土压力pmin, 即最小上覆土压力.人们一般采用土层自重p0=γH对上覆土压力进行归一化, 则归一化松动土压力pmin/p0为
| $ \frac{{{\mathit{p}_{\min }}}}{{{\mathit{p}_0}}} = 1 - \frac{{2\tanh \;\;(\mathit{mL}/2)}}{{\gamma \mathit{mL}}}. $ | (14) |
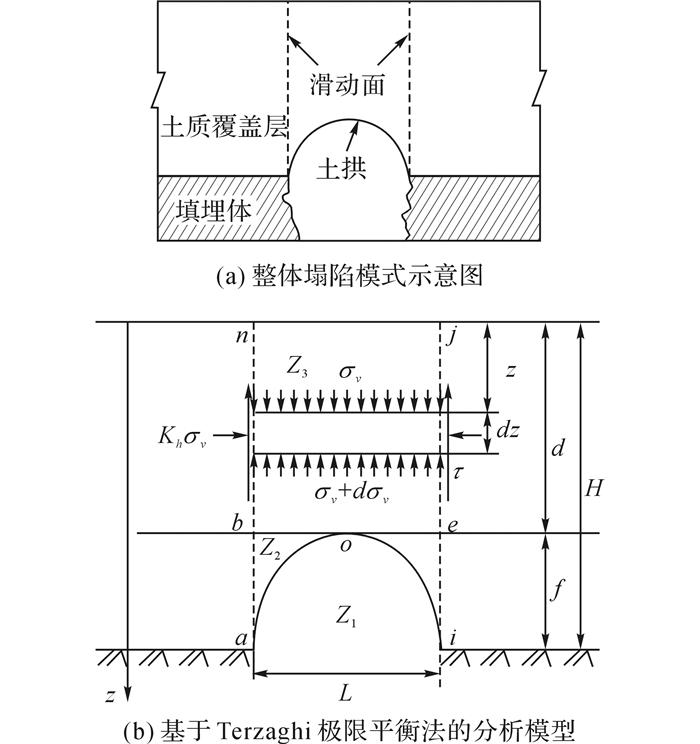
如图 2(a)所示给出整体塌陷破坏模式示意图.Terzaghi[11]曾根据极限平衡法建立了该塌陷模式的计算模型, 此处借鉴Terzaghi极限平衡法建立了整体塌陷的力学模型.图 2(b)给出了该模型示意图, 坐标轴自土层表面指向下方.以内部塌陷拱顶高度处和沉陷区边缘为界将土体分成3个区域:Z1为内部塌陷区域(aoi围成区域), Z2为沉陷区中拱顶以下和拱面上方合围的区域(abo和oei围成区域), Z3为沉陷区拱顶以上的矩形沉陷区域(bnje围成区域).该模型引入如下假定:1)Z1区域中拱形面由内部塌陷产生;2) 拱形上方土体沿竖直滑动面整体向下移动;3) 忽略Z2区域土体自重和该区域与侧壁的摩擦力;4) Trapdoor充分下移后, 滑动面上的摩擦力充分发挥, 且Z3区域土体均达到极限状态.
|
图 2 整体塌陷力学模型 Fig. 2 Mechanical modeling of external failure |
根据图 2(b)所示的微分土条在竖直方向的受力平衡可得
| $ \frac{{{\rm{d}}{\sigma _\mathit{v}}}}{{{\rm{d}}\mathit{z}}} + \frac{{2\tau }}{\mathit{L}} = \gamma . $ | (15) |
式中:σv为土体竖向应力, τ为微分土条边缘处达到极限状态时的抗剪强度, 可利用式(9) 计算得到.
引入边界条件σv|z=0=0, 可得滑动面上沿深度任意点处的剪力:
| $ \begin{array}{l} \tau (\mathit{z}) = ({\mathit{c}_0} + \mathit{wk}_\mathit{w}^\mathit{c}) + \left( {\frac{{\mathit{L}\gamma }}{2} - ({\mathit{c}_{\rm{0}}} + \mathit{wk}_\mathit{w}^\mathit{c})} \right)\\ \;\;\;\;\;\;\;\;\;\;\left( {1 - \exp \left[{-2{\mathit{K}_{\rm{h}}}\frac{\mathit{z}}{\mathit{L}}\tan \;({\phi _0} + \mathit{wk}_\mathit{w}^\phi )} \right]} \right). \end{array} $ | (16) |
式中:Kh为侧向土压力系数.Krynine[25]通过Mohr-Coulomb极限平衡应力圆分析得出
| $ {\mathit{K}_{\rm{h}}} = (1 - {\rm{si}}{{\rm{n}}^2}\phi )/(1 + {\rm{si}}{{\rm{n}}^2}\phi ). $ | (17) |
离心试验[9]表明, 局部沉陷产生过程中, 沉陷区上方土体向下运动, 而沉陷区边缘土体保持不动, Z3区域土体与周边区域土体逐渐远离, 土体处于主动状态.考虑土单元主应力旋转现象的存在, Kh取Krynine值较为合理[10].
对τ(z)沿深度积分可得到竖直滑动面上阻止土体下移的总摩阻力为
| $ \begin{array}{l} {\mathit{F}_{{\rm{re}}}}{\rm{ = 2}}\int_{\rm{0}}^\mathit{d} {\tau {\rm{(}}\mathit{z}{\rm{)d}}\mathit{z = }\gamma \mathit{Ld + }\frac{{(2({\mathit{c}_{\rm{0}}} + \mathit{wk}_\mathit{w}^\mathit{c}) - \mathit{L}\gamma )\mathit{L}}}{{2{\mathit{K}_{\rm{h}}}\tan ({\phi _0} + \mathit{wk}_\mathit{w}^\phi )}}} \\ \;\;\;\left( {1 - \exp \left[{-2{\mathit{K}_{\rm{h}}}\frac{\mathit{d}}{\mathit{L}}\tan \;({\phi _0} + \mathit{wk}_\mathit{w}^\phi )} \right]} \right). \end{array} $ | (18) |
土层受到向下运动的致塌力为土体自重:
| $ {\mathit{F}_{{\rm{ap}}}}{\rm{ = }}\gamma \mathit{Ld}\mathit{.} $ | (19) |
定义一个安全系数K:
| $ \mathit{K}{\rm{ = }}\frac{{{\mathit{F}_{{\rm{re}}}}}}{{{\mathit{F}_{{\rm{ap}}}}}}{\rm{.}} $ | (20) |
当K>1时, 土层不发生整体塌陷;当K=1时, 土层处于极限平衡状态;当K<1时, 土层将产生整体塌陷, 此时沉陷区上覆土压力为沉陷区上方土体自重γH, 归一化上覆土压力等于1.
由式(18) 可知安全系数K的大小与土体的含水率存在很大关系, 是否产生整体塌陷受到土层含水率的明显影响.
2 黄土局部沉陷离心模型试验为验证上述理论模型, 利用蔺港[9]开发的整套局部沉陷模拟系统, 进一步开展了不同含水率黄土土层局部沉陷离心模型试验.
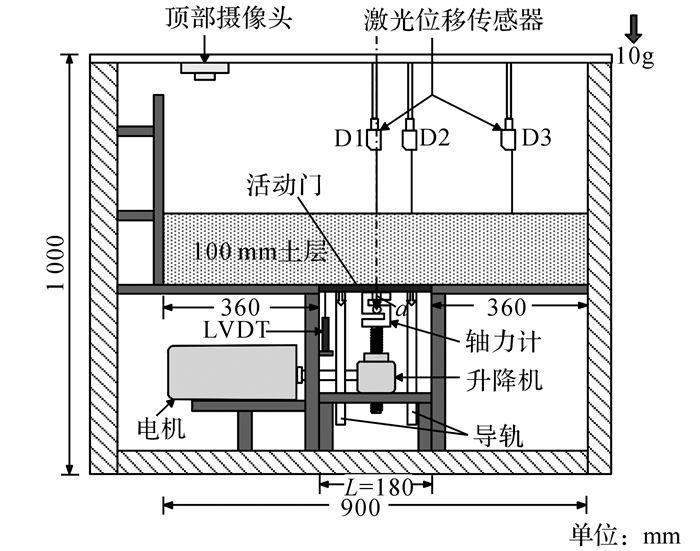
2.1 离心模型试验该离心模拟系统主要包括平面应变模型箱和Trapdoor装置(见图 3).模型箱尺寸为1.0 m(长)×0.45 m(宽)×1.0 m(高), 模型箱前面安装有有机玻璃观察窗.Trapdoor装置包括刚性基础、活动门、升降机、导轨、轴力计、电机、LVDT等.升降机通过螺杆与一块180 mm宽的铝合金活动门相连, 通过电机控制升降机使得活动门能以0~1.5 mm/min的速度向下移动, 达到模拟局部沉陷的目的;活动门底部安装一只LVDT位移传感器, 用于监测活动门位移, 轴力计安装在活动门下方, 用于监测活动门上覆土压力变化.
|
图 3 模型试验布置图 Fig. 3 Configuration of trapdoor centrifugal model tests |
图 3给出了离心模型试验布置图.Trapdoor装置放置在模型箱下部, 其上布置100 mm厚黄土层.在10 g设计离心加速度下, 模拟原型1.0 m厚土质覆盖层和1.8 m宽度的局部沉陷.局部沉陷宽度依据我国行业规范和相关资料[2, 5]确定.在观察窗外侧安装数码相机, 活动门下降过程中, 相机每隔6 s拍摄一张照片, 并通过PIV技术分析土层位移场发展过程.
模型土体采用西安Q2黄土, 颗粒比重为2.71, 塑限为22%, 液限为36.7%.颗粒级配曲线如图 4所示, we为小于某粒径的土质量分数, ds为粒径.从图 4中可以看出, 模型土体中粒径小于0.075 mm颗粒质量占总质量的96.8%, 根据土的工程分类标准[26]该土属于粉质黏土.图 4中还给出了蔺港所采用的钱塘江粉土的颗粒级配曲线, 可以看出Q2黄土细粒土的含量比粉土高.模型土层采用分层填筑、夯击压实的方式制备, 夯击后每层土的厚度为2.5 cm.

|
图 4 模型试验土体颗粒级配曲线 Fig. 4 Grain size distribution curves of two model soils |
黄土试验共安排2组, 土体含水率w分别为15.6%和24.5%.表 1给出了2组试验的主要参数, 试验编号分别为T4和T5.表中, Sr为土体饱和度;ρd为土体干密度.试验中, 活动门下降速度控制在1 mm/min.T4、T5试验中活动门分别下降25和50 mm后停止.为便于对比, 表 1中也给出了蔺港[9]试验工况, 分别标号T1~T3.
| 表 1 钱塘江粉土试验[9]和西安黄土试验 Table 1 Test programs for Qiantang Jiang silt and Xian loess |
为获得土体抗剪强度参数, 开展了不同含水率的钱塘江粉土和西安黄土的室内直剪试验.试验中, 控制粉土的含水率为10%、16.3%和18%;黄土的含水率为12.4%、15.6%和24.5%.2种土的干密度与表 1所列一致;分别施加100、200、300和400 kPa的法向压力.离心试验中活动门下降速度较快, 因开展快剪试验, 根据土工试验方法标准[27], 设定快剪试验施加的剪切速率为0.8 mm/min.
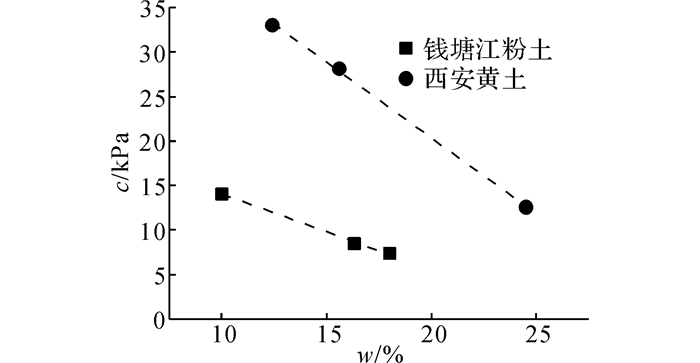
图 5~7给出直剪试验结果, 试验数据表明, 粉土和黄土的c和ϕ均随含水率增加近似线性减小, 含水率对c的影响较对ϕ的影响更为明显.该变化规律与其他学者试验结果近似[21-22].经计算得到式(10) 和(11) 中各参数值, 钱塘江粉土对应的c0、ϕ0、kwc和kwϕ值分别为22.6、39.7、-0.85和-0.61;西安黄土分别为54.4、30.0、-1.70和-0.48.

|
图 5 抗剪强度和竖向应力关系曲线 Fig. 5 Relationships between shear strength and vertical stress of two model soils |

|
图 6 内摩擦角与含水率关系 Fig. 6 Relationships between internal friction angle and water content of two model soils |
|
图 7 总黏聚力与含水率关系 Fig. 7 Relationships between apparent cohesion and water content of two model soils |
图 8给出了T4试验(含水率为15.6%)的土层破坏情况.当活动门沉降量为0.3 mm(对应原型沉降为3 mm)时, 如图 8(a)所示, 活动门两侧边缘处产生向沉陷区域倾斜的2条裂缝T4-1和T4-2, 此时可以认为土拱已经形成, 局部沉陷产生;随着沉降量的继续增大, 裂缝T4-1和T4-2连通形成拱形破坏面, 当沉降量为25 mm时(对应原型沉降为250 mm)时, 破坏面如图 8(b)所示, 此时破坏面下方土体与上方明显脱离, 而上方土体保持完好, 仅产生如图 1(a)所示的内部塌陷.

|
图 8 T4试验破坏过程 Fig. 8 Failure process of T4 |
图 9给出了T5试验(含水率为24.5%)的土层破坏过程.如图 9(a)所示, 活动门沉降量为5.9 mm(对应原型中为59 mm)时, 活动门两侧边缘处产生向沉陷区域倾斜的2条裂缝T5-1和T5-2, 土体表面也产生2条裂隙, 可以认为此时内部塌陷已经产生;当活动门沉降量增加到35 mm(对应原型中为350 mm)时, 如图 9(b)所示, 活动门边缘区域土层已形成新的几乎贯通的竖向裂隙T5-5和T5-6, 土层产生整体塌陷.

|
图 9 T5试验破坏过程 Fig. 9 Failure process of T5 |
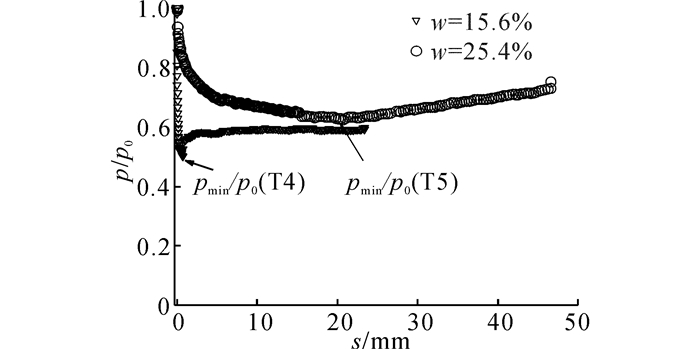
将轴力计监测得到的活动门上方荷载除以活动门宽度得到沉陷区上覆土压力p, 再对其进行归一化处理得到归一化上覆土压力p/p0.图 10给出了归一化上覆土压力p/p0与活动门位移s的关系曲线.由图可知, 随着含水率的增大达到上覆土压力最小值pmin(即松动土压力)所需的沉降位移也增大, T4和T5分别为0.72、20.7 mm, 该规律同蔺港的试验结果一致.T4试验仅发生内部塌陷, 上覆土压力随位移发展逐渐趋于稳定;T5试验中, 整体塌陷发生后, 土体随活动门下移不断塌落, 直到活动门达到最大位移(50 mm), 上覆土压力仍有增加的趋势.将土层发生整体塌陷后测得的上覆土压力最大值, 作为实测最大上覆土压力, 则图 10得到T5的归一化实测最大上覆土压力值pmax/p0=0.76.
|
图 10 归一化上覆土压力-活动门位移关系曲线 Fig. 10 Relationships between normalized soil pressure on trapdoor with settlement |
通过PIV图像处理技术, 得到了T1~T5试验中发生内部塌陷时拱形破坏面与竖直方向之间倾斜角度ϕs实测值, 表 2中给出了该值列表.ϕs实测结果表明, 随着含水率增大2种土层的ϕs均呈现出减小的规律.与表 2中给出的土体内摩擦角ϕ对比, 发现两者随含水率的变化规律一致, 且数值上也较为接近, 误差绝对值介于0.2°~4.3°.该试验数据有效验证了Villard等[8]、Yamamoto等[19]和Abbo等[20]的理论和数值分析成果, 说明ϕs采用总应力指标中内摩擦角参数对通常的土体具有适用性.
| 表 2 离心试验结果和理论计算结果对比 Table 2 Comparison of Centrifuge test results and theoretical results |
表 2中给出T1~T5试验获得的归一化松动土压力值.将非饱和土直剪试验得到的ϕ及L、H代入式(14) 得到pmin/p0的理论计算结果.该结果也在表 2中给出.对比2组数据, 其误差小于10%.理论计算结果和试验结果有较好的一致性, 验证了内部塌陷模型的合理性.
3.2 整体塌陷安全系数与pmin/p0通过安全系数K值可判断土层是否发生整体坍塌.将直剪试验得到的ϕ、c及L、H和拱形高度f代入式(18)~(20), 得到计算结果见表 2.T1和T4试验算得的K值均大于1, 与离心试验中观察到未发生整体塌陷的现象相符合;T2、T3和T5试验算得的K值均小于1, 与离心试验中观察到发生整体塌陷的现象一致.
表 2中给出了实测和理论归一化最大上覆土压力pmax/p0值.对比表中T2、T3和T5试验的实测与理论结果, 可以看出实测结果均接近理论值.T5试验中由于土体延展性较好的, 在试验沉降位移内土体尚未完全坍塌(见图 9(b)), 因此实测值较小.上述2方面的对比验证了整体塌陷模型的合理性.
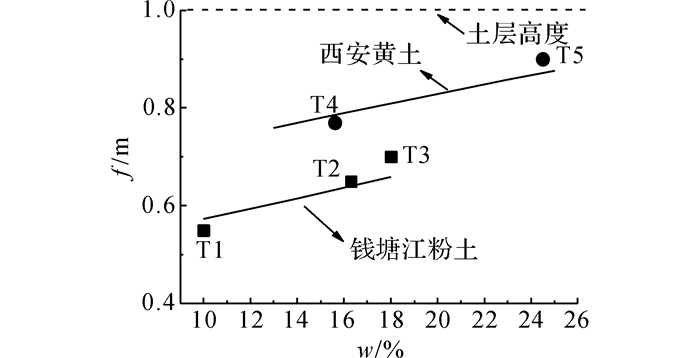
4 含水率变化影响分析 4.1 含水率对内部塌陷拱形破坏面高度的影响将非饱和土直剪试验获得的ϕ0和kwϕ及L和H代入式(12), 得到如图 11所示的粉土和黄土拱形破坏面高度随含水率变化曲线, 从图中可以看出, 拱形破坏面高度随着含水率增加近似线性增加.为了同试验数据对比, 图中用方形黑点和圆形黑点分别给出了粉土和黄土离心模型试验中拱形破坏面高度实测值, 计算结果和试验结果有较好的一致性.对比2类土的拱形破坏面高度变化曲线可以看出, 具有较高细颗粒含量的黄土(见图 4)能够形成较高的拱形面, 这与人们的实际经验一致.
|
图 11 拱形破坏面高度f随含水率的变化关系 Fig. 11 Relationships between arch hight and water content |
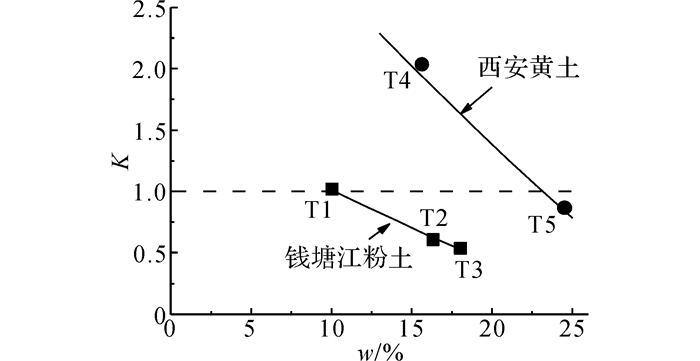
将非饱和土直剪试验获得的土体强度参数ϕ0、c0、kwc、kwϕ及L、H和f代入式(18)~(20), 计算得到粉土和黄土的整体塌陷安全系数K随含水率的变化关系, 如图 12所示, 由图可见, 2种土的安全系数均随含水率的增大近似线性减小.图中方形黑点和圆形黑点分别表示采用粉土和黄土直剪试验数据计算得到的各试验的安全系数值, 该值在表 2中已给出.参考式(18) 可以看出, 不同于内部塌陷模式, c(w)和ϕ(w)均对抵抗整体塌陷有贡献.根据图 6和7, 并参考kwc和kwϕ的数值, 可以发现, c(w)受含水率变化影响更为显著, 说明c(w)的变化对安全系数的影响更为明显.将图 12中水平虚线与曲线的交点为K=1所对应的含水率, 定义为临界含水率.在该含水率下土层处于发生整体破坏的临界点, 当土层含水率大于临界值, 会发生整体塌陷.图中对应粉土和黄土的临界含水率分别为10.3%和23.2%.
|
图 12 安全系数K随含水率的变化关系 Fig. 12 Relationships between K and water content |
对比2种土的安全系数随含水率的变化曲线可以看出, 在相同含水率下, 黄土有较高的整体稳定性, 如含水率15.6%、饱和度56%的T4试验(见表 1)安全系数达到2.04(见表 2), 不发生整体塌陷;而如含水率16.3%、饱和度47.4%的T1试验安全系数仅为0.61, 会发生整体塌陷.
综合含水率对内部塌陷和整体塌陷影响的分析, 可以看出, 在干旱和半干旱地区, 黄土是用作土质覆盖层较好的工程材料, 其发生整体塌陷对应的临界含水率较高, 但在覆盖层厚度设计中, 应考虑内部塌陷发生时的破坏面高度.
5 结论土质覆盖层利用非饱和土具有的水分储存和释放能力实现防渗闭气, 因此认识土层含水率变化对覆盖层破坏过程和模式的影响成为合理设计土质覆盖层结构和准确评估覆盖层服役性能的关键.本文基于土拱效应原理, 采用结构拱假定和Terzaghi极限平衡法分别建立能够考虑土层含水率的覆盖层内部塌陷模型和整体塌陷理论分析模型, 推导出了内部塌陷拱形破坏面高度与含水率关系表达式及判别整体塌陷是否发生的安全系数公式.通过包括钱塘江粉土和西安黄土的5组离心模型试验数据与理论计算结果对比, 验证了2种塌陷模型的合理性和预测精度.利用钱塘江粉土和西安黄土抗剪强度指标随含水率变化规律, 分别讨论了含水率对土质覆盖层内部塌陷拱形破坏面高度和整体塌陷安全系数的影响, 首次揭示了含水率对土质覆盖层破坏模式的影响规律.上述研究主要获得以下结论:
(1) 通过不同含水率黄土局部沉陷离心模型试验, 进一步验证了不同含水率下非饱和土层存在不同的破坏模式, 即内部塌陷和整体塌陷;当整体塌陷出现时, 一般情况下内部塌陷已经产生;
(2) 理论模型分析表明, 内部塌陷阶段形成一条悬链线形破坏面, 拱脚与竖直倾斜面夹角取土体内摩擦角, 此模式下的松动土压力为拱形破坏面下土体自重在塌陷区宽度上的平均值;
(3) 试验结果显示整体塌陷时沉陷区土体沿竖直滑动面下移最终产生几乎贯通的裂隙, 理论和试验数据对比表明, 安全系数能够有效判断整体塌陷产生, 提出的临界含水率概念能通过土体含水率简便判断土层发生整体塌陷的风险;
(4) 钱塘江粉土和西安黄土的直剪试验数据表明, 土体总黏聚力和内摩擦角随土体含水率增大而减小, 导致内部塌陷拱形破坏面高度随含水率增加, 整体塌陷安全系数随含水率减小, 说明含水率增加会对土质覆盖层稳定性造成不利影响;对比2种土, 相同含水率下黄土具有较高的整体稳定性, 整体塌陷对应临界含水率较高, 是用作土质覆盖层较好的工程材料.
| [1] | KOEMER R M, SOONG T Y. Leachate in landfills: the stability issues[J]. Geotextiles & Geomembranes, 2000, 18(18): 293–309. |
| [2] |
柯瀚, 陈云敏, 谢焰, 等. 适宜降解条件下填埋场的沉降模型及案例分析[J].
岩土工程学报, 2009, 31(6): 929–938.
KE Han, CHEN Yun-min, XIE Yan, et al. Settlement analysis of landfills under optimal decomposition conditions and case study[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 929–938. |
| [3] | QIAN X D, KOERNER R M, GRAY D H. Geotechnical aspects of landfill design and construction[M]. New Jersey, USA: Prentice-Hall, Inc., 2002. |
| [4] |
CJJ176-2012. 生活垃圾卫生填埋岩土工程技术规范[S]. 北京: 中国建筑工业出版社, 2012.
CJJ176-2012. Technical code for geotechnical engineering of municipal solid waste sanitary landfill [S]. Beijing: China Architecture and Building Press, 2012. |
| [5] |
詹良通, 焦卫国, 孔令刚, 等. 黄土作为西北地区填埋场覆盖层的可行性及设计厚度分析[J].
岩土力学, 2014, 35(12): 3361–3369.
ZHAN Liang-tong, JIAO Wei-guo, KONG Ling-gang, et al. Feasibility analysis of using loess as soil cover material for landfills in Northwest China and its analysis of design thickness[J]. Rock and Soil Mechanics, 2014, 35(12): 3361–3369. |
| [6] |
吴子树, 张利民, 胡定. 土拱的形成机理及存在条件的探讨[J].
成都科技大学学报, 1995(2): 15–19.
WU Zi-shu, ZHANG Li-min, HU Ding. Studies on the mechanism or arching action in loess[J]. Journal of Chengdu University of Science and Technology, 1995(2): 15–19. |
| [7] |
贺可强, 王滨, 万继涛. 枣庄岩溶塌陷形成机理与致塌模型的研究[J].
岩土力学, 2002, 23(5): 564–574.
HE Ke-qiang, WANG Bing, WAN Ji-tao. Study on forming mechanism of Zaozhuang karst collapse and collapse model[J]. Rock and Soil Mechanics, 2002, 23(5): 564–574. |
| [8] | VILLARD P, GIRAUD H, GOURC J P. A geosynthetic reinforcement solution to prevent the formation of localized sinkholes[J]. Canadian Geotechnical Journa, 2011, 37(5): 987–999. |
| [9] |
蔺港. 局部沉陷诱发腾发型覆盖层破坏的理论与试验研究[D]. 杭州: 浙江大学, 2014.
LIN Gang. Theoritial and Experimental study of fracture caused by differential subsidence in Evapotran-spiration Landfill Cover [D]. Hangzhou: Zhejiang University, 1993. |
| [10] | IGLESIA G R, EINSTEIN H H, WHITMAN R V. Investigation of soil arching with centrifuge tests[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2014, 140(2): 248–256. |
| [11] | TERZAGHI K. Theoretical soil mechanics[M]. 4th ed, New York: John Wiley and Sons, Inc, 1943. |
| [12] | 刘丹珠, 张家发, 李少龙, 等. 基于土拱理论的土体坍塌机理研究[J]. 长江科学院院报, 2011, 28(5): 35–41. |
| [13] | BERBAUMER A. Die dimensionerung des tunnelmauerwerks[M]. Leipzig: Engelmann, 1913. |
| [14] | 胡敏云, 夏永承, 高渠清. 无锚撑桩排式支护护壁桩侧土压力计算方法[J]. 岩石力学与工程学报, 2000, 19(4): 517–521. |
| [15] | MARSTON A, ANDERSON A O. The theory of loads on pipes in ditches and tests of cement and clay drain tile and sewer pipe[R]. IA: Iowa Engineering Experiment Station, Iowa State College, 1913. |
| [16] |
蔺港, 孔令刚, 詹良通, 等. 基于太沙基土拱效应考虑基质吸力影响的松动土压力计算模型[J].
岩土力学, 2015, 36(7): 2095–2104.
LIN Gang, KONG Ling-gang, ZHAN Lang-tong, et al. An analytical model for loosening earth pressure considering matric suction based on Terzaghi soil arch effect[J]. Rock and Soil Mechanics, 2015, 36(7): 2095–2104. |
| [17] |
贾海莉, 王成华, 李江洪. 关于土拱效应的几个问题[J].
西南交通大学学报, 2003, 38(4): 398–402.
JIA Hai-li, WANG Cheng-hua, LI Jiang-hong. Discussion on some Issues in theory of soil arch[J]. Journal of Southwest Jiaotongs University, 2003, 38(4): 398–402. |
| [18] | 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002: 330-333. |
| [19] | YAMAMOTO K, LYAMIN A V, WILSON D W, et al. Stability of dual circular tunnels in cohesive-frictional soil subjected to surcharge loading[J]. Canadian Geotechnical Journal, 2013, 50(12): 41–54. |
| [20] | ABBO A J, WILSON D W, SLOAN S W, et al. Undrained stability of wide rectangular tunnels[J]. Computers & Geotechnics, 2013, 53(3): 46–59. |
| [21] | IGLESIA G R. Trapdoor experiments on the centrifuge, a study of arching in geomaterials and similitude in geotechnical models[D]. MA: Dept of Civil Engineering, MIT, 1991. |
| [22] |
申春妮, 方祥位, 王和文, 等. 吸力、含水率和干密度对重塑非饱和土抗剪强度影响研究[J].
岩土力学, 2009, 30(5): 1347–1351.
SHEN Chun-ni, FANG Xiang-wei, WANG He-wen, et al. Research on effects of suction, water content and dry density on shear strength of remolded unsaturated soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1347–1351. |
| [23] |
林鸿州, 李广信, 于玉贞, 等. 基质吸力对非饱和土抗剪强度的影响[J].
岩土力学, 2007, 28(9): 1931–1336.
LIN Hong-zhou, LI Guang-xin, YU Yu-zhen, et al. Influence of matric suction on shear strength behavior of unsaturated soils[J]. Rock and Soil Mechanics, 2007, 28(9): 1931–1336. |
| [24] |
龚壁卫. 非饱和击实膨胀土总应力强度探讨[J].
长江科学院院报, 1998(3): 40–42.
GONG Bi-wei. Discussion on shear strength of total stress of unsaturated compacted expansive soil[J]. Journal of Yangtze River Scientific Research Institute, 1998(3): 40–42. |
| [25] | KRYNINE D P. Discussion of ‘Stability and stiffness of cellular cofferdams' by Karl Terzaghi[J]. Transactions of the American Society of Civil Engineers, 1945, 110(1): 1120–1186. |
| [26] |
GB/T50145-2007. 土的工程分类标准[S]. 北京: 中国计划出版社, 2008.
GB/T50145-2007. Standard for engineering classification of soil [S]. Beijing: China Planning Press, 2008. |
| [27] |
GB/T50123-1999. 土工试验方法标准[S]. 北京: 中国计划出版社, 1999.
GB/T50123-1999. Standard for soil test method[S]. Beijing: China Planning Press, 1999. |


