钢绞线是用多根高强度钢丝在绞线机上进行螺旋形绞合制成的一种钢拉索, 具有很高的承载力, 适用于桥梁拉索, 张力结构及不直接与混凝土接触的预应力结构中[1].钢绞线制作工艺复杂, 同一截面各钢丝与中心轴的夹角不同, 且钢丝与钢丝存在摩擦, 因此钢绞线截面实际应力并不是均匀分布的.而现有一般的结构分析中为简化计算通常假定钢绞线截面等应力分布, 即不考虑钢丝转角和钢丝间摩擦的影响, 这与钢绞线的实际受力情况是不符的.因此精确研究钢绞线截面应力分布, 对于钢绞线结构设计、选型及使用维护等方面都具有重要意义[2].国内外很多学者对钢绞线进行了有益探索, Chiang[3]利用有限元法和实验方法, 研究了影响钢绞线轴向刚度和轴向应力变化的主要因素.孙庆凯等[4]建立了钢绞线的三维实体模型, 分析了钢绞线的柔软性能, 但未分析钢绞线截面应力分布情况.Ghoreishi等[5]利用多种线性静力分析模型对1×7钢绞线进行了有限元分析, 但只考虑部分钢丝之间摩擦的影响.
本文以1×7、1×19钢绞线为研究对象, 建立几何模型, 研究钢绞线截面应力在载荷作用下的分布规律.同时研究了钢绞线内部摩擦对于截面应力分布的影响.为验证本文分析结果的正确性, 与已有文献的数值分析结果进行了比对.
1 钢绞线模型建立 1.1 空间几何模型钢绞线侧丝是绕钢绞线中心轴线的一次螺旋线, 侧丝的展开如图 1所示.钢绞线长lr, 侧丝的展开线长度为ls, 侧丝在钢绞线中的螺旋半径、捻角和转角分别为rr、βr和θr[6].

|
图 1 侧丝在钢绞线中沿捻向的展开图 Fig. 1 Developed pattern of strands and wires |
由图 1可得, 一次螺旋线方程的表达式为
| $ \left( \begin{array}{l} {\mathit{x}_\mathit{A}}\\ {\mathit{y}_\mathit{A}}\\ {\mathit{z}_\mathit{A}} \end{array} \right) = \left( \begin{array}{l} {\mathit{r}_{\rm{r}}}{\rm{cos}}\;{\mathit{\theta }_{\rm{r}}}\\ {\mathit{r}_{\rm{r}}}{\rm{sin}}\;{\mathit{\theta }_{\rm{r}}}{\rm{ }}\\ {\mathit{r}_{\rm{r}}}{\mathit{\theta }_{\rm{r}}}{\rm{tan}}\;{\mathit{\beta }_{\rm{r}}} \end{array} \right). $ | (1) |
式中:xA、yA、zA为外层钢丝中心线的坐标.
1.2 有限元模型如图 2所示为1×7、1×19钢绞线有限元模型, 直径D分别为9和15 mm, 钢丝直径为3 mm.钢绞线的捻距为公称直径的14~18倍, 本文取捻距为15D, 基于对称性, 计算时取1/6捻距即长度分别为22.5和37.5 mm的钢绞线.钢丝的弹性模量E=200 GPa, 泊松比μ=0.3.

|
图 2 钢绞线有限元模型和网格划分 Fig. 2 A finite element mesh of steel strand |
采用20节点实体单元Solid95对1×7、1×19钢绞线进行网格划分.考虑到网格太大时计算精度不够, 模型无法收敛;当网格太小时, 计算需要消耗较多时间, 兼顾计算精度和计算效率, 本模型在钢绞线截面上将每根钢丝分成24等份, 沿钢绞线长度方向将钢丝分别分成8等份和13等份, 划分后1×7钢绞线生成28 763个节点、6 804个单元, 1×19钢绞线生成104 861个节点、24 624个单元.
2 不考虑摩擦影响的截面应力分布先不考虑钢丝间的摩擦.在模型一端(z=0处)施加固端约束, 另一端(z=2.5D处)分别施加σq为100、200、300、400 MPa面荷载, 研究钢绞线截面的应力分布规律.
当σq=100 MPa荷载作用下, 1×7、1×19钢绞线等效应力如图 3(a)、(b)所示, 对于单根钢丝, 靠近钢绞线中心部位的等效应力较小, 外侧逐渐变大, 但是差别不大.中心钢丝等效应力为100 MPa左右, 外层钢丝等效应力为100~120 MPa.由于侧丝呈空间一次螺旋线结构, 其应力在钢绞线截面呈扇形分布.钢绞线z轴方向应力值变化不大, 在截面呈均匀分布, 大小为100 MPa左右, 如图 3(c)、(d)所示.在σq=300 MPa荷载作用下, 1×7、1×19钢绞线的应力如图 4所示, 其分布规律与100 MPa时相同.在普通结构设计中, 通常只关注钢绞线的轴向受力(z向应力), 此时可按均匀性考虑.

|
图 3 当σq=100 MPa轴向荷载作用下钢绞线(z=2.5D)处应力图 Fig. 3 Stress distribution for cross-section at the end of steel strand(z=2.5D) under tensile force of 100 MPa |

|
图 4 当σq=300 MPa轴向荷载作用下钢绞线(z=2.5D)处应力图 Fig. 4 Stress distribution for cross-section at the end of steel strand(z=2.5D) under tensile force of300 MPa |
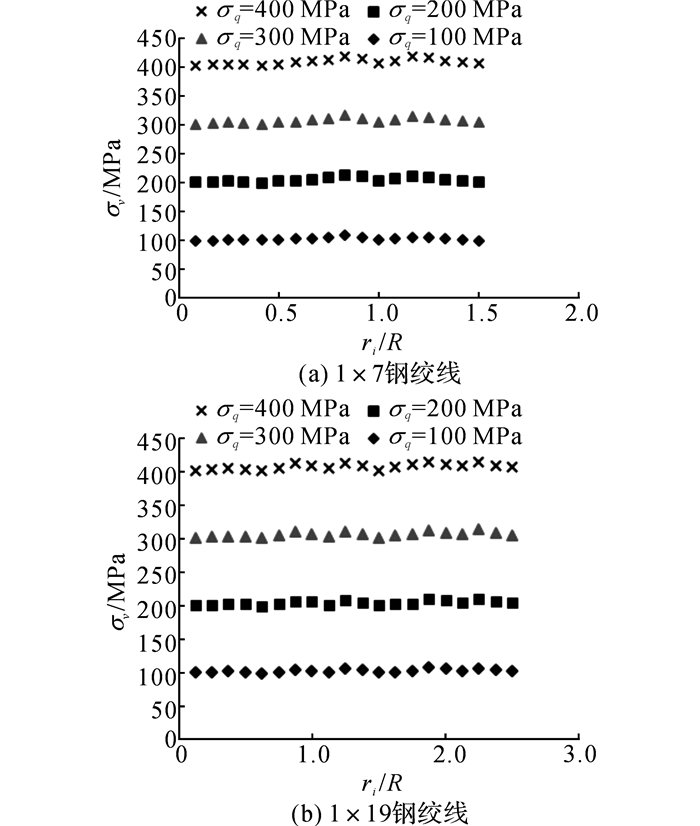
为了研究钢绞线截面应力分布情况, 将截面分成如图 5所示若干层.截面各层节点的平均等效应力如图 6所示.随着点到圆心距离ri的增加, 各层的等效应力值σv除略有波动外基本上与所施加外荷载大小相等.中心钢丝上的等效应力值略小, 外层钢丝的等效应力值稍大.随着荷载的增加, 截面等效应力值的波动也略有增加.

|
图 5 钢绞线截面分层示意图 Fig. 5 Layering diagrammatic sketch of steel strand cross section |
|
图 6 钢绞线(z=2.5D)处节点等效应力 Fig. 6 Stress of cross-section at end of steel strand(z=2.5D) under tensile force |
为了进一步验证有限元模型的准确性, 将分析所得结果与Feyer[7]提出的数值分析结果进行对比, 结果如表 1、2所示.
| 表 1 不同分析方法所得的1×7钢绞线截面应力值 Table 1 Stress of cross-section of 1×7 steel strand with different analysis methods |
| 表 2 不同分析方法所得的1×19钢绞线截面应力值 Table 2 Stress of cross-section of the 1×19 steel strand with different analysis methods |
其中
| $ {\sigma _{\mathit{t}{\rm{, }}\mathit{k}}}{\rm{ = }}\frac{{\frac{{{{\cos }^3}{\alpha _\mathit{k}}}}{{1 + {\nu _\mathit{k}}{{\sin }^2}{\alpha _\mathit{k}}}}{\mathit{E}_\mathit{k}}\mathit{S}}}{{\sum\nolimits_{\mathit{i} = 0}^\mathit{n} {\left( {\frac{{{\mathit{z}_\mathit{i}}{{\cos }^3}{\alpha _\mathit{i}}}}{{1 + {\nu _\mathit{i}}{{\sin }^2}{\alpha _\mathit{i}}}}{\mathit{E}_\mathit{i}}{\mathit{A}_\mathit{i}}} \right)} }}. $ | (2) |
式中:σt,k为第k层钢丝的轴向拉应力, αk为第k层的捻角, νk为第k层钢丝的泊松比, Ek为第k层钢丝的弹性模量, S为轴向外荷载, αi为第i层的捻角, νi为第i层钢丝的泊松比, Ei为第i层钢丝弹性模量, Ai为第i层钢丝的面积, zi为第i层钢丝的数量, n为钢绞线截面钢丝的层数, 从里到外, 第1层取n =0.
由表 1、2可得, 本文采用ANSYS分析得到的轴向应力σz与Feyer数值计算得到的轴向应力σt,k相差不大, 且中心钢丝的轴向应力较大, 外层钢丝的轴向应力较小.因此, 可以认为本文采用ANSYS不考虑摩擦分析所得的结果是正确的.
3 考虑摩擦影响的截面应力分布事实上, 钢绞线内部存在摩擦, 且摩擦磨损降低了钢绞线的强度和使用寿命, 因此研究内部摩擦对钢绞线的影响十分必要.钢绞线内部钢丝的接触包括:层内钢丝的接触、外层与内层间的钢丝接触、内层与中心钢丝接触.由于捻制成型时, 钢丝之间具有一定的相对位移, 从而导致磨损较大[8].本文采用罚函数法描述钢绞线内钢丝之间的摩擦, 即用“弹簧”在两个面之间建立接触关系.当两面接触时, 弹簧起作用;当两面分开时, 弹簧不起作用.本文使用TARGE170和CONTA174单元进行摩擦分析, 接触表面相互作用模型采用不分离, 允许滑动模型, 取摩擦系数为0.15[9].
在σq=100 MPa荷载作用下, 1×7、1×19钢绞线考虑摩擦后的截面等效应力如图 7(a)、(b)所示, 由于钢丝之间的相互作用, 层与层钢丝接触处的等效应力最大, 中心钢丝的等效应力值次之, 外层钢丝的等效应力值最小.钢绞线z轴方向应力在接触处略有变化, 在截面的大部分区域变化不大, 其值在100 MPa左右, 如图 7(c)、(d)所示, 与不考虑摩擦时所得的z轴方向应力值(图 3(c)、(d))相比, 变化不大, 在钢绞线截面呈均匀分布.在钢绞线精细化分析时, 钢绞线内钢丝承受拉伸、弯曲、扭转等作用, 此时需要通过等效应力值分析钢丝的受力状态, 因此截面应按不均匀受力考虑, 同时需考虑摩擦作用对其影响.

|
图 7 σq=100 MPa轴向荷载作用下钢绞线(z=2.5D)处应力图 Fig. 7 Stress distribution for cross-section at the end of steel strand(z=2.5D) under tensile force of 100 MPa |
为了进一步研究考虑摩擦时钢绞线截面等效应力分布情况, 同样将截面分成如图 5所示若干层, 各层等效应力如图 8所示, 随着点到圆心距离ri的增加, 各点的等效应力值先增加后减少, 在接触点处形成突变, 达到最大值.对于1×7钢绞线如图 8(a)所示, 中心钢丝上的等效应力值略大, 外层钢丝的等效应力值稍小.对于1×19钢绞线如图 8(b)所示, 中心钢丝的等效应力值最大, 第2层钢丝的等效应力值次之, 第3层钢丝的等效应力值最小.

|
图 8 钢绞线(z=2.5D)处节点等效应力 Fig. 8 Stress of cross-section at end of steel strand(z=2.5D) under tensile force |
为了进一步验证有限元模型的正确性, 建立1×7钢绞线模型, 钢绞线直径为5 mm, 承受轴向均布荷载作用.基于对称性, 计算时取1/6捻距即长度为37.5 mm钢绞线.钢丝的弹性模量E=190 GPa, 泊松比μ=0.3.使用TARGE170和CONTA174单元进行摩擦分析, 钢丝间摩擦系数取0.15.将分析所得结果与易贤人[10]实验所得结果进行对比, 结果如表 3所示.
| 表 3 不同分析方法所得的1×7钢绞线截面应变值 Table 3 Strain of cross-section of 1×7 steel strand with different analysis methods |
由表 3可得本文所得应变与实验所得应变基本接近, 当外荷载σq=286 MPa时, 误差δ最大为5.48%.随着外荷载的增加, 误差越来越小, 当σq=715 MPa时, δ=1.18%.因此, 可以认为本文采用ANSYS考虑摩擦分析所得的结果是正确的.
4 结论(1) 当不考虑摩擦作用时, 由于钢绞线螺旋成形, 导致受力状态下钢绞线截面应力分布不均匀.钢绞线中心钢丝等效应力略小, 外层钢丝逐渐变大, 其等效应力在钢绞线截面呈扇形分布.钢绞线z轴方向应力值变化不大, 在截面基本呈均匀分布.
(2) 当考虑摩擦作用时, 由于摩擦和钢绞线螺旋成形的共同影响, 钢丝接触处的等效应力最大, 中心钢丝的等效应力次之, 外层钢丝的等效应力最小.钢绞线z轴方向应力在接触处略有变化, 在截面的大部分区域变化不大, 与不考虑摩擦时所得的z轴方向应力值相比差别不大.
(3) 在整体结构设计中, 钢绞线以轴向受力为主, 通常只关注钢绞线的轴向受力(z向应力), 此时可按截面应力均匀考虑.在钢绞线精细化分析时, 需要通过等效应力值分析钢丝承受拉伸、弯曲、扭转等复杂作用, 此时应按截面不均匀受力考虑, 同时需考虑摩擦作用对其影响.
| [1] | 钱若军, 杨联萍. 张力结构的分析、设计、施工[M]. 南京: 东南大学出版社, 2001: 5-21. |
| [2] |
张德坤, 葛世荣, 朱真才. 提升钢丝绳的钢丝微动摩擦磨损特性研究[J].
中国矿业大学学报, 2002, 31(9): 367–370.
ZHANG De-kun, GE Shi-rong, ZHU Zhen-cai. Friction and wear performance on fretting wear of steel wires in hoisting ropes[J]. Journal of China University of Mining & Technology, 2002, 31(9): 367–370. |
| [3] | CHIANG Y J. Characterizing simple-stranded wire cables under axial loading[J]. Finite Elem Anal Des, 1996, 24(2): 49–66. DOI:10.1016/S0168-874X(97)80001-E |
| [4] |
孔庆凯, 万鹏. 钢绞线的基本力学性能及其有限元方法模拟[J].
工程结构, 2003, 23(1): 20–22.
KONG Qing-kai, WAN Peng. Basic mechanical properties and finite element method of the strand wire[J]. Engineering Structure, 2003, 23(1): 20–22. |
| [5] | GHOREISHI S R, MESSAGER T, CARTRAUD P. Validity and limitations of linear analytical models for steel wire strands under axial loading, using a 3D FE model[J]. International Journal of Mechanical Sciences, 2007, 49(11): 1251–1261. DOI:10.1016/j.ijmecsci.2007.03.014 |
| [6] |
马军, 葛世荣, 张德坤. 钢丝绳股内钢丝应力—应变分布的计算模型及数值模拟[J].
机械工程学报, 2009, 45(4): 259–264.
MA Jun, GE Shi-rong, ZHANG De-kun. Calculating model and numerical simulation of stress-strain distribution of wires within strands[J]. Journal of Mechanical Engineering, 2009, 45(4): 259–264. |
| [7] | FEYRER. Wire ropes, tension, endurance, reliability[J]. Berlin, Springer-Verlag, 2007, 21(2): 1–10. |
| [8] |
浦汉军. 起重机用不旋转钢丝绳寿命研究[D]. 广州: 华南理工大学, 2012.
PU Han-jun. Study on theory and life estimation of the non-rotating rope used in crane[D]. Guangzhou: South China University of Technology, 2012. |
| [9] | WANG DG. Effect of displacement amplitude on fretting fatigue behavior of hoisting rope wires in low cycle fatigue[J]. Tribol Int, 2012, 52: 178–189. DOI:10.1016/j.triboint.2012.04.008 |
| [10] |
易贤人. 钢绞线偏轴应变测量方法及实验研究[J].
华中科技大学学报, 2008, 25(3): 211–214.
YI Xian-ren. Measurement method and experimental study of prestressed strand deflection axial strain[J]. Journal of Hua Zhong University of Science and Technology, 2008, 25(3): 211–214. |



