绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)凭借其功耗小、驱动简单、热稳定性高、开关速度快等优点, 在现代电力电子技术中得到了越来越广泛的应用, 在较高频率的大、中型功率模块应用中占据了主导地位, 已广泛地渗透到电力系统、交通、冶金、国防等各个领域[1-2].
通过叠层封装技术, 半导体器件IGBT通常以功率模块的形式应用到市场中, 传统焊接式IGBT模块由热膨胀系数不同的材料叠装而成[3].在实际运行过程中, IGBT模块将承受外部环境与自身损耗共同引起的温度波动, 在各层材料中产生不同的膨胀或收缩变形, 相互约束在焊料层产生交变应力应变[4].当焊料层中不可恢复的非弹性应变积累到一定程度, 将引起焊层裂纹损伤的形成.裂纹损伤在模块内部产生热集中效应, 引起局部温度和热应力升高, 最终导致焊料层断裂和IGBT模块的完全失效[5].焊料层的疲劳寿命直接决定了IGBT模块的可靠服役时间, 基于焊料层失效机理和裂纹损伤的研究对提高IGBT模块可靠性有重要意义.
目前, 有限元分析(finite element analysis, FEA)被广泛地应用于功率器件的封装失效机理、损伤缺陷等研究中, 它克服了加速老化实验周期长、研发成本高等缺点[6-7], 在高保真还原器件材料、结构特性的基础下能够实现对封装模块的多物理场耦合分析.基于有限元分析技术的IGBT模块可靠性研究已经取得了一定成果.董少华等[8-10]获得IGBT模块焊料层在热循环条件下的应力应变分布, 并以热应力最小化为目标函数, 提出封装模块的优化设计;Jamil等[11-12]证明了功率循环相对于温度循环能够更加合理地反映功率器件的实际运行状态;Ishikawa等[13-15]实现了对IGBT模块的寿命预测.同时, Haleh等[16-23]针对IGBT模块焊料层中易存在的空洞和裂纹缺陷进行研究.张小玲等[16-19]分析获得焊料层空洞的大小和位置对模块热性能及热应力的影响规律;Shinohara等[20-23]揭示了功率循环下IGBT模块焊料层裂纹的演化过程.
空洞缺陷可以通过封装工艺的改进来有效避免[16], 而裂纹损伤是随服役进程产生的一种热疲劳失效, 在服役过程中无法避免[3], 因此, 对焊料层裂纹缺陷的研究更具有实际意义.裂纹尖端形状特殊, 在有限元仿真时存在网格划分难度大、尖端的奇异性容易造成仿真结果不收敛等问题, 国内外对焊料层裂纹缺陷的研究较少.本文在全面掌握IGBT模块封装结构、断裂力学理论、有限元仿真技术的基础上, 建立考虑焊料层黏塑性效应的热-力耦合模型.探究IGBT模块焊料层在功率循环作用下的失效机理以及裂纹损伤对IGBT模块热特性和疲劳寿命的影响.通过加速老化实验对仿真结果进行验证, 研究成果能够为IGBT模块寿命预测和可靠性评估提供有效的理论支撑.
1 功率循环下焊料层失效机理分析 1.1 IGBT模块有限元模型以型号为SKM50GB12T4的IGBT模块为仿真原型, 在ANSYS有限元仿真软件中建立等比例几何模型, 如图 1所示.综合考虑IGBT模块本身的传热性能及计算复杂度, 对几何模型进行以下简化.1) 散热器结构复杂, 不利于有限元网格划分和计算, 并且散热器的作用可以通过设置边界条件来弥补, 因此在仿真中, 忽略散热器来提高计算效率;2) 铝键合线对IGBT模块温度分布的影响较小[24], 且本文的研究重点主要为封装模块焊料层, 因此建模时将铝键合线予以忽略.

|
图 1 IGBT模块有限元分析模型结构图(SKM50GB12T4) Fig. 1 FEM of IGBT module(SKM50GB12T4) |
IGBT模块由不同材料叠装而成, 假定各层材料均为各向同性, 通过实际测量及查阅模块Datasheet参数获得IGBT模块材料尺寸以及弹性热力学参数, 如表 1、2所示.表中,T为Sn3.5Ag焊料层所承受的温度.特别地, 由于构成焊料层的焊锡材料熔点较低(Sn3.5Ag钎料熔点Tm=429 ℉), 电子器件的服役温度一般将达到熔点温度一半以上, 此时黏塑性力学行为将成为焊料层变形的主要形式, 弹性力学参数不能准确描述焊料层的力学响应过程.文献[25]的研究表明, Anand本构模型能够有效地描述焊点的黏塑性特性, 可以有效地用于电子封装中焊点的可靠性模拟, 因此采用Anand参数来描述焊料层的非弹性特性, 具体参数如表 3所示.表中, A为常数, Q为活化能, ζ为应力乘子, m为应变率灵敏指数,
| 表 1 IGBT模块各部分结构尺寸 Table 1 Geometry Parameters of IGBT Module |
| 表 3 Sn3.5Ag钎料黏塑性Anand本构方程的材料参数 Table 3 Anand constant of Sn3.5Ag solder material |
为了补偿建模时忽略掉的散热器作用, 在铜基板底部设置强制对流换热系数模拟散热器效应, 经验强制对流换热系数为4 000 W/(m2·℃)[27].基板侧面与空气自然对流换热, 换热系数为10 W/(m2·℃), 环境温度取25 ℃.结构分析时, 将基板底面四个角固定, 如图 1所示.
功率循环通过功率的“开”、“断”来模拟IGBT模块在工作状态下的升降温过程.在ANSYS中, 功率以热生成率HG的形式加载到IGBT芯片上, HG的计算方法为
| $ {H_{\rm{G}}} = P/V. $ | (1) |
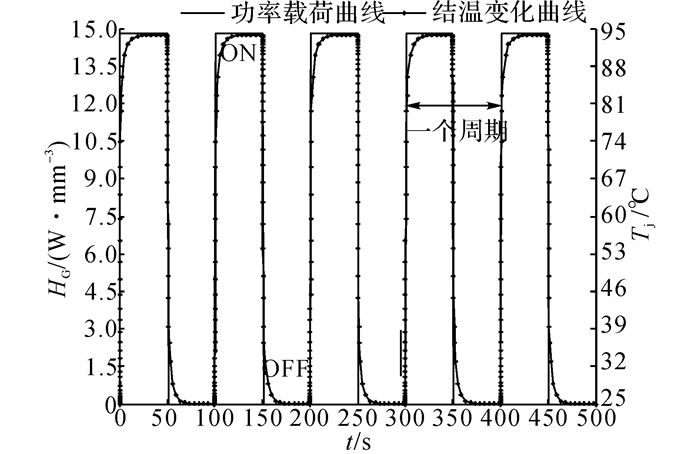
式中:P为施加在器件上的功率, V为热源体积.每个功率循环周期为100 s, 由4个载荷步组成:导通时间为49 s, 开-断转换时间1 s, 关断时间为49 s, 断-开转换时间为1 s.通过损耗公式计算得到在额定电流(50 A)下的IGBT芯片导通损耗为108 W, 即热生成率为14.8 W/mm3, 功率载荷曲线如图 2所示.图中,Tj为IGBT芯片结温.
|
图 2 功率循环载荷曲线及结温变化曲线 Fig. 2 Power cycle profile and time history of temperature |
经过瞬态热分析, 可得IGBT模块在50 s时的温度分布如图 3所示.可知, 在功率载荷作用下, 模块温度分布非均匀, 最高结温出现在IGBT芯片正中节点号为4 979的节点处, 为93.744 ℃, 热量沿着芯片向铜基板传递, 温度从上往下、从内到外逐级递减, 在铜基板边缘处达到模块温度最低值, 为26.299 ℃.节点4 979随时间的温度波动情况如图 4所示.图中,σ为等效应力, εin为非弹性应变.可以看出, 在一个周期内模块结温波动ΔTj≈69 ℃, 结温变化规律与载荷曲线相一致, IGBT器件导通关断转换过程中会造成结温的迅速变化, 开关保持阶段结温逐渐趋于稳定.

|
图 3 功率循环下模块温度分布(50 s) Fig. 3 Temperature distribution on module (50 s) |
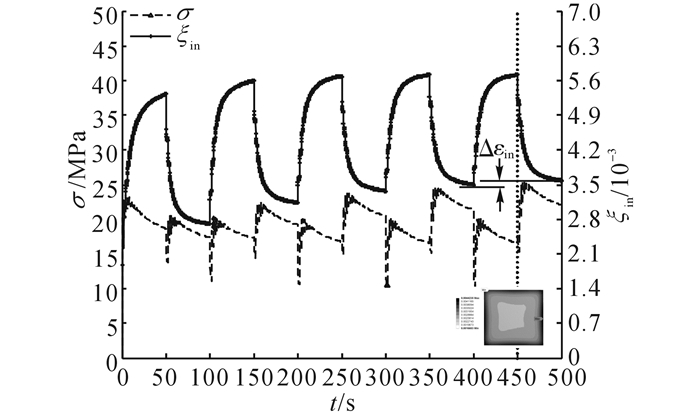
将温度分析结果代入力学分析模块, 求解得到IGBT模块在功率载荷作用下承受的应力应变.由于温度分布的影响, 靠近热源的芯片焊料层相对DBC(direct bonded copper)焊料层承受更大的热应力, 更易发生疲劳失效[8], 因此以芯片焊料层作为研究对象.图 4右下方为功率循环405 s时芯片焊料层的非弹性应变分布云图.可以看出, 焊料层边缘是应变集中的主要区域, 焊料层疲劳损伤往往从边缘萌生, 随时间向中心发展.其中, 位于边缘的331节点承受最大的非弹性应变, 取该节点作进一步分析, 获得331节点在功率循环过程中的应力应变曲线, 如图 4所示.可以看出, 等效应力在器件开关状态保持过程中逐步减小, 这是由于焊料层产生的黏塑性形变引起了应力松弛现象, 导通阶段的应力松弛比关断阶段更加明显;非弹性应变的变化与结温变化规律基本一致, 应变随结温的上升而增加, 随结温的下降而减少.值得注意的是, 在每一循环周期内, 应变上升幅值总是大于下降幅值, 使得循环结束时的非弹性应变大于循环初始时的非弹性应变, 即焊料层在每一循环周期内产生了非弹性应变积累.当这种不可恢复的非弹性应变积累到一定程度后将会导致焊料层中裂纹的萌生和扩展, 最终引起焊料层断裂失效.
|
图 4 芯片焊料层331节点应力应变变化曲线 Fig. 4 Time history of stress and inelastic strain at node 331 |
由上述分析可知, 芯片焊料层是IGBT模块中最脆弱的部分之一, 疲劳失效表现为边缘裂纹的萌生和扩展.在芯片焊料层边缘处预置多种长度的裂纹, 建立含有裂纹损伤的IGBT模块有限元模型.三维有限元模型所划分的单元和节点数目非常庞大, 加上裂纹本身形状的复杂性, 基于三维模型的有限元计算效率非常低, 因此综合考虑研究重点及计算效率, 取图 3中的横向切片建立二维有限元模型, 如图 5所示.在仿真过程中, 设置初始裂纹设置为0.067 5 mm, 为焊料层长度的1%, 预置裂纹处的有限元单元作删除操作, 不再参与计算热力耦合分析.由断裂力学理论可知, 裂纹尖端存在应力集中效应.为了保证仿真结果的收敛性和精确性, 在进行网格划分时, 考虑以下几点.1) 裂纹尖端采用三角奇异单元, 单元围绕裂纹尖端按环形扫掠方式展开;2) 为了得到精确的计算结果, 设置裂纹尖端尺寸为10-5 mm, 在远离裂纹尖端的区域, 单元尺寸适当放大.

|
图 5 计及裂纹损伤IGBT模块有限元模型 Fig. 5 FEM of IGBT module considering crack |
对裂纹模型施加如图 2的功率循环载荷, 进行热分析, IGBT模块在450 s时温度趋于稳定, 温度分布如图 6(a)所示.图中,L为裂纹长度.可以看出, 当芯片焊料层中存在L=0.067 5 mm裂纹时, 模块最高结温出现在IGBT芯片正中, 结温相对于完整模型的结温(见图 3) 有微小的增加(从93.744 ℃上升到93.892 ℃).同时, 在裂纹区域温度存在明显的不连续现象, 这是由于裂纹的阻热效应改变了IGBT模块的热量流通路径.当裂纹从0.067 5 mm扩展到0.337 5 mm时, IGBT模块在450 s时的温度分布如图 6(b)所示.可以看出, 裂纹的阻热效应随着长度的增加越发明显, 一方面结温发生了明显的上升(从93.744 ℃上升到98.039 ℃), 另一方面温度分布发生了改变(结温最高点从芯片正中转移到裂纹上方).综上所述, 焊料层中裂纹损伤会对IGBT模块内部的热传导产生阻碍作用, 使模块结温增大, 温度分布发生改变, 在可靠性分析时, 应对裂纹损伤予以重点关注.

|
图 6 IGBT模块温度分布云图 Fig. 6 Temperature distribution of IGBT module |
热阻是表征功率器件散热性能的主要参数.热阻越大, 说明功率模块散热性能越差.根据IGBT模块热学模型[24]可知, 模块稳态结壳热阻为
| $ {R_{{\rm{th - jc}}}} = \frac{{{T_{\rm{j}}} - {T_{\rm{c}}}}}{{{P_{\rm{l}}}}}. $ | (2) |
式中:Tc为IGBT模块壳温, Pl为引起结温变化的功率损耗.由式(2) 可以看出, 在功率损耗一定的条件下, 模块结温上升的本质可以描述为模块热阻的增大.为了获得焊料层裂纹损伤对IGBT模块热特性的影响, 探究裂纹长度与IGBT模块热阻之间的关系.首先, 定义相对热阻Rn表征热阻的相对变化情况:
| $ {R_{{\rm{n}}\left( i \right)}} = \frac{{{R_{\rm{m}}}\left( i \right)}}{{{R_{\rm{i}}}}}. $ | (3) |
式中:Ri为在一定载荷作用下无裂纹损伤的IGBT模块结壳热阻, Rm(i)为相同载荷条件下裂纹长度比例为i时的IGBT模块结壳热阻.在芯片焊料层中预置15组长度的裂纹损伤, 通过施加相同的功率循环载荷(P=108 W), 热分析获得IGBT模块温度分布(t=450 s).将不同裂纹长度对应的Tj和Tc代入式(2)、(3), 计算得到相对热阻, 如表 4所示.表中,Rth为热阻.可以看出, IGBT模块热阻随裂纹长度的增加而增大, 这是因为裂纹损伤致使IGBT模块散热面积减小, 而裂纹越长, IGBT模块导热性能越差.
| 表 4 裂纹参数与热阻数值仿真数据(P=108 W) Table 4 Thermal resistance with respect to crack length |
在上述结论基础上, 增加3组功率循环仿真实验, 功率损耗分别为23.1、54、86 W.通过热分析获取不同裂纹长度对应的相对热阻, 如图 7所示.可以看出, 4种功率载荷作用下相对热阻随裂纹长度的变化规律基本一致, 当焊料层无裂纹或裂纹长度较小时, 裂纹的增长对模块热特性的影响不大, 而一旦焊料层裂纹扩展到某一阶段, 裂纹的继续增长将引起模块热阻近指数增大, 此时继续服役将导致焊料层在短时间内迅速失效.为了防止IGBT模块失效带来的严重后果, 当检测到模块结壳热阻发生快速增大的初期, 应及时对IGBT模块进行维护和更换.

|
图 7 相对热阻随裂纹长度比例变化规律 Fig. 7 Correlation between crack length ratio and relative thermal resistance |
根据不同的建模方法可知, 目前IGBT模块的寿命模型主要分为解析模型和物理模型两大类.其中, 解析模型描述了模块寿命与加速老化实验中各变量之间的关系, Coffin-Manson模型是目前应用最广泛的解析模型,
| $ {N_{\rm{f}}} = \alpha {(\Delta {T_{\rm{j}}})^{ - n}}. $ | (4) |
式中:Nf为失效循环周期数;ΔTj为功率循环中的结温波动值;α、n为特征常数, 一般通过实验数据拟合获得.
物理模型是基于模块内部疲劳老化和应力应变物理机制建立的寿命模型, 根据力学参量的不同, 主要分为应力型、应变型、能量型和断裂力学型等.其中, 基于应变的寿命模型将IGBT模块的寿命与焊料层中最大非弹性应变增量相关联, 如下所示:
| $ {N_{\rm{f}}} = A{(\Delta {\varepsilon _{{\rm{in}}}})^{ - m}}. $ | (5) |
式中:Δεin为每周期内非弹性应变的变化范围, 包含与时间无关的塑性应变和与时间相关的蠕变应变, Δεin通过有限元仿真计算获得;A、m为特征常数, 通过实验数据拟合获得.
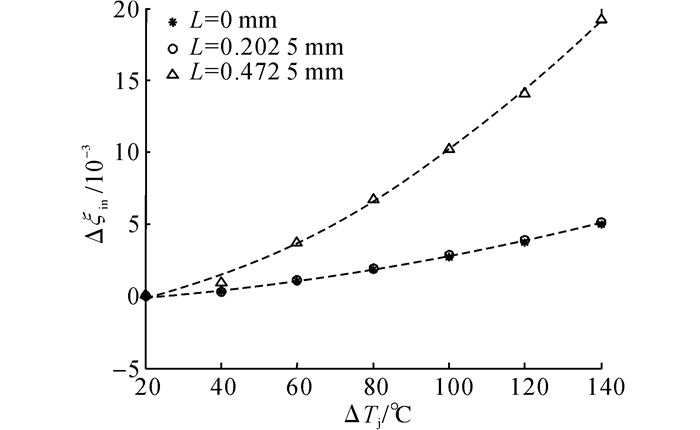
基于L=0 mm、0.202 5 mm、0.472 5 mm三种不同损伤程度的有限元模型, 施加如表 5所示的功率循环载荷.通过热-力耦合分析, 取循环第四周期应力应变曲线, 计算获得模型在周期内非弹性应变增量Δεin, 如图 8所示.可以看出, 在相同的ΔTj载荷下, 不同损伤强度模块产生的Δεin不同, 裂纹越长, IGBT模块Δεin越大, IGBT模块寿命越短.仿真结果说明, IGBT模块的疲劳寿命不仅与ΔTj相关, 还与模块焊料层疲劳损伤程度相关.当模块存在裂纹损伤时, 基于ΔTj的Coffin-Manson解析模型不能准确地预测IGBT模块寿命, 此时应使用基于应力应变参量的物理寿命模型来进行IGBT模块寿命评估.
| 表 5 功率循环仿真条件 Table 5 Condition of power cycle test |
|
图 8 不同损伤模型下结温波动值与非弹性应变的关系 Fig. 8 Correlation between ΔTj and Δεin under differentmodule |
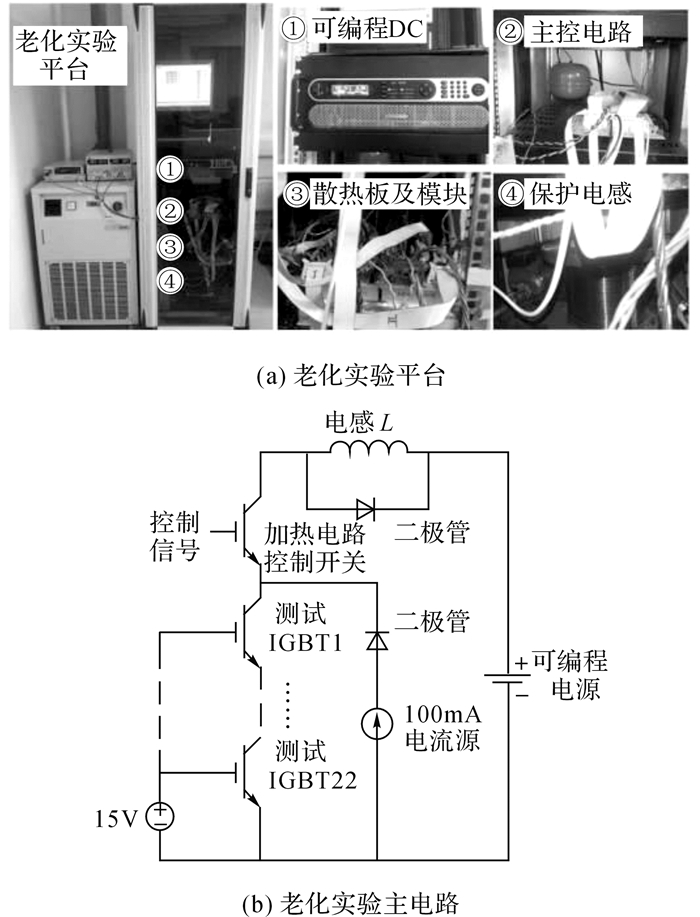
通过加速老化实验, 测量IGBT模块实时结壳热阻, 通过结壳热阻评估模块疲劳失效过程, 验证有限元仿真结果.老化实验装置及主电路如图 9所示, 为了保证IGBT器件同时开通与关断, 电路将11个型号为SKM50GB12T4功率模块(22个IGBT器件)进行串联.为了获得IGBT模块结壳热阻, 须准确测量Tj.通过温度箱实验获得100 mA电流下集射极电压Vce与Tj的关系式, 如下所示:
| $ {T_{\rm{j}}} = 436.972{\rm{ }}3{V_{{\rm{ce}}}} + 293.718{\rm{ }}3. $ | (6) |
|
图 9 老化实验装置及主电路 Fig. 9 Aging test rig and main electrical circuit |
在老化实验中, 图 9(b)所示电路左下角的驱动电压源恒导通, 上位机输出控制信号控制测试模块的导通和关断.具体的实验流程如图 10所示, 当器件导通时, 测试IGBT模块将被加热, 一旦温度传感器检测到模块壳温达到上限阈值, 控制IGBT关断.关断瞬间导通与模块并联的100 mA电流源, 通过测量得到Vce, 代入式(6), 计算得到关断前瞬间IGBT芯片的结温.此时, 结温可以近似为芯片最大结温Tjmax.打开固定在IGBT模块下的散热器, 之后进入冷却步骤, 当测定到模块壳温达到设定的下限值时冷却结束, 此时Tc≈Tjmin, 周期内的ΔTj=Tjmax-Tjmin.最后, 将ΔTj、导通功率P代入式(2), 计算得到模块热阻, 其中, P由导通时的电流和电压相乘得到.
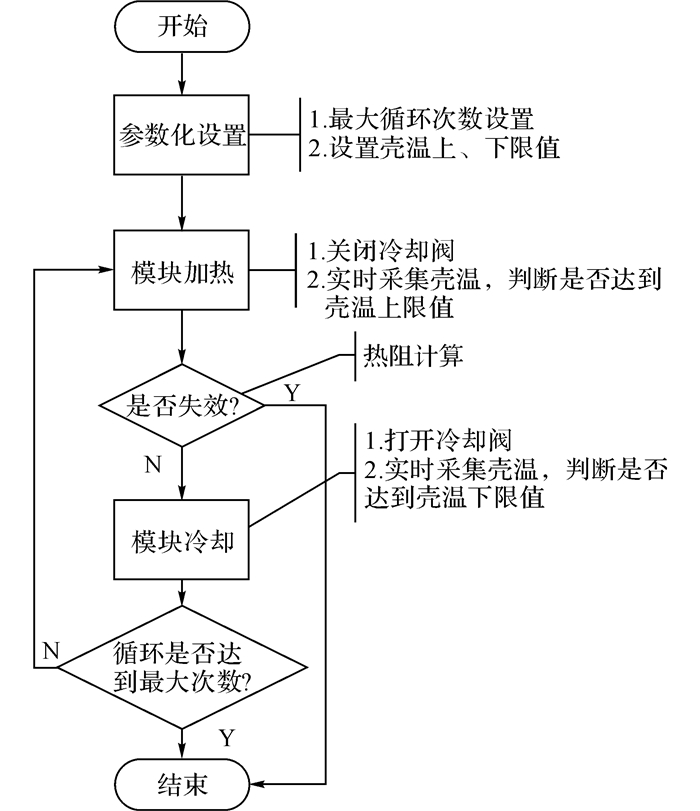
|
图 10 加速老化实验流程图 Fig. 10 Aging test rig and main electrical circuit |
基于上述老化实验平台, 首先设计老化实验1.在实验1中, 控制电路的导通时间, 使每周期内结温波动ΔTj为94.3 ℃, 随着老化周期数的增加, 相对热阻逐渐增大, 如图 11所示.图中,N为功率循环周期数.由于焊料层的疲劳老化程度与模块结壳热阻Rth-jc正相关[4, 28].由图 11可知, 在焊料层老化初期, 结壳热阻的变化率很小;当焊料层老化到一定程度时, 结壳热阻将随时间近指数增长, 与图 7中通过有限元仿真得到的热阻变化规律相一致.
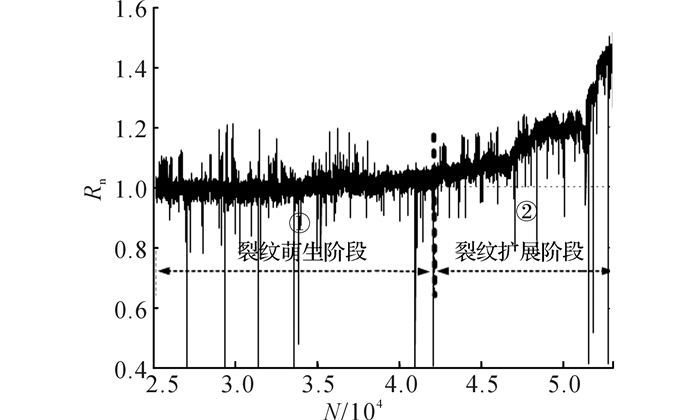
|
图 11 恒定功率循环下模块相对热阻变化情况 Fig. 11 Normalized Rth of module under power cycling test |
在实验2中, 首先对完整IGBT模块在大结温载荷(ΔTj=112 ℃)下进行加速老化, 在功率循环10 376次后, 测量到模块热阻基本未改变, 如图 12所示, 说明此时焊料层未产生较大的疲劳损伤.之后, 缩短电路导通时间, 使周期内结温波动减小到ΔTj≈40 ℃.保持小ΔTj下的功率循环, 老化60 000次后, 发现模块热阻的改变非常小, 说明此时IGBT模块焊料层中未产生影响模块热特性的大裂纹损伤.通过将实验2与实验1的结果进行对比发现, ΔTj越大, 模块老化速度越快, 模块焊料层中缺陷更容易萌生和扩展.
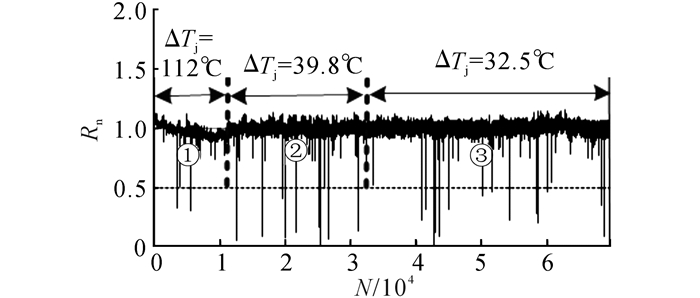
|
图 12 功率循环下未老化模块的相对热阻变化情况 Fig. 12 Normalized Rth of unaged module |
在实验3中, 首先在大结温载荷(ΔTj=119 ℃)下对模块进行加速老化.在功率循环10 952次后, 测量发现模块热阻相对于初始值有了显著增加(Rth=1.41Ri); 如图 13所示, 说明此时焊料层中产生了较大的疲劳缺陷.此后, 缩短电路导通时间, 使周期内结温波动减小到ΔTj≈40 ℃.在小结温波动下开展老化实验发现, 随着功率循环周期的增加, 模块热阻不停攀升.将该实验结果与实验2结果进行对比发现, 相同结温波动ΔTj(≈40 ℃)对完整模块和缺陷模块的疲劳老化效果不同, 缺陷模块服役在相同ΔTj下会有更快的老化速度和更低的服役寿命.该规律与有限元仿真结果图 8所得的结论一致.
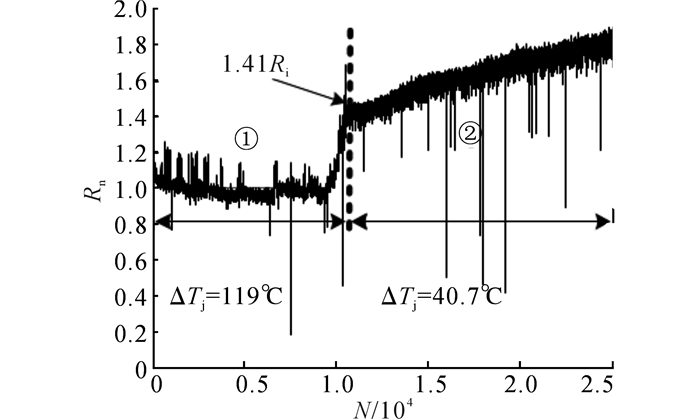
|
图 13 功率循环下老化模块的相对热阻变化情况 Fig. 13 Normalized Rth of module under large ΔTj and then small ΔTj |
(1) 焊料层疲劳失效是IGBT模块的主要失效模式之一, 疲劳损伤往往从边缘萌生, 并随着老化进程逐步向中心扩展.在模块功率循环过程中, 焊料层将产生应力应变的积累;当不可恢复的非弹性应变积累到一定程度时, 焊料层将会发生疲劳失效.
(2) 裂纹的存在会引起IGBT模块热阻的增加, 裂纹长度与模块热阻之间存在明显的阶段性特征:在裂纹未萌生和萌生初期, 裂纹对模块散热参数的影响较小, 随着裂纹长度的增加, 热阻基本不变;一旦模块损伤到某一阶段, 随着裂纹的继续扩展, 模块热阻将近似指数增大, 继续服役将使功率模块在短时间内失效.综合考虑模块运行的可靠性与经济性, 对功率模块更换维护的最佳时间应选在检测到模块热阻快速增大的初期.
(3) IGBT模块的疲劳寿命不仅与功率循环条件相关, 而且受焊料层疲劳现状的影响.当焊料层中出现裂纹时, 施加相同的结温波动载荷, 模块的寿命将低于健康模块.因此, 在对IGBT模块进行寿命评估时, 应充分考虑焊料层的疲劳累积效应.建立基于内部疲劳老化的物理寿命模型相对于目前解析寿命模型, 能够更准确地进行IGBT模块寿命评估.
| [1] | BALIGA B J. Fundamentals of power semiconductor devices[M]. New York: Springer, 2008. |
| [2] |
唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J].
电工技术学报, 2014, 26(6): 17–23.
TANG Yong, WANG Bo, CHEN Ming, et al. Reliability and on-line evaluation of IGBT modules under high temperature[J]. Transactions of China Electro-technical Society, 2014, 26(6): 17–23. |
| [3] | WEI Lai, CHEN Min-you, RAN Li, et al. Small junction temperature cycles on die-attach solder layer in IGBT[C]//2015 17th European Conference on Power Electronics and Applications. Geneva:[s.n.], 2015: 1-10. |
| [4] | CHOI U M, BLAABJERG F, LEE K B. Study and handling methods of power IGBT module failures in power electronic converter systems[J]. Power Electronics IEEE Transactions, 2015, 30(5): 2517–2533. DOI:10.1109/TPEL.2014.2373390 |
| [5] |
郭祥辉. 电子封装结构超声显微检测与热疲劳损伤评估[D]. 北京: 北京理工大学, 2015.
GUO Xiang-hui. Ultrasonic nondestructive testing and thermal fatigue evaluation of electronic packaging[D]. Beijing: Beijing Institute of Technology University, 2015. |
| [6] | OH H, HAN B, MCCLUSKEY P, et al. Physics-of-failure, condition monitoring, and prognostics of insulated gate bipolar transistor modules: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2413–2426. DOI:10.1109/TPEL.2014.2346485 |
| [7] | KOJI S, NAOKO I, TOSHIKI K, et al. Thermal and structural simulation techniques for estimating fatigue life of an IGBT module[C] // 2008 20th International Symposium on Power Semiconductor Devices and IC's. Orlando: IEEE, 2008: 181-184. |
| [8] |
董少华. IGBT器件热可靠性的研究[D]. 济南: 山东大学, 2014.
DONG Shao-hua. The research of thermal reliability of insulated gate bipolar transistor (IGBT)[D]. Jinan: Shandong University, 2014. |
| [9] |
翟超. IGBT模块封装热应力研究[D]. 杭州: 浙江大学, 2013.
ZHAI Chao. Research of thermal stress in IGBT module[D]. Hangzhou: Zhejiang University, 2013. |
| [10] |
张雪垠. 基于FEM的功率IGBT模块功率循环可靠性研究[D]. 上海: 上海交通大学, 2014.
ZHANG Xue-yin. Research on IGBT module power cycling reliability based on FEM method[D]. Shanghai: Shanghai Jiao Tong University, 2014. |
| [11] | JAMIL W, PAUL S H. Simulating package behavior under power dissipation using uniform thermal loading[J]. IEEE Transactions on Advanced Packaging, 2001, 24(1): 60–65. DOI:10.1109/6040.909626 |
| [12] | JAMIL W, PAUL S H. Non-uniform temperature and strain fields in a powered package[J]. IEEE Transaction on Components and Packaging Technologies, 2000, 23(3): 521–527. DOI:10.1109/6144.868852 |
| [13] | ISHIKAWA S, TOHMYOH H, WATANABE S, et al. Extending the fatigue life of Pb-free SAC solder joints under thermal cycling[J]. Microelectronics Reliability, 2013, 53(5): 741–747. DOI:10.1016/j.microrel.2013.02.011 |
| [14] | HUANG X, WU W, CHOU P. Fatigue life and reliability prediction of electronic packages under thermal cycling conditions through FEM analysis and acceleration models[C] // 14th International Conference onElectronic Materials and Packaging (EMAP). Lantau Island: IEEE, 2012: 1-6. |
| [15] | LV X, ZHENG L, KONG X, et al. The research of relationship between the void of DBC and the temperature distribution[J]. International Symposium on Advanced Packaging Materials (APM). Xiamen: IEEE, 2011: 168–171. |
| [16] | HALEH A, MICHAEL G P. 电子封装技术与可靠性[M]. 中国电子学会电子制造与封装技术分会, 译审. 北京: 化学工业出版社, 2012. |
| [17] |
田蕴杰, 张小玲, 谢雪松, 等. IGBT热疲劳工作对焊料层可靠性的影响[J].
固体电子学研究与进展, 2014(03): 288–292.
TIAN Yun-jie, ZHANG Xiao-ling, XIE Xue-song, et al. Thermal fatigue effects on IGBT die attach reliability[J]. Research and Progress of SSE, 2014(03): 288–292. |
| [18] |
蒋长顺, 谢扩军, 许海峰, 等. 封装中的界面热应力分析[J].
电子与封装, 2006, 6(8): 23–26.
JIANG Chang-shun, XIE Kuo-jun, XU Hai-feng, et al. Interfacial thermal stress analysis in packaging[J]. Electronics and Packaging, 2006, 6(8): 23–26. |
| [19] |
吴煜东, 常桂钦, 彭勇殿, 等. 焊层空洞对IGBT模块热应力的影响[J].
大功率变流技术, 2014(01): 17–23.
WU Yu-dong, CHANG Gui-qin, PENG Yong-dian, et al. Effect of solder voids on IGBT thermal and stress performance[J]. High Power Converter Technology, 2014(01): 17–23. |
| [20] | SHINOHARA K, YU Q. Fatigue life evaluation accuracy of power devices using finite element method[J]. International Journal of Fatigue, 2011, 33(9): 1221–1234. DOI:10.1016/j.ijfatigue.2011.03.009 |
| [21] | MOROZUMI A, YAMADA K, MIYASAKA T, et al. Reliability of power cycling for IGBT power semiconductor modules[C] // Industry Applications Conference. Chicago: IEEE, 2003: 1912-1918. |
| [22] | SHINAOHARA K, YU Q. Fatigue evaluation of power devices[C] // Electronic Packaging Technology and High Density Packaging. Beijing: IEEE, 2009:1277-1283. |
| [23] | TAKAGI K, YU Q, SHIBUTANI T, et al. Study of thermal fatigue life caused by dispersion of solder joint[C] // 11th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems. Orlando: IEEE, 2008: 883-888. |
| [24] |
李皎明, 余岳辉, 白铁城, 等. 晶闸管的瞬态热阻抗及其结温温升的研究[J].
微纳电子技术, 2001, 38(2): 52–55.
LI Jiao-ming, YU Yue-hui, BAI Tei-cheng, et al. Research of thyristor's transient thermal impedance and junction temperature rise[J]. Semiconductor Information, 2001, 38(2): 52–55. |
| [25] | TSENG H K, WU M. Electro-thermal-mechanical modeling of wire bonding failures in IGBT[C] // 8th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT). Taipei: IEEE, 2013: 152-157. |
| [26] | DONGKAIS. 无铅焊料互联及可靠性[M]. 刘建影, 孙鹏, 译. 北京: 电子工业出版社, 2008: 252-256. |
| [27] |
吴煜东, 常桂钦, 彭勇殿, 等. 焊层空洞对IGBT模块热应力的影响[J].
大功率变流技术, 2014(01): 17–23.
WU Yu-dong, CHANG Gui-qin, PENG Yong-dian, et al. Effect of solder void on IGBT thermal and stress performance[J]. High Power Converter Technology, 2014(01): 17–23. |
| [28] | STUPAR A, BORTIS D, DROFENIK U, et al. Advanced setup for thermal cycling of power modules following definable junction temperature profiles[C] //International Power Electronics Conference (IPEC). Sapporo: IEEE, 2010: 962-969. |



