助力外骨骼负载特征与驱动特征耦合效应
西南交通大学 机械工程学院, 四川 成都 610031
摘要: 针对助力外骨骼在蹲起姿态中由不同负载特征所引起的驱动失效问题, 为了研究负载特征对关节驱动的影响, 建立考虑负载特征的助力外骨骼蹲起姿态动力学模型, 研究负载特征与关节驱动特征的耦合关系.基于Lagrange动力学理论及矩阵理论, 推导出多刚体系统动力学建模矩阵法, 得到助力外骨骼关节驱动力矩及驱动功率方程.通过人体机器多视觉运动捕捉测量实验及非线性拟合, 得到各关节的角位移、角速度及角加速度.研究结果表明：负载质量与踝关节及膝关节驱动特征为线性强耦合, 与髋关节驱动特征为分段线性弱耦合；负载位置与髋关节驱动特征为分段线性强耦合, 负载姿态与髋关节驱动特征为分段非线性耦合, 负载位置及负载姿态与踝关节及膝关节驱动特征无耦合效应.
关键词: 蹲起姿态 助力外骨骼 负载特征 驱动特征 耦合效应
Coupling effect between load characteristics and joint driving characteristics of powered exoskeleton
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
Abstract: Aiming at the drive failure issue of the powered exoskeleton which was caused by different load characteristics in the squat stance, the dynamic model was established by considering the effects of the load characteristics on the powered exoskeleton. The coupling effect between the load characteristics and the joint driving characteristics was discussed in order to analyze the effect of the load characteristics on the joint driving characteristics. The dynamic modeling matrix method of multi-body system was deduced from the Lagrange dynamic theory and matrix theory. The joint driving torque and the driving power of the powered exoskeleton were worked out. The angular displacement, angular velocity and angular acceleration of all joints were obtained from the somatic data acquisition experiment and nonlinear data-fitting. Results showed that there was linear strong coupling between the load mass and the driving characteristics on the ankle and the knee, and there was piecewise linear weak coupling between the load mass and the driving characteristics on the hip. The piecewise linear coupling between the load position and the driving characteristics on the hip was strong, and the coupling between the load posture and the driving characteristics on the hip was nonlinear, but there was no coupling effect between the load position as well as load posture and the driving characteristics on the ankle and the knee.
Key words: squat stance powered exoskeleton load characteristics driving characteristics coupling effect
1.2 系统势能和广义力
1.3 系统动能
1.4 多体系统拉格朗日动力学方程矩阵法
3 助力外骨骼蹲起姿态运动特征分析
3.1 蹲起姿态运动特征测量实验
3.2 关节角位移非线性拟合
4 仿真计算及分析
4.2 负载特征对踝关节及膝关节驱动特征的影响
助力外骨骼是一种能量自主且与人体运动姿态保持一致的助力可穿戴系统, 能够增强穿戴者的负载能力及作战持久力[1-6].目前, 国内外学者对助力外骨骼进行了相关研究.Ghan等[7-9]分析BLEXX增强型外骨骼动力学问题, 研究控制算法及控制策略；贾山等[10-12]研究下肢外骨骼步行工况下动力学问题, 提出关节驱动器设计和控制策略；Otten等[13]研究外骨骼机器人的力矩闭环控制策略及阻抗控制算法；Zanotto等[14]研究人机膝关节不重合性对穿戴者行走步态的影响；杨巍等[15]研究步行姿态人机耦合系统动力学建模问题和外骨骼结构设计及系统控制问题.
由于穿戴者要背负不同的重物载荷, 在各种运动姿态下, 不同的负载特征对穿戴者及外骨骼的运动、驱动及动力学等特性产生影响.Gregorczyk等[16]研究不同负载质量对穿戴者新陈代谢及步态生物力学的影响；Lee等[17]利用主成分分析法, 分析步行中负载质量对下肢运动学的影响；Majumdar等[18]研究负载质量的变化对士兵脚底作用力的影响；Schiffman等[19]研究穿戴外骨骼时负载质量对系统稳定性极限及姿态摆动的影响；Lawrence等[20]研究人体下蹲时, 不稳定负载对脚底作用力及肌肉活动的影响；Sahli等[21]研究负载质量对髌骨关节动力学特性影响；Cotter等[22]研究人体蹲起姿态中, 负载质量及蹲起深度对膝关节动力学特性的影响.
综合国内外的文献来看, 目前还没有学者研究负载质量、负载位置及负载姿态对助力外骨骼蹲起姿态下关节驱动力矩及驱动功率的影响.由于蹲起姿态是单兵常见的战术动作, 当穿戴者背负大载荷时, 负载的质量、体积、挂载方式及质量分布对穿戴者蹲起顺畅性及舒适性产生影响, 容易产生蹲起失效问题.研究发现, 产生这些问题的原因之一是因为在设计助力外骨骼驱动系统及控制系统时, 没有考虑负载特征对驱动特征的影响, 所以有必要研究负载特征与驱动特征的耦合关系, 为系统驱动控制的优化及驱动失效问题的解决提供理论基础.本文推导了多体系统动力学建模矩阵法, 建立了考虑负载特征的助力外骨骼动力学模型.通过人体机器多视觉运动捕捉测量实验及非线性拟合, 得到各关节运动曲线方程, 最后对助力外骨骼负载特征与关节驱动特征耦合效应进行研究.
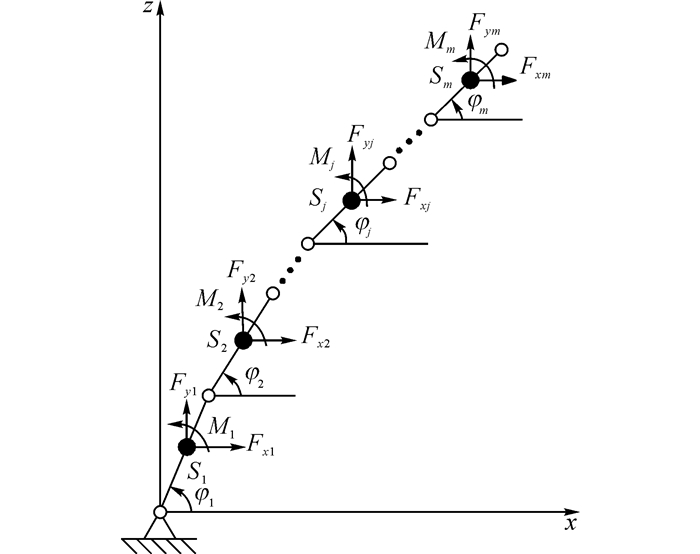
1 多体系统动力学建模矩阵法 1.1 多体系统描述为了方便公式的推导和问题的描述, 采用串联开链机构对多体系统进行描述, 如图 1所示.多体系统有m个杆件, n个广义坐标q1, q2, …, qn. Sj为第j个杆件的质心, 假设系统作用有m个外力和外力矩, 并且都作用于每个杆件的质心, Fxj、Fzj、Mj分别为第j个杆件的质心处受到的外部作用力及作用力矩, 第j个杆件的质心坐标xj、zj和角位移φj都表示为qi的函数, 其中j=1, 2, …, m；i=1, 2, …, n.
| $ \left. \begin{array}{l} {x_j} = {f_{xj}}\left( {{q_1},{q_2}, \cdots ,{q_n}} \right),\\ {z_j} = {f_{zj}}\left( {{q_1},{q_2}, \cdots ,{q_n}} \right),\\ {\varphi _j} = {f_{\varphi j}}\left( {{q_1},{q_2}, \cdots ,{q_n}} \right). \end{array} \right\} $ | (1) |
|
图 1 多体系统模型 Fig. 1 Multi-body system model |
对式(1) 进行求导, 得到第j个杆件质心速度及角速度：
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot x}_j}}\\ {{{\dot z}_j}}\\ {{{\dot \varphi }_j}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {f_{xj}^{\left( 1 \right)}}&{f_{xj}^{\left( 2 \right)}}& \cdots &{f_{xj}^{\left( n \right)}}\\ {f_{zj}^{\left( 1 \right)}}&{f_{zj}^{\left( 2 \right)}}& \cdots &{f_{zj}^{\left( n \right)}}\\ {f_{\varphi j}^{\left( 1 \right)}}&{f_{\varphi j}^{\left( 2 \right)}}& \cdots &{f_{\varphi j}^{\left( n \right)}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}\\ {{{\dot q}_2}}\\ \vdots \\ {{{\dot q}_n}} \end{array}} \right] = \mathit{\boldsymbol{J}}\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}\\ {{{\dot q}_2}}\\ \vdots \\ {{{\dot q}_n}} \end{array}} \right]. $ | (2) |
式中：J为雅可比矩阵；fkj(i)为偏类速度,
| $ f_{kj}^{\left( i \right)} = \frac{{\partial {f_{kj}}}}{{\partial {q_i}}} = \frac{{\partial {k_j}}}{{\partial {q_i}}},k = x,z,\varphi . $ | (3) |
每个杆的质量为mj, 则系统势能为
| $ {E_{\rm{p}}} = \sum\limits_{j = 1}^m {{m_j}g{z_j}} . $ | (4) |
式(4) 对广义坐标qi求偏导数, 可得
| $ \frac{{\partial {E_{\rm{p}}}}}{{\partial {q_i}}} = \sum\limits_{j = 1}^m {{m_j}g\frac{{\partial {z_j}}}{{\partial {q_i}}}} = \sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( i \right)}} . $ | (5) |
为了便于推导及后续计算, 假设系统受到m个外力和外力矩, 且都作用于对应杆的质心, 系统n个驱动关节受到驱动力矩τi的驱动, 则系统的广义力可以表示为
| $ \begin{array}{l} {Q_i} = {F_i} + {\tau _i} = \sum\limits_{j = 1}^m {\left( {{F_{xj}}\frac{{\partial x}}{{\partial {q_i}}} + {F_{zj}}\frac{{\partial {z_j}}}{{\partial {q_i}}} + {M_j}\frac{{\partial {\varphi _j}}}{{\partial {q_i}}}} \right) + {\tau _i}} = \\ \;\;\;\;\;\;\;\sum\limits_{j = 1}^m {\left( {{F_{xj}}f_{xj}^{\left( i \right)} + {F_{zj}}f_{zj}^{\left( i \right)} + {M_j}f_{\varphi j}^{\left( i \right)}} \right) + {\tau _i}} . \end{array} $ | (6) |
多体系统有n个广义坐标qi, 每个杆件的质量为mj, 绕质心的转动惯量为Jj, 则系统总动能为
| $ \begin{array}{l} {E_{\rm{k}}} = \frac{1}{2}\sum\limits_{j = 1}^m {\left\{ {{m_j}\left[ {{{\left( {\sum\limits_{i = 1}^n {f_{xj}^{\left( i \right)}{{\dot q}_i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {f_{zj}^{\left( i \right)}{{\dot q}_i}} } \right)}^2}} \right] + } \right.} \\ \;\;\;\left. {{J_j}{{\left( {\sum\limits_{i = 1}^n {f_{\varphi j}^{\left( i \right)}{{\dot q}_i}} } \right)}^2}} \right\} = \\ \;\;\;\frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}& \cdots &{{J_{1n}}}\\ {{J_{21}}}&{{J_{22}}}& \cdots &{{J_{2n}}}\\ \vdots & \vdots &{}& \vdots \\ {{J_{n1}}}&{{J_{n2}}}& \cdots &{{J_{nn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}\\ {{{\dot q}_2}}\\ \vdots \\ {{{\dot q}_n}} \end{array}} \right] = \\ \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}}. \end{array} $ | (7) |
式中：Jil为等效转动惯量, i=l=1, 2, …, n,
| $ {J_{il}} = \sum\limits_{j = 1}^m {\left[ {{m_j}\left( {f_{xj}^{\left( i \right)}f_{xj}^{\left( l \right)} + f_{zj}^{\left( i \right)}f_{zj}^{\left( l \right)}} \right) + {J_j}f_{\varphi j}^{\left( i \right)}f_{\varphi j}^{\left( l \right)}} \right]} . $ | (8) |
系统总动能对每个广义速度求偏导数, 可得
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_1}}}}\\ {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_2}}}}\\ \vdots \\ {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_n}}}} \end{array}} \right] = \frac{1}{2}\\ \left[ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0 \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}} + \left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}}\\ \left[ {\begin{array}{*{20}{c}} 0&1& \cdots &0 \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}} + \left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}}\\ \vdots \\ \left[ {\begin{array}{*{20}{c}} 0&0& \cdots &0 \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}} + \left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]\left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}& \cdots &{{{\dot q}_n}} \end{array}} \right]^{\rm{T}}} \end{array} \right] \\ = \left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}\\ {{{\dot q}_2}}\\ \vdots \\ {{{\dot q}_n}} \end{array}} \right]. $ | (9) |
对式(9) 求导, 可得
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_1}}}} \right)}\\ {\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_2}}}} \right)}\\ \vdots \\ {\frac{{\rm{d}}}{{{\rm{d}}n}}\left( {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_n}}}} \right)} \end{array}} \right] = \left[ {\mathop {{J_{il}}}\limits_{n \times n} } \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot q}_1}}\\ {{{\ddot q}_2}}\\ \vdots \\ {{{\ddot q}_n}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{11}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{12}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{1n}}}}{{\partial {q_n}}}}\\ {\frac{{\partial {J_{21}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{22}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{2n}}}}{{\partial {q_n}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{n1}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{n2}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{nn}}}}{{\partial {q_n}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot q_1^2}\\ {\dot q_2^2}\\ \vdots \\ {\dot q_n^2} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{11}}}}{{\partial {q_2}}} + \frac{{\partial {J_{12}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{11}}}}{{\partial {q_1}}} + \frac{{\partial {J_{13}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{1\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{1n}}}}{{\partial {q_{\left( {n - 1} \right)}}}}}\\ {\frac{{\partial {J_{21}}}}{{\partial {q_2}}} + \frac{{\partial {J_{22}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{21}}}}{{\partial {q_3}}} + \frac{{\partial {J_{23}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{2\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{2n}}}}{{\partial {q_{\left( {n - 1} \right)}}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{n1}}}}{{\partial {q_2}}} + \frac{{\partial {J_{n2}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{n1}}}}{{\partial {q_3}}} + \frac{{\partial {J_{n3}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{n\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{nn}}}}{{\partial {q_{\left( {n - 1} \right)}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}{{\dot q}_2}}\\ {{{\dot q}_1}{{\dot q}_3}}\\ \vdots \\ {{{\dot q}_{\left( {n - 1} \right)}}{{\dot q}_n}} \end{array}} \right]. $ | (10) |
系统总动能对每个广义坐标求偏导数, 可得
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {E_{\rm{k}}}}}{{\partial {q_1}}}}\\ {\frac{{\partial {E_{\rm{k}}}}}{{\partial {q_2}}}}\\ \vdots \\ {\frac{{\partial {E_{\rm{k}}}}}{{\partial {q_n}}}} \end{array}} \right] = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{11}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{22}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{nn}}}}{{\partial {q_1}}}}\\ {\frac{{\partial {J_{11}}}}{{\partial {q_2}}}}&{\frac{{\partial {J_{22}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{nn}}}}{{\partial {q_2}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{11}}}}{{\partial {q_n}}}}&{\frac{{\partial {J_{22}}}}{{\partial {q_n}}}}& \cdots &{\frac{{\partial {J_{nn}}}}{{\partial {q_n}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot q_1^2}\\ {\dot q_2^2}\\ \vdots \\ {\dot q_n^2} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{12}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{13}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{\left( {n - 1} \right)n}}}}{{\partial {q_1}}}}\\ {\frac{{\partial {J_{12}}}}{{\partial {q_2}}}}&{\frac{{\partial {J_{13}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{\left( {n - 1} \right)n}}}}{{\partial {q_2}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{12}}}}{{\partial {q_n}}}}&{\frac{{\partial {J_{13}}}}{{\partial {q_n}}}}& \cdots &{\frac{{\partial {J_{\left( {n - 1} \right)n}}}}{{\partial {q_n}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}{{\dot q}_2}}\\ {{{\dot q}_1}{{\dot q}_3}}\\ \vdots \\ {{{\dot q}_{\left( {n - 1} \right)}}{{\dot q}_n}} \end{array}} \right]. $ | (11) |
多体系统拉格朗日动力学方程的一般形式为
| $ {Q_i} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial {E_{\rm{k}}}}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial {E_{\rm{k}}}}}{{\partial {q_i}}} + \frac{{\partial {E_{\rm{p}}}}}{{\partial {q_i}}}. $ | (12) |
将式(5)、(6)、(10)、(11) 代入式(12), 可得多体系统拉格朗日动力学方程的矩阵表达形式：
| $ \begin{array}{l} \mathit{\boldsymbol{Q = \tau + F = }}\\ \left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}& \cdots &{{J_{1n}}}\\ {{J_{21}}}&{{J_{22}}}& \cdots &{{J_{2n}}}\\ \vdots & \vdots &{}& \vdots \\ {{J_{n1}}}&{{J_{n2}}}& \cdots &{{J_{nn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot q}_1}}\\ {{{\ddot q}_2}}\\ \vdots \\ {{{\ddot q}_n}} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{11}}}}{{\partial {q_1}}} - \frac{1}{2}\frac{{\partial {J_{11}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{12}}}}{{\partial {q_2}}} - \frac{1}{2}\frac{{\partial {J_{22}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{1n}}}}{{\partial {q_n}}} - \frac{1}{2}\frac{{\partial {J_{nn}}}}{{\partial {q_1}}}}\\ {\frac{{\partial {J_{21}}}}{{\partial {q_1}}} - \frac{1}{2}\frac{{\partial {J_{11}}}}{{\partial {q_2}}}}&{\frac{{\partial {J_{22}}}}{{\partial {q_2}}} - \frac{1}{2}\frac{{\partial {J_{22}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{2n}}}}{{\partial {q_n}}} - \frac{1}{2}\frac{{\partial {J_{nn}}}}{{\partial {q_2}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{n1}}}}{{\partial {q_1}}} - \frac{1}{2}\frac{{\partial {J_{11}}}}{{\partial {q_3}}}}&{\frac{{\partial {J_{n2}}}}{{\partial {q_2}}} - \frac{1}{2}\frac{{\partial {J_{22}}}}{{\partial {q_3}}}}& \cdots &{\frac{{\partial {J_{nn}}}}{{\partial {q_n}}} - \frac{1}{2}\frac{{\partial {J_{nn}}}}{{\partial {q_n}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot q_1^2}\\ {\dot q_2^2}\\ \vdots \\ {\dot q_n^2} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {J_{11}}}}{{\partial {q_2}}} + \frac{{\partial {J_{12}}}}{{\partial {q_1}}} - \frac{{\partial {J_{12}}}}{{\partial {q_1}}}}&{\frac{{\partial {J_{11}}}}{{\partial {q_1}}} + \frac{{\partial {J_{13}}}}{{\partial {q_1}}} - \frac{{\partial {J_{13}}}}{{\partial {q_1}}}}& \cdots &{\frac{{\partial {J_{1\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{1n}}}}{{\partial {q_{\left( {n - 1} \right)}}}} - \frac{{\partial {J_{\left( {n - 1} \right)\left( n \right)}}}}{{\partial {q_1}}}}\\ {\frac{{\partial {J_{21}}}}{{\partial {q_2}}} + \frac{{\partial {J_{22}}}}{{\partial {q_1}}} - \frac{{\partial {J_{12}}}}{{\partial {q_2}}}}&{\frac{{\partial {J_{21}}}}{{\partial {q_3}}} + \frac{{\partial {J_{23}}}}{{\partial {q_1}}} - \frac{{\partial {J_{13}}}}{{\partial {q_2}}}}& \cdots &{\frac{{\partial {J_{2\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{2n}}}}{{\partial {q_{\left( {n - 1} \right)}}}} - \frac{{\partial {J_{\left( {n - 1} \right)\left( n \right)}}}}{{\partial {q_2}}}}\\ \vdots & \vdots &{}& \vdots \\ {\frac{{\partial {J_{n1}}}}{{\partial {q_2}}} + \frac{{\partial {J_{n2}}}}{{\partial {q_1}}} - \frac{{\partial {J_{12}}}}{{\partial {q_n}}}}&{\frac{{\partial {J_{n1}}}}{{\partial {q_3}}} + \frac{{\partial {J_{n3}}}}{{\partial {q_1}}} - \frac{{\partial {J_{13}}}}{{\partial {q_n}}}}& \cdots &{\frac{{\partial {J_{n\left( {n - 1} \right)}}}}{{\partial {q_n}}} + \frac{{\partial {J_{nn}}}}{{\partial {q_{\left( {n - 1} \right)}}}} - - \frac{{\partial {J_{\left( {n - 1} \right)\left( n \right)}}}}{{\partial {q_n}}}} \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}{{\dot q}_2}}\\ {{{\dot q}_1}{{\dot q}_3}}\\ \vdots \\ {{{\dot q}_{\left( {n - 1} \right)}}{{\dot q}_n}} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( 1 \right)}} }\\ {\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( 2 \right)}} }\\ \vdots \\ {\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( n \right)}} } \end{array}} \right].\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(13) \end{array} $ |
将式(13) 改写为
| $ \mathit{\boldsymbol{\tau = A}}\left[ {\ddot q} \right] + \mathit{\boldsymbol{B}}\left[ {{{\dot q}^2}} \right] + \mathit{\boldsymbol{C}}\left[ {\dot q\dot q} \right] + \mathit{\boldsymbol{G}} - \mathit{\boldsymbol{F}}. $ | (14) |
式中：τ为关节驱动力矩矢量矩阵,
| $ \mathit{\boldsymbol{\tau = }}{\left[ {\begin{array}{*{20}{c}} {{\tau _1},}&{{\tau _2},}&{ \cdots ,}&{{\tau _n}} \end{array}} \right]^{\rm{T}}}; $ | (15) |
A为等效转动惯量n×n阶矩阵,
| $ \mathit{\boldsymbol{A = }}\left[ {{J_{il}}} \right]; $ | (16) |
B为离心力n×n阶矩阵,
| $ \mathit{\boldsymbol{B = }}\left[ {\frac{{\partial {J_{il}}}}{{\partial {q_l}}} - \frac{1}{2}\frac{{\partial {J_{ll}}}}{{\partial {q_i}}}} \right]; $ | (17) |
C为科里奥利力, 是n×n(n-1)/2阶矩阵,
| $ \mathit{\boldsymbol{C = }}\left[ {\frac{{\partial {J_{ir}}}}{{\partial {q_r}}} + \frac{{\partial {J_{is}}}}{{\partial {q_s}}} - \frac{{\partial {J_{rs}}}}{{\partial {q_i}}}} \right]; $ | (18) |
G为重力矢量矩阵,
| $ \mathit{\boldsymbol{G = }}{\left[ {\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( 1 \right)}} ,\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( 2 \right)}} , \cdots ,\sum\limits_{j = 1}^m {{m_j}gf_{zj}^{\left( n \right)}} } \right]^{\rm{T}}}; $ | (19) |
F为外力广义力矢量矩阵,
| $ \mathit{\boldsymbol{F = }}\left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^m {\left( {{F_{xj}}f_{xj}^{\left( 1 \right)} + {F_{zj}}f_{zj}^{\left( 1 \right)} + {M_j}f_{\varphi j}^{\left( 1 \right)}} \right)} }\\ {\sum\limits_{j = 1}^m {\left( {{F_{xj}}f_{xj}^{\left( 2 \right)} + {F_{zj}}f_{zj}^{\left( 2 \right)} + {M_j}f_{\varphi j}^{\left( 2 \right)}} \right)} }\\ \vdots \\ {\sum\limits_{j = 1}^m {\left( {{F_{xj}}f_{xj}^{\left( n \right)} + {F_{zj}}f_{zj}^{\left( n \right)} + {M_j}f_{\varphi j}^{\left( n \right)}} \right)} } \end{array}} \right]. $ | (20) |
一般情况下, 基于拉格朗日动力学方程分析动力学问题时, 首先需要求出系统总动能；然后对系统总动能的广义坐标及广义速度求偏导, 并且对系统总动能的广义速度的偏导数求导；最后将广义力及以上结果代入拉格朗日方程, 得到系统动力学方程.这种求解方法十分繁琐, 特别对于复杂多刚体动力学模型是一个巨大的挑战, 很容易出错, 不便于检查, 最后将动力学方程写成矩阵形式是很复杂的过程.
本文基于Lagrange动力学理论及矩阵理论, 推导出多刚体系统动力学建模矩阵法.根据这种方法, 只需要得到多刚体系统的雅可比矩阵及等效转动惯量矩阵, 并对等效转动惯量的每一个广义坐标求偏导数, 根据式(14)~(20) 可得动力学方程的矩阵表达形式.该方法简单高效, 模块化计算, 便于检查和编程计算, 并且能够直接得到矩阵形式.
2 助力外骨骼蹲起姿态动力学建模负载特征主要是指助力外骨骼背负重物的质量(负载质量)、重物质心与躯干质心之间的距离(负载位置)及重物质心和躯干质心连线与躯干的角度(负载姿态).如图 2所示为考虑负载特征的助力外骨骼蹲起姿态矢状面内多体系统动力学模型.假设在蹲起姿态运动过程中, 重物质心与躯干的相对位置不变, 由于蹲起过程中, 左、右边对称, 计算时只取左边结构建模.O1、O2、O3分别为踝关节、膝关节、髋关节, S1、S2、S3、S4分别为小腿、大腿、躯干、重物的质心, l1、l2、l3分别为小腿、大腿、躯干的长度, l4为负载位置, lS1、lS2、lS3分别为小腿质心、大腿质心、躯干质心到踝关节、膝关节、髋关节的长度, φ1、φ2、φ3分别为小腿、大腿、躯干与x轴的夹角, φ4为重物质心和躯干质心连线与x轴的夹角, θ为负载姿态, 其中φ4=φ3-θ.系统自由度为3, 选取踝关节角位移φ1、膝关节角位移φ2及髋关节角位移φ3为广义坐标q1、q2、q3, 即φ1=q1, φ2=q2, φ3=q3.由式(1)~(3), 可得
| $ \begin{array}{l} \mathit{\boldsymbol{J = }}\\ \left[ {\begin{array}{*{20}{c}} { - {l_{{\rm{S1}}}}\sin {q_1}}&0&0\\ {{l_{{\rm{S1}}}}\cos {q_1}}&0&0\\ 1&0&0\\ { - {l_1}\sin {q_1}}&{ - {l_{{\rm{S2}}}}\sin {q_2}}&0\\ {{l_1}\cos {q_1}}&{{l_{{\rm{S2}}}}\cos {q_1}}&0\\ 0&1&0\\ { - {l_1}\sin {q_1}}&{ - {l_{\rm{2}}}\sin {q_2}}&{ - {l_{{\rm{S3}}}}\sin {q_3}}\\ {{l_1}\cos {q_1}}&{{l_2}\cos {q_2}}&{{l_{{\rm{S3}}}}\cos {q_3}}\\ 0&0&1\\ { - {l_1}\sin {q_1}}&{ - {l_{\rm{2}}}\sin {q_2}}&{ - {l_{{\rm{S3}}}}\sin {q_3} - {l_4}\sin \left( {{q_3} - \theta } \right)}\\ {{l_1}\cos {q_1}}&{{l_2}\cos {q_2}}&{{l_{{\rm{S3}}}}\cos {q_3} - {l_4}\cos \left( {{q_3} - \theta } \right)}\\ 0&0&1 \end{array}} \right]. \end{array} $ | (21) |
|
图 2 考虑负载特征的助力外骨骼力学模型 Fig. 2 Dynamic model of powered exoskeleton in consideration of load characteristics |
设小腿、大腿及躯干(包括背架、电源、电气设备、电池及髋部结构)分别为m1、m2、m3, 负载质量为m4, 绕质心的转动惯量为J1、J2、J3、J4, 其中J4为负载质心S4绕S3的转动惯量, 每根杆的质心到对应关节的长度lSj(j=1, 2, 3) 为杆长lj的一半, 则每根杆绕质心的转动惯量为
| $ \left. \begin{array}{l} {J_j} = \frac{1}{{12}}{m_j}l_j^2,j = 1,2,3;\\ {J_4} = {m_4}l_4^2. \end{array} \right\} $ | (22) |
由式(8)、(16)、(21), 可得
| $ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} {\left( {\frac{1}{3}{m_1} + {m_2} + {m_3} + {m_4}} \right)l_1^2}&{\left( {\frac{1}{2}{m_2} + {m_3} + {m_4}} \right){l_1}{l_2}\cos \left( {{q_1} - {q_2}} \right)}&{\frac{1}{2}\left( {{m_3} + {m_4}} \right){l_1}{l_3}\cos \left( {{q_1} - {q_3}} \right) + {m_4}{l_1}{l_4}\cos \left( {{q_1} - {q_3} + \theta } \right)}\\ {}&{\left( {\frac{1}{3}{m_2} + {m_3} + {m_4}} \right)l_2^2}&{\frac{1}{2}\left( {{m_3} + {m_4}} \right){l_2}{l_3}\cos \left( {{q_2} - {q_3}} \right) + {m_4}{l_2}{l_4}\cos \left( {{q_2} - {q_3} + \theta } \right)}\\ {{\rm{symmetry}}}&{}&{\left( {\frac{1}{3}{m_3} + \frac{1}{4}{m_4}} \right)l_3^2 + \left( {2{l_4} + {l_3}\cos \theta } \right){m_4}{l_4}} \end{array}} \right].\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(23) $ |
式中：A为对称矩阵.由式(17) 可得,
| $ \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} 0&{\left( {\frac{1}{2}{m_2} + {m_3} + {m_4}} \right){l_1}{l_2}\sin \left( {{q_1} - {q_2}} \right)}&{\frac{1}{2}\left( {{m_3} + {m_4}} \right){l_1}{l_3}\sin \left( {{q_1} - {q_3}} \right) + {m_4}{l_1}{l_4}\sin \left( {{q_1} - {q_3} + \theta } \right)}\\ {}&0&{\frac{1}{2}\left( {{m_3} + {m_4}} \right){l_2}{l_3}\sin \left( {{q_2} - {q_3}} \right) + {m_4}{l_2}{l_4}\sin \left( {{q_2} - {q_3} + \theta } \right)}\\ {{\rm{antisymmetry}}}&{}&0 \end{array}} \right].\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(24) $ |
式中：B为反对称矩阵.由式(18) 得到系统科里奥利力矩阵为零.由式(19) 可得
| $ \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {\left( {\frac{1}{2}{m_1} + {m_2} + {m_3} + {m_4}} \right)g{l_1}\cos {q_1}}\\ {\left( {\frac{1}{2}{m_2} + {m_3} + {m_4}} \right)g{l_2}\cos {q_2}}\\ {\frac{1}{2}\left( {{m_3} + {m_4}} \right)g{l_3}\cos {q_3} + {m_4}g{l_4}\cos \left( {{q_3} - \theta } \right)} \end{array}} \right]. $ | (25) |
助力外骨骼在蹲起过程中, 假设人体与外骨骼之间没有相互作用力, 外力广义力矢量矩阵式(20) 为零.由式(14)、(23)~(25) 及以上分析可得考虑负载特征变化的助力外骨骼蹲起姿态多体系统3个关节驱动力矩动力学方程：
| $ \mathit{\boldsymbol{\tau = A}}\left[ {\ddot q} \right] + \mathit{\boldsymbol{B}}\left[ {{{\dot q}^2}} \right] + \mathit{\boldsymbol{G}}. $ | (26) |
式中：τ为踝关节关节驱动力矩τ1、膝关节驱动力矩τ2及髋关节驱动力矩τ3.助力外骨骼蹲起姿态驱动关节驱动功率为
| $ {P_i} = \left| {{\tau _i}{{\dot q}_i}} \right|;i = 1,2,3. $ | (27) |
如图 3所示为人体蹲起姿态数据测量试验.实验者负重为10 kg, 该实验进行3次测量, 每次测量实验蹲起时间由实验者自行决定, 如表 1所示.表中, cl1、cl2及cl3分别为第1次、第2次及第3次测量.实验测量设备为一套六相机Qualisys光学运动捕捉系统, 该实验测量了人体头部、肩部、胸部、髋关节、膝关节、踝关节、脚掌、脚后跟和脚尖共23个反射标记点三维坐标数据, 采样频率为200 Hz.
|
图 3 蹲起姿态数据测量实验 Fig. 3 Data measurement experiment in squat posture |
|
表 1 蹲起时间 Table 1 Squat time |
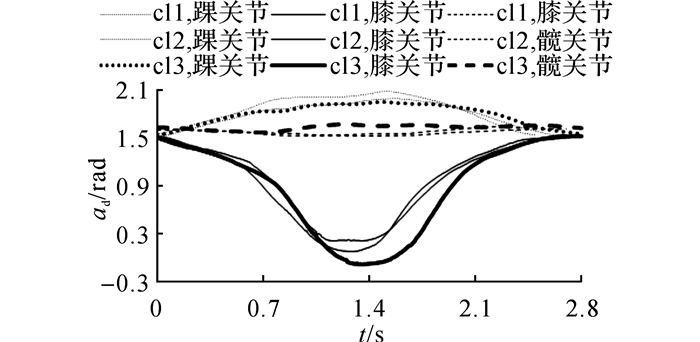
研究发现, 蹲起姿态中, 人体在额状面内的摆动幅度小, 运动主要发生在矢状面内且左、右运动状态很相似.研究各关节运动特征时, 只需选取矢状面内的左边肢体坐标计算.选取踝关节、膝关节、髋关节及肩部矢状面内的测量值, 通过计算得到踝关节角位移、膝关节角位移及髋关节角位移曲线, 如图 4所示.图中，ad为关节角位移.
|
图 4 关节角位移曲线 Fig. 4 Joint angular displacement curves |
为了得到各关节角位移运动方程, 选择傅里叶级数作为基函数, 采用非线性最小二乘法对各关节测量曲线进行非线性拟合, 得到踝关节、膝关节及髋关节角位移拟合方程：
| $ {\varphi _{{\rm{cl}}i}} = {a_0}/2 + \sum\limits_{w = 1}^n {\left( {{a_w}\cos \left( {w\omega t} \right) + {b_w}\sin \left( {w\omega t} \right)} \right)} . $ | (28) |
式中：i=1, 2, 3分别为踝关节、膝关节、髋关节, n为拟合阶次, ω为角频率, a0、aw、bw为常系数.对式(28) 求一、二阶导, 分别得到关节角速度及角加速度及角加速度如下：
| $ \left. \begin{array}{l} {{\dot \varphi }_{{\rm{cl}}i}} = \omega \sum\limits_{w = 1}^n {w\left( {{b_w}\cos \left( {w\omega t} \right) - {a_w}\sin \left( {w\omega t} \right)} \right)} ,\\ {{\ddot \varphi }_{{\rm{cl}}i}} = {\omega ^2}\sum\limits_{w = 1}^n {{w^2}\left( {{a_w}\cos \left( {w\omega t} \right) - {b_w}\sin \left( {w\omega t} \right)} \right)} . \end{array} \right\} $ | (29) |
|
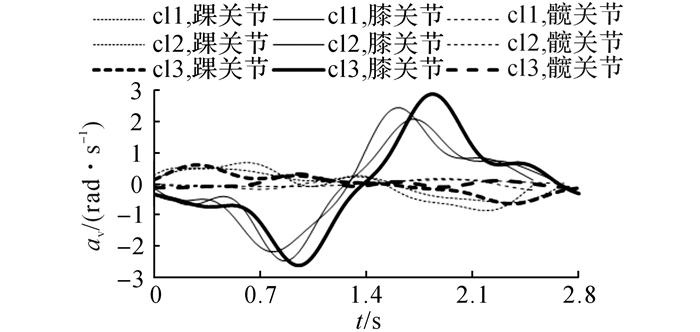
图 5 关节角速度曲线 Fig. 5 Joint angular velocity curves |
|
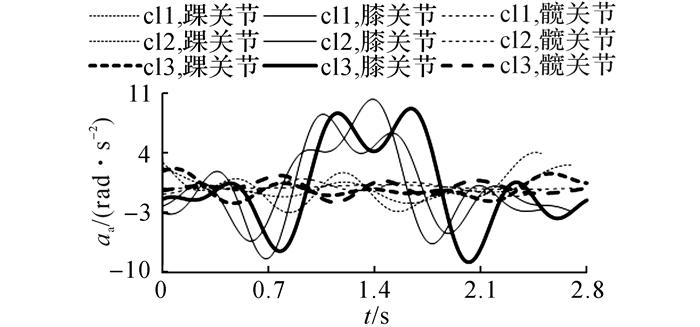
图 6 关节角加速度曲线 Fig. 6 Joint angular acceleration curves |
助力外骨骼系统结构的基本参数如下：m1=0.6 kg, m2=0.9 kg, m3=8 kg；l1=0.364 m, l2=0.466 m, l3=0.46 m, 蹲起时间t=2.7 s, g=9.8 m/s2.因为助力外骨骼与穿戴者的运动形式相同, 助力外骨骼的角位移如式(28) 所示, 角速度av及角加速度aa分别如图 5、6所示.
为了方便描述, 定义kxy为负载特征对各关节驱动特征的影响因子, 含义为3次测量试验的各工况各关节驱动特征最大值对负载特征值变化率的平均值, 其中x=1, 2, …, 6对应6种工况, y=1, 2, 3对应踝关节、膝关节及髋关节.
4.1 计算工况为了满足实际作战需求, 穿戴者需要背负不同质量、不同体积、不同挂载方式及不同质量分布的重物.这些情况影响助力外骨骼关节驱动特征, 产生驱动失效问题, 导致蹲起过程不顺畅, 影响穿戴者的舒适性, 容易产生穿戴疲劳.需要研究助力外骨骼负载特征与关节驱动特征之间的耦合关系.
在矢状面内, 穿戴者背负不同的重物可以用负载质量m4、负载位置l4和负载姿态θ来完全描述, 采用控制变量法, 分别讨论m4、l4和θ对关节驱动力矩及驱动功率的影响.将负载特征与驱动特征耦合效应分为6种工况进行研究, 如表 2所示.助力外骨骼实验样机的重物由6块钢板组成, 并挂在背架不同悬挂点上, 每块钢板的质量为10 kg, 厚度为0.045 m.只取矢状面内左边结构进行计算, 所以m4∈[0, 30], l4∈[0, 0.27], θ∈[0, π], 而定量取值随意.
|
|
表 2 负载特征与驱动特征耦合效应的6种计算工况 Table 2 Six kinds of calculation working conditions for coupling effect between load characteristics and driving characteristics |
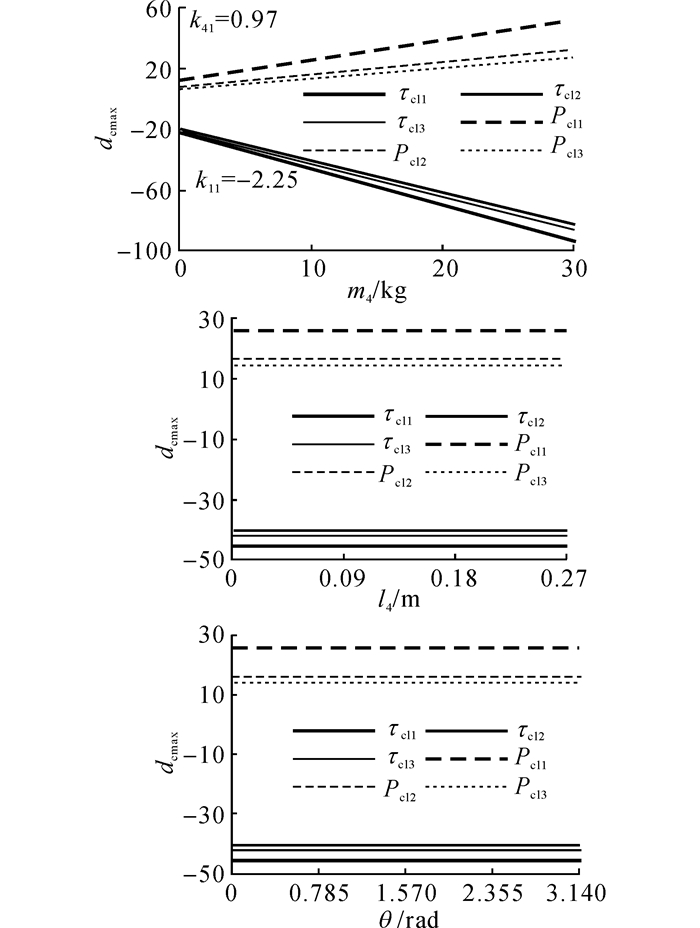
如图 7所示为踝关节驱动特征最大值dcmax随负载特征的变化曲线.图中, τcl1、τcl2及τcl3分别为每次测量实验的关节驱动力矩最大值, Pcl1、Pcl2及Pcl3分别为每次测量实验的关节驱动功率最大值.随着负载质量的变化, 踝关节的驱动力矩及驱动功率最大值呈线性变化, 所以负载质量对踝关节的驱动力矩及驱动功率都有影响, 影响因子分别为-2.25及0.97, 影响因子较大；负载位置及负载姿态对踝关节的驱动特征没有影响.
|
图 7 踝关节驱动特征最大值随负载特征的变化曲线 Fig. 7 Curves of ankle driving characteristics maximum with load characteristics variation |
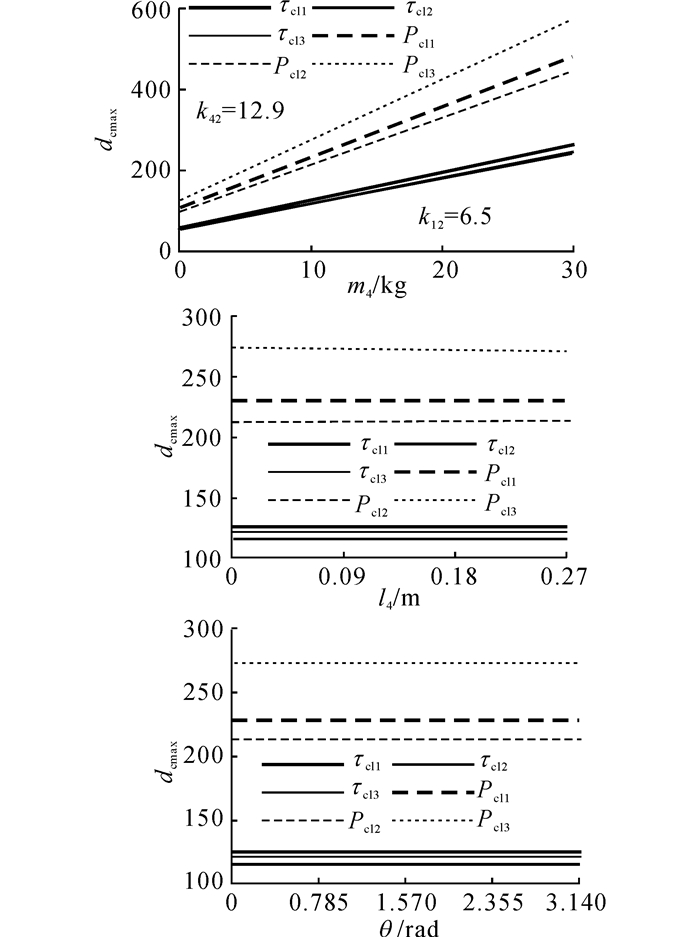
如图 8所示为膝关节驱动特征最大值随负载特征的变化曲线.随着负载质量的变化, 膝关节的驱动力矩及驱动功率最大值呈线性变化, 所以负载质量对膝关节的驱动力矩及驱动功率都有影响, 影响因子分别为6.5及12.9, 影响因子较大；负载位置及负载姿态对膝关节的驱动特征没有影响.
|
图 8 膝关节驱动特征最大值随负载特征的变化曲线 Fig. 8 Curves of knee driving characteristics maximum with load characteristics variation |
由以上分析可知, 负载质量与踝关节及膝关节驱动特征为线性强耦合, 负载位置及负载姿态与踝关节及膝关节驱动特征无耦合效应.
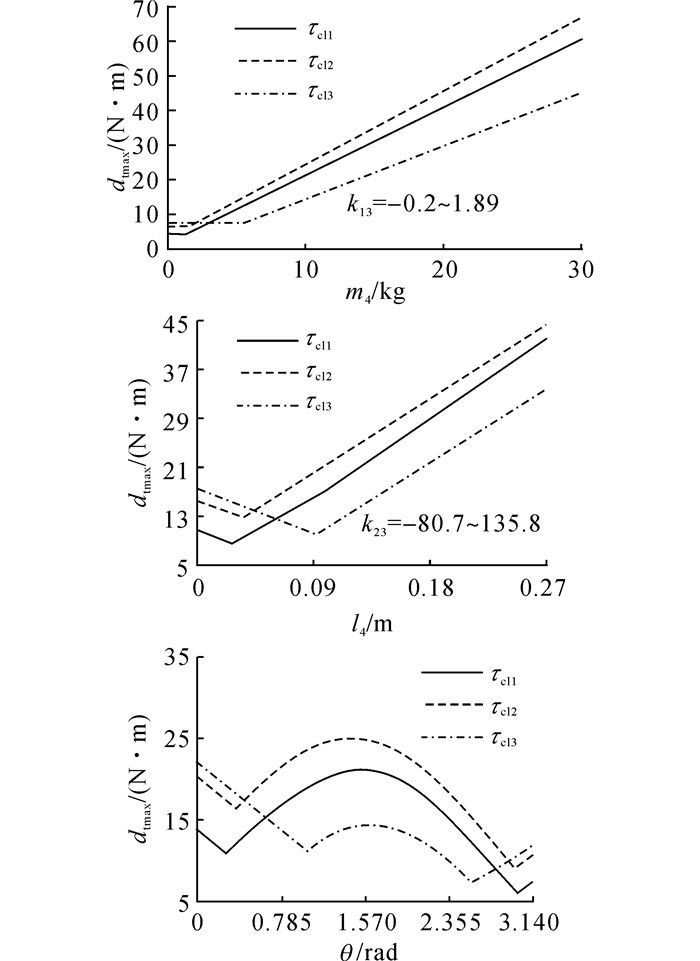
4.3 负载特征对髋关节驱动特征的影响负载特征变化对髋关节驱动特征的影响较复杂, 如图 9所示为髋关节驱动力矩最大值dtmax随负载特征的变化曲线.随着负载特征的变化, 髋关节的驱动力矩最大值呈分段线性及非线性变化, 所以负载特征对髋关节的驱动力矩都有影响.负载质量对髋关节驱动力矩的影响因子从前段的-0.2到后段的1.89, 影响因子较小；负载位置对髋关节驱动力矩的影响因子从前段的-80.7到后段的135.8, 影响因子较大；两者都为分段线性影响, 负载姿态对髋关节驱动力矩的影响较复杂, 为分段非线性影响.
|
图 9 髋关节驱动力矩最大值随负载特征的变化曲线 Fig. 9 Curves of hip driving torque maximum with load characteristics variation |
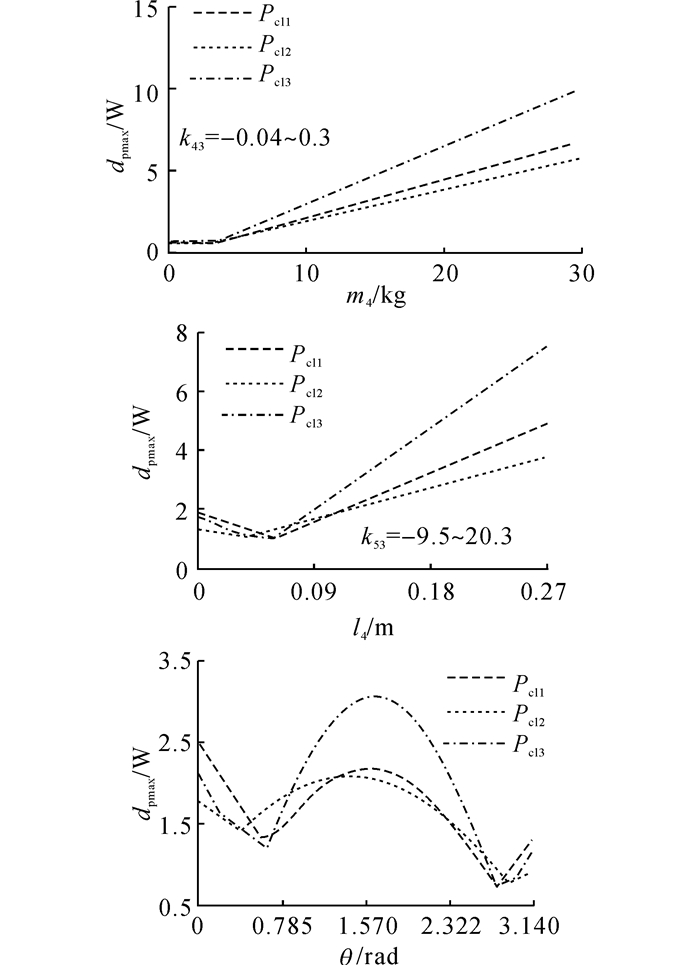
如图 10所示为髋关节驱动功率最大值随负载特征的变化曲线, 影响情况与图 9相似.负载质量对髋关节驱动功率的影响因子从前段的-0.04变化为后段的0.3, 影响因子较小；负载位置对髋关节驱动功率的影响因子从前段的-9.5到后段的20.3, 影响因子较大；两者都为分段线性影响, 负载姿态对髋关节驱动功率的影响较复杂, 为分段非线性影响.
|
图 10 髋关节驱动功率最大值随负载特征变化曲线 Fig. 10 Curves of hip driving power maximum with load characteristics variation |
通过以上分析可知, 负载质量与髋关节驱动特征为分段线性弱耦合, 负载位置与髋关节驱动特征为分段线性强耦合, 负载姿态与髋关节驱动特征为分段非线性耦合, 耦合效应的强弱需要进一步讨论.
4.4 负载特征对各关节驱动特征最大值出现时刻的影响如表 3所示为不同测量实验时, 负载特征对各关节驱动特征最大值出现时刻的影响情况.表中, Tyz为对应关节的驱动特征最大值出现的时刻, 其中y=1, 2, 3对应踝关节、膝关节及髋关节, z=1, 2对应驱动力矩最大值及驱动功率最大值.由表 3可知, 3次测量试验中, 随着负载特征的变化, 踝关节T11平均出现在1.38 s处, T12平均出现在1.14 s处, 膝关节T21平均出现在1.37 s处, T22平均出现在1.41 s处, 所以踝关节及膝关节驱动特征最大值出现的时刻不随负载特征的变化而变化, 只与测量试验的运动形式有关；髋关节T31平均出现时刻由1.37 s漂移到1.52 s, T32平均出现时刻由1.12 s漂移到1.5 s, 所以髋关节驱动特征最大值出现的时刻不仅与测量实验的运动形式有关, 还与负载特征有关, 这表明负载特征能影响髋关节驱动特征时变规律, 不能影响踝关节及膝关节驱动特征的时变规律.
|
|
表 3 关节驱动特征最大值的时刻值 Table 3 Time value of joint driving characteristics maximum |
综合以上所有分析可知, 负载质量与踝关节及膝关节驱动特征为线性强耦合, 与髋关节驱动特征为分段线性弱耦合；负载位置与髋关节驱动特征为分段线性强耦合, 负载姿态与髋关节驱动特征为分段非线性耦合, 而负载位置及负载姿态与踝关节及膝关节驱动特征无耦合效应.这表明负载质量容易造成踝关节及膝关节驱动失效, 负载位置容易造成髋关节驱动失效.另外, 负载特征变化使髋关节驱动特征最大值出现时刻产生漂移, 改变了髋关节驱动特征的时变规律.由于穿戴者在一定的环境中都有相对固定的蹲起方式, 穿戴者对髋关节驱动特征最大值出现的时刻有习惯性预判.当负载特征变化时, 髋关节驱动特征最大值出现的时刻发生变化, 若穿戴者没有意识调整, 则容易造成蹲起不稳定、不顺畅, 产生蹲起失效问题.
5 结论(1) 负载特征影响髋关节驱动特征的时变规律, 但不影响踝关节和膝关节驱动特征的时变规律.
(2) 负载质量与踝关节及膝关节驱动特征为线性强耦合, 与髋关节驱动特征为分段线性弱耦合.
(3) 负载位置与髋关节驱动特征为分段线性强耦合, 负载姿态与髋关节驱动特征为分段非线性耦合, 负载位置及负载姿态与踝关节及膝关节驱动特征无耦合效应.
下一步工作需要研究整体模型额状面内负载特征变化对关节驱动特征的影响, 有必要研究人-机-负载三者耦合对驱动特征的影响.
参考文献
| [1] | ZOSS A B, KAZEROONI H, CHU A. Biomechanical design of the Berkeley lower extremity exoskeleton (BLEEX)[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(2): 128–138. DOI:10.1109/TMECH.2006.871087 |
| [2] | KAZEROONI H. Hybrid control of the Berkeley lower extremity exoskeleton (BLEEX)[J]. The International Journal of Robotics Research, 2006, 25(5/6): 561–573. |
| [3] | ZOSS A, KAZEROONI H. Design of an electrically actuated lower extremity exoskeleton[J]. AdvancedRobotics, 2006, 20(9): 967–988. |
| [4] | ONEN U, BOTSALI F M, KALYONCU M, et al. Design and actuator selection of a lower extremity exoskeleton[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 623–632. DOI:10.1109/TMECH.2013.2250295 |
| [5] | DOLLAR A M, HERR H. Lower extremity exoskeletons and active orthoses: challenges and state-of-the-art[J]. IEEE Transactions on Robotics, 2008, 24(1): 144–158. DOI:10.1109/TRO.2008.915453 |
| [6] | HERR H. Exoskeletons and orthoses: classification, design challenges and future directions[J]. Journal of NeuroEngineering Rehabilitation, 2009, 6(21): 1–9. |
| [7] | GHAN J, STEGER R, KAZEROONI H. Control and system identification for the Berkeley lower extremity exoskeleton (BLEEX)[J]. Advanced Robotics, 2006, 20(9): 989–1014. DOI:10.1163/156855306778394012 |
| [8] | KAZEROONI H. Human augmentation and exoskeleton systems in Berkeley[J]. International Journal ofHumanoid Robotics, 2007, 4(3): 575–605. DOI:10.1142/S0219843607001187 |
| [9] | KAZEROONI H, STEGER R. The Berkeley lowerextremity exoskeleton[J]. Journal of Dynamic Systems, Measurement, and Control, 2006, 128(1): 14–25. DOI:10.1115/1.2168164 |
| [10] |
贾山, 王兴松, 路新亮, 等. 基于踝关节处人机位姿误差的外骨骼摆动腿控制[J].
机器人, 2015, 37(04): 403–414.
JIA Shan, WANG Xing-song, LU Xin-liang, et al. Control of the exoskeleton's swing leg based on the human-machine posture error at ankle joint[J]. Robot, 2015, 37(04): 403–414. |
| [11] |
贾山, 韩亚丽, 路新亮, 等. 基于人体特殊步态分析的下肢外骨骼机构设计[J].
机器人, 2014, 36(04): 392–401.
JIA Shan, HAN Ya-li, LU Xin-liang, et al. Design of lower exoskeleton based on analysis on special human gaits[J]. Robot, 2014, 36(04): 392–401. |
| [12] |
韩亚丽, 贾山, 王兴松. 基于人体生物力学的低功耗踝关节假肢的设计与仿真[J].
机器人, 2013, 35(03): 276–282.
HAN Ya-li, JIA Shan, WANG Xing-song. Design and simulation of an ankle prosthesis with lower power based on human biomechanics[J]. Robot, 2013, 35(03): 276–282. |
| [13] | OTTEN A, VOORT C, STIENEN A, et al. LIMPACT: a hydraulically powered self-aligning upper limb exoskeleton[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2285–2298. DOI:10.1109/TMECH.2014.2375272 |
| [14] | ZANOTTO D, AKIYAMA Y, STEGALL P, et al. Knee joint misalignment in exoskeletons for the lower extremities: effects on user's gait[J]. IEEE Transactions on Robotics, 2015, 31(4): 978–987. DOI:10.1109/TRO.2015.2450414 |
| [15] |
杨巍, 张秀峰, 杨灿军, 等. 基于人机5杆模型的下肢外骨骼系统设计[J].
浙江大学学报:工学版, 2014(03): 430–435.
YANG Wei, ZHANG Xiu-feng, YANG Can-jun, et al. Design of a lower extremity exoskeleton based on5-bar human machine model[J]. Journal of Zhejiang University: Engineering Science, 2014(03): 430–435. |
| [16] | GREGORCZYK K N, HASSELQUIST L, SCHIFFMAN J M, et al. Effects of a lower-body exoskeleton device on metabolic cost and gait biomechanics during load carriage[J]. Ergonomics, 2010, 53(10): 1263–1275. DOI:10.1080/00140139.2010.512982 |
| [17] | LEE M, ROAN M, SMITH B. An application of principal compo nent analysis for lower body kinematics between loaded and unloaded walking[J]. Journal of Biomechanics, 2009, 42(14): 2226–2230. DOI:10.1016/j.jbiomech.2009.06.052 |
| [18] | MAJUMDAR D, PAL M S, PRAMANIK A, et al. Kinetic changes in gait during low magnitude military load carriage[J]. Ergonomics, 2013, 56(12): 1917–1927. DOI:10.1080/00140139.2013.835871 |
| [19] | SCHIFFMAN J M, GREGORCZYK K N, BENSEL C K, et al. The effects of a lower body exoskeleton load carriage assistive device on limits of stability and postural sway[J]. Ergonomics, 2008, 51(10): 1515–1529. DOI:10.1080/00140130802248084 |
| [20] | LAWRENCE M A, CARLSON L A. Effects of an unstable load on force and muscle activation during a parallel back squat[J]. Journal of Strength and Conditioning Research, 2015, 29(10): 2949–2953. DOI:10.1519/JSC.0000000000000955 |
| [21] | SAHLI S, REBAI H, ELLEUCH M H, et al. Tibiofemoral joint kinetics during squatting with increasing external load[J]. Journal Sport Rehabilitation, 2008, 17(3): 300–315. DOI:10.1123/jsr.17.3.300 |
| [22] | COTTER J A, CHAUDHARI A M, JAMISON S T, et al. Knee joint kinetics in relation to commonly prescribed squat loads and depths[J]. Journal of Strength and Conditioning Research, 2013, 27(7): 1765–1774. DOI:10.1519/JSC.0b013e3182773319 |