高速列车运营速度的不断提高会引起列车周围的气流加速, 流场结构改变显著.位于列车顶部且作为高速列车动力来源重要组成部分的受电弓的周围流场流速剧增且更加复杂, 气流不仅直接影响列车减阻降噪, 而且会引起受电弓产生涡激振动, 进一步恶化弓网的受流质量^[1].

国内外学者利用实车试验、风洞试验、数值模拟等方法对受电弓的空气动力学、噪声、弓网动力学以及振动响应方面进行了大量研究^[2].Ikeda等^[3]描述了在低噪声喇叭的轴线上周期性的布置孔可以减少气动噪声, 并将其应用在受电弓上, 试验证明这种多孔圆柱有效抑制了受电弓噪声.Lee等^[4-5]对矩形和流线型的1/4缩比弓头模型进行风洞试验, 对比分析了2种外形下的受电弓气动性能及构件对总阻力和总升力的贡献, 研究了弓头形状改变后的尾流.Manabe等^[6]通过受电弓实验可知, 受电弓噪声与车速的六次方呈正比, 弓头和斜杆是噪声的主要来源, 并发现合适的不等径圆柱和在弓头截面上加缝隙可以有效地降低噪声.Ikeda等^[7]设计了一种新型弓头外形, 可以明显地改变受电弓压力分布, 风洞试验证明该新型弓头的空气动力学性能良好.Lee等^[8]利用风洞试验和实车试验测试了不同车速下受电弓气动力和时速300 km/h实车试验中的弓网接触力, 比较了受电弓在风洞试验和实车试验中的弓网接触力, 分析了受电弓的空气动力学特性.Yi等^[9]采用亚格子-玻尔兹曼方法, 分析简单平头受电弓模型噪声产生机理；研究方形和圆形截面形状的弓头气动噪声, 可知由气流分离伴随产生的涡脱落引起的噪声, 提出并验证了一种受电弓的降噪设计.Shi等^[10]结合流场和声场, 分析300 km/h车速的列车气动噪声, 得知受电弓噪声是由涡旋脱落引起的, 单臂受电弓噪声源主要集中在弓头、连接部位、基座等区域, 受电弓气动噪声主要由低频和中频构成.Pombo等^[11]研究风载荷和轨道激扰对高速列车上多个受电弓与接触网受电弓相互作用的影响.

张弘等^[12-15]利用风洞试验对受电弓气动力进行初步研究, 得到受电弓气动力随车速的变化规律.赵萌等^[16]研究横风下受电弓气动力, 得到受电弓气动力及力矩随侧风速度及角度呈非线性变化的规律.李瑞平等^[17]通过对受电弓气动抬升力的计算分析, 得到受电弓各部件的传递系数, 从而确定了弓头升力对受电弓整体升力的贡献量最大.郭迪龙等^[18]利用分离涡数值模拟方法, 对受电弓非定常气动性能进行研究, 得到了明线上受电弓弓头气动力的幅频特性.

据文献[9, 10, 12]可知, 导流装置对受电弓噪声有明显的改善效果, 但对受电弓非定常气动性能的影响相对较少涉及.本文采用延时分离涡方法(DDES)对安装无和翼板式、小浴盆式以及大浴盆式三种导流装置的列车非定常气动特性进行模拟研究, 对比分析受电弓各构件非定常的阻力和升力及波动特性, 确定一种有效改善受电弓气动力及波动的导流装置形式.

Spalart等在1997年提出分离涡模拟(detached eddy simulation, DES), 此后于2006年说明模型应力损失的问题时提出了DDES, 主体思想是延迟了DES方法进入LES(large eddy simulation)的区域, 尽量保证边界层内不会进入LES.基于该方法可以大大地减少计算时间和网格数量.对于LES区域的亚格子应力模型, 采用标准Smagorinsky模型处理^[19].

在数值计算中, 来流风速v=60 m/s, 马赫数小于0.3, 可以忽略空气压缩性.将模型列车高度H视为特征长度, 列车周围流场处于强湍流状态.采用基于S-A湍流模型的DDES方法, 可以很好地求解整个流场.

计算软件采用商业软件Fluent, 在国家超算广州中心的天河2号超级计算机上, 采用5×24个CPU进行并行计算.为了使计算较快收敛和保证结果精度等, 将定常计算获得的流场作为非定常计算的初始流场, 采用PISO方法求解质量守恒方程.对流项采用一阶迎风格式离散, 扩散项采用中心差分格式离散, 时间采用二阶隐式推进.根据文献[2]可知, 将Courant Number设置为1, 根据时间步长计算公式可知, Δt=Δ/v, v_max≥1.5v, 其中Δ为最小网格尺寸, Δt=0.5×10^-4 s.定常计算采用Realizable κ-ε湍流模型, 速度-压力耦合采用PISO算法, 对流项采用一阶迎风格式离散, 扩散项采用QUICK格式离散.

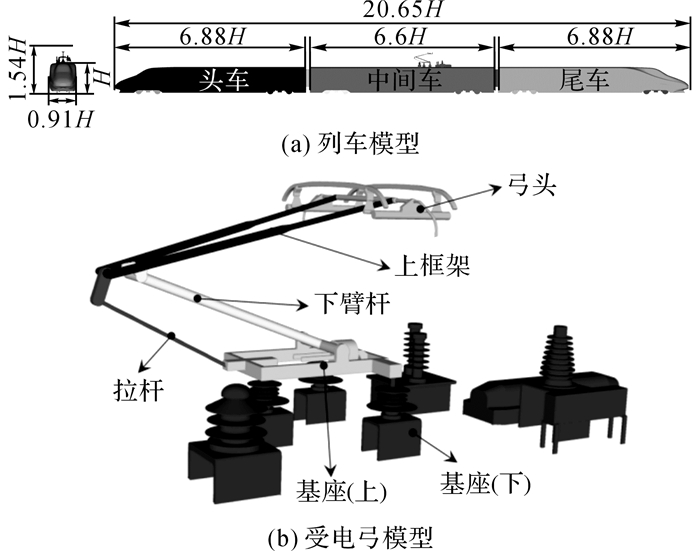
在模拟计算中, 采用头车(6.88 H)+中间车(6.6 H)+尾车(6.88 H)3车编组、缩比为1:8的高速列车作为计算模型, 车长为20.65 H, 其中H为车高, 并作为特征长度.受电弓模型采用DSA250型动车组受电弓, 且位于中间车, 列车及受电弓模型如图 1所示.列车和受电弓模型表面均进行了必要且合理的简化.

图 1

图 1 列车及受电弓模型 Fig. 1 Model of train and pantograph

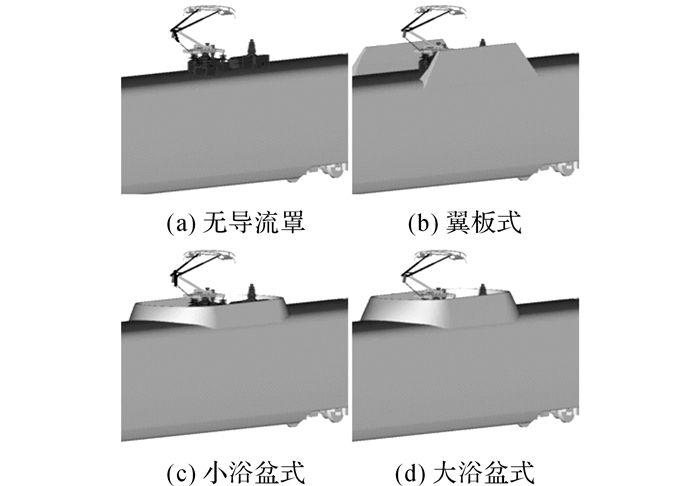
该研究的导流装置形式有3种：翼板式、小浴盆式和大浴盆式, 如图 2所示.

图 2

图 2 受电弓周围导流设备 Fig. 2 Diversion equipment around pantograph

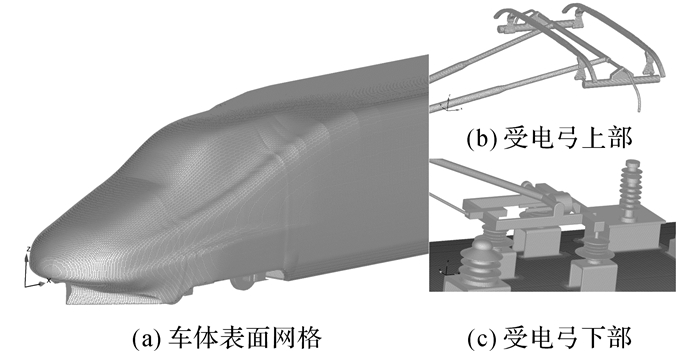
根据文献[20]的网格划分方法, 对流线型车体、导流装置和受电弓等主要关心的区域进行网格加密, 远离列车区域对受电弓气动力及周围流场结构的影响有限, 故设置相对较稀疏.由于需要准确地模拟附面层、扑捉到导流装置和受电弓处流场结构的发展以及细小漩涡的发展和脱落, 车体壁面第一层网格小于0.001 m.采用自适应网格技术, 保证物面第一层网格y+满足湍流模型的要求, 空间体网格3 000万以上, 列车及受电弓表面网格如图 3所示.

图 3

图 3 列车及受电弓表面网格 Fig. 3 Grid on surface of train and pantograph

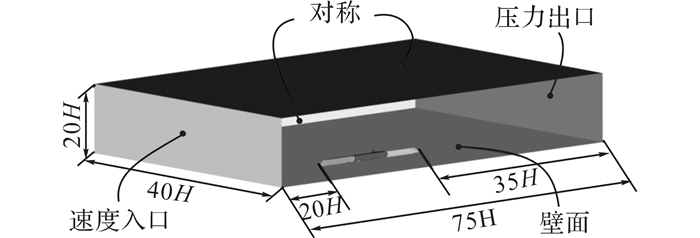
为了保证流场充分发展, 避免边界对列车周围流场结构的影响.计算域X方向长75H, Y方向宽为40H, Z方向高为20H.为了避免速度入口边界的影响, 列车头部鼻尖点距入口边界20H；为了避免出口边界条件对列车流场及尾涡变化的影响, 尾涡区域长35 H.列车计算区域如图 4所示.

图 4

图 4 列车计算区域示意图 Fig. 4 Train numerical computational domain

对计算域的边界进行设置, 以便获得唯一解, 计算流域的边界设置如图 4所示.列车表面给定无滑移壁面边界条件；流域前端面为速度入口边界条件, 速度设置如下：X方向速度分量为列车运行速度v, Y方向速度分量和Z方向速度分量均为0.顶面及流域两侧面采用对称边界条件, 后端面设置为压力出口边界条件, 相对压强P_out=0 Pa.地面给定无滑移固壁边界条件.在定常计算时, 车体和地面近壁面区域流场采用标准壁面函数控制模拟.

为了便于分析, 定义各气动力系数系数如下.

C_d=D/(0.5ρv²S),

C_l=L/(0.5ρv²S).

式中：ρ=1.225 kg/m³；v为来流速度；S为参考面积, 此处为模型列车中部等截面区域, 由于计算列车模型为1:8缩比模型, 取S=0.175 m²；D为阻力；L为升力；C_d为侧向力系数；C_l为升力系数.

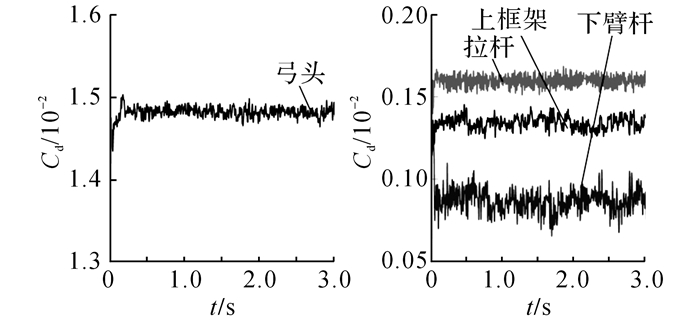
如图 5所示为当侧滑角β=0°时, 无倒流装置时的受电弓各构件非定常阻力系数时程曲线.可以看出, 受电弓各构件所受的阻力波动明显.在计算开始的一段时间内, 气动力波动显著, 这是由于流场没有充分发展造成的；在计算时间大于0.5 s后, 气动力呈现出稳定的波动, 这是由受电弓周围有规律的涡脱造成的, 因此, 将位于0.5~3.0 s间的气动力作为本文分析数据使用.

图 5

图 5 β=0°下的受电弓各构件阻力系数时程曲线 Fig. 5 Time history curve of drag coefficient for each components of pantograph at sideslip of 0°

通过试验所得的压力及压差波形与数值计算所得的波形曲线具有较高的吻合度.

为了验证该计算方法的正确性, 保证计算结果的可靠性与准确度, 在中国空气动力研究与发展中心低速所8 m×6 m大型低速风洞进行风洞试验, 列车风洞试验如图 6(a)所示, 试验列车为1:8缩比的3车编组钢骨架木质动车组模型.在试验中, 来流风速为v=60 m/s.

图 6

图 6 动车组模型 Fig. 6 Model of EMU

采用与风洞试验中模型、尺寸及布置尽可能一致的数值计算模型, 如图 6(b)所示.为了保证数值计算与风洞试验中的马赫数、雷诺数等相似参数的一致, 数值计算中的来流速度与风洞试验中一致；对于数值计算中的来流湍流参数, 当采用DDES方法时, 选择修正的湍流黏性定义, 本次计算给定0.001 m²/s.

如表 1所示为通过动车组数值计算所得的非定常气动力系数的均方根(简称N)与风洞试验数据(简称T).可知, 列车各节车阻力系数具有很好的吻合度, 相差不超过10%.考虑到列车底部结构复杂以及加工误差, 且数值计算中采用的模型无法与试验中列车与路基之间的安装达到完全一致, 导致数值计算和风洞试验中列车升力系数相差相对较大, 差距在40%以上.

表 1

表 1 算法验证用数值计算结果与风洞试验数据对比 Table 1 Comparison of numerical results in algorithm validation with wind tunnel test data 类型 Cd Cl 头车 中间车 尾车 头车 中间车 尾车 T 0.147 5 0.083 7 0.162 8 -0.045 7 -0.025 0 0.097 1 N 0.146 5 0.082 9 0.173 4 -0.064 8 -0.012 0 0.140 2

表 1 算法验证用数值计算结果与风洞试验数据对比 Table 1 Comparison of numerical results in algorithm validation with wind tunnel test data

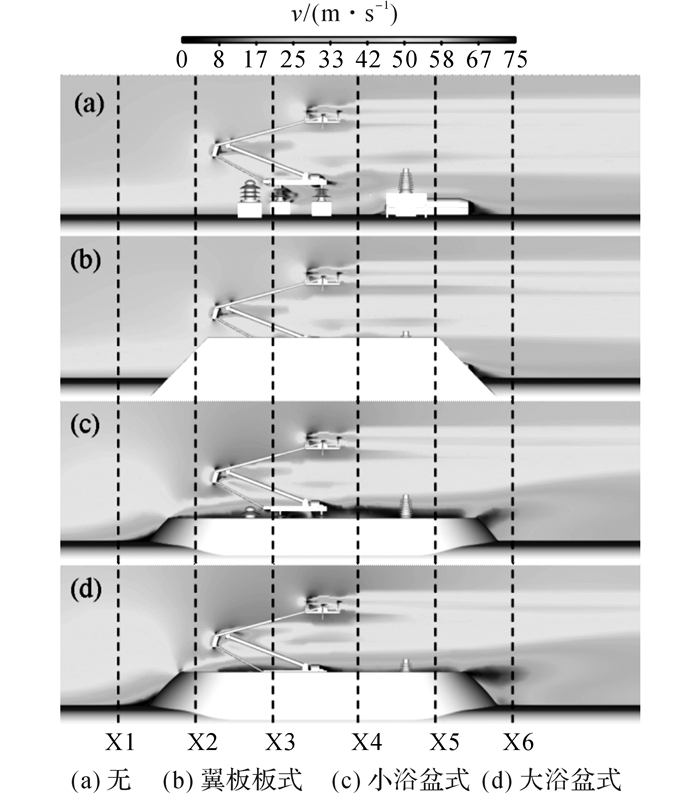
如图 7、8所示分别为安装不同导流装置的列车顶部及受电弓表面压力分布云图和纵剖面速度云图.图中，p为压力，v为合速度.可知, 由于翼板式导流装置前、后无遮挡, β=0°下的受电弓表面压力影响相对较小；浴盆式导流装置显著影响了受电弓及车体表面的压力分布, 由于受电弓基座及绝缘子等位于浴盆内部, 流经此处的气流减少, 浴盆内形成负压区.考虑到基座、绝缘子等对气动噪声的影响可能会较大, 对以杆件为主要构件的受电弓的影响很小, 因此本文未予以关注.浴盆前缘斜坡对气流的导流会引起气流加速, 绕流经过受电弓区域；加速并受到扰动的气流作用在受电弓构件上, 加剧了受电弓气动力的波动.与翼板式倒流装置相比, 浴盆式导流装置显著改变了受电弓下部区域流场结构, 未改变受电弓上部区域的主要流场结构.

图 7

图 7 受电弓表面压力分布 Fig. 7 Pressure distribution of pantograph

图 8

图 8 流场纵剖面速度分布 Fig. 8 Velocity distribution of longitudinal profile for flow

如图 9所示为安装不同导流装置的列车顶部不同横截面的速度云图.图 9中的所标位置对应图 8中的各截面, 每种方案各6个截面.对比不同方案下相同位置处的截面, X1截面位于受电弓前部, 浴盆式导流装置前端对气流的阻滞和导流作用致使导流装置前部区域处于负压状态.随着截面后移, 从X2~X5截面可以看出, 导流装置对受电弓周围流场结构的改变显著, 浴盆内部处于负压状态；在导流装置的影响下, 受电弓下部区域流场流速显著减小；受电弓上部区域气流受到导流装置导流加速, 流速明显增大.

图 9

图 9 列车不同位置横截面速度分布云图 Fig. 9 Velocity distribution for different cross section of train

如表 2所示为β=0°和30°下, 不同形式导流装置下受电弓各部件的阻力系数均方根.可知, 受电弓各构件对总阻力的贡献差异显著, 侧滑角改变了受电弓各构件对总阻力的贡献；当β=0°时, 弓头阻力最大, 其余依次为拉杆、上框架和下臂杆；当β=30°时, 弓头和上框架阻力接近, 且均较大, 其余依次为下臂杆和拉杆.不同导流装置对受电弓的气动性能有明显影响, 当β=0°和30°时, 翼板式对受电弓绝大部分构件的阻力有改善作用, 其他形式的导流装置会导致部分受电弓构件阻力增加.

表 2

表 2 受电弓部件阻力系数均方根 Table 2 RSM of pantograph unsteady drag coefficient 10-3 导流装置 0°侧滑角 30°侧滑角 弓头 上框架 下臂杆 拉杆 弓头 上框架 下臂杆 拉杆 无 14.784 1.338 0.866 1.595 10.712 9.372 9.045 3.124 翼板式 14.540 1.224 0.783 1.584 13.050 10.573 5.203 2.708 小浴盆式 14.241 1.410 0.892 1.740 12.198 11.805 8.980 3.213 大浴盆式 15.883 1.191 1.101 1.641 12.571 12.640 5.972 3.116

表 2 受电弓部件阻力系数均方根 Table 2 RSM of pantograph unsteady drag coefficient

如表 3所示为β=0°和30°下, 不同形式导流装置下受电弓各部件的非定常阻力系数标准差.阻力系数标准差可以用来衡量受电弓各部件阻力波动程度.从表 3可知, 导流装置显著改变了受电弓各部件阻力波动, 侧滑角明线加剧了受电弓各主要部件的阻力波动.当β=0°时, 小浴盆式和大浴盆式导流装置均显著加剧了受电弓各构件阻力的波动, 翼板式导流装置减小了上框架、下臂杆和拉杆的阻力波动；当β=30°时, 受电弓各构件的阻力波动明显加剧, 且翼板式导流装置明显改善了受电弓构件的阻力波动程度.

表 3

表 3 受电弓部件阻力系数标准差 Table 3 SD of pantograph unsteady lift coefficient 10-4 导流装置 0°侧滑角 30°侧滑角 弓头 上框架 下臂杆 拉杆 弓头 上框架 下臂杆 拉杆 无 0.555 0.368 0.666 0.332 2.822 3.250 5.910 0.798 翼板式 0.658 0.301 0.534 0.241 2.795 3.127 3.949 0.721 小浴盆式 1.690 0.479 1.078 0.342 3.003 3.847 6.727 1.057 大浴盆式 1.881 0.371 0.824 0.609 3.612 3.525 4.197 1.130

表 3 受电弓部件阻力系数标准差 Table 3 SD of pantograph unsteady lift coefficient

如表 4所示为β=0°和30°下, 不同形式导流装置下受电弓各部件的升力系数均方根.可知, 受电弓各部件对总升力的贡献差异明显, 侧滑角改变受电弓一些构件的升力方向, 弓头受到正升力, β=30°下小浴盆式和大浴盆式导流装置使上框架受正升力.相对阻力而言, 导流装置对受电弓主要构件的升力影响相对较大；不同形式的导流装置在改变受电弓各构件的升力效果方面差异明显, 不适合的导流装置会增大受电弓构件升力.

表 4

表 4 受电弓部件升力系数均方根 Table 4 RSM of pantograph unsteady lift coefficient 10-4 导流装置 0°侧滑角 30°侧滑角 弓头 上框架 下臂杆 拉杆 弓头 上框架 下臂杆 拉杆 无 -1.032 -1.468 1.243 -0.301 9.000 -4.551 20.715 -5.539 翼板式 -1.541 -1.206 1.200 -0.274 6.167 -13.401 8.118 -4.457 小浴盆式 -0.866 -1.580 1.133 -0.359 11.430 6.035 16.540 -4.704 大浴盆式 -1.134 -1.198 1.371 -0.382 14.111 6.728 7.947 -1.849

表 4 受电弓部件升力系数均方根 Table 4 RSM of pantograph unsteady lift coefficient

如表 5所示为β=0°和30°下, 不同形式导流装置下的受电弓各部件非定常升力系数标准差.可知, 导流装置显著改变了受电弓各部件升力波动.当β=0°时, 翼板式导流装置减弱了弓头升力的波动, 大浴盆式略微减弱了上框架升力波动, 翼板式减弱了下臂杆升力波动, 翼板式减弱了拉杆升力动.当β=30°时, 受电弓各构件的升力波动加剧, 导流装置均加剧弓头和上框架的升力波动, 翼板式和大浴盆式均降低了下臂杆的升力波动, 且大浴盆式尤为突出, 导流装置均加剧了拉杆的升力波动.

表 5

表 5 受电弓部件升力系数标准差 Table 5 SD of pantograph unsteady lift coefficient 10-4 导流装置 0°侧滑角 30°侧滑角 弓头 上框架 下臂杆 拉杆 弓头 上框架 下臂杆 拉杆 无 1.345 1.037 1.021 0.282 4.856 4.472 8.967 0.552 翼板式 1.078 1.589 0.866 0.189 5.404 4.742 8.127 0.643 小浴盆式 1.412 1.153 1.674 0.355 6.132 5.825 10.045 0.840 大浴盆式 1.640 0.954 1.495 0.347 6.374 5.094 6.179 0.830

表 5 受电弓部件升力系数标准差 Table 5 SD of pantograph unsteady lift coefficient

通过流场计算获得受电弓构件在时间区间[t₁, t₂]内的非定常气动力系数时程曲线, 基于在离散情况下成立的Parseval定理和Wiener-Khinchin定理, s(t)的谱密度和s(t)的自相关组成一个傅里叶变换对,$ \int_{{t_1}}^{{t_2}} {{{\left[{s\left( t \right)} \right]}^2}{\rm{d}}} t = \int_{{f_2}}^{{f_1}} {{{\left[{S\left( f \right)} \right]}^2}{\rm{d}}} f$.其中, 采样时长为[t₁, t₂], 采样频率为f₂, 其中f₁=1/(t₂-t₁).

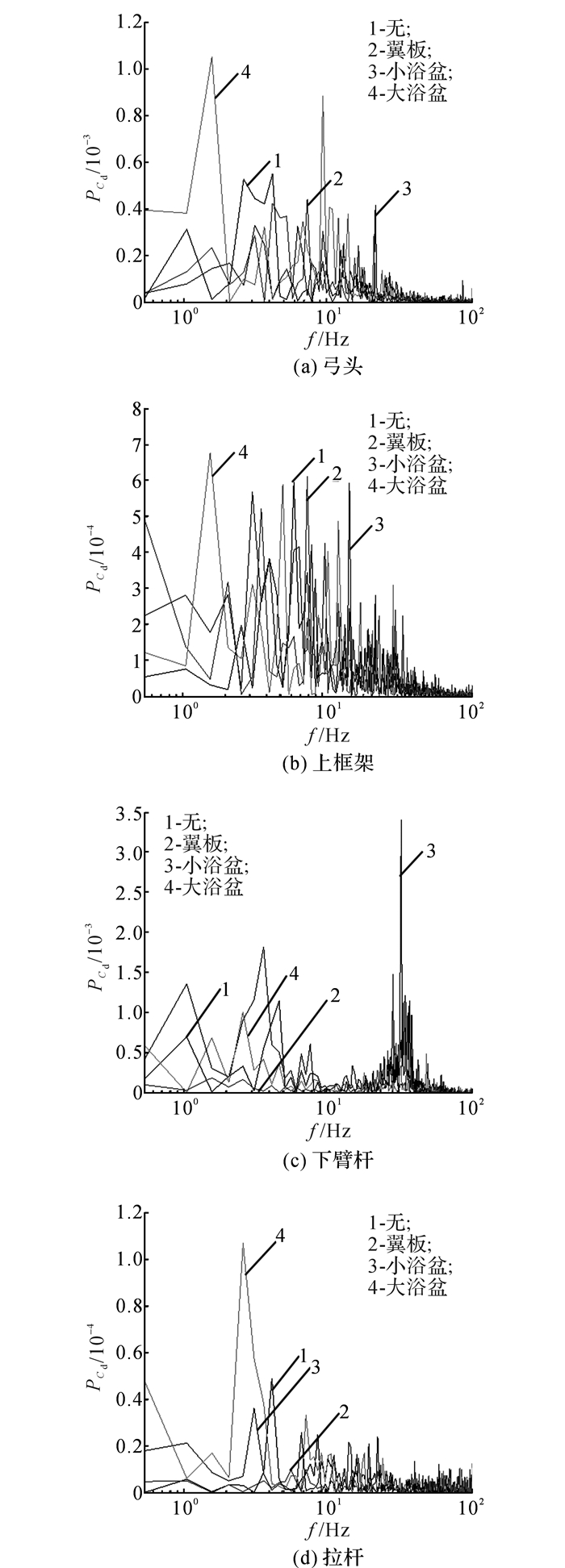
β导致受电弓气动力波动显著, 主要分析当β=30°时的受电弓各构件气动力系数波动特性.如图 10所示为受电弓各构件阻力系数的功率谱密度谱P_Cd.可知, 导流装置明显改变了受电弓构件阻力系数的功率谱密度及分布规律, 翼板式和小浴盆式明显改善了弓头的波动强度, 大浴盆式增加了弓头阻力的波动强度；带宽均主要位于30 Hz以下.不同导流装置下的上框架的阻力波动强度基本一致, 主要涡脱频率存在明显差异；带宽主要位于40 Hz以下.下臂杆阻力的波动主要存在2个带宽：一个在10 Hz以下, 一个在35 Hz左右.翼板式和大浴盆式导流装置显著降低了下臂杆的波动强度, 大浴盆式导流装置增强了下臂杆阻力的波动.拉杆阻力波动带宽主要位于40 Hz以下, 翼板式和小浴盆式明显改善了拉杆阻力波动强度, 且翼板式效果最好, 大浴盆式显著加剧了拉杆阻力波动强度.

图 10

图 10 受电弓各构件阻力系数的功率谱密度 Fig. 10 PSD for unsteady drag coefficient of pantograph

如图 11所示为受电弓各构件升力系数的功率谱密度P_Cl.可知, 导流装置明显改变了受电弓各构件升力系数波动功率谱密度幅值及在频率上的分布规律, 小浴盆式导流装置增加了弓头和上框架升力波动强度, 其他导流装置对弓头和上框架升力的波动强度无明显差异, 带宽均在60 Hz以下.下臂杆升力波动频率主要集中在35 Hz左右, 小浴盆式导流装置加剧了下臂杆升力波动强度, 翼板式和大浴盆式导流装置明显减弱了下臂杆阻力波动强度, 且大浴盆式效果相对更好.导流装置均明显增加了拉杆升力波动强度, 大浴盆式尤为突出.综合比较可知, 翼板式导流装置对受电弓的阻力和升力具有相对较好的改善作用.

图 11

图 11 受电弓各构件升力系数的功率谱密度 Fig. 11 PSD for unsteady lift force coefficient of pantograph

(1)0°侧滑角下, 浴盆式导流装置显著影响了受电弓及车体表面压力分布, 改变了受电弓下部区域流场结构, 浴盆内部处于负压状态；相对翼板式倒流装置而言, 浴盆式导流装置显著改变了受电弓下游车辆顶部流场结构, 流速显著减小, 受电弓上部区域流速增加, 未改变该区域的主要流场结构.

(2)0°和30°侧滑角下, 翼板式改善了受电弓各部件阻力系数及波动特性, 其他形式的导流装置增加了部分受电弓构件的阻力系数及波动.

(3) 侧滑角改变了受电弓部分构件的升力方向.相对阻力而言, 导流装置对受电弓主要构件的升力影响相对较大；0°侧滑角下, 翼板式导流装置均减弱了弓头、下臂杆和拉杆的升力波动, 大浴盆式略微减弱了上框架升力波动.30°侧滑角下, 受电弓各构件的升力波动加剧, 对于弓头和上框架, 导流装置均加剧了升力波动；对于下臂杆, 翼板式和大浴盆式均降低了升力波动, 大浴盆式尤为突出；对于拉杆, 导流装置均加剧了升力波动.

(4) 对于30°侧滑角, 不同导流装置对受电弓各构件气动力的波动改变有明显差异, 不合适的导流装置会增加受电弓气动力的波动强度.综合比较可知, 翼板式导流装置对受电弓气动力波动强度有相对较好的改善作用.