气液两相流广泛存在于动力、石油、能源、化工等工业过程中, 气液比例是否合适直接影响输出产品的质量和系统的性能.近年来, 与数字图像处理技术相结合的低成本、高精度、快速度的方法在两相流领域备受关注.当含气率较高时, 气泡易重叠, 形状复杂不易检测.精确分割气液两相流的重叠气泡至关重要.
目前, 现有的分割重叠目标的方法有多种[1-3]:阈值法[4-5]、区域法[6-7]、边缘法[8-9]等.阈值法, 如基于萤火虫算法的二维熵多阈值快速图像分割方法[10], 改善了分割复杂图像和多目标图像时存在计算量大、计算时间长的问题.区域法, 如基于分水岭算法与自动种子区域生长相结合的分割算法[11], 有效解决了分水岭算法的过分割现象.边缘法通过寻找边缘凹陷信息的凹点并进行匹配连接, 对复杂的重叠目标分离效果较理想.目前, 边缘法的具体方法主要有两种:曲率尺度空间法[12]和弦点距离累积法[13].在曲率尺度空间法的基础上, 提出KD曲率[14]的概念估计曲率.基于离散KD曲率角点检测技术[15], 减小了角点检测复杂性, 大大提高了效率和灵活性.
现有的凹点检测分割和轮廓重构存在以下3个问题.1) 通过曲率尺度空间算法得到的凹点对局部变化和噪声高度敏感, 同时高斯平滑尺度的选择影响一些薄弱凹点和假凹点的检测性能.2) 通过计算得出的候选凹点一般为凹点群, 须进一步进行凹点筛选得出分割点.3) 现有的重叠气泡轮廓重构采用普通连接两两凹点得到的分割线[16], 不能真实地反映重叠部分的轮廓信息.本文提出基于凹凸变换与圆周拟合的重叠气泡轮廓重构方法, 通过对轮廓的质心距离曲线进行凹凸性变换特性分析, 提取凹点后选取分割路径, 最后利用圆周拟合插值算法对重叠部分的气泡轮廓重构.本文将凹点分析转换并量化为距离曲线凹凸性变换特性分析, 计算更简单, 并且通过高斯平滑后检测得出的候选凹点为分割点, 降低了对噪声的敏感度, 同时简化了凹点筛选步骤.通过圆周拟合, 将重叠气泡遮挡部分轮廓进行重构, 便于后续对单个气泡进行分析.该方法的分割质量和准确率较高, 具有较好的抗噪声能力, 重构还原度高, 解决了目前重叠气泡分割和轮廓重构问题.
1 气泡预处理和轮廓提取使用佳能单反相机进行图像采集, 最大分辨率为5 184×3 456, 自动聚焦, 曝光时间为(1/100~1/250) s, 在反应器中心正前方2 m处拍摄.逆光拍摄会受到背光影响, 造成背景亮度不均匀, 不利于预处理, 因此, 背景采用黑布进行拍摄, 能够增强气泡的对比度.经由相机拍摄管道内的流速较低阶段的气液两相流, 得到气泡原始图像如图 1(a)所示.由于气泡与光源的距离不同以及背光等影响, 采集得到的图像亮度有较大差别, 气泡轮廓附近的亮度较高.由于图像中包含较多噪声, 首先对气泡图像进行平滑滤波.高斯滤波是一种线性平滑滤波, 适用于消除高斯噪声.如图 1(b)所示为高斯滤波结果, 不仅消除了噪声, 增强图像对比度, 而且保护了气泡的边缘轮廓信息.按图像的灰度特性, 采用最大类间方差法将图像分成背景和气泡目标两个部分.如图 1(c)所示为采用最大类间方差法的二值化结果, 有效地分割背景和气泡.由于受阴影及高光等因素的影响, 二值化后的目标多存在孔洞及一些小面积区域, 需要进一步进行孔洞填充和小面积区域去除, 结果如图 1(d)、(e)所示.可见, 气泡区域已经被提取出来.采用最优的阶梯型边缘检测算法, 即Canny算法进行边缘检测, 如图 1(f)所示为Canny边缘算法检测结果.可见, 气泡目标区域的轮廓被很好地提取出来, 便于后续处理.

|
图 1 气泡图像预处理和轮廓提取 Fig. 1 Bubble image pre-process and contour extraction |
重叠气泡团经边缘检测后得出轮廓曲线L, 令P1, P2, P3, …, Pn为轮廓曲线L上的n个点, 它们的质量分别是m1, m2, …, mn, (xi, yi)为轮廓L上第i个点的坐标.曲线L围成目标区域的质心位置为
| $ {X_{\rm{c}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }},{Y_{\rm{c}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}, $ | (1) |
由于计算的是曲线上的点的质量, 可以简化为每个点的质量均为1, 则质心位置公式简化为
| $ {X_{\rm{c}}} = \frac{{\sum\limits_{i = 1}^n {{x_i}} }}{n},{Y_{\rm{c}}} = \frac{{\sum\limits_{i = 1}^n {{y_i}} }}{n}. $ | (2) |
曲线L上的点Pi与质心Pc的距离为
| $ \overrightarrow {{P_i}{P_{\rm{c}}}} = \sqrt {{{\left( {{x_i} - {x_{\rm{c}}}} \right)}^2} + {{\left( {{y_i} - {y_{\rm{c}}}} \right)}^2}} . $ | (3) |
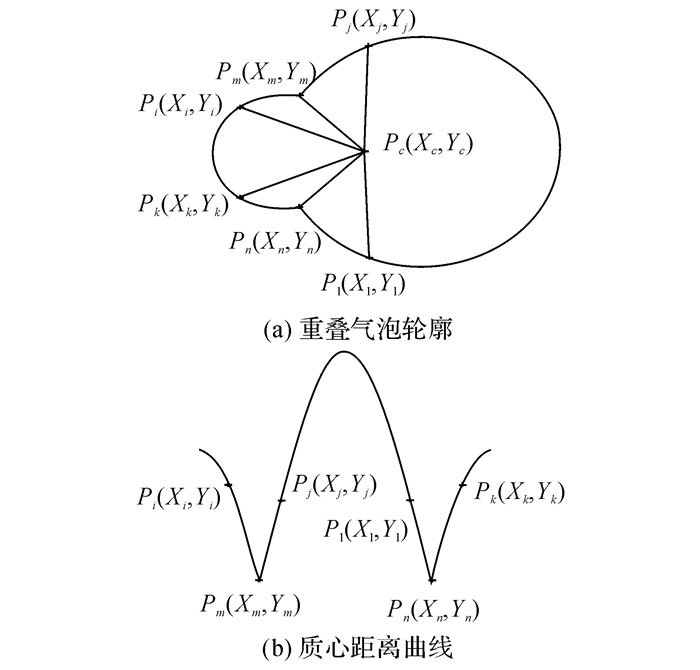
如图 2(a)所示, Pi、Pm、Pj、Pk、Pn、Pl分别为曲线L上的点, Pc为该曲线L围成的区域质心.通过计算曲线L上的每个点与质心间的距离D, 得出图 3(b)的距离曲线.可以看出, 对于同一个气泡来说, Pn、Pk、Pi、Pm均属于同一气泡上的轮廓曲线L1, 按顺时针方向计算可知, 轮廓曲线L1上的点与质心的距离先变大再变小, 在两气泡凹点处, 与质心距离为局部极小值点, 故寻找计算出与质心距离曲线的极小值点作为凹点.
|
图 2 曲线凹凸性变换 Fig. 2 Curve concave-convex transformation |
|
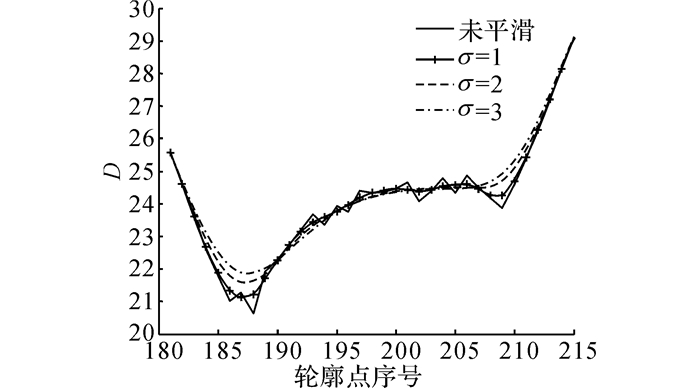
图 3 高斯平滑曲线 Fig. 3 Curve smoothing by Gaussian function |
由于轮廓提取后的曲线噪声较多, 计算轮廓上的点到质心的距离曲线往往含有较多的噪声, 不易于根据凹凸性变换选取凹点, 因此曲线平滑是十分必要的.通常情况下, 短边缘使用小的平滑尺度, 长边缘使用大的平滑尺度.选取尺度过大或过小都容易导致重要特征的丢失或者噪声的抑制性较差.
采用高斯平滑曲线, 高斯函数为
| $ G\left( {x,y} \right) = \frac{1}{{2{\rm{\pi }}{\sigma ^2}}}\exp \left( { - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right). $ | (4) |
可得不同平滑尺度滤波器的标准值σ下的高斯平滑曲线结果, 如图 3所示.
为了改善平滑效果, 对于不同长度的曲线选取不同的σ[15].σ的选取标准如下:
| $ \sigma = \left\{ \begin{array}{l} 1,0 < n \le 100;\\ 2,100 < n \le 200;\\ 3,n > 200. \end{array} \right. $ | (5) |
式中:n为曲线长度.
首先根据重叠气泡团所在位置的坐标极值点形成一个矩形窗口, 作为目标区域进行分析, 如图 4(a)所示.对重叠气泡团图像进行预处理后, 在矩形窗口中气泡团中标记质心位置(Xc, Yc), 如图 4(b)所示, 标记出质心位置.采用Canny算法进行边缘检测, 得出气泡团轮廓, 如图 4(c)所示.

|
图 4 气泡团目标区域的凹点检测 Fig. 4 Concave point detection of bubble region |
基于曲线凹凸性变换算法, 求出轮廓点到质心距离的极小值点, 即为凹点.由于未经高斯平滑的轮廓噪声较多, 如图 5(a)所示, 曲线不平滑, 较粗糙, 容易识别出较多的伪凹点;高斯平滑后, 可得图 5(b)所示的4个凹点.将对应凹点映射至轮廓坐标上, 得出图 4(d)所示的凹点检测结果.

|
图 5 高斯平滑尺度选择 Fig. 5 Gauss smoothing scale selection |
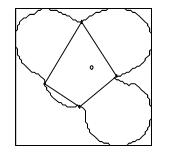
在分割点检测结束后, 需要完成分割路径的选择.以分割线长度最短为准则[17], 即所选取的两个相邻凹点之间的距离应尽量短, 以任一凹点为起点, 顺时针方向连接相邻两个凹点, 如图 6所示, 气泡被粗略地分割出来.
|
图 6 分割路径选择 Fig. 6 Segmentation path selection |
分割后的重叠气泡轮廓是不完整的.为了实现重叠部分轮廓的重构, 基于最小二乘法圆周拟合插值算法进行轮廓匹配重构.最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配, 是一种曲线拟合的方法之一.如图 7所示, 令拟合的圆周曲线方程为

|
图 7 最小二乘法圆周拟合 Fig. 7 Least square circle fitting |
| $ {R^2} = {\left( {x - A} \right)^2} + {\left( {y - B} \right)^2}. $ | (6) |
展开后为
| $ {R^2} = {x^2} - 2Ax + {A^2} + {y^2} - 2By + {B^2}. $ | (7) |
令a=-2A, b=-2B, c=A2+B2-R2, 可得圆周曲线方程的另一个形式:
| $ {x^2} + {y^2} + ax + by + c = 0. $ | (8) |
求出参数a、b、c, 可以求得圆心坐标和半径的参数:
| $ A = \frac{a}{{ - 2}},B = \frac{b}{{ - 2}},R = \frac{1}{2}\sqrt {{a^2} - {b^2} - 4c} . $ |
令轮廓曲线上的点(xi, yi)到圆心的距离为di, 如图 7所示, 则
| $ d_i^2 = {\left( {{x_i} - A} \right)^2} + {\left( {{y_i} - B} \right)^2}. $ | (9) |
点到圆心的距离的平方与半径的平方之差为
| $ \begin{array}{l} {\delta _i} = d_i^2 - {R^2} = {\left( {{x_i} - A} \right)^2} + {\left( {{y_i} - B} \right)^2} - {R^2} = \\ \;\;\;\;\;\;x_i^2 + y_i^2 + a{x_i} + b{y_i} + c. \end{array} $ | (10) |
令Q(a, b, c)为δi的平方和, 则
| $ \begin{array}{l} Q\left( {a,b,c} \right) = \\ \;\;\;\;\sum {\delta _i^2} = \sum {{{\left( {x_i^2 + y_i^2 + a{x_i} + b{y_i} + c} \right)}^2}} . \end{array} $ | (11) |
求出参数a、b、c, 使得Q(a, b, c)最小.
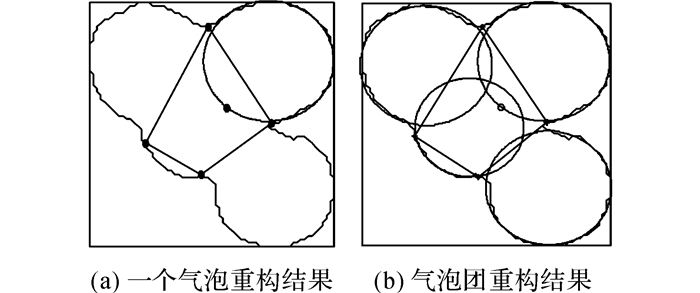
对图 7中的一个气泡, 利用最小二乘法进行圆周拟合[18].当Q(a, b, c)最小时, 求出参数分别为a=-259, b=952, c=243 046, 圆心坐标为(129, 476), 半径R=17.根据该圆的方程绘制圆周, 重构的结果如图 8(a)所示.
|
图 8 轮廓重构圆周拟合 Fig. 8 Contour reconstruction circle fitting |
将目标轮廓坐标按顺时针方向排列, 对两分割点间的轮廓点排列后的直角坐标数据进行采集.利用最小二乘法计算得出每两个分割点间的单个气泡轮廓拟合出的圆周的圆心坐标和半径.以计算的单个气泡的圆心为原点, 以R为半径进行圆周拟合的插值运算, 得到曲线轮廓, 即为重叠气泡目标的重构轮廓曲线.气泡团拟合的最终结果如图 8(b)所示.
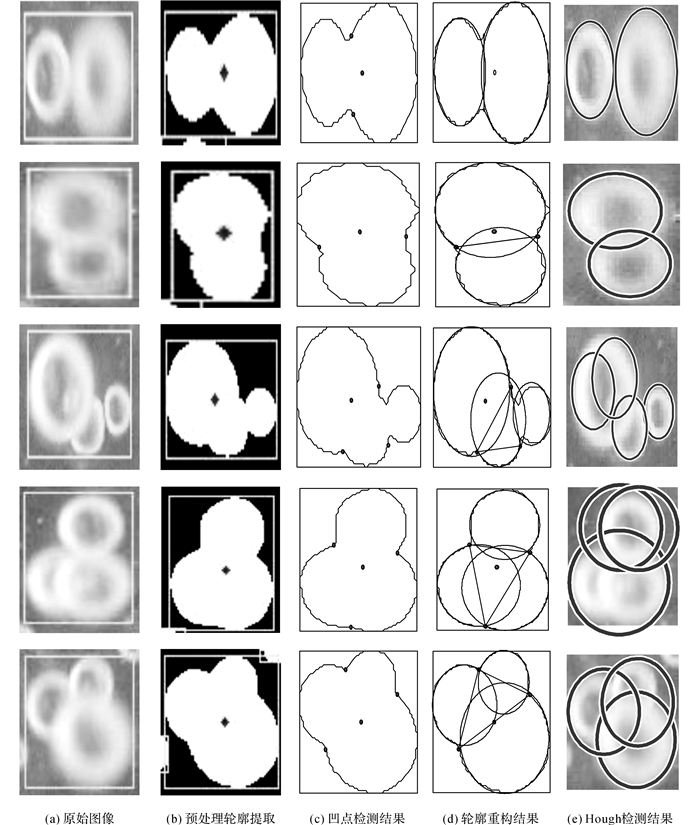
4 实验结果和分析对气液两相流中的部分重叠气泡进行分割, 可得结果如图 9所示.其中, 如图 9(a)所示为原始图像目标区域, 如图 9(b)所示为预处理后轮廓提取的结果图像.可以看出, 气泡轮廓被很好地提取出来.如图 9(c)所示为高斯平滑后基于曲线凹凸性变换方法得出的凹点检测结果.进行分割路径的选择后, 如图 9(d)所示为基于最小二乘圆周拟合算法的轮廓重构结果.如图 9(e)所示为Hough变换检测圆算法的结果.可以看出, 采用本文算法基本能够准确地对气液两相流中的重叠气泡进行分割提取, 对重叠部分的轮廓能够较精准地进行重构.
|
图 9 气液两相流中重叠气泡分割提取结果 Fig. 9 Results of overlapped bubbles segmentation in gas-liquid two-phase flow |
选取4组重叠气泡团图像进行测试.为了反映本文算法和Hough变换算法的性能, 选择准确率、召回率和F值作为评价指标.首先对重叠气泡团图像中包含的实际气泡进行人工计数, 得出实际气泡个数K.然后运用算法识别检测得出的气泡个数Ki, 其中正确识别的气泡个数为Li(由式(15) 计算得到的重合度在50%以上的检出气泡被认为是正确识别), i取1或2, 分别表示本文算法和Hough变换重构算法.
准确率评估的是识别检出的气泡中正确识别所占的比例.准确率的计算公式为
| $ p = \frac{{{L_i}}}{{{K_i}}} \times 100\% . $ | (12) |
召回率评估的是实际气泡中正确识别所占的比例.召回率的计算公式为
| $ r = \frac{{{L_i}}}{K} \times 100\% . $ | (13) |
当准确率和召回率两个指标出现矛盾时, 常用F值作为综合这两者指标的评估指标, 用于综合反映整体的指标.F值的计算公式为
| $ F = \frac{{p \times r \times 2}}{{p + r}} \times 100\% . $ | (14) |
如表 1所示为本文算法和Hough变换检测圆算法测试结果的性能比较.表中,K为实际气泡个数.
| 表 1 重叠气泡目标分割两种方法性能比较 Table 1 Performance comparison of two methods for overlapped bubbles segmentation |
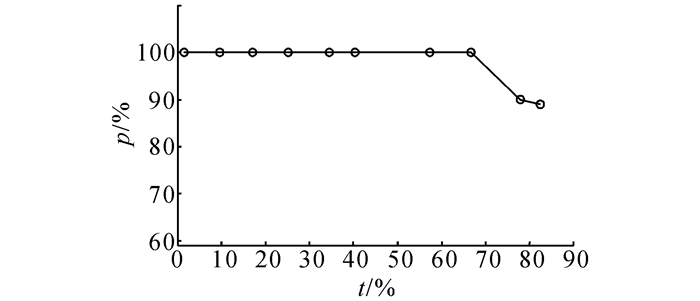
当气泡重叠率较大时, 检测得出的气泡准确率会受到影响, 一般地, 重叠率越大, 准确率越低.如图 10所示为从图像中进行10次采样得出的气泡重叠率t与气泡检测准确率的关系曲线.
|
图 10 气泡重叠率与气泡检测准确率曲线 Fig. 10 Curve about bubble overlapped rate and bubble detection accuracy |
由表 1可以看出, 本文算法的平均准确率为90.90%, 平均召回率为86.47%, F值的平均值为88.61%;Hough变换算法的平均准确率为77.46%, 平均召回率为91.38%, F值的平均值为83.56%.可见本文算法的平均准确率高于Hough变换, 平均召回率略低于Hough变换, 从综合两个指标的F来看, 本文算法的整体综合性能优于Hough变换算法, 但优势不明显.这是因为表 1只是简单地计算了气泡的检出个数的准确度, 没有计算每个检出气泡的精确度.在气液两相流中, 计算气液比例时更重要的参数是气泡的尺寸, 因此, 与检出气泡的个数相比, 更重要的是每一个气泡的检出精度.在这方面, 本文算法与Hough变换相比, 优势非常大.下面进一步比较这两种算法的气泡检出精度.
为了计算气泡的检出精度, 分别获取原始图像中气泡目标的面积A(像素)与算法分割重构后气泡目标的面积Ai(像素), 计算定位误差和重合度来进行分割和重构效果的评价.定位误差的计算公式如下:
| $ e = \frac{{\left| {A - {A_i}} \right|}}{A} \times 100\% . $ | (15) |
式中:i取1或2, 分别表示本文算法和Hough变换重构算法.
重合度的计算公式如下:
| $ c = \frac{{{A_i} \cap A}}{A} \times 100\% . $ | (16) |
式中:Ai∩A表示既在原始图像上又在分割重构的气泡目标图像上的像素点个数, 即重合区域的面积, 重合度越高, 说明分割效果越好.选取10幅气泡测试图像, 对分割得到的定位误差和重合度等进行分析, 如表 2所示为本文算法和Hough变换检测圆算法测试的有效性对比分析结果.表中,S为重合面积.
| 表 2 重叠气泡目标分割有效性对比分析 Table 2 Effectiveness comparative analysis of overlapped bubbles segmentation |
由表 2可看出, 本文算法的平均定位误差为11.26%, 平均重合度为93.89%, 最小定位割误差为3.46%;Hough变换检测算法的平均定位误差为46.42%, 平均重合度为79.61%, 最小定位误差为10.10%.由此可见, 本文的平均定位误差低于Hough变换检测算法35.16%, 平均重合度高14.28%, 证明了本文算法对重叠气泡的分割和轮廓的重构是有效可行的, 检出精度比Hough变换高.
5 结语目前, 气液两相流中对重叠气泡的分割提取相关的技术尚未形成完整的理论.为了实现对重叠气泡的准确分割, 本文提出基于曲线凹凸性变换与圆周拟合的重叠气泡分割与轮廓重构方法.将大量轮廓点二维坐标信息量化为距离问题, 并转换为对曲线的凹凸性分析问题.运用最小二乘圆周拟合算法重构重叠轮廓, 还原度较高.实验结果表明, 基于曲线凹凸性变换算法, 利用最小二乘圆周拟合算法进行重叠气泡的分割和轮廓重构, 识别检测得到的F值的平均值为88.61%, 高于Hough变换检测算法5.05%, 平均定位误差为11.26%, 平均重合度为93.89%, 分割效果较好, 噪声敏感度低, 重构还原度高.本文算法是有效可行的, 为重叠气泡的分割与轮廓重构提供了新的思路, 为后续对气泡的尺寸和分布等研究工作的展开奠定了基础.
| [1] | LIAO M, ZHAO Y Q, LI X H, et al. Automatic segmentation for cell images based on bottleneck detection and ellipse fitting[J]. Neurocomputing, 2015, 173(3): 615–622. |
| [2] |
王丹丹, 徐越, 宋怀波, 等. 融合K-means与Ncut算法的无遮挡双重叠苹果目标分割与重建[J].
农业工程学报, 2015, 31(10): 227–234.
WANG Dan-dan, XU Yue, SONG Huai-bo, et al. Fusion of K-means and Ncut algorithm to realize segmentation and reconstruction of two overlapped apples without blocking by branches and leaves[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(10): 227–234. DOI:10.11975/j.issn.1002-6819.2015.10.030 |
| [3] |
王乐乐, 雍晓东, 李然, 等. 图像处理技术在气泡特性研究中的应用[J].
四川大学学报:工程科学版, 2012, 44(supple.2): 188–192.
WANG Le-le, YONG Xiao-dong, LI Ran, et al. Image processing technology in the application of bubble characteristics research[J]. Journal of Sichuan University: Engineering Science Edition, 2012, 44(supple.2): 188–192. |
| [4] | LIU L M, YANG N, LAN J H, et al. Image segmentation based on gray stretch and threshold algorithm[J]. Optik-International Journal for Light and Electron Optics, 2015, 126(6): 626–629. DOI:10.1016/j.ijleo.2015.01.033 |
| [5] | LONG J W, SHEN X J, CHEN H P. Adaptive minimum error thresholding algorithm[J]. Acta Automatica Sinica, 2012, 38(7): 1134. DOI:10.3724/SP.J.1004.2012.01134 |
| [6] |
胡敏, 蔡慧芬. 基于形态学标记连通的分水岭图像分割[J].
电子测量与仪器学报, 2011, 25(10): 864–869.
HU Min, CAI Hui-fen. Watershed segmentation based on morphological marker-connection[J]. Journal ofElectronic Measurement and Instrument, 2011, 25(10): 864–869. |
| [7] |
刘荣, 彭艳敏, 唐粲, 等. 基于分水岭与图割的自动分割方法[J].
北京航空航天大学学报, 2012, 38(5): 636–641.
LIU Rong, PENG Yan-min, TANG Can, et al. Object auto-segmentation based on watershed and graph cut[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 636–641. |
| [8] |
徐越, 李盈慧, 宋怀波, 等. 基于Snake模型与角点检测的双果重叠苹果目标分割方法[J].
农业工程学报, 2015, 31(1): 196–203.
XU Yue, LI Ying-hui, SONG Huai-bo, et al. Segmentation method of overlapped double apples based on Snake model and corner detectors[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(1): 196–203. |
| [9] | CARMONA-POYATO A, MADRID-CUEVAS F J, MEDINA-CARNICER R, et al. Polygonal approximation of digital planar curves through break point suppression[J]. Pattern Recognition, 2010, 43(1): 14–25. DOI:10.1016/j.patcog.2009.06.010 |
| [10] |
陈恺, 陈芳, 戴敏, 等. 基于萤火虫算法的二维熵多阈值快速图像分割[J].
光学精密工程, 2014, 22(2): 517–523.
CHEN Kai, CHEN Fang, DAI Min, et al. Fast image segmentation with multilevel threshold of two dimensional entropy based on firefly algorithm[J]. Optics and Precision Engineering, 2014, 22(2): 517–523. |
| [11] |
杨家红, 刘杰, 钟坚成, 等. 结合分水岭与自动种子区域生长的彩色图像分割算法[J].
中国图象图形学报, 2010, 15(1): 63–68.
YANG Jia-hong, LIU Jie, ZHONG Jian-cheng, et al. A color image segmentation algorithm by integrating watershed with automatic seeded region growing[J]. Journal of Image and Graphics, 2010, 15(1): 63–68. DOI:10.11834/jig.20100111 |
| [12] | KONUR U, GVRGEN F S, VAROL F, et al. Computer aided detection of spina bifida using nearest neighbor classification with curvature scale space features of fetal skulls extracted from ultrasound images[J]. Knowledge-Based Systems, 2015, 85(C): 80–95. |
| [13] | BORRELLI V, ORGERET R. Error term in pointwise approximation of the curvature of a curve[J]. Computer Aided Geometric Design, 2010, 27(7): 538–550. DOI:10.1016/j.cagd.2010.06.001 |
| [14] | CHEN S T, MENG H, ZHANG C, et al. A KD curvature based corner detector[J]. Neurocomputing, 2016, 173(2): 434–441. |
| [15] |
韦冬冬, 赵豫红. 基于凹点匹配的重叠图像分割算法[J].
计算机与应用化学, 2010, 27(1): 99–102.
WEI Dong-dong, ZHAO Yu-hong. An image segment algorithm for overlapped particles based on concave points matching[J]. Computers and Applied Chemistry, 2010, 27(1): 99–102. |
| [16] | WANG W X. Binary image segmentation of aggregates based on polygonal approximation and classification of concavities[J]. Pattern recognition, 1998, 31(10): 1503–1524. DOI:10.1016/S0031-3203(97)00145-3 |
| [17] |
俞龙江, 杨英, 孙圣和. 基于最小二乘拟合法的焊点形状检测[J].
仪器仪表学报, 2007, 7(28): 1255–1258.
YU Long-jiang, YANG Ying, SUN Sheng-he. Solder joint shape inspection using least square fitting[J]. Chinese Journal of Scientific Instrument, 2007, 7(28): 1255–1258. |



