在复杂流程工业过程中, 每天都能够采集并保存大量的过程数据, 这些数据能够有效反映出工业运行过程中的实际状况, 因此基于数据驱动的故障检测和故障分类方法得到了越来越广泛的应用.在实际的工业过程中, 带有标签的故障数据往往很难获得, 若只有非常少量的带标注样本对分类器进行训练, 则容易造成过拟合、泛化能力弱等问题.每天被海量保存下来的无标签故障样本包含了丰富的工况信息, 若能够加以利用, 则模型性能往往能够得到改善[1].收集并标注故障类数据, 需要耗费领域专家的时间和精力, 成本较高, 机器学习领域中的主动学习是解决训练过程中这一问题的有效途径.相较于随机选择, 主动学习能够用更少的样本更好地描述各类数据的特征[2], 从而降低人工标注的成本.唐明珠等[3]将主动学习用于工业故障检测, Yan等[4]将主动学习用于过程监测中, 均取得了出色的效果.
主动学习的核心思想是选择对当前分类器最有利的样本.如Tong等[5]采用不确定性度量采样策略, 在每一次的迭代中选择最靠近当前分类面的样本;Wang等[6-7]采用基于投票委员会的采样策略, 选择委员会中假设预测分歧最大的样例, 但是以上两种方法容易采样到孤立点.Cohn等[8]提出基于泛化误差减小的采样策略, 选择能给基准分类器带来最大误差缩减的样本, 但是计算成本较高昂.基于不确定性的采样方法中, 信息熵常常作为度量准则, 但是表现出了一定的缺陷, 如熵严重受到不重要类别概率的影响[9].针对该问题, Joshi等[10]提出基于最优次优标号类属概率差(best versus second-best, BvSB)的主动学习方法, 并在多分类问题中取得了较好的性能.
在实际流程工业过程中, 由于发生频率不同, 采集到的正常样本与故障样本以及不同的故障样本之间数量往往不平衡.针对这个问题, 可以通过包括算法层面的改进[11], 对分类模型本身进行调整或者对样本数据进行数据层面的重构[12], 如重采样处理等, 以此来缓解不平衡数据对分类性能带来的不利影响.通过对不平衡数据集进行有效处理, 不仅可以提高分类的准确率, 而且避免了主动学习中采集到重复、无意义样本点的问题.
针对上述方法中存在的弊端, 综合考虑了有标签故障样本少且标注代价昂贵以及数据集类别不平衡的问题, 本文提出基于改进的BvSB和改进的加权支持向量机(weighted SVM, WSVM)的工业故障分类方法, 通过TE过程进行实验研究, 验证了提出方法的有效性和可行性.
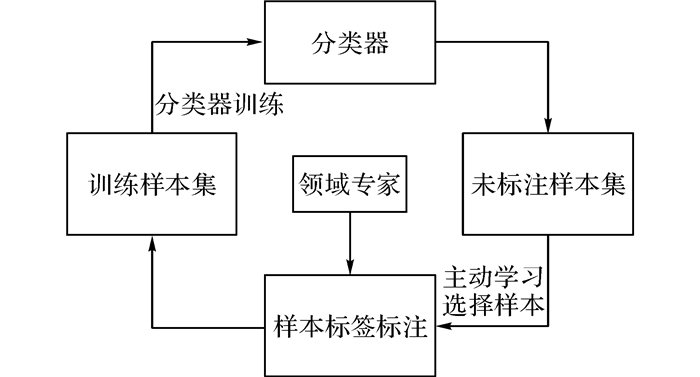
1 改进的BvSB主动学习主动学习通过构造一定的选择机制, 将对于当前分类器性能改善最有价值的样本挑选出来提交给专家进行标注, 并用于更新训练集和分类模型, 从而高效地改善分类器的性能, 对于小样本的监督学习问题是一个有效的解决途径.典型的主动学习框架如图 1所示.
|
图 1 典型分类模型中的主动学习框架 Fig. 1 Typical framework of classication with active learning |
基于不确定性采样策略的主动学习中, 信息熵是最广为使用的度量准则, 设未标注样本集为U={x1, x2, …, xn}, 所有的类别标签为Y={1, 2, …}.通过现存的少量有标签样本训练得到的分类模型对所有的未标注样本集进行分类测试, 可以求得样本xi隶属于各个类别yi的概率, 记为p(yi|xi).信息熵的计算公式如下:
| $ E = \arg \mathop {\max }\limits_{{x_i} \in U}-\sum\limits_{{y_i} \in Y} {p\left( {{y_i}\left| {{\mathit{\boldsymbol{x}}_i}} \right.} \right)} logp\left( {{y_i}|{\mathit{\boldsymbol{x}}_i}} \right). $ | (1) |
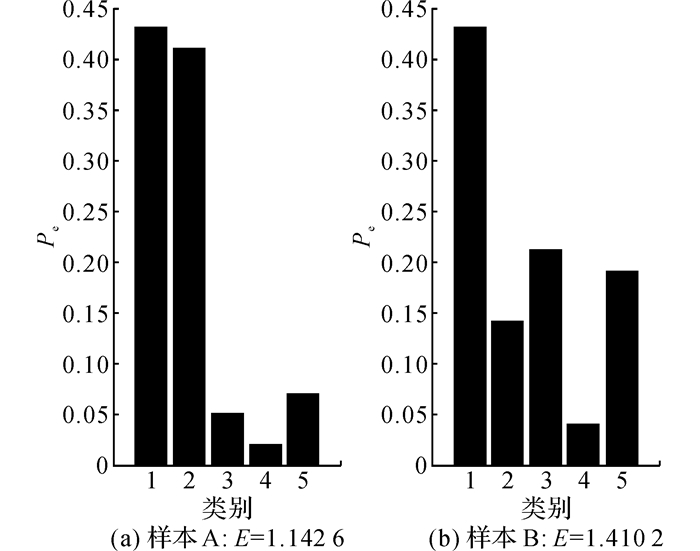
样本熵越高, 说明样本类别属性越模糊, 往往能给模型带来更大的信息量和价值.在主动学习的过程中, 会遍历所有的无标签样本并计算对应的熵值, 将熵值最大的这部分样本提交给专家标注从而扩充有监督学习样本集, 能达到快速改善分类器性能的目的.然而在多分类问题中, 熵值容易受到不重要类别概率的影响[9].图 2中,Pe为类别预测隶属度.如图 2所示, 在一个多分类问题中, 有样本A和样本B.可以看出, 样本A属于前两个类别的概率非常接近, 其类别属性难以判断, 样本B相对样本A来说, 不确定度相对较低.计算结果是不确定度更大的样本A信息熵更小.
|
图 2 熵在多分类中不能有效评估样本不确定度的例子 Fig. 2 Illustration of entropy's poor performance in determining sample uncertainty in multi-class classification problems |
针对不重要类别较小的概率能够构成样本较大信息熵的问题, Joshi等[10]提出更加贪婪的评估策略BvSB.在BvSB准则中, 只有最高估计概率值的两个类别被用来衡量样本分类的不确定度.即对于一个新样本, 进行分类测试后, 如果将类别概率最高的两个值分别记为P(yBest|xi)和P(ySecond_Best|xi), 则BvSB的计算公式如下:
| $ \begin{array}{l} {\rm{BvSB}} = \arg \mathop {\min }\limits_{{x_i} \in U} \left( {\mathop {\min }\limits_{y \in Y, y \ne {y_{{\rm{Best}}}}} \left( {P\left( {{y_{{\rm{Best}}}}|{\mathit{\boldsymbol{x}}_i}} \right)} \right)-\left( {P\left( {y|{\mathit{\boldsymbol{x}}_i}} \right)} \right)} \right) = \\ \arg \mathop {\min }\limits_{{x_i} \in U} \left( {P\left( {{y_{{\rm{Best}}}}|{\mathit{\boldsymbol{x}}_i}} \right)-P\left( {{y_{{\rm{Second}}\_{\rm{Best}}}}|{\mathit{\boldsymbol{x}}_i}} \right)} \right). \end{array} $ | (2) |
BvSB准则虽然在多分类问题中对于样本分类的不确定性起到了较好的评估作用, 但是仅仅考虑样本的信息度是不够的.样本的代表性在选择过程中具有非常重要的意义[13].
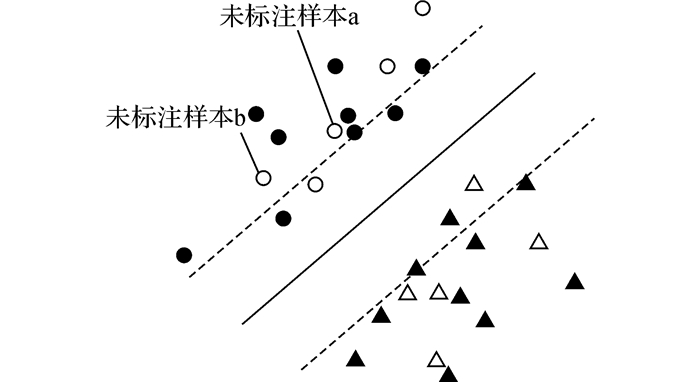
如图 3所示, 黑色圆点代表类别1中已标注样本, 黑色三角点代表类别2中已标注样本, 灰色圆点和灰色三角点分别代表类别1和类别2的未标注样本.图中, 黑色实线代表支持向量机训练得到的最大间隔分离超平面, 两条虚线为间隔边界.由图 3可知, 以BvSB准则作为信息度度量, 样本a比样本b离分类边界更近, 最优次优类属概率差值更小.在进行主动选择时, 优先选择样本a进行人工标注.然而从图 3可以看出, 样本a周围有两个与其相似的已标注样本, 样本a的加入并不能对分类边界的调整起到明显的作用, 所以选择样本a进行标注意义不大.样本b虽然信息度度量上不如a更有价值, 但是加入样本冗余性的考量后, 可以看出样本b对于分类面的改善可能比样本a更大.基于这个想法, 在BvSB的基础上, 提出综合考虑样本中的孤立点以及样本信息冗余问题的改进BvSB算法.
|
图 3 BvSB存在的代表性度量缺失问题 Fig. 3 Illustration of lack of representativeness measurement for sample selection in BvSB |
为了不采样到孤立点, 通过采用基于平均密度的算法检测出孤立点并从未标注样本集中剔除.孤立点是在低密度区域中的对象, 在一个数据集中若存在孤立点, 则孤立点的密度往往会明显小于平均密度.具体算法如下.
定义1 平均距离 将未标注样本集中的n个样本两两计算距离dij, 有
| $ {\bf{DR}} = \left[\begin{array}{l} {d_{11}}\;\;{d_{12}}\;\; \cdot \;\; \cdot \;\; \cdot \;\;{d_{1n}}\\ {d_{21}}\;\;{d_{22}}\;\; \cdot \;\; \cdot \;\; \cdot \;\;{d_{2n}}\\ \cdot \;\;\;\;\; \cdot \;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \\ \cdot \;\;\;\;\; \cdot \;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \\ \cdot \;\;\;\;\; \cdot \;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \\ {d_{n1}}\;\;{d_{n2}}\;\; \cdot \;\; \cdot \;\; \cdot \;\;\;{d_{nm}} \end{array} \right]. $ | (3) |
所有对象的平均距离为
| $ D = \frac{{\sum\limits_{i = 1}^{n-1} {\sum\limits_{j = i + 1}^n {{d_{ij}}} } }}{{C_n^2}}. $ | (4) |
定义2 最大样本距离为
| $ {d_{\max }} = \max \left( {{d_{ij}}} \right);\;\;i, j = 1, 2, ..., n. $ | (5) |
定义3 样本邻域 样本邻域是以样本点xi为球心、r为半径的一个球形范围.根据文献[14]得出的结论可知, 当r取
定义4 总体平均密度为
| $ \bar p = \frac{n}{{t{{\left( {\frac{{\sqrt 3 }}{2}{d_{\max }}} \right)}^m}}}. $ | (6) |
式中:n为未标注样本集的总个数, m为经过预处理之后的样本维度, t为常系数.
定义5 单个样本的邻域密度为
| $ p\left( {{\mathit{\boldsymbol{x}}_i}, r} \right) = \frac{{{n_i}}}{{{{\left( {\frac{{\sqrt 3 }}{2}aD} \right)}^m}}}. $ | (7) |
式中:ni为样本xi指定邻域内的未标注样本个数;a为可调系数, 取值为(0, 1], 随着需要处理的数据量和数据集的维数而改变.
由此可以判定, 对于孤立点, 邻域密度会明显小于平均密度, 这类样本在进行主动学习选择的时候将被剔除, 避免将这类样本加入训练集后造成误差传播反而使分类器性能下降.
在主动学习过程中, 综合考虑样本的信息度和样本的代表性.首先, 根据BvSB准则, 计算每个未标注样本在初始分类器下得到的最优次优概率差;其次, 在主动学习的过程中, 通过计算未标注样本与已标注样本集的余弦相似性来度量样本的代表性, 避免选择到一些相似度太高的未标注样本, 从而有效地解决样本冗余性的问题.未标注样本与已标注样本集的相似性即样本代表性的计算公式如下:
| $ {d_{\cos }}\left( {{\boldsymbol{x}_i}, L} \right) = \frac{1}{k}\sum\limits_{{x_j} \in {L_k}} {{d_{\cos }}\left( {{\boldsymbol{x}_i}, {\boldsymbol{x}_j}} \right)} . $ | (8) |
式中:L表示已标注样本集, Lk表示与未标注样本余弦相似性最大的k个已标注样本构成的集合, 本文中k取5.dcos(xi, xj)为未标注样本xi与已标注样本xj的余弦相似性, 计算公式为
| $ \begin{array}{l} {d_{\cos }}\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) = \frac{{\left| {\mathit{\Phi} \left( {{\mathit{\boldsymbol{x}}_i}} \right) \cdot \mathit{\Phi} \left( {{\mathit{\boldsymbol{x}}_j}} \right)} \right|}}{{\left\| {\mathit{\Phi} \left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right\|\left\| {\mathit{\Phi} \left( {{\mathit{\boldsymbol{x}}_j}} \right)} \right\|}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\left| {K\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right)} \right|}}{{\sqrt {K\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_i}} \right)K\left( {{\mathit{\boldsymbol{x}}_j}, {\mathit{\boldsymbol{x}}_j}} \right)} }}. \end{array} $ | (9) |
式中:K(·, ·)为核函数, Φ(xi)和Φ(xj)分别为样本xi和xj经过Φ映射到特征空间中对应的坐标值.
为了得到样本信息度与代表性的综合评价指标, 对样本的BvSB度量值和平均余弦距离进行统一的去量纲归一化标准处理, 可得
| $ \begin{array}{l} {\rm{rule}}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \lambda \times {\rm{normalized\_bvsb}}\left( i \right) + \\ \left( {1-\lambda } \right) \times {\rm{normalized\_cos}}\;{\rm{distance}}\left( i \right). \end{array} $ | (10) |
式中:λ∈[0,1], 通过λ和(1-λ)来分别表示样本分类不确定度的权重和未标注样本与已标注样本余弦相似性的权重.最优次优类属概率差越小, 余弦相似性越低, 则信息量越大, 样本的相似性、冗余性越低, 计算得到的综合指标rule越低.当λ=0.5时, 表示样本的信息度和代表性一样重要;当λ=1时, 只考虑样本的信息度, 退化成改进的BvSB方法;当λ=0时, 只考虑未标注样本与现有样本的相似度, 即只衡量了样本的代表性.一般情况下, 样本的信息含量对于分类决策边界的调整有重要的作用, 而新样本与已标注样本保持区分度也能减少数据集的冗余.为了平衡样本的信息度和代表性, 取λ为0.5.将所有未标注样本的rule进行排序, 找到rule最小的样本进行主动学习, 并加入到训练集中用于快速改善分类器的性能.
2 改进的加权支持向量机在实际流程工业过程中, 正常工况数据易获取, 故障样本难以获得, 且不同类型的故障发生频率不同, 导致不同类型的故障之间的样本数量不同.不平衡的样本数据对于分类器寻找最好的分类面会有一定的影响.支持向量机在训练的过程中产生的最优分类超平面会向间隔区域中的少数类样本倾斜.这种偏差行为导致在主动学习的过程中, 会采集到重复的、无意义的样本, 而且训练得到的分类器分类精度会受到影响.目前, 针对不平衡数据集, 主要有两种处理方法:1) 算法层面的改进, 如加权的代价敏感支持向量机;2) 数据层面的改进, 如重采样等, 通过增加少数类样本或者舍弃多数类样本来调整数据集的不平衡程度.
构造有区别的误分类代价(different error cost, DEC), 即赋予少数类和多数类不同的惩罚因子, 从而在进行不平衡分类时, 通过更大的误分类代价来突出少数类样本的重要性, 由此降低不平衡率对支持向量机分类器偏向性的影响.受到文献[7, 15]的启发, 提出改进的加权SVM算法.对不同样本采用不同的权重系数, 不同类别赋予不同的权值, 从而形成不同的惩罚系数, 减少了样本分布不平衡时对主动学习和分类精度的影响.原始最优化问题可以描述如下:
| $ \begin{array}{l} \mathop {\min }\limits_{\omega, b, \xi } \;\;\;\frac{1}{2}{\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + C\left( {{\lambda _i}\sum\limits_{i = 1}^n {{s_i}{\xi _i}} + \lambda _j^*\sum\limits_{j = n + 1}^{n + k} {s_j^*\xi _j^*} } \right);\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\forall _{i = 1}^n{y_i}\left( {\mathit{\boldsymbol{\omega }}\cdot{\mathit{\boldsymbol{x}}_i} + b} \right) \ge 1-{\xi _i}, \;\\ \forall _{j = n + 1}^{n + k}\widehat {{y_i}}\left( {\mathit{\boldsymbol{\omega }}\cdot{\mathit{\boldsymbol{x}}^*}_i + b} \right) \ge 1-{\xi ^*}_i, \;\;\\ \forall _{i = 1}^n{\xi _i} \ge 0, {\rm{ }}\forall _{j = n + 1}^{n + k}{\xi ^*}_i \ge 0. \end{array} $ | (11) |
式中:si、sj*分别为已标注样本和未标注样本中不同样本的权重, λi、λj*为类的权重,
| $ \begin{array}{l} \mathop {\max }\limits_\alpha \sum\limits_{i = 1}^{n + k} {{\alpha _i}-\frac{1}{2}} \sum\limits_{i = 1}^{n + k} {\sum\limits_{j = 1}^{n + k} {{\alpha _i}{\alpha _j}{y_i}{y_j}K\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right)} } ;\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\sum\limits_{i = 1}^{n + k} {{\alpha _i}{y_i}} = 0;\\ \;\;\;0 \le {\alpha _i} \le {\lambda _i}{\mathit{\boldsymbol{s}}_i}C, \;\;i = 1, 2, ..., n;\\ \;\;\;0 \le {\alpha _j} \le \lambda _j^*\mathit{\boldsymbol{s}}_j^*C, \;\;j = n + 1, ..., n + k; \end{array} $ | (12) |
求得最优解α*=[α1*, α2*, …, αn+k*]T.
计算
| $ {\mathit{\boldsymbol{\omega }}^*} = \sum\limits_{i = 1}^{n + k} {\alpha _i^*{y_i}{\mathit{\boldsymbol{x}}_i}.} $ | (13) |
选择α*的一个正分量αj*, 计算
| $ {b^*} = {y_j}-\sum\limits_{i = 1}^{n + k} {\alpha _i^*{y_i}K\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right).} $ | (14) |
求得分类超平面
| $ {\mathit{\boldsymbol{\omega }}^*} \cdot \mathit{\boldsymbol{x}} + {b^*} = 0. $ | (15) |
最终构造的决策函数为
| $ f\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm sgn}} \left( {\sum\limits_{i = 1}^{n + k} {\alpha _i^*{y_i}K\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_i}} \right) + {b^*}} } \right). $ | (16) |
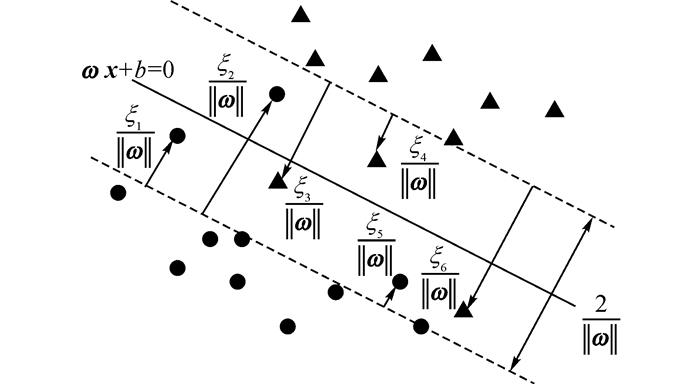
通过引入核技巧, 使用非线性变换将输入空间对应一个特征空间, 将超曲面模型对应于超平面模型, 从而将分类问题转化为在特征空间中求解线性支持向量机来完成.如图 4所示, 将对偶问题的解α*=[α1*, α2*, …, αn+k*]T中对应于αi*>0的样本点(xi, yi)的实例xi称为软间隔的支持向量.图中, 实线表示最优分离超平面, 虚线表示间隔边界, 圆点和三角点分别表示类别1和类别2的样本点.同时, 图 4中标出了实例xi到间隔边界的距离
|
图 4 软间隔的支持向量 Fig. 4 Support vectors in soft margin SVM |
加权支持向量机中, 单个样本的权重系数确定可以采取如下方法:初始时每个样本的权重参数取相同值, 即1, 相当于没有对样本引入权重的区分度.首先通过初始已有的少量已标注样本训练, 得到初始分类器f(0);然后在f(0)的基础上, 通过改进的主动学习算法中提出的综合rule值作为依据选择m个待学习样本, 并在标记后加入到训练样本集中.在此时得到的训练集中, 包含了初始训练样本和通过主动学习挑选出的新样本.由图 4可知, 一个二分类软间隔支持向量机学习得到的最优分离超平面为ω*·x+b*=0, 间隔边界的距离为
支持向量域描述方法(SVDD)[19]是一种单分类的算法, 通过找到能够包含该组数据最小半径的超球体, 以便能对这组数据进行描述, 奇异点应该分布在超球体的外面.为了减少奇异点的影响, 增加模型的鲁棒性, 使用松弛变量把它们排除在超球体的外面.本文提出基于SVDD, 确定加权支持向量机在处理多分类不平衡问题时各类别权值的计算方法.对于训练数据中的每一个类别构建一个超球体, 通过计算超球体的半径来找到合适的类权值.
SVDD的优化目标可以简单地描述为找到一个中心为a、半径为R的最小球面:
| $ F\left( {R, \mathit{\boldsymbol{a}}, {\xi _i}} \right) = {R^2} + C\sum\limits_i {{\xi _i}} . $ | (17) |
使得该球面满足
| $ \left. {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{x}}_i}-\mathit{\boldsymbol{a}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_i}-\mathit{\boldsymbol{a}}} \right) \le {R^2} + C\sum\limits_i {{\xi _i}} ;}\\ {{\xi _i} \ge 0.} \end{array}} \right\} $ | (18) |
除了个别极端数据外, 在支持向量域的数据描述中, 大部份训练数据都包含在球面内.
引入拉格朗日乘子, 化简后可以得到
| $ \begin{array}{l} L\left( {R, a, {\alpha _i}, {\xi _i}, {\gamma _i}} \right) = {R^2} + C\sum\limits_i {{\xi _i}}-\\ \sum\limits_i {{\alpha _i}} \left\{ {{R^2} + {\xi _i}-\left( {\left\| {\mathit{\boldsymbol{x}}_i^2} \right\|-2\mathit{\boldsymbol{a}}\cdot{\mathit{\boldsymbol{x}}_i} + {{\left\| \mathit{\boldsymbol{a}} \right\|}^2}} \right)} \right\} - \sum\limits_i {{\gamma _i}{\xi _i}} . \end{array} $ | (19) |
求取L对R、a、ξi的偏导数, 并取值为0,
| $ \left. \begin{array}{l} \frac{{\partial L}}{{\partial R}} = 0:\sum\limits_i {{\alpha _i} = 1;} \\ \frac{{\partial L}}{{\partial \mathit{\boldsymbol{a}}}} = 0:\mathit{\boldsymbol{a}} = \frac{{\sum\nolimits_i {{\alpha _i}{x_i}} }}{{\sum\nolimits_i {{\alpha _i}} }} = \sum\limits_i {{\alpha _i}{x_i};} \\ \frac{{\partial L}}{{\partial {\xi _i}}} = 0:C-{\alpha _i}-{\gamma _i} = 0. \end{array} \right\} $ | (20) |
| $ \left. \begin{array}{l} \max \;L = \sum\limits_i {{\alpha _i}\left( {{\mathit{\boldsymbol{x}}_i} \cdot {\mathit{\boldsymbol{x}}_i}} \right)-\sum\limits_{i, j} {{\alpha _i}{\alpha _j}\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right);} } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\forall i, 0 \le {\alpha _i} \le C, \sum\limits_i {{\alpha _i} = 1.} \end{array} \right\} $ | (21) |
支持向量是式(21) 中满足0 < αi < C的数据点, R是任意一个支持向量到中心点a的距离.通过SVDD求取得到的半径R描述了每一个类别的样本分布特性.由于分类平面会向少数类即分布更紧密的类别倾斜, 为了平衡样本数据, 取半径R的倒数为每个类别的权重λ.通过如上的参数求取和设定方法, 充分考虑了样本点在特征空间的分布情况对于分类面倾斜的影响, 得到了一个能够处理不平衡数据的改进加权支持向量机.
3 算法描述基于改进的BvSB和改进的WSVM的故障分类算法描述如下:初始时, 总样本集主要由两部分构成:少量的已标注样本和大量的未标注样本.首先通过已标注样本集来训练加权支持向量机, 可以得到一个初始的分类模型.通过基于平均密度的孤立点检测方法找到未标注样本集中的孤立点并从主动学习的候选样本中删除, 并以综合评价样本代表性和信息度的选择指标作为依据, 从未标注样本中选取多个最有利用价值的样本提交给领域专家进行标注并将标注后的样本迭代添加到已标注样本集中形成新的不断扩展的训练样本集.用扩展后的已标注样本集来训练得到新的分类模型, 循环多次执行直到加权支持向量机的分类精度或者最大的迭代次数达到了初始设定值.
具体步骤如下所示.
输入:已标注样本集L, 未标注样本集U, 每轮迭代时主动学习挑选的样本数m, 期望分类精度η, 最大迭代次数tmax, 加权支持向量机中每个样本的权值si, 每种类别的权值λi以及支持向量机中的相关参数.
输出:对于当前已标注样本集训练得到的分类模型的分类准确率.
1) 初始化所有输入参数.用现有的已标注样本训练加权支持向量机得到初始分类模型f(0), 计算该分类模型的分类准确率.
2) 判定是否满足结束迭代训练的条件.分别对迭代次数和分类准确率进行判定, 若满足, 则跳出循环结束学习, 不满足, 则转步骤3).
3) 对未标注样本集U, 依据式(3)~(7) 计算每个未标注样本的邻域样本密度与未标注样本集的平均样本密度, 若求得的样本邻域密度远小于总体平均密度, 则判定该样本为孤立样本, 从未标注样本集中删除, 不再进入待学习的行列.
4) 依据式(2) 计算第t轮迭代时剩余的未标注样本集Ut-1(t=1, 2, …)中, 所有剩余未标注样本的BvSB即最优次优类属概率差值, 将该值作为信息度度量的依据;依据式(8)、(9) 计算所有剩余未标注样本与其相似性最大的k个已标注样本的平均余弦距离, 本文中k取5, 将该值作为代表性度量的依据.
5) 依据式(10) 计算标准化处理后能综合评价待学习样本信息度和代表性的指标值rule.
6) 依据rule对当前所有未标注样本进行排序, 第t轮迭代中将值最小的前m个样本选取作为待学习样本集utAL.
7) 将第t轮选择的utAL提交给领域专家进行标注, 同时对有标签训练集和无标签训练集进行更新:Lt=Lt-1∪{utAL}, Ut=Ut-1\{utAL}.
8) 用更新后的已标注样本集训练加权支持向量机, 首先找到更新后的训练集样本中所有位于分类模型f(t-1)的分类间隔中间的样本点, 将这部分样本点赋予相对于间隔外样本点两倍的权重, 同时将不同类别的样本构成的超球体求取分布半径作为惩罚因子选取的依据, 并将迭代次数t=t+1, 重新训练得到新的分类模型f(t), 并计算新模型的分类准确率.
9) 判定是否满足结束迭代训练的条件.分别对迭代次数和分类准确率进行判定, 若满足, 则跳出循环结束学习;不满足, 则转步骤3).
4 实验及相关分析TE过程是田纳西伊斯特曼化学品公司创建的, 是基于一个真实化工过程建立的仿真平台[20].该过程较好地模拟了实际工业过程运行的许多特征, 常常作为故障诊断领域的一个标准问题来研究.TE过程包含21个预设定的故障来模拟常见异常状况, 其中16个是已知的, 5个是未知的[21].
4.1 实验设置如表 1所示,从TE数据中选择3组比较常见的故障(见表 2)作为实验数据集, 验证本文提出的基于改进主动学习和改进加权支持向量机算法的有效性.表 2中,Ns、Nc分别为样本数和特征数,Nas为每轮主动学习挑选样本个数.数据集的描述如下.
| 表 1 TE过程故障列表 Table 1 Process disturbances in TE |
| 表 2 工业故障识别实验数据 Table 2 Fault classification Experimental setup |
为了验证算法的正确性和有效性, 通过实验比较了多种算法的性能, 包括随机采样(random)、信息熵度量(entropy)采样、最优次优概率差度量采样(bvsb)、改进的BvSB采样(ibvsb)、基于BvSB和加权支持向量机(WSVM)采样(bvsb-wsvm)和基于改进的BvSB和改进的加权支持向量机(WSVM)采样(ibvsb-wsvm).其中, 前四种采样方法都使用的是标准支持向量机作为分类器.所有用于实验的样本集, 随机选择其中一半的数据作为训练集, 另外一半的数据为测试集.训练集中已标记的比例均为10%.在进入分类模型训练之前, 考虑到样本集的特征维数较高, 通过PCA对数据进行有效的预处理, 保持数据信息度的同时将其映射至低维空间, 降低了计算复杂度, 并去除数据噪声.
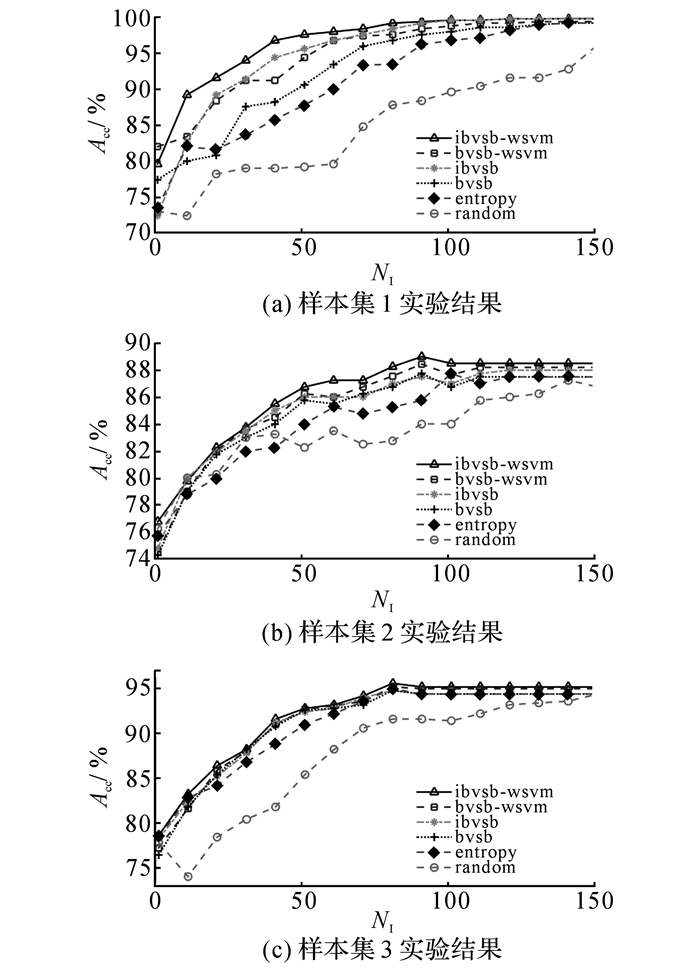
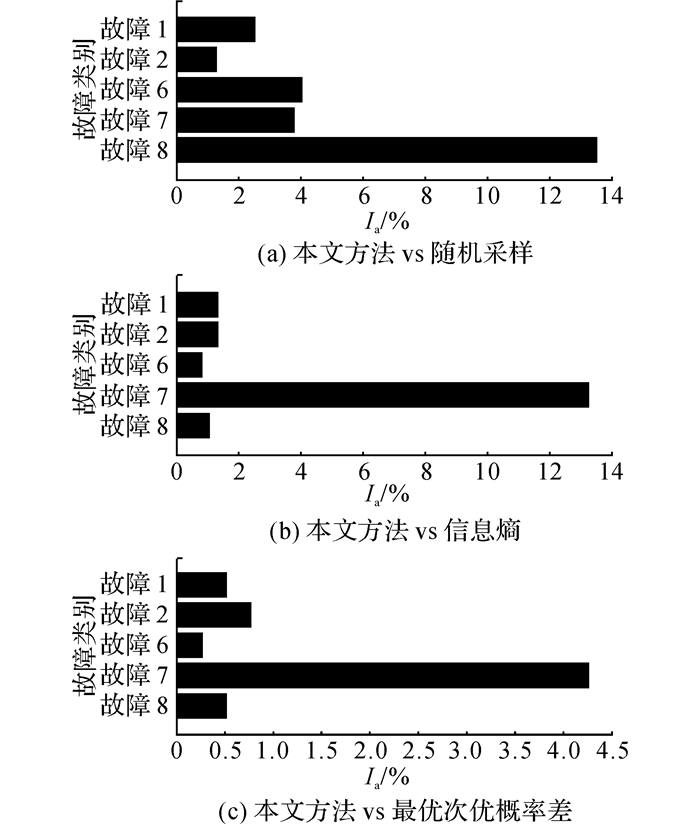
4.2 实验结果图 5中,NI为迭代次数,Acc为准确率.从图 5可以看出, 随着主动学习的不断迭代进行, 分类器的训练集不断扩展, 分类性能有效地得到改善.在迭代的前期, 可能各种算法的区别并不能明显的体现, 这是因为有监督学习训练样本量太小时, 分类性能都不会太好.但是也可以明显看出, 各种主动学习挑选的样本对于分类器的改善都明显地优于随机采样, 说明以信息度作为采样依据是有意义的.通过(ibvsb-wsvm)和(bvsb-wsvm)、(ibvsb-wsvm)和(ibvsb)以及(bvsb-wsvm)和(bvsb)的结果对比, 可以更加清晰地看到, 无论是主动学习的样本选择机制, 还是不平衡支持向量机中独立样本权值和类别惩罚因子的确定, 本文提出的方法都取得了更好的效果.综合实验结果可以看出, 本文提出的基于改进的BvSB和改进的WSVM的主动学习和故障分类算法, 因为综合考虑了孤立点, 样本的代表性和信息度, 以及类不平衡数据对于分类器分类精度的影响, 通过有效的权值参数求取, 在迭代次数相同时, 可以获得更高的分类准确率.且在迭代到一定数量后分类准确率趋于一个稳定值时, 此时的故障分类精度往往优于使用原始标准支持向量机得到的结果.以样本集2为例, 图 6给出在进行一定次数的迭代之后, 本文方法相对于现有算法在各个类别上分类准确率提高的具体数值.图中,Ia为提高的准确率.
|
图 5 主动学习算法在各数据集上的性能比较 Fig. 5 Classification accuracy comparison among different active learning methods on multiple datasets |
|
图 6 改进的BvSB+WSVM与其他算法在样本集2上各类别的分类准确率比较 Fig. 6 Classication accuracy comparison for each class in dataset2 between modified BvSB+WSVM and other approaches |
为了更直观地说明本文算法在节省人工标注负担上所起的作用, 表 3给出各算法在以上各数据集上达到相同分类准确率时需要通过人工标注的样本个数.表中,N为人工标记样本个数.由表 3可以看到, 本文提出的算法在达到相同的故障检测和分类准确率时, 需要专家标注的样本数明显少于其他算法, 可以有效地节约人工标注的时间和成本.
| 表 3 达到相同分类准确率时各算法需要标记的样本数 Table 3 Number of samples needed to be labeled for different approaches when achieving same classication accuracy on multiple datasets |
由于在流程工业过程中, 故障样本标注的代价非常昂贵, 为了减少样本的标注代价, 本文提出了一种有效的通过主动学习的策略来解决标注问题的途径.该算法综合考虑了待标注样本的信息度和代表性, 并剔除了其中的孤立点样本, 更高效的达到通过少量样本标注就能快速提高分类器性能的目的.首先, 根据样本对支持向量机作用的不同, 赋予各个样本不同的权重, 对于学习得到的分类模型的实际性能有了促进和提高.同时, 由于在实际的流程工业过程中, 获取的正常样本与故障样本以及各类别故障样本的个数和分布往往是不平衡的, 且在主动学习过程中, 不是各类别依次学习, 所以也会形成样本数据的不平衡.通过充分考虑样本分布对于分类面倾斜的影响, 构建每个类别的超球体, 用求取的半径参数作为惩罚因子选择依据.在寻找最优分类面时, 由于综合考虑对训练集中的不同样本和不同类别赋予了不同的权重参数, 得到了改进的加权支持向量机作为分类模型, 有效避免了主动学习过程中采集到重复、无意义样本的问题, 同时提高了分类准确率.将所提出的方法用于TE过程的故障分类识别, 实验结果验证了方法的有效性和可行性.完全通过主动学习来进行样本的标注会花费人力成本, 如何把人工标注和有可信度的机器自动标注结合起来, 将是今后工作中的一个重要研究方向.
| [1] | JAIN P, KAPOOR A. Active learning for large multi-class problems[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009. |
| [2] | DASGUPTA S. Coarse sample complexity bounds for active learning[J]. Neural Information Processing Systems, 2005, 18: 235–242. |
| [3] |
唐明珠, 阳春华, 桂卫华. 基于改进的QBC和CS-SVM的故障检测[J].
控制与决策, 2012, 27(10): 1489–1493.
TANG Ming-zhu, YANG Chun-hua, GUI Wei-hua. Fault detection based on modified QBC and CS-SVM[J]. Control and Decision, 2012, 27(10): 1489–1493. |
| [4] | YAN Z, CHEN J. Enhancing quality of statistic monitoring models by training set eesign with active learning approach[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 151(2016): 201–218. |
| [5] | TONG S, KOLLER D. Support vector machine active learning with applications to text classification[J]. Journal of Machine Learning Research, 2012, 2(1): 45–66. |
| [6] | WANG R, KWONG S, CHEN D. Inconsistency-based active learning for support vector machines[J]. Pattern Recognition, 2012, 45(10): 3751–3767. DOI:10.1016/j.patcog.2012.03.022 |
| [7] |
徐海龙, 别晓峰, 冯卉, 等. 一种基于QBC的SVM主动学习算法[J].
系统工程与电子技术, 2015, 37(12): 2865–2871.
XU Hai-long, BIE Xiao-feng, FENG Hui, et al. Active learning algorithm for SVM based on QBC[J]. System Engineering and Electronics, 2015, 37(12): 2865–2871. DOI:10.3969/j.issn.1001-506X.2015.12.31 |
| [8] | COHN D A, GHAHRAMANI Z, JORDAN M I. Active learning with statistical models[J]. Journal of Artificial Intelligence Research, 1996, 4(1): 705–712. |
| [9] |
陈荣, 曹永锋, 孙洪. 基于主动学习和半监督学习的多类图像分类[J].
自动化学报, 2011, 37(8): 954–962.
CHEN Rong, CAC Yong-feng, SUN Hong. Multiclass image classification with active learning and semi-supervised learning[J]. Acta Automatica Sinica, 2011, 37(8): 954–962. |
| [10] | JOSHI A J, PORIKLI F, PAPANIKOLOPOULOS N. Multi-class active learning for image classification[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009. |
| [11] | PERRY T, BADER-EL-DEN M, COOPER S. Imbalanced classification using genetically optimized cost sensitive classifiers[C]//2015 IEEE Congress on Evolutionary Computation. Sendai: IEEE, 2015. |
| [12] | BURNAEV E, EROFEEV P, PAPANOV A. Influence of resampling on accuracy of imbalanced classification[C]//Proceedings of the 8th International Conference on Machine Vision. Barcelona:[s.n.], 2015. |
| [13] | YANG Y, MA Z, NIE F, et al. Multi-class active learning by uncertainty sampling with diversity maximization[J]. International Journal of Computer Vision, 2015, 113(2): 113–127. DOI:10.1007/s11263-014-0781-x |
| [14] |
施化吉, 周书勇, 李星毅, 等. 基于平均密度的孤立点检测研究[J].
电子科技大学学报, 2007, 36(6): 1286–1288.
SHI Hua-ji, ZHOU Shu-yong, LI Xing-yi, et al. Average density-based outliers detection[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(6): 1286–1288. |
| [15] |
金鑫, 李玉鑑. 面向非平衡数据处理的样例惩罚支持向量机[J].
武汉大学学报:理学版, 2012, 58(2): 139–143.
JIN Xin, LI Yu-jian. Support vector machine with example dependent costs for dealing with imbalanced data[J]. Journal of Wuhan University: Natural Science Edition, 2012, 58(2): 139–143. |
| [16] | GE Z, SONG Z, GAO F. Review of recent research on data-based process monitoring[J]. Industrial and Engineering Chemistry Research, 2013, 52(10): 3543–3562. DOI:10.1021/ie302069q |
| [17] | LIU Y, LIAN J, BARTOLACCI M R, et al. Density-based penalty parameter optimization on C-SVM[J]. The Scientific World Journal, 2014(2014): 851814. |
| [18] |
金鑫, 李玉鑑. 不平衡支持向量机的惩罚因子选择方法[J].
计算机工程与应用, 2011, 47(33): 129–133.
JIN Xin, LI Yu-jian. Error-cost selection for biased support vector machines[J]. Computer Engineering and Applications, 2011, 47(33): 129–133. DOI:10.3778/j.issn.1002-8331.2011.33.038 |
| [19] | TAX D M, DUIN R P. Support vector data description[J]. Machine Learning, 2004, 54(1): 45–66. DOI:10.1023/B:MACH.0000008084.60811.49 |
| [20] | DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers and Chemical Engineering, 1993, 17(3): 245–255. DOI:10.1016/0098-1354(93)80018-I |
| [21] |
石向荣. 面向过程监控的非线性特征提取方法研究[D]. 杭州: 浙江大学, 2014.
SHI Xiang-rong. Study on nonlinear feature extraction for process monitoring[D]. Hangzhou: Zhejiang University, 2014. |



