2. 浙江树人大学 信息科技学院, 浙江 杭州 310015
2. College of Information Technology, Zhejiang Shuren University, Hangzhou 310015, China
重大装备导电结构件的亚表面缺陷的检测问题, 是航空航天、轨道交通、材料加工、制造装配等重要领域需要研究解决的课题[1-3].目前, 可使用的常规无损检测方法有很多种, 如射线法、渗透法、超声法、电磁超声法和涡流法等, 但是单一检测方法具有各自的特点和适用范围, 对于亚表面不同位置、尺寸微小、扩展角度多样的复杂缺陷, 采用单一无损检测方法无法获得稳定可靠的检测信号[4-6].
电涡流(eddy current test, ECT)和超声(ultrasonic testing, UT)是两种典型的无损检测方法, ECT有趋肤效应, 对导体表面缺陷的检测灵敏度高, 但检测的深度有限;UT存在表面检测盲区, 适用于较深缺陷的检测.综合利用ECT和UT的检测信息可以获得更准确的检测结论[7-8].目前, ECT/UT复合检测技术在国内外都有一定的研究, 刘轶等[9]用低频涡流和超声来检测振动筛的大梁裂纹;陈金贵等[10]设计了涡流-超声旋转探头, 对无缝钢管进行检测;Hans[11]在铁路检测系统中, 同时使用超声和涡流检测技术互相补充、佐证检测同一部位缺陷;刘轶等[9-11]论证了ECT/UT具有互补性, 使用两者对同一目标进行检测可以增加检测的范围和精度, 但两者检测数据的处理是独立进行的.Habibalahi[12]结合脉冲涡流检测和超声检测, 用人工神经网络对检测数据进行融合分析, 实现对受重物体的压力进行测量;Li等[13]提出基于D-S证据理论的ECT和UT数据融合方法, 对缺陷进行定量化评估;Habibalahi等[12-13]综合利用ECT和UT的检测信息, 采用多传感器数据融合技术来处理ECT/UT检测数据, 实现ECT和UT的复合检测.
目前, 国内外专家对多传感器数据融合技术进行了大量的研究, 提出了许多数据融合的算法[14-16], 如加权平均融合、人工神经网络、D-S证据理论等.马丽丽等[17]提出多传感器卡尔曼滤波融合算法, 具有较高的滤波精度, 能够成功消除测量的系统误差;Yue等[18]提出基于图像融合的模糊聚类方法, 能够重构更高精度的电气层图像;Balakrishnan等[19]提出基于离散小波变换的ECT融合成像技术, 提高了对缺陷的识别能力;Edwards等[20]设计一种加权逻辑函数, 对脉冲涡流和电磁超声检测数据进行融合, 对导体表面和近表面缺陷进行检测.ECT/UT信号融合属于异源信息融合问题, 考虑到ECT和UT对不同深度亚表面缺陷的检测能力不同的实际情况, 本文提出基于拟合方差的优化D-S融合模型, 根据拟合方差对证据权重进行修正, 能够在两者的检测结论存在不一致的情形下, 通过数据融合获得准确可靠检测结论, 解决不同深度的亚表面缺陷分类和定量化估计问题.
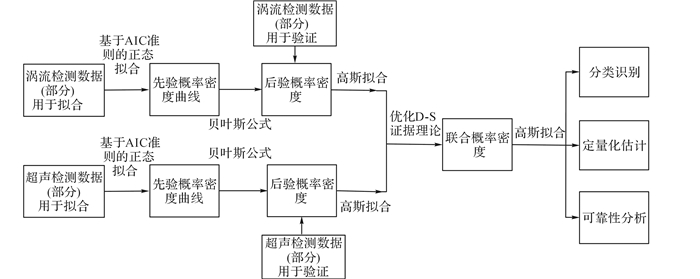
1 理论研究提出基于拟合方差的优化D-S证据理论的导电结构亚表面缺陷ECT/UT复合检测方法原理框图, 如图 1所示.
|
图 1 基于拟合方差的优化D-S证据理论的ECT/UT复合检测方法原理框图 Fig. 1 ECT/UT integrative detection principle block diagram based fitting variance optimized D-S evidence theory |
首先对不同深度的亚表面缺陷进行多次查扫, 获得检测数据.一部分检测数据用于拟合来获得先验概率密度, 利用基于赤池信息量准则(AIC准则)的正态拟合方法对样本数据进行正态拟合, 获得缺陷在不同埋藏深度条件下, 涡流和超声检测值的概率分布;另一部分检测数据用于验证, 将先验概率密度转换成不同检测值条件下, 缺陷埋藏深度的后验概率分布.然后对后验概率分布进行高斯拟合, 提取拟合方差对证据权重进行优化, 并用D-S证据理论对后验概率密度进行融合, 获得联合概率密度.最后对联合概率密度进行高斯拟合, 提取联合概率密度分布、联合概率密度拟合期望和联合概率密度拟合方差作为指标, 分别来表示缺陷的分类识别、定量化估计和检测的可靠性.
1.1 基于AIC准则的正态拟合方法在样本数据充足的条件下, 同一缺陷的检测数据分布具有正态特征.对于不同深度的缺陷, 本文认为正态分布的期望和方差是随缺陷埋藏深度变化的多项式函数[20], 多项式函数的阶数通过AIC准则确定.
赤池信息量准则(AIC)是在统计分析中有着广泛应用的信息量准则, 是赤池弘次在研究信息论特别是在解决时间序列的拟合定阶问题中提出来的[21].假设模型的误差服从正态分布, 计算公式为
| $ {\rm{AI}}{{\rm{C}}_k} = n{\rm{log}}({\rm{RSS}}/n) + 2k. $ | (1) |
式中:k为多项式的阶数, n为拟合数据的种类, RSS为拟合后的残差平方和.当两个拟合模型之间存在较大差异时, 该差异体现于上式右边第一项, 当第一项差异不显著时, 第二项起主要作用.增加自由参数能够提高拟合的优良性, 为了尽量避免出现过度拟合的情况, 最优模型应是AIC值最小的那个方案.
1.2 基于拟合方差的优化D-S证据理论D-S证据理论是一种决策层融合算法, 特点是可以将不完整的信息证据, 乃至有一定冲突的证据, 完成相应的推理或决策, 融合规则如下.
| $ \begin{array}{l} {m_1} \oplus {m_2}\left( C \right) = \\ \left\{ {\begin{array}{*{20}{c}} {0,}&{C = \varphi ;}\\ {\frac{1}{{1 - K}}\sum\limits_{A \cap B = C} {{m_1}\left( A \right)\cdot{m_2}(B),} }&{C \ne \varphi .} \end{array}} \right. \end{array} $ | (2) |
| $ K = \sum\limits_{A \cap B = \phi } {{m_1}\left( A \right)\cdot{m_2}(B).} $ | (3) |
式中:m1(A)和m2(B)为ECT和UT对亚表面缺陷检测得到的两类BPA, m1⊕m2(C)为融合后的联合概率密度分布, A、B、C为各证据对应的焦元, K为冲突因子.传统D-S证据理论认为每条证据的权重是相同的, 在实际情况中, 证据之间往往存在差异性, 某些证据需要被加强, 某些证据需要被弱化.本文提出用拟合方差对证据权重, 重新计算BPA, 再用D-S证据理论进行证据组合, 获得联合概率密度分布.
为了求取拟合方差, 先通过贝叶斯准则将先验概率转换获得后验概率, 以此作为独立证据的BPA(基本概率分布), 离散序列的贝叶斯公式为
| $ P\left( {{D_i}\left| A \right.} \right) = \frac{{P\left( {A\left| {{D_i}} \right.} \right)P\left( {{D_i}} \right)}}{{\sum\limits_j {\left( {A\left| {{D_j}} \right.} \right)P\left( {{D_j}} \right)} }}. $ | (4) |
式中:P(D)为某种缺陷存在的概率;P(A|D)为存在缺陷D的条件下, 检测值为A的概率;P(D|A)是在检测值为A的条件下, 存在缺陷D的概率.
对后验概率进行高斯拟合, 得到后验概率密度曲线, 并求取拟合方差.拟合方差可以体现正态分布概率集中度和置信区间的宽窄.在同样的检测阈值的前提下, 拟合方差越小.可见, 拟合方差与检测可靠性成反比关系, 对ECT和UT的拟合方差求倒数, 再进行归一化求得基于拟合方差的优化权重w(E)和w(U), 并用下式对BPA进行修正:
| $ \left. \begin{array}{l} m\left( {E\prime } \right) = w\left( E \right) \times m\left( E \right) + \left[{1-w\left( E \right)} \right] \times m\left( U \right), \\ m\left( {U\prime } \right) = w\left( U \right) \times m\left( U \right) + \left[{1-w\left( A \right)} \right] \times m\left( U \right). \end{array} \right\} $ | (5) |
式中:m(E)和m(U)为ECT和UT的BPA分布.将由权重缩小而产生的冗余概率以一定比例分配给证据空间, 以凸显大权重证据的概率分布特征, 并保证概率和为1.
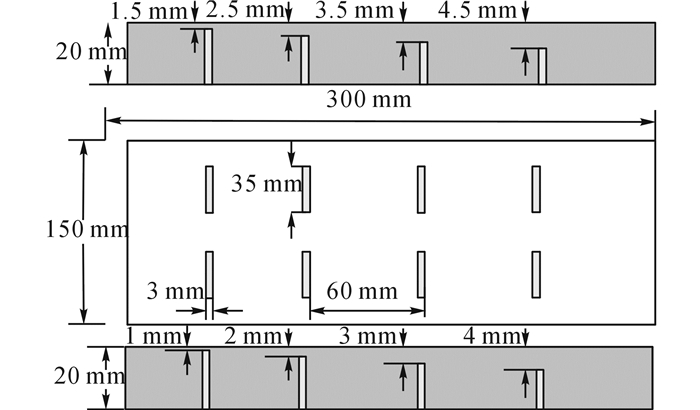
2 实验设计与数据分析 2.1 实验设计实验采用的试件如图 2所示, 300 mm×150 mm×20 mm的铝板试件上, 包含长度为35 mm、宽度为3 mm、离表面距离为1、1.5、2、2.5、3、3.5、4、4.5 mm的缺陷.
|
图 2 试件与缺陷示意图 Fig. 2 Diagrammatic sketch of specimen and defect |
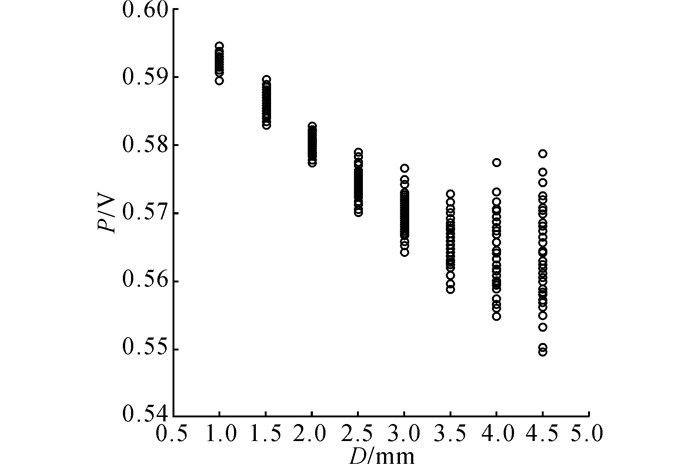
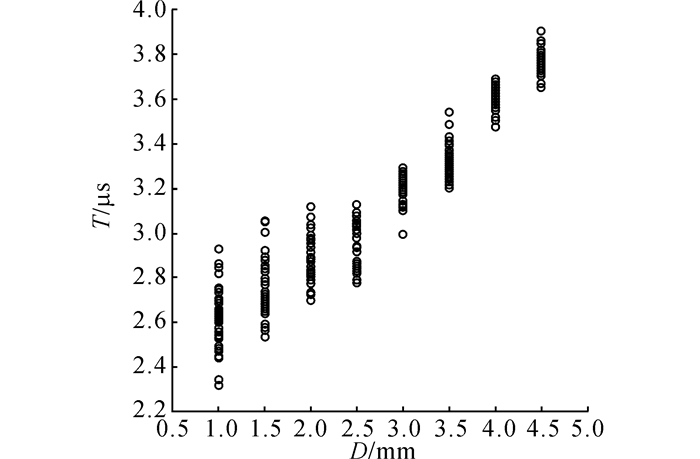
对于ECT实验, 根据经验知识可知, 激励频率fe为400 Hz, 提离l在0.10~0.20 mm下随机变化;对于UT实验, 采用食用油作为耦合剂, 根据经验知识可知, 采样频率fu为6 MHz.用涡流和超声波对一组缺陷检测50次, 获得50组涡流测试信号和50组超声测试信号, 对涡流信号提取波形峰值电压、对超声信号提取第一缺陷波(first defect wave, FDW)回波时间作为各自的特征, 40组用作数据拟合, 10组用来验证结果.如表 1、2所示为随机抽取的10组涡流检测和超声检测获得的特征数据;如图 3、4所示为对应的检测特征数据的分布图.图中, D为缺陷埋藏深度, P为涡流检测特征, T为超声检测特征.
| 表 1 涡流信号峰值电压(fe=400 Hz, l=0.10~0.20 mm) Table 1 Peak voltage of ECT signal (fe=400 Hz, l=0.10~0.20 mm) |
| 表 2 超声信号第一缺陷波回波时间(fu=6 MHz) Table 2 FDW echo time of UT signal (fu=6 MHz) |
|
图 3 涡流信号峰值电压分布 Fig. 3 Peak voltage distribution of ECT signal |
|
图 4 超声信号第一缺陷波回波时间分布 Fig. 4 FDW echo time distribution of UT signal |
在获得ECT和UT的检测数据之后, 认为检测数据具有正态分布特征, 采用基于AIC准则的正态拟合方法来获得电涡流检测特征和超声检测特征的概率分布.如表 3、4所示为涡流检测特征数据和超声检测特征数据的期望和方差的AIC拟合值.
| 表 3 涡流检测特征数据期望和方差AIC拟合值 Table 3 AIC value of fitting expectation and variance of ECT feature |
| 表 4 超声检测特征数据期望和方差AIC拟合值 Table 4 AIC value of fitting expectation and variance of UT feature |
从表 3、4中, 取AIC值最小的k作为拟合阶数.可见, 对于ECT数据的期望和方差, 应分别采用线性拟合和三阶多项式拟合;对于UT数据的期望和方差, 都采用二阶多项式拟合, 确定以下的拟合公式(系数待定)[22]:
| $ \begin{array}{l} p\left( {y\left| x \right.} \right) = \frac{1}{{\sqrt {2{\rm{\pi }}} \left( {{a_2}{x^2} + {b_2}x + {c_2}} \right)}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{exp}}\left( {\frac{{-{{\left( {y-{a_1}{x^2}-{b_1}x - {c_1}} \right)}^2}}}{{2{{\left( {{a_2}{x^2} + {b_2}x + {c_2}} \right)}^2}}}} \right). \end{array} $ | (6) |
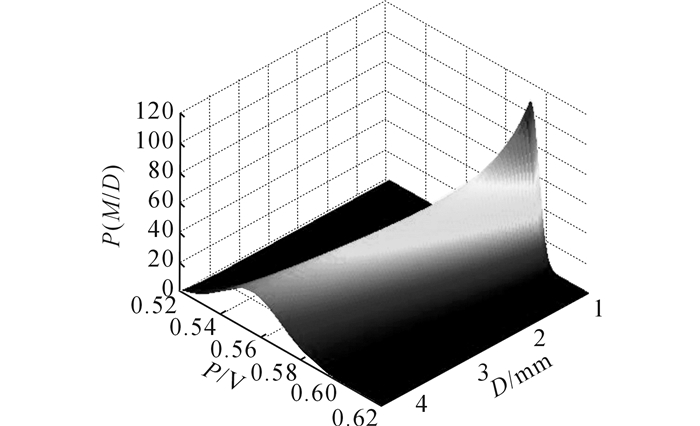
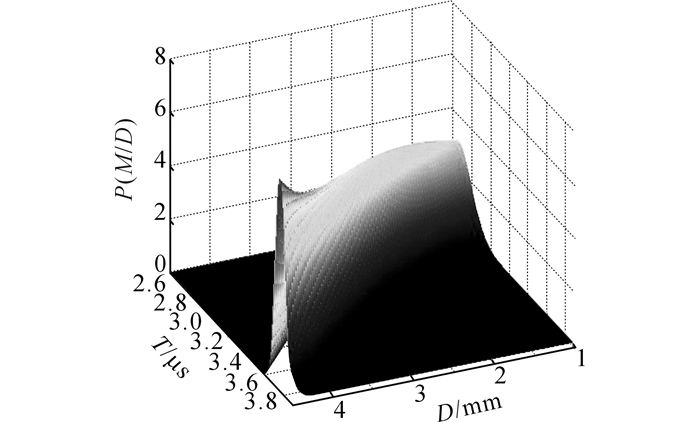
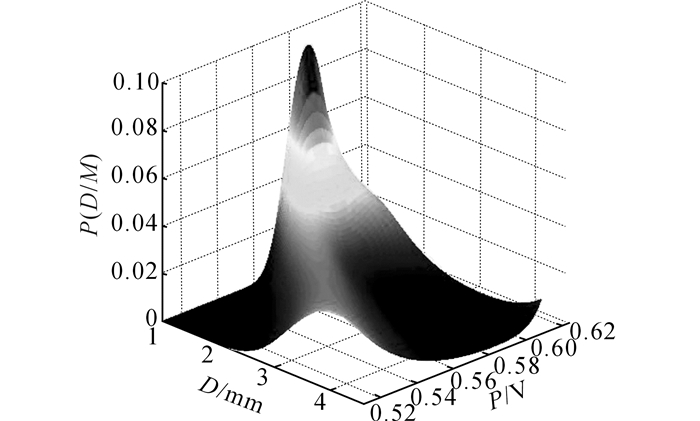
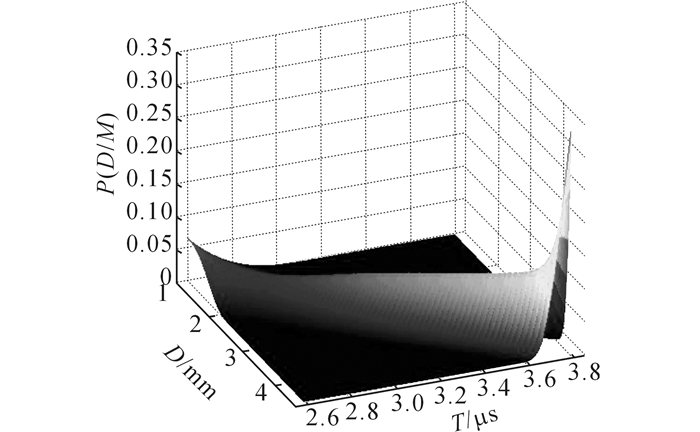
利用正态分布模型分别对涡流和超声的40组数据进行拟合, 确定正态分布模型的各个待定系数.其中, x为缺陷埋藏深度, y为检测值.对于涡流检测数据:a1=0, b1=-0.010 78, c1=0.602 2;a2=0.053 03, b2=-0.011 59, c2=0.002 388.对于超声检测数据:a1=-0.027 92, b1=0.165 8, c1=-2.278;a2=0.010 67, b2=-0.165 8, c2=0.294 1.涡流检测特征数据和超声检测特征数据的正态拟合先验概率密度P(M/D)分布如图 5、6所示, 涡流检测特征数据和超声检测特征数据的后验概率密度P(D/M)分布如图 7、8所示.
|
图 5 涡流检测特征数据正态分布 Fig. 5 Normal distribution of ECT feature |
|
图 6 超声检测特征数据正态分布 Fig. 6 Normal distribution of UT feature |
|
图 7 涡流检测特征数据后验概率分布 Fig. 7 Posteriori probability distribution of ECT feature |
|
图 8 超声检测特征数据后验概率分布 Fig. 8 Posteriori probability distribution of UT feature |
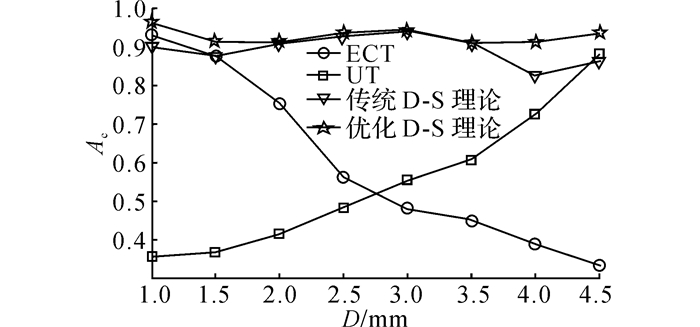
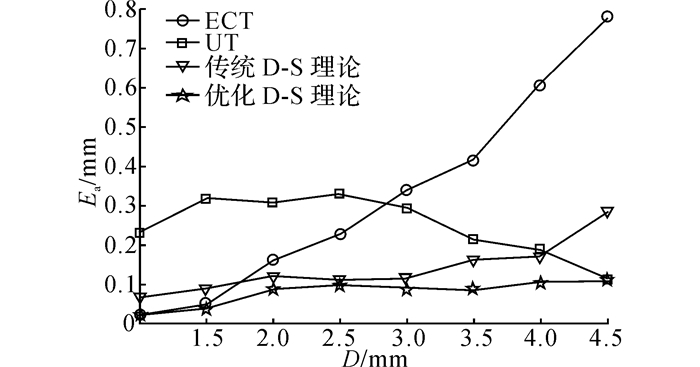
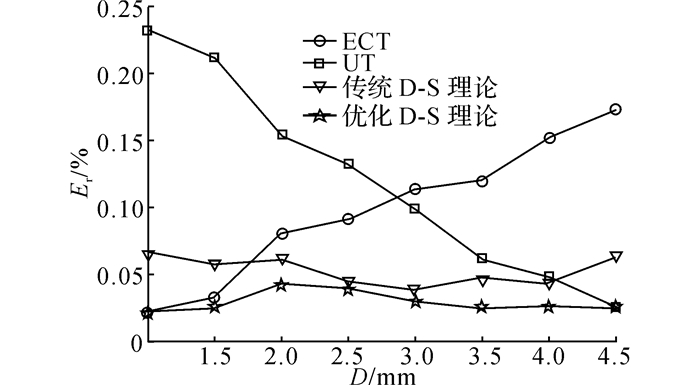
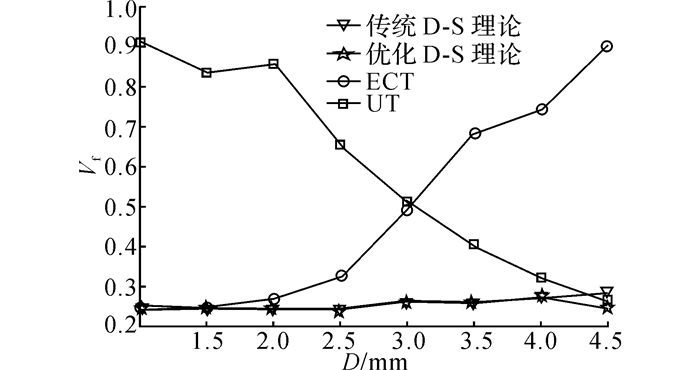
用余下的10组检测数据进行验证, 将检测值代入后验概率分布曲面, 得到对应的后验概率密度;利用常规D-S证据理论和优化D-S证据理论对后验概率密度进行融合, 获得联合后验概率分布, 以此作为8组不同深度的缺陷的分类结果, 并进行比较, 概率分布如表 5和图 9所示.可见, 复合检测的分类准确度Ac高于单一模式检测, 在某种检测方法对特定的缺陷检测能力较差的情况下, 用优化D-S证据理论的复合检测方法优于传统D-S证据融合.对后验概率密度和联合概率密度进行高斯拟合, 拟合的曲线(部分)如图 10所示.可见, ECT/UT复合检测的联合后验概率密度较集中, 拟合曲线比单一检测的后验概率密度曲线狭窄.本文认为, 正态拟合曲线的期望表示检测缺陷的埋藏深度;方差表示检测的可靠性, 如表 6、7和图 11、12所示为10组不同深度缺陷数据的定量化估计的平均误差(绝对误差Ea和相对误差Er), 如表 8和图 13所示为10组不同深度缺陷数据的后验概率密度曲线的平均拟合方差Vf.为了能够清楚地体现检测可靠性的变化, 对正态拟合曲线在拟合期望±0.3 mm的置信区间内的概率Pci进行计算, 结果如表 9所示.
| 表 5 不同埋藏深度缺陷单一检测和复合检测的分类准确度 Table 5 Classification accuracy for single and integrative method of different buried depth defects |
|
图 9 不同埋藏深度缺陷单一检测和复合检测的分类准确度 Fig. 9 Classification accuracy for single and integrative method of different buried depth defects |
| 表 6 不同埋藏深度缺陷单一检测和复合检测定量化估计绝对误差 Table 6 Quantitative estimates absolute error for single and integrative method of different buried depth defect |
| 表 7 不同埋藏深度单一检测和复合检测定量化估计相对误差 Table 7 Quantitative estimate relative error for single and integrative method of different buried depth defect |
| 表 8 不同埋藏深度缺陷单一检测和复合检测的平均拟合方差 Table 8 Average fitting variance for single and integrative method of different buried depth defects |
| 表 9 不同埋藏深度缺陷单一检测和复合检测拟合期望±0.3mm置信区间概率 Table 9 ± 0.3 mm confidence interval probability for single and integrative method of different buried depth defects |

|
图 10 不同埋藏深度缺陷单一检测和复合检测的后验概率拟合曲线 Fig. 10 Posteriori probability fitting curve for single and integrative method of different buried depthdefects |
|
图 11 不同埋藏深度缺陷单一检测和复合检测定量化估计绝对误差 Fig. 11 Quantitative estimates absolute error for single and integrative method of different buried depth defect |
|
图 12 不同埋藏深度缺陷单一检测和复合检测定量化估计相对误差 Fig. 12 Quantitative estimate relative error for single and integrative method of different buried depth defect |
|
图 13 不同埋藏深度缺陷单一检测和复合检测的拟合方差 Fig. 13 Fitting variance for single and integrative method of different buried depth defects |
从表 8、9和图 13可见, ECT/UT复合检测与单一检测相比, 对于2~4 mm下的缺陷, 检测的准确性和可靠性上都有较大提升, 优化D-S理论的复合检测方法的检测结果最准确.对于较浅的缺陷(2 mm以下)和较深的缺陷(4 mm以上), 基于传统的D-S理论的复合检测方法与单一ECT和UT的性能相近, 基于优化D-S理论的复合检测方法能够进一步地提高检测性能.
3 结语针对导电结构件的亚表面缺陷检测难题, 本文设计基于拟合方差的优化D-S证据理论的ECT/UT复合检测方法.提出基于AIC的拟合的方法, 获得独立的ECT和UT的概率分布曲线;提出根据拟合方差对证据权重进行优化, 利用D-S证据理论对后验概率密度进行融合获得联合概率密度分布, 实现ECT/UT复合检测.通过设计相关实验、分析检测数据、求取联合概率密度指标, 可以证明该方法对于不同深度的亚表面缺陷检测具有较好的准确性和可靠性, 缺陷分类准确度达90%以上, 缺陷定量化估计误差在5.5%以下, 拟合期望±0.3 mm置信区间概率在90%左右, 相比单一检测和基于传统的D-S理论的复合检测方法, 均有不同程度的提升.在实际应用中, 对于成形较复杂的亚表面缺陷, 可以先利用最优特征提取方法对ECT和UT数据进行特征提取, 再运用本方法进行复合检测, 在检测数据充足的情况下, 能够得到准确的检测结果.
| [1] | ARJUN V, SASI B. Optimization of pulsed eddy current probe for detection of sub-surface defects in stainless stell plates[J]. Sensors and Actuators, 2015, 26(3): 69–75. |
| [2] | BRUDAR B. How to distinguish surface and subsurface cracks using electromagnetic ndt methods[J]. NDT international, 1984, 17(4): 221–223. DOI:10.1016/0308-9126(84)90024-5 |
| [3] |
齐勇, 李勇, 陈振茂. 基于GMFM的脉冲涡流检测亚表面腐蚀缺陷成像技术[J].
空军工程大学学报:自然科学版, 2013, 14(5): 120–125.
QI Yong, LI Yong, CHEN Zhen-mao. Research of pulsed eddy current testing for defect imaging based on gradient magnetic field measurement[J]. Journal of Air Force Engineering University: Natural Science Edition, 2013, 14(5): 120–125. |
| [4] | DIRAISON Y, JOUBERT P Y, PLACKO D. Characterization of subsurface defects in aeronautical riveted lap-joints using multi-frequency eddy current imaging[J]. NDT and E International, 2009, 42(2): 133–140. DOI:10.1016/j.ndteint.2008.10.005 |
| [5] | JEFFERSON C, PRASHANTH A V. Damage quantification in polymer composites using a hybrid NDT approach[J]. Composites Science and Technology, 2013, 83(5): 11–21. |
| [6] | GRYS S, VOKOROKOS L. Size determination of subsurface defect by active thermograph-simulation research[J]. Infrared Physics and Technology, 2014, 62(2): 147–153. |
| [7] |
张清华. 基于超声和涡流的复合式无损检测技术[D]. 广州: 华南理工大学, 2010.
ZHANG Qing-hua. Technique of complex NDT based on ultrasonic and eddy current testing[D].Guangzhou: South China University of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10561-2010228930.htm |
| [8] |
李国厚. 导电结构涡流/超声检测与评估技术研究[D]. 杭州: 浙江大学, 2012.
LI Guo-hou. Study on ECT/UT and evaluation technology of the conductive structures[D]. Hangzhou: Zhejiang University, 2012. http://d.wanfangdata.com.cn/Thesis/Y2047880 |
| [9] |
刘轶, 许晓东. 基于超声与低频涡流技术的振动筛大梁裂纹检测方法研究[J].
煤矿机械, 2015(02): 45–51.
LIU Yi, XU Xiao-dong. Study on beam crack detection method for shaker based on ultrasound and low-frequency eddy[J]. Coal Mine Machinery, 2015(02): 45–51. |
| [10] |
陈金贵, 黄颖. 无缝钢管超声涡流联合探伤方法研究[J].
中国设备工程, 2013, 1(2): 88–94.
CHEN Jin-gui, HUANG Yin. Research of eddy current and ultrasonic joint inspection for seamless steel pipe[J]. China Plant Engineering, 2013, 1(2): 88–94. |
| [11] | HANS M T. Advantage of a combined ultrasonic and eddy current examination for railway inspection trains[C]//Proceedings of the ECNDT.[S.l.]: IEEE, 2006:176-188. |
| [12] | HABIBALAHI A M. Improving pulse eddy current and ultrasonic testing stress measurement accuracyusing neural network data fusion[J]. Science Measurement and Technology, 2015, 9(4): 514–521. |
| [13] | LI G H, HUANG P J, CHENG P H, et al. Application of multi-sensor data fusion in defects evaluation based on Dempster-Shafer theory[C]//Instrumentation and Measurement Technology Conference.[S. l.]: IEEE, 2011: 1-5. |
| [14] | LUIS F R, TIAGO M. A Bayesian approach for NDT data fusion: the Saint Torcato church case study[J]. Engineering Structures, 2015, 84(2): 120–129. |
| [15] | LIU J, TIAN G Y, et al. Investigation of thermal imaging sampling frequency for eddy current pulsed thermograph[J]. NDT&E International, 2014, 62(3): 85–92. |
| [16] |
阮晴, 罗飞路, 王鹏. 基于BP网络和DS证据理论的超声检测缺陷识别[J].
兵工自动化, 2011, 30(9): 72–76.
RUAN Qing, LUO Fei-lu, WANG Peng. Flaws identification in ultrasonic testing based on BP network and D-S evidence theory[J]. Ordnance Industry Automation, 2011, 30(9): 72–76. |
| [17] |
马丽丽, 张曼. 多传感器集中式增量卡尔曼滤波融合算法[J].
计算机工程与应用, 2014, 3(11): 229–232.
MA Li-li, ZHNAG Man. Multi-sensor centralized incremental Kalman filtering fusion algorithm[J]. Computer Engineering and Applications, 2014, 3(11): 229–232. DOI:10.3778/j.issn.1002-8331.1308-0396 |
| [18] | YUE S, WU T. Fuzzy clustering based ET image fusion[J]. Information Fusion, 2013, 14(7): 487–497. |
| [19] | BALAKRISHNAN S, CACCIOLA M. Development of image fusion methodology using discrete wavelet transform for eddy current images[J]. NDT and E International, 2012, 51(12): 51–57. |
| [20] | EDWARDS R S, SOPHINB A, DIXONA S, et al. Data fusion for defect characterizations using a dual probe system[J]. Sensors and Actuators A: Physical, 2007, 31(14): 222–228. |
| [21] |
刘璋温. 赤池信息量准则AIC及其意义[J].
数学的实践与认识, 1980, 3: 65–73.
LIU Zhang-wen. Akaike information criterion AIC and its significance[J]. Mathematics in Practice and Theory, 1980, 3: 65–73. |
| [22] | HORN D, MAYO M R. NDE reliability gains from combining eddy-current and ultrasonic testing[J]. NDT and E International, 2010, 21(33): 351–362. |



