2. 西北工业大学 计算机学院, 陕西 西安 710072
2. School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China
随着智能移动设备(智能手机、平板电脑等)的广泛普及, 利用内置的位置感知装置进行移动轨迹数据的记录与存储.通过挖掘分析其中的内涵式价值信息, 为基于位置的服务(location-based service, LBS)相关应用提供知识支撑, 逐渐成为普适计算领域的一项热点问题.近年来, 已吸引了来自学术界与工业界的广泛关注与深入研究.通过对历史移动轨迹数据中所蕴含的价值知识进行挖掘分析, 从中抽取出具有大概率意义上的普适性行为模式, 可以为智能交通、商业精准营销、军事物流等领域提供移动轨迹预测方面的决策依据[1-6].
Chen等[7-8]通过移动模式抽取与模式树索引, 构建研究面向特定用户的移动轨迹预测问题.Tiwari等[9]借助于地图匹配技术, 将原始移动轨迹转换为以路段表示的序列数据, 同时通过计算查询轨迹与历史轨迹之间基于距离的相似度矩阵实现轨迹预测的目的.Simmons等[10]通过对驾驶员驾驶习惯的观察学习, 构建隐马尔科夫模型以实现对特定用户移动轨迹的预测.Monreale等[11]基于移动轨迹模式挖掘, 利用决策树构建预测器实现对移动轨迹的预测过程.在现实中, 由于数据获取渠道的有限性与单一性, 同时考虑到移动对象的隐私保护问题, 实际所获取到的移动轨迹数据相对于其所覆盖的城市空间环境而言, 具有稀疏、不均匀以及不充分的特征[12-13].这些特征不仅表现在轨迹位置点相对于空间区域的整体覆盖不充分, 同时表现在数据集中分布与数据缺失现象在不同区域同时并存.上述特征对于移动轨迹建模与知识发现带来了难以回避的挑战与困难.此外, 随着城市规模的不断扩展以及城市道路交通情况的复杂化, 移动轨迹数据的稀疏性特征将会在应用层进一步凸显.
针对上述移动轨迹空间分布所存在的稀疏、不均匀以及不充分等特性, 如何在数据有限的客观约束条件下充分发掘其中所蕴含的内涵价值与规律知识?如何从多角度、多层次实现对移动模式的准确刻画与建模过程, 以在最大程度上支撑移动对象未来轨迹预测方面的现实应用问题?在稀疏分布条件下, 如何有效克服基于历史轨迹相似度计算与模式匹配方法所构建在线轨迹预测模型的内在缺陷?考虑到上述问题, 本文提出双层多粒度移动轨迹知识发现与模式挖掘方法, 分别在粗粒度层与细粒度层对历史移动轨迹数据进行建模挖掘.以所发掘的多粒度知识为基础, 融合构建在线移动轨迹混合式预测模型.通过现实数据(深圳市出租车GPS采集数据集)的实验测试, 验证了本文方法的有效性与适用性.
1 移动轨迹双层多粒度语义建模移动轨迹数据空间分布的稀疏性使其具有内在的多粒度建模与表示的客观需求.本文定义区域级粗粒度与路网节点级细粒度的双层多粒度语义模型, 分别以覆盖空间多粒度划分集合R与城市路网节点集合V对原始移动轨迹数据进行数据语义转换.通过对语义化轨迹数据的模式挖掘与抽取, 产生对移动轨迹特征模式在不同层次上的刻画与知识表述.
1.1 移动轨迹覆盖空间区域多粒度划分移动轨迹在空间维度的无限连续特性在轨迹间近似性比较分析、有限元素简约表示以及频繁模式特征提取等方面造成了较大的阻碍.若对每条轨迹数据所表征的地理空间数据进行连续化链表表达, 则会占用大量的内存空间资源.此外, 由于移动个体、客观环境以及采样过程多重因素的相互影响, 即使同一个用户不同时间在相同的路径上也不可能产生完全一致的两条轨迹.有必要对移动轨迹所覆盖的空间区域进行离散化划分, 以生成一组互不重叠的空间完全划分集合.具体的形式化描述如下:对于所限定的移动轨迹覆盖空间范围S, 通过离散化划分操作得到有限元素集合, 则S=∪Ri, 1≤i≤m, 且满足Ri∩Rj=Ø, i≠j, 其中Ri(1≤i≤m)为划分后得到的离散区域元素.
现有的移动轨迹建模、模式分析以及相关应用方面的文献大多采用等尺度规则网格划分的方法, 对覆盖空间范围S进行离散化划分.这种传统方法未能考虑移动轨迹在空间范围S上的分布特征, 对于稀疏性分布移动轨迹而言, 将会产生部分划分区域轨迹点集中分布、部分划分区域极少甚至没有轨迹点的情况.等尺度规则网格空间划分方法无法对轨迹点集中分布的区域作进一步的细粒度分解与区分, 因而不能从移动群体行为特征的意义上得出更精确的模式表示与知识解释.同时, 未包含任何轨迹空间点的网格单元作为后续语义数据转换与分析过程中的无效元素, 对于空间网格划分过程、离散空间数据结构存储以及算法运行效率等方面而言均属于冗余数据.
针对等尺度规则网格空间划分存在的缺陷, 已有部分研究在空间划分过程中结合移动轨迹数据地理空间分布特征, 实现与轨迹点空间分布相匹配的多粒度空间划分过程[13].通过多粒度空间划分可以有效应对数据稀疏性分布所带来的相关问题, 同时可以有效区分城市不同功能区定位所带来的热点区域.以k-d tree数据结构实现对轨迹覆盖空间的多粒度划分过程, 作为一种分割k维数据空间的数据结构表示方法, k-d tree通过逐级展开的递归过程实现对超平面空间的自适应划分.对于移动轨迹空间位置点, k-d tree划分方法分别以二维平面的x轴与y轴, 对所覆盖的空间范围进行分割.在每一次分割的过程中, 保证所分割的两个对称子空间所包含的轨迹位置点的数量相等, 如此递归运行直至满足用户所给定的空间划分数目.
在得到k-d tree空间离散划分之后, 基于离散划分区域集合, 利用地理空间位置匹配的方法实现对原始移动轨迹数据进行语义转换, 即将原始轨迹Tr转换为以离散区域元素表示的语义序列数据.对转换后的语义序列数据进行频繁序列模式挖掘过程, 以抽取粗粒度区域层移动轨迹行为模式.对应的模式挖掘算法在下一节进行相应地阐述.
1.2 基于地图匹配的移动轨迹路网节点映射区域层次的移动轨迹模式反映的是移动群体在离散空间区域载体上的移动规律与模式, 其对于稀疏分布条件下的移动模式抽取可以显著扩展内在的空间覆盖范围, 同时可以有效提升在线预测轨迹与历史移动模式知识之间的匹配程度.粗粒度的区域层次知识发现对于移动模式的空间表示精确性而言具有一定程度的损失, 同时单一粗粒度层次的移动轨迹模式表示对于稀疏条件下的移动轨迹预测过程知识支撑而言较有限.考虑在不同粒度层次上对群体移动行为模式进行多角度的特征抽取与规律刻画, 有效增强对群体移动行为的规律认识与理解, 有效扩展对轨迹预测应用方面的模式储备.具体而言, 借助于外在的城市路网地图数据, 在细粒度的路网层次上对群体移动行为模式进行表示与模式挖掘, 作为粗粒度区域级上的移动轨迹模式的有益补充与增强.
考虑城市路网拓扑数据G={V, E}, 其中V={vi, i=1, 2, …, n}表示路网节点集合, E={ei, i=1, 2, …, m}表示路径段, ei的两端分别为相应的路网节点.基于地图匹配方法, 原始移动轨迹数据可以转化为以路网节点为元素的时间序列数据Tr′={…(vi, ti)…}, 其中vi表示路网节点, ti为相应的时间戳信息.需要注意的是, 本文的匹配过程剔除了路网拓扑结构数据中的路径E信息, 只利用了路网节点V信息, 其原因在于一旦确定了与某个路段ei相连接的两个端点(路网节点), 则在这一路段上的移动轨迹形态可以通过线性插值的方式进行直接拟合.此外, 可以在极大程度保证原始轨迹数据形态特征的基础上, 有效地约简轨迹数据的规模.
2 移动轨迹多粒度知识发现与预测 2.1 移动轨迹多粒度知识发现基于上述粗粒度移动轨迹区域建模表示与细粒度路网节点映射表示的双层多粒度建模方法, 设计相应的移动轨迹模式挖掘算法.本文以序列模式挖掘算法为基础, 针对区域表示序列与路网节点序列挖掘相应的频繁移动模式.频繁移动模式定义为:Ri(vi)→Rj(vj), 其中Ri, Rj∈R, vi, vj∈V, 且i≠j, 其意味着移动对象按照时间先后顺序依次通过Ri离散区域(vi路网节点)与Rj离散区域(vj节点).下面给出多粒度双层移动轨迹模式挖掘算法.
算法1 双层多粒度移动模式挖掘算法.
输入:D={Tri, i=1, 2, …, k}
V={vi, i=1, 2, …, n};R={Ri, i=1, 2, …, m}
输出:Patt={Pi, i=1, 2, …, l}
FOR EACH Tri∈D DO
[Tr Ri, Tr Vi]←Transform(Tri, R, V)
END FOR
[Patt R, Patt V]←SeqMine(Tr R, sup/Tr V, sup′)
FOR EACH Patt R (Patt V) DO
TreeIndex←Contain(Patt V, Patt R)
Patt←TreeIndex
END FOR
所挖掘的细粒度移动轨迹模式与粗粒度区域层表示移动模式并非简单地属于相同移动模式在不同语义层次上的表示.原因如下.1) 粗粒度区域对细粒度路网节点具有语义层次包含关系, 在细粒度上的互不关联元素, 在更抽象的粗粒度语义层可能是具有强关联关系的元素对.2) 路网节点集合规模远大于离散划分空间集合, 因此原始GPS轨迹数据在路网节点语义转换序列数据中的分布会比在离散区域语义转换序列数据中的分布更稀疏.在粗粒度移动轨迹模式挖掘中的最小支持度的设置应大于细粒度移动轨迹模式挖掘中的最小支持度, 即sup>sup′.本文中, sup与sup′分别取10%和5%.
2.2 多粒度双层移动模式映射索引结构针对所挖掘的多粒度双层移动轨迹模式集合, 按照粗粒度离散区域表示在空间范围上对于细粒度路网节点的包含关系, 构建相应的双层移动模式映射索引结构, 以实现对粗粒度区域级移动模式与细粒度路网节点级移动模式的关联存储, 即分别在粗粒度层与细粒度层以父节点与子节点结构表示移动模式的序列关系, 同时在粗粒度层与细粒度层之间建立指针索引结构, 以反映路网节点与离散区域之间的映射包含关联关系.
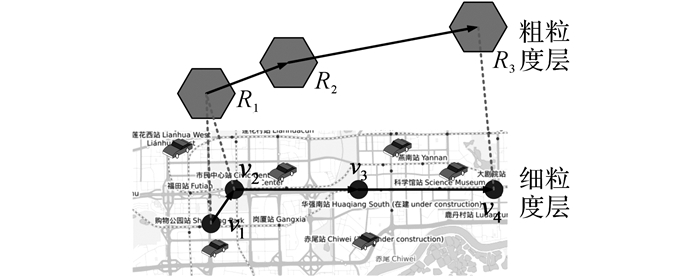
如图 1所示, 圆形图标表示细粒度路网节点层移动轨迹模式, 所表示的路网层移动模式为:v1→v2→v3→v4;六边形图标表示粗粒度层, 相应的移动轨迹模式为:R1→R2→R3, 其中路网节点v1、v2对应空间划分区域R1, v4对应空间划分区域R3, 区域R2不存在对应的细粒度层移动模式路网节点元素.
|
图 1 多粒度双层移动轨迹模式映射结构 Fig. 1 Multi-granularity double layer moving track pattern mapping structure |
通过对粗粒度区域层与细粒度路网节点层移动行为模式的双层融合表示与结构索引, 提出面向在线移动轨迹预测的混合模型(moving trajectory hybrid prediction, MTHP), 相应的流程如图 2所示.

|
图 2 在线移动轨迹混合预测模型 Fig. 2 Hybrid prediction model of online moving trajectory |
具体如下.以第1部分移动轨迹语义建模中的离散划分区域集与路网地图节点数据集为基础, 对在线查询轨迹Trqu分别进行转换, 从而生成多粒度语义序列数据Sequ.以2.2部分所构建的双层多粒度移动模式映射索引结构为模式匹配基础, 利用模式序列后缀匹配原则, 分别以Sequ与所挖掘的粗/细粒度层模式集合Patt进行相似度匹配计算;在匹配计算的过程中, 基于粗粒度层区域表示和路网节点表示之间的包含映射关联关系, 实现粗粒度层预测结果与细粒度层预测结果的合并与互补操作, 以生成预测轨迹Trpre.此外, 对Trqu轨迹进行增量式空间范围检索过程, 以Trqu轨迹的空间范围为查询条件对粗、细粒度二次转换语义数据集进行检索查询, 以返回与在线预测轨迹Trqu属同一空间范围的历史轨迹小数据集, 在预测结果Trpre的基础上进行二次修正, 从而提升在线移动轨迹的预测精度.相应的在线移动轨迹混合预测算法形式化表示如下.
算法2 在线移动轨迹动态预测算法.
输入:Patt={Pi, i=1, 2, …, l};Trqu;
输出:Trpre
Sequ←Transform (Trqu, R, V)
FOR EACH Pi∈Patt DO
Trpre←PattMatch(Pi, Sequ)
END FOR
Similar Trs←Retrieval (D, Trqu)
Trpre←modificaton (Trpre, Similar Trs)
3 实验结果及分析实验运行环境如下:Intel Core i3 CPU, 2.40 GHz, 内存为4.00 GB, 操作系统为Windows 7, 所有的实验采用Java实现.实验中采用的数据集为广东省深圳市300辆出租车近10天的真实GPS数据, 其中包括约41 000条完整移动轨迹, 含1 279 465个GPS轨迹点, 里程数为23万公里.以36 000条移动轨迹数据作为训练数据, 其余5 000条轨迹数据作为测试数据.
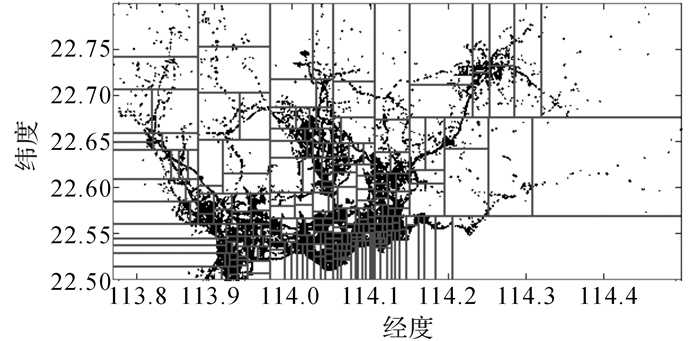
通过k-d tree划分方法实现对所覆盖空间的多粒度离散划分, 离散划分区域的数量对最终的预测性能会产生较大的影响.在离散区域划分的过程中, 若选择较少的区域划分参数值, 则所获得的离散划分区域数量减少, 同时区域覆盖面积会相应地增大, 从而造成最终轨迹预测的精度下降;若选择较大的区域划分参数值, 则获得的离散划分区域数量增大, 区域面积相应地减小.过多的离散划分区域无益于甚至会恶化历史轨迹稀疏、不均匀分布所带来的相关问题, 同时会增大预测算法运行所占用的资源与时间开销.基于k-d tree的离散区域划分数量取值应适中.通过分别对离散划分区域数量为128、256以及512三种不同情况下的算法性能进行分析, 同时考虑内存空间与在线运行时间的约束条件, 本文选取256个离散区域划分集合作为实验验证部分的参数取值.相应的划分结果如图 3所示,包含GPS轨迹位置点的数量为1 078 806, 划分区域参数设置为256, 划分后的离散区域中轨迹位置点分布平均值约为4 200, 方差为0.393 1.等尺度规则网格方法在256个划分区域下, 轨迹位置点的分布方差为14.37.比较可知, 基于k-d tree的划分方法有效克服了等尺度规则网格空间划分所产生的轨迹点分布不均问题.
|
图 3 基于k-d tree的多粒度空间划分 Fig. 3 Divisions of multi-granularity space based on k-d tree |
基于所划分的256个离散区域集合以及所提取的1 572个城市路网节点集合, 对原始轨迹数据进行语义转换与双层多粒度频繁移动模式挖掘过程, 得到的部分粗粒度区域级移动模式如图 4所示.

|
图 4 粗粒度区域级移动轨迹模式图示 Fig. 4 Moving trajectory patterns on coarse-grain area level |
利用粗粒度区域级移动模式与细粒度路网节点级移动模式双层映射索引结构, 实现对在线移动轨迹的预测实验.移动轨迹预测评价指标选取以所预测的移动轨迹序列与实际轨迹位置点之间的均方差公式进行比较(mean square deviation, MSD), 具体为
| $ \begin{align} & \frac{\left| \text{T}{{\text{r}}_{\text{pre}}}\text{-T}{{\text{r}}_{\text{real}}} \right|}{\left| \text{T}{{\text{r}}_{\text{real}}} \right|}= \\ & \ \ \ \ \ \sum\nolimits_{i=1}^{k}{\frac{{{({{x}_{i}}-x_{i}^{'})}^{2}}+{{({{y}_{i}}-y_{i}^{'})}^{2}}}{k}}. \\ \end{align} $ | (1) |
式中:Trreal与Trpre分别表示真实轨迹与预测轨迹;Trreal为轨迹位置点,是以原始采集数据(经纬度坐标系数据点xi与yi)表示;Trpre为预测位置点,是以细粒度坐标点(x′i与y′i)表示, 其中以粗粒度离散区域表示的部分转化为相应的划分区域的中心位置点位置来表示.
将提出的在线移动轨迹混合预测方法MTHP与粗粒度区域模式匹配方法(region pattern matching, RPM)、细粒度路网节点模式匹配方法(urban network pattern matching, UNPM)进行实验比较.其中Trqu轨迹取测试轨迹长度的30%进行预测实验, 预测轨迹长度分别取5、7与10 km, 分别对1 000~5 000条测试轨迹进行实验测试, 结果取平均值.
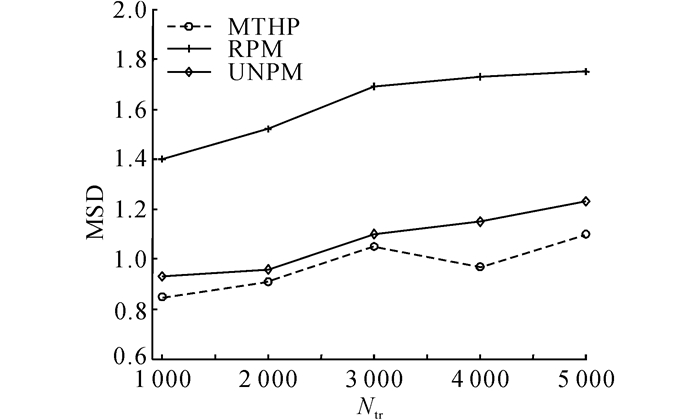
如图 5所示为3种不同预测方法与真实轨迹之间的均方差结果.图中,Ntr为测试轨迹数量.可以看出, 提出的MTHP预测方法显著优于RPM和UNPM方法, 预测精度分别提升了40.17%和14.03%.其中RPM方法的效果最差, 原因在于RPM方法中的区域表示本身较UNPM中的路网节点表示精度低, 同时相应的移动模式语义表示粒度较大, 因此造成最终得到的预测结果存在较大偏差.此外, 在MTHP方法中, 建立在增量式历史轨迹检索基础之上的Trpre预测结果二次修正对于提升最终的输出结果具有提升作用.
|
图 5 移动轨迹预测均方差差MSD比较 Fig. 5 Comparison of moving trajectory prediction MSD |
如图 6所示为3种不同方法的可预测轨迹比率rpre(ratio of predictable trajectories, RPT)结果.该指标反映的是在数据稀疏分布客观约束条件下, 可预测轨迹数量相比于全部测试轨迹数量的比值.从图 6可以看出, 提出的MTHP方法在双层多粒度移动模式支持下取得了较高的RPT值;RPM方法次之, UNPM方法最差.原因在于RPM方法的区域元素规模较小, 在一定程度上缓解了数据稀疏问题;移动模式的区域表示扩大了预测轨迹Trqu的匹配范围;UNPM方法所具有的更大规模节点数量以及更细粒度模式表示方式均有效地减小了预测轨迹Trqu的匹配范围.

|
图 6 移动轨迹可预测比率比较 Fig. 6 Comparison of predictability rate of moving trajectory |
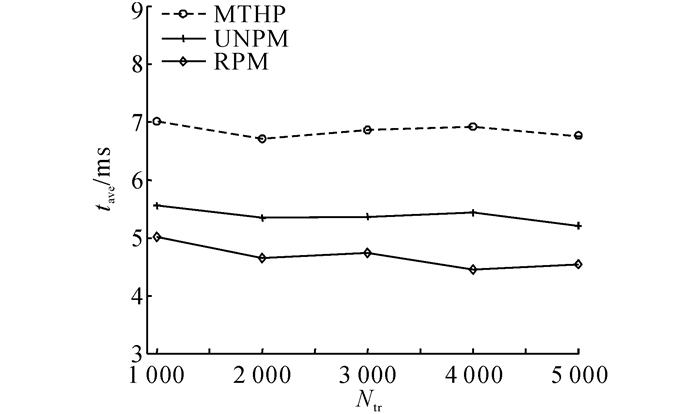
对3种不同预测方法的平均运行时间开销tave进行实验比较分析, 结果如图 7所示.由于MTHP方法混合了粗粒度与细粒度双层知识表示与模式匹配过程, 因此该方法的平均运行时间开销与单层UNPM方法与RPM方法相比最长.此外, 对在线查询轨迹的增量式相似轨迹检索过程增加了算法的运行时间;然而, 每条查询轨迹平均耗时为7 ms的运算速度对于绝大多数的应用均可满足.UNPM方法由于所采用的路网节点数量远大于RPM方法的离散区域数量, 在对历史轨迹检索与匹配过程中所耗费的时间显著高于粗粒度区域知识方法RPM.
|
图 7 移动轨迹预测平均运行时间比较 Fig. 7 Comparison of average running time of moving trajectory prediction |
本文提出基于多粒度知识发现的移动轨迹预测方法MTHP, 分别在区域级粗粒度层与路网节点级细粒度层展开对移动轨迹的建模与模式抽取.通过双层多粒度移动模式的关联映射结构化表示, 实现在线查询轨迹粗/细语义层的结果融合与互补.在真实数据集下进行实验验证.结果表明, 本文提出的MTHP比基于单层语义模式匹配预测方法在预测精度及可预测比率两方面均取得了较大的提升, 具有较好的预测效果.
| [1] | DEGUCHI Y, KURODA K, SHOUJI M, et al. HEV charge/discharge control system based on navigation information [R]. Yokohama: Nissan Motor, 2004. |
| [2] | KARBASSI A, BARTH M. Vehicle route prediction and time of arrival estimation techniques for improved transportation system management [C] // Proceedings of Intelligent Vehicles Symposium. Columbus: IEEE, 2003: 511-516. |
| [3] | FROEHLICH J, KRUMM J. Route prediction from trip observations [R]. Seattle: University of Washington, 2008. |
| [4] | CHEN C, ZHANG D, MA X, et al. Crowddeliver: planning city-wide package delivery paths leveraging the crowd of taxis[J]. IEEE Transactions on Intelligent Transportation Systems, 2016(99): 1–19. |
| [5] | DAI J, YANG B, GUO C, et al. Personalized route recommendation using big trajectory data [C]//2015 IEEE 31st International Conference on Data Engineering. Seoul: IEEE, 2015: 543-554. |
| [6] | ZHANG S, QIN L, ZHENG Y, et al. Effective and efficient: large-scale dynamic city express[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3203–3217. DOI:10.1109/TKDE.2016.2604806 |
| [7] | CHEN L, LV M, CHEN G. A system for destination and future route prediction based on trajectory mining[J]. Pervasive and Mobile Computing, 2010, 6(6): 657–676. DOI:10.1016/j.pmcj.2010.08.004 |
| [8] | CHEN L, LV M, YE Q, WOODWARD J. A personal route prediction system based on trajectory data mining[J]. Information Sciences, 2011, 181(7): 1264–1284. DOI:10.1016/j.ins.2010.11.035 |
| [9] | TIWARI V S, ARYA A, CHATURVEDI S. Route prediction using trip observations and map matching [C] //2013 IEEE 3rd International Advance Computing Conference (IACC). Ghaziabad: IEEE, 2013: 583-587. |
| [10] | SIMMONS R, BROWNING B, ZHANG Y, et al. Learning to predict driver route and destination intent [C] // IEEE Intelligent Transportation Systems Conference. Toronto: IEEE, 2006: 127-132. |
| [11] | MONREALE A, PINELLI F, TRASARTI R, et al. Wherenext: a location predictor on trajectory pattern mining [C] // Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris: ACM, 2009: 637-646. |
| [12] | XUE A Y, ZHANG R, ZHENG Y, et al. Destination prediction by sub-trajectory synthesis and privacy protection against such prediction [C] // 2013 IEEE 29th International Conference on Data Engineering (ICDE). Brisbane: IEEE, 2013: 254-265. |
| [13] | XUE A Y, QI J, XIE X, et al. Solving the data sparsity problem in destination prediction[J]. The VLDB Journal, 2015, 24(2): 219–243. DOI:10.1007/s00778-014-0369-7 |




