2. 中国科学院 计算技术研究所, 北京 100190;
3. 北京市移动计算与新型终端重点实验室, 北京 100190;
4. 中国科学院大学, 北京 100190
2. Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. Beijing Key Laboratory of Mobile Computing and Pervasive Device, Beijing 100190, China;
4. University of Chinese Academy of Sciences, Beijing 100190, China
随着基于位置的服务(location based services, LBS)在移动互联网的迅猛发展, 许多定位解决方案不断涌现, 如GPS定位、地磁定位、超声波定位、射频(RFID)定位等.上述定位方案均存在一些局限性:GPS信号由于易受到建筑或其他障碍物的阻挡, 只适用于室外环境;超声波易受物体遮挡, 存在传输受限问题;基于射频的定位方法探测范围较小, 且需要专门的设备支撑;地磁信号易受电磁干扰, 难以精准采集, 因而定位效果较差.随着移动互联网的发展, 具备Wi-Fi通信模块的智能终端逐年普及, 环境中的Wi-Fi信号日渐丰富, 无线接入点(access point, AP)越来越多, 这些都为基于Wi-Fi定位方法[1]的普及实施提供了有利条件.基于蓝牙4.0技术的低功耗蓝牙(bluetooth low energy, BLE)具有扫描速度快、连接迅速、功耗超低等特性, 适逢苹果公司推出iBeacon[2]技术, 基于iBeacon技术的BLE定位方法逐渐成为研究热门.
现有的Wi-Fi[3-6]和低功耗蓝牙[7-9]单模定位方法定位精度较低, 定位系统鲁棒性较差;由于蓝牙信源不够广泛, 定位系统的普适性无法满足需求.另外, 已有的指纹定位方法均需采集大量标定数据进行模型训练, 带来了极大的人工成本.针对这些问题, 本文的贡献如下.
1) 将Wi-Fi和低功耗蓝牙进行有效的特征融合, 充分利用了这两种定位手段的优势.
2) 半监督流形学习方法的引入有效利用了无标定数据, 从而减少了训练数据采集的工作量.
1 相关工作在单模室内定位研究领域, Torteeka等[10]基于Wi-Fi传感器, 将模糊集合理论和K近邻方法相结合, 对K个最近邻样本进行权重分配, 提升了定位精度和鲁棒性.Ma等[11]针对Wi-Fi定位对训练样本进行预分类, 对定位样本分别利用改进的欧式距离判别方法和联合概率方法估计位置并进行加权, 最终提升了定位精度, 减少了计算耗时.Zhu等[12]基于BLE传感器进行位置估计:离线训练阶段利用对数正态分布来训练传播模型同时结合高斯函数对RSS进行过滤;在线定位阶段, 算法先使用滑动窗减少信号的异常波动, 同时基于三边关系定理提出基于距离权重的方法过滤异常信号值, 最后利用泰勒级数展开对定位结果进行纠正.Faragher等[13]对BLE信号衰落和设备的电力损耗进行量化分析, 然后对BLE信源的分布密度、广播功率和频率等参数进行优化并应用于位置估计, 与基于Wi-Fi的指纹算法相比, 在不同的BLE部署密度下, 定位精度均有所提升.
上述文献从不同的角度对定位算法的精度、鲁棒性等进行提升.受限于Wi-Fi信号和BLE信号的固有特征, Wi-Fi定位方法在精度上难以满足实际的应用需求;室内环境中部署的BLE设备数量较少, 无法做到大面积覆盖, 基于BLE的单模定位技术难以胜任大面积、长距离定位工作.
由于单一传感器[14-16]信息存在一定的局限性, 多传感器信息融合逐渐受到研究人员的重视.研究人员将GPS、基站、Wi-Fi、射频、蓝牙和惯导等多种传感器信息进行融合, 并应用于定位实践, 取得了一定的提升效果.Chen等[17]结合WLAN与集成了GPS定位模块和惯性传感器的定位模块(multi-sensor positioning, MSP), 实现了室内室外无缝定位系统. Radu等[18]将步行航位推算(pedestrian dead reckoning, PDR)和Wi-Fi指纹进行融合来做位置估计, 相比两者中的任何一种单模方法, 该方法的定位误差控制在2 m左右. Zhuang等[19]提出用于大面积复杂环境中移动机器人定位的混合传感系统, 在结构明显的走廊区域, 该系统利用视觉信息并基于预定义的混合拓扑图进行姿态跟踪;对于半结构化的办公环境, 系统采用激光扫描的方式进行连续姿态调整, 结合卡尔曼滤波作姿态平滑.通过有效的地图建模和简单的计算, 该系统在实时定位时表现良好.Colombo等[20]对可穿戴设备的位置估计进行研究, 通过结合惯性传感器和其他传感器如摄像头来进行位置计算, 利用双层扩展卡尔曼滤波(extended Kalman filter, EKF)串联来平滑定位结果.最终该方法在短时定位上取得了厘米级的定位效果.Ayllon等[21]将音频信号和惯性传感器进行融合, 利用波达方向(direction of arrival, DOA)和惯性数据来作位置估计.该方法在无需任何参考点数据, 同时也不需要在结点之间进行同步调整的情况下有效控制了定位误差.在WiFi和蓝牙多模融合方面, 王睿等[22]针对两种传感器的定位结果, 在决策层通过对结果设置不同权重进行融合, 在一定程度上提升了定位精度和鲁棒性.
上述多模融合方法仅仅把多种传感器数据简单融合在一起, 没有有效地提取传感器信号之间的关联特征, 而关联特征往往能在多模信息融合过程中发挥重要作用.本文提出基于Wi-Fi和BLE的混合定位方法, 将Wi-Fi和BLE的原始特征进行融合, 并融入二者之间的互相关特征[23], 有效利用了Wi-Fi和BLE信号的定位优势.此外, 本文通过引入半监督流形约束方法解决了训练指纹定位模型所需的标定数据采集工作量问题.
2 融合特征提取方法在真实环境中, WLAN信号和BLE信号呈现高动态变化, 只提取信号的单一特征往往造成定位效果不佳.此外, 定位终端获取到的原始信号无法直接用于模型训练和位置计算, 需要进行预处理.
2.1 信号预处理由于真实环境中的Wi-Fi和BLE信号具有不确定性, 信号波动较大, 需要针对采集到的Wi-Fi和BLE的同步信号数据作预处理, 去掉偏差较大的信源的信号值, 才能用于进一步的特征提取工作.环境变化对信号的影响近似服从正态分布, 假定某参考点经过多次扫描得到来自相同信源的信号序列RSS={rss1, rss2, …,rssn}, 均值μ和标准差σ表示如下:
| $ \mu {\rm{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {{\rm{rs}}{{\rm{s}}_i}} ,\sigma = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{\rm{rs}}{{\rm{s}}_i} - \mu } \right)}^2}} } . $ |
概率密度函数为
| $ f\left( {{\rm{rss}}} \right) = \frac{1}{{\sigma \sqrt {2{\rm{\pi }}} }}\exp \left( { - \frac{{{{\left( {{\rm{rss}} - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right). $ | (1) |
通过融入信号过滤机制, 完整预处理步骤如下.
1) 统计相同参考点接收到来自同一信源的RSS序列, 计算正态分布参数μ和σ.
2) 根据式(1) 计算f(rssi), 确定概率阈值, 过滤掉低于阈值的RSS信号, 然后对剩余RSS信号计算均值.
3) 统计所有参考点的信源出现频次, 然后按照出现次数降序排列, 最终选择前n个稳定信源.
4) 重新生成所有参考点的Wi-Fi和BLE信号数据.
2.2 融合特征提取相关性分析[24]揭示同一信号序列在不同时刻或不同信号序列在不同时刻的线性联系或依赖关系, 被广泛应用于信号特定频率成分提取、线性定位和相关测速以及图像配准等领域.两个连续信号序列X、Y的互相关函数定义为
| $ {R_{XY}}\left( \tau \right) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_0^T {{x^ * }\left( t \right) * y\left( {t + \tau } \right){\rm{d}}t} . $ | (2) |
离散化计算公式为
| $ {R_{XY}}\left( \tau \right) = \sum\limits_{ - \infty }^\infty {{x^ * }\left( t \right) * y\left( {t + \tau } \right)} . $ | (3) |
两个传感器信号序列的互相关序列取决于这两组信号序列的相似程度.假设两个具有有限强度的信号序列rb(n)和rw(n), 它们之间的互相关性可以表示如下:
| $ \mathop {{R_{{\mathit{\boldsymbol{r}}_b}{\mathit{\boldsymbol{r}}_w}}}}\limits^ \wedge \left( m \right) = \left\{ \begin{array}{l} \sum\limits_{n = 0}^{N - m - 1} {{\mathit{\boldsymbol{r}}_{n + m}}{\mathit{\boldsymbol{r}}_{{w_n}}}} ,\;\;\;m \ge 0;\\ \mathop {{R_{{\mathit{\boldsymbol{r}}_w}{\mathit{\boldsymbol{r}}_b}}}}\limits^ \wedge \left( { - m} \right),\;\;\;\;m < 0. \end{array} \right. $ | (4) |
式中:m=…, -2, -1, 0, 1, 2, …表示由于延迟导致时间参数的转变, 下标rb、rw表示序列的相关程度.若信号序列rb(n)和rw(n)的有限样本数均为N, 则它们互相关的样本个数为2N-1;若信号序列rb(n)和rw(n)的有限样本数分别为N和M, 且N>M, 则它们的互相关样本个数为2N-1.
假设某时刻WLAN设备搜索到的Wi-Fi信号序列rw={rw1, rw2, …, rwn}和BLE信号序列rb={rb1, rb2, …, rbm}, 互相关函数序列定义为
| $ {\mathit{\boldsymbol{r}}_c}\left( m \right) = E\left[ {\mathit{\boldsymbol{r}}_w^ * \left( n \right) * {\mathit{\boldsymbol{r}}_b}\left( {n + m} \right)} \right]; - \infty < n < + \infty . $ | (5) |
计算得到向量rc=[rc1, rc2, …, rc2max(n, m)-1]T, 长度为2max(n, m)-1.通过式(5) 计算得到互相关特征, 再结合现有WiFi和BLE特征, 总共得到如下5项特征组合, 如表 1所示.
| 表 1 指纹特征列表 Table 1 Fingerprint feature list |
为了快速训练模型, 同时能够利用无标定样本进行半监督学习, 分别引入极速学习机(extreme learning machine, ELM)和半监督极速学习机(semi-supervised extreme learning machine, SELM), 然后提出基于融合信息的半监督流形约束方法(fusion feature semi-supervised extreme learning machine, FF-SELM)并应用于实际定位问题.
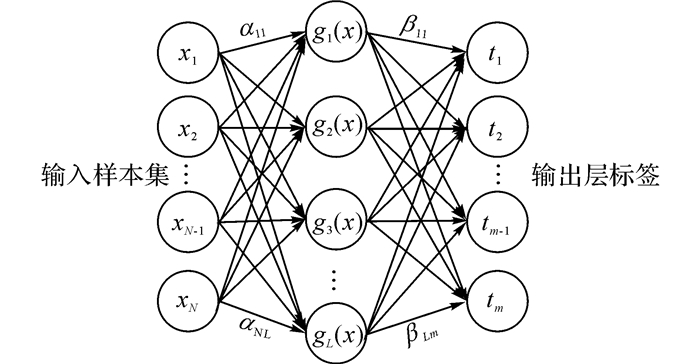
3.1 极速学习机模型ELM[25]是一种单隐层前馈神经网络(single hidden layer feedforward neural network, SLFN), 网络结构如图 1所示.对于一个输入向量x∈Rn和具有L个隐层节点的ELM, 输出形式定义如下:
| $ \sum\limits_{i = 1}^L {{\beta _i}G\left( {{\mathit{\boldsymbol{a}}_i},{b_i},x} \right)} ;{\mathit{\boldsymbol{a}}_i} \in {{\bf{R}}^L},{\mathit{\boldsymbol{b}}_i} \in {\bf{R}},{\mathit{\boldsymbol{\beta }}_i} \in {{\bf{R}}^m}. $ | (6) |
|
图 1 ELM网络结构 Fig. 1 Network structure of ELM |
式中:ai=[ai1, ai2, …, ain]T为连接输入向量与第i个隐层节点的权值, ai=[ai1, ai2, …, ain]T;bi为第i个隐层节点的偏置参数;G(ai, bi, x)为第i个隐层节点的输出;βi=[βi1, βi2, …βim]T表示连接第i个隐层节点与输出节点的权值.
假设g(x)为隐层节点的激励函数, 则
| $ G\left( {{\mathit{\boldsymbol{a}}_i},{b_i},\mathit{\boldsymbol{x}}} \right) = g\left( {{\mathit{\boldsymbol{a}}_i} \cdot \mathit{\boldsymbol{x}} + {b_i}} \right);{\mathit{\boldsymbol{a}}_i} \in {{\bf{R}}^n},{b_i} \in {\bf{R}}. $ | (7) |
对于N个训练样本{(xj, tj)|j=1, 2, …, N}, xj=[xj1, xj2, …, xjn]T, 可用矩阵表示如下:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{H = }}{\left[ {\begin{array}{*{20}{c}} {G\left( {{a_1},{b_1},{x_1}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_1}} \right)}\\ \vdots &{}& \vdots \\ {G\left( {{a_1},{b_1},{x_N}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_N}} \right)} \end{array}} \right]_{N \times L}},\\ \mathit{\boldsymbol{\beta = }}{\left[ {\begin{array}{*{20}{c}} {\beta _1^{\rm{T}}}\\ \vdots \\ {\beta _L^{\rm{T}}} \end{array}} \right]_{L \times m}},\mathit{\boldsymbol{T}} = {\left[ {\begin{array}{*{20}{c}} {t_1^{\rm{T}}}\\ \vdots \\ {t_N^{\rm{T}}} \end{array}} \right]_{N \times m}}. \end{array} \right\} $ | (8) |
根据式(6) 可得Hβ=T, 即期望获得具有L个隐层节点的SLFN零误差逼近这N个样本.
根据文献[25]可知, 参数ai和bi只需在初始阶段随机指定.设H†为H的伪逆矩阵[26-27], 则β的求解如下:
| $ \mathit{\boldsymbol{\beta = }}{\mathit{\boldsymbol{H}}^{\mathit{\dagger} }}\mathit{\boldsymbol{T = }}{\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{T}}. $ | (9) |
针对式(8) 进行优化, 即等价于求解下式:
| $ \arg \mathop {\min }\limits_\beta \left( {\left\| {\mathit{\boldsymbol{H\beta }} - \mathit{\boldsymbol{T}}} \right\|} \right). $ | (10) |
为了保证指纹定位算法预测精确度, 需要采集大量的标定样本进行模型训练.由于人工采集大批量的标定数据工作量巨大, 非标定数据的获取相比更加容易, 针对该问题, 引入半监督极速学习机(semi-supervised ELM, SELM)[28]进行解决, 并引入图的拉普拉斯(Laplacian)算子[29]作流形约束, 以均衡模型的经验风险和学习函数f的复杂度.使用图的平滑度函数S(f)来表示模型复杂性[30], 定义为
| $ S\left( \mathit{\boldsymbol{f}} \right) = \sum\limits_{i,j} {{W_{ij}}{{\left( {{f_i} - {f_j}} \right)}^2}} = {\mathit{\boldsymbol{f}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{\rm{a}}}\mathit{\boldsymbol{f}}. $ | (11) |
式中:La为图的拉普拉斯算子.根据文献[31]可知, La=D-W,
| $ \arg \mathop {\min }\limits_\beta \frac{1}{2}\left( {{{\left\| {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{T}}} \right\|}^2} + \lambda {\mathit{\boldsymbol{f}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{\rm{a}}}\mathit{\boldsymbol{f}}} \right). $ | (12) |
式(12) 中的后半部分为流形约束项.由Hβ=f, 可得
| $ \begin{array}{l} \arg \mathop {\min }\limits_\mathit{\boldsymbol{\beta }} l\left( \mathit{\boldsymbol{\beta }} \right) = \\ \;\;\;\arg \mathop {\min }\limits_\mathit{\boldsymbol{\beta }} l\left[ {\frac{1}{2}\left( {{{\left\| {\mathit{\boldsymbol{JH\beta }} - \mathit{\boldsymbol{T}}} \right\|}^2} + \lambda {{\left( {\mathit{\boldsymbol{H\beta }}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{L}}_{\rm{a}}}\mathit{\boldsymbol{H\beta }}} \right)} \right]. \end{array} $ | (13) |
根据前文所述, H已知且包含所有的标定数据集和非标定数据集, 维度变为(l+u)×L.通过对式(13) 求导, 可得
| $ \mathit{\boldsymbol{\beta = }}{\left( {\left( {\mathit{\boldsymbol{J}} + \lambda \mathit{\boldsymbol{L}}_{\rm{a}}^{\rm{T}}} \right)\mathit{\boldsymbol{H}}} \right)^\mathit{\dagger }}\mathit{\boldsymbol{JT}} $ | (14) |
式(12)、(14) 中λ被置为0, 意味着非标定样本数据被忽略, 则β退化为式(9) 的结果.
3.3 基于融合信息的半监督流形约束定位方法根据3.2节, 通过特征提取得到提出的互相关特征, 组合原始Wi-Fi特征和BLE特征得到融合特征xi表示如下:
| $ {\mathit{\boldsymbol{x}}_i} = \left\{ {{\mathit{\boldsymbol{r}}_b},{\mathit{\boldsymbol{r}}_w},{\mathit{\boldsymbol{r}}_c}} \right\}. $ | (15) |
假定经筛选后, 相对稳定的Wi-Fi信源和BLE信源个数分别为w=20和b=10, 互相关特征维度为k, 由互相关特征计算规则, 可得维度k=39, 从而向量xi可以表示为
| $ {\mathit{\boldsymbol{x}}_i} = {\left[ {{\mathit{\boldsymbol{r}}_{{b_1}}}, \cdots ,{\mathit{\boldsymbol{r}}_{{b_{10}}}},{\mathit{\boldsymbol{r}}_{{w_1}}}, \cdots ,{\mathit{\boldsymbol{r}}_{{w_{20}}}},{\mathit{\boldsymbol{r}}_{{c_1}}}, \cdots ,{\mathit{\boldsymbol{r}}_{{c_{39}}}}} \right]^{\rm{T}}}. $ | (16) |
由式(7) 可知, 当特征维度为n时, ai∈Rn, 即ai=[ai1, ai2, …, ain]T, 而此时融合特征的维度为b+w+k, 从而连接输入向量与第i个隐层节点的权值向量ai=[ai1, ai2, …, aib+w+k]T.
综上所述, 对于l条标定训练样本数据集:{(xi, ti)|xi∈Rb+w+k, ti∈Rm, i=1, 2, …, l}, u条非标定样本集:{xi|xi∈Rb+w+k, i=1, 2, …, u}.整个位置估计过程可以表示如下.
1) 随机给ai和bi赋值, 设置隐层节点数为L.
2) 计算矩阵H(H的维度为(l+u)×L).
3) 计算图的拉普拉斯算子La, La、D和W的维数均为(l+u)×(l+u).
4) 计算β.
5) 利用训练得到的模型f=Hβ进行预测.
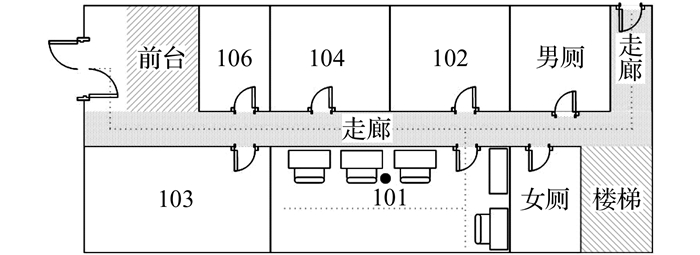
4 实验验证及分析 4.1 实验环境和数据采集实验数据采集场景设于某科研综合楼一层.该实验覆盖范围长约为20.3 m, 宽约为8.04 m, 总体布局如图 2所示.
|
图 2 训练数据采集和算法测试场景 Fig. 2 Scene of training data calibrating and algorithmtesting |
采集数据终端设备为华为荣耀6 Plus, 操作系统为Android4.4.2.通过对定位实验区域进行网格划分, 并结合自主开发的Wi-Fi、BLE同步采集客户端, 共采集有效数据5 676条, 训练数据和测试数据比例为1:1.为了验证Wi-Fi和BLE的互相关特征的稳定性, 在实验区域选一固定参考点(灰色标记处), 采集了2 151条指纹数据.
通过仿真算法进行实验对比, 算法运行环境为MATLAB R2015a, Windows 10操作系统;硬件环境为Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz, 16 GB内存.
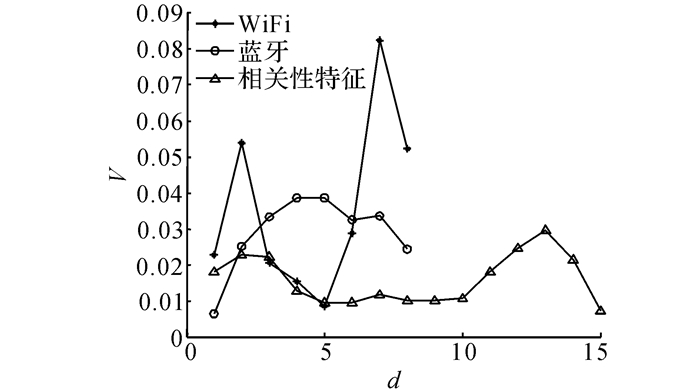
4.2 特征稳定性对比分析对2 151条指纹数据进行统计后, 分别选取8个较稳定的Wi-Fi和BLE信源并编号;然后将RSS信号值进行对齐, 同时缺失的信号值用最小值补充(BLE是-110 dBh, Wi-Fi是-100 dBh), 另外通过特征提取得到15维(2X8-1维)互相关特征.分别计算Wi-Fi特征、BLE特征和互相关特征, 其中互相关特征由式(4) 在MATLAB中Xcorr函数实现计算得到.通过计算3种序列每一维度的RSS信号值, 经0-1归一化处理后的方差, 并求所有维度方差的均值, 实验结果如图 3所示.图中,d为特征维度,V为特征方差.通过对比原始的Wi-Fi特征、BLE特征以及相关特征的方差曲线可知, Wi-Fi特征方差曲线和BLE特征方差曲线起伏不定, 波动较大, 而互相关特征方差曲线最稳定, 特征方差均值在三者中最小.相对于原始信号特征来说, 互相关特征更加稳定, 更有利于提高定位精度.
|
图 3 特征稳定性对比 Fig. 3 Comparison of features stability |
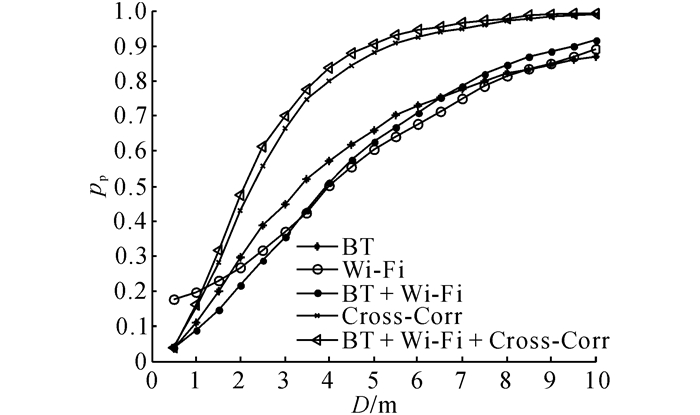
针对2.2节特征提取共得到的5种特征组合, 分别基于提出的FF-SELM方法进行模型训练和位置预测, 对比训练、预测时间和不同误差距离下的测试精度, 结果如表 2和图 4所示.表中,tt、tp分别为训练时间和测试时间,pt、pp分别为训练精度和测试精度.图 4中,D为误差距离.
| 表 2 5种特征组合训练时间及定位精度对比 Table 2 Comparison of training time and localization precision in five feature combinations |
|
` 图 4 5种不同特征组合下的定位精度对比 Fig. 4 Comparison of localization precision in five different feature combinations |
在时间消耗方面, 5种特征组合的训练时间总体十分接近, 由于ELM模型的复杂度只与隐层节点的数量有关, 对输入特征的维度不敏感, 提出的融合特征方法没有因为特征维度变长而显著增加计算耗时;在定位精度方面, 只使用Wi-Fi特征时定位精度最低, 是因为Wi-Fi信号存在波动, 单纯Wi-Fi难以取得高精度的定位效果, 而BLE信号覆盖范围显著低于Wi-Fi, 从而纯BLE的定位精度优于纯Wi-Fi;另外, 使用融合特征时定位精度最高, 与其他特征组合相比, 平均精度的提升幅度在20%以上, 最高达到了30.19%.融合特征由于充分利用了Wi-Fi和BLE信号所包含的信息, 同时吸收了互相关特征稳定性好这一特点, 从而定位精度最优, 证明了提出的融合特征策略的有效性.
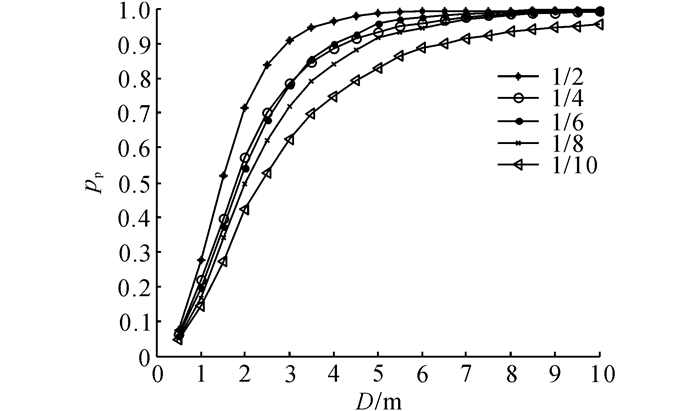
4.4 标定数据量对定位精度的影响分析为了验证标定数据量对FF-SELM模型精度的影响, 保持训练样本集总数不变, 将训练样本集分为标定样本集Trainl和非标定样本集Trainu, 其中非标定样本集中每条样本均不包含参考点的物理坐标;将l/(l+u)分别取值为1/10、1/8、1/6、1/4、1/2, 对模型进行训练, 然后测试模型的定位精度, 结果如图 5所示.分析可知, 随着标定数据的增加, FF-SELM模型的定位精度逐渐上升, 表明训练标定数据量越多, 定位模型效果越好.此外, 当标定数据比例为1/10, 误差距离为5 m时, 定位精度达到80%以上, 证明了提出的半监督流形约束定位方法能够充分利用非标定样本来提升模型的精度.
|
图 5 不同标定数据量下模型定位精度对比 Fig. 5 Comparison of localization precision by using different radio of calibration data |
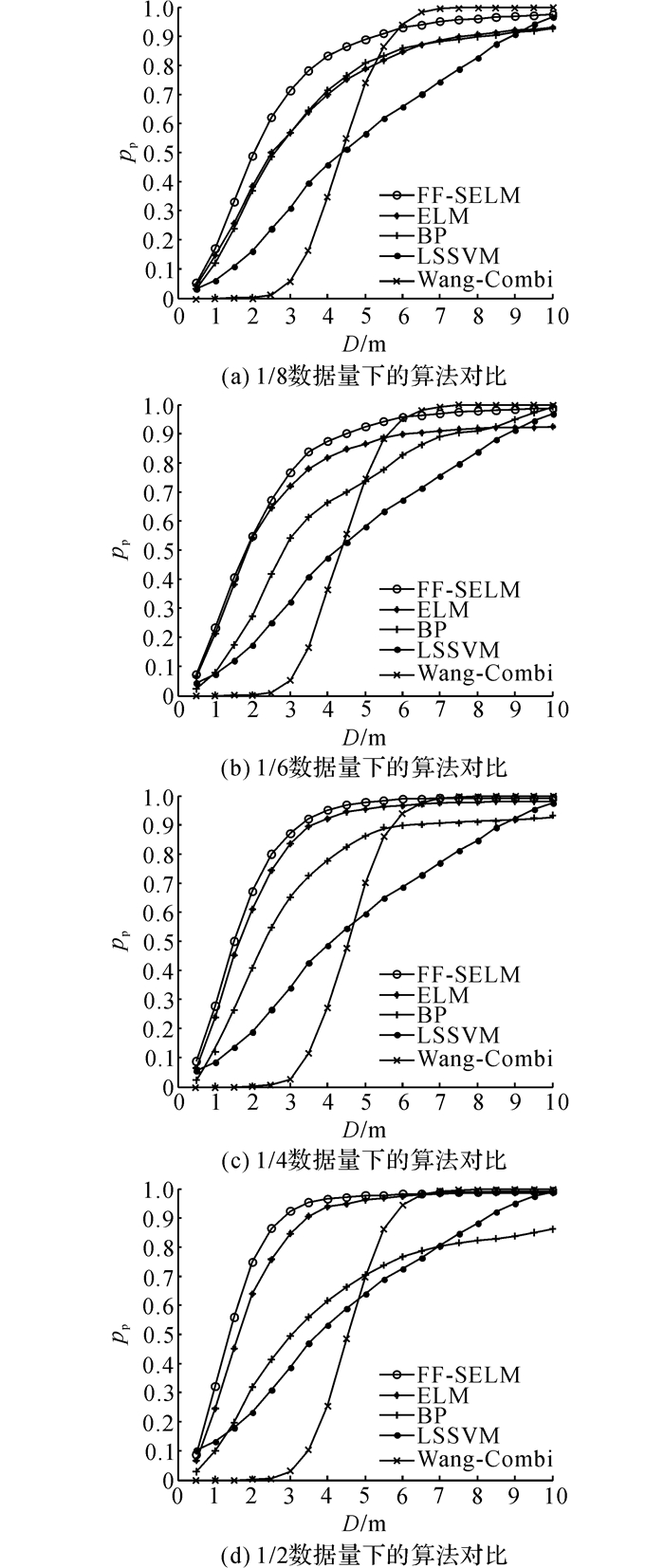
为了验证不同指纹模型算法的优劣, 选取了最小二乘支持向量机(LSSVM)算法、BP神经网络、ELM算法以及王睿等[22]提出的Wang-Combi融合算法与本文提出的FF-SELM进行对比.保持训练数据总量不变, 将l/(l+u)分别取值为1/8、1/6、1/4、1/2, 其中LSSVM、BP、ELM和Wang-Combi不具有半监督学习能力, 只使用标定样本集进行训练.最终结果如图 6所示.分析可知, 随着标定数据量的增加, 5种定位算法的定位精度均稳步提升, 且提出的FF-SELM方法在1/8标定数据量误差距离为5 m时, 精度接近90%;FF-SELM与ELM方法的定位精度优于另外3种方法, 且本文的FF-SELM优于ELM方法.这是由于本文方法基于ELM, 保留了ELM算法的优势, 同时引入了半监督流形约束方法, 能够充分利用非标定数据进行模型训练, 定位精度比ELM模型高;对比本文方法和Wang-Combi方法可知, 当误差距离不超过6 m时, 本文方法均优于Wang-Combi方法, 特别当误差距离为1~4 m时优势特别明显.另外, Wang-Combi方法在不同标定数据量下的定位精度变化不明显, 这是由于Wang-Combi方法采用划分网格方式进行定位, 而归属同一网格的指纹特征十分接近, 且笔者对每一个网格中的所有指纹只取均值, 因而该方法对标定训练样本的数据量不敏感.
|
图 6 不同标定数据比例下, 5种算法的定位精度比较 Fig. 6 Comparison of localization precision in five algorithms by using different ratio of calibration data |
本文针对Wi-Fi单模定位方法精度难以满足实际应用需求和BLE单模定位方法难以胜任大面积、长距离定位工作的问题, 提出基于融合特征的半监督流形约束定位方法.该方法首先对异常Wi-Fi和BLE信号进行过滤, 然后提取互相关特征, 并进行特征融合, 同时引入半监督流形约束方法来充分利用非标定数据训练模型.实验表明, 通过提取Wi-Fi和BLE信号的互相关特征, 能够有效减少因环境中信号波动给定位造成的偏差, 有效融合了Wi-Fi和蓝牙信号的定位优势.与其他指纹定位算法相比, 本文方法在提升了鲁棒性的同时, 定位精度提升了20%以上, 模型计算耗时并没有因为特征维度增加而显著上升.此外, 半监督流形约束方法的引入将标定数据减少了90%, 大大减小了标定数据采集工作量.
下一步工作将深入挖掘Wi-Fi信号和BLE信号之间的关联特征, 减少因信号波动给模型带来的影响;此外, 将继续挖掘BLE信号的传播规律, 以期与Wi-Fi信号进行深入融合, 从而提升本文模型的定位精度和鲁棒性.
| [1] | HONKAVIRTA V, PERL T, ALI-LYTTY S, et al. A comparative survey of WLAN location fingerprinting methods [C]// 6th Workshop on Positioning, Navigation and Communication. Hannover: IEEE, 2009:243-251. |
| [2] | NEWMAN N. Apple ibeacon technology briefing[J]. Journal of Direct, Data and Digital Marketing Practice, 2014, 15(3): 222–225. DOI:10.1057/dddmp.2014.7 |
| [3] | CHEN Z Y. Mining individual behavior pattern based on significant locations and spatial trajectories[C]// 2012 IEEE International Conference on Pervasive Computing and Communications Workshops. Lugano: IEEE, 2012: 540-541. |
| [4] | CHEN Z Y, WANG S Q, CHEN Y Q, et al. InferLoc: calibration free based location inference for temporal and spatial fine-granularity magnitude [C]// 2012 IEEE 15th International Conference on Computational Science and Engineering. Lugano: IEEE, 2012: 453-460. |
| [5] | CHEN Z Y, CHEN Y Q, WANG S Q, et al. A supervised learning based semantic location extraction method using mobile phone data [C]//2012 IEEE International Conference on Computer Science and Automation Engineering. Zhangjiajie: IEEE, 2012: 548-551. |
| [6] | CHEN Z Y, ZHOU J Y, CHEN Y Q, et al. Combing multiple linear regression and manifold regularization for indoor positioning from unique radio signal [C]// 2009 Joint Conferences on Pervasive Computing. Taibei: IEEE, 2009: 611-614. |
| [7] | CHEN Z Y, CHEN Y Q, GAO X Y, et al. Unobtrusive sensing incremental social contexts using fuzzy class incremental learning [C]// 2015 IEEE International Conference on Data Mining. Atlantic City: IEEE, 2015: 71-80. |
| [8] | CHEN Z Y, CHEN Y Q, HU L S, et al. ContextSense: unobtrusive discovery of incremental social context using dynamic bluetooth data [C]//Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. Seattle: ACM, 2014:23-26. |
| [9] | CHEN Z Y, CHEN Y Q, WANG S Q, et al. Inferring social contextual behavior from bluetooth traces [C]//Proceedings of the 2013 ACM Conference on Pervasive and Ubiquitous Computing Adjunct Publication. Zurich: ACM, 2013: 267-270. |
| [10] | TORTEEKA P, CHUNDI X I U. Indoor positioning based on Wi-Fi fingerprint technique using fuzzy k-nearest neighbor [C]// 2014 11th International Bhurban Conference on IEEE Applied Sciences and Technology. Islamabad: IEEE, 2014: 461-465. |
| [11] | MA R, GUO Q, HU C, et al. An improved WiFi indoor positioning algorithm by weighted fusion[J]. Sensors, 2015, 15(9): 21824–21843. DOI:10.3390/s150921824 |
| [12] | ZHU J Y, LUO H Y, CHEN Z L, et al. RSSI based Bluetooth low energy indoor positioning [C]// 2014 International Conference on IEEE Indoor Positioning and Indoor Navigation. Busan: IEEE, 2014: 526-533. |
| [13] | FARAGHER R, HARLE R. Location fingerprinting with bluetooth low energy BLEs[J]. IEEE Journal on Selected Area in Communications, 2015, 33(11): 2418–2428. DOI:10.1109/JSAC.2015.2430281 |
| [14] | GAO X Y, CHEN Z Y, TANG S, et al. Adaptive weighted imbalance learning with application to abnormal activity recognition[J]. Neurocomputing, 2016, 173: 1927–1935. DOI:10.1016/j.neucom.2015.09.064 |
| [15] | GAO X Y, HOI S C H, ZHANG Y D, et al. SOML: sparse online metric learning with application to image retrieval [C]//AAAI. Quebec City: [s. n.], 2014: 1206-1212. |
| [16] | ZHAO Z T, CHEN Z Y, CHEN Y Q, et al. A class incremental extreme learning machine for activity recognition[J]. Cognitive Computation, 2014, 6(3): 423–431. DOI:10.1007/s12559-014-9259-y |
| [17] | CHEN Y, CHEN R, PEI L, et al. Knowledge-based error detection and correction method of a multi-sensor multi-network positioning platform for pedestrian indoor navigation [C]// 2010 IEEE/ION Position Location and Navigation Symposium. Indian Wells: IEEE, 2010: 873-879. |
| [18] | RADU V, LI J, KRIARA L, et al. Poster: a hybrid approach for indoor mobile phone localization [C]// International Conference on Mobile Systems, Applications, and Services. Low Wood Bay: ACM, 2012:527-528. |
| [19] | ZHUANG Y, WANG K, WANG W, et al. A hybrid sensing approach to mobile robot localization in complex indoor environments[J]. International Journal of Robotics and Automation, 2012, 27(2): 198–205. |
| [20] | COLOMBO A, FONTANELLI D, MACII D, et al. Flexible indoor localization and tracking based on a wearable platform and sensor data fusion[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(4): 864–876. DOI:10.1109/TIM.2013.2283546 |
| [21] | AYLLON D, SANCHEZ-HEVIA H, GIL-PITA R, et al. Indoor blind localization of smartphones by means of sensor data fusion [C]// Sensors Applications Symposium. Zadar: IEEE, 2015. |
| [22] |
王睿, 赵方, 彭金华, 等. 基于WI-FI和蓝牙融合的室内定位算法[J].
计算机研究与发展, 2011(supple.2): 28–33.
WANG Rui, ZHAO Fang, PENG Jin-hua, et al. Combination of WI-FI and bluetooth for indoor localization[J]. Journal of Computer Research and Development, 2011(supple.2): 28–33. |
| [23] | WANG D L, BROWN G J. Computational auditory scene-analysis: principles, algorithms, and applications[M]. Piscataway: Wiley-IEEE, 2006. |
| [24] | ORFANIDIS S J. Optimum signal processing: an introduction[M]. London: Macmillan, 1988. |
| [25] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks [C]// Proceedings of 2004 IEEE International Joint Conference on Neural Networks. Budapest: IEEE, 2004: 985-990. |
| [26] | RAO C R, MITRA S K. Generalized inverse of matrices and its applications[M]. New York: Wiley, 1971. |
| [27] | SERRE D. Matrices: theory and applications[J]. Mathematics, 2002(32): 218–221. |
| [28] | LIU J, CHEN Y, LIU M, et al. SELM: semi-supervised ELM with application in sparse calibrated location estimation[J]. Neurocomputing, 2011, 74(16): 2566–2572. DOI:10.1016/j.neucom.2010.12.043 |
| [29] | CHUNG F R K. Spectral graph theory[M]. Washington: American Mathematical Society, 1997: 55. |
| [30] | BELKIN M, MATVEEVA I, NIYOGI P. Regularization and semi-supervised learning on large graphs[C]//International Conference on Computational Learning Theory. Berlin: Springer, 2004: 624-638. |
| [31] | BELKIN M, NIYOGI P, SINDHWANI V. Manifold regularization: a geometric framework for learning from labeled and unlabeled examples[J]. Journal of Machine Learning Research, 2006, 7(1): 2399–2434. |




