在现代社会中, 身份认证在许多场合都有着重要的应用, 其中人脸识别因其具有自然、友好等优势有着更广阔的应用前景.二维人脸识别技术已经有几十年的研究历史, 但仍然存在对光照、姿态和化妆敏感等缺陷.三维人脸识别利用脸部曲面的几何信息(如:曲率、法向量和测地距离等)进行身份识别, 正成为近几年学术界的研究热点.尽管与二维人脸识别相比有较大的优势, 三维人脸识别仍然面临受表情变化干扰的巨大挑战, 由表情变化引起的人脸非刚性形变会导致识别算法难以区分2个人脸之间的差异是由表情变化引起的还是由类间差异引起的.为了解决表情变化影响识别的问题, 许多解决方案相继被提出, 主要分为3类:基于空域的直接匹配、基于局部特征的匹配以及基于整体特征的匹配[1].
基于空域的直接匹配不提取特征, 直接进行曲面相似度匹配.常用方法有最近邻迭代点法(interative closest piont, ICP)[2], 该算法是一种刚性匹配算法, 迭代地计算曲面之间在几何空间上的刚性变换, 以使两者对齐误差最小, 但表情变化属于非刚性形变, 导致这一算法稳定性不强.Mian等[3]提出利用鼻子和额头等近似刚性的区域进行ICP匹配的方法来增强算法稳定性.基于局部特征的匹配主要利用人脸曲面上关键点周围区域的几何统计信息, 受表情变化影响较小, 具有高稳定性和高辨识度, 并受到众多研究人员的关注.其中, Wang等[4]提出从深度图中提取Gabor、LBP和Haar特征, 通过增强和训练弱分类器选择分离性最高的特征.Smeets等[5]采用MeshDOG的方法利用平均曲率进行关键点检测并提取关键点周围的Meshsift特征.Xu等[6]提出在深度图和强度图中提取Gabor局部特征, 采用线性判别分析(LDA)与AdaBoost结合的学习机制对提取到的Gabor特征进行降维, 从而得到鲁棒性较强的特征.本文所提出的算法就属于这一类算法.基于整体特征的匹配算法提取人脸模型的整体特征, 如Cai等[7]提出利用2个形状之间的映射提取非刚性形变进行人脸识别.Alosaimi等[8]提出采用可形变三维人脸模型来判断不同人脸之间的差异是由表情变化引起的还是由类间差异引起的.
在这些方法中, 局部特征匹配算法是针对表情变化问题最有效的解决方法, 对遮挡、杂波也有很强的鲁棒性.为克服表情变化影响, 本文提出一种基于关键点和局部特征的三维人脸识别算法.
1 关键点检测本文提出的关键点由两部分组成:1) 由有价值轮廓线均匀采样得到的关键点集P1;2) 由平均曲率筛选得到的关键点集P2.
1.1 关键点集P1由于过人脸对称面的中心侧面轮廓线被认为具有很好的表征性和鲁棒性, 而且一般认为鼻子附近区域具有最好的稳定性[9], 由中心侧面轮廓线的鼻子部分组成的轮廓线稳定性和表征性更好, 如图 1所示.因此, 本文选择由有价值轮廓线中的点组成关键点集P1.

|
图 1 中心侧面轮廓线和有价值轮廓线对比(不同线型代表不同个体) Fig. 1 Comparison of center profiles and valuable profiles (different linetypes represent different persons) |
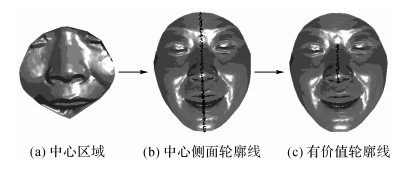
提取中心侧面轮廓线, 中心侧面轮廓线即人脸对称面与人脸曲面的交线.采用中心区域人脸镜像匹配法[10]确定人脸对称面, 中心区域取人脸曲面上以鼻尖点[11]为球心、50 mm为半径的区域, 如图 2(a)所示.设中心区域曲面为F, 初始对称面为S, 本文S选为yoz平面, 中心侧面轮廓线提取步骤如下.
|
图 2 价值轮廓线的提取步骤 Fig. 2 Extraction steps of valuable profiles |
1) 计算曲面F关于S的镜像曲面F′.
2) 使用ICP算法将F′向F对齐, 得到旋转和平移矩阵, 将旋转和平移矩阵应用在整个原始人脸曲面上得到对齐后的人脸曲面.
3) 取原始人脸曲面和对齐后的人脸曲面的均值得到新的人脸曲面, 用主成分分析法提取新得到人脸曲面的3个相互垂直的主轴方向, 将第一、二、三主成分对应的主方向分别作为y轴、x轴、z轴, 对称面S′即此时坐标下的yoz平面.
4) 计算对称面S′与原始人脸曲面的交线, 即为中心侧面轮廓线, 如图 2(b)所示.
根据鼻尖点的位置从中心侧面轮廓线中截取出有价值轮廓线, 如图 2(c)所示, 并将有价值轮廓线中的点均匀采样后作为关键点集P1, 如图 3(a)所示.

|
图 3 由有价值轮廓线、平均曲率及两者结合得到的关键点集 Fig. 3 Keypoints detected by valuable profile, mean curvature, and both |
受文献[12]的启发, 提出平均曲率剪枝算法.平均曲率能够充分地表示曲面的几何信息、有效地平滑噪声, 并且使用平均曲率可以得到稳定的关键点, 因此使用平均曲率来表示关键点的特性, 并对人脸曲面上的点进行筛选得到由该算法检测到的关键点集P2, 检测过程如下.
对于顶点p, 其平均曲率Cmean(p)由最大主曲率Cmax(p)和最小主曲率Cmin(p)计算得到, 如下式:
| $ {C_{{\rm{mean}}}}\left( p \right) = \left( {{C_{\max }}\left( p \right) + {C_{\min }}\left( p \right)} \right)/2. $ | (1) |
式中:对于顶点p, 设其邻域为N(p), M为邻域内点的个数, 则其邻域的平均曲率μ(p)计算如下:
| $ \mu \left( p \right) = \frac{1}{M}\sum\limits_{q \in N\left( p \right)} {{C_{{\rm{mean}}}}\left( q \right)} . $ | (2) |
为了筛选出稳定的关键点, 定义:如果一个顶点的平均曲率满足以下两式之一, 则认为其为关键点:
| $ \left| {{C_{{\rm{mean}}}}\left( p \right)} \right| \ge \left( {1 + a} \right)\left| {\mu \left( p \right)} \right|,a \ge 0; $ | (3) |
| $ \left| {{C_{{\rm{mean}}}}\left( p \right)} \right| \le \left( {1 - b} \right)\left| {\mu \left( p \right)} \right|,b \le 1. $ | (4) |
式中:a和b是限定|Cmean(p)|和|μ(p)|差大小的2个参数, 用来选择关键点.由以上定义筛选出的关键点如图 3(b)所示.
1.3 关键点如图 3(c)所示, 由有价值轮廓线和平均曲率筛选得到的关键点算法得到的关键点大部分分布在眼睛、眉毛、鼻子和嘴巴区域, 而类间差异也主要集中在这些地方, 利用这些关键点周围的空间结构信息能够较好地表征人脸特征.
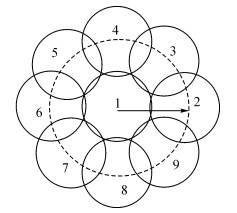
2 局部特征构造一种较为复杂的关键点局部特征, 包括形状指数直方图、倾斜角直方图和方向角直方图.利用形状指数、倾斜角以及方向角可以准确地表征关键点处曲面的几何信息, 使用直方图统计某一区域的几何信息具有平移、旋转、缩放不变性等特点.局部特征的空间结构采用DAISY描述符[13]的结构, 如图 4所示, 这样可以包含更多地关键点与其邻域之间的几何特性.关键点局部特征构造过程由3个步骤组成, 具体描述如下.
|
图 4 关键点局部特征的空间结构 Fig. 4 Spatial structure of keypoint local feature |
为了实现DAISY描述符的旋转不变性, 需要确立规范化方向[14].对于人脸曲面上的关键点p, 其邻域N(p)定义如下:
| $ N\left( p \right) = \left\{ {q\left| {{d_g}\left( {p,q} \right) < R} \right.} \right\}. $ | (5) |
式中:dg(p, q)为点p到点q的测地距离, R为半径.
1) 将所有的点q∈N(p)及其法向量n(q), 转换到如下临时局部坐标系中:
| $ C = \left\{ {\mathit{\boldsymbol{t}}\left( {p'} \right),\mathit{\boldsymbol{t}}\left( {p'} \right) \times \mathit{\boldsymbol{n}}\left( {p'} \right),\mathit{\boldsymbol{n}}\left( {p'} \right)} \right\}. $ | (6) |
式中:p′为转换后的p, 单位法向量n(p′)为z轴, t(p′)为人脸曲面在p′点的切平面T(p′)中随机选择的单位向量.
2) 将转换后的q′及其法向量n(q′)映射到切平面T(p′), 相应的夹角θ(q′)和模长m(q′)为
| $ \left. \begin{array}{l} \theta \left( {q'} \right) = \arctan \left[ {{\mathit{\boldsymbol{n}}_y}\left( {q'} \right)/{\mathit{\boldsymbol{n}}_x}\left( {q'} \right)} \right],\\ m\left( {q'} \right) = \sqrt {\mathit{\boldsymbol{n}}_x^2\left( {q'} \right) + \mathit{\boldsymbol{n}}_y^2\left( {q'} \right)} . \end{array} \right\} $ | (7) |
式中:
| $ \begin{array}{l} {\mathit{\boldsymbol{n}}_x}\left( {q'} \right) = \mathit{\boldsymbol{t}}\left( {p'} \right) \cdot \mathit{\boldsymbol{n}}\left( {p'} \right),{\mathit{\boldsymbol{n}}_y}\left( {q'} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{t}}\left( {p'} \right) \times \mathit{\boldsymbol{n}}\left( {p'} \right) \times \mathit{\boldsymbol{n}}\left( {p'} \right). \end{array} $ |
3) 在临时坐标系下的切平面T(p′)上构造一个高斯权重梯度直方图, 宽为360, 每一个单位覆盖1°.高斯权重描述如下:
| $ w\left( {p',q'} \right) = {\rm{mag}}\left( {q'} \right) \cdot {G_\sigma }\left( {{d_g}\left( {p',q'} \right)} \right). $ | (8) |
式中:标准差σ设置为半径R的一半.
本文选择大于高斯权重梯度直方图峰值80%的方向作为规范化方向.若有多个规范化方向存在, 分别以各个规范化方向为基础计算关键点p′的局部特征, 然后将各个规范化方向得到的关键点特征进行串联作为关键点p′的特征.下文以1个规范化方向d(p′)为例说明关键点局部特征的构造过程.d(p′)确定之后, 邻域内的所有点都转换到新的坐标系下:
| $ C' = \left\{ {d\left( {p'} \right),d\left( {p'} \right) \times \mathit{\boldsymbol{n}}\left( {p'} \right),\mathit{\boldsymbol{n}}\left( {p'} \right)} \right\}. $ | (9) |
局部特征的空间构造是在新坐标系C′下的切平面T(p′)上进行的, 以关键点p′及其8个邻域点为圆心得到9个圆, 并按逆时针排序, 如图 4所示.其中8个邻域点由以关键点p′为圆心从规范化方向处开始均匀采样得到.
2.3 关键点局部特征描述在新的局部坐标系下, 计算每个圆形区域的形状指数直方图、倾斜角直方图和方向角直方图.
1) 记k为圆形区域内的点, 计算圆形区域的形状指数直方图hs, 长度为8, 点k的形状指数由下式计算得到:
| $ S\left( k \right) = \frac{1}{2} - \frac{1}{{\rm{\pi }}}\arctan \frac{{{C_{\max }}\left( k \right) + {C_{\min }}\left( k \right)}}{{{C_{\max }}\left( k \right) - {C_{\min }}\left( k \right)}}. $ | (10) |
式中:S(k)以一个标准方差为k到圆心测地距离的高斯核为权重.
2) 计算倾斜角直方图ha, 长度为8, 倾斜角度α定义为每点法向量n(k)与规范化方向d(p′)的夹角:
| $ \alpha \left( k \right) = \arccos \frac{{\mathit{\boldsymbol{n}}\left( k \right) \cdot d\left( {p'} \right)}}{{\left| {\mathit{\boldsymbol{n}}\left( k \right)} \right| \times \left| {d\left( {p'} \right)} \right|}}. $ | (11) |
式中:α(k)以其法向量和关键点的法向量之间的夹角作为权重:
| $ \phi \left( k \right) = \frac{{\mathit{\boldsymbol{n}}\left( k \right) \cdot \mathit{\boldsymbol{n}}\left( {p'} \right)}}{{\left| {\mathit{\boldsymbol{n}}\left( k \right)} \right| \times \left| {\mathit{\boldsymbol{n}}\left( {p'} \right)} \right|}}. $ |
3) 计算方向角直方图hd, 长度为8, 首先对圆形区域内的点进行下采样, 方向β定义为圆形区域内下采样后任意两点k1和k2之间的连线l(k1, k2)与关键点法向量n(p′)之间的夹角:
| $ \beta \left( {{k_1},{k_2}} \right) = \arccos \frac{{l\left( {{k_1},{k_2}} \right) \cdot \mathit{\boldsymbol{n}}\left( {p'} \right)}}{{\left| {l\left( {{k_1},{k_2}} \right)} \right| \times \left| {\mathit{\boldsymbol{n}}\left( {p'} \right)} \right|}}. $ | (12) |
串联计算得到的3个直方图, 得到第n个圆的特征:
| $ {h_n} = \left( {{h_{{\rm{s}}n}},{h_{{\rm{a}}n}},{h_{{\rm{d}}n}}} \right) $ | (13) |
其中, hsn为第n个圆的形状指数直方图, han为第n个圆的倾斜角直方图, hdn为第n个圆的方向角直方图.以上描述的各个直方图都需要归一化为单位向量, 以便于消除非均匀采样的影响.将9个圆形区域的特征串联得到关键点p′的特征:
| $ f = \left( {{h_1},{h_2}, \cdots ,{h_9}} \right). $ | (14) |
为了在2个人脸曲面上找到对应的关键点, 采用角度γ进行关键点匹配.设点fi和fj分别为库集和测试集人脸曲面上第i、j个关键点的特征:
| $ {\gamma _{i,j}} = \arccos \left( {\frac{{\left\langle {{f_i},{f_j}} \right\rangle }}{{\left\| {{f_i}} \right\| \cdot \left\| {{f_j}} \right\|}}} \right). $ | (15) |
对测试集人脸曲面中每个关键点i, 计算其与库集人脸曲面上每个关键点j之间的角度γi, j, 将得到的角度按降序排序.依据文献[15], 如果第一个值和第二个值的比值小于0.8, 则匹配可以被接受; 否则匹配失败, 并把关键点匹配成功的对数作为身份识别的依据.
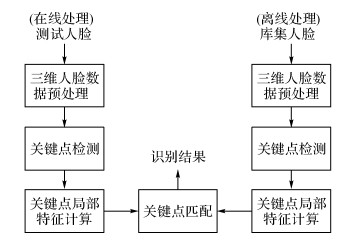
4 实验在i5处理器的Windows操作系统上通过Matlab R2015b平台进行三维人脸识别实验, 实验处理流程如图 5所示.
|
图 5 基于关键点和局部特征的三维人脸识别实验处理流程图 Fig. 5 Experimental process flow chart of 3D face recognition based on keypoints and local feature |
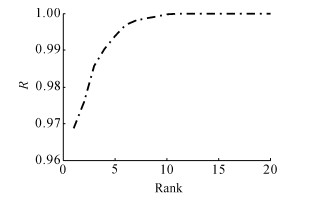
1) 实验一.本实验采用FRGC v2.0数据库.该库采集了466个对象的4 007张人脸点云, 包含微笑、吃惊、生气等带表情的人脸, 实验选取每人的第一张作为库集, 其余的作为测试集.采用R1RR(rank-one recognition rate)作为识别性能指标, 分别以形状指数直方图、形状指数直方图结合倾斜角直方图为局部特征以及本文提出的局部特征进行身份识别实验, 得到了86.7%、90.7%和96.9%的识别率.实验证明使用本文提出的局部特征能够有效地提高识别率, 同时使用累积匹配曲线(cumulative match curve, CMC)作为识别性能指标, 得到本文算法的CMC曲线如图 6所示,其中R为识别率.这个结果同样证实本文提出的算法可以很好地完成人脸识别.
|
图 6 基于FRGC v2.0数据库得到的累积匹配曲线 Fig. 6 Cumulative match curve (CMC) of FRGC v2.0 database |
2) 实验二.本实验基于Bosphorus数据库, 该数据库采集了105个对象的4 666张人脸点云, 表情种类丰富, 且表情幅度较大.本实验采用194张中性人脸作为库集, 有表情人脸作为测试集.实验中以中性人脸作为库集, 不同表情的人脸作为测试集, 测试集表情为生气、厌恶、害怕、高兴、伤心、惊讶时, R1RR分别为94.4%、89.9%、95.7%、96.9%、98.5%、98.6%.当以所有表情人脸作为测试集时, R1RR为95.8%.由此可知, 在表情较大的情况下, 本文提出的算法仍能很好地完成识别.
4.2 与其他算法对比实验本实验选取和实验一相同的数据集与其他针对表情变化的算法进行对比, 并以R1RR为识别性能指标, 以便于进一步检验本文算法的性能.Ratyal等[16]为了克服表情变化的影响, 提出对人脸进行区域划分, 并使用主成分分析法提取特征, 构造多个区域分类器, 对各个区域的特征进行融合, 但是人脸区域很难划分准确, 导致识别性能不高, 仅获得95.1%的识别率.Lei等[17]为了消除表情变化的影响, 提出融合近似刚性的鼻子区域和眼睛前额区域的几何特征, 然后用支持向量机进行训练和分类;但是只利用这些区域会丢失人脸曲面上的其他信息, 因此识别性能不高, 识别率为95.6%.Zhang等[18]通过提取关键点处的多阶特征以提高对表情的鲁棒性, 获得了96.1%的识别率.本文提出的算法获得了96.9%的识别率, 因此本文算法识别效果较好.
5 结语本文提出了一种基于关键点和局部特征的三维人脸识别算法来实现表情变化下的人脸特征表达, 并通过在FRGC v2.0数据库上进行的3种局部特征的对比验证了本文提出的特征能够有效的提高识别率.在Bosphorus数据库上进行了身份识别实验, 并在FRGC v2.0数据库上与3种算法进行了对比, 结果表明本文算法的识别能力较强, 并对表情变化具有一定的鲁棒性, 但是耗时较长.三维人脸识别除了面临表情变化的影响外, 也面临着遮挡的巨大挑战, 遮挡会使得人脸的三维数据丢失, 在未来的研究中, 主要致力于遮挡问题的解决.
| [1] |
王跃明, 潘纲, 吴朝晖. 三维人脸识别研究综述[J].
计算机辅助设计与图形学学报, 2008, 20(7): 819–829.
WANG Yue-ming, PAN Gang, WU Zhao-hui. Summary of 3D face recognition research[J]. Journal of Computer-Aided Design and Computer Graphics, 2008, 20(7): 819–829. |
| [2] | CHEN Y, MEDIONI G. Object modelling by registration of multiple range images[J]. Image and vision computing, 1992, 10(3): 145–155. DOI:10.1016/0262-8856(92)90066-C |
| [3] | MIAN A, BENNAMOUN M, OWENS R. An efficient multimodal 2D-3D hybrid approach to automatic face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(11): 1927–1943. DOI:10.1109/TPAMI.2007.1105 |
| [4] | WANG Y, LIU J, TANG X. Robust 3D face recognition by local shape difference boosting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(10): 1858–1870. DOI:10.1109/TPAMI.2009.200 |
| [5] | SMEETS D, KEUSTERMANS J, VANDERMEULEN D, et al. meshSIFT: Local surface features for 3D face recognition under expression variations and partial data[J]. Computer Vision and Image Understanding, 2013, 117(2): 158–169. DOI:10.1016/j.cviu.2012.10.002 |
| [6] | XU C, LI S, TAN T, et al. Automatic 3D face recognition from depth and intensity Gabor features[J]. Pattern Recognition, 2009, 42(9): 1895–1905. DOI:10.1016/j.patcog.2009.01.001 |
| [7] | CAI L, DA F. Nonrigid-deformation recovery for 3D face recognition using multiscale registration[J]. Computer Graphics and Applications, IEEE, 2012, 32(3): 37–45. DOI:10.1109/MCG.2010.99 |
| [8] | ALOSAIMI F, BENNAMOUN M, MIAN A. An expression deformation approach to non-rigid 3D face recognition[J]. International Journal of Computer Vision, 2009, 81(3): 302–316. DOI:10.1007/s11263-008-0174-0 |
| [9] | CHANG K I, BOWYER K W, FLYNN P J. Multiple nose region matching for 3D face recognition under varying facial expression[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(10): 1695–1700. DOI:10.1109/TPAMI.2006.210 |
| [10] | PAN G, WANG Y M, WU Z H. Finding symmetry plane of 3d face shape [C]//18th International Conference on Pattern Recognition (ICPR). Hong Kong: IEEE, 2006: 1143-1146. |
| [11] | LI X, DA F. Efficient 3D face recognition handling facial expression and hair occlusion[J]. Image and Vision Computing, 2012, 30(9): 668–679. DOI:10.1016/j.imavis.2012.07.011 |
| [12] | CHEN H, BHANU B. 3D free-form object recognition in range images using local surface patches[J]. Pattern Recognition Letters, 2007, 28(10): 1252–1262. DOI:10.1016/j.patrec.2007.02.009 |
| [13] | TOLA E, LEPETIT V, FUA P. Daisy: An efficient dense descriptor applied to wide-baseline stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 815–830. DOI:10.1109/TPAMI.2009.77 |
| [14] | LI H, HUANG D, MORVAN J M, et al. Towards 3D face recognition in the real: a registration-free approach using fine-grained matching of 3D keypoint descriptors[J]. International Journal of Computer Vision, 2014, 113(2): 128–142. |
| [15] | MAES C, FABRY T, KEUSTERMANS J, et al. Feature detection on 3D face surfaces for pose normalisation and recognition [C]// 2010 Fourth IEEE International Conference on Biometrics: Theory Applications and Systems (BTAS), September 27-29, 2010. Washington DC: IEEE, 2010: 1-6. |
| [16] | RATYAL N I, TAJ I A, BAJWA U I, et al. 3D face recognition based on pose and expression invariant alignment[J]. Computers and Electrical Engineering, 2015, 46: 241–255. DOI:10.1016/j.compeleceng.2015.06.007 |
| [17] | LEI Y J, BENNAMOUN M, EL-SALLAM A A. An efficient 3D face recognition approach based on the fusion of novel local low-level features[J]. Pattern Recognition, 2013, 46(1): 24–37. DOI:10.1016/j.patcog.2012.06.023 |
| [18] | ZHANG G, WANG Y. Robust 3D face recognition based on resolution invariant features[J]. Pattern Recognition Letters, 2011, 32(7): 1009–1019. DOI:10.1016/j.patrec.2011.02.004 |



