2. 河北工业大学 控制科学与工程学院, 天津 300130;
3. 智能康复装置与检测技术教育部工程研究中心, 天津 300130
2. School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China;
3. Engineering Research Center of Intelligent Rehabilitation and Detecting Technology, Tianjin 300130, China
由于生产安全事故、交通事故等因素, 不同程度地增加了下肢残疾的风险, 穿戴高性能的智能假肢是大腿截肢者重返社会的重要保障.近年来, 国内外有关智能假肢的研究越来越多.1990年, Zahedi发明了世界上第一个智能下肢假肢IP(intelligent prosthesis)[1];Sup等[2]提出的Power Knee动力膝可以使假肢穿戴者完成上下楼梯等复杂步态;Hitt等[3]提出了一种利用可调节弹簧驱动机构实现的能量优化的动力踝关节假肢.德国的奥托博克(Otto Bock)公司推出的智能假肢C-Leg[4]是当今世界新型的智能仿生腿的代表.Dingwell等[5]研发了一套假肢步态实时检测、分析系统, 该系统可以直观地显示出假肢穿戴者运动过程中两只脚的步态对称性.
从上世纪八十年代初开始, 国内也开展了智能假肢方面的研究.谭冠政等[6]研发了智能假肢步速测量数字电路实现实时测量;喻洪流等[7]设计了一种基于神经网络控制的智能假肢;王人成[8]提出利用肌肉电信号识别步态, 从而制定控制策略, 并研发了一种多连杆假肢膝关节机构;高云园等[9]利用髋、膝、踝关节角度和足底压力信号设计下肢运动姿势识别系统.步态识别技术是智能假肢研制的关键环节之一, 是智能假肢研究的一个热点.
表面肌电信号(surface electromyography, SEMG)是人体运动过程中神经肌肉活动发出的微弱生物电信号, 发生于大脑动作意愿产生之后, 肌肉真正收缩之前, 更接近人体原始运动意图的信号, 被广泛应用在康复医学和步态识别中[10-12].当人在上下楼梯、上下坡、平地行走时, 髋关节、膝关节屈伸范围表现出显著差异, 考虑到这2类信息在不同步态时表现出的显著性不同, 本文选择髋关节角度、膝关节角度信号、下肢表面肌电信号作为步态识别的信息源.
近年来, 国内以人工神经网络(尤其是BP神经网络)及智能算法为基础的步态识别方法得到了广泛的应用[13-15], 但是传统BP神经网络存在着收敛速度缓慢、容易陷入局部极小值、难以确定隐层节点个数、学习结果对初始权值向量敏感等不足, 影响了BP神经网络在步态识别中的进一步应用.齐美彬等[16]根据人体运动的规律性和重复性特点, 利用隐马尔科夫模型识别人体步态, 然而隐马尔科夫模型计算的复杂程度随着特征向量维度增大而成比例增加, 庞大的计算量制约着隐马尔科夫模型的广泛应用.佘青山等[17]将支持向量机(support vector machine, SVM)方法引入了下肢假肢步态识别, 目前SVM在步态识别领域被大量使用, 但SVM存在计算量大、核函数必须满足Mercer条件等缺点.相关向量机(relevance vector machine, RVM)[18]是一种新的机器学习方法, RVM中没有需要调整的参数, 核函数也不需要满足Mercer条件.虽然可有效解决非线性和小样本问题, RVM在本质上仍属于二分类器, 只能单模型单输出, 且核函数的构造或选择至今没有完善的理论依据[19].由于不同核函数对应不同信息源的特征空间和非线性映射, 因此多核函数对步态特征的描述能力更强, 使用多个核函数可以提高决策函数的性能[20-21].为了克服单个核函数的RVM的不足, 本文提取髋关节、膝关节角度、下肢表面肌电信号的特征值, 并对每种信号选用相应的核函数进行空间映射, 利用萤火虫优化(glowworm swarm optimization, GSO)算法确定核函数参数, 最后利用多核相关向量机(multiple kernel relevance vector machine, MKRVM)识别步态, 实验结果验证该方法的有效性.
1 多核学习相关向量机构造MKRVM模型, 最常用的方法将不同特性的核函数进行组合, 获得多核函数.假设来自特征空间s、大小为N的训练样本集为
| $ {X^s} = \left\{ {{x_i}, {t_i}} \right\}_{i = 1}^N, x \in {{\rm{R}}^D}. $ |
其中, t∈{1, 2,…, C}表示类别标签, s∈{1, 2, …, S}表示特征空间数目, R为实数,D为特征向量维数.当核函数确定时, 基核矩阵表示为Ks, 定义多核矩阵
| $ {K^\beta }\left( {{x_i}, {x_j}} \right) = \sum\limits_{s = 1}^S {\left[{{\beta _s}{K^s}\left( {x_i^s, x_j^s} \right)} \right]} . $ | (1) |
式中:Kβ为多核函数, βs≥0为基核函数的权值, Ks(xis, xjs)为第s个基核函数
引入辅助回归目标Y∈RL×N和权重参数W∈RN×L, 可得标准噪声回归模型[22]:
| $ {y_{nl}}\left| {{w_l}, {k_n} \sim {N_{ynl}}} \right.\left( {{k_n}{w_l}, 1} \right). $ | (2) |
式中:ynl为Y的第n行、第l列的元素;wl为W的第l列;knβ为kβ的第n行;Nx(m, v)表征x服从均值为m、方差为v的正态分布.
引入多项概率联系函数如下式, 将回归目标转化为类别标签:
| $ {t_n} = i, {y_{ni}} > {y_{nj}}, \forall j \ne i. $ | (3) |
为确保模型的稀疏性, 为权重向量引入零均值、方差为αnl-1的标准正态先验分布.由先验参数αnc组成的矩阵表示为A∈RN×L, αnl服从超参数为a、b的Gamma分布.该分层贝叶斯模型结构如图 1所示.
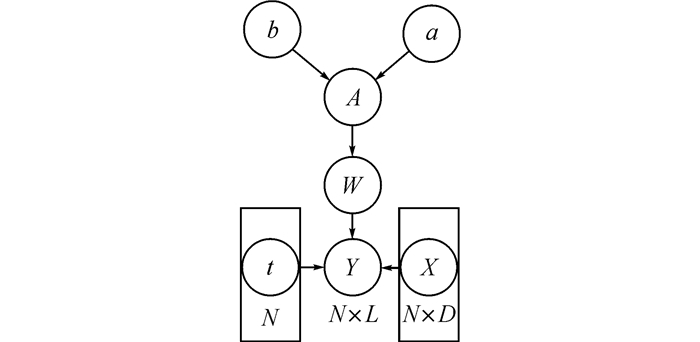
|
图 1 分层贝叶斯模型结构示意图 Fig. 1 Diagram of hierarchical Bayesian model structure |
由最大后验概率估计方法可得
| $ \hat W = \arg \max P\left( {W\left| {Y, A, K} \right.} \right). $ | (4) |
因此给定类别时, 基于最大后验概率(MAP)的权重更新方法为
| $ {{\hat W}_l} = {\left( {K{K^{\rm{T}}} + {A_l}} \right)^{ - 1}}KY_l^{\rm{T}}. $ | (5) |
根据式(5), 可以得出辅助变量的E-step形式.若∀c≠i, 可得下式[23]:
| $ {{\hat y}_{\mathit{ln}}} \leftarrow {{\hat w}_l}{k_n} - \frac{{{\varepsilon _{p\left( u \right)}}\left\{ {{N_u}\left( {\hat w_l^{\rm{T}}{k_n} - \hat w_i^{\rm{T}}{k_n}, 1} \right)} \right\}}}{{{\varepsilon _{p\left( u \right)}}\left\{ {\mathit{\Phi }\left( {u + \hat w_i^{\rm{T}}{k_n} - \hat w_l^{\rm{T}}{k_n}} \right)} \right\}}}. $ | (6) |
式中:ε为标准正态分布p(u)=N(0, 1) 的期望, 表示为u~N(0, 1);Φ为高斯累计分布函数.
Gamma分布的均值为
| $ {{\tilde a}_l} = \frac{{2a + 1}}{{w_l^2 + 2b}}. $ | (7) |
实验对象共36个人, 其中20男16女, 年龄在20~40岁.实验对象均签署了知情同意书, 所有实验对象在参加实验之前需接受训练并熟悉整个实验过程, 每种步态匀速走40次, 从中选出最具规范的20次, 每种步态共得到了20×36=720组数据.本文对髋关节、膝关节角度信号、下肢表面肌电信号的采集使用的设备为Delsys公司的Trigno无线EMG肌电采集系统.如图 2所示为传感器模块, 每个EMG传感器都内嵌1个角度传感器, 该系统包括1个基站和多个无线模块, 实际采集数据时需要通过无线发射到基站, 电脑利用EMGworks采集、分析软件显示采集的数据.3种信号的采样频率均为1 000 kHz.按照下肢肌肉群在行走时步态动作不同阶段的作用和贡献大小, 选择4块大腿上关键区域的肌群:阔筋膜张肌、股内侧肌、半腱肌、长收肌[24].阔筋膜张肌完成屈髋任务;股内侧肌是膝关节强有力的伸肌, 可以屈曲髋关节;半腱肌主要作用是伸髋屈膝以及膝关节的外旋;长收肌内收、外旋、微屈髋关节.安放传感器前需要用砂纸对皮肤进行轻微打磨, 去除皮肤角质层, 用医用酒精进行擦拭, 以增强信号的拾取能力.实验平台由台阶、平面和斜坡连接而成, 本文主要对平地行走、上坡、下坡、上楼梯和下楼梯5种步态来进行数据采集和分析.数据处理平台是宏基PC, 软件平台是MatlabR2012a, 主频2.00 GHz, 内存2.00 GB.

|
图 2 肌电信号传感器模块 Fig. 2 Electromyography sensor module |
基于MKRVM人体步态识别过程包括下肢表面肌电、髋关节、膝关节角度信号的采集、信号归一化处理、特征提取、选取核函数以及核函数参数的优化、基于MKRVM的步态分类等几个环节, 如图 3所示为相应的算法流程图.
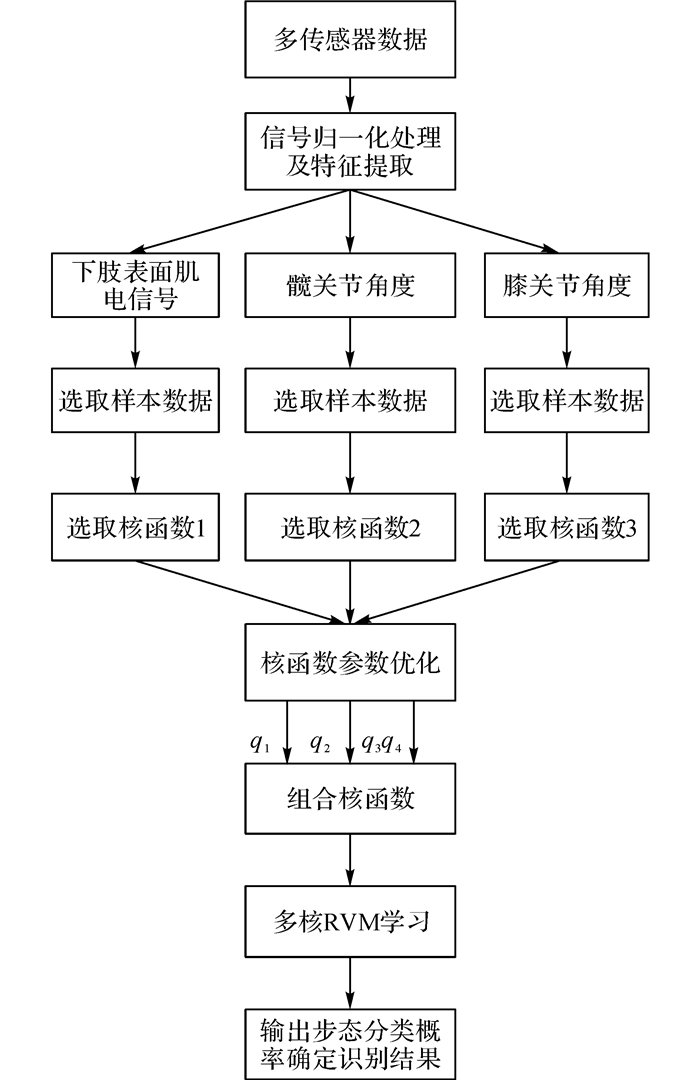
|
图 3 基于MKRVM人体步态识别方法流程图 Fig. 3 Flow chart of Locomotion-Mode recognition based on MKRVM |
肌电信号的幅值作为肌肉收缩力的间接反映, 两者间的关系并非固定, 电极位置、皮肤性质和皮肤温度的细微变化等多种因素可能导致肌电信号在不同时刻的差异.为了克服这种微弱信号的不确定性因素, 选择合适的参考值进行归一化处理.常用的方法是选择最大自主收缩值(maximum voluntary contraction, MVC)作为肌肉收缩的参考[25], 消除给定测试条件的影响, 将测试值由毫伏值转化为所选参考值的百分数, 如图 4所示, Q为采样点数, U为肌电信号幅值.幅值归一化处理并不是改变SEMG曲线的形状, 只是改变纵轴的缩放比例.
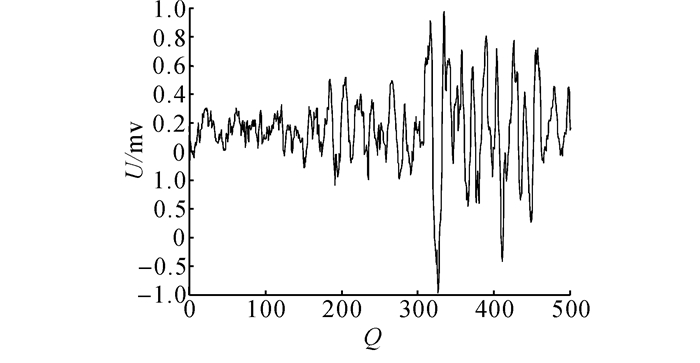
|
图 4 归一化后的SEMG信号曲线 Fig. 4 SEMG signal curve after normalization |
时间归一是在单步周期内选取均匀分布的500个离散点, 将连续的肌电信号变成一个一维数组, 进而利用同等动作条件下的多个有效单步周期进行平均, 得到该动作的单步肌电模型.由于髋关节、膝关节角度值具有明确直观的意义, 因此角度信号只进行时间归一, 不作幅值归一.
2.4 特征提取如何选择传感器信息特征是步态识别关键的一个环节, 如果能从待识别对象中选取出有效特征, 分类器就能比较容易地实现对不同步态的分类.由于SEMG信号属于生物电信号, 可重复性差, 一个特征只能从一个角度描述信号, 本文从时域、频域、时频域来提取SEMG信号特征[26].
SEMG直方图是常用的时域特征.何涛等[27]的研究表明,当肌肉收缩时, SEMG表现为偏离其图中的准线, 收缩程度越大, SEMG偏离准线越远.当人体上楼、上坡时, 主要是由大腿伸肌作用, 而在大腿屈肌处采集的SEMG信号相对较弱;当人体下楼、下坡时, 大腿屈肌的信号较强而大腿伸肌的信号相对较弱.本文利用表面肌电信号最大波幅比值作为肌电信号特征.首先设定一个阈值Bmax, 表面肌电信号的幅值大于+Bmax或小于-Bmax的采样点应删除.两端作限幅处理后, 将该区间的表面肌电信号采样点分成N等分后画出直方图, 由于本文利用表面肌电信号最大波幅比值来识别5种步态, 选择2路表面肌电信号的波幅直方图.
| $ v = \frac{{\max \left( A \right)}}{{\max \left( B \right)}}. $ | (8) |
式中:A为伸肌直方图的幅值;B为屈肌直方图的幅值;υ为两路表面肌电信号最大波幅比值, 选择髋关节半腱肌作为伸肌, 选择髋关节阔筋膜张肌为屈肌.
如图 5所示为5种步态的表面肌电信号直方图, R为对应幅值区间内信号个数.
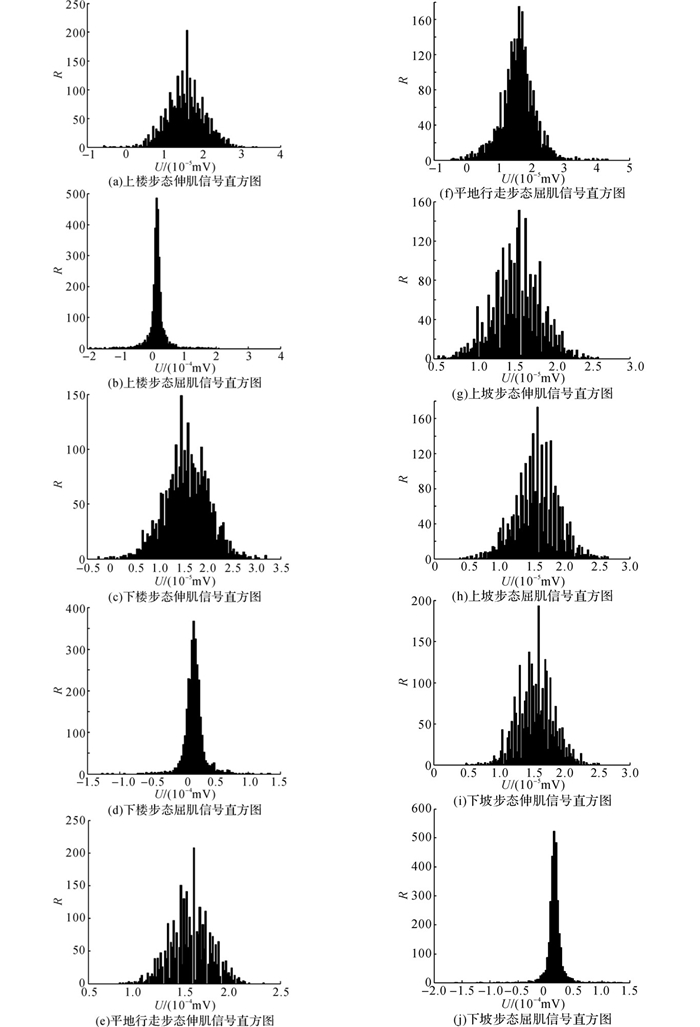
|
图 5 5种步态下伸肌和屈肌的表面肌电信号直方图 Fig. 5 Surface electromyography histograms of extensors and flexors in five locomotion modes |
功率谱是一种比较常用的频域方法, 不同实验对象同一步态的SEMG信号有区别, 同一实验对象在不同时间同一步态, 其功率谱也会有一定的改变.功率谱比值能够适应非特定人的SEMG特征提取.本文选用4块肌肉的肌电信号功率谱比值作为肌电信号频域特征.
| $ \chi = \frac{{{P_0}}}{P} = \frac{{\int_{{f_0} - n}^{{f_0} + n} {P\left( f \right){\rm{d}}f} }}{{\int_{ - \infty }^\infty {P\left( f \right){\rm{d}}f} }}. $ | (9) |
式中:χ为肌电信号功率谱比值;P(f)为功率谱密度函数;f0为功率谱最大值处的频率;n为积分范围.f0是方程d P(f)/d(f)=0的解, 如有多个解, 取P(f)为最大值时的f0.
实验表明, 当n=15 Hz时, 特征值差异较大.因为表面肌电信号能量集中在10~400 Hz, 分母在该范围内积分.由于表面肌电信号是非平稳特性的生理信号, 小波包变换可以根据要求将信号分解到各个频率范围之内, 提高了信号的自适应能力, 选择小波包能量比作为步态特征.多次实验后, 将4块肌肉表面肌电信号作4层小波包分解, 选用Matlab小波包工具中的db2小波包,计算出16个频段的投影系数, 设E4j(j=0, 1, …, 15) 表示重构信号S4j(j=0, 1, …, 15) 对应的能量:
| $ {E_{4j}} = \int {{{\left| {{S_{4j}}\left( t \right)} \right|}^2}{\rm{d}}t} = \sum\limits_{k = 1}^n {{{\left| {{X_{jk}}} \right|}^2}} . $ | (10) |
式中:Xjk(j=0, 1, …, 15;k=1, 2, …, n)为重构信号S4j的投影系数.
表面肌电信号各频段的能量表示为
| $ \vartheta = \left[{{E_{40}}, {E_{41}}, \cdots, {E_{414}}, {E_{415}}} \right]. $ | (11) |
为了避免运算量过大, 将能量值简化处理:
| $ E = {\left( {\sum\limits_{j = 0}^{15} {{{\left| {{E_{4j}}} \right|}^2}} } \right)^{1/2}}. $ | (12) |
小波包能量比表示为
| $ \sigma = \left[{\frac{{{E_{40}}}}{E}, \frac{{{E_{41}}}}{E}, \cdots, \frac{{{E_{414}}}}{E}, \frac{{{E_{415}}}}{E}} \right]. $ | (13) |
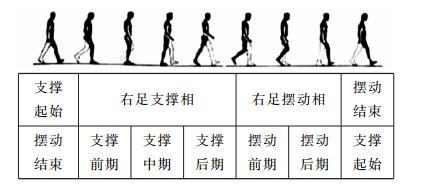
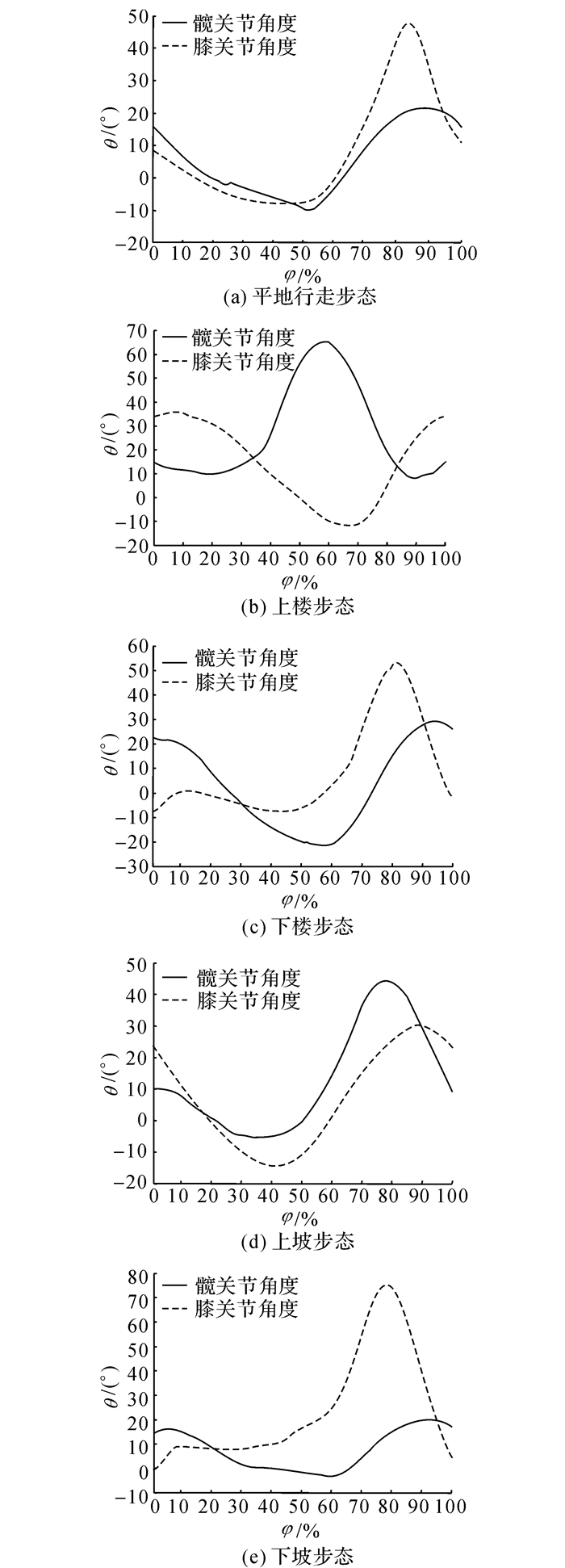
人体行走过程是一个典型的节律性运动, 如图 6所示为人体行走步态周期, 人体的步态由摆动相和支撑相周期性交替组成, 约分别占步态周期的60%和40%.支撑相可细分为支撑前、中、后期, 支撑前期占10%;支撑中期占40%;支撑后期占10%.摆动相则分为摆动前期、后期, 摆动前期占20%;摆动后期占20%[17].如图 7所示为一位实验对象5种步态髋关节和膝关节角度信号, φ为当前时刻在步态周期的百分比.不同步态髋关节、膝关节角度的变化有很好的区分性和规律性, 可以作为步态识别的重要信息, 为了提取细分运动模式下的角度特征, 本文计算髋关节、膝关节角度在细分运动模式下每0.1 s内的均值作为角度特征值, 计算公式为
|
图 6 人体行走步态周期示意图 Fig. 6 Human gait cycle diagram while walking |
|
图 7 5种步态下髋关节、膝关节角度在步态周期不同时刻曲线图 Fig. 7 Hip and knee joint angles vary with moments in one gait cycle in five locomotion modes |
| $ \tilde \omega = \sum\limits_{i = 1}^N {{\varepsilon _i}/\left( {N{\varepsilon _{\max }}} \right)} . $ | (14) |
式中:εi为不同步态下髋关节、膝关节角度值;εmax为髋关节、膝关节角度的最大值;N为0.1 s内传感器的采样点数.
2.5 不同肌肉组合特征的步态识别结果分析实验针对下述A、B、C、D、E这5种不同的肌肉组合提取特征并分别进行识别:
A组:阔筋膜张肌、股内侧肌、半腱肌、长收肌;
B组:阔筋膜张肌、股内侧肌、半腱肌;
C组:阔筋膜张肌、股内侧肌、长收肌;
D组:阔筋膜张肌、半腱肌、长收肌;
E组:股内侧肌、半腱肌、长收肌.
2.6 核函数的选择以及优化确定核函数是MKRVM算法的关键步骤之一, MKRVM算法中4种常用的核函数如下.
1) 线性核函数:
| $ k\left( {x, x'} \right) = xx'. $ | (15) |
2)p1阶多项式核函数:
| $ k\left( {x, x'} \right) = {\left( {{x^{\rm{T}}} \cdot x' + 1} \right)^{{p_1}}}. $ | (16) |
3) 径向基核函数:
| $ k\left( {x, x'} \right) = \exp \frac{{ - {{\left\| {x - x'} \right\|}^2}}}{{2p_2^2}}. $ | (17) |
4) Sigmoid核函数:
| $ k\left( {x, x'} \right) = \tanh \left( {{p_3}xx' + {p_4}} \right). $ | (18) |
在式(15)~ (18) 中:p1>0为核阶数;p2>0为核宽度;p3、p4为Sigmoid核函数参数.本文选择具有快速、准确的GSO[28]智能优化算法对MKRVM核函数中的每个参数进行优化.
2.7 实验结果分析把每一类数据的前30个样本作为训练样本, 后30个样本作为测试样本.MKRVM输出是[ppd, psl, pxl, psp], 即当前样本属于各种步态的概率, 其中ppd、psl、pxl、psp分别表示平地行走、上楼、下楼、上坡的概率, 之后将结果最大概率值位置1, 其余置0, 可得[0,0,0]T表示平地行走;[0, 1, 0, 0]T表示上楼;[0, 0, 1, 0]T表示下楼;[0, 0, 0, 1]T表示上坡,
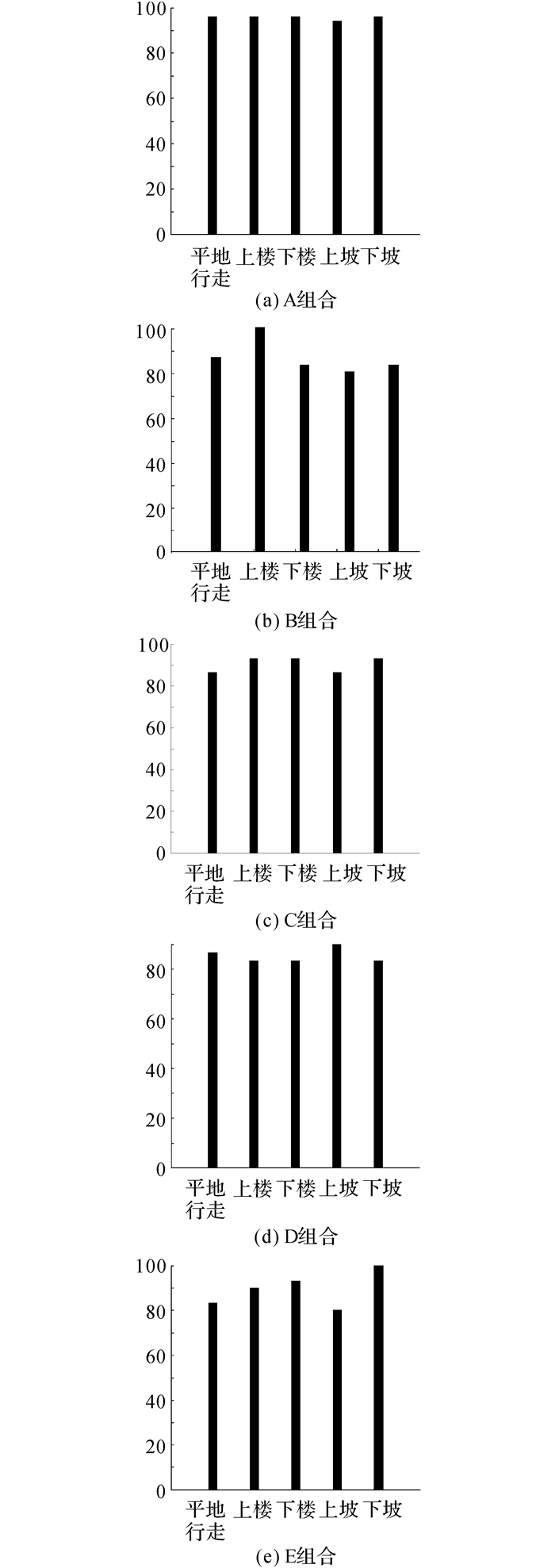
本文对下肢不同肌肉组合的特征值进行识别, 寻找分类效果理想的肌肉组合.A组合对阔筋膜张肌、股内侧肌、半腱肌、长收肌四块肌肉提取特征值进行识别, 识别结果如图 8所示, ζ表示每种步态的平均识别率.A组合由于包含的肌电信息相对较多, 所反映的步态信息相对较多, 平均识别率为95.52%.
|
图 8 A、B、C、D、E肌肉特征组合识别结果 Fig. 8 Recognition results of muscle feature combination A, B, C, D and E |
B组合对阔筋膜张肌、股内侧肌、半腱肌3块肌肉提取特征值进行步态识别, 识别结果如图 8(b)所示, 在减少长收肌情况下的平均识别率为86.7%, 共有20组测试样本识别错误, 包括4组平地行走步态误识别为下楼梯, 5组下坡步态误识别为平地行走, 6组上坡步态误识别为平地行走, 5组下楼梯步态误识别为下坡.
C组合对阔筋膜张肌、股内侧肌、长收肌提取特征值进行步态识别, 结果如图 8(c)所示, 识别结果优于B组合.该组合的识别结果中有14组样本出现错误, 其中4组上坡步态误识别为上楼梯, 2组上楼步态误识别为平地行走, 2组下楼步态误识别为上楼, 4组平地行走步态误识别为下坡, 2组下坡步态误识别为平地行走.该组合识别效果比B组合好, 较A组合差.
D组合对阔筋膜张肌、半腱肌、长收肌提取特征值, 进行步态识别, 识别结果如图 8(d)所示, 整体识别率最低.该组合共有22组样本识别错误, 其中5组上楼步态误识别为上坡步态, 3组上坡步态误识别为上楼步态, 4组平地行走步态误识别为下坡步态.5组下楼步态误识别为下坡步态.5组下坡步态误识别为上坡步态.
E组合对股内侧肌、半腱肌、长收肌提取特征值, 进行步态识别, 识别结果如图 8(e)所示, 识别率低于C组合.该组合共有15组样本识别错误, 其中4组平地行走步态误识别为上楼梯步态, 3组上楼步态误识别为上坡步态, 2组下楼步态误识别为下坡步态, 6组上坡步态误识别为下坡步态.
通过以上分析, 可以看出:大腿肌肉对行走步态贡献率不同, 肌肉选取的准确性也是保证识别准确率的重要因素, 其中A组合识别率最高, 因此选取4块肌肉.通过对单核SVM和单核RVM作对比实验来分析不同步态特征的核函数性能.由于SVM含有惩罚因子C, 在分类时需要设置, 采用交叉验证网格搜索方法[29]得到C=6.65, 核函数的参数p1=1.56, p2=4.95, p3=2.80, p4=5.66.为了便于比较, 同时采用交叉验证网格搜索方法来确定RVM核函数参数, 单核RVM的核函数参数p′1=3.55, p′2=2.46, p′3=2.85, p′4=1.77.
如表 1所示为单核分类器识别结果, 其中σSVM为SVM识别率, σRVM为RVM识别率.3种信号特征的核性能有明显区别, 对于表面肌电信号特征, SVM与RVM的最优核函数为径向基核函数;对于髋关节角度特征, SVM最优核函数为Sigmoid核函数, RVM最优核函数为径向基核函数;对于膝关节角度特征, SVM与RVM的最优核函数为Sigmoid核函数.因此多源信号的最优核组合如下:表面肌电信号选择径向基核函数, 髋关节角度选择径向基核函数, 膝关节角度选择Sigmoid核函数.
| 表 1 不同特征下单核分类器识别结果 Table 1 Recognition results of single kernel classifiers using different features |
采用GSO算法[28]对MKRVM的核函数参数寻优, 算法参数设置如下:荧光素初值l0=5, 邻域的变化率β=0.06, 控制萤火虫邻居数量的阈值mi=5, 萤火虫的感知范围rq=5, 运动步长S=0.05, 荧光素的更新率ω=0.4, 荧光素的挥发系数λ=0.3, 最大迭代次数为100, 种群规模为30.下肢表面肌电信号最优核函数为径向基核函数, 核函数参数p2=0.42;髋关节角度最优核函数为径向基核函数, 核函数参数p2=1.65;膝关节角度最优核函数为Sigmoid核函数, 核函数参数p3=4.28、p4=1.79.
将单核分类器对不同特征100次的识别结果取平均值, 如表 2所示为单核RVM与MKRVM识别结果对比, 其中ttra为训练时间, trec为识别时间, σ为识别率.从表中可以看出, 利用GSO优化核函数参数训练过程需要5.820 s, 识别过程需要0.063 s, 训练时间长于单核RVM与SVM方法, 识别时间少于单核SVM方法, 实际应用中训练过程一般是离线进行的, 而人们更关心的是识别时间.通过对比实验可以发现, MKRVM由于融合了下肢表面肌电信号、髋关节角度信号、膝关节角度信号特征, 并对每种特征选用了合适的核函数及核参数, 具有更高的识别率.
| 表 2 单核与多核分类器性能对比结果 Table 2 Performance comparison of single kernel and multi kernel classifier |
如表 3所示为利用不同分类器步态的识别情况, 对于160个测试样本, MKRVM的识别率达到94.50%, 高于BP的84.09%、SVM的85.38%和RVM的90.33%.由于BP神经网络采用梯度下降的学习算法, 易陷入局部最小化, BP神经网络识别结果较差.单核RVM由于相关向量少, 稀疏性高, 因此其测试时间相比SVM要短, 分类的正确率优于SVM.在对每一类步态的识别率中, 除上坡的识别率要低于RVM, MKRVM对于其余步态的识别率均高于BP、SVM和RVM的识别率.作为对比的同类方法中, 文献[14]方法的识别率为90.16%;文献[15]方法的识别率为90.00%;文献[17]方法的识别率为85.00%.
| 表 3 不同分类器的识别率 Table 3 Recognition rates of different types of classifier |
经过对实验结果的分析不难看出, 由于MKRVM融合了多源信号的步态信息, 能够更为全面地描述步态特征, 且使用多个核函数的组合比使用单一核函数的推广性更好, 因此该方法的性能明显优于BP和SVM方法及其他同类方法.
3 结语表面肌电信号和髋关节、膝关节角度分别体现了人体步态的某些特征, 为了克服传统单一核函数只能反映某一类数据对应步态特性的不足, 通过研究多源信号特点, 选择表面肌电信号最大波幅比值、肌电信号功率谱比值和小波包能量比, 以及细分运动模式下髋关节、膝关节角度每0.1s内的均值作为特征值.
为不同信号选取合适的核函数, 利用GSO确定核函数参数, 利用MKRVM识别步态.实验结果表明, 本文采用的MKRVM识别方法对5种步态(平地行走、上楼、下楼、上坡、下坡)的平均识别率优于基于单一核函数的方法, 为步态识别的研究提供了一种新途径.
由于本文搭建的是基于PC机的多源信息采集系统, 该方法距离实用还有一定的差距, 如何提升系统鲁棒性的同时加强算法的实时性是今后的研究重点.
| [1] | DATTA D, HOWITT J. Conventional versus microchip controlled pneumatic swing phase control for tranfemoral amputees: user's verdict[J]. Prosthesis and Orthotics International, 1998, 22(2): 129–135. |
| [2] | SUP F, BOHARA A, GOLDFARB M. Design and control of a powered transfemoral prosthesis[J]. International Journal of Robotics Research, 2008, 27(2): 263–273. DOI:10.1177/0278364907084588 |
| [3] | HITT J, SUGAR T, HOLGATE M, et al. Robotic transtibial prosthesis with biomechanical energy regeneration[J]. Industrial Robot, 2013, 36(5): 441–447. |
| [4] | KAHLE J T, HIGHSMITH M J, HUBBARD S L. Comparison of non-microprocessor knee mechanism versus C-Leg on prosthesis evaluation questionnaire, stumbles, falls, walking tests, stair descent, and knee preference[J]. Journal of Rehabilitation Research and Development, 2008, 45(1): 1–14. DOI:10.1682/JRRD.0000.00.0000 |
| [5] | DINGWELL J B, DAVIS B L, FRAZIER D M. Use of an instrumented treadmill for real-time gait symmetryevaluation and feedback in normal and transtibial amputee subjects[J]. Prosthetics and Orthotics International, 1996, 20(2): 101–110. |
| [6] |
谭冠政, 吴立明. 国内外人工腿(假肢)研究的进展及发展趋势[J].
机器人, 2001, 23(1): 91–96.
TAN Guan-zheng, WU Li-ming. Progress and development trend towards study of artificial legs (prostheses) in foreign countries and China[J]. Robot, 2001, 23(1): 91–96. |
| [7] |
喻洪流, 钱省三, 沈凌, 等. 基于小脑模型神经网络控制的步速跟随智能膝上假肢[J].
中国组织工程研究与临床康复, 2007, 11(31): 6233–6235.
YU Hong-liu, QIAN Sheng-san, SHEN ling, et al. Intelligent above-knee prosthesis following healthy leg gait with cerebellar model articulation controller[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2007, 11(31): 6233–6235. DOI:10.3321/j.issn:1673-8225.2007.31.036 |
| [8] |
王人成. 我国假肢技术的研究与进展[J].
中国康复医学杂志, 2012, 27(11): 1058–1060.
WANG Ren-cheng. The prosthetic technology research and development of our country[J]. Chinese Journal of Rehabilitation Medicine, 2012, 27(11): 1058–1060. DOI:10.3969/j.issn.1001-1242.2012.11.017 |
| [9] |
高云园, 孟明, 罗志增, 等. 利用多源运动信息的下肢假肢多模式多步态识别研究[J].
传感器技术学报, 2011, 24(11): 1574–1578.
GAO Yun-yuan, MENG Ming, LUO Zhi-zeng, et al. Multi-Mode and gait phase recognition of lower limb prosthesis based on multi-source motion information[J]. Chinese Journal of Sensors and Actuators, 2011, 24(11): 1574–1578. |
| [10] | ZHANG F, LIU M, HUANG H. Effects of locomotion mode recognition errors on volitional control of powered above-knee prostheses[J]. IEEE Transaction on Neural Systems and Rehabilitation Engineering, 2015, 23(1): 64–72. DOI:10.1109/TNSRE.2014.2327230 |
| [11] | YOUNG A J, SIMON A M, HARGROVE L J. A training method for locomotion mode prediction using powered lower limb prostheses[J]. IEEE Transaction on Neural Systems and Rehabilitation Engineering, 2014, 22(3): 671–677. DOI:10.1109/TNSRE.2013.2285101 |
| [12] |
佟丽娜, 侯增广, 彭亮. 基于多路sEMG时序分析的人体运动模式识别方法[J].
自动化学报, 2014, 40(5): 810–820.
TONG Li-na, HOU Zeng-guang, PENG Liang. Multi-channel sEMG time series analysis based human motion recognition method[J]. Acta Automatic Sinica, 2014, 40(5): 810–820. |
| [13] |
马玉良, 马云鹏, 张启忠, 等. GA-BP神经网络在下肢运动步态识别中的应用研究[J].
传感技术学报, 2013, 26(9): 1183–1188.
MA Yu-liang, MA Yun-peng, ZHANG Qi-zhong, et al. Gait phase recognition of lower limb based on GA optimized BP neural network[J]. Chinese Journal of Sensors And Actuators, 2013, 26(9): 1183–1188. |
| [14] |
刘磊, 杨鹏, 刘作军. 基于多源信息和广义回归神经网络的下肢运动模式识别[J].
机器人, 2015, 37(3): 310–317.
LIU Lei, YANG Peng, LIU Zuo-jun. Lower limblocomotion modes recognition based on multiple-source information and general regression neural network[J]. Robot, 2015, 37(3): 310–317. |
| [15] |
袁娜, 杨鹏, 刘作军. 利用平均影响值和概率神经网络的步态识别[J].
哈尔滨工程大学学报, 2015, 36(2): 1–5.
YUAN Na, YANG Peng, LIU Zuo-jun. Gait recognition based on the mean impact value and probability neural network[J]. Journal of Harbin Engineering University, 2015, 36(2): 1–5. |
| [16] |
齐美彬, 王倩, 蒋建国. 非规范视角步态识别研究[J].
仪器仪表学报, 2008, 29(10): 2058–2061.
QI Mei-bin, WANG Qian, JIANG Jian-guo. Research on nonstandard view gait identification[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2058–2061. DOI:10.3321/j.issn:0254-3087.2008.10.008 |
| [17] |
佘青山, 高云园, 孟明. 下肢EMG的小波支持向量机多类识别方法[J].
华中科技大学学报:自然科学版, 2010, 38(10): 75–79.
SHE Qing-shan, GAO Yun-yuan, MENG Ming. Multiclass recognition of lower limb EMG using wavelet SVM[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2010, 38(10): 75–79. |
| [18] | TIPPING M E. Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211–244. |
| [19] | LI W X, LIAN L M. Multiple faces tracking based on relevance vector machine[J]. Journal of Software, 2012, 7(4): 810–813. |
| [20] |
汪洪桥, 孙富春, 蔡艳宁, 等. 多核学习方法[J].
自动化学报, 2010, 36(8): 1037–1049.
WANG Hong-qiao, SUN Fu-chun, CAI Yan-ning, et al. On multiple kernel learning methods[J]. Acta Automatica Sinica, 2010, 36(8): 1037–1049. |
| [21] |
张凯军, 梁循. 一种改进的显性多核支持向量机[J].
自动化学报, 2014, 40(10): 2288–2294.
ZHANG Kai-jun, LIANG Dun. An improved domain multiple kernel support vector machine[J]. Acta Automatica Sinica, 2014, 40(10): 2288–2294. |
| [22] | PSORAKIS I, DAMOULAS T, GIROLAMI M A. Multiclass relevance vector machines: sparsity and accuracy[J]. IEEE Transactions on Neural Networks, 2010, 21(10): 1588–1598. DOI:10.1109/TNN.2010.2064787 |
| [23] | DAMOULAS T, GIROLAMI M A. Combining feature spaces for classification[J]. Pattern Recognition, 2009, 42(11): 2671–2683. DOI:10.1016/j.patcog.2009.04.002 |
| [24] | HUANG H, ZHANG F, HARGROVE L J, et al. Continuous locomotion-mode identification for prosthetic legs based on neuromuscular-mechanical fusion[J]. IEEE Transactions on Biomedical Engineering, 2011, 58(10): 2867–2875. DOI:10.1109/TBME.2011.2161671 |
| [25] |
陈玲玲. 肌电信号的运动模式识别及其在膝上假肢中的应用研究[D]. 天津: 河北工业大学, 2010: 56.
CHEN Ling-ling. Motion pattern recogniton based on emg and its application research on ak prosthesis [D]. Tianjin: Hebei University of Technology. 2010: 56. |
| [26] |
丁其川, 熊安斌, 赵新刚, 等. 基于表面肌电的运动意图识别方法研究及应用综述[J].
自动化学报, 2016, 42(1): 13–25.
DING Qi-chuan, XIONG An-bin, ZHAO Xin-gang, et al. A review on researches and applications of sEMG-based motion intent recognition methods[J]. Acta Automatica Sinica, 2016, 42(1): 13–25. |
| [27] |
何涛, 胡洁, 夏鹏, 等. 基于ReliefF算法与遗传算法的肌电信号特征选择[J].
上海交通大学学报, 2016, 50(2): 204–208.
HE Tao, ZOU Hu-Jie, XIA Peng, et al. Feature selection of EMG signal based on relieff algorithm andgenetic algorithm[J]. Journal of Shanghai JiaotongUniversity, 2016, 50(2): 204–208. |
| [28] |
龙文, 蔡绍洪, 焦建军, 等. 求解约束优化问题的萤火虫算法及其工程应用[J].
中南大学学报:自然科学版, 2015, 46(4): 1260–1267.
LONG Wen, CAI Shao-hong, JIAO Jian-jun, et al. Firefly algorithm for solving constrained optimization problems and engineering applications[J]. Journal of Central South University: Science and Technology, 2015, 46(4): 1260–1267. |
| [29] |
王雪刚, 邹早建. 基于果蝇优化算法的支持向量机参数优化在船舶操纵预报中的应用[J].
上海交通大学学报, 2013, 47(6): 884–888.
WANG Xue-gang, ZOU Zao-jian. FOA-based SVM parameter optimization and its application in ship manoeuvring prediction[J]. Journal of Shanghai Jiaotong University, 2013, 47(6): 884–888. |



