2. 常州大学 城市轨道交通学院, 江苏 常州 213164
2. School of Urban Rail Transit, Changzhou University, Changzhou 213164, China
高速列车的振动噪声问题[1], 特别是车内噪声[2], 已经逐渐成为影响其可靠商业运营的关键因素[3].根据传递路径的不同, 车内噪声的来源可以分为空气传声和结构传声2种主要形式[4].对于空气传声, 控制空气声源、增强车体的密封和隔声性能是降低该路径噪声的主要措施.对于结构传声, 控制结构振动、提高连接部件的隔振和减振性能是降低该路径噪声的有效方法.高速列车车体多为铝型材结构, 研究铝型材的声振性能是开展车内减振降噪工作的重要基础.Xie等[5]基于统计能量分析(statistical energy analysis, SEA)建立了轨道车辆铝型材的声学特性仿真模型.研究结果显示, 在力载荷激励下, SEA模型的预测结果和试验结果较为接近, 但在声载荷激励下, 两者的吻合情况并不理想.Park等[6]使用有限元方法(finite element method, FEM), 研究了铝型材内部结构参数优化对其轻量化及隔声性能的影响.通过内部结构优化, 铝型材在减重6 %的情况下, 800 Hz以上的隔声性能依然优异.此外, 在铝型材内部填充聚氨酯泡沫, 可以进一步提高其在全频段的隔声性能.沈火明等[7]使用周期子结构方法, 研究了铝型材腹板倾角对其隔声性能的影响.计算结果表明, 铝型材加上板结构的隔声效果最优, 加下板结构的隔声效果最差.两者在腹板倾角为55°时隔声量差值达到6.9 dB.罗乐等[8]基于结构-声耦合法建立了铝型材的隔声预测模型, 分析了车体不同区域铝型材的隔声特性.研究发现, 面密度最大的地板铝型材的隔声性能明显优于顶板, 但次于侧墙, 面密度并不是判断铝型材隔声性能的唯一指标.王瑞乾等[9]通过实验室测试, 研究了在铝型材表面喷涂阻尼对其减振降噪效果的影响.结果显示, 随着阻尼层厚度的增加, 铝型材的隔声效果呈现提升趋势, 尤其是在500 Hz以上的中高频段.
就国内高速列车铝型材而言, 目前还缺少有关其声振特性的系统性研究.本文以国内典型高速列车的地板铝型材作为研究对象, 结合试验测试、仿真分析等手段详细研究其声振特性, 并在此基础上提出一种新的铝型材声振特性等效建模方法.
1 地板铝型材隔声特性测试高速列车地板铝型材的隔声测试在声学实验室内进行.根据ISO 140-3[10]等相关标准规定, 使用混响室-混响室方法测试试件的隔声量.实验中2个混响室的容积如下:5 414 mm×4 100 mm×3 300 mm(发声室)和4 457 mm×4 196 mm×3 300 mm(受声室).测试样件的几何尺寸为985 mm ×970 mm.地板铝型材隔声测试现场照片如图 1所示.

|
图 1 地板铝型材隔声测试现场照片 Fig. 1 Test photographs of sound transmission loss measurement of floor aluminum extrusion |
在发声室使用B & K 4292型12面无指向声源输出粉红噪声作为激励, 频率范围为中心频率100 Hz ~ 3 150 Hz的1/3频带.在发声室和受声室内, 分别无规则布置6个B & K 4190型麦克风, 同时测得2个混响室的平均声压级L1和L2.将测试结果代入下式, 得到试件的频率隔声量:
| $ R = {L_1} - {L_2} + 10\lg \frac{{St}}{{0.16V}}. $ | (1) |
式中:S为试件表面积, t为受声室混响时间, V为受声室容积.
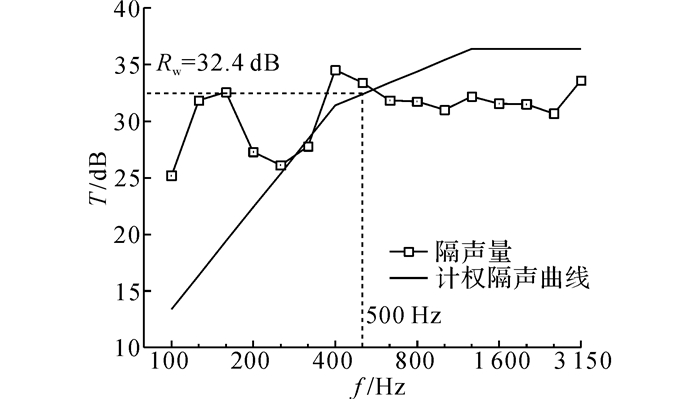
地板铝型材的隔声测试结果如图 2所示.f为1/3频程中心频率, T为隔声量.可见, 地板铝型材的隔声量频率曲线在中心频率250 Hz的1/3频带出现低谷, 在中心频率500 Hz以上的1/3频带基本平稳而略呈上下波动状.其隔声单值评价量Rw=32.4 dB.
|
图 2 地板铝型材隔声测试结果 Fig. 2 Test results of sound transmission loss of flooraluminum extrusion |
高速列车地板铝型材的阻尼损耗因子使用半功率带宽法和行波法2种方法进行识别.
将地板铝型材和B & K 3626型激振器分别用弹性绳固定并作自由悬挂.使用激振器对铝型材车外一侧进行激励, 依次随机激励3个位置, 激励输入是上限截止频率为5 000 Hz的白噪声.同时在车内一侧随机布置10个B & K 4508型加速度计进行拾振, 如图 3所示.

|
图 3 半功率带宽法阻尼测试现场照片 Fig. 3 Test photographs of damping using half-power bandwidth method |
当激励频率等于结构的固有频率时, 系统发生共振, 通过识别此时的共振频率及其半功率带宽获得试件的阻尼.阻尼损耗因子的计算公式如下:
| $ \eta = \frac{{{f_2} - {f_1}}}{{{f_n}}}. $ | (2) |
式中:n为节点数,fn为共振频率, f1和f2分别为共振曲线峰值下降3 dB时对应的半波宽频率.
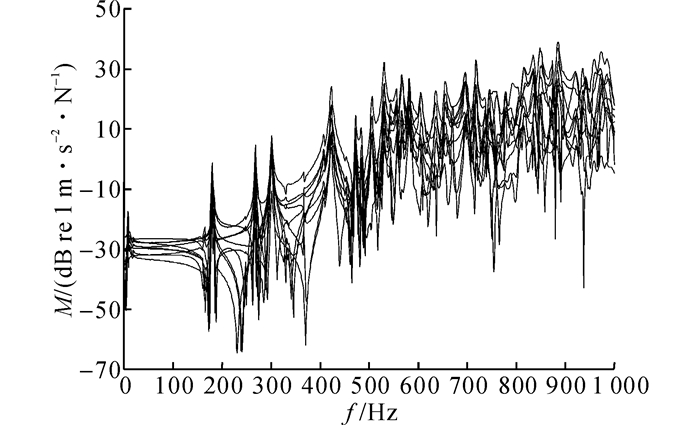
如图 4所示为地板铝型材在第一个激励点位置时, 10个加速度测点的频响函数(0~1 000 Hz)测试结果.由图 4可见, 在500 Hz以上地板铝型材各个测点的频响函数峰值密集且相互交错, 即结构出现了局部模态.局部模态呈现高频密集分布, 使用半功率带宽法识别阻尼会出现困难[11].因此, 使用行波法对其进行识别.
|
图 4 半功率带宽法加速度频响函数测试结果 Fig. 4 Test results of acceleration frequency response function using half-power bandwidth method |
行波法的推导基于梁结构模型[12].弯曲波沿梁的长度方向传播时振幅会明显衰减, 而衰减的程度与其阻尼损耗因子密切相关.x0和x1两点之间的振动速度(或者加速度)可以表示为
| $ \begin{array}{l} {\underline v _1} = {\underline v _0}\exp \left[{-{\rm{j}}\bar k\left( {{x_0}-{x_1}} \right)} \right] = \\ \;\;\;\;\;\;\;{\underline v _0}\exp \left[{{\rm{k''}}\left( {{x_0}-{x_1}} \right)} \right]\exp \left[{-{\rm{jk'}}\left( {{x_0}-{x_1}} \right)} \right]. \end{array} $ | (3) |
式中:v0和v1分别为两点的振动速度, v表示复数, j表示虚部, k为波数, k′和k″分别为复波数k的实部和虚部.
那么, x0和x1两点之间的相位差可以表示为
| $ {\phi _{01}} = {\rm{k'}}\left( {{x_1} - {x_0}} \right) = \frac{{2{\rm{\pi }}}}{\lambda }\left( {{x_1} - {x_0}} \right). $ | (4) |
式中:λ为波长.
振幅的衰减可以表示为
| $ \ln \frac{{{v_0}}}{{{v_1}}} = 10\lg \frac{{\left| {v_0^2} \right|}}{{\left| {v_1^2} \right|}} = 8.7{\rm{k''}}\left( {{x_1} - {x_0}} \right). $ | (5) |
通过测试相位以及振幅的衰减可以确定波数的实部和虚部.对于阻尼损耗因子并不是非常大的结构而言, 弯曲刚度的实部可以通过下式获得:
| $ B' = {\omega ^2}m'\frac{1}{{{{\rm{k}}^{'4}}}} = {\omega ^2}m'{\left( {\frac{{{x_1} - {x_0}}}{{{\phi _{01}}}}} \right)^4}. $ | (6) |
式中:ω为角频率, m′为被测结构单位长度的质量.
阻尼损耗因子可以表示为
| $ \eta = 4\frac{{{\rm{k''}}}}{{{\rm{k'}}}}\frac{{{{D'}_{\rm{B}}}\lambda }}{{13.6}}. $ | (7) |
式中:D′B表示单位长度上振动级的衰减, 可表示为
| $ \left( {{x_1} - {x_0}} \right){{D'}_{\rm{B}}} = 10\lg \frac{{\left| {v_0^2} \right|}}{{\left| {v_1^2} \right|}}. $ | (8) |
如图 5所示为使用行波法测试地板铝型材阻尼的现场照片.使用激振器激励铝型材车外一侧, 每个试件激励2个位置, 激励输入同样是上限截止频率5 000 Hz的白噪声.在同一侧布置10个加速度计进行拾振.加速度计和激振点分布在同一水平直线上, 距离激振点分别为0、2、4、8、12、16、24、32、48和64 cm.

|
图 5 行波法阻尼测试现场照片 Fig. 5 Test photograph of damping measurement using vibration attenuation method |
如图 6所示为地板铝型材在第一个激励点位置时, 中心频率1 000 Hz的1/3频程加速度频响函数及其线性拟合曲线(用于获得斜率).图中,D为加速度计和激振点之间的距离.

|
图 6 行波法加速度频响函数测试结果 Fig. 6 Test results of acceleration frequency response function using vibration attenuation method |
通过式(7) 计算得到地板铝型材在中心频率1 000 Hz的1/3频带的阻尼损耗因子, 为0.004.其他频带的阻尼损耗因子也可以通过类似方法获得.
对于地板铝型材在500 Hz以下频率的阻尼, 基于半功率带宽法, 首先将每个加速度测点的频率阻尼识别结果换算到1/3频程[13], 然后将10组数据进行算术平均, 再将3个激励点位置的结果进行算术平均, 得到地板铝型材在整体模态时的阻尼损耗因子.对于地板铝型材在500 Hz以上频率的阻尼, 基于行波法, 将第一个激励点位置的结果和第二个激励点位置的结果进行算术平均, 得到地板铝型材在局部模态时的阻尼损耗因子.
将采用半功率带宽法和行波法识别得到的阻尼损耗因子在频域进行合并, 得到地板铝型材在中心频率为100~3 150 Hz的1/3频程阻尼损耗因子.
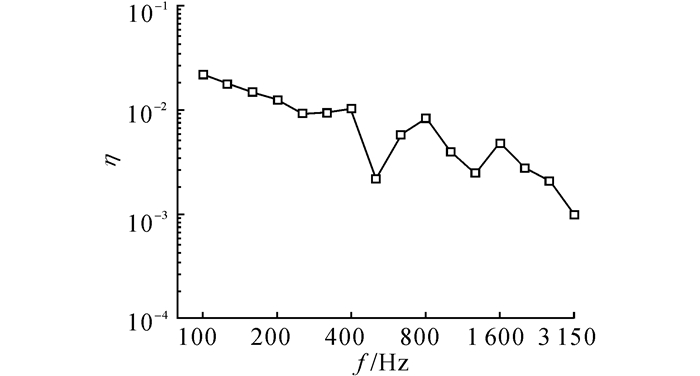
如图 7所示为地板铝型材的阻尼损耗因子结果.由图 7可见, 地板铝型材的阻尼损耗因子随着频率的提高基本呈现下降趋势.在中心频率为500和1 250 Hz的1/3频带出现局部阻尼低谷.
|
图 7 地板铝型材阻尼损耗因子测试结果 Fig. 7 Test results of damping loss factor of floor aluminum extrusion |
基于半功率带宽法中地板铝型材的加速度频响函数结果, 使用模态计数法[14], 通过统计共振峰的数量获得地板铝型材的模态密度.
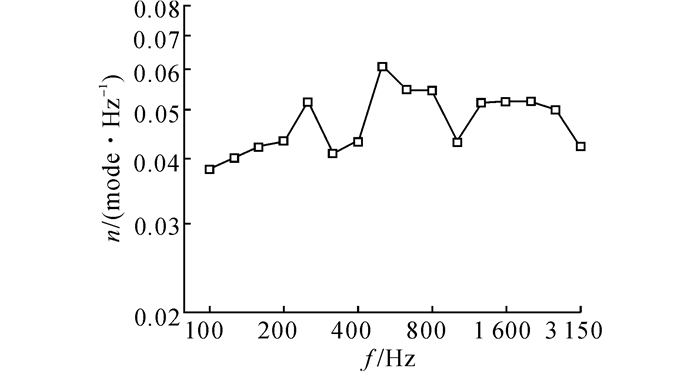
如图 8所示为地板铝型材的模态密度结果.其中,n为模态密度(对数坐标).由图 8可见, 地板铝型材的模态密度在频率分布上的差异基本不大.在中心频率为250、500和1 600 Hz附近的3个1/3频带存在局部峰值.
|
图 8 地板铝型材模态密度测试结果 Fig. 8 Test results of modal density of floor aluminum extrusion |
辐射声功率测试基于声强法[15], 在混响室-半消声室中进行.将地板铝型材安装于混响室-半消声室的洞口.其中, 铝型材车外一侧朝向混响室, 车内一侧朝向半消声室.在混响室内使用激振器激励铝型材, 每个试件激励3个位置, 激励输入是上限截止频率为5 000 Hz的白噪声.在半消声室内使用B & K3599型声强探头对地板铝型材进行离散点上的声强扫描, 铝型材表面划分为6×6的网格, 按S型路线进行逐格测试.同时在该侧地板铝型材表面布置10个加速度计拾振.如图 9所示为地板铝型材振动声辐射测试的现场照片.

|
图 9 地板铝型材振动声辐射测试现场照片 Fig. 9 Test photographs of sound radiation power measurement of floor aluminum extrusion |
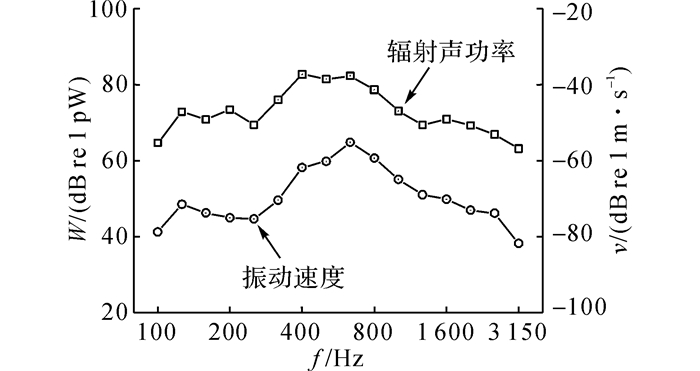
将3个激励位置的测试结果进行算术平均, 得到地板铝型材的辐射声功率和表面振动速度(对加速度进行积分)结果, 如图 10所示.其中W为辐射声功率.
|
图 10 地板铝型材辐射声功率和振动速度测试结果 Fig. 10 Test results of sound radiation power andvelocity of floor aluminum extrusion |
基于SEA理论[14], 子系统1(如:板子系统)流入子系统2(如:空腔)的能量为
| $ {W_{12}} = \omega {\eta _{12}}{E_1} = \omega {\eta _{12}}{m_1}\left\langle {\overline {{v^2}} } \right\rangle . $ | (9) |
式中:η12为子系统1到子系统2的耦合损耗因子, E1为子系统1的振动能量, m1为子系统1的质量,
对于板件而言, 振动辐射到半空间的声功率为
| $ {W_{{\rm{rad}}}} = \rho c\sigma S\left\langle {\overline {{v^2}} } \right\rangle . $ | (10) |
式中:σ为板的声辐射效率;S为板的表面积;ρ和c分别为空气的密度和空气中的声速, 这里定义在20℃时, ρ × c = 415 N·s/m2.
令W12=Wrad, 那么板和空腔的耦合损耗因子(也称作辐射损耗因子)可以表示为
| $ {\eta _{12}} = \frac{{{W_{12}}}}{{\omega {m_1}\left\langle {\overline {{v^2}} } \right\rangle }} = \frac{{\rho c\sigma S}}{{\omega {m_1}}}. $ | (11) |
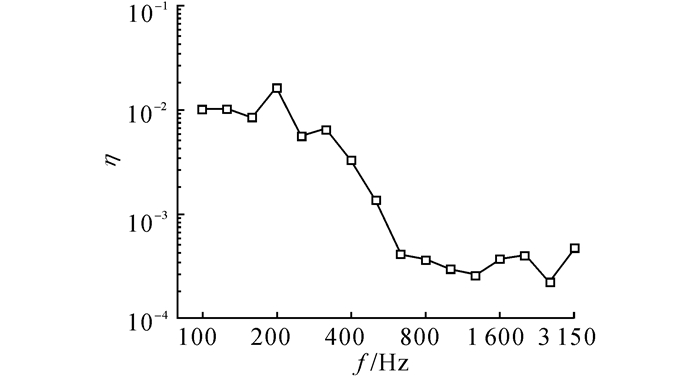
通过式(11) 可以计算得到地板铝型材和空腔之间的耦合损耗因子, 如图 11所示.由图 11可见, 地板铝型材和空腔之间的耦合损耗因子在中心频率为200 Hz的1/3频带出现局部峰值, 之后基本随着频率的提高呈现下降趋势.在中心频率为1 250 Hz以上的1/3频带略有上升, 在中心频率为2 500 Hz的1/3频带出现局部低谷.
|
图 11 地板铝型材耦合损耗因子测试结果 Fig. 11 Test results of coupling loss factor of flooraluminum extrusion |
地板铝型材声振特性的仿真分析基于混合有限元-统计能量分析方法[16](hybrid method of finite element and statistical energy analysis, FE-SEA).
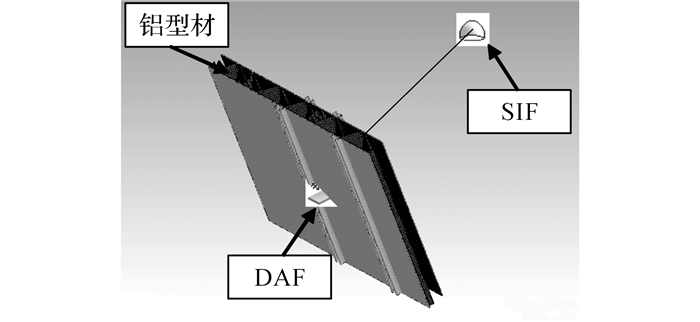
3.1 混合FE-SEA隔声模型根据隔声试验中地板铝型材的几何尺寸, 建立FE模型, 并划分实体单元网格.基于混合FE-SEA方法建立地板铝型材的隔声预测模型.如图 12和13所示分别为地板铝型材的FE模型和隔声预测模型.

|
图 12 地板铝型材FE模型 Fig. 12 FE model of floor aluminum extrusion |
|
图 13 地板铝型材隔声预测混合FE-SEA模型 Fig. 13 Prediction model of sound transmission loss of floor aluminum extrusion based on hybrid FE-SEA |
将2.1节测试得到的地板铝型材阻尼损耗因子在FE子系统中进行定义.在铝型材车外一侧, 施加混响声场(diffuse acoustic field, DAF), 模拟声源激励;在铝型材车内一侧, 连接半无限流体(semi-infinite fluid, SIF)子系统, 模拟自由声场.
在隔声试验中, 地板铝型材安装于2个混响室之间的洞口.铝型材的四周分别采用2个螺栓与洞口工装紧固, 并用密封胶进行密封.考虑到铝型材的尺寸和工装安装尺寸之间的误差及其离散点螺栓的固定方式, 铝型材的实际边界条件是十分复杂的.因此, 分别计算地板铝型材四边简支和四边自由2种边界条件下的隔声量.铝型材的结构模态分析调用外部NASTRAN求解器.
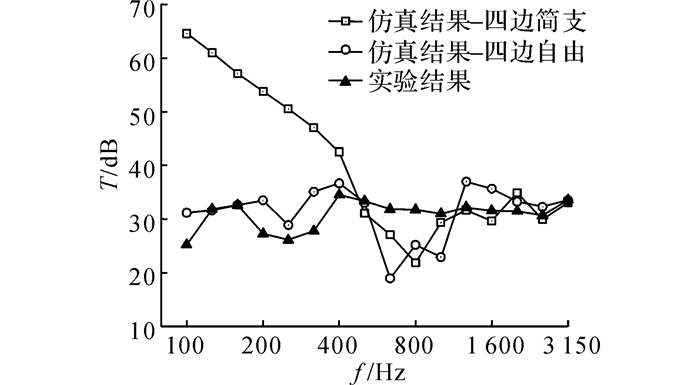
如图 14所示为地板铝型材的隔声量预测结果.可见, 当地板铝型材四边自由时, 其隔声量预测结果和试验结果更为接近.当地板铝型材四边简支时, 中心频率为500 Hz以下的1/3频带隔声量明显偏高.这是因为在隔声试验中, 地板铝型材的四周虽然使用螺栓紧固, 但是由于螺栓数量较少(每边2个), 同时铝型材四周和洞口工装之间存在一定的安装间隙, 其边界条件可能更加接近于自由边界.当仿真计算中使用四边简支边界条件时, 相对于自由边界, 额外增加了结构的刚度, 使得铝型材的第一阶模态频率大幅提高, 进而导致中心频率为500 Hz以下的1/3频带的中低频隔声量受到刚度控制.
|
图 14 基于混合FE-SEA模型的隔声量预测结果 Fig. 14 Prediction results of sound transmission loss based on hybrid FE-SEA model |
选取2.3节地板铝型材辐射声功率测试中第一个激振点位置作为研究对象, 将试验中的激振力频谱输入到振动声辐射预测模型之中.同样计算地板铝型材四边简支和四边自由两种边界条件下的辐射声功率.
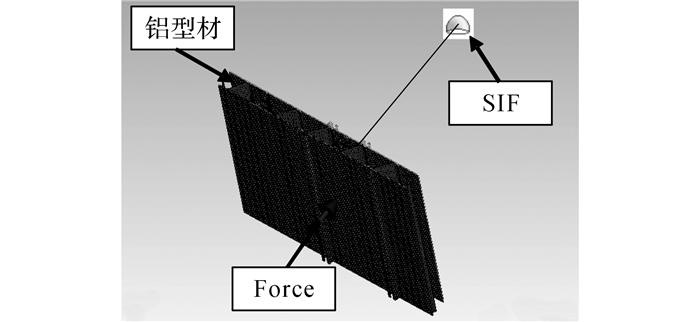
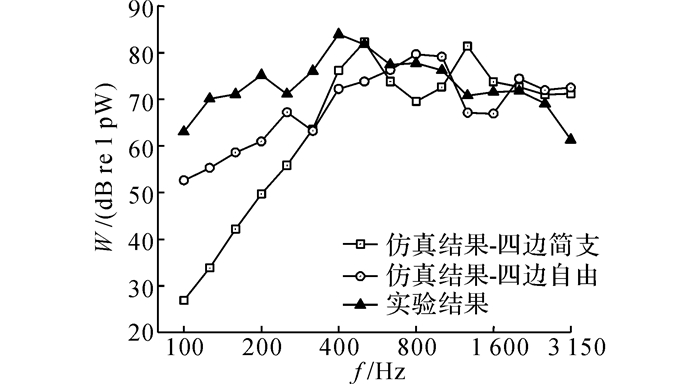
如图 15和16所示分别为地板铝型材振动声辐射混合FE-SEA模型和预测结果.由图 16可见, 地板铝型材四边自由时, 其辐射声功率预测结果和试验结果更为接近.这是因为辐射声功率试验的安装洞口和隔声试验的安装洞口采用的是相同类型的固定工装.因此, 对于文中声学实验室测试的试件隔声量以及辐射声功率, 在仿真计算中采用四边自由边界条件进行模拟更加合适.这同时也为混合FE-SEA模型中使用地板铝型材的阻尼损耗因子测试结果(阻尼测试为自由边界条件)的合理性提供了依据.
|
图 15 地板铝型材振动声辐射预测混合FE-SEA模型 Fig. 15 Prediction model of sound radiation power of floor aluminum extrusion based on hybrid FE-SEA |
|
图 16 基于混合FE-SEA模型的辐射声功率预测结果 Fig. 16 Prediction results of sound radiation power based on hybrid FE-SEA model |
对于铝型材等复杂结构的声振特性仿真分析, 当使用FEM建模时, 单元的合理划分、网格数量的有效控制都将对计算结果的准确性和时效性产生影响.往往结构越复杂, 计算越困难.SEA能够简化建模过程, 且计算耗时少.如果直接根据铝型材结构划分子系统, 又会面临子系统模态数过低、不满足该方法前提条件的情况.如何针对铝型材等复杂结构进行声学仿真等效建模, 使其同时达到建模过程简单、计算高效准确, 是一个值得研究的问题.宋士柯[17]根据振动模态理论对铝型材的等效模型进行了探讨.张媛媛等[18]分析了铝型材的截止频率并对整体模态下的铝型材等效板进行了研究.不难看出, 上述方法都是基于FEM, 通过将等效板的模态参数调试成与铝型材结构一致, 进而实现铝型材的等效.这类方法存在明显的频率制约, 即等效板主要适合于中低频(结构表现为整体模态)的简化模拟.本节基于SEA原理, 通过使用SEA的关键参数赋值, 对铝型材进行单层板等效, 拓展其中高频等效建模方法.
SEA以能量为核心, 将结构划分为若干子系统, 通过建立子系统之间的能量-功率流平衡方程, 描述整个动力学稳态系统.外界激励以输入功率的形式出现在能量-功率流平衡方程中, 子系统之间的相互作用通过损耗因子总矩阵来体现, 方程所求解的能量向量则代表着各个子系统的能量.子系统间的能量-功率流平衡方程的一般形式[14]如下:
| $ \mathit{\boldsymbol{LE = }}\frac{1}{\omega }{\mathit{\boldsymbol{P}}_{{\rm{in}}}}. $ | (12) |
式中:E为系统能量矩阵, Pin为系统输入功率矩阵, 具体表达式分别为
| $ \mathit{\boldsymbol{E = }}{\left\{ {{E_1}, {E_2}, {E_3}, \cdots, {E_N}} \right\}^{\rm{T}}}. $ | (13) |
| $ {\mathit{\boldsymbol{P}}_{{\rm{in}}}} = {\left\{ {{P_{{\rm{in}}, 1}}, {P_{{\rm{in}}, 2}}, {P_{{\rm{in}}, 3}}, \cdots, {P_{{\rm{in}}, N}}} \right\}^{\rm{T}}}. $ | (14) |
L为包含内损耗因子和耦合损耗因子的系统能量损耗矩阵, 矩阵元素为
| $ {\mathit{\boldsymbol{L}}_{ij}} = \left\{ \begin{array}{l} - {\eta _{ij}}, i \ne j;\\ \sum\limits_{k = 1}^N {{\eta _{ik}}, i = j} . \end{array} \right. $ | (15) |
其中, 内损耗因子和耦合损耗因子由系统本身决定, 且耦合损耗因子满足互易定理:
| $ {n_i}{\eta _{ij}} = {n_j}{\eta _{ji}}. $ | (16) |
式中:ni、nj分别为子系统i和j的模态密度, ηij、ηji分别为振动能量从子系统i传至子系统j和从子系统j传至子系统i的耦合损耗因子.
上述方程代表了使用SEA方法对复杂系统进行求解的最基本表达式.可以发现, 子系统的模态密度、内损耗因子(阻尼损耗因子)、子系统之间的耦合损耗因子是SEA的关键参数.基于此, 下面将研究使用单层板结构, 通过重置以上关键参数, 进行地板铝型材声振特性等效建模的可行性.
4.1 隔声预测等效SEA模型如图 17所示为地板铝型材隔声预测等效SEA模型.建立一块和隔声试件几何尺寸相同的单层铝板;根据发声室、受声室的容积分别建立2个声腔;在发声室声腔上施加DAF;在单层板子系统中定义地板铝型材的模态密度、内损耗因子, 在单层板和声腔的面连接中定义耦合损耗因子, 并且使单层板的质量和地板铝型材相等, 受声室声腔的吸声系数和实际受声室相同.

|
图 17 地板铝型材隔声预测等效SEA模型 Fig. 17 Equivalent model of sound transmission loss prediction of floor aluminum extrusion based on SEA |
如图 18所示为使用等效SEA模型计算得到的地板铝型材隔声量结果.由图 18可见, 等效SEA模型计算得到隔声量在中心频率为500 Hz以上的1/3频带和试验结果基本吻合较好, 而在500 Hz以下存在一定差异.这可能和地板铝型材在中心频率为500 Hz以下主要表现为整体模态, 模态数较低, 并不能完全满足SEA的前提条件有关.

|
图 18 基于等效SEA模型的隔声量预测结果 Fig. 18 Prediction results of sound transmission loss based on equivalent SEA model |
此外, 在中心频率为2 500 Hz附近的1/3频带, 仿真结果和试验结果的趋势略有差异.这可能和铝型材的阻尼分布特性有关.等效模型中输入的实际上是地板铝型材的平均阻尼, 而其真实结构由于在高频区段模态十分密集, 阻尼特性是相当复杂的.
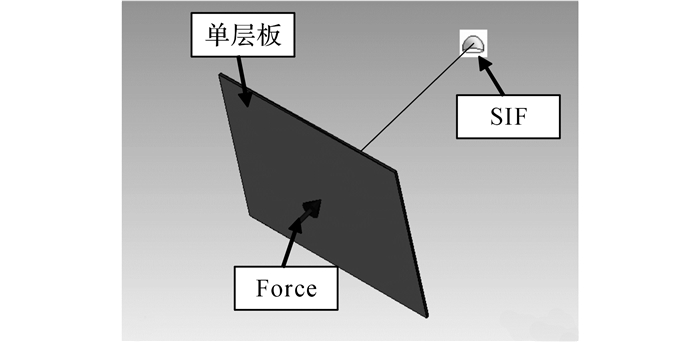
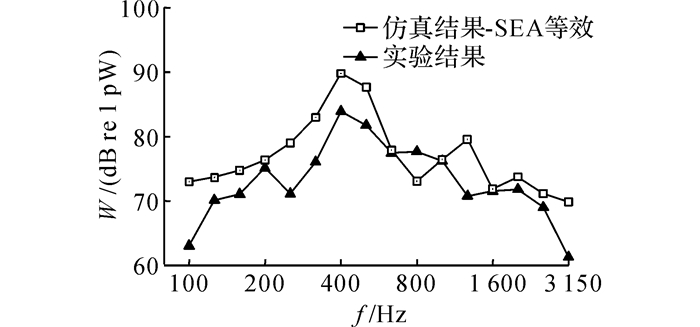
4.2 声辐射预测等效SEA模型如图 19和20所示分别为地板铝型材振动声辐射预测等效SEA模型和预测结果.由图 20可见, 采用等效SEA模型计算得到的地板铝型材辐射声功率和试验结果在频率分布上基本一致.与图 19相比, 当将等效SEA模型用于隔声预测时, 地板铝型材的仿真结果和试验结果在中心频率500 Hz以下的1/3频带差异明显, 但是当将其用于辐射声功率预测时, 相应的仿真结果和测试结果则基本在全频段均吻合较好.这可能与载荷激励的输入形式有关, 需要在今后进一步深入研究.
|
图 19 地板铝型材振动声辐射预测等效SEA模型 Fig. 19 Equivalent model of sound radiation power prediction of floor aluminum extrusion based on SEA |
|
图 20 基于等效SEA模型的辐射声功率预测结果 Fig. 20 Prediction results of sound radiation power based on equivalent SEA model |
(1) 在声学实验室的安装洞口, 使用少量螺栓对铝型材四周进行离散式紧固, 其测试边界条件和仿真计算中的四边自由更为符合.
(2) 将声学实验室测试得到的铝型材关键SEA参数赋值于单层板, 等效之后的SEA模型隔声量、辐射声功率预测结果在中高频和试验结果吻合较好.该方法适用于铝型材的中高频等效建模.
(3) 在力载荷激励下, 铝型材的等效SEA模型的辐射声功率预测结果和试验结果在全频段吻合度较高;但在声载荷激励下, 其隔声预测结果和试验结果在中低频吻合度略差.
| [1] | PARK B, JEON J Y, CHOI S, et al. Short-term noise annoyance assessment in passenger compartments of high-speed trains under sudden variation[J]. Applied Acoustics, 2015, 97: 46–53. DOI:10.1016/j.apacoust.2015.04.007 |
| [2] |
张捷, 肖新标, 韩健, 等. 高速列车车内客室端部噪声分布特性与声学模态分析[J].
机械工程学报, 2014, 50(12): 97–103.
ZHANG Jie, XIAO Xin-biao, HAN Jian, et al. Characteristics of noise distribution at the ends of the coach and acoustic modal analysis of high-speed train[J]. Journal of Mechenical Engineering, 2014, 50(12): 97–103. |
| [3] | JIN X. Key problems faced in high-speed train operation[J]. Journal of Zhejiang University-SCIENCE A: Applied Physics and Engineering, 2014, 15(12): 936–945. |
| [4] | EADE P W, HARDY A E J. Railway vehicle internal noise[J]. Journal of Sound and Vibration, 1977, 51(3): 403–415. DOI:10.1016/S0022-460X(77)80083-7 |
| [5] | XIE G, THOMPSON D J, JONES C J C. A modelling approach for the vibroacoustic behaviour of aluminium extrusions used in railway vehicles[J]. Journal of Sound and Vibration, 2006, 293(3-5): 921–932. DOI:10.1016/j.jsv.2005.12.015 |
| [6] | PARK I S, LEE J K, KIM S H, et al. Sound insulation design of the aluminum extruded panel for a high speed train [C] // Proceedings of STECH'12. Seoul: [s.n.], 2012: 1-3. |
| [7] |
沈火明, 张玉梅, 肖新标, 等. 高速列车波纹外地板低噪声优化设计[J].
交通运输工程学报, 2011, 11(2): 65–71.
SHEN Huo-ming, ZHANG Yu-mei, XIAO Xin-biao, et al. Low noise optimization design of external corrugated floor for high speed train[J]. Journal of Traffic and Transportation Engineering, 2011, 11(2): 65–71. |
| [8] |
罗乐, 郑旭, 郝志勇, 等. 基于结构-声耦合法研究高铁铝型材的隔声性能[J].
中南大学学报:自然科学版, 2015, 46(9): 3513–3519.
LUO Le, ZHENG Xu, Hao Zhi-yong, et al. Sound insulation performance analysis of high-speed train aluminum extrusions based on structure-sound coupling method[J]. Journal of Central South University: Science and Technology, 2015, 46(9): 3513–3519. |
| [9] |
王瑞乾, 肖新标, 刘佳, 等. 高速列车阻尼喷涂式铝型材减振降噪特性试验[J].
噪声与振动控制, 2014, 34(4): 52–55.
WANG Rui-qian, XIAO Xin-biao, LIU Jia, et al. Experiments on vibration and noise reduction effect of sprayed-damping section aluminum applied to high-speed trains[J]. Noise and Viibration Control, 2014, 34(4): 52–55. |
| [10] | International Organization for Standardization. ISO 140-3. Measurement of sound insulation in buildings and of building elements-part 3: Laboratory measurements of airborne sound insulation of building elements [S]. Switzerland: International Organization for Standardization, 1995. |
| [11] | XIE G. The vibroacoustic behavior of aluminium extrusions used in railway vehicles [D]. UK: University of Southampton, 2004. |
| [12] | CREMER L, HECKL M, PETERSSON B A T. Structure-borne Sound[M]. 3rd ed. Berlin: Springer-Verlag, 2005. |
| [13] | VATTI K K. Damping estimation of plates for statistical energy analysis [D]. USA: University of Kansas, 2011. |
| [14] | LYON R H, DEJONG R G. Theory and Application of Statistical Energy Analysis[M]. 2nd ed. London: Butterworth-Heinemann, 1995. |
| [15] | International Organization for Standardization. ISO 9614-1. Acoustics-Determination of sound power levels of noise sources using sound intensity-Part 1: Measurement at discrete points [S]. Switzerland: International Organization for Standardization, 2009. |
| [16] | COTONI V, SHORTER P, LANGLEY R. Numerical and experimental validation of a hybrid finite element-statistical energy analysis method[J]. The Journal of theAcoustical Society of America, 2007, 122(1): 1–12. DOI:10.1121/1.2744126 |
| [17] |
宋士柯. 中空挤压铝型材的等效模型研究[D]. 北京: 北京交通大学, 2014.
SONG Shi-ke. The study on equivalent model of hollow aluminum extrusion [D]. Beijing: Beijing Jiaotong University, 2014. |
| [18] |
张媛媛, 沈火明, 肖新标, 等. 高速列车铝型材外地板结构振动与隔声量分析[J].
重庆理工大学学报:自然科学, 2014, 28(1): 28–32.
ZHANG Yuan-yuan, SHEN Huo-ming, XIAO Xin-biao, et al. Research on vibration and transmission loss of aluminum alloy external floor for high-speed train[J]. Journal of Chongqing University of Technology: Natural Science, 2014, 28(1): 28–32. |



