正交异性钢桥面板具有自重轻、材料利用率高、适用范围广、承载力大、便于施工等优点, 已成为大与特大跨径桥梁普遍采用的桥面结构类型.然而越来越多的工程实例表明, 正交异性钢桥面板疲劳裂纹是主要病害, 有关疲劳性能的研究也受到越来越多的关注[1-3].有关正交异性钢桥面板疲劳裂纹问题的研究有助于改善纵肋对接焊接部位、纵肋与桥面板焊接部位等的抗疲劳性能.
传统的疲劳分析方法一般将疲劳过程分为2个阶段, 即疲劳裂纹形成和扩展阶段.对于疲劳裂纹形成阶段, 一般是基于试验应力-寿命曲线(S-N曲线), 采用Miner线性疲劳损伤累积理论进行分析[4];对于疲劳裂纹扩展阶段, 一般是基于断裂力学理论, 采用Paris公式进行分析[5].从已有的研究工作[6-8]看, 目前基本上是采用上述2种方法.邓扬等[6]采用长期监测数据和S-N曲线, 提出了大跨桥梁焊接细节疲劳可靠度评估方法.顾萍等[7]针对铁路正交异性钢桥面板典型疲劳裂纹依据断裂力学揭示了裂纹扩展速率与应力场的关系, 并进行了疲劳寿命估算.郑淳[8]提出了基于线弹性断裂问题可靠度分析的响应面-样条边界元法和重要抽样蒙特卡洛-样条边界元法.实际上, Miner线性疲劳损伤累积理论是一种唯象的经验理论, “损伤”没有与疲劳破坏的物理机制相联系;且断裂力学中的Paris公式仅适用于宏观裂纹的稳定扩展阶段, 无法对疲劳裂纹形成阶段进行分析.另外, 在疲劳失效过程中, 如何定量考虑微观效应对疲劳寿命的影响是研究中的难点问题.
疲劳破坏过程本质上是一个从微观到宏观的跨尺度行为, 发展跨尺度的疲劳分析方法已成为热点研究问题[9].近年来, 约束应力区的概念被用来连接不同尺度下的材料缺陷, 形成了多个多尺度嵌套的裂纹扩展模型[10-15].研究表明, 基于约束应力区的跨尺度裂纹模型可将疲劳裂纹形成阶段与扩展阶段统一在一个模型中进行描述, 而不用划分为2个不同阶段并分别采用完全不同的模型进行分析[16].目前已发表的研究工作中基于约束应力区的跨尺度裂纹模型均是针对平面裂纹问题, 没有对三维条件下的裂纹跨尺度扩展问题进行研究.
本文基于约束应力区的概念, 采用有限元法求解应力强度因子, 通过将跨尺度应力强度因子作为裂纹扩展的控制参量, 建立三维表面半椭圆疲劳裂纹扩展的跨尺度分析模型, 并将其应用于正交异性钢桥面板细节的疲劳寿命分析.将分析结果与已有试验结果进行比较, 以验证方法的可行性和有效性, 并分析微观效应对疲劳裂纹扩展行为及疲劳寿命的影响.
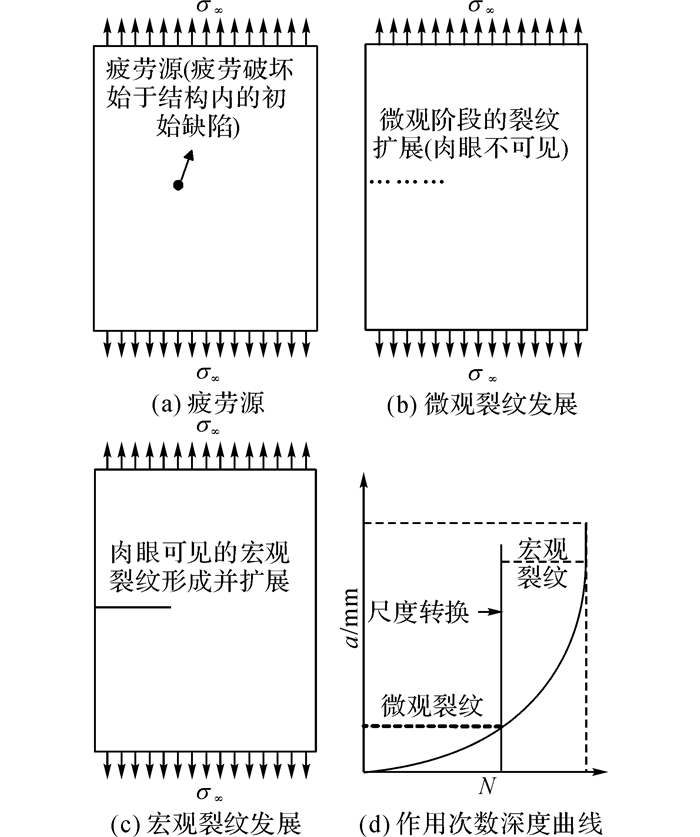
1 约束应力区概念构件的疲劳破坏过程是从一个微观缺陷处开始, 逐步扩展的过程.当裂纹扩展到肉眼可见时, 成为宏观裂纹, 宏观裂纹的扩展最终导致构件的断裂破坏, 疲劳破坏过程如图 1所示, 图中σ∞为远场应力, N为作用次数, a为裂纹深度.
|
图 1 材料的疲劳破坏示意图 Fig. 1 Schematic digram of material fatigue failure |
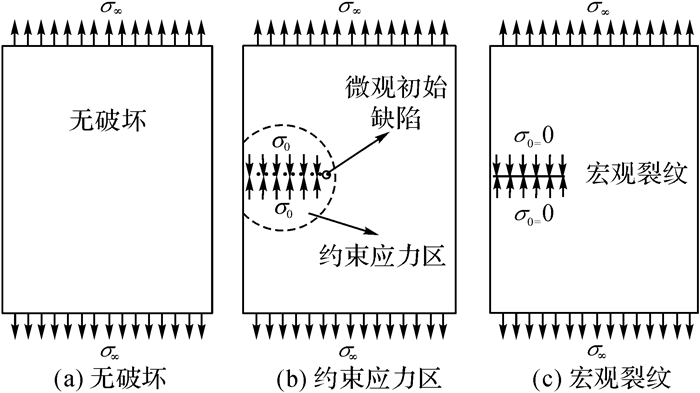
材料的约束应力区概念[16]如图 2所示.如图 2(a)为材料完好无损, 如图 2(b)是在微观缺陷处切开, 切口处有约束应力σ0存在.定义约束应力比σ*=σ0/σ∞.如当σ*=σ0/σ∞=1时, 相当于材料无损伤;如当0 < σ*=σ0/σ∞ < 1时, 表明材料存在一定程度的损伤, 但又没有完全裂开;如当σ*=σ0/σ∞=0时, 相当于形成宏观裂纹, 材料完全裂开, 如图 2(c)所示.可见, 约束应力比σ*可作为描述材料损伤程度的一个变量.在疲劳破坏从微观缺陷到宏观断裂的全过程中, 约束应力区尺寸从微观缺陷的尺度发展到宏观尺度, 同时约束应力的大小逐渐减少至0.
|
图 2 材料的约束应力区示意图 Fig. 2 Schematic diagram of material restraining stress zone |
求解应力强度因子的方法有解析法、数值解法等.解析法只适用于简单问题, 大多数问题(尤其是三维问题)没有解析解, 只能采用数值解法, 如有限元法、有限差分法、边界元法等.本文通过ANSYS软件采用有限元法计算应力强度因子.
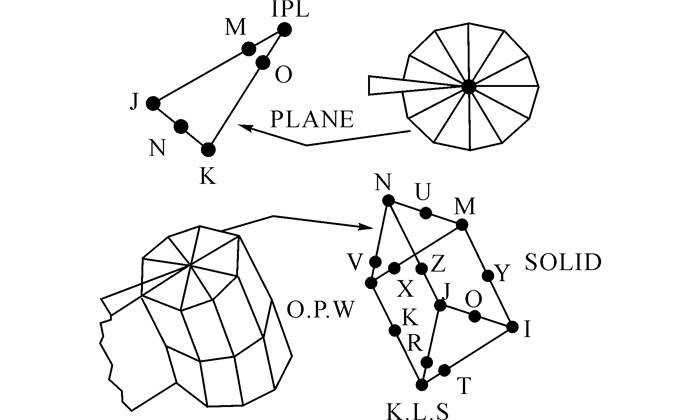
在线弹性断裂力学问题中, 裂纹尖端应力、应变场是奇异场, r为距裂纹尖端的距离, 随着r→0, 应力、应变以r-1/2趋于无穷大.因此, 在有限元分析中, 围绕裂纹尖端的单元应是二项式的奇异单元, 如图 3所示, 图中, “PLANE”表示平面裂纹问题, “SOLID”表示三维裂纹问题.在计算完成后, 就可以使用通用后处理器POST1中的“KCALC命令(K Calculate)”来计算应力强度因子.使用“KCALC命令”首先定义描述裂纹尖端的局部坐标系, 局部坐标系中的X轴应与裂纹开裂面平行.然后定义沿裂纹面的路径, 当计算应力强度因子时, 若是平面问题还需要指定分析类型是平面应力还是平面应变.对于薄板的分析, 可定义为平面应力;对于其他分析, 在裂纹尖端附近及其渐近位置, 一般应考虑为平面应变问题.最后, 还需指定模型是具有对称边界条件的半裂纹模型, 还是具有反对称边界条件的半裂纹模型, 或是整体裂纹模型.
|
图 3 围绕裂纹尖端的二项式奇异单元 Fig. 3 Binomial singular element of around crack tip |
本文以一个含表面半椭圆裂纹的有限厚度板来验证有限元模型计算应力强度因子的可行性和准确性.模型主要参数如下:长150 mm, 宽75 mm, 高8 mm, 弹性模量E=206 Gpa, 泊松比ν =0.3, 远场应力σ∞ =100 MPa.
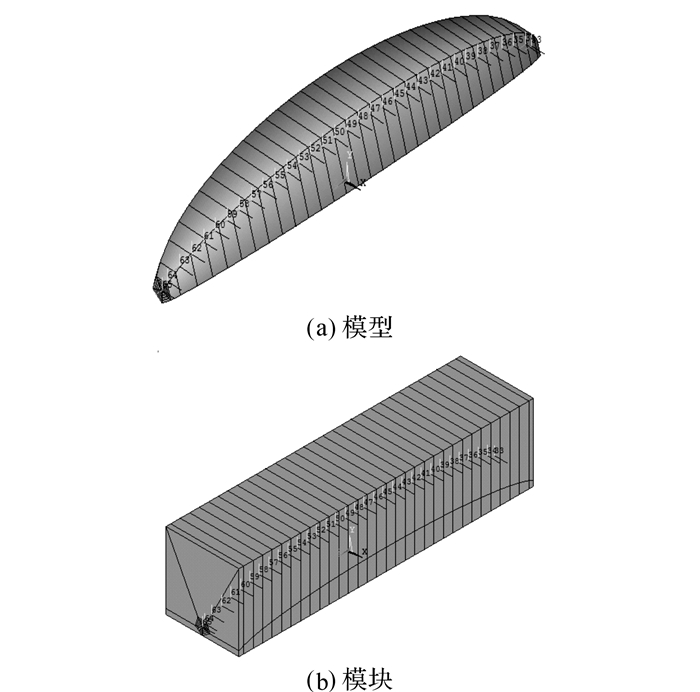
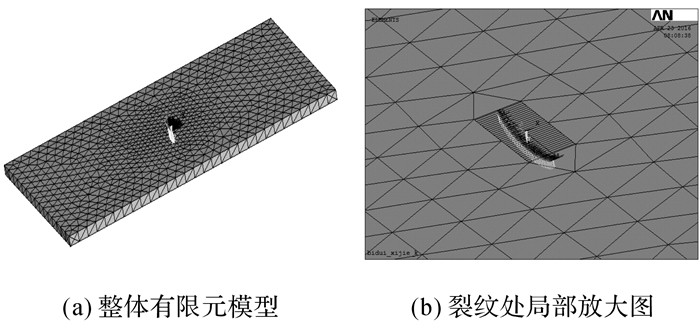
建立计算三维裂纹问题的应力强度因子有限元模型的方法,主要有逐节点直接建模方法和实体建模方法.本文裂纹体共分为5层单元, 采用逐节点直接建模方法.首先建立裂纹前缘节点;然后建立裂纹体其他节点, 并将靠近裂纹前缘的中间节点移动到1/4位置;最后用Solid95单元建立单元, 其中裂纹尖端第一层单元为奇异单元, 如图 4(a)所示.裂纹体外又建立过渡单元, 最终形成裂纹体模块, 如图 4(b)所示.将裂纹体模块放入已进行单元划分的有限厚度板中, 两者使用接触单元进行连接, 接触算法使用多点约束算法(muliti point constraint, MPC), 接触面行为设定为绑定, 完成后的模型如图 5所示.
|
图 4 用于计算应力强度因子的三维裂纹模型 Fig. 4 Three dimensional crack model for stress intensity factor calculation |
|
图 5 用于计算应力强度因子的有限元(FE)模型 Fig. 5 Finite element(FE) model for calculation stress intensity factor |
ANSYS软件的计算结果与文献[17]中公式
| $ {K_1} = M\frac{{\sigma \;\sqrt {{\rm{\pi }}a} }}{{E\left( k \right)}}. $ |
的计算结果及对比如表 1所示, 其中a为半椭圆的短轴值, b为半椭圆的长轴值.通过比较可知, 采用ANSYS软件计算三维裂纹问题的裂纹尖端应力强度因子可行, 本文建立的有限元模型计算结果具有足够的精度.
| 表 1 ANSYS软件与文献[17]公式计算结果的对比 Table 1 Comparison between calculation results of software ANSYS and Reference [17] |
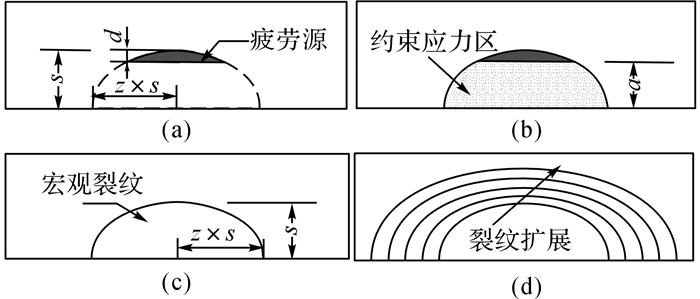
材料微观缺陷的形态多种多样.断裂力学研究成果表明, 将不同形态的缺陷简化为半椭圆形, 是偏于安全的.基于前述约束应力区的概念建立三维表面半椭圆宏/微观跨尺度裂纹扩展模型, 如图 6所示.假定三维体内有疲劳源(微观缺陷), 如图 6(a)所示, 在疲劳源处将三维体局部切开, 考虑到宏观裂纹形成后为半椭圆形, 因此假定切开后的形状亦为半椭圆形(该半椭圆与初始宏观裂纹相同, 长短轴比记作z, 短轴记作s, 长轴即为z×s, 切口处有约束应力σ0, 如图 6(b)所示.试验开始时, σ*≈1, 约束应力区深度a很小.随着荷载作用次数N的增加, σ*逐渐减小, 最终降为0, 而约束应力区深度a逐渐增加, 最终约束应力区成为自由表面.疲劳裂纹也由微观缺陷逐渐发展为宏观可见裂纹, 如图 6(c)所示;宏观可见裂纹逐渐发展, 出现疲劳破坏, 如图 6(d)所示.
|
图 6 宏/微观跨尺度裂纹扩展示意图 Fig. 6 Schemtic diagram of micro/macro trans-scale crack propagation |
微观缺陷在三维体内的埋深为变量, 由半椭圆的短轴长度s决定.微观缺陷为半椭圆顶端的部分区域(微观缺陷尺度为μm), 假定d=1 μm.初始微观缺陷的大小可通过选取不同长短轴比z的半椭圆顶端来进行模拟.
基于线弹性断裂力学理论中的叠加原理, 分别施加远场应力σ∞和约束应力σ0(σ0=σ*×σ∞), 存在约束应力时的应力强度因子可表示为
| $ K_{{\rm{mic}}}^{{\rm{mac}}} = {\sigma _\infty } \times f\left( {z、a、s、{\sigma ^*}} \right). $ | (1) |
如前所述, σ*与a有关, 两者之间的关系体现了材料疲劳损伤的演化特性, 因无具体试验结果, 假定σ*从0.9减小到0, 其关系为
| $ {\sigma ^*} =-0.9 \times \frac{a}{s} + 0.9, a < s. $ | (2) |
因此, 约束应力条件下的应力强度因子可进一步表示为
| $ K_{{\rm{mic}}}^{{\rm{mac}}} = {\sigma _\infty } \times f\left( {z、a、s} \right). $ | (3) |
以
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C{\left( {\Delta K_{{\rm{mic}}}^{{\rm{mac}}}} \right)^m}. $ | (4) |
式中:C、m为材料参数.
在疲劳裂纹进入宏观尺度后, 假定半椭圆裂纹扩展过程中长短轴比例维持不变, 可得到宏观尺度下的应力强度因子计算公式:
| $ {K^{{\rm{mac}}}} = {\sigma _\infty }\times{f}\left( {z、a} \right). $ | (5) |
式中:a为宏观表面半椭圆裂纹深度.
根据Paris公式, 有
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C{\left( {\Delta {K^{{\rm{mac}}}}} \right)^m}. $ | (6) |
式(3) 与式(5) 的应力强度因子可采用ANSYS软件, 通过建立有限元模型进行求解, 相应的函数关系式可通过对数值结果的拟合得到.
通过对疲劳裂纹扩展速率的积分, 可获得疲劳裂纹随循环荷载作用次数N的变化规律, 当a扩展为极限裂纹深度时,疲劳寿命为
| $ {N_{\rm{f}}} = \int_0^s {\frac{1}{{C{{\left( {\Delta K_{{\rm{mic}}}^{{\rm{mac}}}} \right)}^m}}}{\rm{d}}a + } \int_s^{{a_{{\rm{max}}}}} {\frac{1}{{C{{\left( {\Delta {K^{{\rm{mac}}}}} \right)}^m}}}{\rm{d}}a} . $ | (7) |
式中:amax为荷载作用Nf次后的极限裂纹扩展深度, Nf即为构件的疲劳寿命.
式(7) 即为三维表面半椭圆裂纹的宏/微观跨尺度扩展模型.式(7) 将a定义为一个描述裂纹发展程度的变量, 微观阶段为约束应力区深度的变化, 宏观阶段为宏观裂纹深度的变化.通过a的变化, 实现了疲劳裂纹从微观到宏观的尺度转换.
4 疲劳寿命计算结果与试验结果比较U肋与桥面板焊接部位是正交异性钢桥面板易于出现疲劳破坏的位置, Ya等[18]进行了正交异性钢桥面板的桥面板与U肋焊缝疲劳试验, 采用高渗透性蓝色墨水浸入的方法记录了宏观裂纹形成时(应力幅出现变化, 裂纹形成自由表面)的缺陷形状及大小.研究结果表明, 宏观裂纹形成时为大小不一(mm尺度)的近似半椭圆形.选取该部位作为研究对象, 采用三维表面半椭圆裂纹跨尺度扩展模型进行疲劳寿命分析, 并与文献[19]试验结果进行比较, 以验证本文模型用于该细节疲劳寿命分析的可行性和有效性.
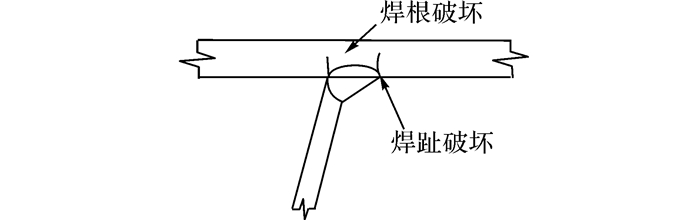
Sim等[20]根据全尺寸的正交异性钢桥面板疲劳试验结果, 指出桥面板与U肋焊缝存在焊趾疲劳破坏和焊根疲劳破坏, 但主要是焊趾疲劳破坏, 如图 7所示.因此, 在本文采用的有限元模型中, 桥面板与U肋焊缝假定为焊趾疲劳破坏.
|
图 7 钢桥面板与U肋焊缝疲劳破坏类型 Fig. 7 Fatigue failure types of steel bridge deck and U rib welded joint |
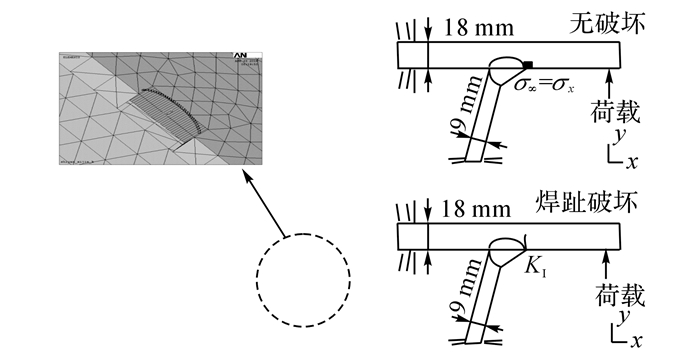
根据文献[19]建立有限元分析模型, 桥面板与U肋焊接部位主要承受弯拉作用.在本文有限元分析中, 荷载主要是远场荷载和约束应力.首先假定焊缝在初始状态完好无损, 采用在桥面板施加竖向面荷载, 并对桥面板一端及U肋底部施加固定约束, 模拟桥面板与U肋承受的弯拉作用, 得到跨尺度计算模型中的远场应力σ∞.然后建立桥面板与U肋焊缝裂纹有限元模型:一是在桥面板处施加与焊缝无损伤时相同的竖向面荷载;二是根据前述约束应力区概念得到约束应力σ0,并在裂纹面施加约束应力, 得到应力强度因子KⅠ.所建立的有限元模型如图 8所示.该细节部位裂纹同时受拉应力和剪应力作用, 属于张开型(Ⅰ型)、复合型(Ⅱ型)裂纹.根据数值计算结果, Ⅱ型应力强度因子KⅡ数值很小, 可忽略不计, Ⅰ型裂纹是该部位疲劳破坏的主因.因此, 取KⅠ作为Kmicmac和Kmac的近似结果.有限元计算的目的在于拟合出式(3) 与式(5) 的函数关系式, 采用多项式进行拟合, 即
|
图 8 钢桥面板与U肋焊缝应力强度因子有限元模型 Fig. 8 FE model of steel bridge deck and U rib welded joint for stress intensity factor |
| $ \begin{array}{l} K_{{\rm{mic}}}^{{\rm{mac}}} = {\sigma _\infty } \times \left( {{p_0} + {p_1} \times a + {p_2} \times z + {p_3} \times s + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_4} \times {a^2} + {p_5} \times z \times a + {p_6} \times a \times s + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{p_7} \times {z^2} + {p_8} \times {s^2}} \right), \end{array} $ | (8) |
| $ \begin{array}{l} {K^{{\rm{mac}}}} = {\sigma _\infty } \times \left( {{q_0} + {q_1} \times a + {q_2} \times z + {q_3} \times {a^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_4} \times z \times a + {q_5} \times {z^2} + {q_6} \times z \times {a^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{q_7} \times {z^2} \times a + {q_8} \times {a^3}} \right). \end{array} $ | (9) |
假定一个远场应力σ∞值, 计算出不同约束应力区深度和宏观裂纹深度对应的Kmicmac和Kmac, 进行拟合, 得到p、q值, 如表 2所示.
| 表 2 多项式系数p、q的拟合值 Table 2 Fitting values for polynomial coefficients p and q |
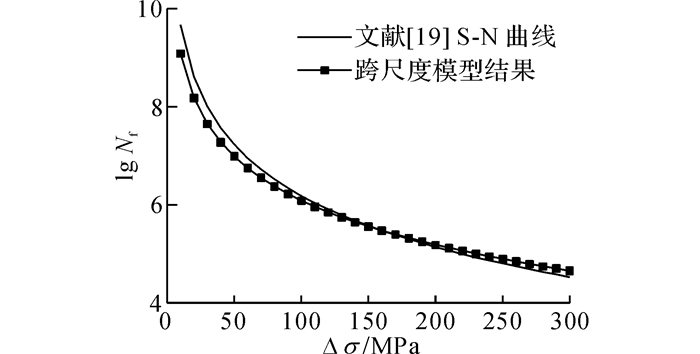
将式(8)、(9) 代入式(7), 通过数值积分可获得疲劳过程的a~N关系曲线及试件的疲劳寿命.参考文献[19]给出的试验S-N(应力-寿命)曲线(如图 9所示), 利用位于曲线中间位置的一个试验数据点, 即Δσ=150 MPa, Nf=105.6, 通过打靶计算, 可确定式(4) 与式(6) 中的2个材料疲劳性能参数C和m, C=4.761×10-13, m=3.至此, 式(7) 中的所有宏/微观参量都已确定.采用数值积分, 可得到与不同应力幅Δσ对应的疲劳寿命的对数lg Nf, 如图 9所示.结果表明, 跨尺度裂纹模型与试验S-N曲线几乎完全一致, 本文建立的跨尺度裂纹模型可正确反映U肋与桥面板焊接部位疲劳破坏从微观到宏观发展的全过程, 且具有较好的精度.
|
图 9 跨尺度模型计算结果与文献[19] S-N曲线的对比 Fig. 9 Comparison of S-N curve obtained from trans-scale model with experimental S-N curve given in Reference [19] |
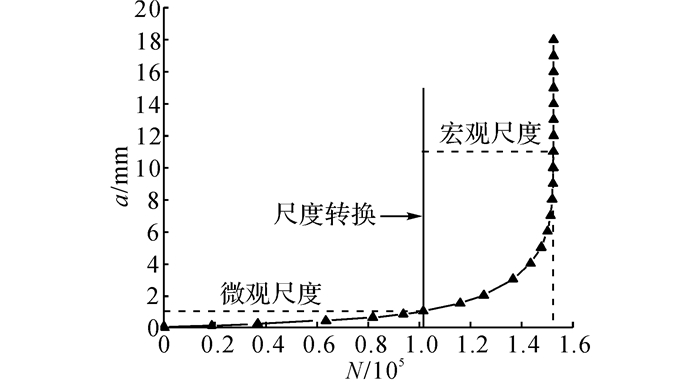
如前所述, 疲劳过程分为2个阶段, 即疲劳裂纹形成和扩展阶段.为量化各个阶段的疲劳寿命, 令Δσ∞=200 MPa, z=5, s=1 mm, 得到裂纹深度a随循环次数N变化的曲线, 如图 10所示.
|
图 10 当远场应力幅为200 MPa、长短轴比为5、短轴长1 mm时的裂纹深度与循环次数关系曲线 Fig. 10 Relation curve between crack depth and cycle index with far field stress amplitude of 200 MPa, axial ratio of 5 and short axis of 1 mm |
由图 10可见, 疲劳裂纹寿命由裂纹形成寿命与扩展寿命组成, 其中形成寿命约占疲劳寿命的66%, 说明疲劳寿命的大部分在裂纹形成阶段.同时, 当裂纹深度超过11 mm后(占总厚度的61.1%), 疲劳寿命几乎不再增加, 且当裂纹深度由7 mm提高到11 mm时, 其疲劳寿命也仅增加了约1.5%, 表明极限裂纹深度对疲劳寿命影响甚微.
5 微观效应对扩展行为对疲劳寿命的影响材料微观因素对疲劳寿命有很大影响, 在疲劳分析中的困难之处是如何考虑微观因素的影响.以前的研究工作主要是通过总结大量疲劳试验数据, 得出疲劳寿命的概率分布规律, 以此来描述微观因素的影响.在本文所建立的跨尺度疲劳裂纹扩展模型中, σ*的演变路径与约束应力尖端区的形状与尺寸代表着材料微观因素对材料疲劳破坏过程的影响.因此通过少量的疲劳试验数据, 拟合出模型中的待定参数, 即可定量分析与考察材料微观因素对疲劳破坏过程的影响.当然, 由于难以通过试验观测材料疲劳破坏的微观发展过程, 对σ*的演变路径进行合理假设, 考虑2种可能的情况:一是线性变化(模式1), 二是抛物线变化(模式2).通过假设不同的裂尖区尺寸, 模拟材料初始微观缺陷对疲劳破坏过程的影响.
假定σ*从0.9减小到0, 模式1为线性变化.模式2按抛物线变化, 假设约束应力(代表着材料疲劳损伤的程度)在开始阶段下降的慢, 接近形成宏观裂纹时下降加快(即损伤速度加快).
模式1:
| $ {\sigma ^*} =-0.9 \times \frac{a}{s} + 0.9, a < s. $ |
模式2:
| $ {\sigma ^*} =-0.92 \times {\left( {\frac{a}{s}} \right)^2} + 0.02 \times \frac{a}{s} + 0.9, a < s. $ |
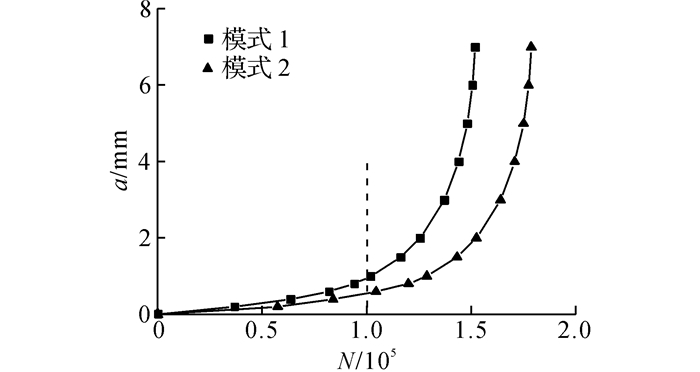
令Δσ∞=200 MPa, z=5, s=1 mm, 不同约束应力演化模式, 得到裂纹发展深度a随循环次数N变化的一组曲线, 如图 11所示.可见材料微结构的演化特性将影响裂纹深度的发展.
|
图 11 当远场应力幅为200 MPa、长短轴比为5、短轴长1 mm时,不同约束应力区演化模式下的裂纹深度与循环次数关系曲线 Fig. 11 Relation curve between crack depth and cycle index with far field stress amplitude of 200 MPa, axial ratio of 5 and short axis of 1 mm under different evolution models of constraintstess |
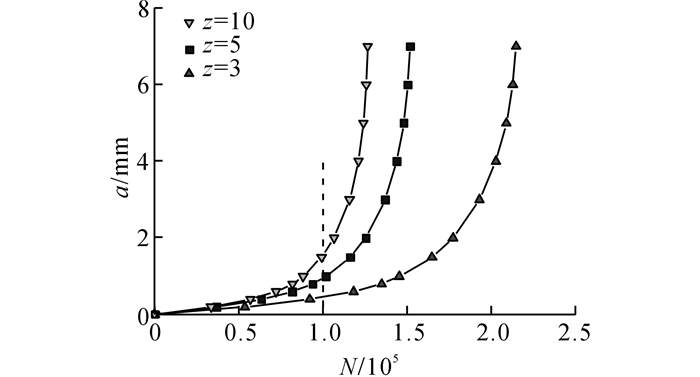
约束应力区为半椭圆形状, 半椭圆顶端为微观缺陷区.对于不同形状与大小的微观缺陷, 可通过选取不同长短轴比z的半椭圆顶端来进行模拟.因此, 微观缺陷对裂纹扩展行为的影响可体现为参数z对数值模拟结果的影响.采用上述模型及参数, 令Δσ∞=200 MPa, s=1, 采用约束应力演化模式1, 考虑不同大小的微观缺陷, 得到裂纹发展深度a随循环次数N变化的一组曲线, 如图 12所示.可见微观缺陷的大小对疲劳破坏有较大影响.
|
图 12 当远场应力幅为200 MPa、短轴长1 mm、处于演化模式1时,不同微观缺陷大小下的裂纹深度与循环次数关系曲线 Fig. 12 Relation curve between crack depth and cycle index with far field stress amplitude of 200 MPa, short axis of 1 mm and evolution mode 1 under different microdefect sizes |
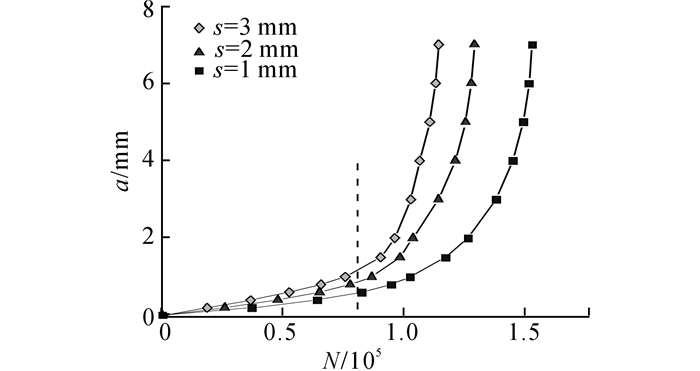
微观缺陷在三维体内的埋深为变量, 由半椭圆的短轴值s决定.令Δσ∞=200 MPa, z=5, 采用约束应力演化模式1, 考虑不同埋深的微观缺陷, 得到裂纹发展深度a随循环次数N变化的一组曲线, 如图 13所示.可见微观缺陷的埋深也对疲劳破坏有较大影响.
|
图 13 当远场应力幅为200 MPa、短轴长1 mm、处于演化模式1时,不同微观埋深下的裂纹深度与循环次数关系曲线 Fig. 13 Relation curve between crack depth and cycle index with far field stress amplitude of 200 MPa, short axis of 1 mm and evolution mode 1 under different micro buried depths |
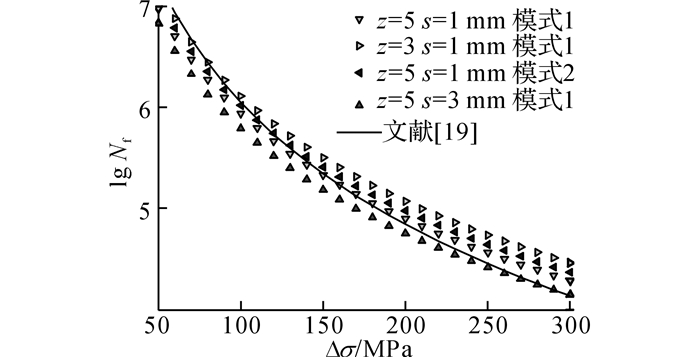
目前, 针对正交异性钢桥面板纵肋与顶板间的疲劳破坏, 研究人员均进行了大量的试验, 得到了各自的S-N曲线, 但疲劳试验数据较为发散.本文采用不同的约束应力演化模式及微观缺陷, 计算疲劳寿命, 并与S-N曲线[19]进行比较, 结果如图 14所示.由图可见, 微观效应对疲劳寿命有较大的影响, 是疲劳试验数据具有很大发散性的主要原因.
|
图 14 文献[19]与不同约束应力演化模式及微观缺陷下的S-N曲线比较 Fig. 14 Experimental S-N curve in Reference [19] compared with S-N curves computed by using our trans-scale model for various evolution modes and various micro-defects |
(1) 疲劳破坏具有典型的多尺度特征.基于约束应力区的概念, 采用有限元法拟合得到Kmicmac和Kmac的表达式, 并采用ΔKmicmac和ΔKmac作为控制参量, 建立了表面半椭圆疲劳裂纹扩展统一模型, 可将疲劳破坏全过程在一个理论框架内进行统一描述.
(2) 本文基于约束应力区概念, 采用有限元法计算应力强度因子, 建立的疲劳裂纹跨尺度分析方法能够正确描述正交异性钢桥面板纵肋与桥面板焊接部位的疲劳破坏行为.
(3) 本文提出的跨尺度模型可分析材料微观效应对疲劳破坏过程的影响.数值模拟结果表明, 微观效应对疲劳寿命有很大影响, 是疲劳试验数据具有很大发散性的主要原因.
| [1] |
刘扬, 李明, 鲁乃唯, 等. 随机车流作用下悬索桥钢箱梁细节疲劳可靠度[J].
长安大学学报:自然科学版, 2016, 36(2): 44–51.
LIU Yang, LI Ming, LU Nai-wei, et al. Fatigue reliability for steel box girder details of suspension bridge under random traffic flow[J]. Journal of Chang'an University: Natural Science Edition, 2016, 36(2): 44–51. |
| [2] |
张清华, 崔闯, 卜一之, 等. 港珠澳大桥正交异性钢桥面板疲劳特性研究[J].
土木工程学报, 2014, 47(9): 110–119.
ZHANG Qing-hua, CUI Chuang, BU Yi-zhi, et al. Study on fatigue features of orthotropic decks in steel box girder of Hong Kong-Zhuhai-Macao Bridge[J]. China Civil Engineering Journal, 2014, 47(9): 110–119. |
| [3] |
张高楠, 石广玉, 王晓丹. 正交异性钢桥面板焊缝的疲劳寿命评估方法[J].
固体力学学报, 2013, 33: 216–223.
ZHANG Gao-nan, SHI Guang-yu, WANG Xiao-dan. Evaluation the approaches for fatigue life prediction of welded joints of orthotropic steel decks[J]. Chinese Journal of Solid Mechanics, 2013, 33: 216–223. |
| [4] | MINER M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics, 1945, 12(3): A159–A164. |
| [5] | PARIS P C. The growth of cracks due to variations in load [D]. Bethlehem: University of Lehigh, 1962. |
| [6] |
邓扬, 丁幼亮, 李爱群, 等. 钢箱梁焊接细节基于长期监测数据的疲劳可靠性评估:疲劳可靠度指标[J].
土木工程学报, 2012, 45(3): 86–92.
DENG Yang, DING You-liang, LI Ai-qun, et al. Fatigue reliability assessment for welded of steel box girders using long-term monitoring data: fatigue reliability indices[J]. China Civil Engineering Journal, 2012, 45(3): 86–92. |
| [7] |
顾萍, 周聪. 铁路正交异性钢桥面板典型疲劳裂纹寿命估算[J].
铁道学报, 2012, 34(1): 97–102.
GU Ping, ZHOU Cong. Estimation of fatigue life of typical cracks of orthotropic steel decks of railways bridges[J]. Journal of the China Railway Society, 2012, 34(1): 97–102. |
| [8] |
郑淳. 基于断裂力学的公路钢桥疲劳寿命可靠度方法研究[D]. 广州: 华南理工大学, 2013.
ZHEN Chun. Research on fatigue reliability evaluation of highway steel bridges based on fracture mechanics [D]. Guangzhou: South China University of Technology, 2013. |
| [9] | SIH G C. Multiscale fatigue crack initiation and propagation of engineering materials: structural integrity and microstructural worthiness[M]. New York: Springer, 2008. |
| [10] | SIH G C, TANG X S. Dual scaling damage model associated with weak singularity for macroscopic crack possessing a micro-/meso-scopic notch tip[J]. Theoretical and Applied Fracture Mechanics, 2004, 42(1): 1–24. DOI:10.1016/j.tafmec.2004.06.001 |
| [11] | TANG X S, SIH G C. Weak and strong singularities reflecting multiscale damage: micro-boundary conditions for free-free, fixed-fixed and free-fixed constraints[J]. Theoretical and Applied Fracture Mechanics, 2005, 43(1): 5–62. DOI:10.1016/j.tafmec.2004.12.002 |
| [12] | SIH G C, TANG X S. Simultaneous occurrence of double micro/macro stress singularities for multiscale crack model[J]. Theoretical and Applied Fracture Mechanics, 2006, 46(2): 87–104. DOI:10.1016/j.tafmec.2006.07.001 |
| [13] | SIH G C, TANG X S. Asymptotic micro-stress field dependency on mixed boundary conditions dictated by micro-structural asymmetry: Mode I macro-stress loading[J]. Theoretical and Applied Fracture Mechanics, 2006, 46(1): 1–14. DOI:10.1016/j.tafmec.2006.05.007 |
| [14] | TANG X S, SIH G C. Equilibrium mechanics model of multiscaling by segmentation: asymptotic solution for macro-meso-micro damage in anti-plane shear deformation[J]. Theoretical and Applied Fracture Mechanics, 2005, 44(1): 1–15. DOI:10.1016/j.tafmec.2005.05.001 |
| [15] | SIH G C, TANG X S. Triple scale segmentation of non-equilibrium system simulated by macro-micro-atomic line model with mesoscopic transitions[J]. Theoretical and Applied Fracture Mechanics, 2005, 44(2): 116–145. DOI:10.1016/j.tafmec.2005.06.002 |
| [16] | TANG X S. Scatter of fatigue data owing to material microscopic effects[J]. Sci China Phys Mech Astron, 2014, 57(1): 90–97. DOI:10.1007/s11433-013-5333-9 |
| [17] | 李庆芬, 胡胜海, 朱世范. 断裂力学及其工程应用[M]. 哈尔滨: 哈尔滨工程大学出版社, 2008: 34-36. |
| [18] | YA S, YAMADA K, ISHIKAWA T. Fatigue evaluation of Rib-to-Deck welded joints of orthotropic steel bridge deck[J]. Journal of Bridge Engineering, 2011, 16(4): 492–499. DOI:10.1061/(ASCE)BE.1943-5592.0000181 |
| [19] |
荣振环, 张玉玲, 刘晓光, 等. 大跨度斜拉桥正交异性板疲劳试验研究[J].
钢结构, 2009, 24(5): 13–16.
RONG Zhen-huan, ZHANG Yu-ling, LIU Xiao-guang, et al. Fatigue experimental research on orthotropic plate of long-span cable-stayed bridge[J]. Steel construction, 2009, 24(5): 13–16. |
| [20] | SIM H B, UANG C M, SIKORSKY C. Effects of fabrication procedures on fatigue resistance of welded joints in steel orthotropic decks[J]. Journal of Bridge Engineering, 2009, 14(5): 366–373. DOI:10.1061/(ASCE)1084-0702(2009)14:5(366) |



