热声发电具有结构简单、环保、可利用低品位能源等优点, 在中小型太阳能发电、工业废热回收、冷热电联产及分布式能源系统方面具有较好前景.
美国Los Alamos实验室的Backhaus等[1]率先研制了高效行波热声发电机.该发电系统主要由1个行波环路和2个对称布置的直线发电机组成, 其热电效率达到18%, 对应的发电功率为39 W.中科院理化所的Wu等[2]之后对斯特林型热声发电系统进行了一系列研究, 于2014年研制出一台1 kW级热声斯特林发电系统, 其最大输出电功达到了1 043 W, 对应热电效率为17.7%.同年, Wu等[3]设计的三级双作用热声发电系统输出电功率达到了1.57 kW, 最大热电效率达16.8%.2015年, Bi等[4]设计的三级行波热声发动机输出电功率已达4.69 kW.然而, 直线电机的输入阻抗并没有同热声发动机的输出声阻抗形成良好匹配.因此, 热声发电系统的性能仍然有相当大的提升空间.正如在电路中, 负载阻抗需要与电路相匹配从而使得电路有高的输出电功率及效率.在声场中, 直线电机和谐振管可视作环路部分的声负载, 其与声源——行波环路的阻抗匹配, 对系统性能有重要的影响.实现热声发动机与直线电机之间的良好阻抗匹配, 是提升热声发电系统总体性能的有效途径之一.
2012年浙江大学的Sun等[5]等设计搭建了一台行波热声发电系统, 以氦气为工质, 工作压力为3.0 MPa, 频率为65 Hz.其最大输出电功达到了345.3 W, 最高的热电效率为12.33%.通过实现热声发动机与直线电机的良好匹配, 2014年, 在2.48 MPa工作压力下, 该热声发电系统实现了473.6 W的电功输出[6].在3.16 MPa工作压力下, 该发电系统实现了750 W的电功率输出, 热电效率达到16.3%.
本文将热声发电系统进行解耦, 通过Design Environment for Low-amplitude Thermoacoustic Engines (DeltaEC)软件分别分析热声发动机和直线电机的阻抗特性,对热声发电系统整机进行数值模拟和实验研究.从声阻抗特性层面成功实现热声发动机与直线电机间的良好匹配, 揭示行波热声发电系统的性能变化规律和工作特性.
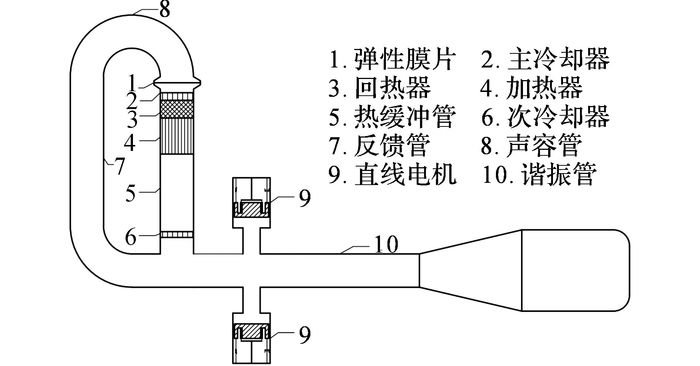
1 实验系统和数理模型 1.1 热声发电系统实验装置如图 1所示为斯特林型热声发电系统的示意图.该系统主要由行波热声发动机(参数见表 1)和2台直线发电机所(参数见表 2)组成.其中发动机主要由声学管路和换热器类部件组成.声学管路主要包括声容管、惯性管、热缓冲管、谐振管、气库等;换热器类部件包括主冷却器、回热器、加热器以及次冷却器.直线发电机为动磁式, 额定电压(峰值)为280 V, 额定电流(峰值)为4 A, 活塞额定位移振幅为6.5 mm, 最大耐压为6.0 MPa.
|
图 1 行波热声发电系统示意图 Fig. 1 Schematic of traveling-wave thermoacoustic electric generating system |
| 表 1 行波热声发动机主要参数 Table 1 Major parameters of traveling-wave thermoacousticengine |
| 表 2 直线发电机的参数 Table 2 Parameters of linear alternators |
本实验采用瑞士Huba提供的静态压力传感器, 型号为511.933 003 142, 量程为0~4 MPa, 满量程精度为±0.3%, 响应时间为1 ms;同时采用美国PCB公司提供的动态压力传感器, 型号为102B15, 动态压力的最大量程为1 379 kPa, 满量程精度为1.0%, 响应时间小于1 μs, 频率响应范围为0.5 ~500 000 Hz.温度测量包括加热器温度和主水冷器冷却水进出口温度, 均采用K型热电偶, 通过Keithley2700和7700模块进行数据采集.加热功率测量采用精度为0.5级的HB404P智能数显功率表, 外接负载的电功率、电流和电压采用Aitek公司的AWE2101系列功率分析仪进行测量.
一般将热声发电系统视作整体来进行优化和设计, 但这种方式忽略了热声发动机和直线电机本身的最优工况, 这可能导致设计得到的最优性能仍然有较大的提升空间.因此, 本文采用“解耦法”优化该行波热声发电系统.
1.2 热声发动机及直线电机理论模型热声发动机的输出阻抗特性的理论计算依据线性热声理论进行.Xiao等[7-10]的研究使线性热声理论得到了发展.热声发动机频域内的动量方程、连续性方程及能量方程[10]如下:
| $\frac{{{\rm{d}}{p_1}}}{{{\rm{d}}x}} = \frac{{{\rm{j}}\omega {\rho _{\rm{m}}}}}{{1 - {f_\upsilon }}}\frac{{{U_1}}}{A}.$ | (1) |
| $\begin{array}{l} \frac{{{\rm{d}}{U_1}}}{{{\rm{d}}x}} = - \frac{{{\rm{j}}\omega A}}{{\gamma {p_{\rm{m}}}}}\left[ {1 + \left( {\gamma - 1} \right){f_\kappa }} \right] \times \\ \quad \quad \quad \frac{{{f_\kappa } - {f_\upsilon }}}{{\left( {1 - {f_\upsilon }} \right)\left( {1 - \Pr } \right)}}\frac{{{U_1}}}{{{T_{\rm{m}}}}}\frac{{{\rm{d}}{T_{\rm{m}}}}}{{{\rm{d}}x}}. \end{array}$ | (2) |
| $\begin{array}{l} \frac{{{\rm{d}}{T_{\rm{m}}}}}{{{\rm{d}}x}} = \\ \frac{{H - \frac{1}{2}{\mathop{\rm Re}\nolimits} \left[ {{p_1}{U_1}\left( {1 - \frac{{{f_\kappa } - {{\tilde f}_\upsilon }}}{{\left( {1 + \Pr } \right)\left( {1 - {f_\upsilon }} \right)}}} \right)} \right]}}{{\frac{{{\rho _{\rm{m}}}{c_{\rm{p}}}{{\left| {{U_1}} \right|}^2}}}{{2A\omega \left( {1 - {{\Pr }^2}} \right){{\left| {1 - {f_\upsilon }} \right|}^2}}}{\mathop{\rm Im}\nolimits} \left[ {{f_\kappa } + \Pr {{\tilde f}_\upsilon }} \right] - \left( {Ak + {A_{\rm{s}}}{k_{\rm{s}}}} \right)}} \end{array}$ | (3) |
式中:p1、U1、Tm及H分别为复合压力振幅、复合体积流率、工质平均温度及总功流;ω、γ、Pr及pm分别为角频率、绝热指数、普朗特数及平均压力;fκ和fυ分别为黏性函数和黏性函数;k和ks分别为气体和固体的导热系数;A和As分别为气体和固体的横截面积;x为沿声波传递方向的坐标.DeltaEC由Los Alamos实验室根据该线性热声理论编写出来的, 之后在热声研究中受到广泛应用.
2台电机的参数基本一致, 因此忽略其微小差别, 则能得到以下控制方程[10-11]:
| $Bl \cdot {\upsilon _1} = {I_1} \cdot \left( {\frac{{{R_1}}}{2} + {r_{\rm{e}}} + {\rm{j}}\omega {L_{\rm{e}}} - {\rm{j}}\frac{1}{{2\omega {C_{\rm{e}}}}}} \right).$ | (4) |
| $\left( {{p_1} - {p_{{\rm{1,b}}}}} \right)A = Bl \cdot {I_1} + {R_{\rm{m}}}{\upsilon _1} + \frac{K}{{{\rm{j}}\omega }}{\upsilon _1} + {\rm{j}}\omega M{\upsilon _1}.$ | (5) |
| ${\upsilon _1}A = \frac{{{\rm{j}}\omega {V_{\rm{b}}}}}{{\gamma {p_{\rm{m}}}}}{p_{{\rm{1}},{\rm{b}}}}.$ | (6) |
式中:v1、I1、p1、p1, b及R1分别为电机的速度振幅、电流、驱动压力、背腔压力及外接负载.
在热声学中, 声阻抗Za定义如下:
| ${Z_{\rm{a}}} = \frac{{{p_{\rm{1}}}}}{{{U_1}}}.$ | (7) |
将式(4)~(6) 代入式(7) 中, 可得2台电机的声阻抗为
| ${Z_{\rm{a}}} = \frac{1}{{2{A^2}}}\left[ {\left( {{R_{\rm{m}}} + \frac{{{R_{\rm{e}}}B{l^2}}}{{R_{\rm{e}}^2 + X_{\rm{e}}^2}}} \right) + {\rm{j}}\left( {{X_{\rm{m}}} + \frac{{{X_{\rm{e}}}B{l^2}}}{{R_{\rm{e}}^2 + X_{\rm{e}}^2}}} \right)} \right].$ | (8) |
式中:Xm=ωM-(K+γpmA2/Vb)/ω为力抗, Re=Rl/2+re为电阻, Xe=ωLe-1/(2ωCe)为电抗.因此其性能[5]为
| ${W_1} = \frac{1}{2}\frac{{{{\left| {\Delta {p_1}} \right|}^2}{A^2}B{l^2}{R_{\rm{1}}}}}{{{{\left( {B{l^2} - {X_{\rm{m}}}{X_{\rm{e}}} + {R_{\rm{m}}}{R_{\rm{e}}}} \right)}^2} + {{\left( {{X_{\rm{m}}}{R_{\rm{e}}} + {X_{\rm{e}}}{R_{\rm{m}}}} \right)}^2}}}.$ | (9) |
| ${\eta _{{\rm{a - e}}}} = \left( {{W_{\rm{a}}} - {W_{\rm{m}}}} \right)\frac{{{R_1}}}{{{R_{\rm{e}}}}} = \frac{{B{l^2}{R_{\rm{e}}}}}{{B{l^2}{R_{\rm{e}}} + 2{R_{\rm{m}}}\left( {R_{\rm{e}}^2 + X_{\rm{e}}^2} \right)}}$ | (10) |
在DeltaEC软件中, 直线电机可用IESPEAKER部件来模拟, 并可通过给予一定的输入参数使其工作, 也可以结合热声发动机耦合成行波热声发电系统进行模拟计算.
2 行波热声发动机输出特性在DeltaEC的发动机模型中, 去除图 1中的直线发电机, 改为具有可变声阻抗的部件, 从而计算出不同阻抗下发动机的输出特性, 即输出声功、效率等参数.
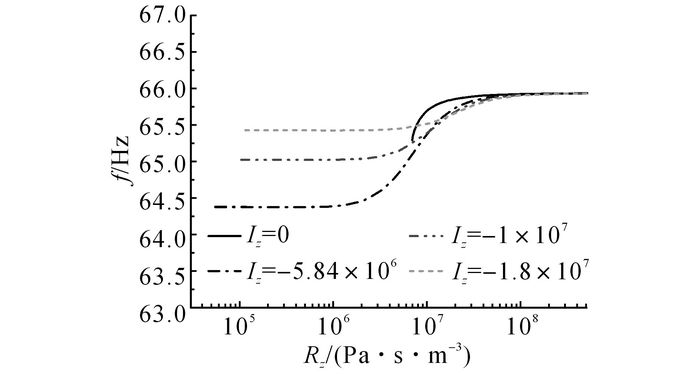
如图 2所示为热声发动机工作频率f随声阻抗Z的变化规律.发动机频率随声阻抗实部RZ的增大而增大, 随声阻抗虚部IZ绝对值的增大而减小.工作频率最后稳定在65.9 Hz.当发动机连接直线发电机处阻抗实部小于1.0×107 Pa·s/m3时, 频率变化相对较快, 这是因为在该声阻抗实部区域, 行波热声发动机的声功和效率都处于急剧增大的趋势, 发动机未处于良好的工作状态中;而当声阻抗实部大于2.0×107 Pa·s/m3时, 频率的升高趋势逐渐平稳下来.当声阻抗实部大于1.0×107 Pa·s/m3时, 工作频率处于65.5~65.9 Hz.可见, 输出声阻抗对系统的工作频率的影响较为微弱, 尤其是在声阻抗实部大于1.0×107 Pa·s/m3的区域.
|
图 2 行波热声发动机工作频率随声阻抗变化的规律 Fig. 2 Working frequency of rmoacoustic engine varies with acoustic impedance of acoustic load |
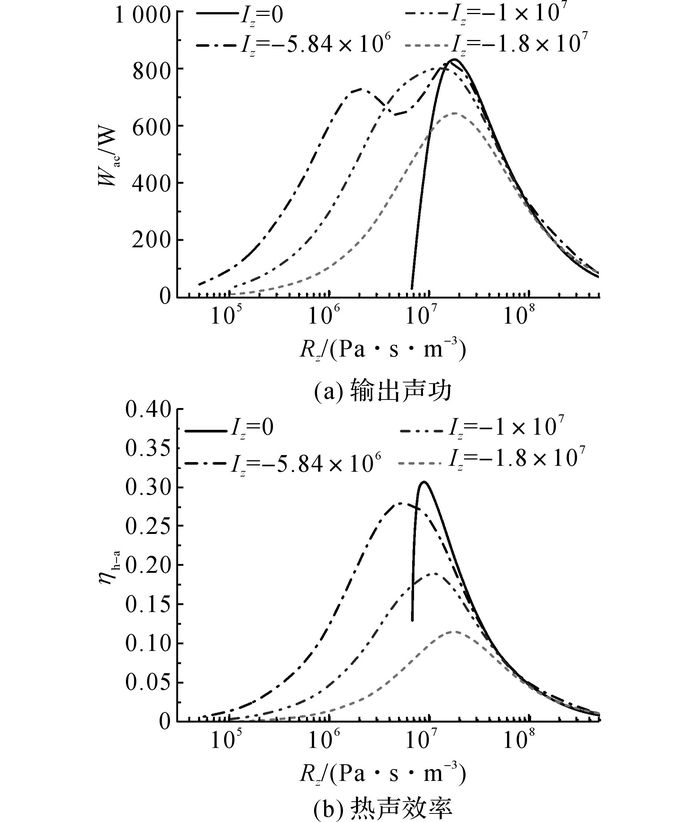
如图 3所示为声功Wac及效率ηh-a随发动机谐振管处(即图 1中直线发电机位置)阻抗实部和虚部的变化规律.模拟结果显示, 发动机最大输出声功可以达到800 W, 热声效率达到30%.在不同声阻抗虚部的情况下, 发动机产生的声功及效率随阻抗实部的增大有相同的趋势, 即先增大再减小.每条曲线声功及效率最大处基本位于较小的声阻抗实部范围内, 但两者范围不完全重叠, 当阻抗虚部从0变化到-1.8×107 Pa·s/m3时, 最优输出声功对应的实部阻抗在1.0×107~3.0×107 Pa·s/m3, 而最优热声转化效率对应的阻抗实部则稍小, 范围为5.0×106~2.0×107 Pa·s/m3.
|
图 3 行波热声发动机输出声功及其效率随声阻抗变化的规律 Fig. 3 Output acoustic power and thermal-to-acoustic efficiency of thermoacoustic engine vary with impedance of acoustic load |
从图 3可得, 声阻抗虚部对于系统的输出特性具有显著影响.当声阻抗虚部为0时, 计算得到的最大输出声功及热声效率均为该热声发电机在所有阻抗条件下的最大值.这是因为由于谐振管的存在, 热声发动机本身已处于谐振状态, 在声功输出时表现为纯声阻性.根据匹配原理, 外接负载为纯阻性时能达到最优匹配特性.此外, 当声阻抗实部小于6.5×106 Pa·s/m3时, 谐振管处输出声功已减小到0, 表明该热声发动机无法工作于低于该阻抗实部的声阻抗区域内.当声阻抗虚部低于0时, 发动机的工作性能略有下降, 尤其是当阻抗虚部为-1.8×107 Pa·s/m3时, 即负载具有较大容抗时, 输出声功及热声效率下降明显.但是, 热声发动机所能工作及性能较优的声阻抗实部区域有所增大.
3 直线发电机的输入特性直线电机的阻抗虚部较小时能更好地与发动机匹配, 根据式(8), 则力抗Xm和电抗Xe需要接近0.直线电机的声阻抗受工作频率、外接电阻及串联电容的影响.为了保证电机声阻抗虚部较小, 需要在电功输出电路上串联一个合适的电容.在该系统中, 外接电容为9.6 μF.
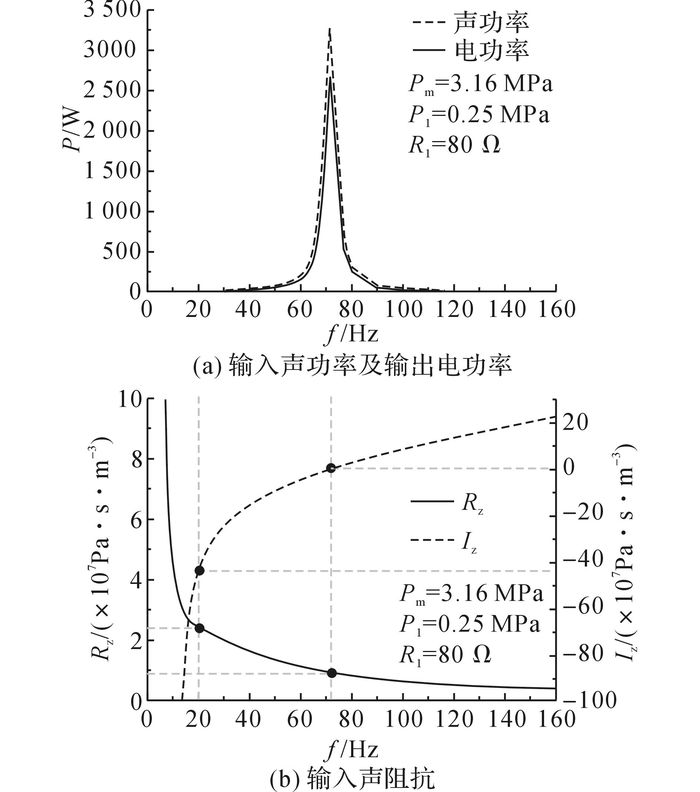
如图 4所示为直线电机输入声功率Wac、输出电功率We及输入声阻抗随工作频率的变化规律.工作压力Pm=3.16 MPa, 压力振幅Pl=0.25 MPa, 外接电阻Rl=80 Ω.当发电机工作在72 Hz左右, 即接近电机的机械谐振状态时, 其输入声功及输出电功均达到最大值, 分别为3 242.7 W及2 659.6 W.根据图 4(a), 工作频率对电机影响巨大, 当工作频率偏离谐振点时, 电机的输入声功及输出电功率将大幅度下降.图 4(b)为工作频率对发电机输入声阻抗的影响.当频率从20 Hz增大到140 Hz时, 输入声阻抗实部从2.40×107 Pa·s/m3迅速减小到4.54×106 Pa·s/m3, 虚部则从-3.89×108 Pa·s/m3增大到1.83×108 Pa·s/m3.当频率约72 Hz时, 声阻抗实部为9.5×106 Pa·s/m3, 虚部恰好为0.此时, 直线发电机为纯声阻性声学元件, 在系统压力振幅一定时, 发电机能获得最大输入声功和最大的输出电功.当工作频率为20 Hz时, 声阻抗虚部为-3.89×108 Pa·s/m3, 发电机处于极大的容抗状态, 因而引出声功能力急剧减弱.
|
图 4 直线电机输入声功、输出电功及其输入声阻抗随工作频率变化的规律 Fig. 4 Input acoustic power, output electric power and acoustic impedance of linear alternator vary with working frequency |
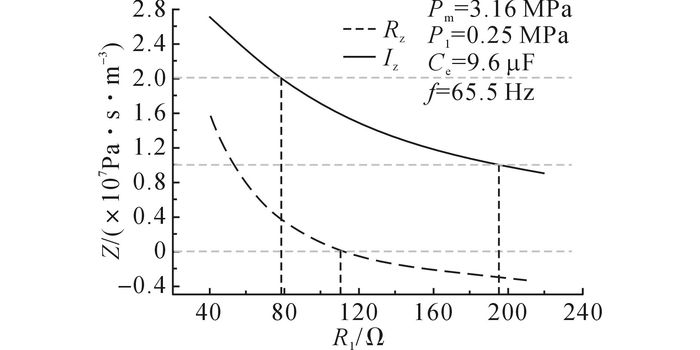
如图 5所示为直线发电机声阻抗Z随外接负载Rl的变化曲线.其中, 工作频率为65.5 Hz.可见, 当外接负载从40 Ω增大到220 Ω时, 声阻抗实部从2.7×107 Pa·s/m3减小到9.0×106 Pa·s/m3, 声阻抗虚部从1.6×107 Pa·s/m3减小到-3.4×106 Pa·s/m3.根据前文所述的发动机最优输出声阻抗范围, 则要调节直线发电机的输入声阻抗与之匹配, 可得最优外接负载范围为80~200 Ω.
|
图 5 直线发电机声阻抗随外接负载变化的规律 Fig. 5 Acoustic impedance of linear alternators varies with load resistance |
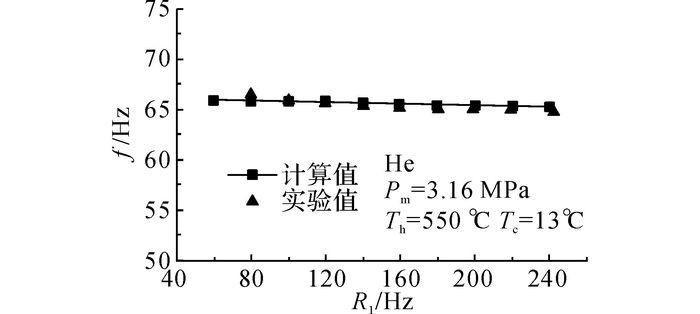
行波热声发动机与直线发电机之间首先是系统工作频率的匹配.当行波热声发动机以氦气为工质时, 其工作频率在65 Hz左右, 而直线电机的最优工作频率在72 Hz左右, 因而两者已经取得了较好的匹配.如图 6所示为两者耦合后热声发电系统工作频率的变化规律, 其中加热温度Th=550 ℃, 冷却水温度Tc=13 ℃.系统工作频率在实验和理论计算中, 均随着外接负载的增大而略有减小.单工作频率基本稳定在65.5 Hz左右, 与热声发动机工作频率一致, 与直线发电机的最优工作频率匹配也较好.
|
图 6 热声发电系统工作频率随外接负载变化的规律 Fig. 6 Working frequency of thermoacoustic electric generating system varies with load resistance |
如图 7所示为不同加热温度下行波热声发电系统的工作性能.加热温度越高, 而冷端温度不变, 则回热器两端温度梯度越大, 热声振荡的驱动力也就越大, 系统发电功率和效率也相应越高.图 7(a)为热声发电系统输出电功率We的理论和实验对比结果.由图可得, 在该负载范围内, 理论与实验数据均呈先增大后减小的趋势, 在外接负载约为100 Ω时有最大值, 且理论和实验结果较接近.图 7(b)为系统发电效率ηh-e的理论和实验对比结果.随着外接负载的增大, 实验和理论发电效率均先增大后减小.当外接负载较大(大于160 Ω)时, 实验发电效率明显下降.在模拟结果中, 效率增长趋势放缓且呈减小趋势.这是因为随着外接负载的增大, 直线电机声阻抗实部不断减小, 逐渐偏离了最优声阻抗范围.

|
图 7 热声发电系统发电量及发电效率随外接负载变化的规律 Fig. 7 Power and thermal-to-electric efficiency of thermoacoustic electric generating system varies with load resistance at different temperatures |
实验发电效率明显低于理论发电效率.原因主要为以下3个方面:1) 实验过程中热量损失大, 如通过辐射、对流及管壁导热造成的热量耗散;2) 加热器传热效率较低, 特别是加热器外周的电加热管传热距离过大, 而谐振管及环路的内壁不够光滑和存在明显的截面突变, 会造成一定的流动损失;3) 存在声直流等非线性效应原因造成的损失.此外, 最优输出电功对应的外接负载约100 Ω, 而最优热电效率对应的外接负载则在160 Ω左右, 相对更大.这与声阻抗匹配机理及图 2所得的结论是相符的.
值得注意的是, 外接负载为100到180 Ω时, 实验中系统发电功率及热电效率均较高.此时发电机输入声阻抗实部从1.7×107 Pa·s/m3减小到1.1×107 Pa·s/m3, 声阻抗虚部从9.4×105 Pa·s/m3减小到-2.8×106 Pa·s/m3.由前文可知, 该外接负载范围对应的直线发电机输入声阻抗区域与热声发动机的输出声阻抗正好呈良好匹配, 既保证发动机声功输出能力, 也保证了直线电机的发电能力.这说明该行波热声发电系统实现了发动机与直线电机之间的良好耦合.
5 结论(1) 该热声发动机的稳定工作频率在65.5 Hz左右, 而当声功引出处阻抗实部为1.0×107~2.0×107 Pa·s/m3, 阻抗虚部小于106 Pa·s/m3量级时, 发动机的输出声功及效率高.
(2) 直线电机的高效工作频率在72 Hz左右, 当串联电容为9.6 μF, 外接负载为80~200 Ω时, 直线电机的输入声阻抗处于发动机最优输出声阻抗范围内.
(3) 在模拟实验中, 在550 ℃工作温度下, 数值模拟得到该热声发电系统的最大发电功率达到520 W, 最高热电效率达到24.4%;在实际实验中, 该热声发电系统最大发电功率达到481 W, 最高热电效率为15.1%.两者结果相近, 且系统工作频率、发电量和发电效率随外界负载变化规律一致性较高.
| [1] | BACKHAUS S, TWARD E, PETACH M. Traveling-wave thermoacoustic electric generator[J]. Applied Physics Letters, 2004, 85(6): 1085–1087. DOI:10.1063/1.1781739 |
| [2] | WU Z H, ZHANG L M, DAI W, et al. Investigation on a 1 kW traveling-wave thermoacoustic electrical generator[J]. Applied Energy, 2014, 124: 140–147. DOI:10.1016/j.apenergy.2014.02.063 |
| [3] | WU Z H, YU G Y, ZHANG L M, et al. Development of a 3 kW double-acting thermoacoustic Stirling electric generator[J]. Applied Energy, 2014, 136: 866–872. DOI:10.1016/j.apenergy.2014.04.105 |
| [4] | BI T J, WU Z H, ZHANG L M, et al. Development of a5 kW traveling-wave thermoacoustic electric generator[J]. Applied Energy, 2017, 185: 1355–1361. DOI:10.1016/j.apenergy.2015.12.034 |
| [5] | SUN D M, WANG K, ZHANG X J, et al. A traveling-wave thermoacoustic electric generator with a variableelectric RC load[J]. Applied energy, 2013, 106: 377–382. DOI:10.1016/j.apenergy.2013.01.051 |
| [6] | WANG K, SUN D M, ZHANG J, et al. Operating characteristics and performance improvements of a 500W traveling-wave thermoacoustic electric generator[J]. Applied Energy, 2015, 160: 853–862. DOI:10.1016/j.apenergy.2015.03.085 |
| [7] | XIAO J H. Thermoacoustic heat transportation and energy transformation Part 1: formulation of the problem[J]. Cryogenics, 1995, 35(1): 15–19. DOI:10.1016/0011-2275(95)90419-G |
| [8] | XIAO J H. Thermoacoustic heat transportation and energy transformation Part 2: isothermal wall thermoacoustic effects[J]. Cryogenics, 1995, 35(1): 21–26. DOI:10.1016/0011-2275(95)90420-K |
| [9] | XIAO J H. Thermoacoustic heat transportation and energy transformation Part 3: adiabatic wall thermoacoustic effects[J]. Cryogenics, 1995, 35(1): 27–29. DOI:10.1016/0011-2275(95)90421-B |
| [10] | SWIFT G W, GARRETT S L. Thermoacoustics: aunifying perspective for some engines and refrigerators[J]. The Journal of the Acoustical Society of America, 2003, 113(5): 2379–2381. DOI:10.1121/1.1561492 |
| [11] |
吴张华, 罗二仓, 戴巍. 热声发电之直线发电机的理论研究[J].
太阳能学报, 2008, 29(4): 493–497.
WU Zhang-hua, LUO Er-cang, DAI Wei. Theoretical investigation on linear alternator in thermoacoustic power generation system[J]. Acta Energiae Solaris Sinica, 2008, 29(4): 493–497. |



