拉削加工技术具有加工精度高、加工范围广、生产效率高和操作简便等优点, 被广泛应用于航空航天器械、海洋装备和汽车零部件等高精密加工制造领域.然而伴随着关键部件的高精化标准逐渐升高, 大量学者开始致力于研究如何实现拉削加工精密化、平稳化和高效化.因此, 建立准确的拉削负载计算模型, 优化拉刀和拉削过程的工艺参数, 抑制拉削过程的振动, 对提高关键部件的加工精度具有非常重要的理论与实际意义.
目前许多学者对拉削负载的建模进行了大量的研究工作, 普遍采用了动力学原理[1-2]、能量转换原理[3-4]、统计学[5-7]、微单元积分[8-10]、热力学原理[11]、有限元理论[12-13]、材料应变特性[14-15]等方法来构建拉削负载模型.例如, Schroeter等[1]引入Kienzle方程, 构建了拉削的动力学系统模型, 并采用试验数据拟合参数来预测拉削负载.Hossam等[4]引入能量转化原理, 构建了基于加工表面拉刀连续刀齿拉削负载模型.仇健等[7]引用统计学中的多因素方法, 构建了切削速度、切削深度、每齿进给量相关的切削力预测公式.魏兆成等[10]引入微分思想, 构建了基于进给方向和刀具接触界面任意变化的铣削力模型. Vogtel等[11]引入热力学原理, 通过对工件进行有限元模拟构建了线性回归方程拟合前角、齿升量等参数, 预测拉削负载.Schulze等[12]引入了变化的齿升量, 构建有限元模型模拟拉削负载.李炳林等[15]引用斜角切削理论, 构建了切屑通过时剪切区的应力、应变、应变率和温度的控制方程, 从而准确预测拉削负载.
上述文献涉及的研究内容, 一方面大都将拉刀的齿升量设定为常量, 没有考虑刀齿齿升量的变化, 同时也没有考虑拉削过程中刀齿宽度与工件接触的情况;另一方面忽略了拉削过程中刀齿后刀面与工件已加工表面的刮削效应, 以及多齿参与拉削的动特性.因此, 拉削负载特性的计算模型有待于进一步研究.
本文基于经典拉削负载模型和大量的拉削试验, 考虑工件的圆弧效应和切削与刮削并存原理, 建立单个刀齿的拉削负载计算模型;根据刀齿和工件接触的周期特性, 建立多齿拉削负载计算模型;对多齿拉削负载计算模型进行试验和仿真验证.
1 拉削负载计算模型 1.1 建模分析矩形槽拉削加工系统如图 1所示, 系统主要由床身、主油缸、导向柱、溜板、夹刀装置、端板、拉刀等组成.主油缸通过溜板和夹刀装置驱动拉刀, 拉刀穿过工件内孔, 实现对工件内孔矩形槽的加工, v为拉削速度.

|
图 1 矩形槽拉削加工系统示意图 Fig. 1 Diagrammatic sketch of rectangular groove broach |
若只考虑拉刀与工件接触部分, 可以将上述拉削加工系统简化为拉刀与工件接触状态, 如图 2所示.拉刀垂直于工件截面穿过工件, 实现逐齿拉削.其中, 拉刀在长度方向上由许多平行刀齿组成, 每个刀齿的绝对齿升量为δi(i为刀齿序号, i=1, 2, 3, …, n);每个刀齿之间间距相同,为p;工件长度为lw.根据绝对齿升量δi, 可以将拉刀刀齿分为粗拉区l1和精拉区l2.因此, 拉削负载在各个区域有不同的拉削负载特性.

|
图 2 拉刀与工件接触示意图 Fig. 2 Diagrammatic sketch of broach tool and workpiece contacting |
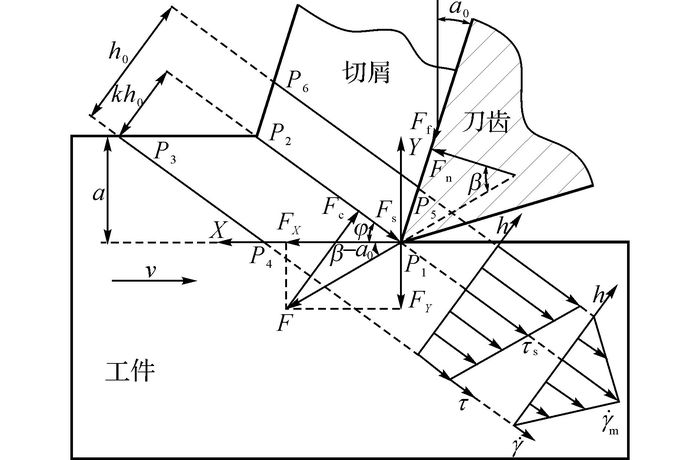
根据拉削过程中刀齿的受力分析可知, 拉削负载包括沿X方向的拉削力FX和沿Y方向的正压力FY, 如图 3所示.其中正压力表示为
|
图 3 拉削过程单个刀齿剪切区应力和应变率 Fig. 3 Single tooth shear zone stress and strain rate of broaching processing |
| $ {F_Y} = {F_X}\tan \left( {\beta - {\alpha _0}} \right). $ | (1) |
式中:β为刀齿摩擦角, α0为刀齿前角.
根据式(1) 可知, FY可由FX求得, 因此, 拉削负载特性主要由拉削力FX决定, 本文针对FX进行研究.经大量的拉削加工试验有如下发现.
1) 在拉削初始阶段, 如图 4所示,由于工件的加工表面是曲面, 并非所有刀齿齿宽都参与拉削,即工件的圆弧效应.
2) 拉削过程存在明显的“切削”过程和“刮削”过程.
3) 刀齿在拉削过程中会呈现切削和刮削占比不同的情况.
4) 拉削过程中与工件接触的刀齿数量会发生周期性变化.
根据如图 3所示的受力分析, 实际拉削负载FX中不仅包含切削力特性FX1和刮削力特性FX2, 同时需考虑在拉削过程中切削与刮削有不同的占比, 及刀齿数在拉削过程中的周期特性变化.基于上述特征, 本文先从单齿拉削负载建模入手, 详细分析单齿拉削过程的负载计算模型, 然后根据多齿拉削周期性, 建立多齿拉削负载动特性计算模型.
1.2 单齿拉削负载计算模型如图 2所示, 单齿拉削主要出现在工件长度lw小于刀齿间距d的情况.该工况下的单齿拉削负载FX模型由切削力特性FX1和刮削力特性FX2组成.
1.2.1 单齿拉削负载FX1的受力分析及计算方法如图 3所示为刀齿拉削过程中的受力状态, 平行四边形P1P2P3P4和P1P2P6P5区域构成了拉削加工的剪切应变区.其中P3P4是起始剪切面, P5P6是终止剪切面, P1P2是主剪切面;h0为剪切带厚度;k为不等分系数;主剪切面P1P2到初始剪切面P3P4的距离为kh0;τ为剪切区的剪切应力分布;
如图 3所示, 假设剪切面上的剪切应力τ是均匀分布的, 则单个刀齿剪切力Fs和剪切应力τ成比例, 因此, 单个刀齿切削负载可描述为
| $ \begin{array}{l} {F_{X1}} = {F_{\rm{s}}} \cdot \frac{{\cos \left( {\beta - {\alpha _0}} \right)}}{{\cos \left( {\varphi + \beta - {\alpha _0}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\frac{{{\tau _{\rm{s}}}A}}{{\sin \varphi }} \cdot \frac{{\cos \left( {\beta - {\alpha _0}} \right)}}{{\cos \left( {\varphi + \beta - {\alpha _0}} \right)}}. \end{array} $ | (2) |
式中:τs是主剪切面P1P2上的剪切应力, A是拉削过程切削层剖面面积, φ是刀齿剪切角.其中α0为常数, 其他参数的计算如下.
1) 剪切角φ.根据Grzesek[16]提出的剪切带厚度h0和切削层厚度a与剪切角φ的关系式, 得出剪切角的计算式为
| $ \varphi = \arcsin \frac{a}{{10{h_0}}} = \arcsin \frac{{{\delta _i} - {\delta _{i - 1}}}}{{10{h_0}}}. $ | (3) |
其中:h0采用文献[17]测得的典型值0.025 mm.
2) 摩擦角β.根据Merchant[15]提出的剪切角φ与摩擦角β的关系式, 得出摩擦角的计算式为
| $ \beta = \frac{{\rm{\pi }}}{2} + {\alpha _0} - 2\varphi . $ | (4) |
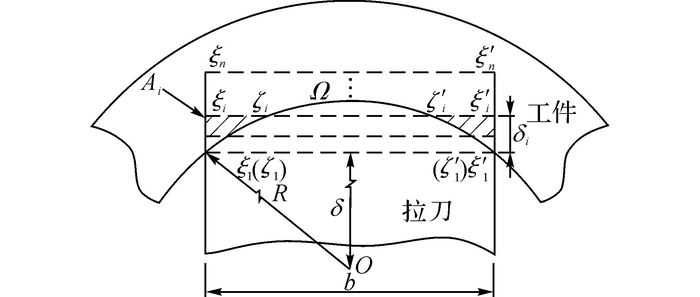
3) 切削层剖面面积A.考虑工件的圆弧效应, 大多数刀齿通过工件时, 每个刀齿的切削层剖面面积A不是恒定的, 如图 4所示.图中b为拉刀宽度;Ai为第i个刀齿的切削层剖面面积, A0=0;R为拉削工件的内径;δ为工件圆弧中心到拉刀的距离;当δi≥R-δ时, 设i=iN,N是自然数.
|
图 4 切削层剖面积Ai的计算原理图 Fig. 4 Calculation principle diagram of cutting area Ai |
根据刀齿与工件的几何关系, Ai的表达式为
| $ {A_i} = \left\{ \begin{array}{l} b{\delta _i} - \left( {{S_0} - {S_i}} \right) - \sum\limits_{j = 1}^{i - 1} {{A_j}} ,\;\;\;\;\;\;0 < i < {i_N};\\ b{\delta _i} - {S_0} - \sum\limits_{j = 1}^{i - 1} {{A_j}} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = {i_N};\\ b\left( {{\delta _i} - {\delta _{i - 1}}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{i_N} < i < n; \end{array} \right. $ | (5) |
式中:S0为线段ξ1ξ1′和弧ξ1Ωξ1′组成的面积;Si为线段ζiζi′和弧ζiΩζi′组成的面积, S0和Si的计算式分别为
| $ {S_0} = {R^2}\arccos \frac{\delta }{R} - \frac{1}{2}b\delta , $ | (6) |
| $ {S_i} = {R^2}\arccos \frac{{\delta + {\delta _i}}}{R} - \left( {\delta + {\delta _i}} \right)\sqrt {{R^2} - {{\left( {\delta + {\delta _i}} \right)}^2}} . $ | (7) |
4) 剪切应力τs.依据文献[15]单个刀齿的不等分剪切面分析, 可通过构建单个刀齿拉削过程中的材料控制方程和变形控制方程来预测剪切应力τs.由于实际拉削过程中拉削速度较小, 且对拉刀和工件有充分的冷却, 可不考虑温度对拉削负载的影响.因此, 本文采用简化的Johnson-Cook材料本构方程预测剪切应力τs, 其表示为
| $ \begin{array}{l} {\tau _{\rm{s}}} = {\tau _{\rm{s}}}\left( {h = k{h_0}} \right) = \\ \;\;\;\;\;\;\;\frac{1}{{\sqrt 3 }}\left[ {A + B{{\left( {\frac{{{\gamma _{\rm{s}}}}}{{\sqrt 3 }}} \right)}^{{n_{\rm{s}}}}}} \right]\left[ {1 + C\ln \frac{{{{\dot \gamma }_{\rm{m}}}}}{{{{\dot \gamma }_{\rm{0}}}}}} \right]. \end{array} $ | (8) |
式中:A、B、C、ns是材料常数;
| $ {\gamma _{\rm{s}}} = \frac{1}{{\tan \varphi }}. $ | (9) |
| $ {{\dot \gamma }_{\rm{m}}} = \frac{{4v\cos {\alpha _0}}}{{{h_0}\cos \left( {\varphi - {\alpha _0}} \right)}}, $ | (10) |
在拉削加工过程中, 刀齿前刀面在进行切削的同时, 刀齿与工件之间仍然存在挤压应力, 即刀齿后刀面与已加工表面有摩擦, 从而产生刮削力FX2, 根据大量试验测试, 单齿刮削负载FX2跟刀齿参与拉削的宽度bl和拉削速度v有关, 依据试验数据, 采用最小二乘法, 可以近似描述为
| $ {F_{X2}} = {k_1} \cdot \sin \left( {\frac{{{b_1}}}{v}{k_2}} \right) + {k_3}. $ | (11) |
式中:k1、k2、k3为刮削系数.bl为刀齿参与拉削的宽度, 计算式为
| $ {b_1} = b - {b_i}. $ | (12) |
式中:bi是线段ζiζi′的长度.
1.2.3 单齿拉削负载FX的计算方法综合上述建模分析可知, 单齿拉削负载模型为
| $ {F_X} = \left( {1 - \eta } \right) \cdot {F_{X1}} + \eta \cdot {F_{X2}}. $ | (13) |
式中:η为切削和刮削特性权重系数, 依据试验数据进行系数配比, 其计算式为
| $ \eta = \exp \left( { - \frac{{{\delta _i} - {\delta _{i - 1}}}}{\lambda }} \right). $ | (14) |
式中:λ为平均齿升量, 即满足
| $ \lambda = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{\delta _i} - {\delta _{i - 1}}} \right)} . $ | (15) |
当工件尺寸lw大于拉刀刀齿间距p时, 会导致与工件接触的最大拉刀齿数nm超过1个, 即形成多齿拉削.该情况下, nm与工件截面长度lw及齿距p之间的关系为
| $ {n_m} = \left[ {\frac{{{l_{\rm{w}}}}}{p}} \right]. $ | (16) |
式中:lw为工件长度;[·]为取整运算.
获得刀齿与工件的接触个数nc和时间t的关系如下.
1) 工件与刀齿接触初期阶段.
nc为刀齿与工件接触数量, 每经过时间间隔Δt, nc增加一个, 一直达到nm.nc的计算式为
| $ {n_{\rm{c}}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t < {t_0};\\ \left( {t - {t_0}} \right)/\Delta t,\;\;\;\;\;\;\;\;\;\;{t_0} \le t \le {t_1}. \end{array} \right. $ | (17) |
式中:t0为第一个刀齿接触工件所需时间;t1为nm个刀齿接触工件所需时间, 且满足
| $ {t_1} = {t_0} + \frac{{p\left( {{n_{\rm{m}}} - 1} \right)}}{v}. $ | (18) |
2) 工件与刀齿完全接触阶段.
每经过时间间隔Δt, nc在nm与nm-1之间呈现周期特性, 一直到工件开始离开刀齿, 其接触刀齿数与时间的关系为
| $ {n_{\rm{c}}} = {n_{\rm{m}}} - \frac{{1 - {{\left( { - 1} \right)}^{\left( {t - {t_1}} \right)/\Delta t}}}}{2},\;\;\;\;{t_1} \le t \le {t_2}. $ | (19) |
式中:t2为有刀齿开始脱离工件所需时间, 其计算式为
| $ {t_2} = {t_1} + \frac{{p\left( {n - 2{n_{\rm{m}}} + 2} \right)}}{v}. $ | (20) |
3) 工件逐渐脱离刀齿阶段
每经过时间间隔Δt, nc减少一个, 一直达到0, 其接触刀齿数与时间关系为
| $ {n_{\rm{c}}} = \left\{ \begin{array}{l} {n_{\rm{m}}} - 1 - \left( {t - {t_2}} \right)/\Delta t,\;\;\;\;\;{t_2} \le t < {t_3};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \ge {t_3}. \end{array} \right. $ | (21) |
式中:t3为刀齿全部脱离工件时间, 其计算式为
| $ {t_3} = {t_2} + \frac{{p\left( {{n_{\rm{m}}} - 2} \right)}}{v}. $ | (22) |
基于上述分析可知, 单齿拉削负载计算模型中包含了工件的圆弧效应、切削与刮削效应及切削与刮削在拉削过程中的占比不同情形.结合多齿拉削过程中的刀齿数与工件的接触情况, 其多齿拉削负载动特性计算模型可描述为
| $ {F_{\rm{X}}}\left( t \right) = \left\{ \begin{array}{l} \sum\limits_{j = 1}^{{n_{\rm{c}}}} {\left[ {\left( {1 - \eta } \right){F_{{\rm{X1}}}} + \eta {F_{{\rm{X2}}}}} \right]} ,\;\;\;{t_0} \le t < {t_1};\\ \sum\limits_{j = 1}^{{n_{\rm{c}}}} {\left[ {\left( {1 - \eta } \right){F_{{\rm{X1}}}} + \eta {F_{{\rm{X2}}}}} \right]} ,\;\;\;{t_1} \le t < {t_2};\\ \sum\limits_{j = 1}^{{n_{\rm{c}}}} {\left[ {\left( {1 - \eta } \right){F_{{\rm{X1}}}} + \eta {F_{{\rm{X2}}}}} \right]} ,\;\;\;{t_2} \le t < {t_3};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > {t_3}. \end{array} \right. $ | (23) |
式(23) 即为多齿拉削负载动特性模型, 包含了本文所要讨论的3个特性, 即圆弧效应、切削与刮削效应、刀齿数周期特性.
2 试验设备及方法为验证模型的有效性, 以工业中常用的LG612Ya-800型卧式拉床为试验平台, 如图 5所示.试验拉床最大拉削力为60 kN, 拉削行程为800 mm, 最大拉削速度为6 m/min.拉削负载数据通过2个PTH503压力传感器(量程为0~15 MPa, 综合精度为0.5% FS, 输出信号为4~20 mA, 频率响应为5 ms)从主油缸的无杆腔和有杆腔采样获得.数据采样系统由西门子公司的S7-300型可编程控制器(PLC)的CPU313C集成AD模块实现, 采样周期为2 ms.数据处理和显示系统由工控机和Borland C++软件平台完成.

|
图 5 基于LG612Ya-800型卧式拉床的拉削加工系统试验平台 Fig. 5 Testing platform of broach processing system based on horizontal broaching machine of type LG612Ya-800 |
试验系统其他参数说明如下.
1) 拉刀刀齿参数.
拉刀规格为600 mm×16 mm×40 mm, 刀齿宽度b=40 mm, 刀齿前角α0=15°, 刀齿齿距p=6 mm, 具体刀齿的齿升量如表 1所示.
| 表 1 拉刀刀齿齿升量参数表 Table 1 Parameters of broach tooth lift |
2) 试验材料.
试验工件材质为45#钢, 内径为43 mm, 外径为58 mm, 长度为39 mm, 加工后的矩形槽尺寸为16 mm×1.7 mm× 39 mm.此外, 由文献[19]可知, 式(8) 中的拉削工件材料常数为:A=507 MPa, B=320 MPa, C=0.046 MPa, n=0.28,
| 表 2 拉刀刀齿应变、应变率参数表 Table 2 Parameters of broach tooth strain and strain rate |
| 表 3 刀齿拉削面积参数表 Table 3 Parameters of broaching area of cutters |
3) 试验方法.
本文试验设定拉削速度v=48 mm/s, 通过PLC模拟量采集模块获取压力传感器的压力值, 模块采样频率为200 Hz, 最后通过Borland C++软件读取模块数据.
4) 仿真方法.
本文通过式(23) 计算仿真曲线, 其中切削负载FX1是由工件材料特性、工件和刀具几何尺寸及拉削速度等参数代入式(2) 中求解获取, 式(11) 中刮削力FX2是基于大量试验数据拟合的最优结果, 其中刮削力系数k1、k2、k3是利用最小二乘法拟合获得.相关的仿真计算参数如表 4所示.
| 表 4 拉削负载仿真相关计算参数表 Table 4 Related calculating parameters of broaching load simulation |
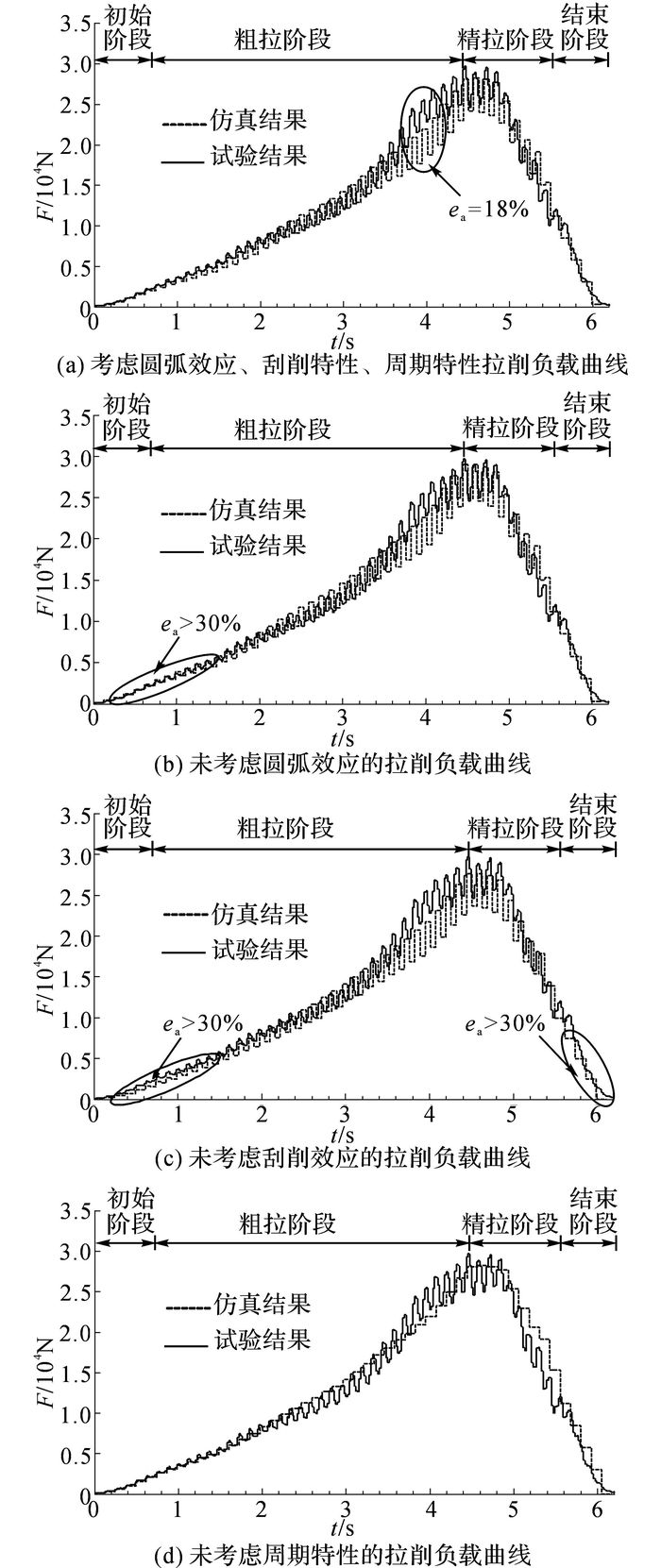
进行20组实际拉削试验, 每组的拉削负载曲线都具有很好的重复性, 本文随机抽取一组曲线进行说明.具体试验和仿真结果如图 6所示, 图中曲线沿时间轴分为4个阶段, 包括刀齿拉削初始阶段、粗拉阶段、精拉阶段和结束阶段.实线表示试验结果, 虚线表示仿真结果.
|
图 6 针对圆弧内孔键槽拉削负载计算模型的仿真与试验结果对比 Fig. 6 Comparisons of calculating model simulation and test results addressed to broaching load of inner hole rectangular groove |
图 6(a)虚线表示综合考虑圆弧效应、刮削效应以及周期特性后的仿真结果, 最大仿真拉削负载为28 266 N, 而试验最大拉削负载为29 721 N, 仿真曲线呈现先增大后减小的趋势, 且为波峰波谷交替变化, 因此与试验数据相比, 仿真结果具有较好的吻合度.在粗拉阶段结束时, 仿真值与试验结果之间达到最大误差ea为18%, 其余阶段均小于13%.产生误差的主要原因有以下2点:首先机床本身的非线性振动导致拉刀拉削方向与拉削驱动力方向存在偏差, 引起拉削负载变化;其次在粗拉阶段, 拉削厚度和宽度都很大, 导致切屑增多, 大量切屑堆积影响了拉削负载的计算精度.图 6(b)虚线表示未考虑圆弧效应的仿真结果, 最大仿真拉削负载为29 019 N, 可见在拉削起始阶段, 仿真结果与试验结果的最大误差ea>30%.图 6(c)虚线表示未考虑刮削效应的仿真结果, 最大仿真拉削负载为27 628 N, 可见在拉削初始阶段和结束阶段, 仿真结果与试验结果的最大误差ea>30%.图 6(d)虚线表示未考虑刀齿数与工件接触周期特性的仿真结果, 其结果未呈现波峰波谷状变化, 但整体变化趋势与试验结果相对一致.
3.1 工件孔圆弧效应对拉削负载的影响对比图 6(a)和图 6(b)的拉削负载特性时域曲线发现, 在工件拉削过程中由于工件内孔处呈现圆弧状, 每个刀齿的拉削面积在加工过程中都存在变化, 如表 4所示.因此, 本文通过精确计算每个刀齿切过工件的面积, 综合考虑圆弧效应的影响, 准确地计算了拉削负载, 其仿真结果平均误差小于13%, 如图 6(a)所示.如图 6(b)表示的仿真值是在未考虑圆弧效应情况下的计算结果, 其仿真结果普遍大于试验结果, 未能准确地反映实际拉削负载, 特别是在拉削初始阶段和粗拉阶段, 其仿真结果最大误差ea超过30%.对比仿真与试验结果可知, 圆弧效应在拉削加工中对计算拉削负载影响较大.因此建立内孔拉削负载计算模型应考虑圆弧效应的影响.
3.2 刀齿刮削效应对拉削负载的影响对比图 6(a)和图 6(c)拉削负载特性时域曲线发现, 在考虑刮削效应的情况下, 仿真结果与实际结果平均误差小于13%, 如图 6(a)所示;而在未考虑刮削效应时, 其仿真结果在拉削过程中小于试验拉削负载, 仿真最大误差ea超过30%, 如图 6(c)所示.以上对比结果证明刀齿在拉削过程中, 后刀面与已加工工件表面相互接触, 存在刮削现象; 同时, 每个齿的齿升量存在差异, 导致切削与刮削占比存在不同.在拉削负载计算中, 综合考虑切削与刮削并存的现象来进行负载建模, 可提高拉削负载的计算精度.
3.3 刀齿接触周期对拉削负载的影响对比图 6(a)和图 6(d)拉削负载特性时域曲线发现, 图 6(d)中虚线是没有考虑周期特性情况下的仿真结果, 其仿真值没有呈阶梯状上升或下降, 仅反映了拉削负载的整体变化趋势, 不能很好拟合实际拉削负载波峰波谷的周期变化特征, 其最大误差ea超过30%.在本文的拉削试验过程中, 参与拉削工件的刀齿齿数为5个或6个, 呈现出齿数的周期变化特性.当考虑拉削负载周期特性时, 其仿真计算结果精度得到大大提高, 如图 6(a)所示.
仿真中的周期特性并没有与实际拉削负载的周期完全拟合, 这主要是受到卧式拉床传动部件运动复杂性和刀齿齿距的加工精度的影响.此外, 拉削阻尼呈非线性变化, 拉削速度在整个过程中并非为一个恒定参数, 造成在部分周期内拉削负载的仿真结果与试验结果误差较大.其次, 工况的复杂性也会产生一定干扰信号从而影响最终采集的试验数据.但是从图 6(a)中看出, 通过本文建立的拉削负载周期特性计算模型, 可以有效地提高拉削负载的计算精度, 证明拉削周期特性是影响计算模型的主要因素.
4 结论(1) 仿真与试验对比结果表明, 工件圆弧效应、刀齿的刮削效应和刀齿的切/刮削占比等因素对圆弧内孔矩形键槽的拉削负载的影响较大, 建立仿真模型时, 应综合考虑这些因素的影响.
(2) 当工件长度lw小于1个齿距d时, 接触工件的齿数在整数0和1之间周期性交替变化, 即单齿拉削.当工件长度lw大于1个齿距d时, 接触工件的齿数在nm与nm-1间周期性变化, 即多齿拉削.基于仿真与试验对比结果分析可知, 刀齿数的周期特性是影响拉削负载计算模型精度的主要因素.
(3) 本文根据试验工况中拉刀刀齿数的周期特性, 将拉削过程划分为工件与刀齿接触初期阶段、工件与刀齿完全接触阶段以及工件与刀齿脱离阶段, 针对不同拉削阶段分别建立多齿拉削负载模型.仿真与试验结果表明, 本文建立的拉削负载动特性计算模型具有较好的计算精度和稳定性, 其平均计算误差ea小于13%, 可为实际拉削加工中工艺参数优化和拉床吨位选型提供良好的理论支撑与技术指导.
| [1] | SCHROETER R B, BASTOS C M, CRICHIGNO FILHO J M. Simulation of the main cutting force in Crankshaft turn broaching[J]. International Journal of Machine Tools and Manufacture, 2007, 47(12): 1884–1892. |
| [2] | CHOLPADI R K, KUTTAN A. Mechanistic force modeling for broaching process[J]. International Journal of Manufacturing Engineering, 2014, 2014: 1–10. |
| [3] | KLOCKE F, GIERLINGS S, BROCKMANN M, et al. Force-based temperature modeling for surface integrity prediction in broaching nickel-based alloys[J]. Procedia CIRP, 2014, 13: 314–319. DOI:10.1016/j.procir.2014.04.053 |
| [4] | HOSSAM A K, ALI H, BEHNAM M I, et al. An energy based analysis of broaching operation: cutting forces and resultant surface integrity[J]. CIRP Annals-Manufacturing Technology, 2012, 61(1): 107–110. DOI:10.1016/j.cirp.2012.03.004 |
| [5] |
董辉跃, 朱灵盛, 章明, 等. 飞机蒙皮切边的螺旋铣削方法[J].
浙江大学学报:工学版, 2015, 49(11): 2033–2039.
DONG Hui-yue, ZHU Ling-sheng, ZHANG Ming, et al. Orbital milling method of aircraft skins trimming[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(11): 2033–2039. |
| [6] |
李刚, 王扬渝, 王慧强, 等. 基于斜角切削模型的机夹式球头铣刀切削力预测研究[J].
制造技术与机床, 2014, 6: 86–89.
LI Gang, WANG Yang-yu, WANG Hui-qiang, et al. Cutting force prediction of ball end mill based on oblique cutting model[J]. Manufacturing Technology and Machine Tools, 2014, 6: 86–89. DOI:10.3969/j.issn.1005-2402.2014.01.025 |
| [7] |
仇健, 李晓飞, 马晓波, 等. 硬质合金立铣刀高速铣削铝合金切削力实验研究[J].
中国机械工程, 2012, 23(13): 1555–1560.
Qiu Jian, LI Xiao-fei, MA Xiao-bo, et al. Experimental study of cutting forces on high speed milling aluminum alloy using carbide end mill[J]. China Mechanical Engineering, 2012, 23(13): 1555–1560. DOI:10.3969/j.issn.1004-132X.2012.13.010 |
| [8] | HOSSEINIH A, KISHAWY H A. Prediction of cutting forces in broaching operation[J]. Journal of Advanced Manufacturing Systems, 2013, 12(1): 1–14. DOI:10.1142/S0219686713500017 |
| [9] |
吴继华, 刘战强. 正交微切削中切削力预测模型研究[J].
武汉理工大学学报:交通科学与工程版, 2010, 34(1): 130–133.
WU Ji-hua, LIU Zhan-qiang. Predaction of forces in orthogonal micro-cutting based on strain gradient theory[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2010, 34(1): 130–133. |
| [10] |
魏兆成, 王敏杰, 蔡玉俊, 等. 球头铣刀三维曲面加工的铣削力预报[J].
机械工程学报, 2013, 49(1): 178–184.
WEI Zhao-cheng, WANG Min-jie, CAI Yu-jun, et al. Milling force prediction for ball-end milling of 3D curved surfaces[J]. Journal of Mechanical Engineering, 2013, 49(1): 178–184. |
| [11] | VOGTEL P, KLOCKE F, PULS H, et al. Modelling of process forces in broaching Inconel 718[J]. Procedia CIRP, 2013, 8: 409–414. DOI:10.1016/j.procir.2013.06.125 |
| [12] | SCHULZE V, BOVE N, ZANGER F. Simulation of metal cutting process with variable cutting thickness during broaching[J]. Procedia CIRP, 2012, 1: 437–442. DOI:10.1016/j.procir.2012.04.078 |
| [13] | SCHULZE V, BOVE N, ZANGER F. Numerical investigation of the changing cutting force caused by the effects of process machine interaction while broaching[J]. Procedia CIRP, 2012, 4: 140–145. DOI:10.1016/j.procir.2012.10.025 |
| [14] |
凌玲, 李星星, 王学林, 等. OCr18Ni9不锈钢本构模型及其对切削力预测影响分析[J].
中国机械工程, 2012, 23(18): 2243–2248.
LING Ling, LI Xing-xing, WANG Xue-lin, et al. Constitutive model of stainless steel OCr18Ni9 and its influence on cutting force prediction[J]. China Mechanical Engineering, 2012, 23(18): 2243–2248. DOI:10.3969/j.issn.1004-132X.2012.18.021 |
| [15] |
李炳林, 胡于进, 王学林, 等. 基于斜角切削理论的立铣切削力预测研究[J].
中国机械工程, 2011, 22(19): 2283–2288.
LI Bing-lin, HU Yu-jin, WANG Xue-lin, et al. Cutting force prediction based on oblique cutting theory in end milling[J]. China Mechanical Engineering, 2011, 22(19): 2283–2288. |
| [16] | GRZESEK W. Advanced machining processes of metallic materials[M]. London: Elsvier, 2008: 83. |
| [17] | SHAW M C. Metal cutting principles[M]. New York: Oxford University Press, 1984: 55. |
| [18] |
陈刚, 陈忠富, 陶俊林, 等. 45钢动态塑性本构参量与验证[J].
爆炸与冲击, 2005, 25(5): 451–456.
CHEN Gang, CHEN Zhong-fu, TAO Jun-lin, et al. Constitutive parameters and verification of 45 steeldynamic plasticity[J]. Explosion and Shock Waves, 2005, 25(5): 451–456. DOI:10.11883/1001-1455(2005)05-0451-06 |



