2. 浙江纺织服装职业技术学院, 浙江 宁波 315211
2. Zhejiang Fashion Institute of Technology, Ningbo 315211, China
电火花成型加工(die-sinking electrical discharge machining, DEDM)广泛应用在精密模具、航空航天、医疗器械、传感器等各种精密加工领域.由于放电加工中存在工具电极的损耗, 影响了其加工精度, 不少学者就如何补偿电极损耗提高加工精度问题展开了卓有成效的研究[1-4].
当前的电极损耗补偿研究, 主要有在线监测和模型预测2个方向.在线监测主要是通过监测加工状态判断电极损耗状态, 进而实施补偿, Bissacco等[5-9]从有效放电脉冲、放电间隙(开路电压)和电极形状监测补偿等方面进行了研究, 揭示了放电能量的大小是决定电极损耗量的最重要因素, 而与放电脉冲形状的关系不大的规律.这些方法受加工环境和放电参数不同取值的影响很大, 并且很多阈值的设置主要依赖经验, 缺乏理论依据.
模型预测是通过仿真的手段模拟工艺过程, 从而对电极损耗状况进行预测, 进而为补偿提供依据.何磊等[10-13]从均匀损耗法、定长补偿法和均匀损耗微量补偿法等方面进行了研究:根据已有的实验数据, 结合电极损耗原理和加工条件, 预测电极损耗状, 建立补偿模型.与在线监测相比, 由于其补偿在加工前已经完成, 因此电极加工过程连续, 加工效率高.这些研究主要对象为简单棒状的电极, 以电极与工件的体积损耗比率(以下简称相对体积损耗比)小于1%的低损耗量工况为主, 并且集中在微细电火花铣削加工领域, 对于成型电极的损耗问题涉及较少, 而在成型加工中相对体积损耗比1%以上的大损耗量工况是较位常见的, 需要深入研究.
王刚等[14-15]提出了通过电极形状的曲面偏置来补偿电极摇动误差的方法, 利用计算机辅助几何设计直接对电极曲面形状进行修正以消除误差提高加工精度.这种方法适用性强, 通过实验验证, 具有良好的理论和实践指导价值, 为本文的研究提供了思路.但也存在一些需要改进地方:损耗量是通过曲率一次性补偿到电极上的, 忽略了多次放电过程中电极曲率的变化, 在局部曲率较大的地方容易产生过量补偿, 从而降低补偿精度;补偿方向是曲面法向在水平面的投影, 这与实际的加工中的主轴伺服不一致性, 容易出现变形, 影响成型精度.
在电火花放电成型加工中, 零件的成型包含粗加工、半精加工和精加工, 过程中由于采用不同的损耗规准, 需要更换3~4次电极, 带入了装夹误差, 制约了加工效率和成型精度.
针对以上不足, 本文立足电火花成型加工中的精密补偿, 针对损耗率大于1%的大损耗量工况, 通过电极损耗的预变形方法研究, 实现1个电极完成整个精密加工过程, 从而提高成型加工精度和效率.
1 电极损耗预变形补偿原理由于电火花成型加工的特点, 电极的损耗是客观存在的, 如果能够预先对损耗量进行补偿, 则能有效提高成型精度.以加工1个椭圆形工件为例, 分析预变形补偿原理, 如图 1所示.目标工件的形状是椭圆, 如果电极不补偿直接以椭圆形进行加工, 则在损耗后变成了三角形, 显然工件不能获得所需的形状;而原始电极按照一定的规则进行预先补偿变形, 在一定的损耗规则后, 则可能变成了椭圆形, 从而获得目标形状.因此, 通过对电极形状的预先补偿变形, 获得给定精度的工件形状, 即电极预变形的基本思想.要获得预补偿变形的电极形状, 就需要建立模型, 把损耗量补在初始电极上, 实现精密成型.

|
图 1 电极损耗预变形补偿原理 Fig. 1 Compensation theory on pre-deformation ofelectrode wear |
电极损耗与材料、脉宽、加工极性等相关, 影响因素众多, 其与工件的蚀除量成一定比例关系, 而加工过程中加工效率是已知设定量, 因此通过相对体积损耗比[16-18], 可以精确获取电极在一定加工效率下的损耗情况, 其表达式为
| $ f = \frac{{{v_{\rm{d}}}}}{{{v_{\rm{w}}}}} \times 100\% . $ | (1) |
式中:f为相对体积损耗比, vd为电极单位时间内损耗的体积, vw为工件单位时间内损耗的体积.
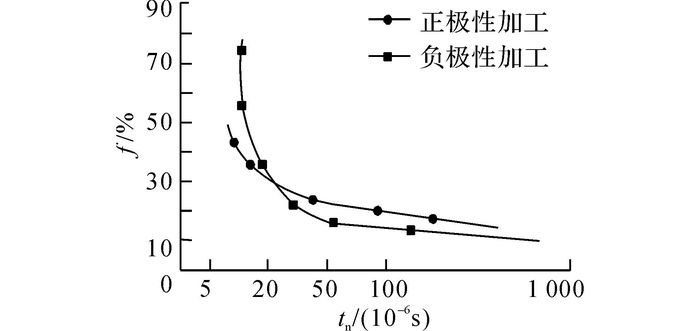
如图 2所示为以铜为工具电极材料, 以钢为工件, 波形为矩形, 在峰值电流If=10 A时的不同加工极性不同脉宽的相对体积损耗比关系表, 图中, tn为放电脉宽.
|
图 2 电极和工件的相对损耗率关系图 Fig. 2 Relative wear ratio between electrode and parts |
因此, 通过确定加工极性、加工效率、材料, 结合相对损耗率, 即可根据式(1) 计算出电极损耗量, 而相对损耗率在一定的工艺条件下是确定的, 其数值通过实验获得.
3 电极预变形补偿 3.1 电极损耗量放电能量的大小是决定电极损耗量的最重要因素, 结合工件的加工效率有
| $ Q = f{V_{\rm{w}}} = ft{v_{\rm{w}}}. $ | (2) |
式中:Q为电极总损量, Vw为工件蚀除体积, t为加工时间.
单次放电过程中电极的损耗量为
| $ q = \frac{{Q\left( {{t_{\rm{d}}} + {t_{\rm{p}}}} \right)}}{t} = {v_{\rm{w}}}\left( {{t_{\rm{d}}} + {t_{\rm{p}}}} \right). $ | (3) |
式中:td为放电时间, td=tn+tf, tf为脉宽,tn为脉冲间隔; tp为空程时间, 由主轴抬刀速度和行程确定; t/(td+tp)为放电次数.
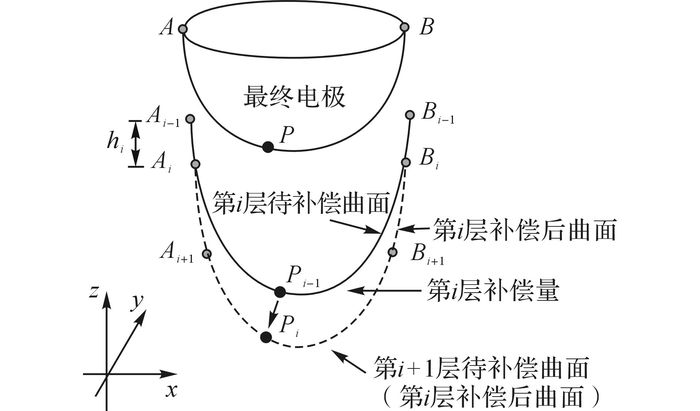
3.2 电极等损耗非均匀分层模型在电火花铣销加工中, 常用等损耗原理进行电极损耗补偿, 即认为电极的损耗只在电极端部并且均匀相等.本文研究的成型加工由于电极曲面的复杂性, 单次的放电成型是电极产生一个体积等量、形状非均匀的损耗.加工中的电极损耗累积, 就是在电极进给方向上一层层剥离相同体积不同形状壳体的过程.因此, 以相同时间为单位, 则每一层剥离层都是体积相同的损耗层, 以如图 3所示的第i层为例子说明分层补偿原理.
|
图 3 非均匀电极损耗量分层补偿原理图 Fig. 3 Layered compensation for non-uniform electrodewear |
如图 3所示, 以电极二维截面为例, 通过点的坐标偏置, 进行分层推导.假设, 从目标形状出发, 点P是目标曲线上的任意一点, 经过(i-1) 层补偿后形成点Ai-1、点Pi-1和点Bi-1组成的第i层待补偿曲线.设hi为第i层补偿量在电极进给方向Z向上的补偿高度, 则点Ai、点Bi的坐标, 是点Ai-1和点Bi-1在进给方向下移hi后, 与第i层待补偿曲线在x-y平面的交点.
要获得电极的预变形补偿形状, 即把第i层待补偿曲线偏置成第i层待补偿后曲线, 就是计算点Pi-1到点Pi的过程, 其首先要计算由第i层待补偿曲线和点Ai、点Pi和点Bi组成的第i层待补偿后曲线形成的该层补偿量, 然后通过计算hi, 即z向的分层厚度获得点Ai、点Bi, 再结合相应的偏置模型获取点Pi坐标.
同理, 进行第i+1层补偿.则有
| $ {Q_i} = \iint\limits_{{D_i}} {\left( {{f_i}\left( {x,y,z} \right) - {f_{i - 1}}\left( {x,y,z} \right)} \right){\text{d}}s}. $ | (4) |
式中:Qi为第i层补偿量, Di为第i层补偿曲面的投影, fi(x, y, z)为第i层补偿后曲面方程, fi-1(x, y, z)为第i层待补偿曲面方程, s为补偿曲面在x-y平面的投影面积.
结合式(3), 有
| $ k{v_{\text{w}}}\left( {{t_{\text{d}}} + {t_{\text{p}}}} \right) = \iint\limits_{{D_i}} {\left( {{f_i}\left( {x,y,z} \right) - {f_{i - 1}}\left( {x,y,z} \right)} \right){\text{d}}s}. $ | (5) |
式中:k为分层系数, 即单层损耗量中包含的放电次数.
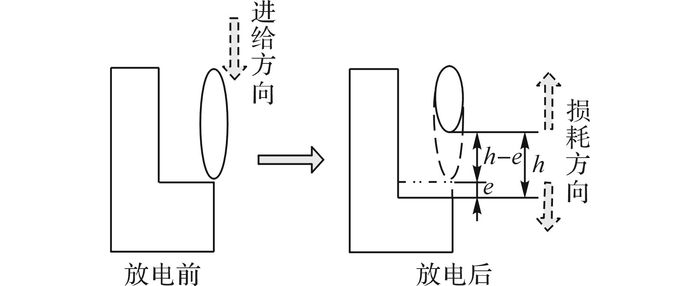
理想变形补偿就是每放1次电进行1次补偿, 其进给方向的补偿高度hi即为每次电极在进给方向上的损耗值.但是在电火花成型加工过程中, 单次脉冲放电时间是以μm计的, 1个成型加工有几百万次放电, 显然以单次放电为单位进行补偿偏置, 计算量过大, 因此本文参考电火花等损耗的原理, 提出了基于放电间隙的分层方法, 如图 4所示.
|
图 4 电极损耗间隙分层补偿原理图 Fig. 4 Discharge gap theory for layered compensation |
该方法以放电间隙为分层厚度, 即认为放电过程都是工具电极从1个无限接近工件的位置开始, 经过电极与工件的不断损耗到达间隙位置, 放电自然结束, 然后通过主轴伺服进给1个放电间隙量后, 再次达到工件和电极无限接近的位置, 进入下一个放电损耗循环.
如图 4所示, 电极与工件从无限接近的位置开始放电, 在工件损耗了e高度、电极损耗了h-e高度后, 自动结束1层的放电损耗.其中, h为放电间隙, 也是主轴单次放电循环的总进给量.
在成型放电过程中, 存在几万甚至几十、上百万次放电, 每次损耗体积都很小, 因此可以忽略形状的影响, 利用高度比来表示相对体积比.令
| $ {h_i} = h - e = ef, $ |
则有
| $ C = \frac{H}{e} = \frac{{\left( {1 + f} \right)H}}{h}. $ | (6) |
式中:c为层数, H为工件在z向的总成型深度, 即主轴的成型进给量.
可知, 单层的损耗量为
| $ {Q_i} = \frac{Q}{c} = \frac{{hf{V_{\rm{w}}}}}{{\left( {1 + f} \right)H}}. $ | (7) |
电极形状非常复杂, 特别是经过若干次损耗后形状发生不规则变化, 要进行式(5) 的计算非常困难.本文通过非均匀有理B样条曲线(non-uniform rational B-splines, NURBS)的拟合, 即把曲面fi(x, y, z)用fi(u, v)来拟合, 在u和v这2个方向进行参数化, 误差控制在小于0.1 μm.图 5(a)是第i层拟合前曲面, 图 5(b)是NURBS拟合后, 在u和v方向的离散曲面Pj, k(u, v)为u向上第j条样条曲线和v向上第k条样条曲线相交的控制点.

|
图 5 电极待补偿曲面离散前后图 Fig. 5 NURBS discretion of the surface to be compensated |
补偿前后离散曲面的表达式为
| $ {f_i}\left( {u,v} \right) = {f_{i - 1}}\left( {u,v} \right) + {\mathit{\boldsymbol{q}}_i}\left( {u,v} \right). $ | (8) |
qi(u, v)为第i层补偿量的矢量偏置矩阵:
| $ {\mathit{\boldsymbol{q}}_i} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_{1,1}}\left( {u,v} \right)}& \vdots &{{\mathit{\boldsymbol{q}}_{1,m}}\left( {u,v} \right)}\\ \vdots &{{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)}& \vdots \\ {{\mathit{\boldsymbol{q}}_{n,1}}\left( {u,v} \right)}& \vdots &{{\mathit{\boldsymbol{q}}_{n,m}}\left( {u,v} \right)} \end{array}} \right]. $ | (9) |
式中:qj, k(u, v)为控制点Pj, k(u, v)的偏置矢量.
因此, 电极补偿就是要计算矢量偏置矩阵, 即计算偏置量的大小和方向.
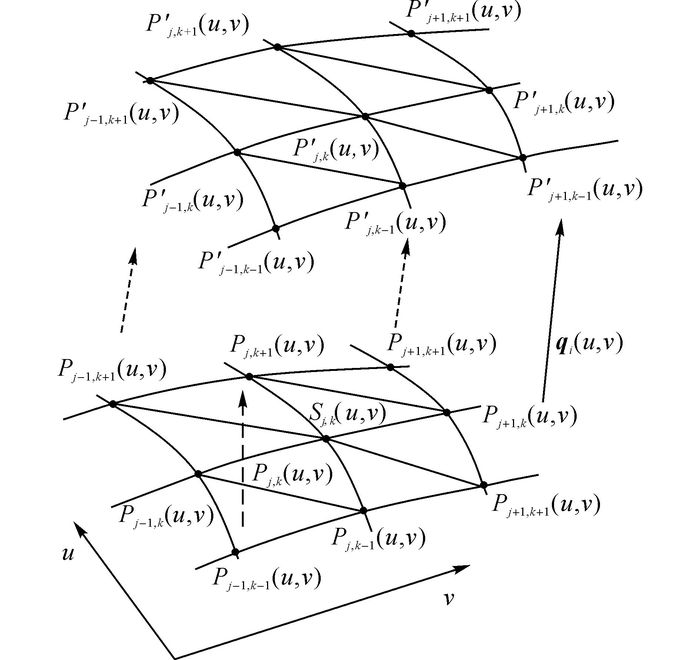
3.2 电极预补偿量矢量模型电火花加工的特点表明, 曲率越大, 放电越集中, 电极的损耗量也就越大, 各控制点偏置量通过曲率的大小进行插值计算.如图 6所示为偏置示意图, Pj, k′(u, v)为点Pj, k(u, v)补偿偏置后的对应点.
|
图 6 电极曲面各点偏置示意图 Fig. 6 Offset sketch of discrete point on electrode curve |
令控制点Pj, k(u, v)在u方向的曲率为Kj(P), 在v方向的曲率为Kk(P), 则点Pj, k(u, v)的平均曲率为
| $ {K_{j,k}}\left( P \right) = \frac{1}{2}\left( {{K_j}\left( P \right) + {K_k}\left( P \right)} \right). $ | (10) |
则有
| $ {a_{j,k}}\left( {u,v} \right) = \frac{{{k_{j,k}}\left( {u,v} \right)}}{{\sum\limits_{k = 1}^n {\sum\limits_{j = 1}^m {{K_{j,k}}\left( {u,v} \right)} } }}. $ | (11) |
式中: αj, k(u, v)为点Pj, k(u, v)的曲率系数, 分母为离散曲面上所有控制点的曲率之和.
控制点的绝对偏置量为
| $ \left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right| = \lambda {a_{j,k}}\left( {u,v} \right). $ | (12) |
式中: λ为偏置量系数.
各点偏置后形成的体积为单层损耗量, 有
| $ \sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = 1}^{m - 1} {\left( {{s_{j,k}}\left( {u,v} \right)\left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right|} \right)} } = {Q_i}. $ | (13) |
式中: sj, k(u, v)为点Pj, k(u, v)右上角的曲面面积, 为点Pj, k(u, v)、Pj+1, k(u, v)、Pj, k+1(u, v)和Pj+1, k+1(u, v)组成的区域.
联立式(12) 和(13), 可得
| $ \left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right| = \frac{{{a_{j,k}}\left( {u,v} \right){Q_i}}}{{\sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = 1}^{m - 1} {\left( {{s_{j,k}}\left( {u,v} \right){a_{j,k}}\left( {u,v} \right)} \right)} } }}. $ | (14) |
结合式(7) 中的Qi求解, 可得离散点的偏置绝对量|qj, k(u, v)|.
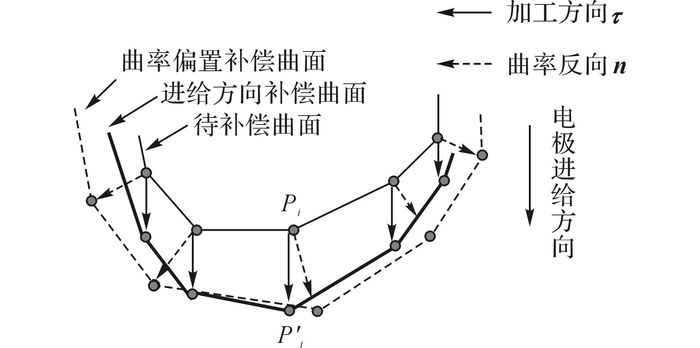
一般的偏置方向多以曲率反向为偏置方向, 这种方法的好处是能获得较为光顺的曲面, 但其补偿精度较差, 如果有凹凸曲面时会发生偏置干涉, 为此本文提出以电极进给方向为偏置方向, 并设计曲面光顺, 如图 7所示为2种不同偏置方法的示意图, 虚线是按曲率的反向进行偏置, 粗实线是按电极进给方向进行偏置, 细实线是待补偿面.
|
图 7 不同偏置方向的电极补偿曲面 Fig. 7 Electrode compensation curve in different offset directions |
如图 7所示, 2种偏置方法在电极底部基本一致, 但是离底部较远的地方出了差异, 特别是曲率变化大的地方.在电火花加工中, 最先放电点一般为电极和工件的最近点, 但是当按曲率进行偏置时, 在离底部较远的地方也进行了较大的补偿, 即认为这些地方也出现了较多的放电, 这与实际加工存在不一致.则有
| $ {\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right) = \left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right|\mathit{\boldsymbol{\tau }} $ | (15) |
因此, 第i层的偏置计算公式为
| $ \left. \begin{array}{l} \left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right| = \frac{{{a_{j,k}}\left( {u,v} \right)\left( {h - e} \right)f{V_{\rm{w}}}}}{{H\sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = 1}^{m - 1} {\left( {{s_{j,k}}\left( {u,v} \right){a_{j,k}}\left( {u,v} \right)} \right)} } }},\\ {{P'}_{j,k}}\left( {u,v} \right) = {P_{j,k}}\left( {u,v} \right) + \left| {{\mathit{\boldsymbol{q}}_{j,k}}\left( {u,v} \right)} \right|\mathit{\boldsymbol{\tau }}. \end{array} \right\} $ | (16) |
以此类推, 通过逐层的矢量化偏置补偿, 最终获取电极的预补偿初始形状.
3.3 偏置曲面光顺处理偏置的曲面由于进行了矢量化偏置变形会出现一些凹凸点, 要进行光顺处理[19-20].由于采用分层补偿, 每补偿一层就要进行光顺;由于补偿过程是电极的局部偏置, 设计计算速度快的选点法[21]3次B样条光顺.光顺处理设计的流程如下:确立光顺准则, 寻找待调整点, 计算调整量, 样条曲线曲面重构, 继续调整直到达到设定要求.
根据能量法, 把应变能最小作为准则, 利用遗传算法求解各点光顺偏置量.离散曲面的应变能为
| $ {E_i} = \sum\limits_{j = 1}^n {{e_j}\left( u \right)} + \sum\limits_{k = 1}^m {{e_k}\left( v \right)} . $ | (17) |
式中:Ei为第i层曲面的总应变能, ej(u)为曲面u方向上第j条样条线应变能, ek(v)为曲面v方向上第k条样条线应变能.
ej(u)和ek(v)的计算公式可参考文献[17]:
| $ \begin{array}{l} {e_j}\left( u \right) = \sum\limits_{i = 1}^{101} {K_j^2\left( {0.01 \times i} \right),{e_k}\left( v \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{101} {K_k^2\left( {0.01 \times i} \right)} . \end{array} $ | (18) |
式中:Kj、Ki分别为第j、i条样条的曲率.
如图 6所示, 偏置后点Pj, k′(u, v)的平均曲率用Kj, k(P′)表示, 计算该点与相连4点的曲率差:
| $ \begin{array}{l} \Delta {K_{j,k}}\left( {P'} \right) = \left| {{K_{j,k}}\left( {P'} \right) - {K_{j - 1,k}}\left( {P'} \right)} \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{K_{j,k}}\left( {P'} \right) - {K_{j + 1,k}}\left( {P'} \right)} \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{K_{j,k}}\left( {P'} \right) - {K_{j,k - 1}}\left( {P'} \right)} \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{K_{j,k}}\left( {P'} \right) - {K_{j,k + 1}}\left( {P'} \right)} \right|. \end{array} $ | (19) |
计算所有点的曲率差, 如果ΔKj, k(P′)最大, 则以点Pj, k′(u, v)为特征点, 点Pj-1, k′、Pj+1, k′、Pj, k+1′、Pj, k-1′和Pj, k′为待调整点, 相应的调整量为Δj-1、Δj+1、Δk+1、Δk-1和Δj, 利用遗传算法求得新的点Pj-1, k、Pj+1, k、Pj, k+1、Pj, k-1和Pj, k.
遗传算法计算过程如下:
1) 设置约束范围, |Δj|<ε.约束范围ε参考精加工度要求, 以0.01为限.
2) 以Δj-1、Δj+1、Δj+1、Δj-1和Δj为基因, 交叉概率为0.8, 变异概率为0.02, 选定20个种群进化300代.
3) 设置适应度函数Ei, 以min (Ei)为准则, 经过遗传变异后得到Δj-1′、Δj+1′、Δj+1′、Δj-1′和Δj′, 得出新的调整点, 插值后生成新的3次B样条.
4) 完成所有曲线光顺后进行曲面重构, 从而完成一个补偿层曲面的光顺
3.4 电极预变形补偿流程建模根据以上推导的方程, 建立如图 8所示的补偿流程模型.

|
图 8 电极损耗的预变形补偿流程模型 Fig. 8 Process model of pre-deformation compensation for electrode wear |
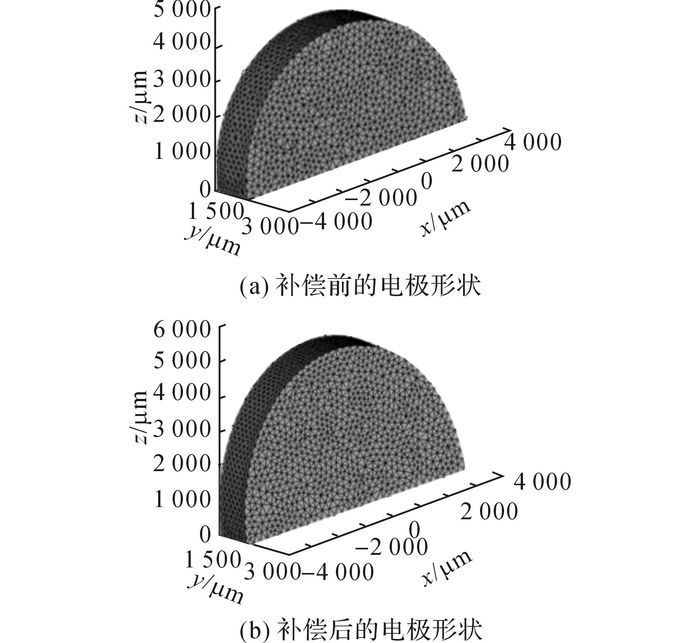
按照图 8所示的流程,利用Matlab软件进行算例分析.算例以一个实际加工的半径为4 cm的半圆形扁平状电极为对象,以相对体积损耗比为11%、z方向进给4 mm为工艺条件进行预变形补偿计算.图 9(a)是未经过补偿的电极形状,图 9(b)是经过补偿后的电极形状.从2个图形对比中可知,经过补偿的电极形状发生了明显的变化,电极的顶部凸起,半圆形变成了半椭圆形.
|
图 9 电极补偿前、后的仿真形状图 Fig. 9 Simulation shape of electrode before and aftercompensation |
结合图 9的算例数据, 进行实验验证.采用博虹电火花机D7130, 用厚度为1.5 mm的铜片电极, 以半径为4 mm的半圆形为目标形状, 以矩形脉冲加工45#钢.加工参数:脉宽为100 μs, 脉间为80 μs, 放电时间为80 ms, 峰值电流为10 A, 加工效率为20 mm3 /min, 抬刀高度为20 mm, 放电间隙为0.08 mm.实验结果通过Dukin Sigma 665型3座标机进行测量, 分辨率为0.1 μm.
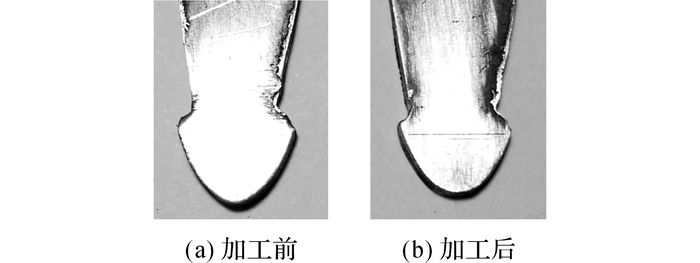
如图 10所示为预变形补偿后的电极加工前后的形状, 如图 11所示为电极几何形状轮廓图.从图中的3条轮廓线可见,补偿后的电极形状在加工后由于损耗的作用出现了变形,但是变形后的形状与目标形状基本一致,表明该补偿方法有效,达到了预期目标.
|
图 10 补偿后电极在放电电火花成型加工(DEMD)前、后的形状对比图 Fig. 10 Shape contrast of compensated electrode before and after DEMD processing |

|
图 11 半圆形电极轮廓图 Fig. 11 Semi-circle shape of electrode |
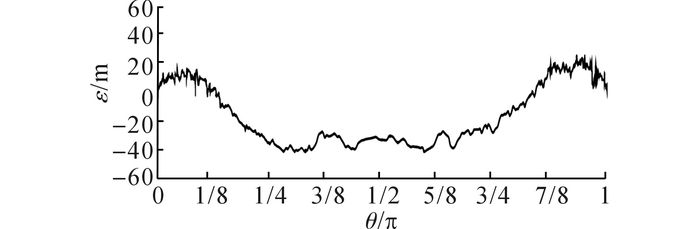
为了精确分析补偿后电极的加工效果, 如图 12所示为预变形补偿电极的实际加工后的形状在半径方向上的误差, 图中ε为误差, θ为沿半径方向的角度.可知, 误差落在[-40 μm, 25 μm], 最大误差低于半径长度的1.000 %;平均几何误差为25 μm, 为加工长度的0.625%, 达到精加工的标准, 误差主要出现在[π/4, 3π/4].
|
图 12 加工后的补偿电极沿半径方向的误差 Fig. 12 Error in radical direction of compensation electrode after processing |
为了进一步验证方法, 在相同损耗率和工艺条件下, 进行其他形状的扁平状电极的加工实验.如图 13所示为短半轴为4 mm, 长半轴分别为9 mm和7 mm的椭圆形补偿加工的电极及其误差比较图.

|
图 13 椭圆形电极放电成型加工后的形状及误差 Fig. 13 Shape and error of elliptical electrodes after DEDM |
从图 13可知, 误差基本落在[-30 μm, 40 μm].最大误差为40 μm, 低于长半轴为7 mm椭圆加工长度的0.571%, 低于长半轴为9 mm椭圆加工长度的0.444%;平均几何误差<30 μm, 误差主要出现在x方向的[-2.5 mm, 2.5 mm].
从图 12和13可以看出, 平均几何误差的变化基本一致.误差主要出现中间位置, 这与实际加工时损耗主要出现的工作区域相吻合.平均几何误差比较均匀, 在靠近电极两侧和底端的部位, 误差变化较为剧烈, 底部主要是排渣困难导致放电不均, 而两侧主要是因为存在工件的拐角尖点, 容易引起各种不稳定的放电导致放电点不确定, 从而引起误差的剧烈变化.
如图 14所示为不同补偿方向的电极, 进行放电加工后所形成的不同工件形状.电极采用短半轴为4 mm, 长半轴为9 mm的椭圆形.图 14(a)是按曲率方向进行分层补偿后的电极进行放电加工后所形成的工件形状, 图 14(b)按进给方向进行分层补偿的电极, 进行放电加工后所形成的工件形状.如图 15所示为这2种工件形状的轮廓对比图.

|
图 14 不同补偿方向的电极经DEDM加工后的工件图 Fig. 14 Parts shape after DEDM with electrodes indifferent compensation directions |
从图 14和图 15可知, 采用电极进给方向进行补偿, 成型零件轮廓均匀, 符合椭圆形的目标形状;采用曲率方向补偿进行加工的工件, 底部的形状和按照电极进给方向补偿成型形状基本一致, 但是形状不均匀, 在开口处出现过量蚀除, 影响了形状的精度.其主要原因是当按曲率方向进行电极补偿时, 由于电极初始端曲率较大, 形成了过多的补偿, 使得电极的端部肥大, 工件的初始加工位置形状变大, 其结果也验证了图 7分析的结果.

|
图 15 不同补偿方向的电极加工后的工件轮廓对比图 Fig. 15 Comparison of parts' outline of processed electrode with different compesation directions |
总之, 本文在加工长度<9 mm、相对体积损耗比为11%的条件下, 成型零件的几何偏差控制在[-40 μm, 40μm], 平均几何误差低于30 μm, 与文献[17]中[-0.1 mm, 0.1 mm]的偏差范围、0.04 mm的平均几何误差相比, 精度提高了25%, 偏差幅度减少了60%, 形状更均匀.图 12和13是不同形状不同尺寸电极的实验结果, 其误差变化的范围、变化机理高度对应, 补偿后的放电加工达到精密成型的标准.图 14和15表明, 采用电极进给方向补偿, 工件轮廓与目标形状一致性更高.因此, 电极损耗分层预补偿方法的有效性和应用价值得到验证.
5 结论(1) 本文针对相对体积损耗比达11%的大损耗量电火花成型加工, 提出了预变形的电极补偿方法, 为几十微米级误差的精密放电加工实现了一次成型, 也为微米级的超精密放电加工减少了电极更换次数, 提高了加工效率.
(2) 基于放电间隙的分层补偿方法, 解决了大损耗量下电极精密补偿的难题, 提高了成型加工的精度;基于电极进给方向的补偿偏置, 修正了按曲率补偿导致形状变异的不足, 进一步提高了形状精度.
(3) 实验结果表明, 成型零件的几何平均误差低于30 μm, 达到了电火花成型精密加工标准, 补偿方法精确有效, 下一步将就相对损耗率的机理展开重点研究.
| [1] | BISSACCO G, TRISTO G, HANSEN H N, et al. Reliability of electrode wear compensation based on material removal per discharge in micro EDM milling[J]. CIRP Annals-Manufacturing Technology, 2013, 62(1): 179–182. DOI:10.1016/j.cirp.2013.03.033 |
| [2] |
丁海娟, 崔海, 张志航, 等. 微细电火花线切割加工表面干摩擦磨损特性[J].
农业机械学报, 2011, 42(1): 228–232.
DING Hai-juan, CUI Hai, ZHANG Zhi-hang, et al. Tribological properties of the micro-WEDM surfaceunder dry friction and wear conditions[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(1): 228–232. |
| [3] | YAN M T, LIN S S. Process planning and electrode wear compensation for 3D micro-EDM[J]. International Journal of Advanced Manufacturing Technology, 2011, 53(1-4): 209–219. DOI:10.1007/s00170-010-2827-8 |
| [4] | HINDUJA S, KUNIEDA M. Modelling of ECM and EDM processes[J]. College International pour la Recherche en Productique Annals-Manufacturing Technology, 2013, 62(2): 775–797. |
| [5] | BISSACCO G, HANSEN H N, TRISTO G, et al. Feasibility of wear compensation in micro EDM milling based on discharge counting and discharge population characterization[J]. College International pour la Recherche en Productique Annals-Manufacturing Technology, 2011, 60(1): 231–234. |
| [6] | MARADIA U, BOCCADORO M, STIRNIMANN J, et al. Electrode wear protection mechanism in meso-micro-EDM[J]. Journal of Materials Processing Technology, 2015, 223: 22–33. DOI:10.1016/j.jmatprotec.2015.03.039 |
| [7] | TIRLA A, POPA M S, POP G M, et al. An electrode wear compensation model regarding the EDM process[J]. Annals of Daaam and Proceedings, 2010, 21(1): 797–798. |
| [8] | NGUYEN V Q, DUONG T H, KIM H C. Precision micro EDM based on real-time monitoring and electrode wear compensation[J]. International Journal of Advanced Manufacturing Technology, 2015, 79(9-12): 1–10. |
| [9] | ALIGIRI E, YEO S H, TAN P C. A new tool wear compensation method based on real-time estimation of material removal volume in micro-EDM[J]. Journal of Materials Processing Technology, 2010, 210(15): 2292–2303. DOI:10.1016/j.jmatprotec.2010.08.024 |
| [10] |
何磊, 裴景玉, 郑博文, 等. 定长补偿电火花铣削加工中锥形电极的形成及稳定性[J].
航空学报, 2014, 35(4): 1165–1172.
HE Lei, PET Jing-yu, ZHENG Bo-wen, et al. Formation and stability of conical electrode in ED-milling with fix-length compensation method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 1165–1172. |
| [11] | TLILI A, GHANEM F, SALAH N B. A contribution in EDM simulation field[J]. International Journal of Advanced Manufacturing Technology, 2015, 79(5-8): 1–15. |
| [12] |
弯艳玲, 廉中旭, 于占江, 等. 微细电火花分层铣削加工实验研究[J].
长春理工大学学报:自然科学版, 2014(5): 37–40.
WAN Yan-ling, LIAN Zhong-xu, YU Zhan-jiang, et al. Research on layered machining experiment by micro-EDM[J]. Journal of Changchun University of Science and Technology: Natural Science Edition, 2014(5): 37–40. |
| [13] | LI J Z, XIAO L, WANG H, et al. Tool wear compensation in 3D micro EDM based on the scanned area[J]. Precision Engineering-Journal of the International Societies for Precision Engineering and Nanotechnology, 2013, 37(3): 753–757. |
| [14] |
王刚, 单岩, 吴荣仁. 电火花摇动加工中的曲面非均匀偏置补偿技术[J].
浙江大学学报:工学版, 2006, 40(9): 1604–1608.
WANG Gang, SHANG Yan, WU Rong-ren. Compensation of electrode orbiting in electrical discharge machining based on non-uniform offsetting[J]. Journal of Zhejiang University: Engineering Science, 2006, 40(9): 1604–1608. |
| [15] |
单岩, 王刚, 吴纬纬. 基于刀轨广义偏置的电火花摇动加工补偿方法[J].
机械工程学报, 2006, 45(10): 261–265.
SHANG Yan, WANG Gang, WU Wei-wei. Electrode orbiting compensation in edm based on generalized offset of tool path[J]. Journal of Mechanical Engineering, 2006, 45(10): 261–265. |
| [16] |
许加利, 李建功, 裴景玉, 等. 相对体积损耗比对微细电火花加工的影响及其测量方法[J].
上海交通大学学报, 2009(9): 1508–1511.
XU Jia-li, LI Jian-gong, PEI Jing-yu, et al. Effects of relative volume wear ratio on micro-EDM process and its method for measuring[J]. Journal of Shanghai Jiaotong University, 2009(9): 1508–1511. |
| [17] | KHAN A A. Electrode wear and material removal rate during EDM of aluminum and mild steel using copper and brass electrodes[J]. International Journal of Advanced Manufacturing Technology, 2008, 39(5/6): 482–487. |
| [18] | TORRES A, PUERTAS I, LUIS C J. Modelling of surface finish, electrode wear and material removal rate in electrical discharge machining of hard-to-machine alloys[J]. Precision Engineering, 2015, 40: 33–45. DOI:10.1016/j.precisioneng.2014.10.001 |
| [19] |
陈仁杰, 刘利刚, 董光昌. 严格顶点约束的网格光顺算法[J].
浙江大学学报:工学版, 2010, 44(8): 1672–1675.
CHEN Ren-jie, LIU Li-gang, DONG Guang-chang. Mesh faring with vertex constraint[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(8): 1672–1675. |
| [20] | WEI P, LU D, HUANG T, et al. Hexahedral mesh smoothing via local element regularization and global mesh optimization[J]. Computer-Aided Design, 2015, 59(C): 85–97. |
| [21] |
秦贤杰, 黄有度. B样条曲线曲面的一种光顺算法[J].
合肥工业大学学报:自然科学版, 2012(3): 429–432.
QIN Xiao-jie, HUANG You-du. A kind of fairing method for B-spline curves and surfaces[J]. Journal of Hefei University of Technology: Natural Science, 2012(3): 429–432. |



