2. 浙江工业大学 固体力学研究所, 浙江 杭州 310014;
3. 浙江大学 流体动力与机电系统国家重点实验室, 浙江 杭州 310027;
4. 浙江大学 高压过程装备与安全教育部工程研究中心, 浙江 杭州 310027
2. Institute of Solid Mechanics, Zhejiang University of Technology, Hangzhou 310014, China;
3. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China;
4. Engineering Research Center of High Pressure Process Equipment and Safety, MOE, Zhejiang University, Hangzhou 310027, China
在绝大多数化学爆炸事故中, 爆炸本身起源于如坑道、仓库和管道等受限空间内[1], 例如:青岛输油管道爆炸事故[2]和天津港危化品仓库爆炸事故[3].鉴于爆炸会对人民财产安全造成严重损失, 对潜在爆炸后果的预测与评估就显得尤为重要.
在爆炸产生的各种危害中, 爆炸冲击波造成的危害最为严重, 危害范围也最广, 故爆炸后果评估的关键在于预测爆炸产生的冲击波强度[4].据此, 一些学者提出了预测爆炸产生冲击波强度的半经验模型, 如TNT当量模型[5]、TNO多能模型[6]和Baker-Strehlow模型[7], 然而此类模型主要适用于开敞空间的爆炸, 对于受限空间中的爆炸, 因模型不能计及空间结构的变形与断裂对爆炸冲击波强度的削弱影响, 故在空间外可能给出远远高于实际大小的爆炸冲击波强度.此外, 传统的半经验模型也无法解析复杂环境状况下局部区域的流动与扩散现象, 无法适应越来越精确的爆炸后果评估需求.
近年来, 计算流体力学(computational fluid dynamics, CFD)方法被越来越广泛的用于爆炸后果预测与评估中.Mercx等[8]应用AutoRealGas软件对海洋平台爆炸过程进行了模拟, 并对爆炸超压以及可能造成的后果进行了分析.Ma等[9]对FLACS软件中湍流尺度的算法进行了改进并将其应用在网架结构气云爆炸模拟中, 模拟得到的超压与实验结果较为一致.Rigas等[10-11]对氢气储存设施以及加氢站的泄漏和爆炸进行了模拟, 分析评估了爆炸后果并提出了相应的安全建议.然而, 绝大多数研究工作中没有计及爆炸流场与空间结构的相互作用, 即空间结构被视作刚体, 这对于密闭或受限空间中的爆炸往往难以给出足够合理的后果预测结果.Ngo等[12]也指出, 如不计及结构的变形与断裂, 计算得到的结构表面超压往往会偏高.实际上, 爆炸流场与空间结构之间存在强烈的流固耦合作用, 爆炸产生的超压促使结构发生变形、断裂, 变形断裂后的空间结构又会进一步制约爆炸流场的演变, 但由于极端变形、局部拓扑变化、流固耦合算法以及多领域交叉等问题, 公开文献中计及结构变形与断裂的爆炸后果研究工作极少.Wang等[13]针对伴随断裂的多物质流固耦合问题发展了一种计算程序, 该程序成功应用于内部气体爆炸作用下管道断裂的模拟中, 模拟得到的管道外超压与实验结果较一致.
本文提出一种计及计算稳定性的流固耦合算法并建立内部气体爆炸作用下管道动态断裂与爆炸流场发展的流固耦合分析模型, 将模拟的管道断裂形貌及爆轰压力历程与试验结果进行对比验证, 进而分析管道内气体爆炸的后果并与现有方法的计算结果进行对比.
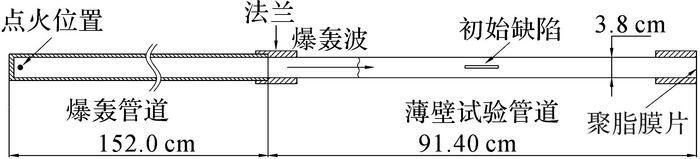
1 数值模型为便于数值模型的验证, 管道爆炸后果分析模型以Chao等[14-16]在2004年和2005年开展的典型试验为基础建立.试验装置示意图如图 1所示, 试验管道与爆轰管道通过法兰连接, 初始时刻两管道内充满按化学计量比例混合的乙烯和氧气.电火花首先将可燃混合气体点燃, 火焰在爆轰管道中加速后转变为爆轰波进入试验管道.试验管道由6061-T6铝合金制成, 其厚度为0.89 mm, 初始表面缺陷位于试验管道中央, 宽度及深度分别为0.30和0.56 mm.在爆轰波作用下, 初始缺陷形成贯穿裂纹并进一步扩展.
|
图 1 气体爆轰加载试验装置示意图 Fig. 1 Schematic diagram of gaseous detonation loading experiment |
对初始气体压力为180 kPa, 初始缺陷长度L为25.4、50.8和76.2 mm三种典型情况下的管道爆炸后果进行研究, 分别对应试验中的Shot 4、Shot 7和Shot 3.本文不考虑火焰到爆轰波的转变过程, 因此建立的数值分析模型由试验管道、内部可燃混合气体和外部空气3部分组成, 如图 2所示.初始表面缺陷作为贯穿缺陷处理, 试验管道由一层拉格朗日网格离散, 内部可燃混合气体和外部空气由欧拉网格离散.在裂纹可能经过的区域, 网格尺寸控制在0.30~0.89 mm, 数值模型共离散约120万个单元.试验管道两端施加固定边界条件, 空气域外侧及管道右侧出口施加无反射边界条件, 管道左侧出口施加壁面边界条件.

|
图 2 管道爆炸流固耦合数值分析模型 Fig. 2 Fluid-structure coupling model for pipe explosion analysis |
材料在冲击或爆炸载荷作用下的应变率往往高达101~106 s-1[17], 其动力学行为由应变硬化、应变率硬化和温度软化3种效应决定, 据此, 采用如下Johnson-Cook型本构方程描述管道的动力学行为:
| $\sigma = ({\sigma _0} + {E_1}\varepsilon )\left( {1 + d{\rm{ln}}\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)\left( {1 - \alpha \frac{T}{{{T_0}}}} \right).$ | (1) |
式中:σ和ε分别为材料的等效应力和等效应变, σ0、
金属材料在高速冲击或爆炸载荷作用下往往会发生热粘塑性失稳, 即以绝热剪切的模式失效.基于此, 通过对形如式(1) 的本构方程进行失稳分析推导得到了适用于高应变率情形下的应变率-应变双变量失效准则[19-20]:
| $\left( {A - \frac{{\alpha \beta {E_1}}}{{{T_0}\rho c}}} \right)\left( {\frac{{{\sigma _0}}}{{{E_1}}} + \varepsilon } \right) + \left( {1 + d{\rm{ln}}\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right) = 1.$ | (2) |
式中:β为塑性功转变为热量的百分比, 取0.9[21].ρ、c分别为材料的密度和比热容, 取ρ=2.78×103 kg/m3, c=896 J/kg/K.A为积分常数, 对应绝热剪切过程中一定的状态, 如绝热剪切带的起始等, 本文根据试验结果取A=0.855.
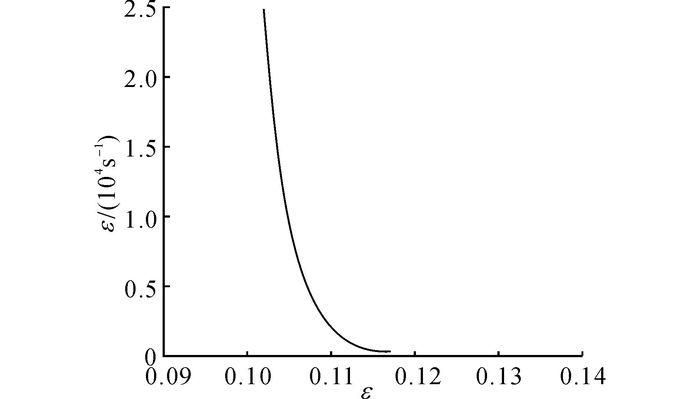
如图 3所示为式(2) 代表的双变量失效准则, 由图可见,临界失效应变随应变率提高而减小.在数值计算中, 当试验管道对应的拉格朗日单元满足临界失效条件时, 则计算程序将其删除, 以此来实现裂纹扩展的模拟.
|
图 3 高应变率下材料双变量失效准则 Fig. 3 Bivariate failure criterion for materials at high-strain-rates |
可燃混合气体的爆轰产物及外部空气均采用理想气体状态方程描述:
| $p = \left( {\gamma - 1} \right){\rho _{\rm{g}}}e.$ | (3) |
式中:p为气体压力, γ为气体的多方指数, ρg、e分别为气体密度和内能.
根据试验条件, 爆轰产物和空气的多方指数分别为1.15和1.40, 初始密度分别为2.28 kg/m3和1.29 kg/m3, 根据理想气体状态方程计算得到空气的初始内能为2.53×102 kJ/m3, 根据CJ爆轰理论计算得可燃混合气体的初始内能为2.04×104 kJ/m3.试验中, 当爆轰波进入试验管道后, 爆轰接近CJ爆轰[15], 相应的爆轰速度DCJ=2.4 km/s, 爆轰压力pCJ=6.1 MPa.
2 流固耦合算法对于拉格朗日网格, 空间网格节点与假想的材料点是一致的, 即网格变形时材料也同时变形, 优点在于能够精确描述结构边界的运动, 一般用于固体结构应力应变的分析.对于欧拉网格, 空间网格与所分析的物质结构是相互独立的, 有限元节点即空间点, 网格在整个分析过程中是始终不变的, 优点在于可处理大变形问题, 多用于流体的分析.
为解决伴随极端变形与断裂的流固耦合问题, 数值模型中管道对应的拉格朗日网格交叠在可燃混合气体和空气对应的欧拉网格之上.在交界面上, 拉格朗日网格作为欧拉网格内流体流动的几何边界, 而欧拉网格则提供给拉格朗日网格压力边界条件.
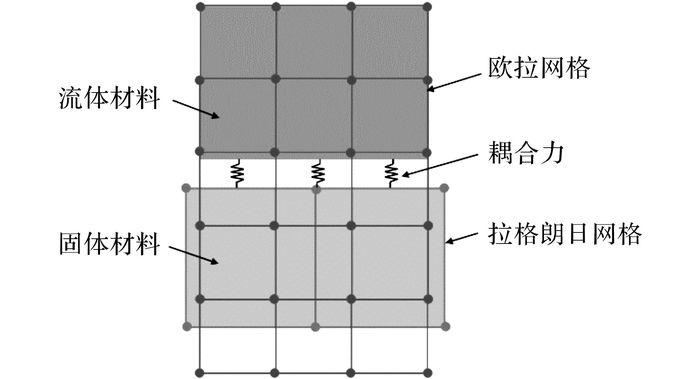
基于罚函数接触算法, 本文提出了一种计及计算稳定性的流固耦合算法.该算法在每个时间步的开始首先检查拉格朗日网格与欧拉网格之间的空间交叠信息, 当固体材料在某个或某些欧拉网格中的体积百分数超过0.5时, 固体材料和流体材料之间的耦合被激活, 如图 4所示, 耦合力正比于接触刚度和穿透深度, 这类似于在固体材料和流体材料之间放置弹簧以实现耦合.
|
图 4 拉格朗日网格与欧拉网格耦合示意图 Fig. 4 Schematic diagram of coupling between Lagrangian and Eulerian grids |
对于密度和刚度都相差很大的材料(例如本研究中的铝合金和气体), 不恰当的接触刚度很容易导致耦合仿真中发生穿透、泄漏和计算不稳定等问题.在计及计算稳定性的流固耦合算法中, 接触刚度的大小综合考虑了计算稳定性、总体时间步长以及节点质量, 由下式计算得到:
| $k = {\rm{max}}\left( {{K_1}\frac{{K{S^2}}}{V},{K_2}\frac{m}{{\Delta {t^2}}}} \right).$ | (4) |
式中:k为接触刚度, K1、K2为接触刚度缩放系数, K为材料的体积模量, S为接触段面积, V为单元体积, m和Δt分别为节点质量和整体时间步长.
3 模型验证在模型验证部分, 对应试验中从左至右的爆轰波传播方向, 数值模型的爆心(点火位置)设置在试验管道的最左侧.数值计算借助动力学分析程序LS-DYNA完成, 材料的本构方程、双变量失效准则以及接触刚度算法通过编写K文件的方式植入到计算程序中.
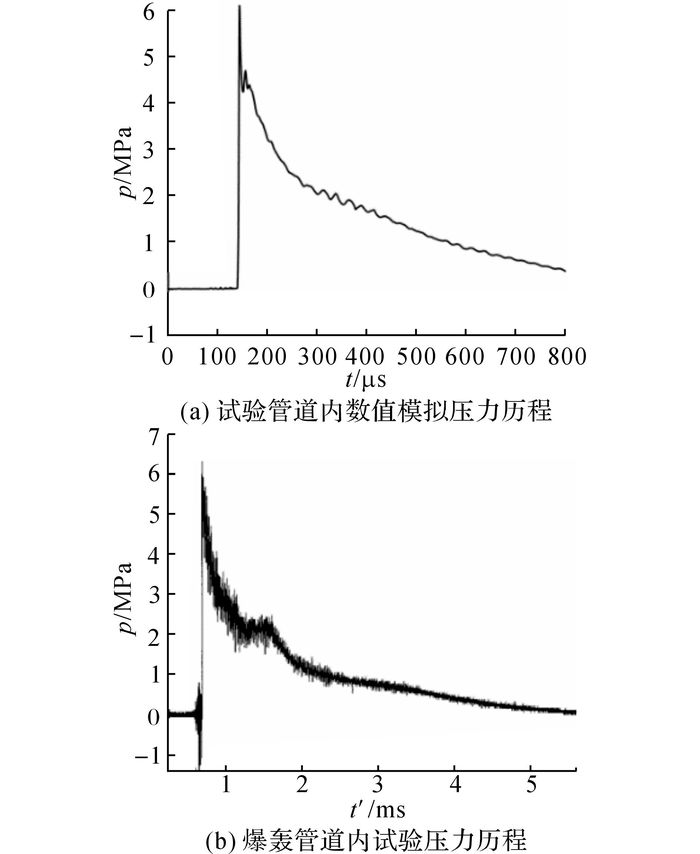
如图 5所示为管道内爆轰压力历程模拟与试验结果对比[15].图 5(a)给出了试验管道内爆轰压力历程的数值模拟结果.由图可见, 当爆轰波传播至测点位置时, 管道内压力迅速上升至爆轰压力6.1 MPa, 之后压力大致按照指数规律衰减.考虑到试验中试验管道上未安装压力传感器, 图 5(b)给出了在爆轰管道内测得的典型压力历程用以与数值模拟结果作对比.由图 5可见,模拟得到的管道内压力历程与试验结果具有较好的一致性, 最大压力值几乎相等.需要指出的是,模拟的试验管道内压力相比在爆轰管道内测得的压力在达到峰值之后衰减的更快, 这主要是由于试验管道上的压力测点与管道破裂处的距离更近, 导致压力更快的泄放掉.
|
图 5 管道内爆轰压力历程模拟与试验结果对比 Fig. 5 Comparison of numerical and experimental detonation pressure traces in tube |
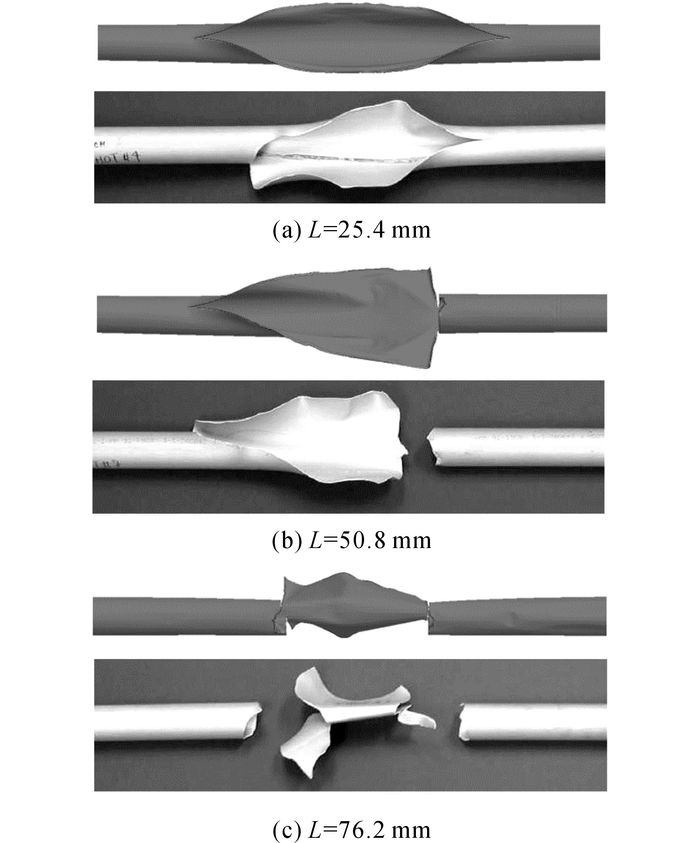
如图 6所示为3种初始缺陷长度情况下模拟得到的管道最终断裂形貌及相应的试验结果[16].由图可见, 3种情况下数值仿真结果都与试验结果具有较好的一致性, 尤其是不同初始缺陷长度下的裂纹分叉行为(L=25.4 mm时无分叉, L=50.8 mm时右侧裂纹分叉, L=76.2 mm时两侧裂纹分叉)得到了很好的数值重现.需要说明的是,在L=25.4 mm和L=50.8 mm两种不同情况下, 试验中左侧裂纹在沿管道轴线方向扩展一段距离后转弯继续沿管道螺旋线方向扩展最后停止, 而数值仿真中左侧裂纹直至停止一直沿管道的轴线方向扩展, 这可能是由于试验中使用的管道难以做到材料力学性能的完全均一, 造成了试验中不对称的裂纹扩展行为.
|
图 6 不同缺陷长度下管道断裂形貌模拟与试验结果对比 Fig. 6 Comparison of numerical and experimental fracture patterns of tubes with different flaw lengths |
为了方便定量研究管道变形及断裂对爆炸冲击波强度的削弱影响, 并消除爆轰波传播方向带来的不对称结果, 在爆炸后果分析中, 将数值模型的爆心设置在试验管道中央, 即与初始缺陷位于管道的同一轴向位置.管道左、右两侧出口均施加无反射边界条件, 其余参数设定与试验对应一致.
4.1 断裂形貌如图 7所示为模拟得到的3种初始裂纹长度对应的管道最终断裂形貌.在L=25.4 mm和L=50.8 mm两种情况下, 裂纹均沿管道轴向方向扩展, 所不同的仅仅是L=50.8 mm对应的最终裂纹长度比L=25.4 mm情况下的稍长一些.在L=76.2 mm情况下, 左、右两侧裂纹在沿管道轴向扩展一段距离后均发生了分叉, 4个分叉裂纹继续沿管道环向扩展直至停止, 管道中间部分塑性变形严重.对比不同点火位置对应的管道最终断裂形貌(图 6与7), 说明试验中L=50.8 mm时左、右两侧裂纹不同的扩展行为是由爆轰波的不对称传播方向导致的.

|
图 7 中心起爆时管道断裂形貌模拟结果 Fig. 7 Numerical fracture patterns of tubes with center detonation source |
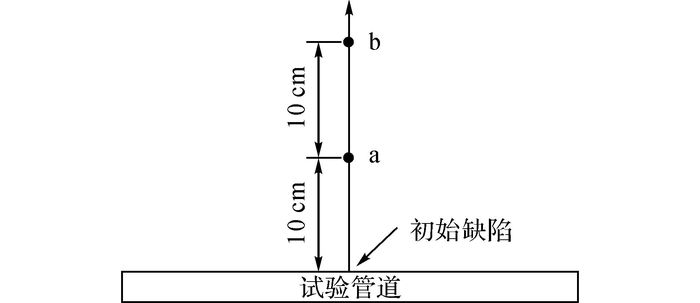
为定量分析管道变形及断裂对爆炸超压的削弱影响, 本文对不考虑上述削弱影响即单纯气体爆轰的情况也进行了数值仿真, 具体实现方法是在数值模型中删除试验管道, 其余参数保持一致.此外, 在管道外初始缺陷上方设置如图 8所示的2个压力测点, 方便对管道外的压力历程进行分析对比.
|
图 8 管道外压力测点位置示意图 Fig. 8 Location of pressure measuring points out of tube |
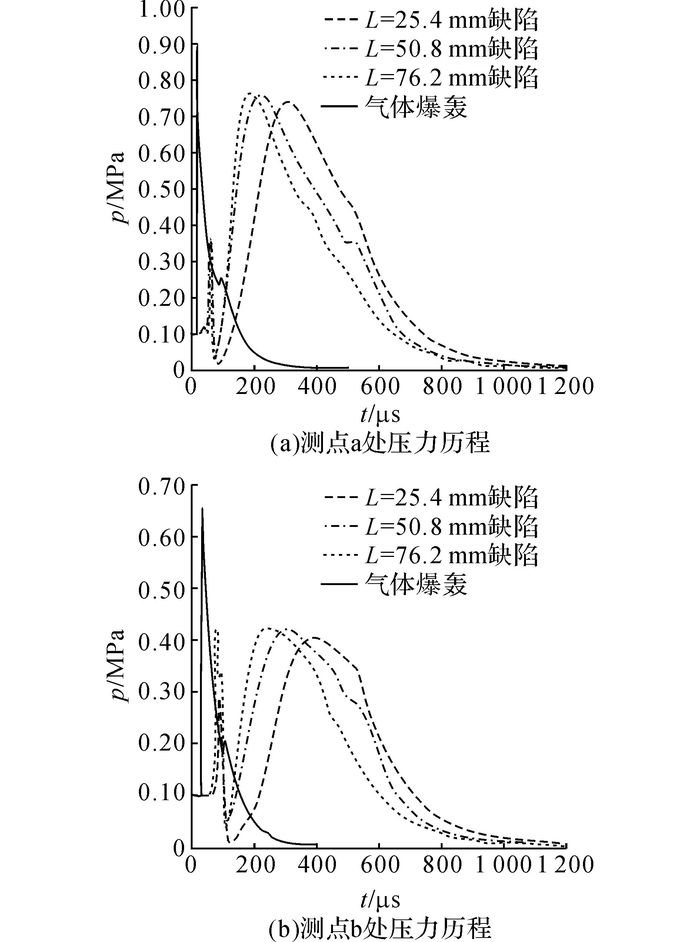
如图 9所示为3种初始缺陷大小以及气体爆轰情况下两测点a、b处的压力历程.由图可见, 管道变形及断裂对爆炸冲击波的压力波形和峰值压力都产生了较大影响.气体爆轰情况下的压力历程符合爆炸冲击波在空间某点的典型压力历程特征:冲击波传播至压力测点时, 压力p迅速上升至峰值压力, 之后衰减至大气压附近.考虑管道变形及断裂情况的压力历程稍稍复杂一些, 两测点处的压力在100 μs之前首先会经历一个迅速上升和下降的过程, 这是由一部分爆轰波初次运动至管道壁面时穿过初始贯穿裂纹继续向外传播经过压力测点造成的;此后压力再次大幅上升至峰值压力并进而衰减至大气压附近, 这是由裂纹进一步扩展后管道内高压气体从管道破裂处向外释放造成的.此外, 相比气体爆轰的情况, 管道变形及断裂延迟了管道外峰值超压的出现时间, 且管道初始缺陷长度越小峰值超压出现时间越晚, 这主要是由于初始缺陷长度越小, 管道在内部气体爆轰作用下越不容易发生破裂, 即裂纹扩展到一定大小所需的时间越长, 导致峰值超压出现的时间越晚.
|
图 9 不同缺陷长度及气体爆轰时两测点处压力历程 Fig. 9 Pressure histories for two measuring points in cases of different flaw lengths and gaseous detonation |
如表 1所示为气体爆轰和3种初始缺陷长度情况下测点处峰值压力的对比.由表可见, 管道变形及断裂对爆炸冲击波强度的削弱作用较为明显, 且管道初始缺陷越小, 削弱作用越大, 这同样是由于初始缺陷长度越小, 管道越不容易发生破裂, 即裂纹扩展到一定长度消耗的能量越大, 导致管道外冲击波峰值压力越小, 即削弱作用越大.两测点a、b处的峰值压力在考虑管道变形及断裂的削弱影响时(L=25.4 mm情况)分别为不考虑上述影响时(气体爆轰情况)的83.1 %和62.2 %.
| 表 1 不同缺陷长度及气体爆轰时测点处峰值压力对比 Table 1 Comparison of peak pressures of measuring pointsin cases of different flaw lengths and gaseousdetonation |
在通过本文方法模拟得到管道外超压分布后, 可根据爆炸超压伤害准则进一步对管道的爆炸后果进行预测或评估.
4.3 与现有方法的对比前已述及, 管道爆炸后果预测与评估的关键在于对管道外冲击波超压的计算, 考虑到目前公开文献中缺少相应的管道爆炸冲击波超压试验数据, 本文将考虑流固耦合效应的管道爆炸后果预测方法与目前广泛使用的TNT当量法及传统CFD方法进行对比分析以说明本文方法的优势.
TNT当量法的实质是将所研究的爆炸按照能量等效原则等效为一定质量TNT的爆炸, 以TNT爆炸产生的冲击波强度来代替所研究爆炸在空间产生的冲击波强度.对于本文给定的管道爆炸, 其等效TNT当量为5.1 g (TNT爆热取4500 kJ/kg), 根据比例定律[4]可计算得到两测点a、b处的峰值压力pso分别为3.15和0.64 MPa.
对于传统CFD方法, 由于在模拟爆炸过程的同时不能模拟管道的变形及断裂, 因此应用该方法进行管道爆炸后果评估时需要在管道上假设一开口或者不考虑管道的存在, 这样CFD方法才能模拟得到空间的爆炸流场及爆炸超压.对于不考虑管道存在的情况, 采用传统CFD方法的仿真结果即4.2节单纯气体爆轰的结果, 两测点a、b处的峰值压力pso分别为0.89 MPa和0.65 MPa.
TNT当量法、传统CFD方法以及本文方法(取L=25.4 mm缺陷的结果)计算得到的两测点a、b处的峰值压力如图 10所示.TNT当量法作为一种半经验方法, 忽略了爆炸物的种类以及形状对爆炸超压的影响, 并且应用于管道内气体爆炸的情况时也忽略了管道变形及断裂对爆炸超压的削弱作用, 因此其给出的峰值超压最高, 是相对最为保守的一种方法.传统CFD方法考虑了爆炸物的具体组成及形状, 并且能解析局部区域的爆炸流场, 但因不能同时模拟爆炸过程及结构变形断裂, 应用于管道内气体爆炸后果评估时仍不能计及管道变形断裂对爆炸超压的削弱影响, 故给出的超压值相比本文方法更高.

|
图 10 各方法计算的管道外峰值压力对比 Fig. 10 Comparison of external peak pressures calculated by different methods |
由以上分析可知, 本文方法最大的优势在于考虑了爆炸流场与管道的流固耦合作用, 即计及了管道变形断裂对爆炸超压的削弱影响, 故相比于传统方法可给出更加合理的管道爆炸后果预测结果.
5 结语本文提出了一种计及计算稳定性的流固耦合算法, 应用该算法实现了气体爆炸流场发展与管道变形断裂的耦合仿真, 应变率-应变双变量失效准则很好地解释了管道的裂纹扩展及分叉行为, 模拟得到的管道最终断裂形貌及内部压力历程与试验结果具有较好的一致性.研究表明管道变形与断裂对爆炸冲击波强度的削弱作用较为明显, 具体表现如下:管道外给定两测点处的冲击波峰值压力在考虑以上削弱影响时为不考虑情况的83.1%和62.2%, 且峰值压力的出现时间明显更晚.
相比难以计及爆炸流场与空间结构相互作用的半经验模型和传统CFD方法, 本文方法充分考虑了管道与爆炸流场的流固耦合作用, 因此可以更加合理地预测管道爆炸的后果.以上结论对管道爆炸后果预测以及管道爆炸事故推演具有重要意义.
| [1] | BAKER W E, COX P A, KULESZ J J, et al. Explosion hazards and evaluation [M]. [S. l.]: Elsevier, 2012. |
| [2] | ZHU Y, QIAN X, LIU Z, et al. Analysis and assessment of the Qingdao crude oil vapor explosion accident: Lessons learnt[J]. Journal of Loss Prevention in the Process Industries, 2015, 33: 289–303. DOI:10.1016/j.jlp.2015.01.004 |
| [3] |
崔甍甍, 范达, 张进军. 天津港"8·12"爆炸事故的教训与启示[J].
中华急诊医学杂志, 2015, 24(10): 1078–1081.
CUI Meng-meng, FAN Da, ZHANG Jin-jun. Lessons and illuminations of Tianjin port "8·12" explosion hazard[J]. Chinese Journal of Emergency Medicine, 2015, 24(10): 1078–1081. DOI:10.3760/cma.j.issn.1671-0282.2015.10.005 |
| [4] | DOBASHI R, KAWAMURA S, KUWANA K, et al. Consequence analysis of blast wave from accidental gas explosions[J]. Proceedings of the Combustion Institute, 2011, 33(2): 2295–2301. DOI:10.1016/j.proci.2010.07.059 |
| [5] | WHARTON R K, FORMBY S A, MERRIFIELD R. Airblast TNT equivalence for a range of commercial blasting explosives[J]. Journal of Hazardous Materials, 2000, 79(1): 31–39. |
| [6] | Van den BERG A C. The multi-energy method: a framework for vapour cloud explosion blast prediction[J]. Journal of Hazardous Materials, 1985, 12(1): 1–10. DOI:10.1016/0304-3894(85)80022-4 |
| [7] | BAKER Q A, TANG M J, SCHEIER E A, et al. Vapor cloud explosion analysis[J]. Process Safety Progress, 1996, 15(2): 106–109. DOI:10.1002/(ISSN)1547-5913 |
| [8] | MERCX W, VAN DEN BERG A C, HAYHURST C J, et al. Developments in vapour cloud explosion blast modeling[J]. Journal of Hazardous Materials, 2000, 71(1): 301–319. |
| [9] | MA G, LI J, ABDEL-JAWAD M. Accuracy improvement in evaluation of gas explosion overpressures in congestions with safety gaps[J]. Journal of Loss Prevention in the Process Industries, 2014, 32: 358–366. DOI:10.1016/j.jlp.2014.10.007 |
| [10] | RIGAS F, SKLAVOUNOS S. Evaluation of hazards associated with hydrogen storage facilities[J]. International Journal of Hydrogen Energy, 2005, 30(13): 1501–1510. |
| [11] | KIM E, PARK J, CHO J H, et al. Simulation of hydrogen leak and explosion for the safety design of hydrogen fueling station in Korea[J]. International Journal of Hydrogen Energy, 2013, 38(3): 1737–1743. DOI:10.1016/j.ijhydene.2012.08.079 |
| [12] | NGO T, MENDIS P, GUPTA A, et al. Blast loading and blast effects on structures-an overview[J]. Electronic Journal of Structural Engineering, 2007, 7: 76–91. |
| [13] | WANG K G, LEA P, FARHAT C. A computational framework for the simulation of high-speed multi-material fluid-structure interaction problems with dynamic fracture[J]. International Journal for Numerical Methods in Engineering, 2015, 104(7): 585–623. DOI:10.1002/nme.4873 |
| [14] | CHAO T W, SHEPHERD J E. Comparison of fracture response of preflawed tubes under internal static and detonation loading[J]. Journal of Pressure Vessel Technology, 2004, 126(3): 345–353. DOI:10.1115/1.1767861 |
| [15] | CHAO T W, SHEPHERD J E. Fracture response of externally flawed aluminum cylindrical shells under internal gaseous detonation loading[J]. International Journal of Fracture, 2005, 134(1): 59–90. DOI:10.1007/s10704-005-5462-x |
| [16] | CHAO T W. Gaseous detonation-driven fracture of tubes [R]. DTIC Document, 2004. |
| [17] | KUNTIYAWICHAI K, BURDEKIN F M. Engineering assessment of cracked structures subjected to dynamic loads using fracture mechanics assessment[J]. Engineering Fracture Mechanics, 2003, 70(15): 1991–2014. DOI:10.1016/S0013-7944(02)00257-6 |
| [18] | LESUER D R, KAY G, LEBLANC M. Modeling large strain, high rate deformation in metals[J]. Engineering Research, Development and Technology, 1999, 100(200): 300. |
| [19] | MA L, HU Y, ZHENG J, et al. Failure analysis for cylindrical explosion containment vessels[J]. Engineering Failure Analysis, 2010, 17(5): 1221–1229. DOI:10.1016/j.engfailanal.2010.02.009 |
| [20] | MA L, XIN J, HU Y, et al. Ductile and brittle failure assessment of containment vessels subjected to internal blast loading[J]. International Journal of Impact Engineering, 2013, 52: 28–36. DOI:10.1016/j.ijimpeng.2012.09.004 |
| [21] |
杨扬, 程信林. 绝热剪切的研究现状及发展趋势[J].
中国有色金属学报, 2002, 12(3): 401–408.
YANG Yang, CHENG Xin-lin. Current status and trends in researches on adiabatic shearing[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(3): 401–408. |



