2. 上海航天控制技术研究所, 上海 201109
2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China
高超声速飞行器是指马赫数大于5的飞行器[1], 是近年来世界航天强国的研究热点, 未来应用前景非常广阔.由于高超声速飞行器飞行包线大, 在稀薄大气层内, 飞行器舵面气动效能急剧下降, 难以提供足够的气动力矩保证扰动下的稳定飞行或期望的机动能力.直接力控制是一种不依赖大气环境, 由侧喷发动机构成的反作用控制系统(reaction control system, RCS)[2]来实现操纵控制的系统, 采用直接力与气动力相结合的复合控制方法[3-4]已成为实现高超声速飞行器稳定飞行的关键技术.
近些年, 国内外学者对复合控制的研究越来越多.刘忠等[5]基于反演法设计复合控制器, 提出利用能量优化逻辑实现侧喷发动机的多输入控制, 并设计模糊小脑模型神经网络[6]以抑制不确定性干扰.王霄婷等[7]研究全空域变质心/RCS复合控制策略, 通过对变质心控制系统力矩配平和闭环响应快速性能的分析, 实现从变质心到RCS控制的切换.耿洁等[8]针对再入飞行器的直气复合控制系统提出鲁棒飞行控制器, 利用线性规划和脉冲调宽调频(pulse-width pulse-frequency, PWPF)[9]方法实现控制分配.总体来说, 复合控制技术研究取得一定进展, 但是在结合稳定性分析的复合控制策略方面的研究很少.
本文提出了基于闭环稳定性判据的复合控制方法, 将稳定性判据作为高超声速飞行器开启侧喷发动机的控制策略.首先, 本文建立基于Winged-Cone的全状态六自由度高超声速飞行器模型, 并以飞行姿态角速度为例, 推导得到适用于高超声速飞行器的闭环稳定性判定方法.其次, 将稳定性判定应用于复合控制器设计中, 根据稳定性判定结果预测飞行器的稳定性, 形成新的直接力开启策略, 提高了传统复合控制的控制能力.最后, 通过实验仿真, 验证基于闭环稳定性判据的复合控制的性能.
1 基于飞行器模型的稳定性判据分析传统的稳定性判定方法主要包括纵向静稳定性、航向静稳定性和横向静稳定性等[10-12].近些年随着飞行器飞行速度和机动性[13]要求大幅提高, 尤其是高超声速飞行器的发展, 稀薄大气飞行时稳定裕度明显下降, 传统的横航向静稳定性判据无法对强耦合[14]、大攻角下的稳定性能做出精确的评估, 因此研究高超声速飞行器的稳定性评估以及控制策略问题显得尤为重要.
本文基于美国Winged-Cone高超声速飞行器全状态六自由度模型[15], 以姿态角速度模型作为稳定性判据的分析依据, 姿态角速度非线性模型表示为
| $ \dot p = - \frac{{{I_{\rm{z}}} - {I_{\rm{y}}}}}{{{I_{\rm{x}}}}}qr - \frac{{{{\dot I}_{\rm{x}}}}}{{{I_{\rm{x}}}}}p + \frac{{{l_{\rm{A}}} + {l_{{\rm{DT}}}}}}{{{I_{\rm{x}}}}}. $ | (1) |
| $ \dot q = - \frac{{{I_{\rm{x}}} - {I_{\rm{z}}}}}{{{I_{\rm{y}}}}}pr - \frac{{{{\dot I}_{\rm{y}}}}}{{{I_{\rm{y}}}}}q + \frac{{{m_{\rm{A}}} + {m_{{\rm{DT}}}}}}{{{I_{\rm{y}}}}}. $ | (2) |
| $ \dot r = - \frac{{{I_{\rm{y}}} - {I_{\rm{x}}}}}{{{I_{\rm{z}}}}}pq - \frac{{{{\dot I}_{\rm{z}}}}}{{{I_{\rm{z}}}}}r + \frac{{{n_{\rm{A}}} + {n_{{\rm{DT}}}}}}{{{I_{\rm{z}}}}}. $ | (3) |
式中:p、q、r为姿态角速度, Ix、Iy、Iz为转动惯量, lA、mA、nA为气动力矩, lDT、mDT、nDT为直接力矩.
气动力矩公式满足
| $ {l_{\rm{A}}} = \hat qbS{C_1}. $ | (4) |
| $ {m_{\rm{A}}} = \hat q\bar cS{C_{\rm{m}}} + {X_{{\rm{cg}}}}\left( {D\sin \alpha + L\cos \alpha } \right). $ | (5) |
| $ {n_{\rm{A}}} = \hat q\bar cS{C_{\rm{n}}} + {X_{{\rm{cg}}}}Y. $ | (6) |
式中:
将姿态角速度模型整理成线性模型, 得扩展状态方程为
| $ \mathit{\boldsymbol{\dot x = }}{\mathit{\boldsymbol{A}}_w}\mathit{\boldsymbol{x + }}{\mathit{\boldsymbol{B}}_w}{\mathit{\boldsymbol{M}}_{\rm{c}}}. $ | (7) |
式中:
| $ \mathit{\boldsymbol{x = w}} - \mathit{\boldsymbol{\bar w}}. $ | (8) |
| $ \mathit{\boldsymbol{w = }}{\left[ {\int {p{\rm{d}}t} ,p,\int {q{\rm{d}}t} ,q,\int {r{\rm{d}}t} ,r} \right]^{\rm{T}}}. $ | (9) |
| $ {\mathit{\boldsymbol{A}}_w} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0\\ 0&{{a_{22}}}&0&{{a_{24}}}&0&{{a_{26}}}\\ 0&0&0&1&0&0\\ 0&{{a_{42}}}&0&{{a_{44}}}&0&{{a_{46}}}\\ 0&0&0&0&0&1\\ 0&{{a_{62}}}&0&{{a_{64}}}&0&{{a_{66}}} \end{array}} \right]. $ | (10) |
| $ {\mathit{\boldsymbol{B}}_w} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ {I_{\rm{x}}^{ - 1}}&0&0\\ 0&0&0\\ 0&{I_{\rm{y}}^{ - 1}}&0\\ 0&0&0\\ 0&0&{I_{\rm{z}}^{ - 1}} \end{array}} \right]. $ | (11) |
| $ {a_{22}} = \frac{{\hat qS{b^2}{C_{1,p}}}}{{{I_x}2V}}. $ | (12) |
| $ {a_{24}} = - \frac{{r\left( {{I_z} - {I_y}} \right)}}{{{I_x}}}. $ | (13) |
| $ {a_{26}} = \frac{1}{{{I_{\rm{x}}}}}\left[ { - q\left( {{I_{\rm{z}}} - {I_{\rm{y}}}} \right) + \frac{{\hat qS{b^2}{C_{1,{\rm{r}}}}}}{{2V}}} \right]. $ | (14) |
| $ {a_{42}} = - \frac{{r\left( {{I_{\rm{x}}} - {I_{\rm{z}}}} \right)}}{{{I_{\rm{y}}}}}. $ | (15) |
| $ {a_{44}} = \frac{{\hat qS{{\bar c}^2}{C_{{\rm{m}},q}}}}{{{I_{\rm{y}}}2V}}. $ | (16) |
| $ {a_{46}} = - \frac{{p\left( {{I_{\rm{x}}} - {I_{\rm{z}}}} \right)}}{{{I_{\rm{y}}}}}. $ | (17) |
| $ {a_{62}} = \frac{1}{{{I_{\rm{z}}}}}\left[ { - q\left( {{I_{\rm{y}}} - {I_{\rm{x}}}} \right) + \frac{{\hat qS{b^2}{C_{{\rm{n}},p}}}}{{2V}}} \right]. $ | (18) |
| $ {a_{64}} = - \frac{{p\left( {{I_{\rm{y}}} - {I_{\rm{x}}}} \right)}}{{{I_{\rm{z}}}}}. $ | (19) |
| $ {a_{66}} = \frac{{\hat qS{b^2}{C_{{\rm{n}},r}}}}{{{I_{\rm{z}}}2V}}. $ | (20) |
式中:V为飞行速度, Cl, p为Cl对p的偏导数, Cl, r为Cl对r的偏导数, Cm, q为Cm对q的偏导数, Cn, p为Cn对p的偏导数, Cn, r为Cn对r的偏导数, w为姿态角速度扩展状态向量, w为期望的角速度扩展状态向量.
设计反馈控制器Mc=Kwx.
式中:Kw为反馈控制矩阵.
则可得状态空间方程为
| $ \mathit{\boldsymbol{\dot x = }}\left( {{\mathit{\boldsymbol{A}}_w} + {\mathit{\boldsymbol{B}}_w}{\mathit{\boldsymbol{K}}_w}} \right)\mathit{\boldsymbol{x = }}{\mathit{\boldsymbol{A}}_c}\mathit{\boldsymbol{x}}. $ | (21) |
从而得到闭环系统的特征矩阵, 即
| $ {\mathit{\boldsymbol{A}}_s} = s\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{A}}_c}. $ | (22) |
式中:s是复变量, Ac为系统矩阵.
将特征矩阵整理得到
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_s} = {\rm{diag}}\left[ {\left( {s + {L_{\dot p,{\rm{cop}}}}} \right),\left( {s + {L_{p,{\rm{cop}}}}} \right),\left( {s + {M_{\dot q,{\rm{cop}}}}} \right),} \right.\\ \;\;\;\;\;\;\;\left. {\left( {s + {M_{q,{\rm{cop}}}}} \right),\left( {s + {N_{\dot r,cop}}} \right),\left( {s + {N_{r,{\rm{cop}}}}} \right)} \right]. \end{array} $ | (23) |
根据劳斯定理, 闭环系统的稳定性判据如下
| $ \begin{array}{l} {L_{\dot p,{\rm{cop}}}} > 0,{L_{p,{\rm{cop}}}} > 0.\\ {M_{\dot q,{\rm{cop}}}} > 0,{M_{q,{\rm{cop}}}} > 0.\\ {N_{\dot r{\rm{,cop}}}} > 0,{N_{r{\rm{,cop}}}} > 0. \end{array} $ | (24) |
式中:L
以上的六参数稳定性判据是基于闭环系统, 可实时预测飞行器的稳定状态, 且与传统的静稳定判据相比, 能适应不同的飞行器模型, 通用性更强.
2 基于稳定性判据的直气复合控制当飞行器飞行状态改变, 尤其是飞行器的气动控制面的效率严重下降时, 难以提供足够的控制力矩, 可采用反作用控制系统的侧喷发动机提供直接力, 形成直气复合控制系统[17], 并通过控制分配算法得到解耦三轴方向的额外力矩.
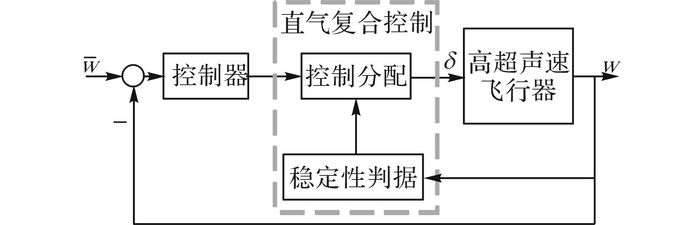
直气复合控制的开启策略[18]一般采用经验公式, 如选用动压、角速度, 通过反复实验得到侧喷发动机开启的阈值, 这种控制策略简单, 但是鲁棒性差、抗干扰能力弱.本文提出利用稳定性判据预测飞行器的稳定性状态, 并结合该判据来设计直接力开启策略的方法, 具体的控制器结构如图 1所示.
|
图 1 基于稳定性判据的复合控制器结构 Fig. 1 Blended controller structure based on stabilitycriterion |
结合图 1的复合控制器结构, 首先通过反馈控制器算法使高超声速飞行器稳定在设定值, 通过稳定性判据判断飞行器的稳定性, 当判断出飞行器即将失稳时, 加入直接力控制量, 采用控制分配算法得到三轴方向的控制力矩作用于飞行器, 从而提高飞行器的稳定性.传统的基于动压开启策略的复合控制方法并不能判断飞行器的稳定性, 而基于稳定性判据的复合控制方法能实时预测和判定飞行器稳定状态, 并能根据需要及时给出三轴方向的直接力控制力矩以保证飞行器稳定, 具有更强的鲁棒性.
直气复合控制在姿态角速度环三轴方向的控制量是定常离散值, 核心是确定直接力作用在飞行器上的时间点和持续长度.通过稳定性判据实时判定高超声速飞行器的稳定状态, 将其作为直气复合控制中直接力的开启条件, 当三轴姿态角速度稳定时, 不开启直接力, 当预测到飞行器即将失稳时开启直接力控制, 控制器设计方法为
| $ {\delta _{\rm{X}}} = \left\{ \begin{array}{l} 0,{L_{\dot p,{\rm{cop}}}} > 0\& {L_{p,{\rm{cop}}}} > 0;\\ 1,其他. \end{array} \right. $ | (25) |
| $ {\delta _{\rm{Y}}} = \left\{ \begin{array}{l} 0,{M_{\dot q,{\rm{cop}}}} > 0\& {M_{q,{\rm{cop}}}} > 0;\\ 1,其他. \end{array} \right. $ | (26) |
| $ {\delta _{\rm{Z}}} = \left\{ \begin{array}{l} 0,{N_{\dot r,{\rm{cop}}}} > 0\& {N_{r,{\rm{cop}}}} > 0;\\ 1,其他. \end{array} \right. $ | (27) |
式中:δX、δY、δZ为三轴方向的直接力开启状态, 0表示不开启该轴向的直接力, 1表示开启该轴向的直接力.
通过上述控制器可以实现飞行器在高超声速机动飞行时进行快速姿态调整, 提高对干扰因素的控制能力.
对于高超声速飞行器的直气复合控制, 由于高超声速飞行时发动机燃料非常有限, 因此以发动机的燃料量为优化指标, 结合式(25)~(27) 所表示的方法, 形成带有约束的控制器, 即
| $ {\delta _X} = \left\{ \begin{array}{l} 0,{L_{\dot p,{\rm{cop}}}} > 0\& {L_{p,{\rm{cop}}}} > 0\& \\ \;\;\;{\delta _{e,\min }} \le {\delta _{\rm{e}}} \le {\delta _{e,\max }};\\ 1,其他. \end{array} \right. $ | (28) |
| $ {\delta _Y} = \left\{ \begin{array}{l} 0,{M_{\dot q,{\rm{cop}}}} > 0\& {M_{q,{\rm{cop}}}} > 0\& \\ \;\;\;{\delta _{a,\min }} \le {\delta _{\rm{a}}} \le {\delta _{a,\max }};\\ 1,其他. \end{array} \right. $ | (29) |
| $ {\delta _Z} = \left\{ \begin{array}{l} 0,{N_{\dot r,{\rm{cop}}}} > 0\& {N_{r,{\rm{cop}}}} > 0\& \\ \;\;\;{\delta _{r,\min }} \le {\delta _{ - {\rm{r}}}} \le {\delta _{r,\max }};\\ 1,其他. \end{array} \right. $ | (30) |
根据式(28)~(30) 的约束控制器, 当舵偏角不饱和且飞行器稳定时, 不加入直接力; 否则, 加入直接力.这样可以保证只有在气动力不足以控制飞行器时才提供直接力, 使侧喷发动机的燃料消耗最小.
在确保飞行器稳定情况下引入直接力以提高控制性能, 直接力控制量采用最小控制能量融合法计算得到, 实现控制力矩到制导指令的映射, 即
| $ {\mathit{\boldsymbol{M}}_c} = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\delta }}_c}. $ | (31) |
需指出, 制导指令表示为
| $ {\mathit{\boldsymbol{\delta }}_{\rm{c}}} = {\left[ {{\delta _e},{\delta _a},{\delta _{\rm{r}}},{\delta _{\rm{x}}},{\delta _{\rm{y}}},{\delta _{\rm{z}}}} \right]^{\rm{T}}}. $ | (32) |
式中:δe, δa, δr为舵偏角, δx, δy, δz为直接力在三轴方向的偏转量.
控制分配算法可以描述为如式(33) 所示的优化问题
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{\delta }}_{\rm{c}}} \in \Pi } f\left( {{\mathit{\boldsymbol{\delta }}_c}} \right) = \mathit{\boldsymbol{\delta }}_c^{\rm{T}}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{\delta }}_c},\Pi :\left\{ {{\mathit{\boldsymbol{\delta }}_c}\left| {{\mathit{\boldsymbol{M}}_c} = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\delta }}_c}} \right.} \right\}. $ | (33) |
可得
| $ {\mathit{\boldsymbol{\delta }}_c} = {\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \right]^{ - 1}}{\mathit{\boldsymbol{M}}_c}. $ | (34) |
式中:Q为权重矩阵, 一般取舵面饱和偏转的对角矩阵的逆矩阵, D称为敏感矩阵.
3 实验仿真本文采用Winged-Cone高超声速飞行器模型, 利用Matlab/Simulink仿真软件研究分析飞行器在不同飞行状态下直接力开启策略的控制性能.依据飞行器在不同飞行状态(高度、速度不同)的气动参数模型, 采用不同的直接力控制策略来分析姿态角变化情况, 并判定飞行器稳定性状况, 从而分析控制策略的性能.
飞行器质量M=136 080 kg, 机翼参考面积S=334.73 m2, 翼展b=18.288 m, 气动弦长c=24.384 m, 速度V=7.48×103 m/s, 高度H=30 km, 转动惯量Ix=1.33×106 kg·m2, Iy=1.33×107 kg·m2, Iz=1.33×107 kg·m2.
以飞行器姿态角速度回路为例, 进行配平计算, 获得稳定工作点, 并借助Simulink完成配平和线性化工作.
设定飞行器为匀速直线平飞, 通过配平使飞行器的力和力矩平衡, 得到配平点如下:
| $ {\left[ {p,q,r,\theta ,\psi ,\phi } \right]^{\rm{T}}} = {\left[ {{0^ \circ },{0^ \circ },{0^ \circ },{{0.566}^ \circ },{0^ \circ },{0^ \circ }} \right]^{\rm{T}}}. $ | (35) |
式中:θ、ψ、φ分别为俯仰角、偏航角、滚转角.
线性化结果分别为
| $ {\mathit{\boldsymbol{A}}_w} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0\\ 0&{ - 0.0149}&0&0&0&{0.0186}\\ 0&0&0&1&0&0\\ 0&0&0&{ - 0.0147}&0&0\\ 0&0&0&0&0&1\\ 0&{ - 7.1026}&0&0&0&{ - 0.016} \end{array}} \right]. $ | (36) |
| $ {\mathit{\boldsymbol{B}}_w} = {10^{ - 6}} \times \left[ {\begin{array}{*{20}{c}} 0&0&0\\ {0.749}&0&0\\ 0&0&0\\ 0&{0.0749}&0\\ 0&0&0\\ 0&0&{0.0749} \end{array}} \right]. $ | (37) |
首先不引入直接力控制, 通过反馈控制器实现飞行器稳定, 如图 2(a)~(c)所示, 根据PD谱[19]分析方法, 得到反馈控制值为
| $ \begin{array}{l} {\mathit{\boldsymbol{K}}_w} = {10^9} \times \left[ {\begin{array}{*{20}{c}} { - 0.3004}&{ - 0.1200}&0\\ 0&0&{ - 3.0020}\\ 0&{0.0976}&0 \end{array}} \right.\\ \;\;\;\;\;\;\;\;\left. {\begin{array}{*{20}{c}} 0&0&{ - 0.0002}\\ { - 1.1990}&0&0\\ 0&{ - 3.0020}&{ - 1.1992} \end{array}} \right]. \end{array} $ | (38) |
当高度由30 km增加到40 km, 速度从7.48×103 m/s改变为4.42×103 m/s时, 动压则由4.88×105 kg/(m·s2)下降到3.78×104 kg/(m·s2), 飞行器控制结果如图 2的(d)~(f)所示, 图中t为时间.

|
图 2 气动力单独控制下仿真对比图 Fig. 2 Comparison when controlled only by aerodynamic force |
从图 2中可知, 通过反馈控制器实现飞行器稳定飞行, 姿态角稳定, 如图(a)~(c), 当高度和速度改变, 动压下降, 飞行器姿态角不稳定, 出现发散现象, 如图(d)~(f).分析可知, 当飞行状态改变, 动压下降时, 飞行器气动舵饱和而无法提供足够的气动力矩, 从而导致飞行器姿态角发散.因此, 可通过引入直接力控制力矩组成复合控制回路来保证飞行器稳定.
3.1 基于传统开启策略的直气复合控制直气复合控制中直接力开启判定条件采用动压和角速度2种方式.
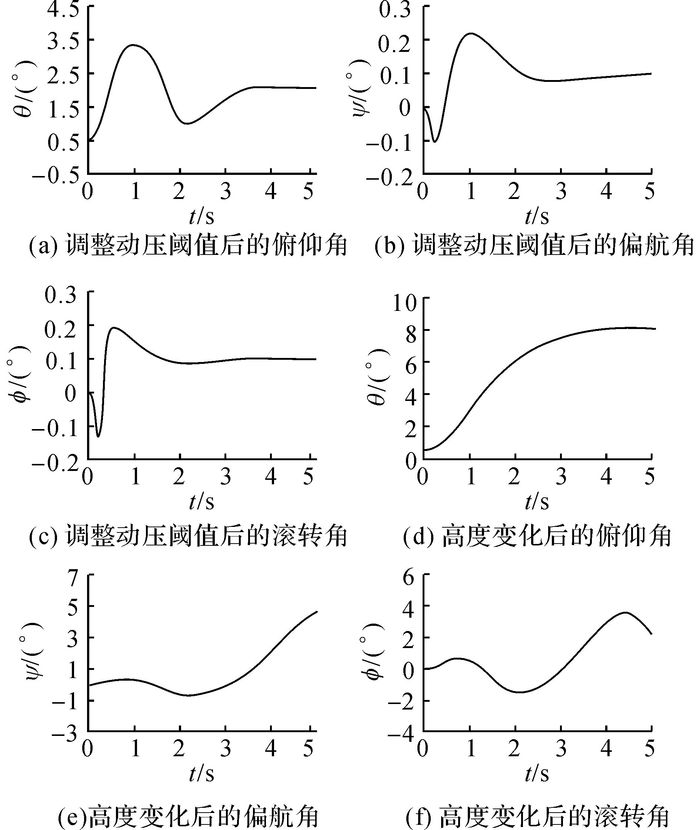
3.1.1 动压开启条件的复合控制器设计动压开启条件的控制器设计是通过调整动压阈值实现复合控制, 即飞行器动压低于阈值时开启直接力.动压阈值一般基于先验数据试凑得到, 本实验得到的动压阈值
|
图 3 基于动压开启策略的直气复合控制图 Fig. 3 Blended control based on dynamic pressure |
根据图 3的结果可知, 基于动压开启策略的直气复合控制器原理简单, 且能控制飞行器稳定, 最终稳定值为[θ, ψ, φ]T=[2°, 0.1°, 0.1°]T, 稳定时间大约为4 s, 如上图(a)~(c).然而该方法基于先验数据, 鲁棒性较差, 譬如当飞行高度增加到50 km, 传统开启策略的复合控制方法失效, 如上图(d)~(f), 综上, 基于动压开启策略的直气复合控制方法对飞行状态的变化不具有适应能力.
3.1.2 角速度开启条件的复合控制器设计类似动压开启条件的分析方法, 以角速度为开启条件设计复合控制器, 仿真结果如图 4(a)~(c)所示为飞行器失稳情况下调整角速度阈值后飞行器稳定飞行的仿真图, (d)~(f)为飞行状态改变后的仿真图, 角速度阈值为

|
图 4 基于角速度开启策略的直气复合控制 Fig. 4 Blended control based on angle velocity |
| $ {\left[ {{p_0},{q_0},{r_0}} \right]^{\rm{T}}} = {\left[ {{3^ \circ }/s,{4^ \circ }/s,{4^ \circ }/s} \right]^{\rm{T}}}. $ | (39) |
分析图 4, 调整得到适当的角速度阈值可以使飞行器稳定飞行, 如图(a)~(c), 但是当飞行状态改变, 如高度改变到50 km时, 基于角速度开启策略的直气复合控制方法不能控制飞行器稳定, 姿态角发散, 如图(d)~(f).
结合分析比较图 3和4, 基于传统开启策略的直气复合控制是依靠经验设计的, 当飞行状态改变时, 开启策略的条件阈值并未及时改变, 易导致高超声速飞行器表现出失稳发散现象.
3.2 基于稳定性判据的直气复合控制当飞行状态改变, 气动力不足时, 利用稳定判据得到的判定结果如下:
| $ \left. \begin{array}{l} {L_{\dot p,{\rm{cop}}}} = 36,{L_{p.{\rm{cop}}}} = - 7.96 \times {10^8};\\ {M_{\dot q,{\rm{cop}}}} = 5.12 \times {10^6},{M_{q,{\rm{cop}}}} = 1.81 \times {10^7};\\ {N_{{\rm{\dot r,cop}}}} = 3.94 \times {10^7},{N_{r{\rm{,cop}}}} = 2.62 \times {10^5}. \end{array} \right\} $ | (40) |
上述参数出现负数, 根据稳定性判据, 此时飞行器出现不稳定.当引入直接力控制后, 高超声速飞行器姿态保持稳定, 控制性能大为改善, 判定结果如下:
| $ \left. \begin{array}{l} {L_{\dot p,{\rm{cop}}}} = 225,{L_{p.{\rm{cop}}}} = 3.84 \times {10^9};\\ {M_{\dot q,{\rm{cop}}}} = 1.20 \times {10^9},{M_{q,{\rm{cop}}}} = 1.79 \times {10^{11}};\\ {N_{{\rm{\dot r,cop}}}} = 4.31 \times {10^{10}},{N_{r{\rm{,cop}}}} = 1.14 \times {10^7}. \end{array} \right\} $ | (41) |
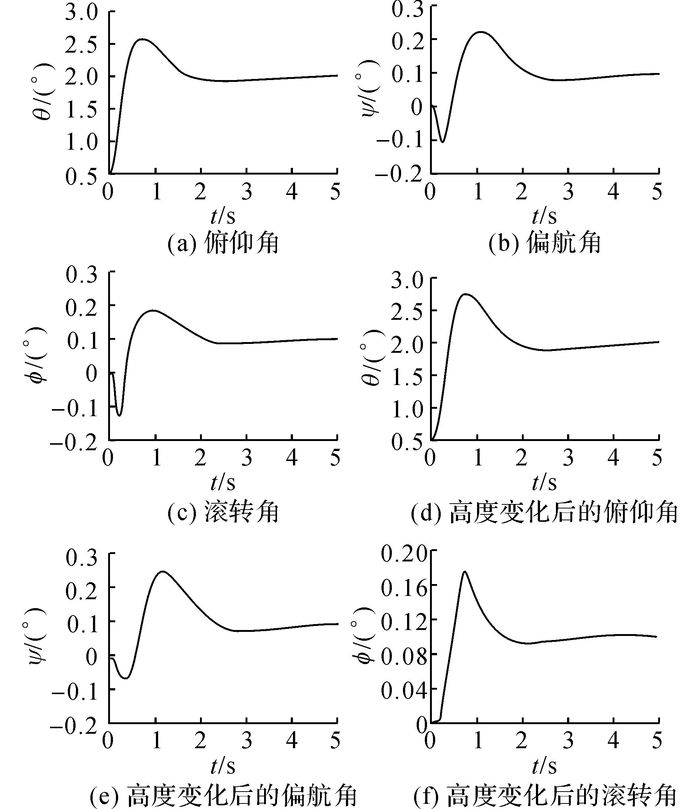
对比上述判定结果, 加入直接力控制后, 飞行器稳定性能提高, 如图 5(a)~(c)所示, 且改变飞行状态(如高度), 依然能稳定控制, 如图 5(d)~(f)所示.
|
图 5 基于稳定性判据的复合控制仿真图 Fig. 5 Blended control based on stability criterion |
结合图 5, 飞行器出现姿态角发散时, 加入直接力控制之后飞行器稳定飞行, 如图(a)~(c), 从图中可知, 飞行器稳定性能良好, 姿态角稳定时间约为4 s.改变飞行高度到50 km, 飞行器姿态角仍然稳定, 稳定时间稍微增加, 大约5 s左右, 如图(d)~(f).综上, 基于稳定性判据的直气复合控制方法能适应不同的飞行状态, 飞行器具有较强的鲁棒性.
结合传统开启策略进行对比分析, 基于稳定性判据的控制方法具有明显的优势.前者是基于经验试凑, 而后者是通过稳定性判据判定出飞行器的稳定性, 相比之下, 后者设计逻辑清晰、控制性能更好, 能适应不同的飞行器模型以及不同的飞行状态.
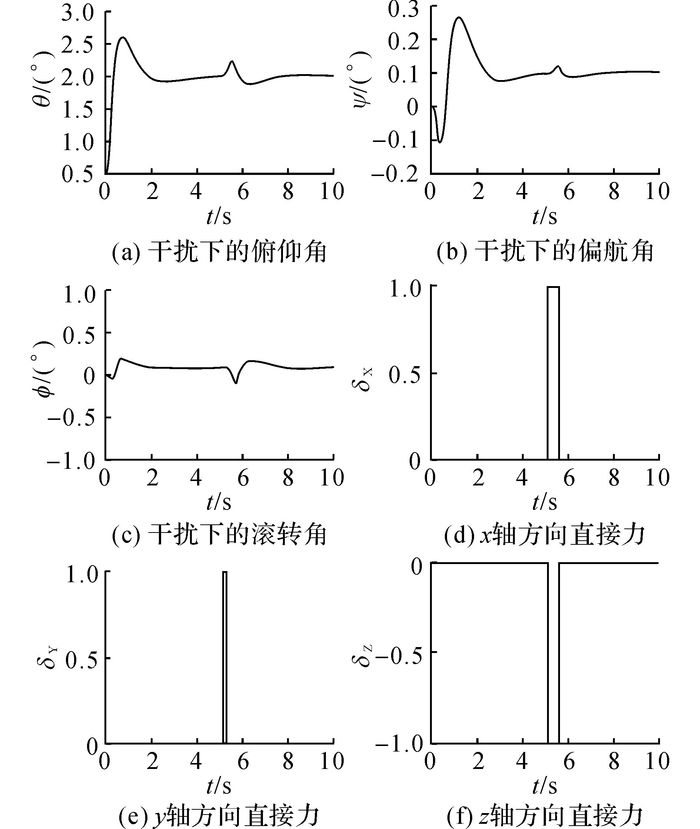
研究基于稳定性判据的直气复合控制器的抗干扰能力, 在仿真第5 s增加对气动参数的阶跃干扰, 如图 6(a)~(c)所示为姿态角变化图, (d)~(f)为直接力控制量.
|
图 6 基于稳定性判据的控制器的抗干扰性能 Fig. 6 Anti-interference performance of controller based on stability criterion |
从图 6中可知, 基于稳定性判据的直气复合控制器具有较强的抗干扰能力, 在飞行器出现一定气动干扰时, 能及时判断和提供直接力控制, 保持飞行器稳定.
仿真研究中设定不同的高度和速度是用于分析不同飞行状态, 并不用于反映飞行器的控制性能, 所以未给出高度、速度仿真曲线.
4 结语本文研究并提出高超声速飞行器新的闭环系统的稳定性判定方法, 并将该判定方法作为复合控制开启三轴方向直接力的条件, 形成新的高超声速飞行器直气复合控制方法.根据提出的思路, 设计出新型的复合控制器, 选取六自由度全状态的Winged-Cone高超声速飞行器模型为对象进行仿真研究和对比验证.在不同飞行状态下分别对无直接力作用的控制器、基于动压和角速度开启策略的传统复合控制器、基于稳定性判据的新开启策略的复合控制器进行仿真对比, 采用设定不同的高度、速度值作为改变飞行状态的方法, 主要以飞行器姿态角作为分析和仿真对象, 根据姿态角的变化来分析稳定性状况, 进而研究有无直接力的控制器以及不同开启策略的控制器的鲁棒性.
仿真研究表明:基于传统直接力开启策略的复合控制方法虽然能在一定程度上弥补气动力的不足, 但不能满足飞行机动性要求, 也无法预测飞行器不稳定状况并做出及时调整, 可能导致飞行器不稳或最终发散.与传统方法相比, 基于稳定性判据的开启策略不依赖飞行器的先验数据, 能适应不同的飞行器模型, 可实时判定飞行器的稳定状态, 能在飞行器即将失稳时及时提供额外直接力控制力矩以保证飞行器稳定, 可作为高机动性控制的技术途径.本文的研究方法主要针对姿态角控制器设计, 在不引入推力、高度、速度控制时, 几种控制器的高度和速度输出可能会在设定值附近变化, 这一问题可通过高超声速飞行器综合控制回路设计给出解决方案.总之, 相比而言, 本文的方法具有更大的适用面和更好的鲁棒性.
| [1] | VOLAND R T, HUEBNER L D, MCCLINTON C R. X-43A hypersonic vehicle technology development[J]. The International Academy Astronautics, 2006, 59(1): 181–191. |
| [2] | DOMAN D B, GAMBLE B J, NGO A D. Quantized control allocation of reaction control jets and aerodynamic control surfaces[J]. Journal of Guidance, Control and Dynamics, 2009, 32(1): 13–24. DOI:10.2514/1.37312 |
| [3] | HIROKAWA R, SATO K, MANABE S. Autopilot design for a missile with reaction-jet using coefficient diagram method [C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Canada: AIAA, 2001: 739-746. |
| [4] | TAUR D R, HSU H T. A composite guidance strategy for SAAMM with side jet controls [C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Canada: AIAA, 2001. |
| [5] | LIU Z, JIA X H. Novel back-stepping design for blended aero and reaction-jet missile autopilot[J]. Journal of Systems Engineering and Electronics, 2008, 19(1): 148–153. DOI:10.1016/S1004-4132(08)60060-2 |
| [6] | SU S F, LEE Z J, WANG Y P. Robust and fast learning for fuzzy cerebellar model articulation controllers[J]. IEEE Transactions on Systems, Man and Cybernetics, 2006, 36(1): 203–208. DOI:10.1109/TSMCB.2005.855570 |
| [7] |
王霄婷, 周军, 林鹏. 再入飞行器变质心/RCS复合控制策略研究[J].
西北工业大学学报, 2011, 29(2): 212–216.
WANG Xiao-ting, ZHOU Jun, LIN Peng. Proposing moving centroid/RCS control strategy for reentry flight vehicle[J]. Journal of Northwestern Polytechnical University, 2011, 29(2): 212–216. |
| [8] | GENG J, SHENG Y Z, LIU X D. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system[J]. Chinese Journal of Aeronautics, 2014, 27(4): 964–976. DOI:10.1016/j.cja.2014.03.013 |
| [9] | SONG G B, BUCK N V, AGRAWAL B N. Spacecraft vibration reduction using pulse-width pulse-frequency modulated input shaper[J]. AIAA Journal of Guidance, Control and Dynamics, 1999, 22(3): 433–444. DOI:10.2514/2.4415 |
| [10] | ZHANG Y Y, LI R F, X T, et al. An analysis of stability and chattering reduction of high-order sliding mode tracking control for a hypersonic vehicle[J]. Information Sciences, 2016, 348(20): 25–48. |
| [11] | ZAHRINGER C, HELLER M, SACHS G. Lateral separation dynamics and stability of a two-stage hypersonic vehicle [C]//12th AIAA International Space Planes and Hypersonic Systems and Technologies. Virginia: AIAA, 2003. |
| [12] | TEODORESCU B C. Lateral directional oscillatory departure criteria for high angle-of-attack flight conditions[J]. University Politehnica of Bucharest Scientific Bulletin, 2006, 68(3): 45–54. |
| [13] | GOMAN M G, KHRAMTSOVSKY A V, KOLENIKOV E N. Evaluation of aircraft performance and maneuverability by computation of attainable equilibrium sets[J]. Journal of Guidance, Control and Dynamics, 2008, 31(2): 329–339. DOI:10.2514/1.29336 |
| [14] | BUSCHEK H, CALISE A J. Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model[J]. Journal of Guidance, Control and Dynamics, 1997, 20(1): 42–48. DOI:10.2514/2.4031 |
| [15] | SHAUGHNESSY J D, PINCKNEY Z, MCMINN J D, et al. Hypersonic vehicle simulation model: winged-cone configuration [R]. Virginia: NASA Langley Research Center, 1990. |
| [16] | SHAO X L, WANG H L. Six-DOF modeling and simulation of a generic hypersonic vehicle for conceptual design studies [C]// AIAA Modeling and Simulation Technologies Conference and Exhibit, Rhode: AIAA, 2004. |
| [17] | XING L D, ZHANG K N, CHEN W H, et al. Optimal control and output feedback considerations for missile with blended aero-fin and lateral impulsive thrust[J]. Chinese Journal of Aeronautics, 2010, 23(4): 401–408. DOI:10.1016/S1000-9361(09)60234-X |
| [18] | INNOCENTI M, THUKRAL A. A blending strategy for missile autopilots using the simplex method [C]// Proceedings of the 1995 American Control Conference. Seattle: IEEE, 1995: 2163-2167. |
| [19] | MICKLE M C, ZHU J J. Bank-to-turn roll-yaw-pitch autopilot design using dynamic nonlinear inversion and PD-eigenvalue assignment [C]//Proceeding of the 2000 American Control Conference, Chicago: IEEE, 2000: 1359-1364. |


