2. 东北师范大学 计算机科学与信息技术学院, 吉林 长春 130117
2. School of Computer Science and Technology, Northeast Normal University, Changchun 130117, China
在大数据时代的背景之下, 分类作为解决信息过载的重要技术之一, 在机器学习和数据挖掘领域中被广泛应用.随机森林算法作为分类技术的一种, 性能优良、分类精度高, 在模式识别、文本分类、商品推荐中应用较多.然而, 国内外研究人员关注的方向主要是随机森林算法在某个具体领域的应用(如:图像分类处理, 人脸识别, 种群判别等), 而关于算法本身的研究较少, 譬如Gall等[1]把霍夫变换应用到随机森林算法中, 形成了霍夫随机森林算法, 特别是在大数据背景下, 对于提升随机森林算法性能和分类精度的研究不够深入.
传统的随机森林算法在训练产生多个基分类器后, 再通过集成学习的方式将这些分类器模型组合起来构成决策森林[2].首先, 这里每个基分类器的训练数据集是随机有放回抽样产生的, 然后, 每个基分类器学习训练时节点分裂的特征选取也是随机产生的一个特征子空间, 有了这2个随机因素的影响, 使得每个基分类器的训练结果虽不足以训练出一个强分类器, 但是每个基分类器之间一般都会有足够的差异性[3-5].随机森林算法通过在不同数据子空间与属性特征子空间中学习, 好比拥有了很多精通不同领域的专家, 最后通过这些专家的投票表决来预测新的数据.
然而, 简单的投票表决方式没有区分每个基分类器之间的分类优势.随机因素的引入虽然得到了差异较明显的基分类器, 但是没有考虑各个分类模型间的性能差距, 所以进行选择性的模型组合, 有利于进一步提高随机森林算法的分类性能.首先分析传统随机森林算法的多数表决机制的不足以及发掘提升性能的途径, 然后给出一种全新的加权投票机制, 用于进一步提升随机森林算法的分类性能和精度.
1 模型组合的相关概念传统的数据挖掘分类算法通常都是由训练集学习得到单分类器, 然后使用此单分类器分类或预测新样本.模型组合(也就是集成学习)思想的出现来源于神经网络算法, Hansen等[6]根据训练集形成多个神经子网络, 通过对各个神经子网络的学习结果进行组合, 从而提高整个神经网络学习器的泛化能力.
模型组合的本质特征在于, 多个模型通常各自携带互补的预测信息, 通过模型组合可以纠正单模型中的独立错误, 从而提供更准确的、鲁棒的预测结果.模型组合过程分为2个步骤:1) 构建多个具有较大差异性的子模型;2) 使用一种集成策略整合各个自模型, 得到最终的模型输出结果.集成策略有很多, 具体策略需要根据模型学习目标自主择优.随机森林算法使用的集成策略是多数表决(majority voting)机制[7], 也是一种简单的模型组合方法, 其思想就是将各分类器预测所属类别数目最多的类别作为最终的分类结果.类似这样的通过各个基分类器的结果投票表决出最终分类结果的策略可以统称为投票策略.投票策略除了多数表决之外还有一票否决、阈值表决等.一票否决投票机制就是体现全体一致原则, 需要所有的分类器结果均是同一个类别才能将其作为最终的分类结果, 例如联合国大会下设常任理事国就具有一票否决权;阈值表决投票机制就是一旦各个分类器的分类结果中某个类别投票数目达到指定阈值, 最终的分类结果就可以使该类别.明显, 对于单标签分类问题, 如果阈值设定超过50%, 那么此时阈值表决就等效于多数表决了.实际生活中, 例如中国宪法的修改, 在被提议后, 需要由全国人大以全体代表的2/3以上多数通过, 这就是一个阈值表决投票机制.
综上, 模型组合中有很多集成策略.随机森林算法默认使用了多数表决机制, 并获得了较好的分类性能.但是具体问题分析时, 仅仅使用多数表决机制是不够完善的.因此, 本文先分析传统的多数表决机制的不足, 然后给出一种全新的加权投票机制用于进一步提升随机森林算法的分类性能.
2 加权的多数表决机制随机森林算法使用的集成策略是多数表决机制, 着重关注的也是随机森林算法中的第2个步骤——组合过程, 但是对于单分类器的训练过程, 各个分类器训练的数据集的随机性以及节点分裂是特征子空间的随机性, 各个单分类器间差异性明显, 这样的弱相关性正是我们需要的.然而, 差异性的劣势在于:1) 各个单分类器的分类能力参差不齐;2) 对于多数表决投票方法而言, 无法突出优秀分类器的分类能力, 整体的分类性能还有进一步提升的可能.因此, 就可以为各个单分类器设定不同的权重, 由最终的加权投票值确定最终的分类结果.这样就可以更好地发挥各个单分类器的个性与优势, 强化分类效果好的单分类器的优势, 弱化分类效果较差的单分类器的劣势, 从而提高学习结果的正确性.
加权的多数表决机制可以表示为如下的预测函数:
| ${F_{{\rm{new}}}}\left( x \right){\rm{argma}}{{\rm{x}}_{y \in 1,{\rm{ }} \ldots ,k}}{f_{{\rm{new}}}}\left( {x,y} \right).$ | (1) |
其中:
| ${{f}_{\text{new}}}\left( x,y \right)=\sum\nolimits_{h\in H}{{{\alpha }_{h}}}\cdot I\left( h\left( x \right)=y \right).$ | (2) |
式中:I(h(x)=y)为指示函数,可表示为
| $I\left( {h\left( x \right) = y} \right) = \left\{ {\begin{array}{*{20}{l}} {1,h\left( x \right) = y为真;}\\ {0,h\left( x \right) = y为假.} \end{array}} \right.$ |
h(x)=y表示用分类器h对样本x分类的结果为y,αh为基分类器h的权重,argmaxy∈{1, …, k} fnew (x, y)表示使得fnew (x, y)最大的x, y得取值,H为分类器集合.
这个新的预测函数Fnew(x)与传统随机森林算法的预测函数F(x)的差别就在于式(2) 中多了基分类器的权重.本文以此公式为基础, 提出一个基于最大共识的模型组合算法(model combination algorithm based on the consensus maximization MCA-CM), 用于进一步提升随机森林算法的分类性能.
3 基于最大共识的模型组合算法 3.1 最大共识定义加权的多数表决机制与普通的多数表决相比, 为每个单分类器h赋予了一个权重αh, 故这个新的投票方法的关键在于分类器权重的计算.首先, 权重定义的实践基础在于发挥各个单分类器的个性与优势, 因此, 此权重应当与各个分类器的分类能力成正比, 即有
| ${\alpha _h} \propto {A_h}$ | (3) |
式中:Ah为分类器h的分类能力.
由式(1) 可以看到, 求解argmax函数时同时扩大或缩小αh的值, 不影响最终的预测结果.故可以把单分类器的分类能力直接作为其权重, 即αh=Ah.为了更好地描述分类器的分类能力, 参考随机森林算法的分类性能指标, 选取分类准确度与OOB(Out-of-Bag, 袋外)误差估计的定义, 使用最大共识(consensus maximization)来表示Ah, 即给出CM的定义如下:
| $\begin{array}{l} {\rm{CM}}\left( {{h_t}} \right) = \\ \frac{{\left( {1 + {\mu ^2}} \right)\left[ {1 - {\rm{OOBerror}}\left( {{h_t}} \right)} \right]{\rm{Accuracy}}\left( {{h_t}} \right)}}{{{\mu ^2}\left[ {1 - {\rm{OOBerror}}\left( {{h_t}} \right)} \right] + {\rm{Accuracy}}\left( {{h_t}} \right)}}. \end{array}$ | (4) |
式中:ht为第t个分类器;Accuracy(ht)为第t个分类器的分类准确度;OOBerror(ht)为第t个分类器的OOB误差率;μ为一个调谐参数, 取值范围是0, 1, 通常取1.
分类器的分类能力可以由经验误差与泛化误差来表示, 这里训练集分类准确度估计的是经验误差(在训练集上的表现), OOB误差估计的则是泛化误差(在未知数据集上的表现), 即这里的泛化能力是分类能力的一个指标.
同样, 参考分类准确度和OOB误差率[8]的定义, 首先可以根据分类器对于样本的预测类别和样本的真实类别是否相同可以构造一个随机森林01评分矩阵, 如表 1所示.表中: scoreij为分类器hj对于训练样本(xi, yi)的评分.如果预测结果与真实类别一致, 则为1, 否则为0, 即scoreij=I(hj(xi)=yi).为表现每个分类器的分类准确度的不同, 故可给出分类器ht的分类准确度为
| 表 1 随机森林01评分矩阵 Table 1 01-rating matrix of random forests |
| ${\rm{Accuracy}}\left( {{h_t}} \right) = \frac{{1 + \sum\nolimits_{i = 1}^n {{\rm{scor}}{{\rm{e}}_{it}}} }}{{1 + \sum\nolimits_{j = 1}^{\left| H \right|} {\sum\nolimits_{i = 1}^n {{\rm{scor}}{{\rm{e}}_{ij}}} } }}.$ | (5) |
另外, 参考OOB误差估计的计算方法, 构造随机森林的Out-of-Bag矩阵如表 2所示.表中:σij为分类器hj的训练集Sj中是否包含样本(xi, yi).如果包含, 值为0, 否则为1, 即σij=I((xi, yi)∉Sj), OOB误差率只关心那些袋外数据(Out-of-Bag Data), 故可以得到OOB误差率计算公式为
| $\text{OOBerror}\left( {{h}_{t}} \right)=\frac{1+\sum\nolimits_{i=1}^{n}{{{\sigma }_{it}}}\cdot I\left( \text{scor}{{\text{e}}_{it}}=0 \right)}{1+\sum\nolimits_{i=1}^{n}{{{\sigma }_{it}}}}.$ | (6) |
| 表 2 随机森林Out-of-Bag矩阵 Table 2 Out-of-Bag matrix of random forests |
在01评分矩阵上的元素依次乘上σij, 这样就可以对应每个分类器来过滤掉袋内数据.但需要注意的是, 这里的OOB误差率与基本的OOB误差估计完全不同, OOB误差估计是基于样本的误差平均, 此处的OOB误差率则是基于分类器的误差平均, 计算每个分类器各自预测袋外数据的误差率.
另外, 式(5)、(6) 的分子分母均有加一操作, 是为了有效预防出现分母为0的情形(如极端情形:所有分类器对于所有样本都分类错误).而式(4) 之所以有调谐参数μ, 是参考F1综合评价指标, 是为了更好地协调经验误差与泛化误差的关系, 既保证了分类器的分类性能, 又考虑了它的泛化能力.
综上, 式(2) 就演变成如下:
| ${f_{{\rm{new}}}}\left( {x,{\rm{ }}y} \right) = {\sum _{h \in H}}{\rm{CM}}\left( h \right)I\left( {h\left( x \right) = y} \right).$ | (7) |
基于最大共识的模型组合算法(MCA-CM), 是受加权的多数表决机制的启发, 针对随机森林算法的特点扩展得来的.因为需要充分考虑各个单分类器的分类能力和泛化能力, 所以才有了如公式(7) 所示的最大共识投票策略.此策略的核心思想就是获得多个基模型的最大限度的联合预测, 这样的最大化共识方法可以减少歧视性的预测结果以及过拟合由于基模型不完善而导致的错误投票.
MCA-CM算法的关键在于CM的计算过程, 主要是根据基分类器的预测结果与训练数据实际所属类别间的差异性构造2个矩阵, 一个是随机森林01评分矩阵, 考虑的是经验误差, 计算的是分类准确度的概率平均;另一个是随机森林Out-of-Bag矩阵, 考虑的是泛化误差, 用于计算OOB误差率的基分类器平均.通过式(6) 可知, 这里的随机森林Out-of-Bag矩阵其实就是表示了随机森林算法构造过程中的袋外数据分布情况.
MCA-CM算法引入了随机森林01评分矩阵和随机森林Out-of-Bag矩阵用于估计各个分类器的经验误差和泛化误差, 可以减少个别分类器的歧视预测和过拟合噪声数据等情况的产生.
3.3 MCA-CM算法描述基于最大共识的模型组合算法的算法框架描述如下:
MCA-CM输入:训练集S, 基分类器集合H
输出:随机森林的预测函数Fnew
1 for (xi, yj)∈S //遍历训练集S
2 for hj∈H
// 遍历随机森林的基分类器集合H
3 scoreij=I(hj(xi)=yi)
//计算01评分矩阵
4 σij=I((xi, yi)∉Sj)
//计算Out-of-Bag矩阵
5 end for
6 end for //遍历结束
7 for hj∈H
//遍历基分类器集合H计算权重CM
8 α=Accuracy (ht)
//通过式(5) 计算分类准确度
9 β=OOBerror (ht)
//通过式(6) 计算OOB误差率
10 CM
//通过式(4) 计算权重CM
11 end for
12
//加权得到新的预测函数
13 return Fnew
在MCA-CM算法的核心框架中, 重要的步骤体现在通过第3步与第4步计算得到的2个矩阵, 然后依据这2个矩阵计算基分类器的权重.分类准确度与OOB误差率的综合评价机制保证了最终预测函数的分类能力和泛化能力.
4 MCA-CM算法的实验分析 4.1 性能指标与评估方法分类的性能指标有分类准确度、召回率、精确度、宏平均召回率、宏平均精确度等指标[9], 在通常情况下, 召回率与精确度是负相关的, 可以综合这2个指标给出评价, 也就是F1指标, 定义如下:
| ${\rm{F}}1 = \frac{{2{\rm{Accuracy}} \cdot {\rm{Recall}}}}{{{\rm{Accuracy}} + {\rm{Recall}}}}.$ | (8) |
式中:Recall为召回率.
推广到多类分类问题中, 就有F1(i)指标和宏平均F1指标(Macro_F1), F1(i)指标就表示类别i的F1指标值, 宏平均F1指标就是所有类别F1指标的平均, 即可表示为:
| ${\rm{F}}1\left( i \right) = \frac{{2{\rm{Accuracy}}\left( i \right)\cdot{\rm{Recall}}\left( i \right)}}{{{\rm{Accuracy}}\left( i \right) + {\rm{Recall}}\left( i \right)}}.$ | (9) |
| ${\rm{Macro}}\_{\rm{F}}1 = \frac{1}{k}\sum\nolimits_{i = 1}^k {{\rm{F}}1} \left( i \right).$ | (10) |
F1指标是评价分类性能的一个有效指标[10], 本文中使用的数据集超过2个类别, 故使用宏平均F1作为主要评价指标, 同时, 为更好地体现数据集的差异性, 将训练集分类准确度A与测试集分类误差E作为一个辅助评价标准.
| $A = \frac{1}{n}\sum\nolimits_{i = 1}^n I \left( {F\left( {{x_i}} \right) = {y_i}} \right).$ | (11) |
| $E = \frac{{\sum {_{\left( {{x_i},{\rm{ }}{y_i}} \right) \in O}} I\left( {F\left( {{x_i}} \right) \ne {y_i}} \right)}}{{\left| O \right|}}.$ | (12) |
式中:O为训练集合.
常见的分类器评估方法有交叉验证(cross vlidation, CV)法和预留(Holdout)法.这2种评估方法的共同点都是将数据集划分为训练集和测试集2部分, 目的也均是为了获得更加可靠和稳定的模型.统计学家Seymour Geisser提出了CV理论, 它是一种常用的评估某算法对独立于训练数据的数据集的泛化能力的方法.交叉验证法主要包括K折交叉验证(K folder cross validation)、K对折交叉验证(K*2 folder cross validation)和留一交叉验证(Leave one out cross validation, LOOCV)这3类方法.
交叉验证法在进行预测估计时, 需要不断地划分数据集与合并数据集, 整个的计算复杂度和空间复杂度都比较高, 从而使得评估运行效率降低.而预留法则不同, 它是从数据集中随机选取确定数量的子集作为训练集, 其他部分则作为测试集即可, 操作简单, 运行效率相较于交叉验证法也高了不少.综合考虑, 本文将采用预留法作为评估方法之一.一般而言, 预留法中需要选取数据集中1/3左右的数据作为测试集, 本文采用的比例为7:3, 即70%的数据作为训练集, 30%的数据作为测试集.
本质上, 分类算法的评估方法是测试学习的分类器的推广能力, 又称为泛化能力.也就是说, 分类器的泛化能力越强, 说明该分类器应用在同质数据集上也能得到比较合理的输出结果.而泛化误差就是描述这一推广到未知新数据能力的一个衡量标准.随机森林算法是在Tree Bagging算法上发展而来, 每棵树的训练集是由初始的总数据集通过随机抽样获得的, 每个样本约有e-1≈0.367的概率不被抽中, 也就表明抽取过程中有接近37%左右的样本无法被抽取出来, 这类数据就被称为上文中所述的OOB数据.而这些数据没有被用于各自基分类器的训练和学习, 天然地可以作为训练集合.而整个的抽取过程就完成了测试集与训练集的划分, 也就是说, 可以使用很少的计算资源就可以评估随机森林算法的泛化能力.与交叉验证法和预留法相比, OOB误差估计法既保证了类似交叉验证法的验证精度与粒度, 又获得了可以比拟预留法的验证效率.因此, 本文也将采用OOB误差估计法作为评估方法之一.
4.2 实验数据集本算法使用的数据集是搜狗实验室数据SogouC数据集, 此数据集属于文本分类语料库(http://www.sogou.com/labs/dl/c.html), 主要数据来源是搜狗新闻网站的文本信息, 这里的数据是经过整理和分类的新闻文本和类别数据, 包括几十个类别, 数据规模有数十万篇文本数据.
主要研究的是模型组合问题, 故直接使用初始数据集进行相关的实验论证, 研究本文提出的模型组合算法能否提高随机森林算法的分类性能.
4.3 实验结果与分析在完整版本的数据子集上进行测试, 整体思想是按照预留法分配70%的数据作为训练集, 剩下30%数据作为测试集.运行结果的评价指标分别是分类准确度、宏平均F1与测试集的误差, 其中分类准确度作为参考, 其余2个分别用于考虑算法的经验误差与泛化误差.
考虑的改进的模型组合策略对随机森林算法的影响情况, 运行条件如下:
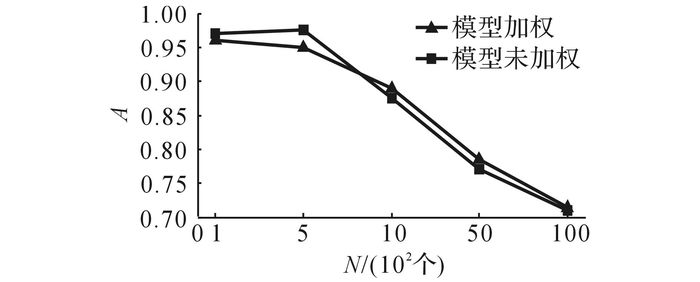
类别数目=10, 构建树的数目=250, 特征子集的选择策略为√, 节点分裂策略选择Gini指标, 出于时间性能考虑, 考虑树的最大深度为10, 样本的特征维度为262 144维.测试结果如图 1所示, 图N为数据集大小.
|
图 1 改进的模型组合算法对分类准确度的影响 Fig. 1 Effect of improved model combination algorithm on classification accuracy |
实验结果显示, 基于最大共识的模型组合算法改进随机森林算法时对于其分类准确度的提升不明显, 毕竟分类准确度仅作为分类性能的参考.
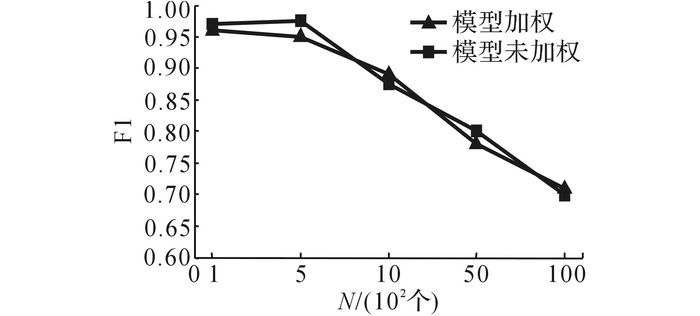
用基于最大共识的模型组合对随机森林算法进行改进时对宏平均F1的影响如图 2所示.
|
图 2 改进的模型组合算法对宏平均F1的影响 Fig. 2 Effect of improved model combinationalgorithm on Macro_F1 |
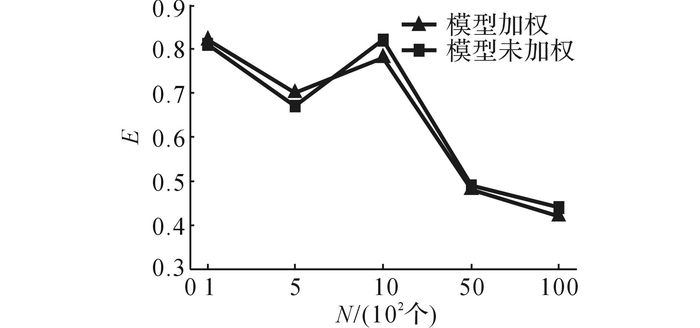
对测试集分类误差的影响如图 3所示.从图 2与3的实验结果可以发现, 基于最大共识的模型组合算法改进随机森林算法由于综合考虑了各个基分类器间经验误差与泛化误差的差异性, 使得其在测试集分类误差的表现均普遍优于没有加权的初始随机森林算法, 而在宏平均F1值的表现上则优势不明显, 这是略侧重于泛化误差的表现.综合看来, 这是由于改进算法兼顾经验误差与泛化误差的关系, 既考虑了改进组合分类器在训练集上的表现, 又想进一步提高其泛化能力, 使得整体分类性能虽有提升, 但还继续存在提升的空间.
|
图 3 改进的模型组合算法对测试集分类误差的影响 Fig. 3 Effect of improved Model CombinationAlgorithm on classification error of test set |
综上, 本文提出的基于最大共识的模型组合算法可以提高随机森林算法的分类能力, 同时也具有较强的泛化能力.虽然提升的幅度不大, 但是对于同类型的多模型组合算法性能的提升应当具有指导意义.
5 结语本文主要介绍了模型组合的相关知识, 分析了随机森林算法中投票表决预测分类的不足, 随后给出了最大共识的概念, 并提出了基于最大共识的模型组合算法用于优化随机森林算法的集成学习过程, 并通过实验进行了验证, 结果证明了新算法的集成学习是有效的, 能够在提高分类精度的同时, 也具有较强的泛化能力.
| [1] | GALL J, LEMPITSKY V. Decision forests for computer vision and medical image analysis[M]. London: Springer, 2013: 143-157. |
| [2] | GRAY K R, ALJABAR P, HECKEMANN R A, et al. Random forest-based similarity measures for multi-modal classification of Alzheimer's disease[J]. NeuroImage, 2013, 65: 167–175. DOI:10.1016/j.neuroimage.2012.09.065 |
| [3] | ZHAI S, XIA T, WANG S. A multi-class boosting method with direct optimization [C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 273-282. |
| [4] | ZHAI S, XIA T, TAN M, et al. Direct 0-1 loss minimization and margin maximization with boosting[C]//Advances in Neural Information Processing Systems. Nevada: [s.n.] 2013: 872-880. |
| [5] | DONG L, LI X, LANG P. Prediction of rockburst classification using Random Forest[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(2): 472–477. DOI:10.1016/S1003-6326(13)62487-5 |
| [6] | HANSEN L K, SALAMON P. Neural network ensembles[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1990, 12(10): 993–1001. |
| [7] | BAUMANN F, CHEN J, VOGT K, et al. Improved threshold selection by using calibrated probabilities for random forest classifiers [C]//Computer and Robot Vision (CRV), 2015 12th Conference on. Halifax: IEEE, 2015: 155-160. |
| [8] | WANG P, JIANG T, FAN G, et al. Prediction of torpedo Initial velocity based on random forests regression[C]//Intelligent Human-Machine Systems and Cybernetics (IHMSC), 2015 7th International Conference on. Hangzhou: IEEE, 2015: 337-339. |
| [9] | KREMIC E, SUBASI A. Performance of Random Forest and SVM in Face Recognition[J]. The International Arab Journal of Information Technology, 2016, 13(2): 287–293. |
| [10] | MARATEA A, PETROSINO A, MANZO M. Adjusted F-measure and kernel scaling for imbalanced data learning[J]. Information Sciences, 2014, 257(2): 331–341. |


