2. 滨州学院 山东省高校航空信息技术重点实验室, 山东 滨州 256603
2. Key Laboratory of Aviation Information Technology in University of Shandong, Binzhou University, Binzhou 256603, China
目标跟踪是计算机视觉领域一项重要的研究课题, 在视频监控、导弹制导、智能交通、人机交互等领域得到了广泛的应用.国内外许多学者[1-4]致力于目标跟踪研究, 取得了引人注目的成果.但是, 由于跟踪视频中存在遮挡、光照变化、尺度变化、运动模糊、背景杂乱等影响跟踪性能的因素, 使得设计一个鲁棒的跟踪算法仍是一项具有挑战性的课题.
近年来, 基于稀疏表示的跟踪算法得到了国内外许多学者的关注, 取得了较好的跟踪性能.受稀疏表示在人脸识别算法领域的成功应用启发, Xue等[5]将稀疏表示引入到目标跟踪领域(tracking using L1 minimization, L1), 假设候选样本可以被目标模板和琐碎模板组成的字典矩阵线性表示, 并在跟踪过程中对目标模板进行更新.但是该算法采用Lasso算法求解L1最小化问题以获得系数的稀疏性, 导致L1算法的计算量大, 难以满足快速跟踪的需求.为此, Bao等[6]提出加速近似梯度算法来提高L1算法的跟踪速度, 但是该算法在对目标模板更新过程中, 没有考虑遮挡因素, 导致部分视频跟踪失败.Wang等[7]提出在线增量正交映射非负矩阵分解的跟踪方法, 引入非负矩阵分解, 保留跟踪目标的局部特征信息, 从而实现鲁棒的跟踪, 但是该算法在求解非负矩阵分解时, 计算量大, 同样难以满足快速跟踪的要求.Jia等[8]提出结构化局部稀疏表示的跟踪算法.Zhong等[9]在稀疏表示的基础上将判别模型和生成模型相结合应用到跟踪领域.Wang等[10]提出基于反向稀疏和局部加权距离的目标算法, 降低了每帧需要求解的L1问题的次数, 提高了运算效率.虽然以上基于稀疏表示的算法取得了较好的跟踪效果, 但是跟踪速度较慢, 难以满足快速跟踪的需要.
为此, 受核协同表示在人脸识别[11]和高光谱图像分类[12]领域的成功应用启发, 本文提出一种基于核协同表示的快速跟踪算法(kernel collaborative presentation with L2 regularization, KCRL2), 把跟踪目标和字典矩阵映射到高维空间, 同时引入L2正则最小均方, 弥补以往基于稀疏表示算法速度上的不足.实验结果表明本文算法能够获得较快的跟踪速度, 同时取得较高的覆盖率和较低的中心点误差.
1 基于稀疏表示的跟踪算法近年来, 稀疏表示算法在计算机视觉领域得到了广泛的应用, Xue等[5]首次将稀疏表示应用到目标跟踪领域, 提出基于稀疏表示的目标跟踪算法.该算法通过对稀疏表示系数进行L1范数约束, 并在候选样本中选取具有最小重构误差的样本作为跟踪目标, 其数学模型为
| $\underset{\mathit{\boldsymbol{w}}}{\mathop{\rm{min}}}\,\left\| \mathit{\boldsymbol{Mw}}-\mathit{\boldsymbol{x}} \right\|_{2}^{2}+\lambda {{\left\| \mathit{\boldsymbol{w}} \right\|}_{1}},\quad \quad \rm{s}\rm{.t}.~\mathit{\boldsymbol{w}}\ge 0.$ | (1) |
式中:M=[D, I, -I]为过完备字典矩阵, 由模板矩阵D, 正琐碎矩阵I和负琐碎矩阵-I构成.模板矩阵D由前几帧的跟踪结果组成, 正、负琐碎矩阵为单位矩阵.w=[aT, e+T, e-T]为稀疏表示系数, 由目标表示系数aT、正、负琐碎系数e+T、e-T构成.x表示观测样本.λ为常数.上标T表示转置.
每个候选样本是跟踪目标的概率由下式来建模:
| $p\left( \mathit{\boldsymbol{x}}|\mathit{\boldsymbol{y}} \right)=\frac{1}{\mathit{\Gamma }}\rm{exp}\ \ \left\{ \ -\alpha {{\left\| \mathit{\boldsymbol{Da}}-\mathit{\boldsymbol{x}} \right\|}^{2}} \right\}~.$ | (2) |
式中:a通过对式(1) 求正则最小化求解, α为系数, 控制高斯核函数的形状, Γ为归一化常数.
2 基于核协同表示的跟踪算法 2.1 核协同表示稀疏表示在目标跟踪领域取得了巨大的成功, 但是该算法由于采用琐碎模板, 导致计算量很大, 难以应用到实时跟踪.为了解决这个问题, 本文引入非线性映射φ(·):Rm→F, 把候选样本x和模板矩阵M映射到高维空间, x→φ(x)=[φ(x1), φ(x2), …, φ(xn)], M→φ(M), 并假设映射后的样本φ(x)可以被映射后的模板矩阵φ(M)线性表示, 则核协同表示的目标函数为
| $\underset{\mathit{\boldsymbol{w}}}{\mathop{\rm{min}}}\,\frac{1}{2}\left\| \varphi \left( \mathit{\boldsymbol{x}} \right)-\varphi \left( \mathit{\boldsymbol{M}} \right)\mathit{\boldsymbol{w}} \right\|_{2}^{2}+f\left( \mathit{\boldsymbol{w}} \right).$ | (3) |
式中:f(w)为规则化项.引进一个核函数κ(xi, xj)=〈φ(xi), φ(xj)〉, 本文中, 核函数为高斯核, 则目标函数(3) 式变为
| $\begin{align} & \underset{\mathit{\boldsymbol{w}}}{\mathop{\rm{min}}}\,\frac{1}{2}\left\| \varphi \left( \mathit{\boldsymbol{x}} \right)-\varphi \left( \mathit{\boldsymbol{M}} \right)\mathit{\boldsymbol{w}} \right\|_{2}^{2}+f\left( \mathit{\boldsymbol{w}} \right)= \\ & \underset{\mathit{\boldsymbol{w}}}{\mathop{\rm{min}}}\,\frac{1}{2}\kappa \left( \mathit{\boldsymbol{x}},\rm{ }\mathit{\boldsymbol{x}} \right)+\frac{1}{2}{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{K}_{MM}}\mathit{\boldsymbol{w}}-{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{K}_{M}}\left( \mathit{\boldsymbol{x}} \right)+f\left( w \right)= \\ & \underset{\mathit{\boldsymbol{w}}}{\mathop{\rm{min}}}\,\frac{1}{2}{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{K}_{MM}}\mathit{\boldsymbol{w}}-{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{K}_{M}}\left( \mathit{\boldsymbol{x}} \right)+f\left( w \right). \\ \end{align}$ | (4) |
式中:KMM为n×n的矩阵:[KMM]ij=κ(mi, mj), KM(x)为n×1的向量:[KM(x)]i=κ(mi, x).n为模板矩阵中列向量的个数, mi为模板矩阵中第i个列向量.因为式(3) 目标函数最终目的是求解表示系数w, 所以式(4) 中最后一行可以把κ(x, x)省略.
2.2 基于核协同表示的目标跟踪算法在式(4) 中, f(w)为规则化项, 传统的基于稀疏表示算法中, f(w)项通常选取L1范数约束, 强调表示系数的稀疏性.但是在Zhang等[13]提出在人脸识别分类任务中, 基于L2约束协同表示的作用比稀疏约束的作用更重要, 并通过实验表明, 基于协同表示的识别分类可以取得比基于L1约束更好的性能, 同时具有更快的运算速度.因此, 本文将目标函数设置成具有L2约束的核协同表示:
| $\underset{w}{\mathop{\rm{min}}}\,\frac{1}{2}{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{K}_{MM}}\mathit{\boldsymbol{w}}-{{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{\mathit{\boldsymbol{K}}}_{M}}\left( \mathit{\boldsymbol{x}} \right)+\frac{\lambda }{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^{2}}.$ | (5) |
式中:λ为使式(5) 解更加稳定的惩罚参数.为了求解最优的表示系数w, 对J(w)求关于w梯度等于0的解:
| $\frac{\partial J\left( \mathit{\boldsymbol{w}} \right)}{\partial \mathit{\boldsymbol{w}}}={{\mathit{\boldsymbol{K}}}_{MM}}\mathit{\boldsymbol{w}}-{{\mathit{\boldsymbol{K}}}_{M}}\left( \mathit{\boldsymbol{x}} \right)+\lambda \mathit{\boldsymbol{w}}=0.$ | (6) |
其中:
| ${{\mathit{\boldsymbol{w}}}^{*}}={{\left( {{\mathit{\boldsymbol{K}}}_{MM}}+\lambda \mathit{\boldsymbol{I}} \right)}^{-1}}{{\mathit{\boldsymbol{K}}}_{M}}\left( \mathit{\boldsymbol{x}} \right).$ | (7) |
令Q=(KMM+λI)-1, Q与候选样本x相互独立, 因此对于每一个候选样本求其表示系数时, Q项可以提前计算, 这样就大大加快了运算速度.
在经典的基于稀疏表示的跟踪算法中, 为了解决跟踪过程中出现的遮挡等干扰因素, 引进正、负琐碎模板I和-I, 该方法假设遮挡等干扰因素服从小噪声的高斯分布, 可以采用L1范数对表示系数进行约束, 并成功的对遮挡等干扰因素进行建模, 从而实现对跟踪目标的准确跟踪.本文方法采用L2范数对表示系数进行约束, 若继续采用琐碎模板对遮挡等干扰因素进行建模, 则会导致跟踪失败.为此, 本文引入方块模板[14]来建模噪声项, 该方法假设若一个像素被遮挡, 则这个像素周围的其他像素也有很大可能性被遮挡.因此, 模板矩阵可以写为:M=[D,E]∈Rd×(k+l).其中, D由(Principal basis vectors, PCA)子空间向量组成, E为方块矩阵.d为模板矩阵中特征向量的维数, k为由PCA子空间组成的模板矩阵中特征向量的个数, l为模板矩阵中组成方块矩阵的特征向量的个数.
2.3 运动模型目标跟踪可以看作是贝叶斯框架下隐形状态变量的推理过程.假设从第1帧到第t帧的跟踪视频组成的矩阵为Xt=[x1, x2, …xt], 则第t帧的隐形状态变量zt可以通过迭代的求解下式获得
| $p\left( {{\mathit{\boldsymbol{z}}_t}\left| {{\mathit{\boldsymbol{X}}_t}} \right.} \right) \propto p\left( {{\mathit{\boldsymbol{x}}_t}{\mathit{\boldsymbol{z}}_t}} \right)\int p \left( {\left. {{\mathit{\boldsymbol{z}}_t}} \right|{\mathit{\boldsymbol{z}}_{t - 1}}} \right)p\left( {\left. {{\mathit{\boldsymbol{z}}_{t - 1}}} \right|{\mathit{\boldsymbol{X}}_{t - 1}}} \right){\rm{d}}{\mathit{\boldsymbol{z}}_{t - 1}}.$ | (8) |
式中:p(zt|zt-1)为连续2帧隐形状态的运动模型, p(xt|zt-1)为观测模型.用仿射变换的6个参数建运动模型p(zt|zt-1), 令zt=[χt, yt, θt, st, αt, φt], χt, yt, θt, st, αt, φt分别表示跟踪目标的水平位置、垂直位置、旋转角度、尺度变换、角度变换和斜角比等.
2.4 观测模型在第t帧, Qt矩阵通过(KMtMt+λI)-1求得, 其中, Mt=[Dt,Et], 同时在第t帧跟踪视频上抽取N个候选样本{xti}i=1N, 对每一个候选样本采用式(9) 求表示系数(不失一般性, 去掉下标t),
| $\begin{align} & \underset{w_{b}^{i},w_{e}^{i}}{\mathop{\rm{min}}}\,\frac{1}{2}\mathit{\boldsymbol{w}}_{b}^{{{i}^{\rm{T}}}}{{\mathit{\boldsymbol{K}}}_{DD}}\mathit{\boldsymbol{w}}_{b}^{i}-\mathit{\boldsymbol{w}}_{b}^{{{i}^{\rm{T}}}}{{\mathit{\boldsymbol{K}}}_{D}}\left( {{\mathit{\boldsymbol{x}}}^{i}} \right)+\frac{1}{2}\mathit{\boldsymbol{w}}_{e}^{{{i}^{\rm{T}}}}{{\mathit{\boldsymbol{K}}}_{EE}}\mathit{\boldsymbol{w}}_{e}^{i}- \\ & \quad \quad \quad \mathit{\boldsymbol{w}}_{e}^{{{i}^{\rm{T}}}}{{\mathit{\boldsymbol{K}}}_{E}}\left( {{\mathit{\boldsymbol{x}}}^{i}} \right)+\frac{\lambda }{2}{{\left\| \mathit{\boldsymbol{w}}_{b}^{i} \right\|}^{2}}+\frac{\lambda }{2}{{\left\| \mathit{\boldsymbol{w}}_{e}^{i} \right\|}^{2}}. \\ \end{align}$ | (9) |
则第i个候选样本对应的系数为
| ${\mathit{\boldsymbol{w}}^i} = {\left[ {\mathit{\boldsymbol{w}}_b^i,\mathit{\boldsymbol{w}}_e^i} \right]^{\rm{T}}} = \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{K}}_M}\left( {{\mathit{\boldsymbol{x}}^i}} \right).$ | (10) |
每个候选样本是跟踪目标的概率可由重构误差求得
| $\mathit{\boldsymbol{p}}\left( {\left. {{\mathit{\boldsymbol{x}}^i}} \right|{\mathit{\boldsymbol{z}}^i}} \right) \propto \left\| \varphi \right.\left( {{\mathit{\boldsymbol{x}}^i}} \right) - \varphi \left( \mathit{\boldsymbol{M}} \right)\left. {{\mathit{\boldsymbol{w}}^i}} \right\|_2^2 = - 2{\mathit{\boldsymbol{w}}^{{i^{\rm{T}}}}}{\mathit{\boldsymbol{K}}_M}\left( {{\mathit{\boldsymbol{x}}^i}} \right) + {\mathit{\boldsymbol{w}}^{{i^{\rm{T}}}}}{\mathit{\boldsymbol{K}}_{MM}}{\mathit{\boldsymbol{w}}^i}.$ | (11) |
为了更好地适应跟踪过程中跟踪目标的状态变化, 需要对模板矩阵中的D进行更新.本文引入遮挡比更新机制[15]来确定是否对D进行更新.每帧中跟踪目标的重构误差项e=Ewe反映跟踪目标的被遮挡及对齐状况.定义2个阈值thr1和thr2来确定重构误差的大小(thr1=0.1, thr2=0.6), 当e<thr1时, 表示跟踪目标中只有极少部分像素被遮挡, 可以直接用跟踪结果对D进行更新.当thr1<e<thr2, 表示跟踪结果部分像素被遮挡, 可以采用均值向量来代替被遮挡的部分, 然后对D进行更新.当thr2<e时, 表明跟踪结果大部分被遮挡, 则该跟踪结果被舍弃, 不用来对D进行更新.
3 实验结果本文算法在Window8操作系统下, Inter(R) Core(TM) i7-5500U CPU@2.40GHz, 8G内存的电脑平台采用MatlabR2014a进行仿真实验.每帧中采样粒子的数目为600个, 每个采样图像块统一缩放为32×32像素, 模板矩阵中基向量的个数为16, 方块矩阵的个数为256, 大小为2×2像素, 每隔5帧对模板矩阵中的基向量进行更新.为了验证本文算法的优越性, 采用12个具有挑战性的视频(分别具有部分遮挡、背景杂乱、尺度变化、光照变化等影响干扰性能的因素)与当前比较流行的6种算法:稀疏原型跟踪算法(online object tracking with sparse prototypes, OSPT[16])、分块跟踪算法(fragments-based tracking, Frag[17])、多示例跟踪算法(tracking with online multiple instance learning, MIL[2])、最小软阈值均方跟踪算法(least soft-threshold square tracking, LSST[15])、L1[5]、连续异常噪声模型跟踪算法(tracking via probability continuous outlier model, PCOM[18-19])进行对比.
3.1 定性对比严重遮挡:存在严重遮挡的occlusion1、caviar1、caviar2视频部分跟踪结果如图 1所示.

|
图 1 含有严重遮挡的occlusion1、caviar1、caviar2视频截图 Fig. 1 Video clips of occlusion1、caviar1、caviar2 with severe occlusion |
从图 1中可以看出, occlusion1视频中人物头部的位置基本不发生变化, 但是存在分别来自左方、右方以及下方书的严重遮挡;caviar1和caviar2目标人物分别存在由近到远以及由远到近的位置移动, 同时存在尺度变化以及旁边其他移动人物的遮挡.由于KCRL2、OSPT、LSST、PCOM算法在跟踪过程中对模板矩阵更新时考虑了遮挡因素, 针对不同的遮挡率, 采用不同的更新机制, 因此对存在严重遮挡的视频跟踪成功.L1算法虽然也是基于稀疏表示原理的跟踪算法, 但是该算法对模板矩阵更新时没有考虑遮挡因素, 所以对存在遮挡的视频跟踪时, 性能不稳定, occusion1出现偏移, caviar1则当出现相似人物干扰时, 跟丢目标人物, caviar2跟踪成功.MIL算法由于采用harr特征, 很容易受到相似物体的干扰, 跟丢目标.
光照变化:存在严重光照变化的car4、car11、singer1、davidindoor视频部分跟踪结果如图 2所示.

|
图 2 含有光照变化的car4、car11、singer1、davidindoor视频截图 Fig. 2 Video clips of car4、car11、singer1、davidindoor with illumination change |
从图 2中可以看出, 当car4视频经过桥洞时, 存在桥洞阴影的变化, 同时存在道面及周围相似树木对跟踪目标汽车的干扰;car11视频, 对面汽车灯光及树枝上的灯光严重影响对目标汽车的跟踪;在singer1视频中, 舞台上方的灯光干扰着对白衣歌者的跟踪, 同时由于摄像机位置的变化, 导致歌者的尺度也存在由大及小的变化;在davidindoor视频中, 目标人物从黑暗的屋子走向明亮的客厅, 同时目标头部存在旋转等影响跟踪性能的因素.从跟踪结果来看, KCRL2、OSPT、LSST、PCOM算法由于在跟踪过程中, 每隔5帧就对模板矩阵进行更新, 所以能够适应跟踪目标的亮度变化, 从而能够对目标进行准确的跟踪, 同时由于采用仿射变换, 能够适应跟踪目标的尺度变化.Frag、MIL算法没有考虑到尺度变换, 所以跟踪过程中目标框的大小是固定的, 影响了跟踪性能, 同时对光照变化比较敏感, 容易跟丢目标.
运动模糊:存在严重运动模糊的jumping、owl、face部分视频跟踪结果如图 3所示.

|
图 3 存在运动模糊的jumping、owl、face视频截图 Fig. 3 Video clips of with motion blur |
从图 3中可以看出, jumping视频, 摄像机不动, 目标人物由于快速上下跳绳, 导致人物头部存在模糊现象;在owl视频中, 门上图片的小熊位置不动, 但是摄像机存在快速的上下左右运动, 导致视频中小熊图像严重模糊;在face视频中, 摄像机及人物头部均存在快速移动, 导致人物头部模糊不清.从跟踪结果来看, KCRL2、LSST算法能够适应目标和摄像机的快速移动导致的运动模糊, 从而准确的进行跟踪.其他6种算法均难以克服运动模糊对跟踪性能的影响, 导致跟踪失败.
背景杂乱:存在严重背景杂乱的football、davidoutdoor部分视频跟踪结果如图 4所示.

|
图 4 背景杂乱的football、davidoutdoor外视频截图 Fig. 4 Video clips of football、davidoutdoor with background clutter |
从图 4中可以看出, football、davidoutdoor视频中, 背景存在很多跟踪目标相似的区域, 同时还存在相似物体的遮挡干扰, 严重影响跟踪性能.KCRL2、LSST算法一直跟踪稳定, 成功的实现了跟踪, 其他算法都偏移到跟踪目标相似的区域.
3.2 定量对比本文采用2个指标:中心点评估(中心点误差曲线和平均中心误差值)和覆盖率评估(覆盖率曲线和平均覆盖率值)对不同算法进行定量对比.中心点误差的定义为
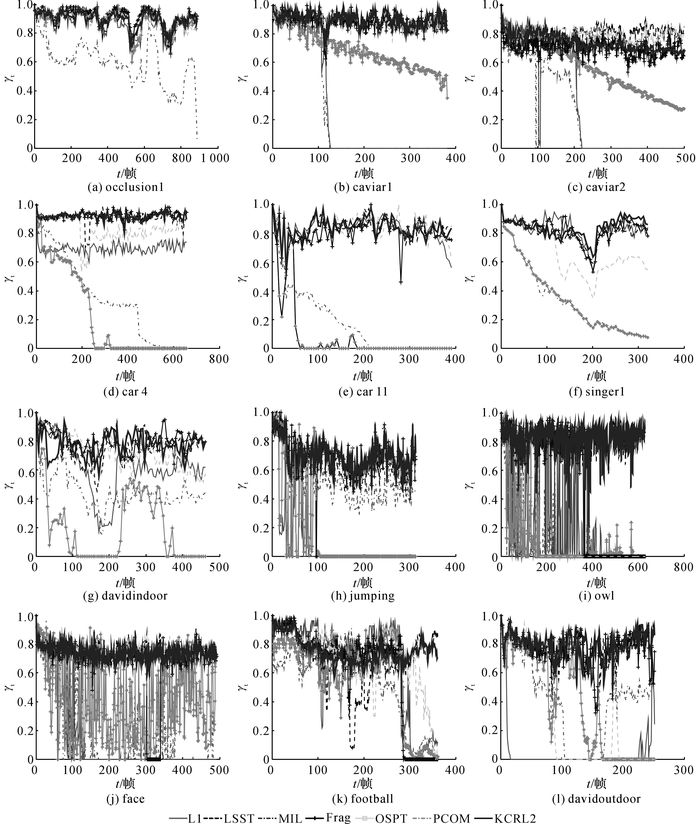
|
图 5 不同算法的覆盖率对比 Fig. 5 Comparison of overlap rates of different algorithms |

|
图 6 不同算法的中心点误差对比 Fig. 6 Comparison of center location error of different algorithms |
| 表 1 不同算法的平均覆盖率对比 Table 1 Comparision of average overlap rates of different algorithms |
| 表 2 不同算法的平均中心点误差对比 Table 2 Comparision of average center location errors of different algorithms |
在基于稀疏表示的跟踪算法中, 算法的复杂度主要在系数的求解上, KCRL2算法通过式(7), w*=(KMM+λI)-1KM(x)进行系数的求解, Q=(KMM+λI)-1可在每次迭代之前求出, 所以系数的求解为w*=QKM(x), 时间复杂度为O(dk+dl+d2).而传统L1算法的时间复杂度为O(m(d2+dk)), m为传统L1算法的迭代次数, m的取值为50到200之间.通过时间复杂度对比, 可见KCRL2算法比传统L1算法跟踪速度上有了很大的提升.
表 3给出了6种算法的跟踪速度对比, s为跟踪速度, 单位为帧/s, 从表 1、2、3可以看出, 虽然MIL、PCOM算法的跟踪速度比KCRL2算法要快, 但是KCRL2算法的跟踪精度上要领先MIL、PCOM算法, 因此本文算法既能能够实现的较快的目标跟踪, 同时具有较高的跟踪精度.
| 表 3 不同算法的跟踪速度对比 Table 3 Comparison of tracking speed of different algorithms |
提出一种基于核协同表示的快速跟踪算法, 在粒子滤波框架下, 在高维空间建立候选样本和字典矩阵的线性模型, 同时引入L2正则化, 加快算法的跟踪速度, 观测模型中引入遮挡因素, 有选择的对模板矩阵进行更新, 实验结果表明, 本文算法能够有效应对跟踪过程中出现的场景光照变化、目标姿态变化、遮挡等问题, 实现快速鲁棒的跟踪.
| [1] |
于慧敏, 曾雄. 结合排序向量SVM的视频跟踪[J].
浙江大学学报:工学版, 2015, 49(6): 1015–1021.
YU Hui-min, ZENG Xiong. Visual tracking combined with ranking vector SVM[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(6): 1015–1021. |
| [2] | BABENKO B, YANG M H, BELONGIE S. Robust visual tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33: 1619–1632. DOI:10.1109/TPAMI.2010.226 |
| [3] | GAO J, LING H, HU W, et al. Transfer learning based visual tracking with gaussian process regression[C]//Proceedings of European Conference on Computer Vision. Zurich: Springer, 2014: 188-203. |
| [4] | MA B, HU H W, SHEN J B, et al. Linearization to Nonlinear Learning for Visual Tracking[C]// Proceedings of IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 4400-4407. |
| [5] | XUE M, LING H B. Robust visual tracking using L1 minimization[C]//Proceedings of IEEE International Conference on Computer Vision. Kyoto: IEEE, 2009: 1436-1443. |
| [6] | BAO C L, WU Y, LING H B, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2012: 1830-1837. |
| [7] | WANG D, LU H C. On-line learning parts-based representation via incremental orthogonal projective non-negative matrix factorization[J]. Signal Processing, 2013, 93: 1608–1623. DOI:10.1016/j.sigpro.2012.07.015 |
| [8] | JIA X, LU H C, Yang M H. Visual tracking via adaptive structural local sparse appearance model[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2012:1830-1837. |
| [9] | ZHONG W, LU H CH, YANG M H. Robust object tracking via sparse collaborative appearance model[J]. IEEE Transaction on Image Processing, 2014, 23(5): 2356–2368. DOI:10.1109/TIP.2014.2313227 |
| [10] | WANG D, LU H CH, XIAO Z Y, el al. Inverse sparse tracker with a locally weighted distance metric[J]. IEEE Transaction on Image Processing, 2015, 24(9): 2646–2657. DOI:10.1109/TIP.2015.2427518 |
| [11] | WANG D, LU H, YANG M H. Kernel collaborative face recognition[J]. Pattern Recognition, 2015, 48(10): 3025–3237. DOI:10.1016/j.patcog.2015.01.012 |
| [12] | LI W, DU Q, XIONG M M. Kernel collaborative representation with tikhonov regularization for hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 48–52. |
| [13] | ZHANG L, YANG M, FENG X. Sparse representation or collaborative representation: which helps face recognition?[C]//Proceedings of IEEE International Conference on Computer Vision. Barcelona: IEEE, 2011, 471-478. |
| [14] | SHI Q, ERIKSSON A, HENGEL A, et al. Is face recognition really a compressive sensing problem?[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Colorado Springs: IEEE, 2011: 553-560. |
| [15] | WANG D, LU H C, Yang M H, et al. Least soft-threshold square tracking[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Porland OR: IEEE, 2013: 2371-2378. |
| [16] | WANG D, LU H C, Yang M H. Online object tracking with sparse prototypes[J]. IEEE Transaction on Image Processing, 2013, 22(1): 314–325. DOI:10.1109/TIP.2012.2202677 |
| [17] | ADAM A, RIVLIN E. Robust fragments-based tracking using the integral histogram[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington: IEEE, 2006: 798-805. |
| [18] | WANG D, LU H CH. Fast and robust object tracking via probability continuous outlier model[J]. IEEE Transaction on Image Processing, 2015, 24(12): 5166–5176. DOI:10.1109/TIP.2015.2478399 |
| [19] | WANG D, LU H CH. Visual tracking via probability continuous outlier model[C]// Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH: IEEE, 2014: 3478-3485. |


