2. 沈阳工业大学 理学院, 辽宁 沈阳 110870
2. School of Science, Shenyang University of Technology, Shenyang 110870, China
细颗粒物在普通电除尘器(electrostatic precipitator)中难以被收集的主要原因在于:由电晕放电引起的离子风会改变内部流场的形态, 使内部流场由均匀分布的层流变为复杂的湍流.细颗粒物更易穿透, 从而难于沉降到收尘极板上.并且, 由于湿式电除尘器(wet electrostatic precipitator)使用沿收尘极板壁面的均匀水膜来达到清灰的目的.水膜的流动会进一步使内部流场复杂化.为了有针对性的提升电除尘器的效率, 更好地理解电除尘器内部颗粒在上述复杂物理条件下的运动状态, 除尘器内部流场必须作为设计运行中的考量因素之一.
目前热门的用于实验室规模电除尘器流场可视化的设备有激光-多普勒速度计(Laser-Doppler velocimetry)以及粒子成像测速仪(Particle Image Velocimetry)等[1-2].Mizeraczyk等[3]使用二维及三维PIV分别研究一次流均匀分布的情况下离子风对除尘器内部流体的影响.并且对其他影响因素, 如不同粒径的颗粒物收集、极线排布方式及不同施加电压等也有研究报道[4-5].
实验手段进行流场分析有着诸多限制, 如静电场对测量的干扰, 观察视角的限制等, 往往造成取得预期的结果并不容易.因此模拟手段开始被广泛运用.其中, 有限元-特征方法(MoC)[6-7], 有限元-边界元(BEM)[8], 有限元-电荷模拟(CSM)[9]有限元-供体网格法(DCM)[10]和有限元差分法(FDM)[11]主要用于在二维模型中获得电场相关特性.主要包括电场及电荷分布, 电晕放电的伏安曲线等.Soldati[12]和Skodras等[13]使用直接数值模拟(DNS)法于多极线电除尘器中分析粒子轨迹.基于上述文献的结论, 无论从理论或实验中, 均已证实离子风的存在对于总收尘效率有着显著的影响.
尽管不同数值化分析方法已有很多报道, 各种模型方法也还是有各自的局限.对于真实工况下的还原还是有很多限制, 并不能完全取代实验的方法.大部分情况下模拟的结果还是需要靠与实际实验比对来做各种修正和完善.
本文采用三维模型计算双高压极线布置下粒子在湿式电除尘器内的运动轨迹, 计算涉及复数物理场效果的耦合分析.研究基于有限元方法模拟得到电场分布、电势分布、粒子荷电量、气流分布、颗粒物轨迹以及极板上的累积量.所使用模拟软件为COMSOL.结果表明除尘器内流体和静电力对粒子运动均有不同程度的影响.
1 模型描述与数值分析方法 1.1 模型描述采用模型为标准线板式除尘器.具体布置方式如图 1所示.风道尺寸为0.6 m×0.2 m×0.2 m.在Y-Z平面上, 左右壁面布置有2块接地收尘极板, 板板间距为0.2 m.2块接地极板分别以1 m/s的速度沿Z轴负方向运动以模拟湿式除尘器内的水膜流动.2根直径为3 mm的高压线电极布置在极板及风道的中央, 在Y轴上的投影坐标分别为0.2及0.4 m.其上依次被加载30和72 kV直流高压电.一次流为流速0.1 m/s的均匀层流.出口压力为0 Pa(表压).一次流方向为沿Y轴正方向流动.在实际工业过程中, 含尘烟气最初(锅炉尾气)的烟温可达到600 ℃以上.在进入湿式除尘器内部之前, 会先经过预氧化装置, 干式静电除尘器, FGD, 低温省煤器等设备.在此过程中烟气温度持续下降.该降温过程可以保证烟气中的湿度一直处于饱和状态.因此在该模拟过程中参数选取如下:风道内烟温为180 ℃.空气黏度μ=1.98×10-5 kg/m·s, 空气密度ρ=0.746 kg/m3, 离子迁移率k=2.4×10-4 m2/V.

|
图 1 三维模型及电极配置图 Fig. 1 Schematic graph of 3-D model and electrodes configuration |
在静电场条件下, 电场E与电势V的关系为
| $ E = - \nabla V. $ | (1) |
同时, 由于电位移矢量D与电场E之间有如下关系:D=ε9εrE, 结合上式则可将高斯定律改写成以下形式:
| $ \nabla \mathit{\boldsymbol{D = }}{\rho _{\rm{v}}}. $ | (2) |
| $ \nabla {\varepsilon _0}{\varepsilon _{\rm{r}}}E = {\rho _{\rm{v}}}. $ | (3) |
对于接地极, 采用如下边界条件定义:
| $ \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{D}} = 0. $ | (4) |
式中:E为电场强度;D为电位移矢量;∇D为对D的拉普拉斯算子;ρv为空间电荷密度;ε0为真空介电常数;εr为相对介电常数;n为极板的法线向量.
1.3 粒子荷电方程不同粒径的粒子在静电场中基本有2种不同的荷电机理, 即扩散荷电及场荷电[14].在该模型中, 为简化计算流程, 在误差不大的情况下仅考虑场荷电效应.相关粒子荷电方程如下:
| $ q\left( t \right) = {q_\infty }\frac{{t/\tau }}{{1 + t/\tau }}. $ | (5) |
| $ {q_\infty } = {\rm{\pi }}{\varepsilon _0}\frac{{3{\varepsilon _{\rm{r}}}}}{{{\varepsilon _{\rm{r}}} + 2}}d_{\rm{p}}^2E. $ | (6) |
| $ \tau = 4\frac{{{\varepsilon _0}E}}{J} $ | (7) |
式中:q∞为饱和荷电量;t为荷电时间;τ为场荷电常数;dp为颗粒物粒径;J为电流密度.
1.4 湍流场描述方程本例中计算湍流场采用了雷诺平均方程(reynolds-averaged navier-stokes, RANs)[15].基本假设流体为可压缩并属于牛顿流体.适用此条件的相关物理场方程为
动量守恒方程:
| $ \begin{array}{l} \rho \left( {u\nabla } \right)u = \\ \;\;\;\;\nabla \left[ { - p\mathit{\boldsymbol{I + }}\left( {\mu + {\mu _T}} \right)\left( {\nabla u} \right)\mathit{\boldsymbol{I}} - \frac{2}{3}\rho \kappa \mathit{\boldsymbol{I}}} \right] + {\mathit{\boldsymbol{F}}_{{\rm{mf}}}}. \end{array} $ | (8) |
质量守恒方程:
| $ \nabla \left( {\rho u} \right) = 0. $ | (9) |
能量守恒方程:
| $ \rho \left( {u\nabla } \right)\kappa = \nabla \left[ {\left( {\mu + \frac{{{\mu _T}}}{{{\sigma _\kappa }}}} \right)\nabla \kappa } \right] + {P_\kappa } - \rho \varepsilon . $ | (10) |
耗散比:
| $ \begin{array}{l} \rho \left( {u\nabla } \right)\kappa = \rho \left( {u\nabla } \right)\kappa = \nabla \left[ {\left( {\mu + \frac{{{\mu _T}}}{{{\sigma _\kappa }}}} \right)\nabla \kappa } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;{C_{e1}}\frac{\varepsilon }{\kappa }{P_\kappa } - {C_{e2}}\rho \frac{{{\varepsilon ^2}}}{\kappa }. \end{array} $ | (11) |
| $ {\mu _T} = \rho {C_\mu }\frac{{{\kappa ^2}}}{\varepsilon }. $ | (12) |
| $ \begin{array}{l} {P_\kappa } = {\mu _T}\left[ {\nabla u:\left( {\nabla u + {{\left( {\nabla u} \right)}^{\rm{T}}}} \right) - \frac{2}{3}{{\left( {\nabla u} \right)}^2}} \right] - \\ \;\;\;\;\;\;\;\frac{2}{3}\rho \kappa \nabla u. \end{array} $ | (13) |
式中:u为速度场;p为压力;ρ为密度;I为单位矩阵;Fmf为主流场向量;κ为湍流动能;ε为涡流耗散比;Pκ为湍动能每单位耗散净产出;μ为层流黏性系数;μT为湍流黏性系数;C, σ为相关常数.
1.5 湍流场造成的粒子运动连续分散相间动量传递方程表达式为[16-17]:流体中均匀分散的粒子同时受到数种力的作用, 如拖拽力, 重力, Basset力, 升力等等.其中最重要的就是流场拖拽力.在该模型中, 拖拽力表现为除尘器内的流场流动对粒子本身的带动作用.为每个计算节点相应的流场动量传递给相应位置粒子的动量.计算关系如下:
| $ \begin{array}{l} {\rho _{\rm{a}}}{\phi _{\rm{a}}}\left[ {\frac{\partial }{{\partial t}}\left( {{u_{\rm{a}}}} \right) + {u_{\rm{a}}}\nabla \cdot \left( {{u_{\rm{a}}}} \right)} \right] = - {\phi _{\rm{a}}}{\nabla _p} + \\ \;\;\;\;\nabla \cdot \left( {{\phi _{\rm{a}}}{\tau _{\rm{a}}}} \right) + {\phi _{\rm{a}}}{\rho _{\rm{a}}}g + {F_{ma}} + {\phi _{\rm{a}}}{F_{\rm{a}}}. \end{array} $ | (14) |
| $ {F_{{\rm{drag,a}}}} = - {{\dot F}_{{\rm{drag,b}}}} = \beta {u_{{\rm{slip}}}}. $ | (15) |
| $ {u_{{\rm{slip}}}} = {u_{\rm{b}}} - {u_{\rm{a}}}. $ | (16) |
式中:g为重力向量方向加速度;φ为粒子直径;Fdrag为拖拽力;uslip为相对滑动速度;Fm为相间动量转移量(即一相施加于另一相上的力);F为其他体积力,下标a、b指的是不同的2个相.
2 结果与讨论 2.1 静电场静电场的模拟结果如图 2所示.其中, 电场强度以切面形式表示, 切面位于各轴中部;电势以等势线形式表示.从图中可以看出电势沿高压线位置向外扩散并均匀分布, 越靠近高压线中心等势线越呈圆形, 越靠近接地极板则等势线开始变为椭圆状.由于两极线距离较近, 风道中央出现一个交联的等势场.

|
图 2 72 kV下电场强度(切面图)及电势(等势线)分布图 Fig. 2 Electric field distribution (multislice plot) andelectric potential distribution (contour plot) under 72 kV |
图中沿极线壁面很短一段范围内属于电场强度较高的区域, 该区域也是实际产生电晕放电的区域.颗粒物在该区域荷电效率最高, 受到的库仑力也最强.然而在距离极线稍远的区域, 电场强度开始明显下降.颗粒荷电效率以及受到的库仑力也随之剧烈下降.其表现出改变原始运动轨迹的趋势也越弱.
2.2 湍流场与流线如图 3所示为施加不同电压后, 在离子风以及壁面移动情况下除尘器内部的气流分布.图中WW(with water)为有壁面水流, NW (no water)为无壁面水流,由图可以看出, 电晕放电产生的离子风对一次流产生了明显的影响.由于离子风的方向是由高压极垂直指向接地极.考虑到电极分布的对称性以及一次流主要为层流, 在一次流流速较低时, 整个流场能产生复杂的湍流运动, 形成数个涡旋.在无壁面移动条件下该结果与已有实验结果相比具有很高的相似性[18].有壁面移动(水流)的条件下的速度场实验结果仍未见报道.

|
图 3 30与72 kV在不同初始流速条件下速度场与流线图 Fig. 3 Velocity field and stream line under 30 kV (left two column) and 72 kV (right two column) with variousprimary flow speed |
由图中可以看出, 由于二次流和一次流的叠加, 使得整体流速产生分布不均的情况.在无一次流条件下, 由电晕产生的离子风造成了风道内部湍流流动并在各线电极前后均产生了不同形态的涡旋.由于两极线相对位置较近, 中间部分的涡旋受到相互间的挤压而直径较小, 相对的, 靠近两侧的涡旋呈现出相对椭圆的形态.在两侧有壁面移动的条件下, 30 kV电压下离子风造成的X-Y平面内的涡旋基本消失, 取而代之的是X-Z平面内由壁面移动造成的涡旋.而72 kV条件下可以看出由离子风造成的涡旋依然一定程度上可见.说明两垂直平面上的涡旋强度基本均等.随着一次流的加入, 涡旋形态出现了明显偏转.位于两极线中部的涡旋融合成了一个.并且在下游处的涡旋较之上游处的涡旋变得更加椭圆.
随着一次流继续上升, 30 kV下由离子风造成的涡旋迅速消失.主要表现为上游处的涡旋消失, 并且在两极线下游处分别出现了明显的涡旋, 该涡旋形成一个速度空腔使得该区域内颗粒物无法有效地向极板方向移动, 并且浪费了极线附近高效荷电和驱进区域.72 kV情况下该涡旋直径更大, 占据了整体风道中的大部分区域.在有壁面移动的条件下, X-Z平面内的涡旋出现明显向下游偏转的趋势.其强度也在减弱.
由结果可推断, 增加一次流速可以有效缓解由离子风和壁面水流造成对整体气流流动的影响, 但在整体风道长度不变的情况下也势必会造成颗粒物停留时间降低.另外加大电压可以使得颗粒物荷电效率提高, 沈欣军等[19]使用PIV粒子测速仪获得了相似条件下除尘器中的真实流场分布, 该测试结果可以做为本文模拟结论的一个有效对比.本论文中, 在给定的条件下, 模拟计算获得的流场结果接近实测流场形态.涡流分布, 涡流直径等均与实验值近似.
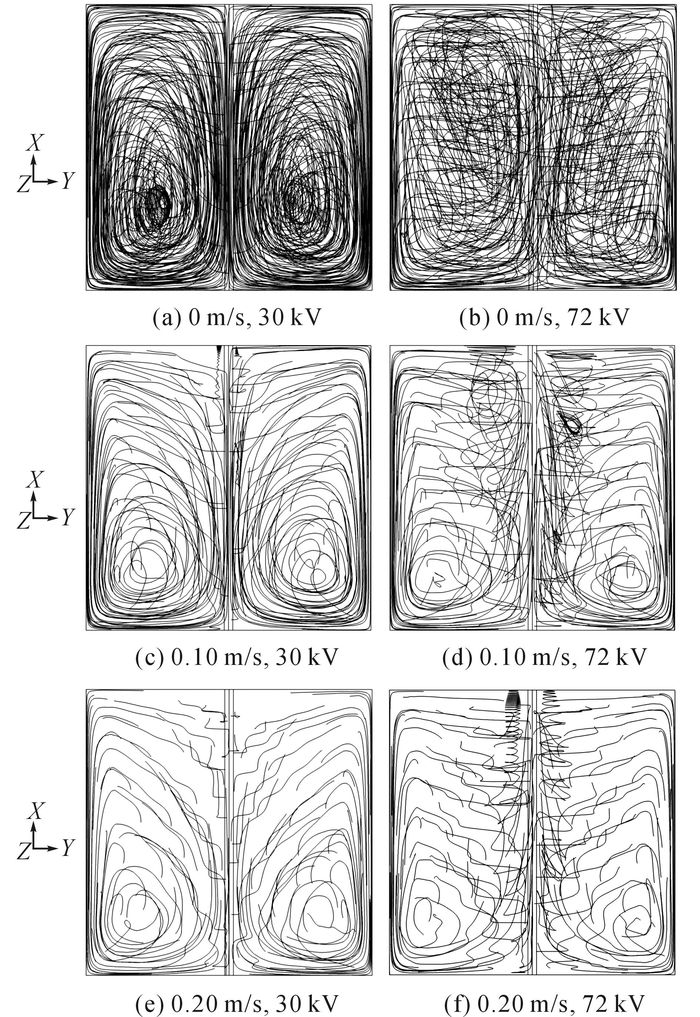
如图 4所示为侧视方向(X-Z平面)下的流线分布情况.由于离子风方向是沿X轴方向, 壁面移动(水流)方向是沿Z轴负方向, 因此在该角度能更加直观显示出壁面移动给整体流场造成的影响.由图可看出, 在电压30 kV下, 侧向风量为0时, 水流造成的涡旋占据绝对主导地位, 随着一次流速上升, X-Z平面上由水流造成的涡旋逐渐减弱.该方向上, 离子风造成的涡旋在该方向上的投影基本以偏移量不大的直线段为主.当电压升高至72 kV, 侧向风量为0时, 侧向流线变得杂乱, 证明在该条件下2种涡流具有同等的强度.随着一次流速增加, 水流造成的涡旋同步下降, 但是也可看出离子风造成的涡旋影响范围也比30 kV下更广.
|
图 4 不同初始流速条件下由壁面移动造成的气流分布流线图 Fig. 4 Stream line of vortices caused by wall function under various primary flow speed |
水膜流动给整体流场产生的影响相比离子风的影响更为持续.结合图 3可以看出X-Y平面内的涡旋一直存在, 虽然其强度也随一次流的增加而减弱, 但是减弱幅度明显小于离子风涡旋的幅度.在水膜流动条件下, 整体流场体现出明显的三维运动的特征.使粒子轨迹变得更加复杂.
2.3 粒子轨迹不同粒径的粒子在除尘器内部的运动状态也不尽相同, 为直观显示各粒径段粒子在给定的多物理场条件下的运动轨迹, 在上述模型中分别释放4种粒子并评判其在流场中的运动轨迹与受力分析, 粒径分别为0.3、1、2.5、10 μm.用于考量的作用力为库仑力, 流场拖拽力以及重力.颗粒物释放方式为一次释放, 由于粒子释放位置及其在该处所受力一致, 则可认为之后进入除尘器的所有粒子均拥有相似的运动轨迹.分布方式为同时在入口处及风道中均匀散布.数量分别为1 000.为使各因素的影响能够充分发挥, 选定电压为72 kV, 一次流速为0.1 m/s, 壁面移动作为对比条件.
如图 5所示分别显示了粒径10 μm粒子在给定条件下的运动轨迹.

|
图 5 上视及平视下粒径为10 μm粒子在电场中的运动轨迹及极板上的沉积 Fig. 5 Trajectory of 10 μm particle in upper and side view and deposit distribution on collecting plates |
每种粒子运动过的轨迹以流线表示.在其他变量均固定的情况下, 由式(5)~(7) 可看出, 粒子荷电量与直径的平方成正比, 因此10 μm粒子受到的库仑力相比其他粒径段的粒子强数个数量级.具体表现为由入口部分进入的粒子还在并未到达第1电极之前就基本完全沉积到收尘极板上, 从图 5(c)中可看出颗粒物均在第1电极上游附近被捕集.
颗粒物在极板上的累计量由定义的边界条件计算得到.给定边界条件如下:
| $ {R_{{\rm{Accumulation}}}} = \sum\nolimits_{p = 1}^{{N_{{\rm{paricles}}}}} {\frac{{{q_m}}}{{{A_{{\rm{face}}}}}}} . $ | (17) |
式中, qm为颗粒物质量流量, 单位为kg/s, Aface为收尘极板上的网格面面积, 单位为m2.
在图 5中, 不同灰度代表了在极板上该区域颗粒物的累积量.越亮表示该处颗粒扬累积量越高,越暗表示累积量越低.从图中可看出, 收集量最高的区域位于极线稍微靠近上游的位置.
值得注意的是, 在风道中散布的粒子显示, 部分位于第1极线上游区域的粒子在电场的驱进下表现出逆向气流方向移动的趋势.且其偏转的位置与由入口释放的粒子偏转的位置基本相同.该处也是此粒径段颗粒在极板上沉积量最大的位置.同时可看出, 在有壁面移动的条件下, 位于风道底部的颗粒比风道顶端的颗粒有更进一步向前移动的趋势.该现象可理解为由壁面移动造成的涡旋在风道底部造成的回流使得颗粒物所受到的重力得到抵消, 致使位于该方向上的颗粒沉降速度下降并向风道中部集中.最终导致该部分颗粒在更加靠近极线的位置附近(电场强度更强)才得以被收集.
如图 6所示为粒径2.5 μm的粒子轨迹及极板沉积量.从图中可以看出, 由入口散布的粒子开始偏移的位置更加接近第1电极, 运动的轨迹也更加向后延伸, 而风道中散布的粒子轨迹也更加明显, 证明其经过了更长时间之后才被收集.在涡流区的粒子开始有随涡流旋转的趋势, 这部分粒子速度明显低于接近极板附近粒子的速度, 其向极板运动的趋势也越低.总的来说, 颗粒物累积最多的位置依然出现于第1极线周围.与图 5结果比较, 所收集的颗粒物在极板上分布开始加宽.

|
图 6 上视及平视下粒径为2.5 μm粒子在电场中的运动轨迹及极板上的沉积 Fig. 6 Trajectory of 2.5 μm particle in upper and side view and deposit distribution on collecting plates |
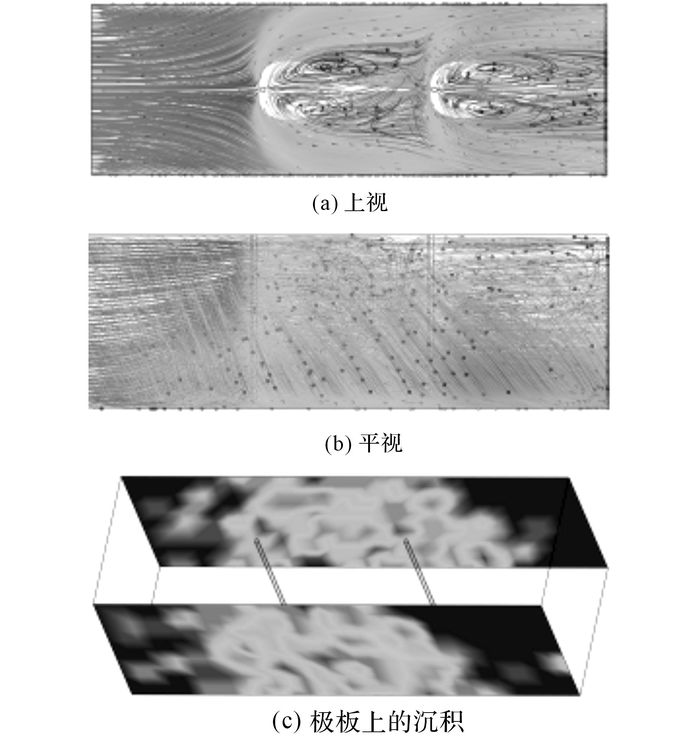
如图 7和8所示分别为粒径1和0.3 μm粒子轨迹及极板沉积量.随着颗粒物直径进一步减小, 其自身所荷电量也急剧降低, 体现为颗粒轨迹在流场中所受到库仑力的偏转也更小.粒子轨迹也在逐渐靠近极线附近(电晕区)之后才开始产生偏转.然而远离电晕区的部分, 也就是靠近极板周围的部分, 库仑力强度随距离增加而下降.颗粒物则有明显重新遵从流场运动轨迹的趋势.由图 7及8中可以看出, 颗粒的运动轨迹基本开始与图 3显示的流线重合.在涡流区中包含的颗粒更多, 加上其相对运动速度较慢, 使得这部分颗粒向收尘极板的运动趋势进一步减弱.意味着他们会更加难以被收集.另外, 越靠近极板, 粒子拥有越大的速度.同时在远离高压极线的区域电场强度也相对更弱.两者结合降低了这部分区域粒子的停留时间.高速区域的粒子速度可达到一次流速的2~3倍.几乎绝大部分颗粒都随着一次流被带出除尘器.造成除尘器对该粒径段的粒子收集效率大大降低, 根据出口截面的统计来看分别只为27.8 %及11.3 %.图 7及8中粒子在极板上的沉积指出, 高效收尘的区域进一步向下游移动直至逐渐模糊, 在下游区脱离第2极线区域后几乎失去对粒子的捕集能力.导致大部分粒子在并未捕集之前就已经离开烟道.

|
图 7 上视及平视下粒径为1 μm粒子在电场中的运动轨迹及极板上的沉积 Fig. 7 Trajectory of 1 μm particle in upper and side view and deposit distribution on collectingplates |
|
图 8 上视及平视下粒径为0.3 μm粒子在电场中的运动轨迹及极板上的沉积 Fig. 8 Trajectory of 0.3 μm particle in upper and side view and deposit distribution on collectingplates |
本文对一次流流速为0.1 m/s, 72 kV情况下壁面移动对收尘效率产生的影响进行了计算对比, 结果如表 1所示.表中, Nd为捕集数量,Ne为逃逸数量,η为捕集效率.
| 表 1 一次流速为0.1 m/s, 72 kV情况下收尘效率总结 Table 1 Collection efficiency summary under primary flow speed at 0.1 m/s |
实际计算所得效率较实验值低, 这与该模拟中使用的粒子释放方式有关.为显示涡流区的粒子轨迹, 粒子采用了入口处释放及烟道内均布释放的双重释放方式.入口处的粒子能受到完整的库仑力, 而烟道内均布的粒子由于所处位置不尽相同, 位于中部, 尤其是下游处的粒子几乎在释放瞬间就离开烟道, 并未有足够的时间受到气流或电场的偏转.若只使用入口处释放, 不仅会使10 μm及2.5 μm粒子收尘效率达到100 %而无法比较, 更会难以显示位于涡旋中粒子的轨迹.
由结果可知, 总的来说壁面移动造成的收尘效率区别明显.有壁面移动的条件下收尘效率较无移动条件下高.尤其对于2.5 μm粒径段, 差距接近20 %.然而随着粒径减小, 该影响也逐渐下降.0.3 μm粒径段捕集效率已无明显差距.一方面由于该粒径段粒子捕集基数已经不高, 另一方面该粒径段的颗粒轨迹已几乎和流场一致.
值得指出的是, 实际湿式除尘器中由于湿度往往处于饱和, 细颗粒物在运动状态下容易与悬浮的水汽颗粒凝并, 成为较大颗粒.因此对于实际操作情况下湿式除尘器对细颗粒物的捕集效率会更高.实际工业操作中影响颗粒物收集效率的因素(包括已知和未知因素)也比模拟中更为复杂.数值模拟中难以还原真实工况下的各种细节, 如灰尘比电阻和颗粒层厚度堆积造成的反电晕等等.模拟中难以重现与实际实验相同的结论.另一方面也表明, 实际湿式除尘器中由于水流流动对整体流场的改变对于细颗粒物收集来说并不占主导因素.
2.5 各颗粒物受力分析为对流场内的粒子进行受力分析, 在72 kV, 一次流速为0.1 m/s, t = 2 s(粒子刚好经过第1极线), 流场的同侧(粒子受到库仑力的矢量方向相同)对4种不同粒径的粒子分别均匀采样100个进行评估.各受力情况平均值如图 9所示.
|
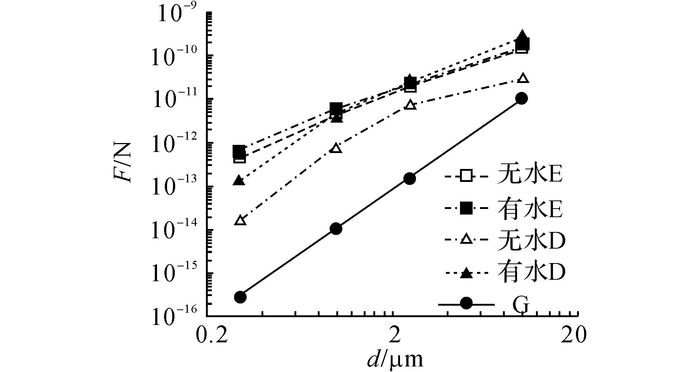
图 9 不同粒径粒子受力分析 Fig. 9 Force analysis of different diameter particles |
由于粒子在除尘器内的运动主要决定于所受到的库仑力(E), 流场拖拽力(D)和重力(G).从图 9中可知, 当壁面无移动, 在高电压下导致粒子运动的第1因素为电场力.由于粒径越大, 颗粒物自身荷电量越多, 故所受到的库仑力越大.其次主导粒子运动的因素为流体的拖拽力.两者的差距在0.3 μm情况下达到2个数量级, 随着粒径的增加, 差距逐渐减小到同一数量级之内.但当加入壁面移动后, 流场拖拽力逐渐上升至与电场力持平.在粒径为10 μm时甚至超过电场力变为第1影响因素.另一方面, 重力对亚微米粒子运动的贡献则小得多.对于粒径为0.3 μm级的粒子, 重力影响仅为电场力的1/5 000.然而重力对粒子运动的影响也随着粒径增加而上升.在达到dp=10 μm时, 三者大小几乎在同一量级.对于大部分除尘器来说, 往往气流方向, 电场力方向以及重力方向三者互相垂直.这也使得颗粒在电场中的运动更加复杂.
在电场中间的粒子受到的库仑力最强, 但是该区域被涡旋所占据.然而远离极线颗粒又具有较高的速度.两方面不利因素造成了现有除尘器对细颗粒物收尘效果不理想.同时该模拟结果也很好地说明这两点也是今后除尘器改造的重点之一.其一就是通过使用不同极线布置方式, 更改极板几何形状等方式抵消涡流的影响, 使得流场分布更加均匀.其二就是通过改造供电方式, 优化场强分布, 使得颗粒在极板附近速度能降低, 从而被捕集.
3 结语本文使用了有限元多物理场耦合的方式对湿式电除尘器内的流场及颗粒物运动进行了数值分析.主要目的是使流场可视化, 以及在电场和流场的双重作用下荷电粒子运动轨迹评估.结论指出, 湿式电除尘器内的流场由于多方面的影响变得相当复杂.并且流场结构对于收尘效率有着不可忽视的影响.在给定的物理条件下, 流场中形成了数个对称涡旋, 垂直面上由于水流的影响也生成了涡旋.虽然随着一次流速上升涡旋的强度有所减弱, 但是涡旋的存在无疑对流场有阻碍作用, 使得颗粒物在流场中的运动趋势更加复杂.
为了更直观的理解颗粒物在上述条件的耦合下的运动轨迹, 不同粒径的粒子在电场中释放并进行受力分析.直观的比较了不同物理场对颗粒的影响.结果表明, 无垂直壁面移动(模拟湿式除尘器壁面水流)情况下, 电场力为粒子运动的主导因素.在电场力作用下, 粒子向极板方向运动, 但同时由于流场的湍流特性造成了粒子运动速度上的差异, 最终影响除尘器收尘效率.在加入垂直壁面移动后, 流场拖拽力对粒子轨迹的影响几乎和电场力处于相同数量级.
流场及颗粒物的可视化分析不仅反映了颗粒物的运动趋势, 而且可以定量的反映阻碍收尘效率提高的主要因素.为进一步优化除尘器结构设计, 提高收尘效率指明方向.
| [1] | YAMAMOTO T, VELKOFF H R. Electrohydrodynamics in an electrostatic precipitator[J]. Journal of Fluid Mechanics, 2006, 108: 1–18. |
| [2] | KALLIO G A, STOCK D E. Flow visualization inside a wire-plate electrostatic precipitator[J]. IEEE Transactions on Industry Applications, 1990, 26(3): 503–514. DOI:10.1109/28.55953 |
| [3] | PODLINSKI J, NIEWULIS A., MIZERACZYK J, et al. ESP performance for various dust densities[J]. Journal of Electrostatics, 2008, 66: 246–253. DOI:10.1016/j.elstat.2008.01.003 |
| [4] | NIEWULIS A., PODLISKI J, MIZERACZYK J. Electrohydrodynamic flow patterns in a narrow electrostatic precipitator with longitudinal or transverse wire electrode[J]. Journal of Electrostatics, 2009, 67: 123–127. DOI:10.1016/j.elstat.2009.01.001 |
| [5] | PODLISKI J, NIEWULIS A, MIZERACZYK J. Electrohydrodynamic flow and particle collection efficiency of a spike-plate type electrostatic precipitator[J]. Journal of Electrostatics, 2009, 67(2/3): 99–104. |
| [6] | DAVIS J L, HOBURG J F. Wire-duct precipitator field and charge computation using finite element and characteristics methods[J]. Journal of Electrostatics, 1983, 14(2): 187–199. DOI:10.1016/0304-3886(83)90006-2 |
| [7] | AL-HAMOUZ Z M. A combined algorithm based on finite elements and a modified method of characteristics for the analysis of the corona in wire-duct electrostatic precipitators[J]. IEEE Transactions on Industry Applications, 2002, 38(1): 43–49. DOI:10.1109/28.980343 |
| [8] | ZHAO L, ADAMIAK K. Numerical Simulation of the Electrohydrodynamic Flow in a Single Wire-Plate Electrostatic Precipitator[J]. IEEE Transactions on Industry Applications, 2008, 44(3): 683–691. DOI:10.1109/TIA.2008.921453 |
| [9] | ELMOURSI A A, CASTLE G S P. Modeling of corona characteristics in a wire-duct precipitator using the charge simulation technique[J]. IEEE Transactions on Industry Applications, 1987, IA-23(1): 95–102. DOI:10.1109/TIA.1987.4504872 |
| [10] | LEVIN P L, HOBURG J F. Donor cell-finite element descriptions of wire-duct precipitator fields, charges, and efficiencies[J]. IEEE Transactions on Industry Applications, 1990, 26(4): 662–670. DOI:10.1109/28.55991 |
| [11] | ANAGNOSTOPOULOS J, BERGELES G. Corona discharge simulation in wire-duct electrostatic precipitator[J]. Journal of Electrostatics, 2002, 54(2): 129–147. DOI:10.1016/S0304-3886(01)00172-3 |
| [12] | SOLDATI A. ON The effects of electrohy drodynamic flows and turbulence on aerosol transport and collection in wire-plate electrostatic precipita tors[J]. Journal of Aerosol Science, 2000, 31(3): 293–305. DOI:10.1016/S0021-8502(99)00055-5 |
| [13] | SKODRAS G, KALDIS S P, SOFIALIDIS D, et al. Particulate removal via electrostatic precipitators — CFD simulation[J]. Fuel Processing Technology, 2006, 87(7): 623–631. DOI:10.1016/j.fuproc.2006.01.012 |
| [14] | MIZUNO A. Electrostatic precipitation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(5): 615–624. DOI:10.1109/94.879357 |
| [15] | WILCOX D C. Turbulence modeling for CFD[M]. 1st edition. [S.l]: DCW Industries, 1993. |
| [16] | VAN WACHEM B G M, SCHOUTEN J C, VAN DEN BLEEK C M, et al. Comparative analysis of CFD models of dense gas-solid systems[J]. AIChE Journal, 2001, 47(5): 1035–1051. DOI:10.1002/(ISSN)1547-5905 |
| [17] | ENWALD H, PEIRANO E, ALMSTEDT A E. Eulerian two-phase flow theory applied to fluidization[J]. International Journal of Multiphase Flow, 1996(22): 21–66. |
| [18] | PODLINSKI J, NIEWULIS A, MIZERACZYK J. Electrohydrodynamic flow in a wire-plate non-thermal plasma reactor measured by 3D PIV method[J]. The European Physical Journal D, 2009, 54(2): 153–158. DOI:10.1140/epjd/e2009-00040-x |
| [19] | SHEN X, ZHENG Q, NING Z, et al. PM 10 and PM 2.5 emission control by electrostatic precipitator (ESP) for coal-fired power plants IV: investigations on electrostatic precipitation by means of 2D PIV Technique[J]. Science & Technology Review, 2014, 32(33): 43–50. |



