机械装备加工能耗分析计算是机械装备绿色设计制造的重要内容.目前, 在全球节能减排的大环境下, 降低制造过程的能量消耗以及污染排放是机械企业的发展方向.
近年来, 国内外学者在机械装备加工能耗分析计算领域做了广泛的研究:Seow等[1]基于产品蕴含能(embodied product energy, EPE)计算框架, 建立了产品制造过程的能耗仿真模型(energy simulation model, ESM), 并使用Arena软件仿真辅助研究.Avram等[2]研究了机床使用过程中的能量需求, 建立了一种基于转矩与角速度乘积的主轴和进给轴加减速功率模型, 为能耗计算提供了参考.Zein等[3]运用公理性方法将机床能耗系统细分到部件层, 从部件层出发分析能耗, 并提出了降低能耗的方法.Mativenga等[4]提出了一种考虑能耗与碳排放关联的切削参数优选方法, 使得机床加工过程能耗降低, 碳排放减少.He等[5]提出一种数控加工过程能量评估方法, 将整个数控加工过程的能量细分.施金良等[6]将主轴启动过程能量看作整体进行研究, 采用实验方法测量主轴从静止启动至不同转速时的能耗, 采用二次函数进行拟合得到主轴启动过程能量模型.Mori等[7]将整个机械加工工艺过程的能量形式化表达, 考虑了机床固定功率、切削进给功率、定位和主轴加减速能耗.何彦等[8]提出了一种数控机床能量源的动态能耗建模与仿真方法, 对数控机床能耗过程的动态性进行了分析.Diaz等[9]通过建立不同种类铣床能耗曲线图, 建立了机床能耗比模型, 改变了传统的测量获得机床加工能耗的方法.刘飞等[10]从面向应用需求出发, 对机电主传动系统的能量模型进行研究, 通过分段建立表格函数和数据拟合函数分析各时段能耗.Schrems等[11]提出了一种制造方案能耗的评价技术, 为选取最低能耗的生成链提供了帮助.陈薇薇等[12]基于切削过程各工艺参数对数控机床切削能好的影响分析, 搭建基于支持向量机数控机床能耗模型, 简化了传统经验公式繁琐的计算过程.金波等[13]提出了一种面向六足步行机器人节能的力矩分配算法, 通过线性约束的二次规划求解问题, 并验证了新力矩分配下的机器人更加节能.任峰等[14]通过提取注塑试验数据, 正交分析过程参数与注射能耗间的关系, 应用智能算法建立工艺参数与单产注射能耗之间的非线性关系, 优化过程参数以达到最小化注塑能耗的目的.Prasad等[15]利用C-MOLD流体仿真软件训练已有注塑加工过程数据, 通过比较误差反向传播算法和Levenberg-Marquardt逼近算法, 以实现注射加工工艺参数的分类预测.
现有的机械装备加工能耗分析计算主要针对机械产品加工过程, 是基于已有的制造环境分析加工过程能耗, 难以在机械装备方案设计阶段考虑加工过程能耗.本文提出了一种基于可信度区间的复杂注塑装备塑化设计方案能耗分析方法.在注塑装备方案设计阶段, 针对注塑过程中能耗高的塑化环节进行能耗计算分析.建立基于可信度二元区间表达的注塑装备设计塑化能耗数学模型, 并通过第二代非劣排序遗传算法无约束优化算法求解能耗模型, 从而分析注塑装备方案设计阶段各相关参数对注塑加工塑化过程能耗的影响, 以指导注塑装备方案设计.
1 注塑装备参数可信度区间表达 1.1 基于可信度的区间数在注塑装备方案设计阶段, 存在大量未知设计参数, 设计人员只能凭借经验或者根据已知参数将大量未知参数标定在一定范围内.此外, 在注塑装备设计方案能耗分析阶段, 不仅需要注塑装备的结构参数, 性能参数, 还需要部分注塑加工过程的工艺参数.在注塑装备方案设计阶段, 工艺参数难以精确获得.因此, 为了在注塑装备方案设计阶段进行能耗分析, 本文采用区间数来表达部分相关参数.
定义1 设R表示实数集.对任意的a, b∈R且, 记
| $ a = \left[ {\underline a ,\bar a} \right] $ |
称[a, a]是a的区间数.其中:a为区间数的下限, a为区间数的上限.
在注塑装备方案设计能耗分析计算过程中, 区间数可以表征不确定的参数.然而, 对于能耗分析计算问题, 往往需要比较不同目标函数的优劣, 因此, 需要对区间数进行个体性能差异比较.本文采用区间可信度的方式来衡量相应区间数个体性能的优劣.
定义2 区间a=[a, a]和b=[b, b], ζ是a和b的极大区间, 记为[ζ, ζ], 其中, ζ=max{a, b, a, b/ζ}.记a大于或等于b的可信度为P(a≥b), 则有
| $ P\left( {a \ge b} \right) = \frac{{d\left( {b,\zeta } \right)}}{{d\left( {a,\zeta } \right) + d\left( {b,\zeta } \right)}} $ |
式中:d定义为两区间下限差与上限差的最大值, 对于d(a, b)有
| $ d\left( {a,b} \right) = \max \left\{ {\left| {\underline a - \underline b } \right|,\left| {\bar a - \bar b} \right|} \right\} $ |
由定义2可推出如下区间占优可信度性质(为区间数占优提供排序基础):
(1) P(a≥b)+ P(a≤b)=1;
(1) P(a≥b)≥0.5, 当且仅当+a≥+b.
1.2 注塑装备参数分类与转换在注塑装备方案设计阶段, 注塑装备各结构模块的具体详细参数未知, 可将参数进行分类处理, 根据不同类型参数的特点进行参数关联与区间化处理.注塑装备的主要参数一般可分为3类:结构参数、性能参数及工艺参数.为达到注塑装备参数规范化存储管理的设计目的, 并有利于实现注塑装备能耗计算, 本文给出了一种规范的注塑装备参数区间表达方法, 支持注塑装备设计参数的组织与表达, 并有利于在已有的注塑装备参数资源库中快速检索.
注塑装备参数区间表达形式如下:
| $ \begin{array}{l} {\rm{Para = }}\left\{ {{\rm{IPara,CPara,Npara,SPara,UPara,}}} \right.\\ \left. {{\rm{CoPara}}} \right\} \end{array} $ |
式中:IPara为参数标识, CPara为参数类型, NPara为参数名称, SPara为参数值区间, UPara为参数值单位, CoPara为关联参数集.
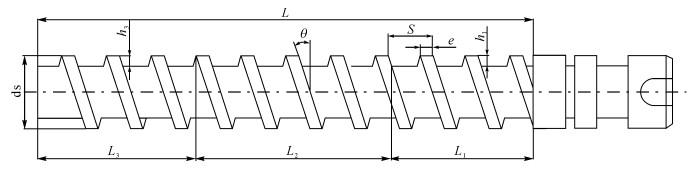
以注塑机主要部件螺杆参数的区间表达为例, 详细说明参数区间表达方法.螺杆设计主要参数有:螺杆长径比、螺杆转速、螺杆材料及考虑螺杆注塑过程能耗的主要参数为螺杆加热时间, 各主要参数形式化表达如表 1所示:表中φ为螺杆长径比, n为螺杆转速, SΔ为螺杆材料, ts为螺杆加热时间, 以表中螺杆长径比的参数区间表达为例, 其中010010表示参数标识, 前三位010为设计方案编号, 后三位010为设计参数编号;StrPara表示该参数属于结构参数集;CapPara表示该参数属于性能参数;ProcPara表示该参数属于工艺参数集; < 100, 160>为参数值可取区间, 当中括号内当参数值唯一时(如 < 38CrMOAl>), 表示该参数值需进行继承操作(下文预处理详细介绍), r/min为参数单位, NULL为空集,表示该项为空,{L, dS}表示螺杆长径比的关联参数集, 其中:L为螺杆长度, dS为螺杆外径, 具体参数如图 1所示.L1为螺杆加料段长度;L2为螺杆塑化段长度;L3为螺杆计量段长度;h1为加料段螺槽深度;h3为计量段螺槽深度;S为螺距;e为螺棱宽度;θ为螺旋升角.
|
图 1 螺杆结构参数示意图 Fig. 1 Schematic diagram of screw structure parameters |
| 表 1 注塑螺杆参数区间表达 Table 1 Parameter interval expression of injection screw |
经过区间分类表达的注塑参数具备一定的广泛性、通用性.但在注塑装备塑化能耗建模过程中, 不能直接调用, 部分参数需经转换处理后, 才能用于建模以及能耗分析.注塑装备参数转换可分为3类:
1) 关联转换
部分注塑装备参数相互之间存在一定关联性, 如果在注塑装备塑化能耗建模过程中, 不考虑这类关联, 会造成参数关系冗余, 导致优化求解过程不收敛等现象.关联操作就是将存在关联关系的参数, 以相互间的数学关系表示, 剔除重复出现的参数的过程.
2) 继承转换
对于部分注塑装备参数, 在参数广义表达时以语义形式表达, 该类参数具有(a)难以直接确定数值(b)能衍生出若干子类参数(c)子类继承父类部分特征等特点.因此, 当具体调用该类参数前对该类参数进行继承操作, 将由该类参数衍生出的若干子参数与该类参数以三元组的形式进行表达:
| $ M = \left\{ {\begin{array}{*{20}{c}} {{p_v}}&{{A_1}}&{{A_{v1}}}\\ {}&{{A_2}}&{{A_{v2}}}\\ {}&{{A_3}}&{{A_{v3}}}\\ {}& \cdots & \cdots \\ {}&{{A_n}}&{{A_{vn}}} \end{array}} \right\} $ |
式中:M为参数名称, pv为参数语义表达, A为继承属性, Av为属性值.若某一衍生参数Ai也属于该类参数, 则继续进行继承操作, 直到遍历所有子类参数.
3) 优化转换
将在方案设计阶段未知的注塑过程工艺参数以区间数的形式表达, 并视为已知参数.而注塑装备设计参数根据具体设计要求确定为已知参数及优化参数.优化操作, 即指注塑装备设计参数在已知参数及优化参数之间的转换, 是能耗建模问题建立的基础.
2 注塑装备塑化能耗模型建立 2.1 塑化方案设计能耗理论模型注塑装备塑化过程能耗主要包括4个部分:1) 物料被填塞进料筒后到物料完全熔融加热圈所消耗的能量QC, 2) 将料筒加热到指定温度所消耗的能量QB, 3) 将螺杆加热到指定温度所消耗的能量QS, 4) 油压马达提供给注塑螺杆的机械能QM, 因此注塑装备塑化阶段能耗QP可表示为
| $ {Q_{\rm{P}}} = {Q_{\rm{C}}} + {Q_{\rm{B}}} + {Q_{\rm{S}}} + {Q_{\rm{M}}}. $ | (1) |
根据注塑过程的具体情况, 现以感应加热的塑化方式为例, 具体分析注塑装备塑化阶段能耗.
(1) 加热圈消耗热能QC
一般的, 物料由固态粒料或粉料经加热由玻璃态经过黏弹态转变为黏流态的过程中, 塑化熔融导热量qH可由导热学傅里叶定理得
| $ {q_H} = \frac{{\kappa \Delta {T_{\rm{H}}}{A_B}}}{{{d_{\rm{m}}}}}. $ | (2) |
式中:ΔTH为物料胚环内外表面温差, K;κ为物料的导热系数, w/(mm·K);dm为物料胚环体的厚度, mm;AB为熔融物料与机筒内表面接触的有效导热面积, mm2.
| $ {{A''}_{\rm{B}}} = {\rm{\pi }}{d_{\rm{B}}}{L_{\rm{B}}}. $ | (3) |
式中:dB为机筒内径, mm;LB为加热机筒的长度, mm.
塑料熔融速率为
| $ {G_C} = \frac{{{q_H}}}{{{e_C}}}. $ | (4) |
式中:eC为物料本身的质量能, J/g.
综上, 加热圈消耗能耗为
| $ {Q_{\rm{C}}} = {G_{\rm{C}}}{h_T} = {h_T}\frac{{\kappa \Delta {T_{\rm{H}}}{\rm{\pi }}{d_{\rm{B}}}{L_{\rm{B}}}}}{{{d_{\rm{m}}}{C_C}}}. $ | (5) |
式中:hT为物料的质量晗, J/g.
(2) 机筒加热消耗热能QB
感应圈通电加热后机筒外表面温度迅速升高, 热源由机筒外表面向内表面传到, 加热机筒到指定温度所消耗的热能:
| $ {Q_{\rm{B}}} = {m_{\rm{B}}}\frac{{{c_{\rm{B}}}\Delta {T_{\rm{B}}}}}{{3600{t_{\rm{B}}}}}. $ | (6) |
式中:mB为注塑机筒重量, kg;cB为注塑机机筒材料的比热容, kJ/(kg·K);tB为机筒加热时间, s;ΔTB为计量段机筒内外表面温差, K.
(3) 加热螺杆消耗热能QS
螺杆在密闭机筒内加热, 螺杆加热到该温度下所需的能耗:
| $ {Q_{\rm{S}}} = {m_{\rm{S}}}\frac{{{c_S}\Delta {T_{\rm{S}}}}}{{3600{t_{\rm{S}}}}}. $ | (7) |
式中:mS为所需螺杆质量, kg;cS为螺杆材料比热容, kJ/(kg·K).s;ΔTS为完成加热时, 螺杆与外部环境的温差, K.
(4) 油马达提供机械能QM
螺杆的前后运动由油压马达提供, 油马达对螺杆施加的机械能为
| $ {Q_{\rm{M}}} = {M_{\rm{M}}}n\frac{{{\mu _T}}}{{9550}} = {10^3}{q_m}\frac{p}{{2{\rm{\pi }}}}n\frac{\mu }{{9550}} $ | (8) |
式中:MM为油马达塑化扭矩, N·m;qm为油马达排量, L/r;p为塑化压力, Pa;μ为油马达效率.
同时, 塑化成型出合格高品质的注塑制品始终是注塑装备方案设计所应考虑的重要因素.只有在保证制品的合格率及高品质的基础上, 研究注塑装备低能耗才有其实际意义.塑化能力是评价注塑装备生产塑化制品能力的指标.螺杆计量段熔料输送能力是决定塑化能力的主要因素.所以可用螺杆计量段的熔体输送能力来表征螺杆的塑化能力, 其塑化能力应为
| $ \begin{array}{l} {q_{\rm{S}}} = \frac{{{{\rm{\pi }}^2}d_{\rm{S}}^2{h_3}n\sin \theta \cos \theta }}{2} - \frac{{{\rm{\pi }}{d_{\rm{S}}}h_3^3{{\sin }^2}\theta }}{{12{\mu _1}}}\frac{{\Delta p}}{{{L_3}}} - \\ \;\;\;\;\;\;\frac{{{{\rm{\pi }}^2}d_{\rm{S}}^2{\delta ^3}\tan \theta }}{{12{\mu _2}e}}\frac{{\Delta p}}{{{L_3}}}. \end{array} $ | (9) |
式中:qS为螺杆塑化能力, cm3/s;μ1为螺槽中熔料的有效黏度, Pa·s;μ2为螺杆与机筒间熔料的有效黏度, Pa·s;δ为螺杆与机筒之间的间隙, cm;Δp为计量段的压力差, MPa.
2.2 注塑装备塑化能耗计算模型对于一般的区间多目标优化问题, 可以表示为
| $ \begin{array}{*{20}{c}} {\min f\left( {x,s} \right) = \left( {{f_1}\left( {x,{s_1}} \right),{f_2}\left( {x,{s_2}} \right), \cdots ,{f_m}\left( {x,{s_m}} \right)} \right)}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;x \in D \subseteq {{\bf{R}}^n}}\\ {{s_i} = {{\left[ {s_i^1,s_i^2, \cdots ,s_i^l} \right]}^{\rm{T}}},s_i^k = \left[ {\underline {s_i^k} ,\overline {s_i^k} } \right],k = 1,2, \cdots ,l} \end{array} $ |
式中:x为n维决策变量, D为x的决策空间, fi(x, ci)(i=1, 2, …, m)为第i个含区间参数的目标函数, si为第i个含区间参数的目标函数中的区间参数集, sik为区间参数集si中的第k个区间参数,
| $ {f_i}\left( {x,{s_i}} \right)\mathop = \limits^{{\rm{def}}} \left[ {\underline {{f_i}\left( {x,{s_i}} \right)} ,\overline {{f_i}\left( {x,{s_i}} \right)} } \right]. $ | (10) |
由本文2.1中的能耗分析, 得到了在注塑装备方案设计阶段塑化过程的能耗计算模型,
| $ \begin{array}{l} {f_1}\left( {x,{s_1}} \right) = {Q_{\rm{P}}} = {Q_{\rm{C}}} + {Q_{\rm{S}}} + {Q_{\rm{B}}} + {Q_{\rm{M}}} = \\ \;\;\;\;\;\;\;{h_{\rm{T}}}\frac{{\kappa \Delta {T_{\rm{H}}}{\rm{\pi }}{d_{\rm{B}}}{L_{\rm{B}}}}}{{{d_{\rm{m}}} \cdot {e_C}}} + {m_{\rm{B}}}\frac{{{c_B}\Delta {T_{\rm{B}}}}}{{3600{t_{\rm{B}}}}} + \\ \;\;\;\;\;\;\;{m_{\rm{S}}}\frac{{{c_{\rm{S}}}\Delta {T_{\rm{S}}}}}{{3600{t_{\rm{S}}}}} + {10^3}{q_m}\frac{p}{{2{\rm{\pi }}}}n\frac{\mu }{{9550}}. \end{array} $ | (11) |
| $ \begin{array}{l} {f_2}\left( {x,{s_2}} \right) = {q_{\rm{S}}} = \frac{{{{\rm{\pi }}^2}d_{\rm{S}}^2{h_3}n\sin \theta \cos \theta }}{2} - \\ \;\;\;\;\;\;\;\frac{{{\rm{\pi }}{d_{\rm{S}}}h_3^3{{\sin }^2}\theta }}{{12{\mu _1}}}\frac{{\Delta p}}{{{L_3}}} - \frac{{{{\rm{\pi }}^2}d_{\rm{S}}^2{\delta ^3}\tan \theta }}{{12{\mu _2}e}}\frac{{\Delta p}}{{{L_3}}}. \end{array} $ | (12) |
根据1.2节中所示, 对相关注塑装备参数进行形式化表达分类, 并进行相关转换处理后确定决策变量与区间参数.如表 2所示.
| 表 2 塑化能耗计算模型决策变量及区间参数列表 Table 2 Decision variables and Interval parameters of energy consumption calculation model |
传统的NSGA-Ⅱ的策略是将种群迭代后优选出各代的最优解, 将其作为下一代迭代的种群, 而作为上一代的非最优解被移除, 该种进化策略大大降低了种群迭代过程中的多样性, 会导致种群迭代过早出现收敛, 陷入局部Pareto最优解, 不利于在全局空间寻求Pareto最优解.
本文采用并行混合进化机制下的NSGA-Ⅱ算法, 具体步骤如下:
1) 根据种群数量, 利用二进制编码方式生成初始群体P
2) 准备一个空的存储空间P*;
3) 第x代父代种群PX产生子代种群QX, 合并父代子代种群产生RX=PX∪QX, 对合并后的种群RX进行非支配排序操作, 并计算种群RX中每一个个体间的拥挤距离.从中选择当前最优的非劣解, 作为下一代父代PX+1.限制当前迭代步下的最优非劣解的范围, 使非最优解也能进行下一代遗传运算.并将RX中最优的非劣解存储到预留空间P*中;
4) 将P*中多步迭代的最优非劣解进行联赛选择, 用共享函数来选择当前群体中优良的个体遗传到下一代群体中, 并保持存储空间中的种群数不超过预设范围.
其中共享函数的实现过程如下:
步骤1:从种群中随机选择x个个体形成集合X;
步骤2:从种群中随机选择2个个体形成集合Y;
步骤3:分别比较步骤1形成的集合X中的个体与步骤2形成的集合Y中的各个个体的优劣, 比较方法如步骤4所示;
步骤4:如果集合Y中的一个个体优于集合X中的所有个体, 而集合Y中的另一个个体劣于集合X中的所有个体, 则将优胜个体遗传到下一代种群中.如果未出现上述情况, 则递归享函数, 从集合Y中选出一个小生境较小的个体遗传到下一代.
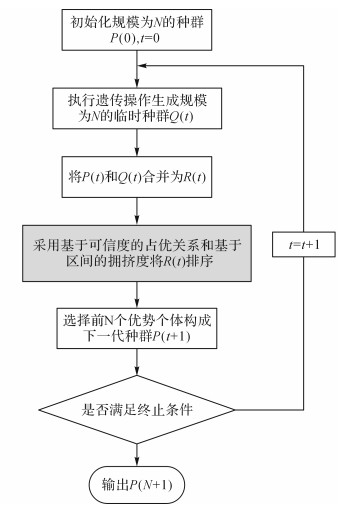
3.2 基于可信度区间的进化优化方法如图 2所示为基于可信度区间的进化优化方法, 具体步骤如下:
|
图 2 基于可信度区间的进化优化方法流程 Fig. 2 Evolutionary optimization method based on confidence interval |
步骤1确定种群规模为N, 设第1代种群为P0, 并设定一个空的存储空间P*.
步骤2对初P0始种群交叉及变异操作, 通过联赛选择生成临时种群Qi.
步骤3合并规模为Pi和Qi, 并记作Ri.
步骤4采用基于可信度的占优排序方法, 对于Qt中排序相等的个体计算其区间拥挤度, 并选取与种群规模相等的占优个体, 构成下一代种群Pi+1.
步骤5判定迭代步长是否到达.如果是, 输出Xn;否则, 迭代步长加一, 转至步骤2.
步骤6如果符合精度要求, 输出结果.如果不符合精度要求, 则跳转到步骤3.
3.3 注塑装备塑化设计方案评价方法考虑最终得到的优化注塑装备塑化设计方案集中, 注塑装备塑化过程能耗及塑化能力的权衡, 本文采用VIKOR方法, 用专家多粒度语言评价优化注塑装备塑化设计方案集中的备选方案, 确定最终的优选塑化设计方案.记注塑装备塑化设计方案专家q人, P={P1, P2, P3, …, Pm}, 第i个专家权重为wi, 备选的注塑装备塑化设计方案集为U={U1, U2, U3, …, Um}, 需要权衡的指标为D={D1, D2, D3, …, Dm}本文中仅涉及注塑装备塑化过程能耗及塑化能力2个评价指标, s=2).具体评价方案如下:
步骤1:确定专家评价值
由q名专家对优化注塑装备塑化设计方案集中的所有涉及方案进行评价, 由此获得第i个专家对第j个方案的第k个指标确定的评价值:
| $ {H_{ijk}} = {\left( {{H_{ijk}}} \right)_{m \times s}}\left( {i = 1,2, \cdots ,q} \right). $ | (13) |
求n个专家的评价值得几何平均数:
| $ \overline {{H_{ijk}}} = {\left( {\prod\limits_{i = 1}^n {{w_i}\left( {{H_{ijk}}} \right)} } \right)^{1/q}}. $ | (14) |
式中:i=1, 2, …, q;j=1, 2, …, m;k=1, 2, …, s.
步骤2:确定指标集中的最优解及最劣解:
| $ f_k^ + = \max {H_{jk}}. $ | (15) |
| $ f_k^ - = \min {H_{jk}}. $ | (16) |
步骤3:确定各专家的权重:
| $ W = \left\{ {{w_1},{w_2},{w_3}, \cdots ,{w_q}} \right\}. $ | (17) |
步骤4:计算注塑装备塑化设计方案集中各备选方案的效益值Sj及遗憾度Rf:
| $ {S_j} = \sum\limits_{k = 1}^s {{w_i}\left( {f_k^ + - {H_{jk}}} \right)/\left( {f_k^ + - f_k^ - } \right)} . $ | (18) |
| $ {R_j} = \max {w_i}\left( {f_k^ + - {H_{jk}}} \right)/\left( {f_k^ + - f_k^ - } \right). $ | (19) |
步骤5:计算注塑装备塑化设计方案集中各备选方案的折中度Cj
| $ \begin{array}{l} {C_j} = v\left( {{S_j} - {S^ - }} \right)/\left( {{S^ + } - {S^ - }} \right) + \left( {1 - v} \right)\left( {{R_j} - {R^ - }} \right)/\\ \;\;\;\;\;\;\;\;\left( {{R^ + } - {R^ - }} \right). \end{array} $ | (20) |
式中:S+=max Sj, S-=min Sj, R+=max Rj, R-=min Rj, v是决策系数, 表示该决策确定的专家人数占所有专家人数的比例.
步骤6:根据步骤5中折中度对注塑装备塑化设计方案集中的方案进行排序
4 注塑装备塑化设计能耗分析实例以某注塑企业XS-Z60型号注塑机为例, 进行注塑装备塑化设计方案能耗分析.根据设计需求, 设计锁模力为500 kN的注塑机塑化模块.由企业提供部分设计需求参数, 可重新整合表 2内容, 得到针对XS-Z60型号注塑机的塑化能耗计算模型决策变量及区间参数表如表 3所示.由1.2中所提, 在注塑装备塑化能耗计算数学模型建立之初, 需对部分注塑装备参数进行预处理.在本文实例中, 将螺杆的相关设计参数(x7~x15)作为数学模型的决策变量, 而剩余的机筒设计参数(x1~x4)及油压马达设计参数(x5~x6)作为已知的区间参数.根据设计需求, 对于XS-Z60型号注塑机, 表 3中的部分参数(x7~x15)作为决策变量, 由于遗传迭代需求, 现确定决策变量初始迭代区间:螺杆重量为5~50 kg, 螺杆材料比热容0.1~10 kJ/(kg), 螺杆转速20~200 r/min, 计量段螺槽深度0.5~5 mm, 螺旋升角5°~30°, 螺杆与机筒间隙0.01~0.5 mm, 螺棱轴向宽度5~50 mm, 计量段长度200~1 000 mm.其中螺杆外径作为注塑机塑化方案中的主要参数, 在设计需求阶段已确定, 对于XS-Z60型号注塑机, 规定螺杆外径38 mm作为已知确定参数.
| 表 3 XS-Z60注塑机塑化能耗计算模型决策变量及区间参数 Table 3 Decision variables and Interval parameters of energy consumption calculation model(XS-Z60) |
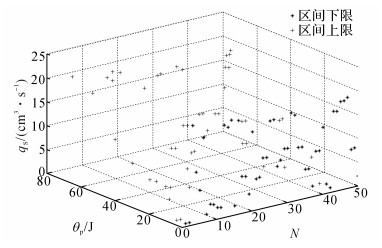
利用第3章所述注塑装备塑化设计方案能耗计算方法, 进行基于可信度区间的进化优化算法计算, 为了减少不必要算法复杂度, 种群规模确定为50;对于本例中的双目标优化问题, 种群进化500代, 采用模拟二进制交叉和多项式变异算子, 交叉和变异算子分别取0.9和0.03且它们分布指标均为20.迭代计算500代后区间最优前沿如图 3所示.
|
图 3 改进NSGA-Ⅱ最优前沿区间表示 Fig. 3 Improved NSGA-Ⅱ optimal frontier interval representation |
由于本文解决的是区间优化问题, 通过遗传算法得到的最优前沿以区间值得上下限表示.至此得到50组优化注塑装备塑化设计方案集, 根据3.3节中的注塑装备塑化设计方案评价方法, 对优化注塑装备塑化设计方案集进行评价排序, 如表 4所示(取前10组).
| 表 4 注塑装备塑化设计优选方案 Table 4 Optimization scheme of molding equipment plastic injection design |
根据注塑装备塑化设计方案评价方法得到的最优设计方案满足塑化成型过程能耗低、塑化能力高的特点, 为注塑装备塑化方案低能耗设计提供了参考.本文提出的理论方法求得的塑化能耗最小方案是基于区间数确定的, 实际方案设计可利用本方法得到的优化参数集, 在此基础上通过实验或使用过程的实际能耗数据, 调整误差参数, 进一步确定塑化能耗最小的螺杆设计参数.本文的目的重点是提供一个面向低能耗的机械装备设计方法, 为机械装备方案设计提供设计指导.
5 结论机械装备加工能耗分析计算是机械产品绿色化设计的重要研究方向, 本文提出了一种基于可信度区间的注塑装备塑化设计方案能耗分析方法, 主要工作与特点有:
(1) 提出基于可信度区间的注塑装备设计方案塑化能耗分析方法, 克服了传统能耗分析只能在整个详细设计完成后才能进行的不足.
(2) 利用基于可信度的区间数统一化表达注塑装备参数, 并根据参数分类及各自特点对注塑装备参数进行关联、继承与优化转换, 根据注塑装备塑化能耗模型, 利用基于可信度区间的改进NSGA-Ⅱ算法实现方案设计阶段的能耗分析.
(3) 提出的能耗分析方法应用于XS-Z60型注塑机塑化方案设计中, 为注塑装备塑化方案能耗分析提供依据.该方法不仅适用于注塑装备, 只要根据具体机械装备构建的能耗模型, 也可实现相应的能耗计算与分析.
| [1] | SEOW Y, RAHIMIFARD S, WOOLLEY E. Simulation of energy consumption in the manufacture of a product[J]. International Journal of Computer Integrated Manufacturing, 2013, 26(7): 663–680. DOI:10.1080/0951192X.2012.749533 |
| [2] | AVRAM O I, XIROUCHAKIS P. Evaluating the use phase energy requirements of a machine tool system[J]. Journal of Cleaner Production, 2011, 19(6/7): 699–711. |
| [3] | ZEIN A, LI W, HERRMANN C, et al. Energy efficiency measures for the design and operation of machine tools: an axiomatic approach[J]. Glocalized Solutions for Sustainability in Manufacturing, 2011(10): 274–279. |
| [4] | MATIVENGA P T, RAJEMI M F. Calculation of optimum cutting parameters based on minimum energy footprint[J]. Cirp Annals, 2011, 60(1): 149–152. DOI:10.1016/j.cirp.2011.03.088 |
| [5] | HE Y, LIU F, WU T, et al. Analysis and estimation of energy consumption for numerical control machining[J]. Proceedings of the Institution of Mechanical Engineers Part b-journal of Engineering Manufacture, 2012, 226(B2): 255–266. |
| [6] |
施金良, 刘飞, 许弟建. 数控机床空载运行时节能决策模型及实用方法[J].
中国机械工程, 2009(11): 1344–1346.
SHI Jin-liang, LIU Fei, XU Di-jian. Decision model and practical method of energy-saving in NC machine tool[J]. China Mechanical Engineering, 2009(11): 1344–1346. DOI:10.3321/j.issn:1004-132X.2009.11.019 |
| [7] | MORI M, FUJISHIMA M, INAMASU Y, et al. A study on energy efficiency improvement for machine tools[J]. Cirp Annals-manufacturing Technology, 2011, 60(1): 145–148. DOI:10.1016/j.cirp.2011.03.099 |
| [8] |
何彦, 林申龙, 王禹林. 数控机床多能量源的动态能耗建模与仿真方法[J].
机械工程学报, 2015(11): 123–132.
HE Yan, LIN Shen-long, Wang Yu-lin. Method for modeling the dynamic energy characteristics of multi-energy sources in CNC machine tool[J]. Journal of Mechanical Engineering, 2015(11): 123–132. |
| [9] | DIAZ N, REDELSHEIMER E, DORNFELD D. Energy consumption characterization and reduction strategies for milling machine tool use[M]. Berlin: Springer Berlin Heidelberg, 2011: 263-267. |
| [10] |
刘飞, 刘霜. 机床服役过程机电主传动系统的时段能量模型[J].
机械工程学报, 2012(21): 132–140.
LIU Fei, LIU Shuang. Multi-period energy model of electro-mechanical main driving system during the service process of machine tools[J]. Journal of Mechanical Engineering, 2012(21): 132–140. |
| [11] | SCHREMS S, EISELE C, ABELE E. Methodology for an energy and resource efficient process chain design[M]. Berlin: Springer Berlin Heidelberg, 2011: 299-304. |
| [12] |
陈薇薇, 张华, 向琴. 基于支持向量机数控机床切削能耗预测方法研究[J].
机械设计与制造, 2014(11): 54–56.
CHEN Wei-wei, ZHANG Hua, XIANG Qin. Research on CNC machine Tool cutting energy consumption prediction based on support vector machine[J]. Machinery Design & Manufacture, 2014(11): 54–56. DOI:10.3969/j.issn.1001-3997.2014.11.015 |
| [13] |
金波, 陈诚, 李伟. 基于能耗优化的六足步行机器人力矩分配[J].
浙江大学学报:工学版, 2012, 46(7): 1168–1174.
JIN Bo, CHEN Cheng, LI Wei. Optimization of energy-efficient torque distribution for hexapod walking robot[J]. Journal of Zhejiang University : Engineering Science, 2012, 46(7): 1168–1174. |
| [14] |
任峰, 杨于光, 林丕. 螺杆参数对注射机塑化单产能耗影响的实验研究[J].
橡塑技术与装备, 2008(10): 7–15.
REN Feng, YANG Yu-guang, LIN Pi. Experimental study of the impact of screw parameters on plastizing uniproducing energy consumption of injection molding machine[J]. China Rubber/Plastics Technology and Equipment, 2008(10): 7–15. DOI:10.3969/j.issn.1009-797X.2008.10.002 |
| [15] | YARLAGADDA P, KHONG C. Development of a hybrid neural network system for prediction of process parameters in injection molding[J]. Journal of Materials Processing Technology, 2001, 118(1/3SI): 110–116. |



