2. 中航工业西安飞机工业(集团)有限责任公司, 陕西 西安 710089
2. AVIC Xian Aircraft Industry (Group) Company LTD., Xian, 710089, China
在飞机数字化装配中, 部件的精准定位依赖于数字化测量仪器的精密测量和数控定位装备的精确定位而实现.数控定位器是飞机数字化装配系统的主要定位设备, 定位精度受定位器制造精度[1]、定位器运动精度、定位器整体刚度与受力变形[2-3]、定位器运行磨损度[4]以及定位器坐标标架标定精度等因素的影响.其中, 定位器坐标标架标定是数控定位系统进行精准定位和调姿的关键所在, 直接影响到单个定位器在装配坐标系下的零点位置、坐标轴方向的确立以及定位器组的协同运动精度(即系统定位精度).
精密运动设备的标定方法主要可以归纳为2种:简单标定和精细标定[5].简单标定包括球面、圆柱面、平面或其他特殊几何外形的设备表面的配合标定;精细标定则采用精密测量仪器测量已选标记点用以计算被测设备的刚体姿态并结合匹配算法进行设备配合的标定方法.此外, 随着国内外标定方法的发展, 出现了介于简单标定和精细标定之间的基于单目或双目照相机的视觉标定[6]方法, 但视觉标定方法对具有几何对称形状的设备更为适用, 且标定精度受所采用的照相机本身的分辨率影响明显.精细标定方法在精密运动设备中运用广泛, 如机器人标定技术和数控机床标定技术, 其中机器人标定技术主要是根据机器人各运动关节之间的运动关系建立运动学模型, 然后利用先进的测量设备测量各运动关节特征点的位姿, 并采用递归最小二乘法、非线性优化算法、遗传算法或神经网络等方法对各待标定参数进行标定计算, 以达到改善机器人运动精度[7]的目的.同样, 数控机床的运动学标定也是首先建立标定模型, 根据数控机床设备上待标定机构的误差关系及其可观性和环链约束来构造实测信息与理论输出信息间的误差泛函, 然后采用各种检测技术对待标定对象的误差进行检测, 再利用一定的数学方法识别标定各运动参数, 最后用标定识别的结果修正数控机床的运动精度[8].总结来说, 标定的主要步骤就是:建立标定模型, 测量待标定点的位姿信息, 采用标定算法确定待标定的参数, 最后根据标定数据修正设备的运动精度.
可移动数控定位器作为数控定位器的一种, 主要用于部件进站与出站干涉较多或部件对接后支撑位置发生改变的飞机数字化装配系统.本文针对可移动数控定位器的坐标标架标定问题, 提出一种基于序列二次规划(sequential quadratic programming, SQP)算法的快速标定方法, 以克服一般精细标定方法的效率问题.
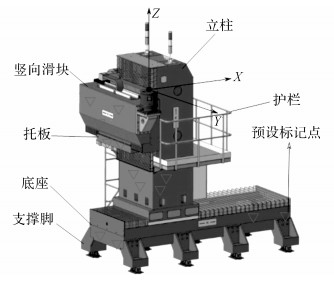
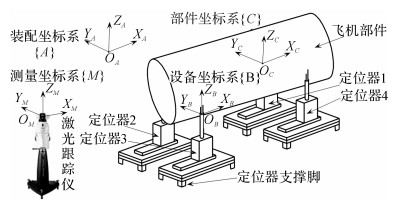
1 可移动式数控定位器坐标标架建立及表征可移动数控定位器, 如图 1所示, 主要由基座、基座支撑脚、竖向滑块、托板、立柱和定位球窝及球头构成.当可移动数控定位器需要整体移动时, 先将转移定位器所需的气垫车运动至定位器基座底部, 定位器支撑脚松开旋紧螺栓, 气垫车气垫充气向上顶起定位器, 从而完成支撑和转运定位器的工作.如图 2所示, 当可移动数控定位器重新移动到装配站位的工作位置时, 需要重新确定数控定位器的设备坐标标架在装配坐标系下的位置, 即需要进行数控定位器坐标标架标定.
|
图 1 定位器设备坐标系及标记点 Fig. 1 Coordinate system and marker points of localizer |
|
图 2 飞机部件数字化装配示意图 Fig. 2 Schematic diagram of digital assembly of aircraftparts |
定位器自身坐标标架可通过如下过程定义:为方便数控定位器坐标标架与现场装配坐标系的方向相协调, 以定位器横向X轴方向为主方向, 以定位器纵向Y轴方向为辅方向, 竖向Z轴方向为次方向, 定位器坐标标架如图 1所示.利用激光跟踪仪跟踪测量横向滑块上的点, 将横向滑块空行程运行一段距离并返回至初始位置, 使得激光跟踪仪记录了点的一系列位置, 通过这些点的位置利用最小二乘法拟合一条直线可得X轴的方向向量;同理可得Y轴的方向向量, 再根据右手法则(向量叉乘)计算得出Z轴的方向向量.将数控定位器各轴运行至设备零点位置, 将支撑球头放入数控定位器相应球窝中, 以球窝为中心旋转支撑球头并利用激光跟踪仪测量支撑球头零件上布置的靶标点位置, 根据测量结果拟合球面, 计算支撑球头的球心坐标, 并将其作为定位器坐标标架的原点.如此, 即可确定数控定位器的坐标标架, 记为{B}.
为了减少数控定位器转站过程中激光跟踪仪转站配置次数、避免转站误差及保证激光跟踪仪的测量效率, 当可移动数控定位器各运动轴停靠在设备零点位置时, 在定位器上预先布置若干标记点, 采用专用装配数据库记录标记点在设备坐标系下的坐标值, 从而表征数控定位器自身的设备坐标标架.标记点位置如图 1所示, 在定位器的基座、立柱、托板和竖向滑块这4个单元体上分别布置若干标记点.选取的标记点应尽量分散在设备的不同侧面且不共线从而可最大限度地表征定位器的位姿信息;同时为了方便激光跟踪仪的测量, 标记点应布置在同一个测量视野范围之内, 去除测量盲点;在各单元体上布置大于3个标记点, 便于剔除测量超差的标记点.
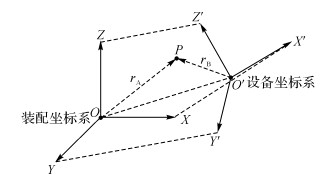
2 基于点匹配的坐标系转换在大型飞机数字化装配过程中, 由于飞机下架转站, 数控定位器故障检修和飞机机身调姿而需要转移冗余定位器等情况, 数控定位器会移位复位和转站换位, 使得其坐标标架位置发生变化, 同时设备坐标系与现场装配坐标系相对关系也发生改变.此时, 必须重新确立数控定位器的坐标标架, 即确立定位器设备坐标系与现场装配坐标系的映射关系, 如图 3所示.若数控定位器位于零点位置, 定位器上标记点在设备坐标系下的坐标位置不变时, 可利用激光跟踪仪测量标记点在装配坐标系下的坐标值, 并通过点到点最佳匹配算法实现数控定位器坐标标架的快速标定.目前常用的点最佳匹配计算算法包括奇异值分解法(SVD)、四元数法(UQ)、双四元数法(DQ)、正交矩阵法(OM)[8]和线性子空间法[9]等.
|
图 3 装配坐标系和设备坐标系映射关系 Fig. 3 Relationship between coordinate system of aircraft components and equipment |
在数控定位器移动到工作位置并完成固定后, 可以利用激光跟踪仪测量数控定位器上的标记点, 将测量结果与装配现场的公共检测点进行点匹配计算, 获得各标记点在装配坐标系下的坐标, 记为rA;同理测量得到设备坐标系下相应各点的坐标为rB.则两刚体坐标系间的转化关系可表示为
| $ {r_A} = \mathit{\boldsymbol{R}}{r_B} + \mathit{\boldsymbol{T}}. $ | (1) |
式中:R为3×3旋转矩阵, T为3维平移列向量.旋转矩阵R可由欧拉角定义的φ, θ, ψ这3个变量表征如下:
| $ \begin{array}{l} \mathit{\boldsymbol{R}} = {\rm{Rot}}\left( {z,\phi } \right){\rm{Rot}}\left( {x,\theta } \right){\rm{Rot}}\left( {z,\psi } \right) = \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} {c\phi }&{ - s\phi }&0\\ {s\phi }&{c\phi }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{c\theta }&{ - s\theta }\\ 0&{s\theta }&{c\theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {c\psi }&{ - s\psi }&0\\ {s\psi }&{c\psi }&0\\ 0&0&1 \end{array}} \right] = \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} {c\phi c\psi - s\phi c\theta s\psi }&{ - c\phi s\psi - s\phi c\theta c\psi }&{s\phi s\theta }\\ {s\phi c\psi + c\phi c\theta s\psi }&{ - s\phi s\psi + c\phi c\theta c\psi }&{ - c\phi s\theta }\\ {s\phi s\psi }&{s\phi c\psi }&{c\theta } \end{array}} \right]. \end{array} $ | (2) |
式中:cx=cos (x), sx=sin(x), Rot(a, b)表示绕a轴旋转b角.
本文的三维平移列向量可由数控定位器球头球心坐标得到:T=rAO, rAO为设备坐标系原点在装配坐标系下的坐标.
利用奇异值分解法(SVD)计算旋转矩阵R的相应参数.记测量点在全局和局部坐标系下的坐标值分别为rAi和rBi, 则点匹配的最小二乘法表达式为
| $ {\Sigma ^2} = \Sigma _{i = 1}^N\left\| {{r_{Ai}} - \mathit{\boldsymbol{R}}{r_{Bi}} - \mathit{\boldsymbol{T}}} \right\|. $ | (3) |
令
| $ \left. \begin{array}{l} \overline {{r_A}} = \frac{1}{N}\sum\limits_{i = 1}^N {{r_{Ai}}} ,\\ \overline {{r_B}} = \frac{1}{N}\sum\limits_{i = 1}^N {{r_{Bi}}} ,\\ {a_{ci}} = {r_{Ai}} - \overline {{r_{Ai}}} ,\\ {b_{ci}} = {r_{Bi}} - \overline {{r_{Bi}}} , \end{array} \right\}. $ | (4) |
式中:rA、rB分别为N个测量点在全局和局部坐标系下的坐标平均值,aci、bci分别为测量点在全局和局部的坐标偏差.
则方程(3) 可以化简为
| $ \left. \begin{array}{l} {\Sigma ^2} = \sum\limits_{i = 1}^N {\left\| {{a_{ci}} - \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{b}}_{ci}}} \right\|} ,\\ {\Sigma ^2} = \sum\limits_{i = 1}^N {\left\| {a_{ci}^{\rm{T}}{a_{ci}} + b_{ci}^{\rm{T}}{b_{ci}} - 2a_{ci}^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{b}}_{ci}}} \right\|} . \end{array} \right\} $ | (5) |
为求式(5) 的最小值, 即转化为求Trace (RH)的最大值, 其中
| $ \mathit{\boldsymbol{H = }}\sum\limits_{i = 1}^N {{b_{ci}}a_{ci}^{\rm{T}}} . $ | (6) |
对矩阵H进行分解, 使得
| $ \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}. $ | (7) |
式中:U, V为单位正交矩阵, Λ是一个对角矩阵.则旋转矩阵可由下式计算可得
| $ \mathit{\boldsymbol{R = V}}{\mathit{\boldsymbol{U}}^{\rm{T}}}. $ | (8) |
如此刚体姿态参数R和T均可确定, 即数控定位器设备坐标系与现场装配坐标系的映射关系也得以确定.
3 数控定位器坐标标架快速标定方法当定位器移位后, 定位器自身的姿态处于未知状态, 同时不确定数控定位器是否运动至零点位置.为了提高定位器标定的效率, 减少定位器各轴调至零点位置的工序, 对数控定位器进行非零位标定.可假设定位器各轴运动至任意位置, 则在定位器除基座上以外的各标记点在设备坐标系下的坐标均可能发生变化.立柱上的标记点在X轴方向位置改变, 托架上的标记点在X和Z轴方向位置改变, 竖向滑块上的标记点在X、Y和Z轴方向位置均发生变化.在对定位器坐标标架进行标定计算时, 必须将立柱、托板和竖向滑块上的标记点在各轴向的偏移量作为相应变量重新进行定位器坐标标架的标定计算, 而SVD方法只能用于数控定位器各轴回零状态下的零位标定, 需要研究专门的标定方法应对此种情况.
记基座、立柱、托架和竖向滑块上的各标记点在设备坐标系下的偏移量分别为Δ1、Δ2、Δ3和Δ4如下所示:
| $ \left. \begin{array}{l} {\Delta _1} = \left( {0,0,0} \right),\\ {\Delta _2} = \left( {{\Delta _{x2}},0,0} \right),\\ {\Delta _3} = \left( {{\Delta _{x3}},0,{\Delta _{z3}}} \right),\\ {\Delta _4} = \left( {{\Delta _{x4}},{\Delta _{y4}},{\Delta _{z4}}} \right). \end{array} \right\} $ | (9) |
利用激光跟踪仪重新测量定位器上的各标记点得到基座、立柱、托板和竖向滑块上各标记点在现场装配坐标系下的坐标值, 分别记为r′A1j、r′A2j、r′A3j和r′A4j.同时, 记重新标定的旋转矩阵为R′, 平移向量为T′=[tx, ty, tz]T, 其中,tx、ty、tz分别为平移向量X、Y、Z方向听分量.旋转矩阵由欧拉角公式(2) 表示, 则带偏移量的点匹配最小二乘表达式如下:
| $ \begin{array}{l} {\Sigma ^2} = \\ \;\;\;\;\sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^n {{{\left\| {{{r'}_{{A_{ij}}}} - \left( {\mathit{\boldsymbol{R}}\left( {{{r'}_{{B_{ij}}}} + {\Delta _i}} \right) + \mathit{\boldsymbol{T'}}} \right)} \right\|}^2}} .} \end{array} $ | (10) |
与此同时, 数控定位器自身存在制造误差和几何误差, 定位器精度指标如表 1所示, 立柱、托板和竖向滑块之间在各轴方向上运行误差小于0.01 mm, 则各偏移量中的参数可设置为如下关系:
| 表 1 定位器精度指标 Table 1 Accuracy index of localizer |
| $ \left. \begin{array}{l} \left| {{\Delta _{x2}} - {\Delta _{x3}}} \right| \le 0.01,\\ \left| {{\Delta _{x3}} - {\Delta _{x4}}} \right| \le 0.01,\\ \left| {{\Delta _{z3}} - {\Delta _{z4}}} \right| \le 0.01. \end{array} \right\} $ | (11) |
由式(10) 和(11) 可知, 根据各标记点的理论值与测量值最小二乘匹配关系, 已知各标记点在三轴方向上各偏移量中的参数不等式关系, 从而求解出旋转矩阵R′、平移向量T′和偏移量Δ.这构成了一个典型的带约束的非线性优化问题, 其数学表达式如下:
| $ \begin{array}{*{20}{c}} {\min \left( {\sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^n {{{\left\| {{{r'}_{{A_{ij}}}} - \left( {\mathit{\boldsymbol{R}}\left( {{{r'}_{{B_{ij}}}} + {\Delta _i}} \right) + \mathit{\boldsymbol{T'}}} \right)} \right\|}^2}} } } \right),}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\mathit{\boldsymbol{A}}{x_i} - {b_i} \le 0,}\\ {x = \left( {{\Delta _{x2}},{\Delta _{x3}},{\Delta _{z3}},{\Delta _{x4}},{\Delta _{y4}},{\Delta _{z4}},\phi ,\theta ,\psi ,{t_x},{t_y},{t_z}} \right).} \end{array} $ | (12) |
式中:A为不等式系数矩阵.
求解式(12) 这类的带约束非线性优化问题, 可利用序列二次规划(sequential quadratic programming, SQP)方法进行计算求解.SQP算法是求解带约束非线性问题最有效的优化算法之一, 具有收敛性较好, 边界搜索能力强, 计算效率高的优点, 被广泛应用于非线性规划(non-linear programming, NLP)问题求解当中[10].SQP方法的主要思想是通过逐次求解二次规划子问题获得优化变量的搜索方向及拉格朗日乘子变量, 从而逼近最优解.二次规划子问题的约束是以有效约束的线性化形式表示的, 目标函数是拉格朗日函数的二次函数的近似, 所用算法是拟牛顿法在该问题Kuhn-Tucker条件[11-12]下的应用.所以拥有拟牛顿法的超线性收敛率, 收敛迅速.
对于一个含约束的非线性规划问题, 有如下形式:
| $ \left. \begin{array}{l} \min f\left( x \right)\\ {\mathit{\boldsymbol{G}}_i}\left( \mathit{\boldsymbol{x}} \right) = 0,i = 1,2, \cdots ,{m_e};\\ {\mathit{\boldsymbol{G}}_i}\left( \mathit{\boldsymbol{x}} \right) \le 0,i = {m_e} + 1, \cdots ,m \end{array} \right\} $ | (13) |
式中:x=[x1, x2, x3, …, xn]T, 为待优化向量.f(x)为目标函数, G(x)=[g1(x), g2(x), g3(x), …, gm(x)]为函数向量, gi(x)为x的线性或非线性函数, 即拉格朗日函数表达式.当i=1~me时, Gi(x)为等式约束;当i=(me+1)~n时, Gi(x)为不等式约束.算法通过拉格朗日(Lagrange)函数的二次近似函数求解二次规划(quadratic programming, QP)子问题如下所示:
| $ L\left( {x,\lambda } \right) = f\left( x \right) + \sum\limits_{i = 1}^n {{\lambda _i}{g_i}\left( x \right)} . $ | (14) |
式中:λ, λi为Lagrange因子.
通过线性化非线性约束条件后可以得到QP子问题, 其目标函数为
| $ \mathop {\min }\limits_{d \in {{\bf{R}}^n}} \frac{1}{2}{d^{\rm{T}}}{\mathit{\boldsymbol{B}}_k}d + {\left( {\nabla f\left( {{x_k}} \right)} \right)^{\rm{T}}}d. $ | (15) |
约束方程为
| $ \left. \begin{array}{l} {\left[ {\nabla {g_i}\left( x \right)} \right]^{\rm{T}}}d + {g_i}\left( x \right) = 0,i = 1,2, \cdots ,{m_e};\\ {\left[ {\nabla {g_i}\left( x \right)} \right]^{\rm{T}}}d + {g_i}\left( x \right) \le 0,i = {m_e} + 1, \cdots ,m. \end{array} \right\} $ | (16) |
式中:d为全变量搜索方向, 符号▽为梯度, 矩阵Bk是Lagrange函数的Hessian矩阵正定拟牛顿近似, 并通过稠密半正定牛顿近似法(dense quasi-newton approximation, BFGS)进行计算, 式(16) 可以通过QP算法求解.得到的解代入新的方程中:
| $ {x_{k + 1}} = {x_k} + {\alpha _k}{\mathit{\boldsymbol{d}}_k}. $ | (17) |
式中:dk为xk指向xk+1的一个向量, 标量步长通过选择适合的线性搜索方法来确定, 从而使得某一指标函数获得足够的减小量.
SQP方法的主要迭代步骤如下[12]:
1) 选取初始点x(1), 给定一个正定对称矩阵B1∈Rn×n以及罚因子r, 令k=1;
2) 利用式(15) 和(16) 求解二次规划子问题, 求出满足子问题Kuhn-Tucker条件的解dk及其对应的拉格朗日乘子λk+1;
3) 针对所选的罚函数从点x(k)沿方向dk进行线性搜索确定步长αk, 并令x(k+1)=x(k)+αkdk;
4) 检验收敛法则, 按一定的准则和精度检验x(k)的最优性, 是则结束迭代, 否则转步骤5);
5) 修改Hessian矩阵, 利用BFGS公式更新Bk为Bk+1, 转步骤2).
利用SQP优化方法理论, 并根据式(12) 分析所得的目标函数和约束条件, 即可进行可移动数控定位器坐标标架的标定和计算.其优化计算模型如图 4所示.
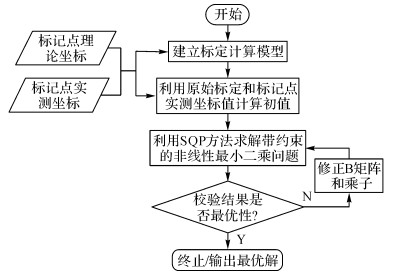
|
图 4 标定优化求解流程 Fig. 4 Solution process of calibration optimization |
由于SQP方法对初值的选取比较敏感, 所以选择合适的初值对于最终的标定结果非常重要.根据上文分析可知待优化的变量x=(Δx2, Δx3, Δz3, Δx4, Δy4, Δz4, ψ, θ, φ, tx, ty, tz)中ψ, θ和φ变化较小, 所以其初始值可设为零;tx, ty和tz的变化也不大, 所以其初始值可以设为原始标定的平移列向量T0=[tx0, ty0, tz0];最关键的是偏移量Δ的确定, 因为偏移量是在数控定位器运动行程内任意变化的, 不存在一个微小变化的范围.但由于所需标定的R和T变化不大, 如此可以利用原始标定的R0和T0以及竖向滑块上的实测和理论坐标平均值计算得出
| $ \left. \begin{array}{l} {\Delta _{40}} = \mathit{\boldsymbol{R}}_0^{ - 1}\left( {{{r'}_{A4}} - {\mathit{\boldsymbol{T}}_0}} \right) - {r_{B4}},\\ {\Delta _{40}} = {\left[ {{\Delta _{x40}},{\Delta _{y40}},{\Delta _{z40}}} \right]^{\rm{T}}},\\ {\Delta _{x20}} = {\Delta _{x40}},\\ {\Delta _{x30}} = {\Delta _{x40}},\\ {\Delta _{z30}} = {\Delta _{z40}}. \end{array} \right\} $ | (18) |
确定目标函数和约束方程如式(12), 初始值为x0=(Δx20, Δx30, Δz30, Δx40, Δy40, Δz40, 0, 0, 0, tx0, ty0, tz0), 利用图 4所示标定优化求解流程优化求解R和T以及偏移量Δ.最终实现可移动数控定位器坐标标架的快速标定.
4 实例分析本文以ARJ机身3段对接现场中机身左4#定位器上对象点测量值分析定位器初始标定的误差和定位器移位后的误差, 从而验证本文所提出的定位器坐标标架标定算法的可行性和精度.激光跟踪仪采用Leica AT901跟踪仪;标定程序模块采用MATLAB语言编写, 包括数据采集、标定参数以及标定误差分析等模块.计算机软硬件环境为:Intel Core i7, cpu @ 2.40GHz, 内存4.00G, 64位操作系统.
定位器标定误差定义为列向量:
| $ {\bf{ei}} = {r_A} - \left( {\mathit{\boldsymbol{B}}{r_B} + \mathit{\boldsymbol{T}}} \right). $ | (19) |
其模长为定位器标定的拟合误差, 令| ei |的平均值:
| $ \bar e = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{\bf{ei}}} \right|} . $ | (20) |
式中:e为定位器标定的平均拟合误差.
4.1 定位器零位标定实例定位器坐标标架零位标定时, 在定位器基座、立柱、托板和竖向滑块上分别选取4个标记点进行测量并记录它们在现场装配坐标系下和定位器设备坐标系下的坐标值分别为(Xa0, Ya0, Za0)和(Xe0, Ye0, Ze0), 如表 2所示.表 2中编号1~4、5~8、9~12和13~16分别代表定位器基座、立柱、托架和竖向滑块上的标记点, 编号17代表由球面布点测量通过拟合球面计算所得的定位器球头中心在装配坐标系下的坐标值.根据这些标记点的坐标值, 利用SVD算法对定位器坐标标架进行标定.如表 3和图 5所示为定位器零位标定各轴向误差和拟合误差.由表 3和图 5可知, 定位器零位标定三轴方向上的标定误差(δx0, δy0, δz0)均不超过0.05 mm, 拟合误差δm0不超过0.06 mm, 平均拟合误差为0.024 mm, 初始零位标定精度满足定位器定位精度0.05 mm.
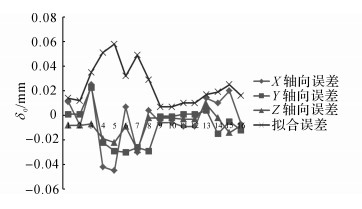
|
图 5 定位器零位标定各轴向误差和拟合误差 Fig. 5 Axial error and fitting error of zero calibration |
| 表 2 定位器上标记点零位标定坐标值 Table 2 Coordinate value of marker points in zero calibration |
| 表 3 定位器零位标定误差和拟合误差 Table 3 Error and fitting error of zero calibration |
当定位器移位后, 当定位器各轴运动至零点位置时, 所标定的各对象点在设备坐标系下的坐标值相对不变.各点在现场装配坐标系下位置随之发生改变, 利用激光跟踪仪重新测量定位器上各标记点在装配坐标系下的坐标值, 然后利用SVD算法重新标定定位器坐标标架.标定误差δSVD如图 6所示, 标定精度与定位器初始标定类似, 在各轴向的标定误差均在0.05 mm之内, 拟合误差不超过0.06 mm且基本低于0.05 mm, 平均拟合误差为0.034 mm, 略高于初始零位标定.
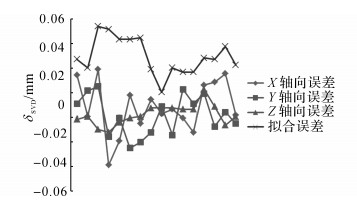
|
图 6 利用SVD算法标定各轴向误差和拟合误差 Fig. 6 Axial error and fitting error of calibration based on SVD |
若定位器各轴处于任意运动位置时, 则定位器除基座上以外的标记点在现场装配坐标系和设备坐标系下的坐标值均发生变化.为了保证定位器标定精度及标定效率, 与定位器各轴运动至零点位置的情况相同, 只测量标记点在现场装配坐标系下的坐标值, 但根据上文分析可知, 零位标定中所采用的SVD算法已不再适用于此类标定计算.利用SQP算法计算出旋转矩阵R和平移向量T以及偏移量Δ.共进行6组标定实验, 其中一组标记点在现场装配坐标系下的坐标值(Xa1, Ya1, Za1)如表 4所示.对比表 4和2可知, 基座上的标记点在装配坐标系下的坐标值变化不大, 而其他标记点由于偏移量Δ的存在变化很大.利用SQP优化算法对定位器进行标定, 标定误差如表 5和图 7所示, 在有偏移量Δ存在的情况下, 文中快速标定算法的标定精度和零位标定时利用SVD算法的标定精度接近, 总体上各轴向标定误差(δx1, δy1, δz1)在-0.03~0.05 mm之内, 拟合误差δm1基本小于0.06 mm, 平均拟合误差为0.024 mm.
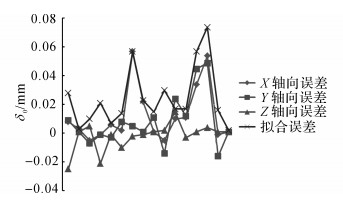
|
图 7 利用SQP算法进行标定的误差 Fig. 7 Error of calibration based on SQP |
| 表 4 标记点在现场装配坐标系下的坐标 Table 4 Coordinate value of gauge points in system of aircraft assembly |
| 表 5 利用SQP算法进行标定的误差 Table 5 Error of calibration based on SQP |
在定位器不做回零处理的情况下, 即定位器标定带有偏移量Δ的情形下, 为了验证不同偏移量Δ对文中快速标定算法拟合误差的影响, 共作6组标定实验.6组标定精度和误差结果如图 8所示.

|
图 8 不同偏移量时标定误差的比较分析(mm) Fig. 8 Calibration error analysis when offsets are different |
由以上SQP算法标定系列误差图可知, 利用SQP优化方法对移位后定位器标定时, 标定结果比较稳定, 各轴向误差基本保持在-0.05~0.05 mm以内, 拟合误差基本保持在0.07 mm以内.各组标定平均拟合误差如表 6所示, 各组标定结果中的偏移量(Δx, Δy, Δz)如表 7所示.从表 6和7分析可知, 每次利用SQP优化算法对定位器坐标标架进行标定时, 各标定序列的平均拟合误差与相对应的偏移量Δ无关, 即标定结果不受偏移量大小的影响.
| 表 6 各标定序列平均拟合误差 Table 6 Average fitting error of calibration sequence |
| 表 7 各标定序列偏移量标定结果 Table 7 Result of deviation value in calibration sequence |
本文针对飞机数字化装配中可移动数控定位器坐标标架快速标定及统一问题, 提出一种基于SQP优化算法的定位器坐标标架快速标定方法, 适用于数控定位器在各轴未归零状态下的坐标标架标定.利用激光跟踪仪测量并记录定位器上标记点, 完成定位器设备坐标系的建立和定位器坐标标架的初始标定.考虑到定位器各轴停靠位置的不确定性, 将标记点在设备坐标系下的偏移量引入作为新的变量, 利用SQP算法建立定位器坐标标架快速标定模型.通过实例分析验证算法有效性, 同时数据分析表明利用SQP算法对定位器坐标标架非零位标定的精度接近于利用SVD方法的零位标定精度, 使得三轴向标定误差基本保持在-0.05~0.05 mm之间, 拟合误差小于0.06 mm, 从而保证数控定位器组的协同定位精度不受影响.标定结果和标定精度稳定可靠, 满足大型飞机数字化装配对数控定位系统的高精度要求.
| [1] |
李晨, 方强, 李江雄. 基于三坐标定位器的大部件调姿机构误差分析[J].
机电工程, 2010, 27(03): 6–13.
LI C, FANG Q, LI J. Error analysis of 3-axis locator based pose adjustment mechanism[J]. Journal of Mechanical and Electrical Engineer, 2010, 27(03): 6–13. DOI:10.3969/j.issn.1001-4551.2010.03.002 |
| [2] |
郭志敏, 蒋君侠, 柯映林. 基于POGO柱三点支撑的飞机大部件调资方法[J].
航空学报, 2009, 30(07): 7–12.
GUO Z, JIANG J, KE Y. Posture alignment for large aircraft parts based on three POGO sticks distributed support[J]. Acta Aero-nautica et Astronautica Sinica, 2009, 30(07): 7–12. |
| [3] |
郭志敏, 蒋君侠, 柯映林. 一种精密三坐标POGO柱设计与精度研究[J].
浙江大学学报:工学版, 2009, 43(09): 9–14.
GUO Z, JIANG J, KE Y. Design and accuracy for POGO stick with three axis[J]. Journal of Zhejiang University :Engineering Science, 2009, 43(09): 9–14. |
| [4] |
应征. 飞机部件数字化调姿过程建模与仿真关键技术研究[D]. 杭州: 浙江大学, 2013.
YING Z. Study on modeling and simulation of alignment pose process of aircraft component [D].Hangzhou: Zhejiang University, 2013. |
| [5] | WANG W, LIU F, YUN C. Calibration method of robot base frame using unit quaternion form[J]. Precision Engineer, 2015, 41(3): 47–54. |
| [6] |
孟晓桥, 胡占义. 摄像机自标定方法的研究与进展[J].
自动化学报, 2003, 29(01): 110–124.
MENG Xiao-qiao, HU Zhan-yi. Recent progress in camera self-calibration[J]. Acta Automation Sinica, 2003, 29(01): 110–124. |
| [7] |
王东署, 李光彦, 徐方, 等. 机器人标定算法及其在打磨机器人中的应用[J].
机器人学报, 2005, 27(06): 491–496.
WANG Dong-shu, LI Guang-yan, XU Fang, et al. Robot calibration algorithms and their application on polishing robot[J]. Robot, 2005, 27(06): 491–496. |
| [8] |
杨晓钧, 李兵, 张东来. 并联机床运动学自标定方法研究[J].
计算机集成制造系统, 2008, 14(09): 1825–1830.
YANG Xiao-jun, LI Bing, ZHANG Dong-lai. Kinematics automatic calibration method for parallel tool[J]. Computer integrated manufacturing system, 2008, 14(09): 1825–1830. |
| [9] |
邓德标, 方源敏, 赵子龙, 等. 空间球状物体的数据采集与分析[J].
测绘科学学报, 2013, 38(05): 146–148.
DENG Di-biao, FANG Yuan-min, ZHAO Zi-long. Data collection and analysis about spatial spherical objects[J]. Science of Surveying and Mapping, 2013, 38(05): 146–148. |
| [10] | EGGERT D W, LORUSSO A, FISHER R B. Estimating 3-D rigid body transformations: a comparison of four major algorithms[J]. Machine Vision and Applications, 1997(9): 272–290. |
| [11] | WANG Z, JEPSON A. A new closed-form solution for absolute orientation [C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington: IEEE, 1994: 129-134. |
| [12] | ZHANG J L, ZHANG X S. A SQP method for inequality constrained optimization[J]. Acta Mathmaticae Applicatea Sinica, 2002, 18(1): 77–84. DOI:10.1007/s102550200005 |


