2. 西安飞机工业(集团)有限责任公司, 陕西 西安 710089
2. AVIC Xi′an Aircraft Industry(Group) Limited Company, Xi′an 710089, China
飞机装配中80%连接孔是沉头孔, 沉头孔的垂直度加工精度对结构件的连接强度和疲劳寿命产生重要影响.波音公司对钛合金螺栓试验表明, 当紧固件沿外载荷作用方向倾斜角度大于2°时, 疲劳寿命降低约47%, 当倾斜角度大于5°时, 疲劳寿命降低95%[1].机器人自动化制孔过程中通常使用法矢修正技术来保证刀具与工件表面的垂直度要求.毕运波等[2]利用激光测距传感器进行法矢修正, 使孔的垂直加工精度平均达到0.5°.法矢修正技术易受到测量环境、传感器精度以及算法的影响, 因此对于法矢修正完的孔必须要进行相应的垂直度检测.目前国内仍然使用人工接触式测量方法完成对沉头孔垂直度的测量, 通过铆钉或窝量规加塞方式, 凭经验判断锪窝孔的垂直度.这种检测方式的效率和精度都无法保证, 且难以直接测量位于飞机某些特殊工位上的孔.
机器视觉测量是一种非接触式测量方法, 具有成本低、精度高等特点, 已经逐渐用于机器人自动化制孔过程中.朱伟东等[3]利用单目相机对飞机部件上的基准孔进行测量, 并将孔圆心的实际位置与理论位置进行对比, 修正飞机部件理论模型和实际装配模型的误差.单目相机的视觉测量只能得到成像平面的二维信息[4], 得到三维信息要求观测目标具有一定的先验条件.沉头孔的几何外形受刀具轮廓约束, 且刀具参数已知, 因此通过构建射影几何模型的方式间接计算出垂直度.但由于沉头孔锪窝段内孔和外孔轮廓不在同一空间平面上, 视觉测量会产生透视投影误差, 并且当刀具与工件表面法矢存在一定夹角时, 沉头孔锪窝段的外孔轮廓是一个空间椭圆, 这样会使透视投影误差更加严重[5].于起峰等[6]提出当目标到摄像系统光心的距离远大于摄像系统焦距时, 透视投影成像关系可以用平行投影近似描述.沉头孔在照相测量过程中, 由于照相机平面与孔面的距离比实际相机的焦距大, 且工业相机的视场很小, 可以用平行投影关系来近似描述, 但依然不能忽略透视投影误差.本文首先介绍沉头孔垂直度检测的应用背景与相关检测方法, 提出了一种利用机器人末端执行器进行沉头孔垂直度检测的新方法.该方法基于平行投影假设, 建立了沉头孔垂直度计算模型, 并对透视投影情况进行算法修正.最后, 通过自动化制孔和视觉测量实验, 验证沉头孔垂直度计算模型的正确性和有效性.
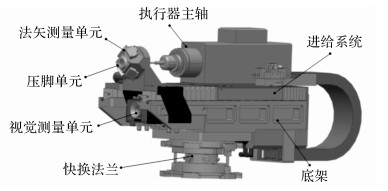
1 沉头孔自动化加工与测量 1.1 制孔末端执行器末端执行器是自动化制孔的执行机构, 由主轴、进给系统、压脚单元、法矢测量单元、视觉测量单元、快换法兰等组成.如图 1所示为浙江大学自主研制的多功能制孔末端执行器, 主轴电机由变频器控制转速, 带动刀具旋转实现切削运动.进给运动由通过丝杠螺母传动实现, 并由光栅尺实时反馈, 精度达到0.005 mm.压脚单元与执行器底座通过滑块导轨相连, 可实现对工件的预紧作用.法矢测量单元由4个测距传感器组成, 对称安装在压脚外表面上, 可以实现对工件表面法向测量[7].视觉测量单元由工业相机和环形光源组成, 固定安装在主轴下方, 并在安装中保证相机光轴与主轴轴线平行.
|
图 1 末端执行器结构图 Fig. 1 End-effector structure |
在制孔加工之前, 首先要对工业相机和激光测距传感器进行标定.其次, 要标定相机和执行器主轴坐标系的手眼关系, 确定相机坐标系与机器人坐标系的坐标转换关系.上述2种标定方法具体参见文献[3].经过手眼标定后, 执行器能在相机坐标系下运动, 并能够以平移方式使工业相机光轴移动到当前执行器主轴轴线位置.
末端执行器在沉头孔加工过程中通常采用钻锪一体式刀具[8], 一次进给即可完成制孔和锪窝操作, 能够严格保证沉头孔直孔段轴线和锪窝孔段轴线同心关系.本文基于机器人自动化制孔系统, 提出如下方案实现沉头孔加工和视觉测量一体化:
1) 进入执行器刀具坐标系模式, 移动末端执行主轴到待加工沉头孔的理论位置;
2) 利用激光测距传感器进行法矢测量与计算, 进而驱动机器人或机床调整执行器主轴与工件表面的垂直关系;
3) 将末端执行器压脚伸出并压紧工件表面, 完成沉头孔加工, 并将压脚收回;
4) 进入相机坐标系模式, 移动工业相机, 使相机光轴移动到当前主轴轴线位置;
5) 工业相机以沉头孔内孔轮廓为参照, 进行自动对焦, 并完成对沉头孔的拍照测量;
6) 回到执行器刀具坐标系模式, 移动执行器主轴到下一个沉头孔的理论加工位置.
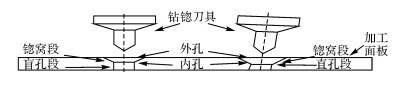
1.3 沉头孔视觉成像分析如图 2所示为沉头孔的2种不同加工成形状态示意图.为便于表述, 将锪窝孔段与直孔段交线称为内孔, 将锪窝孔段与工件表面交线称为外孔.当加工过程中刀具垂直于工件表面时, 沉头孔直孔段是标准的圆柱孔, 锪窝段是标准的圆台孔.由于拍照测量时, 相机光轴与执行器主轴轴线重合, 也即与直孔段轴线重合, 此时沉头孔的图像是一个同心圆结构, 内圆为沉头孔内孔的投影, 外圆为沉头孔外孔的投影.当加工过程中刀具轴线与平面法矢之间存在倾斜角时, 沉头孔的直孔段是一个不规则圆柱体, 锪窝段是一个不规则圆台.由射影几何原理[9]可知, 此时沉头孔图像由一个圆和一个椭圆构成.显然, 该圆是内孔的投影, 椭圆是外孔的投影, 可以通过它们的几何关系计算沉头孔垂直度.
|
图 2 沉头孔加工成形示意图 Fig. 2 Countersink hole forming diagram |
在理想条件下, 不考虑透视投影问题, 沉头孔在相机成像平面内的投影过程可以看作是平行投影, 此时内孔和外孔的成像比例关系不会由于透视投影而失真.如图 3所示为相机测量过程中沉头孔的平行投影示意图, 像平面与加工平面的夹角为φ, 即为垂直度法矢偏差.假设相机的像平面坐标系为M0x0y0z0, 坐标系原点为光轴与像平面的交点M0.沉头孔坐标系为Mexeyeze, 坐标原点为锪窝段所在圆锥的顶点Me.由于相机光轴在拍照测量过程中会移动到当前主轴轴线所在空间位置, 所以像平面坐标系z0轴与沉头孔坐标系ze轴重合.假设内孔圆O1A1B1C1D1和外孔椭圆O2A2B2C2D2在像平面上的投影为O′1(A′1B′1C′1D′1)和O′2(A′2B′2C′2D′2).

|
图 3 沉头孔平行投影示意图 Fig. 3 Countersink hole parallel projection diagram |
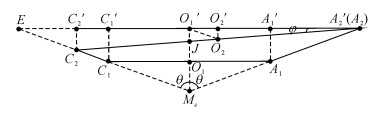
由于内孔和外孔相对xeMeze平面对称, 因此取xeMeze平面的截面表示整个投影过程, 如图 4所示, 沿孔轴线方向平移像平面, 使得点M2和其对应的投影点A′2重合.作线段MeE, A′2E交于点E, 则O′1是A′2E的中点.从图中可以看出, ∠C2A′2C′2=φ.设刀具的锪窝角度为θ, 则受到刀具的轮廓约束, 此时∠EMeO′1=∠C2EC′2=θ.O2和O′2分别是所在线段的中点, 由中位线定理可得:
|
图 4 沉头孔平行投影截面示意图 Fig. 4 Section diagrams of countersink hole parallelprojection |
| $ {{O'}_1}{{O'}_2} = {{A'}_2}{{O'}_2}\tan \varphi \tan \theta . $ | (1) |
由平行投影关系可以看出, O′1O′2是内孔中心和外孔中心在像平面投影的距离, A′2O′2是外孔在像平面的椭圆投影的半长轴, A1O1是内孔在像平面的圆投影的半径.令Δ=O′1O′2, L=A′2O′2, h=A1A′1, R=A1O1, 则
| $ \tan \varphi = \frac{{{{O'}_1}{{O'}_2}}}{{{{A'}_2}{{O'}_2}\tan \theta }} = \frac{\Delta }{{L\tan \theta }}. $ | (2) |
假设沉头孔的窝深为外孔平面到内孔平面的最大距离, 并设其值为h, 则有
| $ h = \frac{{\left( {{{O'}_1}{{O'}_2} + {{A'}_2}{{O'}_2} - {A_1}{O_1}} \right)}}{{\tan \theta }} - \frac{{\left( {\Delta + L - R} \right)}}{{\tan \theta }}. $ | (3) |
由式(2) 可知, tan φ与L、Δ、tan θ相关, 其中L和Δ可以由沉头孔的图像提取出特征值, 而tan θ是由锪窝刀具决定的常量, 因此沉头孔垂直度偏差可以通过视觉测量来获得.同时, 由式(3) 可知, h可以通过L、Δ、R以及tan θ求出.
2.2 孔垂直度计算模型修正在考虑到实际照相测量中, 沉头孔内孔和外孔不在同一个平面上, 由于透视投影会产生近大远小现象, 必然会使内轮廓和外孔轮廓的测量值与真实值之间的比例发生变化.同时, 由于外孔轮廓是一个空间椭圆, 它在像平面上的投影会产生透视畸变.如果仍然按照公式(2) 计算沉头孔的垂直度偏差, 必然会产生计算误差, 因此必须对孔垂直度计算模型进行修正.
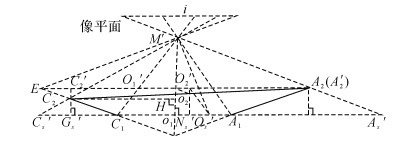
假设照相机的光心在M′处, 根据小孔成像原理, 在拍照测量过程中内孔轮廓和外孔轮廓通过相机光心投影到像平面上.由于改变成像平面上沉头孔轮廓的比例不会影响模型的计算, 为便于与平行投影比较, 将成像平面上的投影等比例放大至沉头孔内孔所在平面上, 如图 5所示.
|
图 5 沉头孔透视投影截面示意图 Fig. 5 Section diagrams of countersunk hole perspectiveprojection |
此时外孔椭圆A2C2的投影位置是A′sC′s, 作C′2G′s, A′2F, O′2N′s垂直于A′sC′s, 作C′2H垂直于M′Me, O′s为A′sC′s的中点.设相机光心M′到沉头孔内孔平面的距离为物距, 设其为p, 则有p=M′O1.假设经过透视投影后, 沉头孔图像中内孔圆中心和外孔椭圆中心的距离为Δ′, 内孔圆直径为R′, 外孔椭圆的半长轴为L′.比较平行投影和透视投影前后图像特征的变化关系, 可得
| $ L' - L = \frac{{{{A'}_{\rm{s}}}F + {{C'}_{\rm{s}}}{{G'}_{\rm{s}}}}}{2}. $ | (4) |
| $ \Delta ' - \Delta = {{O'}_{\rm{s}}}{{N'}_{\rm{s}}} = \frac{{\left( {{{A'}_{\rm{s}}}F + {{C'}_{\rm{s}}}{{G'}_{\rm{s}}}} \right)}}{2}. $ | (5) |
| $ R' = R. $ | (6) |
如果此时仍按照平行投影公式求解出一个角度, 并将其命名为β, 则它满足如下关系:
| $ \tan \beta = \frac{{\Delta '}}{{L'\tan \theta }}. $ | (7) |
由式(4~6) 可得
| $ \tan \beta = \frac{{2\Delta + {{A'}_{\rm{s}}}F - {{C'}_{\rm{s}}}{{G'}_{\rm{s}}}}}{{\left( {2L' + {{A'}_{\rm{s}}}F + {{C'}_{\rm{s}}}{{G'}_{\rm{s}}}} \right)\tan \theta }}. $ | (8) |
因为ΔA2A′sF∽ΔM′A′sO1, 则
| $ {{A'}_{\rm{s}}}F = \frac{{{A_2}F \times {A_2}{{O'}_1}}}{{M'{O_1} - {O_1}{{O'}_1}}} = \frac{{h\left( {L + \Delta } \right)}}{{p - h}}. $ | (9) |
又因为ΔC2C′sG′s∽ΔM′C2H, 则
| $ \frac{{{C_2}{{G'}_{\rm{s}}}}}{{{{C'}_{\rm{s}}}{{G'}_{\rm{s}}}}} = \frac{{M'H}}{{{C_2}H}} = \frac{{\left( {p - {O_1}H} \right)}}{{\frac{1}{2}{A_2}{{C'}_2}}}. $ | (10) |
因为
| $ {{C'}_{\rm{s}}}{{G'}_{\rm{s}}} = \frac{{{O_1}H \times L}}{{p - {O_1}H}}. $ | (11) |
因为O1H=h-O′H1, O′1H=C′2C2=2Ltan φ, 则
| $ {O_1}H = h - {{O'}_1}H = h - 2L\tan \varphi . $ | (12) |
由式(11) 和(12) 可得
| $ {{C'}_{\rm{s}}}{{G'}_{\rm{s}}} = \frac{{\left( {h - 2L\tan \varphi } \right) \times L}}{{p - h + 2L\tan \varphi }}. $ | (13) |
又由式(1) 和(3) 可得
| $ {{A'}_2}{{O'}_2} = L = \frac{{h\tan \theta + R}}{{1 + \tan \theta \tan \varphi }}. $ | (14) |
| $ {{O'}_1}{{O'}_2} = \Delta = \frac{{h{{\tan }^2}\theta \tan \varphi + R\tan \theta \tan \varphi }}{{1 + \tan \theta \tan \varphi }}. $ | (15) |
将式(4)、(8)、(13~15) 代入式(5) 中, 可得
| $ \tan \beta = \frac{{2c + a - b}}{{2\left( {d + a + b} \right)\tan \theta }}. $ | (16) |
其中:
| $ a = \frac{{h{{\tan }^2}\theta \tan \varphi + R\tan \theta \tan \varphi + h\tan \theta + R}}{{1 + \tan \theta \tan \varphi }},\\ b = \frac{{\left[ {h\left( {1 - \tan \theta \tan \varphi } \right) - 2\left( {h\tan \theta + R} \right)\tan \varphi } \right]\left( {h\tan \theta + R} \right)}}{{\left[ {\left( {1 + \tan \theta \tan \varphi } \right)\left( {p - h} \right) + 2\left( {h\tan \theta + R} \right)\tan \varphi } \right]\left( {1 + \tan \theta \tan \varphi } \right)}}, $ |
| $ c = \frac{{h{{\tan }^2}\theta \tan \varphi + R\tan \theta \tan \varphi }}{{1 + \tan \theta \tan \varphi }},d = \frac{{h\tan \theta + R}}{{1 + \tan \theta \tan \varphi }}. $ |
由于沉头孔图像易于提取出L′和Δ′特征, 从而可以间接求解出β.因此, 只要得到β与φ的真实关系, 就能通过β求解得到φ.
2.3 孔垂直度偏差计算由式(16) 可知, tan β与物距p、窝深h、内孔半径R、锪窝角度θ以及垂直度偏差φ相关.其中, β可通过对沉头孔图像进行特征提取得到, 内孔半径R、窝深h由刀具的轮廓决定, 可以认为是常量.同时, 不考虑物距p和窝深h的精度误差.令f(x)=tan β, x=φ, 将透视投影公式化成函数方程形式, 可得
| $ f\left( x \right) = f\left( \varphi \right) = \tan \beta . $ | (17) |
通过对f(x)求导可知, f′(x)在φ=[0,90]区间上是连续的, 因此函数f(x)是一元非线性方程, 对函数的求解可以利用牛顿公式.为区分理论垂直度偏差φ, 将计算得到的垂直度偏差表示为φd.若φd越接近于φ, 说明函数的解越接近于真实值.下面给出牛顿法[10]求解流程:
1) 输入f(x)= tan β作为已知量, 迭代初始值x0设为β, 误差极限ξ设为0.001, 最大迭代次数设为N=10;
2) 设置当前迭代次数n=1;
3) 计算:
4) 若|x-x0| < ξ, 或
(5) 若n < N, 则令n=n+1, x0=x, 并回到步骤(3);否则提示失败.
2.4 孔垂直度计算模型误差分析在机器人自动化制孔过程中, 物距p的精度由相机对焦算法的精度决定, 窝深h的精度由机器人制孔系统的加工精度决定, 两者均存在一定误差变化范围, 且可使计算结果产生偏差.为此, 有必要分析物距p和窝深h对φd的影响.
1) 根据沉头孔制孔加工工艺, 设置h=2 mm, R=3 mm, θ=50°.假设由测量得到β=5°, 分析当p的范围是150±5 mm时φd的偏差变化规律.
2) 设置R=3 mm, θ=50°, 假设由测量得到β=5°, 分析h的范围是2±0.5 mm时φd的偏差变化规律.
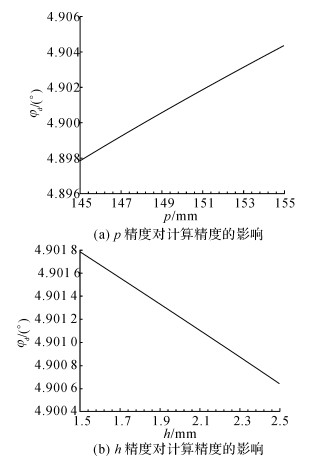
如图 6所示为p与h精度对计算精度的影响,从图 6(a)中可知, φd随着物距p的增加而增加.当物距p从145 mm增加到155 mm, φd只增加了约0.007°, 说明当物距p取值的误差范围较小时, 可以忽略p对φd的影响.从图 6(b)中可知, φd随着h的增加而减少.当窝深h从1.5 mm增加到2.5 mm, φd只减少约0.001 2°, 说明当窝深h取值的误差范围较小时, 可以忽略h对φd的影响.在实际制孔过程中, 物距p和窝深h的精度可达到±1.5 mm[11]和±0.03 mm[8]左右, 因此将p和h设为常量对透视投影公式的计算精度影响非常小.
|
图 6 物距p和窝深h精度对计算精度的影响 Fig. 6 Influence of accuracy of object distance p and deep h on calculation precision |
为避免机器人自身制孔精度对垂直度测量产生影响, 文中将实验分为2个环节:自动化制孔与拍照测量、沉头孔垂直度偏差精密测量.实验采用的加工材料是2024-T3(350 mm×150 mm×5 mm);刀具是硬质合金钻锪刀具(φ5.1 mm×13 mm×100°);制孔平台是浙江大学自行研制的机器人自动化制孔系统, 如图 7所示;相机是Baumer TXG12型工业相机.利用圆心不对称投影方法标定工业相机[12], 标定结果见表 1, 表中f为焦距.实验中沉头孔垂直度的测量工具是ARES COORD3型三坐标测量仪, 测量精度达到0.001 mm.

|
图 7 机器人自动化制孔与测量实验 Fig. 7 Experiment of robot drilling and measuremen |
| 表 1 TXG12型相机参数 Table 1 TXG12 camera parameters |
1) 制孔与拍照测量环节:首先进行法矢修正, 使执行器主轴保证与加工面板的垂直关系.设置窝深参数为1 mm, 按照本文提出的沉头孔加工与测量方案完成沉头孔的制孔与拍照实验.每制完一个孔, 调整末端执行器绕快换法兰轴旋转0.2°, 使当前主轴轴线方向与加工面板表面法矢的夹角增大0.2°.依次进行制孔拍照实验, 总共加工11组沉头孔, 分别对应0°、0.2°、0.4°、0.6°、0.8°、1.0°、1.2°、1.4°、1.6°、1.8°、2.0°.
2) 沉头孔的垂直度精密测量:将制孔完成后的加工面板固定于三坐标测量机上, 操纵球头对第i(i=1~11) 个沉头孔直孔段内壁均匀采点16次, 利用圆柱拟合方法拟合点云数据, 从而获得直孔段轴线向量αi(i=1~11).操纵球头对第i(i=1~11) 个沉头孔外孔周边的面板均匀采点16次, 利用平面拟合方式拟合点云数据, 获得孔周边面板的法矢βi(i=1~11).αi与βi的夹角即为第i个孔的垂直度法矢偏差φi.
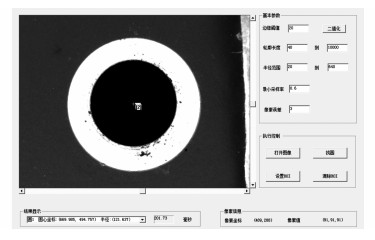
3.3 实验结果沉头孔图像处理需要提取内孔圆轮廓的圆心和半径、外孔椭圆的中心和半长轴.本文首先利用基于Zernike矩的亚像素检测方法检测图像边缘轮廓, 检测精度在0.1个像素.然后利用基于霍夫变换法和最小二乘法相结合的方法提取圆轮廓, 最后在外孔圆轮廓的基础上利用主动Snake模型拟合外孔椭圆轮廓.如图 8所示为实验中工业相机拍摄的沉头孔投影图像.
|
图 8 沉头孔图像处理软件 Fig. 8 Image processing software of countersink hole |
如表 2所示为制孔试验数据处理后得到的相应垂直度偏差值.表中设计值是指由执行器绕法兰轴旋转而产生的垂直度偏差值, 用φh表示;测量值是利用三坐标测量仪精密测量得到的沉头孔垂直度偏差值, 用φl表示;通过平行投影公式计算得到的计算值用φn表示;经过透视投影公式修正后得到的计算值由φk表示;由于三坐标测量仪的精度很高, 这里将三坐标测量仪测量的垂直度法矢φl看作是真实的垂直度偏差φ.
| 表 2 孔垂直度检测实验数据 Table 2 Test data of perpendicularity of the hole |
从实验结果可以看出:
1)φl和φh之间的差值保持在0.246°左右, 说明机器人的法矢修正精度误差在0.246°左右.
2)φl可随φh的增加而较均匀地增加, 而φk不是均匀增加, 说明φk的计算过程中包含了图像处理的误差, 而图像处理误差通常为随机值.
3) 在角度偏差较小时, φn值接近φk, 而当角度逐渐增大时, φn相对于测量值φl的偏差大于φk, 说明加工精度很高时平行投影公式可以替代透视投影公式计算垂直度偏差.
4)φk与φl的标准差是0.03°左右, 说明本文的沉头孔垂直度计算方法能够有效地应用于沉头孔视觉测量过程中, 且该方法具备较高的精度.
4 结语本文提出了一种利用视觉测量技术精密检测沉头孔垂直度法矢偏差的新方法.首先, 利用平行投影关系推导出孔垂直度数学模型.其次, 根据透视几何原理对孔垂直度模型进行了修正, 得到沉头孔垂直度透视投影公式, 并给出基于牛顿法求解该公式的算法步骤.最后, 利用机器人自动化制孔系统进行了沉头孔视觉测量实验.实验结果表明, 沉头孔垂直度的平均视觉测量误差约为0.03°, 验证了本文方法的有效性.
| [1] |
袁红璇. 飞机结构件连接孔制造技术[J].
航空制造技术, 2007, 1: 96–99.
YUAN Hong-xuan. Manufacturing technology of connecting hole in aircraft structures[J]. Aeronautical Manufacturing Technology, 2007, 1: 96–99. DOI:10.3969/j.issn.1671-833X.2007.01.017 |
| [2] |
毕运波, 李永超, 顾金伟, 等. 机器人自动化制孔系统[J].
浙江大学学报:工学版, 2014, 8(7): 1427–1433.
BI Yun-bo, LI Yong-chao, GU Jin-wei, et al. Robotic automatic drilling system[J]. Journal of ZhejiangUniversity: Engineer Science, 2014, 8(7): 1427–1433. |
| [3] | ZHU Wei-dong, MEI Biao, YAN Guo-rui. Measurement error analysis and accuracy enhance-ment of 2D vision system for robotic drilling[J]. Robotics and Compuer-Integrated Manufacturing, 2014, 30(2): 160–171. DOI:10.1016/j.rcim.2013.09.014 |
| [4] | JIANG Z, XU D, TAN M, et al. MEMS Assembly with the simplex focus measure[C]// Proceedings of IEEE International Conference on Mechatronics and Automation. Ontario: [s.n.] 1, 2005: 1118-1122. |
| [5] |
魏振忠, 张广军. 透视投影变换中椭圆中心畸变误差模型及其仿真研究[J].
仪器仪表学报, 2003, 24(2): 160–164.
WEI Zhen-zhong, ZHANG Guang-jun. A distortion error model of the perspective projection of ellipse center and Itssimulation[J]. Chinese Journal of Scientific Instrument, 2003, 24(2): 160–164. |
| [6] |
于起峰, 孙祥一, 邱志强. 从单站光测图像确定空间目标三维姿态[J].
光学技术, 2002, 1(5): 77–82.
YU Qi-feng, SUN Xiang-yi, QIU Zhi-qiang. Approach of determination of object's 3D pose from monoview[J]. Optical Technique, 2002, 1(5): 77–82. |
| [7] |
费少华, 方强, 孟祥磊, 等. 基于压脚位移补偿的机器人制孔锪窝深度控制[J].
浙江大学学报:工学版, 2012, 46(7): 1157–1161.
FEI Shao-hua, FANG Qiang, MENG Xiang-lei, et al. Countersink depth control of robot drilling based on pressure foot displacement compensation[J]. Journal of Zhejiang University: Engineer Science, 2012, 46(7): 1157–1161. |
| [8] |
董辉跃, 曹国顺, 曲巍巍, 等. 工业机器人自动化钻孔及锪窝一体化加工[J].
浙江大学学报:工学版, 2013, 47(2): 201–208.
DONG Hui-yue, CAO Guo-shun, Qu wei-wei, et al. Processing research of industry robots drilling and countersinking automaticly[J]. Journal of Zhejiang University: Engineer Science, 2013, 47(2): 201–208. |
| [9] | F. 罗伊特. 画法几何学[M]. 北京: 机械工业出版社, 1991. |
| [10] | 姚恩瑜, 何勇, 陈仕平. 数学规划与组合优化[M]. 杭州: 浙江大学出版社, 2001. |
| [11] | CHEN C, HWANG R, CHEN Y. A passive auto-focus camera control system[J]. Applied Soft Computing, 2010, 10(1): 296–303. DOI:10.1016/j.asoc.2009.07.007 |
| [12] |
朱伟东, 曹良洪, 梅标, 等. 利用圆心不对称投影精确标定工业相机[J].
光学精密工程, 2014, 22(8): 2267–2273.
ZHU Wei-dong, CAO Liang-hong, MEI Biao, et al. Calibration of industrial cameras using asymmetric circle center projection[J]. Optics and Precision Engineering, 2014, 22(8): 2267–2273. |


