出行选择行为是交通科学领域的研究热点之一, 目前的研究多是在确定环境下开展的, 且假设出行者是完全理性[1-2].事实上, 通勤者面对的是不确定的出行环境, 且并非完全理性, 前景理论(prospect theory, PT)及累积前景理论(cumulative prospect theory, CPT)的提出修正和弥补了对于理性假设的不足, 它将常人的决策行为以及个人的心理感知等因素融入到决策行为分析中.
在参照点选取方面, Katsikopoulos等[3]在路径选择实验中发现不同参照点的出行者表现出不同的风险态度;Avineri等[4]考虑了不同类型出行者参照点的选取对最终的出行决策的影响;Jon等[5]基于调查发现出行者的决策结果取决于自身的参照点.国内的研究大多是在国外研究的基础上进行的, 王伟等[6]考虑出行时间的可靠性与不可靠性, 选择期望-超额出行时间作为参照点;田丽君等[7]假设用户的参照点服从均匀分布, 建立了异质参照点的多用户网络均衡模型.这些研究结果都表明参照点的选取与出行者自身特性相关, 而风险系数也跟参照点有关.
在出行选择等方面, Avineri[8]采用累积前景理论研究不同信息类型对个人出行的影响;Xu等[9]提出了参照点取值方法并分析出行者的路径选择行为;李小静等[10]从价值和可靠性变化2个方面将参照点推广为2个, 研究通勤者的路径选择行为及对待风险的态度;甘佐贤等[11]建立了到达时间与出行感知价值之间的联系, 对累积前景理论在出行决策中的运用进行了分析.在出行联合选择方面, 秦世环[12]综合考虑出行方式选择与路径选择, 根据参照点与风险偏好系数的差异, 建立期望广义出行成本的参照点模型;张波等[13]建立了随机动态用户最优(SDUO)模型用于出发时间与出行路径的同时选择, 并分析不同政策下的出行者选择行为.
上述研究[4]-[7]、[9]-[11]大多是建立在出行者同质的基础上, 虽然有学者开始考虑出行者参照点异质的问题, 但仅假设参照点服从均匀分布[14]或离散分布[15]与实际存在差异;对于出行选择行为的研究多侧重在单维出行决策, 如出行路径、出行方式等, 而对于多维出行决策, 也仅仅将出行路径与出行方式或出发时刻结合, 没有考虑更为复杂的情况, 如三者同时考虑的情况.本文从通勤者异质性的角度出发, 建立异质参照点与风险系数函数, 分析异质通勤者单维出行决策与多维出行决策的区别.
1 通勤者异质性 1.1 偏好到达时间预算在现实生活中, 个体之间往往存在着差异, 本文假设通勤者是异质的, 并根据时间价值的高低对通勤者进行分类.通勤者的偏好到达时间并不是某一确定的时刻, 而是一个大致的区间范围, 即能接受的最早于最晚到达时间, 不同时间价值的通勤者对于到达时间的敏感度β及可靠度γ是不一样的.
在出行选择中, 通勤者出行决策的目的是使到达时间尽可能地接近准时上班时间.假设通勤者最佳偏好到达时间为tb, 能接受的最早到达时间为te, 能接受的最晚到达时间为tl.吕彪等[16]提出路段行程时间近似服从正态分布, 而到达时间等于出发时间加上行程时间, 由正态分布的性质可知, 到达时间仍近似服从正态分布.
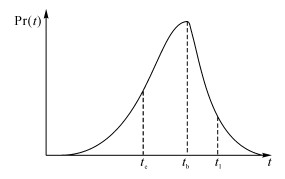
通常, 通勤者迟到受到的惩罚会大于早到, 相对于迟到, 通勤者更倾向于早到, 故te与tb的距离要比tl与tb的距离长, 而相同可靠度下的正态分布中, te与tb的距离与tl与tb的距离是一样的, 这不符合实际.因此, 通勤者的偏好到达时间符合偏态分布.偏态分布函数如图 1所示,其中,Pr(t)为在t时刻到达的可能性.
|
图 1 偏好到达时间分布函数 Fig. 1 Preference arrival time distribution function |
假设偏态分布的概率密度函数为
| $ f\left( t \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _ - }}}\exp \left[ { - \frac{{{{\left( {t - {t_{\rm{b}}}} \right)}^2}}}{{2\sigma _ - ^2}}} \right],\;\;\;t \le {t_{\rm{b}}};\\ \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _ + }}}\exp \left[ { - \frac{{{{\left( {t - {t_{\rm{b}}}} \right)}^2}}}{{2\sigma _ + ^2}}} \right],\;\;\;t > {t_{\rm{b}}}. \end{array} \right. $ | (1) |
式中:σ-为上侧标准差, σ+为下侧标准差,t为到达时间.
根据通勤者到达时间的可靠度的不同, 确定不同时间价值的通勤者偏好到达时间的范围.在预先给定的可靠性度γ下[10], 到达时间的γ悲观值tinf (γ)就是最晚到达时间, 可以表示为
| $ {t_{\inf }}\left( \gamma \right) = \inf \left\{ {{t_1}\left| {\Pr \left\{ {{t_1} \ge {t_{\rm{b}}}} \right\} \le 1 - \gamma } \right.} \right\}. $ | (2) |
根据极限定理, 最晚偏好到达时间服从偏态分布, 即tl~S(tl, σ-, σ+), 故式(2) 可以表示为
| $ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\int\limits_{{t_1}}^{ + \infty } {\frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _ + }}}\exp \left( { - \frac{{{{\left( {t - {t_{\rm{b}}}} \right)}^2}}}{{2\sigma _ + ^2}}} \right){\rm{d}}t \le 1 - \gamma } . $ | (3) |
经推导得到, tl=tb+σ+Φ-1(γ)
式中:Φ-1·为偏态函数的反函数.
在预先给定的可靠度γ下, 到达时间的γ乐观值tsup (γ)就是最早到达时间, 可以表示为
| $ {t_{\sup }}\left( \gamma \right) = \sup \;\;\;\left\{ {{t_{\rm{e}}}\left| {\Pr \left\{ {{t_{\rm{e}}} \le {t_{\rm{b}}}} \right\} \le 1 - \gamma } \right.} \right\}. $ | (4) |
同样式(4) 可以表示为
| $ \begin{array}{l} \max \;{t_{\rm{e}}}\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\int\limits_{ - \infty }^{{t_{\rm{e}}}} {\frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _ - }}}\exp \left( { - \frac{{{{\left( {t - {t_{\rm{b}}}} \right)}^2}}}{{2\sigma _ - ^2}}} \right){\rm{d}}t \le 1 - \gamma } . \end{array} $ | (5) |
推导可得, te=tb-σ-Φ-1(γ)
因此, 偏好到达时间t0的范围为
| $ \left[ {{t_{\rm{b}}} - {\sigma _ - }{\mathit{\Phi }^{ - 1}}\left( \gamma \right),{t_{\rm{b}}} + {\sigma _ + }{\mathit{\Phi }^{ - 1}}\left( \gamma \right)} \right]. $ | (6) |
参照点在累积前景理论中的选择对计算结果以及出行决策有着重要影响, 同时备选方案的收益或损失也是根据参照点划分的.由于不同类型的通勤者对到达时间的敏感性及可靠性要求不同, 所以应该考虑通勤者参照点的异质性[12].
文献[10]和[11]中均假设通勤者在出行中存在2个参照点.本文中, m类通勤者的到达时间范围存在一定的差别, 因此将不同通勤者能接受的最早到达时间tem及最晚到达时间tlm设置为参照点, 即
| $ t_{\rm{e}}^m = {t_{\rm{b}}} - {\sigma _ - }{\mathit{\Phi }^{ - 1}}\left( \gamma \right)\;\;\;t_1^m = {t_{\rm{b}}} + {\sigma _ + }{\mathit{\Phi }^{ - 1}}\left( \gamma \right). $ | (7) |
虽然在两者之间还存在一个最佳偏好到达时间, 这个点显然不是真的的参照点, 而是伪参照点.
1.3 风险偏好风险偏好就是通勤者在风险环境下对出行选择表现出来的心理态度和行为意向, 不同特征的通勤者具有的风险偏好是不同的.但目前的风险偏好系数均采用Kahneman通过实验标定的0.88, 显然这无法正确表达不同类型的通勤者的风险偏好程度.由于风险偏好水平与参照点及期望水平有关, 因此将风险偏好系数与参照点相互关联, 借鉴文献[12]中的结果, 定义各类通勤者的风险偏好系数为
| $ {\theta ^m} = {\left( {1 - \frac{1}{\beta }\left( {t_1^m - t_{\rm{e}}^m} \right)/\sum\limits_m {\left( {t_1^m - t_{\rm{e}}^m} \right)} } \right)^\alpha }. $ | (8) |
式中:α为时间价值系数.
2 出行决策模型累积前景理论通常将个体的决策过程分编辑和评估2个阶段来进行, 在编辑阶段, 依据前面对通勤者参照点的设定, 建立用于描述各备选方案可能发生结果的价值函数V(xk)和累积权重函数π(p);在评估阶段, 通过价值函数和累积权重函数来估计出行选择的前景值.
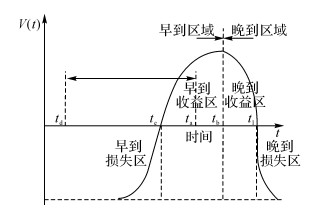
2.1 价值函数如图 2所示, 2个参照点te、tl及伪参照点tb将到达时刻分为了4个时刻:(-∞, te], (te, tb], (tb, tl], (tl, +∞).如果通勤者的实际到达时间早于te或者晚于tl[7], 则此时的价值函数为负值, 被视为损失;如果通勤者的到达时间处于te和tl之间, 则此时的价值函数为正值, 被视为收益.图中Ⅱ区(早到收益)和Ⅲ区(晚到收益)为收益区, Ⅰ区(早到损失)和Ⅳ区(晚到损失)为损失区.
|
图 2 价值函数曲线 Fig. 2 Curve of value function |
由于小汽车的行驶速度快, 路段行程时间比公交车短, 但费用会远大于公交车, 如果仅考虑时间因素, 则通勤者都会偏向选择小汽车.因此, 本文将非时间成本转换为时间成本, 利用广义出行费用函数建立价值函数.通勤者的实际到达时间等于出发时刻加上路段行程时间:
| $ t_{\rm{a}}^m = t_{\rm{d}}^m + {t^m}. $ | (9) |
式中:tdm为m类通勤者的出发时刻;tm为m类通勤者的行程时间, 包括路段上的拥堵时间;
根据实际到达时间tam、偏好到达时间tbm和其他2个参照点, 构建各类通勤者的价值函数:
| $ v\left( {t_{\rm{a}}^m} \right) = \left\{ \begin{array}{l} {v_1} = - {\beta _1}{\left[ {{\alpha ^m}\left( {t_{\rm{e}}^m - t_{\rm{a}}^m} \right) + {C^m}} \right]^{{\theta ^m}}},t_{\rm{a}}^m < t_{\rm{e}}^m;\\ {v_2} = {\beta _2}{\left[ {{\alpha ^m}\left( {t_{\rm{a}}^m - t_{\rm{e}}^m} \right) + {C^m}} \right]^{{\theta ^m}}},t_{\rm{e}}^m \le t_{\rm{a}}^m < t_{\rm{b}}^m;\\ {v_3} = {\beta _3}{\left[ {{\alpha ^m}\left( {t_{\rm{1}}^m - t_{\rm{a}}^m} \right) + {C^m}} \right]^{{\theta ^m}}},t_{\rm{b}}^m \le t_{\rm{a}}^m < t_{\rm{1}}^m;\\ {v_4} = - {\beta _4}{\left[ {{\alpha ^m}\left( {t_{\rm{a}}^m - t_{\rm{1}}^m} \right) + {C^m}} \right]^{{\theta ^m}}},t_{\rm{1}}^m \le t_{\rm{a}}^m. \end{array} \right. $ | (10) |
式中:Cm为m类通勤者的出行费用;αm为m类通勤者的时间价值;βi为损失规避系数, 采用kahneman的标定结果, 收益时β=1, 损失时β=2.25;且0 < θm≤1.
2.2 权重函数本文采用Kahneman给出的权重函数表达式:
当决策者面临收益时:
| $ {w^ + }\left( p \right) = \frac{{{p^\lambda }}}{{{{\left[ {{p^\lambda } + {{\left( {1 - p} \right)}^\lambda }} \right]}^{\frac{1}{\lambda }}}}}. $ | (11) |
当决策者面临损失时:
| $ {w^ - }\left( p \right) = \frac{{{p^\delta }}}{{{{\left[ {{p^\delta } + {{\left( {1 - p} \right)}^\delta }} \right]}^{\frac{1}{\delta }}}}}. $ | (12) |
式中:p为备选方案的主观感知概率, λ为收益参数, δ为损失参数, 根据Kahneman的标定结果, λ=0.61, δ=0.69.
2.3 累积权重函数及前景值以点tb划分的2部分前景值分别为f(xl, pl)和f(xr, pr), 且左右两边均存在收益与损失的情况, 故应分开计算.以左边部分前景值为例:
假设左边有m+n+1个可能的到达时刻, t-ml, …t0l, …tnl, 它们的发生概率为p-ml, …, pnl, 用xl=(x-ml, …, xnl)和pl=(p-ml, …, pnl)表示.
决策权重πi+和πi-由累积概率获得, 过程如下:
| $ {\rm{\pi }}_i^ + = {w^ + }\left( {p_i^1 + \cdots + p_n^1} \right) - {w^ + }\left( {p_{i + 1}^1 + \cdots + p_n^1} \right). $ | (13) |
| $ {\rm{\pi }}_i^ - = {w^ - }\left( {p_{ - m}^1 + \cdots + p_i^1} \right) - {w^ - }\left( {p_{ - m}^1 + \cdots + p_{i - 1}^1} \right). $ | (14) |
| $ {\rm{\pi }}_n^ + = {w^ + }\left( {{p_n}} \right),{\rm{\pi }}_{ - m}^ - = {w^ - }\left( {{p_{ - m}}} \right). $ | (15) |
左边前景值为
| $ f\left( {{x_1},{p_1}} \right) = \sum\limits_{i = - m}^0 {{\rm{\pi }}_i^ - {v_1}\left( {{t_i}} \right)} + \sum\limits_{i = 1}^n {{\rm{\pi }}_i^ + {v_1}\left( {{t_i}} \right)} . $ | (16) |
同样可得到右边前景值为
| $ f\left( {{x_{\rm{r}}},{p_{\rm{r}}}} \right) = \sum\limits_{i = - j}^0 {{\rm{\pi }}_{\rm{i}}^ - {v_{\rm{r}}}\left( {{t_i}} \right)} + \sum\limits_{i = 1}^n {{\rm{\pi }}_{\rm{i}}^ + {v_{\rm{r}}}\left( {{t_{\rm{i}}}} \right)} . $ | (17) |
总的前景值表达式为
| $ \begin{array}{l} f\left( {x,p} \right) = \sum\limits_{i = - m}^0 {{\rm{\pi }}_{\rm{i}}^ - {v_1}\left( {{t_{\rm{i}}}} \right)} + \sum\limits_{i = 1}^n {{\rm{\pi }}_{\rm{i}}^ + {v_1}\left( {{t_i}} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = - j}^0 {{\rm{\pi }}_i^ - {v_{\rm{r}}}\left( {{t_i}} \right)} + \sum\limits_{i = 1}^n {{\rm{\pi }}_i^ + {v_{\rm{r}}}\left( {{t_i}} \right)} . \end{array} $ | (18) |
通勤者出行选择模型求解步骤如下:
Step1:根据各类通勤者的到达时间敏感性β确定到达时间可靠性γ, 然后根据tb, σ-, σ+及α, 按式(2)~(6) 计算得到各类通勤者到达时间的范围;
Step2:计算不同出行方式与出行路径的路段行程时间, 结合出行费用得出各类通勤者的广义出行时间, 并根据出发时刻确定到达时间;
Step3:根据能接受的最早到达时间及最晚到达时间, 按式(7)~(8) 确定各类通勤者的参照点及风险偏好;
Step4:按式(10) 确定各类通勤者的价值函数, 按式(13)~(15) 计算累积概率权重函数;
Step5:根据式(16)~(18) 计算各类通勤者不同出行选择方案的前景值, 选取前景值最大的出行方案.
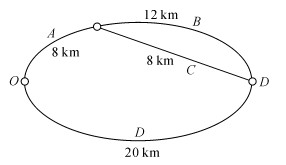
3.2 实例分析路网上存在一个OD点对, 通勤者从起点O出发, 可以经过3条路径到达讫点D, 分别是:从起点O经过路段A和路段B到达终点D、从起点O经过路段A和路段C到达终点D、从起点O经过路段D到达终点D, 如图 3所示.
|
图 3 路网结构图 Fig. 3 Network structure diagram |
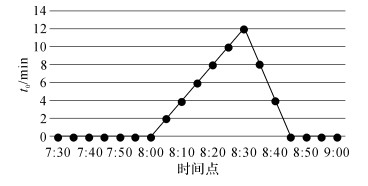
路径1与路径3的路程长度一样, 即自由行程时间一样, 但路径1上小汽车与公交车混合行驶, 相互干扰, 定义干扰因子为φh;路径3上设置了公交专用道, 互不干扰, 但小汽车间由于车道数变少, 相互之间仍有一定干扰, 定义干扰因子为φb;路径2与路径1一样, 小汽车与公交车混合行驶, 但路段C比路段B路程短, 通勤者倾向于选择较短的路径, 导致路段C更容易产生拥挤.假设路段拥挤时间如图 4所示,图中t0为拥挤时间.
|
图 4 拥挤时间函数 Fig. 4 Crowded time function |
定义模型的参数为:Scar=60 km/h, Sbus=40 km/h, LA=8 km, LB=12 km, LC=8 km, LD=20 km, Ccar=5元, Cbus=2元, Cbrt=3元, β=0.08α, γ=ln(1.6+1/β), tp=8:50, σ-2=1, σ+2=0.5, φh=0.75, φb=0.90.
偏态分布函数为
| $ f\left( t \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2{\rm{\pi }}} }}\exp \left[ { - {{\left( {\left( {t - 8:50} \right)/60} \right)}^2}/2} \right],t \le {t_{\rm{b}}};\\ \frac{1}{{\sqrt {\rm{\pi }} }}\exp \left[ { - {{\left( {\left( {t - 8:50} \right)/60 + 0.6} \right)}^2}} \right],t > {t_{\rm{b}}}. \end{array} \right. $ | (19) |
由于通勤者的时间价值不同, 因此其到达时间的可靠性及风险系数也不同.将通勤者分为3类, 15~20为低时间价值, 20~25为中等时间价值, 25~30为高时间价值.
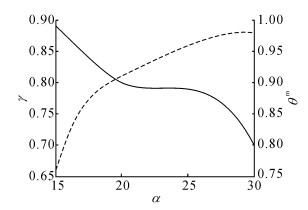
如图 5所示, 随着通勤者时间价值的增加, 到达时间可靠性下降, 并呈现为“S”形, 而风险系数则随着时间价值的增加而增加.可以看出, 低时间价值通勤者的到达时间可靠性较高, 其风险系数较低;而高时间价值通勤者的到达时间可靠性较低, 其风险系数相对较高.
|
图 5 时间价值与可靠性和风险系数的关系 Fig. 5 Relationship between time value and reliability, and risk factor |
根据时间价值与可靠性和风险系数的关系, 选取3类通勤者, 分别为α=15、α=20、α=30.根据Step1-Step3计算异质通勤者的各项, 如表 1所示:
| 表 1 异质通勤者的各项参数 Table 1 Parameters of heterogeneous commuters |
由于可靠性的不同, 通勤者可接受的最早到达时间与最晚到达时间也不相同.α=15的通勤者到达范围相差12分钟, 到达时间可靠性较高, 且其风险偏好系数为0.59, 因此在出行中表现为风险规避;而α=30的通勤者到达范围仅相差4 min, 可见这类通勤者对到达时间要求较高, 且其风险偏好系数为0.95, 在出行中容易表现为风险追求.
通勤者的到达时间由出发时间和行程时间决定, 而行程时间主要由出行方式和出行路径决定, 仅考虑出行时间影响时, 每条路径上小汽车的行程时间都要小于公交车;当综合考虑出行时间与出行费用影响时, 由于时间价值的不同, 各类通勤者受到的影响也不同.α=15和α=20的通勤者时间价值较低, 对出行费用的敏感度较高, 因而小汽车的广义出行时间大于公交车;α=30的通勤者时间价值较高, 对出行费用不敏感, 小汽车的广义出行时间仍小于公交车.
根据Step4-Step5计算各类通勤者不同选择行为的前景值.通勤者一般会以5的倍数选择出发时刻, 如7:10、8:15, 而不是8:07.以5分钟为场景间隔, 得到不同情况下的出行决策结果:
1) 单维出行决策
(1) 在出发时刻方面, 不管哪一类通勤者, 其前景值都表现为先上升后下降的趋势, 这也表明通勤者只有在一定时间范围内出发才会获得收益, 太早或太晚出发都会受到损失.低时间价值的通勤者更偏好早出发, 高时间价值的通勤者偏好晚出发.
(2) 在出行方式方面, 低时间价值的通勤者更偏好选择公交车, 高时间价值的通勤者偏好选择小汽车, 而介于两者之间的通勤者则由出行目的、费用敏感度等决定.
(3) 在出行路径方面, 低时间价值的通勤者更偏好选择路径1, 高时间价值的通勤者偏好选择路径2, 而介于两者之间的通勤者则由出行目的、费用敏感度等决定.
2) 多维出行决策
(1)α=15的通勤者会在8:05出发, 选择公交车经路径1到达工作地;α=20的通勤者会在8:15出发, 选择小汽车经路径1到达工作地;α=30的通勤者会在8:10出发, 选择小汽车经路径2到达工作地.
(2) 对比不同类型通勤者的前景值可以看出, 时间价值低的通勤者在可接受的到达时间范围内到达目的地的概率较大, 可供选择的获得收益的出行方案较多;而时间价值高的通勤者可供选择的能获得收益的出行方案仅有4个.
表 2为2种情况下的出行决策结果对比, 从表中可以发现单维出行决策中, 通勤者仅关注单方面的效益, 如在选择出行方式时, 仅考虑两种出行方式所带来的效益, 没有考虑到出发时刻或出行路径对出行方式的影响, 各决策行为之间是孤立的, 相互之间没有联系;而多维出行决策中, 决策行为之间相互影响, 如不同的出发时刻会导致路段上拥挤时间的不同, 进而影响行程时间, 而路段拥挤时间的不同又会影响到出行路径的选择, 因此2种情况下的决策结果有较大的出入.
| 表 2 单维出行决策与多维出行决策的对比 Table 2 Comparison of one-dimensional travel decision and multi-dimensional travel decision |
最后假设各类通勤者的风险系数为固定常数, 根据Kahneman的标定结果θ=0.88, 代入模型, 与之前的结果进行对比, 可以得出:
(1) 本文中通勤者的风险系数是异质的, 当风险系数为固定常数时, 显然会错误地估计不同类型通勤者在出行选择中的风险态度.由计算结果可知, 风险系数相同的情况下, 模型会高估低时间价值通勤者的前景值, 低估高时间价值通勤者的前景值;
(2) 通勤者在单维出行决策时, 风险系数对出发时刻及出行路径的影响不大, 结果较为相似, 在出行方式, 风险系数高的通勤者倾向于选择小汽车, 风险系数低的通勤者则选择公交车, 如表 3所示;
| 表 3 不同风险系数下的单维出行决策结果 Table 3 One-dimensional travel decision results under different risk factor |
(3) 不同类型通勤者在不同风险系数下的出行决策结果不同.在风险系数相同与不同的情况下, 多维出行决策结果与单维出行决策偏差均较大, 说明在出行决策中假设通勤者的风险系数相同不符合实际情况, 如表 4所示.
| 表 4 不同风险系数下的多维出行决策结果 Table 4 Multi-dimensional travel decision results under different risk factor |
本文从通勤者异质的角度入手, 分析了不同通勤者的出行选择偏好及参照点与风险系数的异质性, 并假设通勤者的到达时间符合偏态分布, 综合考虑出行时间与出行费用对出行选择行为的影响, 建立了基于累积前景理论的多维出行决策模型, 借助实例从单维出行决策、多维出行决策以及风险系数相同等角度分析不同情形下通勤者的出行决策行为.结果表明建立的模型能准确地描述异质通勤者的出行决策行为, 与实际较为符合.在本文中, 通勤者的分类主要依据时间价值, 而在实际中, 通勤者受到多种因素影响, 分类更加复杂;同时路段上拥挤时间受拥挤程度和拥挤时段分布的影响, 拥挤程度又受到通行能力退化及出行需求波动影响, 导致行程时间也随之变化.未来有待进一步研究的方向包括利用聚类分析细化通勤者分类及拥挤时段分布变化、通行能力退化、出行需求波动下的出行决策行为等情况.
| [1] | SMITH M J. The marginal cost taxation of a transportation network[J]. Transportation Research Part B: Methodological, 1979, 13(3): 237–242. DOI:10.1016/0191-2615(79)90015-8 |
| [2] | RABIN M J. Risk Aversion and excepted-utility theory: a calibration theorem[J]. Econometrica, 2000, 68(5): 1281–1292. DOI:10.1111/ecta.2000.68.issue-5 |
| [3] | KATSIKOPOULOS K V, DUSE-ANTHONY Y, FISHER D L, et al. Risk attitude reversals in drivers' route choice when range of travel time information is provided[J]. Human Factors: The Journal of the Human Factors and Ergonomics Society, 2002, 44(3): 466–473. DOI:10.1518/0018720024497718 |
| [4] | AVINERI E, PRASHKER J. Sensitivity to uncertainty: need for a paradigm shift[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1854(1): 90–98. |
| [5] | JOU R C, KITAMURA R, WENG M C, et al. Dynamic commuter departure time choice under uncertainty[J]. Transportation Research Part A: Policy and Practice, 2008, 42(5): 774–783. DOI:10.1016/j.tra.2008.01.017 |
| [6] |
王伟, 孙会君. 基于内生参考点的交通网络均衡模型[J].
应用数学和力学, 2013, 34(2): 190–198.
WANG Wei, SUN Hui-jun. Transportation network equilibrium model based on the endogenous reference point[J]. Applied Mathematics and Mechanics, 2013, 34(2): 190–198. |
| [7] |
田丽君, 黄海军, 许岩. 具有异质参考点的多用户网络均衡模型[J].
管理科学学报, 2014, 17(7): 1–9.
TIAN Li-jun, HUANG Hai-jun, XU Yan. Multi-user Network equilibrium model with heterogeneous reference point[J]. Journal of Management Sciences in China, 2014, 17(7): 1–9. |
| [8] | AVINERI E. A cumulative prospect theory approach to passengers behavior modeling: waiting time paradox revisited[J]. Journal of Intelligent Transportation Systems, 2004, 8(4): 195–204. DOI:10.1080/15472450490523856 |
| [9] | XU H, ZHOU J, XU W. A Decision-making rule for modeling travelers' route choice behavior based on cumulative prospect theory[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(2): 218–228. DOI:10.1016/j.trc.2010.05.009 |
| [10] |
李小静, 刘林忠. 基于累积前景理论的通勤者路径选择模型[J].
交通运输系统工程与信息, 2015, 15(1): 173–178.
LI Xiao-jing, LIU Lin-zhong. Commuter path model selection based on cumulative prospect theory[J]. Transportation Systems Engineering and Information Technology, 2015, 15(1): 173–178. |
| [11] |
甘佐贤, 陈红, 冯微, 等. 基于累积前景理论的出行风险分析[J].
武汉理工大学学报:交通科学与工程版, 2014, 38(4): 909–913.
GAN Zuo-xian, CHEN Hong, FENG Wei, et al. Travel risk analysis based on cumulative prospect theory[J]. Wuhan University of Technology: Transportation Science & Engineering, 2014, 38(4): 909–913. |
| [12] |
秦世环. 基于前景理论的出行方式与路径联合选择行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
QIN Shi-huan. Research Joint choose behavior of travel mode and route based on prospect theory [D]. Harbin: Harbin Institute of Technology, 2013. |
| [13] |
张波, 隽志才, 林徐勋. 基于累积前景理论的出发时间选择SDUO模型[J].
管理工程学报, 2013(1): 68–7.
ZHANG Bo, JUAN Zhi-cai, LIN Xu-xun. SDUO model of choose of departure time based on the cumulative prospect theory[J]. Journal of Industrial Engineering and Engineering, 2013(1): 68–7. |
| [14] |
肖玲玲, 黄海军, 田丽君. 考虑异质出行者的随机瓶颈模型[J].
交通运输系统工程与信息, 2014, 04: 93–98.
XIAO Ling-ling, HUANG Hai-jun, TIAN Li-jun. Stochastic bottleneck model with heterogeneous travelers[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 04: 93–98. DOI:10.3969/j.issn.1009-6744.2014.04.013 |
| [15] |
吴文祥, 黄海军. 考虑地铁车内拥挤和早到与迟到惩罚的通勤者出发时间选择模型[J].
交通运输系统工程与信息, 2009, 01: 128–132.
Wu Wen-xiang, HUANG Hai-jun. Commuters' departure time choice with in-carriage congestion and arrival early /late penalty[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 01: 128–132. DOI:10.3969/j.issn.1009-6744.2009.01.022 |
| [16] |
吕彪, 蒲云, 刘海旭. 多用户类型弹性需求随机期望-超额用户平衡模型[J].
西南交通大学学报, 2012, 03: 516–525.
LU Biao, PU Yun, LIU Hai-xu. Stochastic mean-excess user equilibrium model with multiple classes and elastic demand[J]. Southwest Jiao Tong University, 2012, 03: 516–525. DOI:10.3969/j.issn.0258-2724.2012.03.026 |



