2. 浙江大学 海洋学院 浙江 杭州 310058;
3. 北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京, 100144
2. College of Ocean College, Zhejiang University, Hangzhou 310058, China;
3. Beijing Key Laboratory of Urban Road Intelligent Traffic Control, North China University of Technology, Beijing 100144, China
随着城市交通拥堵问题的日益加剧, 我国很多城市路网的节点交通流运行经常处于过饱和状态, 甚至部分路段的排队长度接近或等于路段长度, 引发排队上溯、形成路段“瓶颈”[1], 造成路口死锁.交叉口死锁将显著增加出行者的出行时间[2], 并对交通安全造成极大影响.在给定的交通需求及路网结构下, 及时识别路段瓶颈并对进行有效控制是消除影响的关键之一.
在通常情况下, 瓶颈控制可分为瓶颈识别和信号参数优化2大部分.在瓶颈识别方面, Ma等[3]基于线圈检测数据, 提出了滚动时间占有率的基本概念及统计方法, 研究了排队长度与基本检测信息的对应关系, 确定了针对不同检测器布设位置的瓶颈触发与消散阈值;朱森来等[4]以交通网络储备容量模型为基础, 提出了宏观交通网络潜在瓶颈路段识别方法, 并设计了储备容量模型的求解算法.在瓶颈控制方面, 赵莹莹[5]分析了瓶颈产生机理, 并依据实时交通流状态提出3类瓶颈控制方法及适用范围;马东方[6]从主动预防和被动消散2个层面设计了区域增容控制和单点瓶颈信号控制的基本流程和实现方法;徐洪峰等[7]分析了环形交叉口的基本特征, 探讨了让行规则与信号控制的利弊, 并以避免交叉口锁死为目标, 提出一种单进口轮放式的信号控制方法, 并取得较好的效果;Weili等[8-10]针对孤立瓶颈交叉口, 以上下游邻接交叉口为调控对象、以排队长度为优化目标、并基于反馈控制的思想提出了一种瓶颈控制实时优化方法;Kitae等[11]通过平衡瓶颈路段上游各路段的排队蔓延速率来减缓排队上溯速率, 但在未知车辆始发点点和目的地的情况下, 并不能很好实现预期目标.
上述方法主要依靠线圈检测数据, 包括断面流量、占有率和瞬时速度等信息, 缺乏对区域交通状态的宏观掌握, 无法精确定位拥堵需求来源并精准优化瓶颈控制方案.
近年来, 视频检测设备在我国很多大中城市日益普及.与传统的线圈检测设备相比, 视频检测设备除能获取通过检测断面的车辆数等信息外, 还能获取车辆通过停车线的车辆牌照、通过时刻等信息, 利用车牌匹配技术可以获取个体车辆在路段上的行程时间.根据我国政府颁布实施的视频检测设备和牌照识别技术的国家标准, 视频检测设备在最不利条件下的识别精度应满足如下要求:流量精度≥85%、含汉字的全牌正确识别率≥90%、拒识率≤0.1%.基于该标准, 在忽略路段进出口驶入与驶离车辆的影响下, 利用车牌匹配可以获取81%以上的车辆行程时间信息, 因此, 可以提取车牌匹配信息获取车辆交通出行量(OD)信息[12].
本文依靠路口现有布设的视频检测设备和线圈检测设备, 综合利用OD信息和流量信息, 针对已识别瓶颈路段的上游区域搜索信号调节的可控制路段, 并基于可控制路段调节量分配模型优化控制节点集合、分配各路段的实际调节量, 完成各节点信号参数优化, 并应用VISSIM仿真实现实施效果评价.
1 瓶颈路段上游控制节点的选取本文中, 瓶颈路段指的是高峰时期易出现过饱和状态, 其排队长度约等于路段长度的路段.利用交叉口之间的OD信息可以精确统计任意一条上游路段相对瓶颈路段的交通需求, 且可区分上游路段相对于瓶颈路段交通需求的路径分布, 为筛选关键路径、甄别可控路段奠定基础.
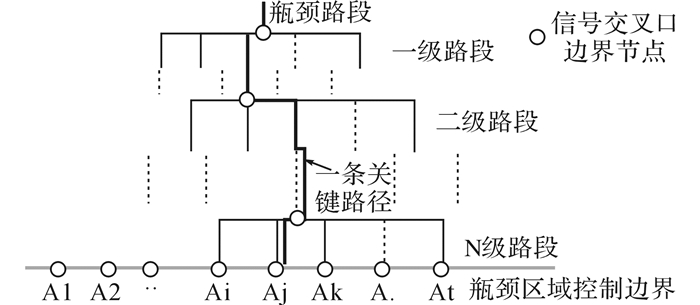
1.1 关键路径与可控制路段关键路径是指瓶颈区域边界节点至瓶颈路段之间可用于瓶颈控制的路径.可控制路段是指一条关键路径中可用于瓶颈控制的路段.各可控制路段所对应的交叉口称之为可控制节点或交叉口.如图 1所示是一条关键路径树状示意图, 其中瓶颈路段在图中最顶端, 与瓶颈路段直接相连的可控制路段为一级可控制路段, 也称一级路段.一级控制路段所对应的交叉口为一级交叉口.与一级控制路段相连但不与瓶颈路段相连的可控制路段为二级控制路段, 也称二级路段.以此类推, 直到瓶颈控制区域边界.瓶颈控制区域边界节点是由交通工程师依据城市具体路网结构、区域信号控制策略等综合确定的可用于瓶颈控制区域边缘交叉口.其中, 图中示黑色粗连线是其中一条典型的关键路径, 其他路段为各级可控制路段.
|
图 1 关键路径树状示意图 Fig. 1 Critical route schematic tree |
视频信息提取出起讫点数据(即O点和D点)后, 需要对车流路径进行优化, 否则会出现冗余路径, Dial算法是一种较为广泛、有效的路径搜索算法, 其借助求解有效路径Dial算法的基本思想, 定义与冗余路径相对应合理路径:合理路径上的每个点到下一个点, 都能远离O点, 靠近D点.
对于O、D之间的第k条路径Pk, 设其经过的交叉口依次为O, Pk1, Pk2, Pk3, …, Pkn, D.令sp(i, j)为路段i和j之间的最短路距离.因此对于任意i, j合理路径应满足条件:
| $ \left. \begin{align} &\text{sp}(O, {{P}_{ki}})<\text{sp}(O, {{P}_{k(i+1)}}), \\ &\text{sp}({{P}_{ki}}, D)>\text{sp}({{P}_{k(i+1)}}, D). \\ \end{align} \right\} $ | (1) |
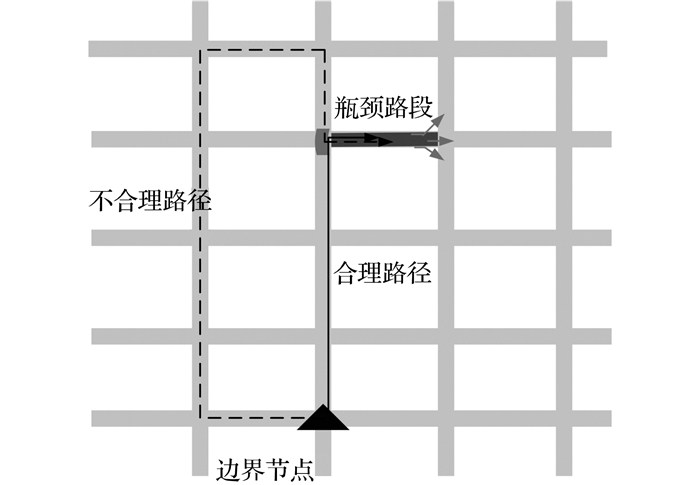
对于指定的某一边界节点和瓶颈节点, 相应的可能路径有多条, 其中某些路径因为路程比较长或者不合理(例如存在环的路径), 需要将之去除(即认为没有交通流从给定的边界节点出发到达瓶颈节点).由于实际路网的复杂程度较高, 在大规模网络中分析合理路径需要对网络进行较多的预处理.如图 2所示为车流路径优化示意图.
|
图 2 车流路径优化 Fig. 2 Traffic route optimization |
在实时控制中, 仅调节上游节点的信号控制参数来消散路段瓶颈可能会致使拥堵的转移, 但是过多的调整上游节点的个数, 瓶颈效果提升的边际效应会大幅降低, 而对于其他交叉口非调整车流的负面相应却显著增加.因此, 只能当上游路段车流对于瓶颈路段交通负荷产生的影响大于一定阈值时才应将其划为可控路段.
假设路段i为瓶颈控制区域中的某级可控路段, 根据OD数据可提取由路段i驶入瓶颈路段m的车辆数数据.路段i相对于瓶颈路段的贡献率αi, m可表示为
| $ {{\alpha }_{i, m}}=\frac{{{q}_{i, m}}}{{{q}_{m}}}. $ | (2) |
式中:qi, m为从路段i到瓶颈路段m的流率(pcu/s), pcu为标准车当量数;qm为瓶颈路段m的流率(pcu/s).
为降低瓶颈控制对非瓶颈路段的影响, 路段i被界定为可控制路段的条件为
| $ {{\alpha }_{i, m}}\ge \delta . $ | (3) |
式中:δ表征为一个贡献率的阈值参数.
同时, 针对路段i本身而言, 其驶入瓶颈路段m的车流流量应在整个进口道流量当中占有较大比重, 否则调整由路段i驶入路段m的流率会导致绿信比的剧烈变化, 对其他交通流产生严重的负面影响.因此, 路段i的转向流量之间应满足:
| $ \frac{{{q}_{i, m}}}{{{q}_{i}}}\ge \sigma . $ | (4) |
式中:σ为转向流量比, 即路段i驶入路段m的流率与路段i本身流率的比值.其中qi为路段i的流率(pcu/s).当路段i驶入瓶颈路段的交通量占该路段交通量一定比例, 即比值大于σ时, 调节该路段的交通流才不会过多的影响其他方向的车流.δ值和σ值可由交通工程师根据实际情况确定.
2 节点优化界定可控制路段与节点后, 应根据实时交通流量估算瓶颈路段驶入流量总调节量, 并以可控制路段的负荷均分为原则实现总调节量的均衡分配并优化信号控制参数.
2.1 瓶颈路段总调节量瓶颈路段总调节量包含2部分, 第1部分为理想消散时间内原方案下瓶颈路段上下游流量差, 第2部分为需要消散的排队车辆数.原方案下瓶颈路段上下游驶入与驶离的流率差为
| $ \Delta {{S}_{\text{d}}}=\sum\limits_{z\in L_{\text{in}}^{^{m}}}{{{q}_{z, m}}}-\sum\limits_{\omega \in L_{_{\text{out}}}^{m}}{{{q}_{m, \omega }}}. $ | (5) |
式中:ΔSd为原方案下游驶离与上游驶入流率差值(pcu/s); qm, ω为由瓶颈路段驶出方向ω的流率(pcu/s);Loutm为瓶颈路段m的下游出口路段集合;qz, m为上游驶入瓶颈路段方向z的流率(pcu/s);Linm为瓶颈路段m的上游驶入路段集合.
为确保在理想消散时段T内消散路段瓶颈, 应计算需要消散的排队车辆数为
| $ \Delta {{S}_{a}}=\frac{\varphi \left( {{L}_{m, }}_{\text{max}}-{{L}_{m, }}\text{idea} \right)}{l}. $ | (6) |
式中:Lm, max为瓶颈触发时的路段排队长度,单位:m, 由于瓶颈检测器布设在离出口道50 m处, 可为路段长度近似替代;Lm, idea为瓶颈控制结束时的路段排队长度, 单位:m;φ为瓶颈路段车道数;l为平均车辆长度, 默认取值6.
在正常情况下, 瓶颈触发时的单位时间内的上游输入必然大于下游输出, 但在路段进出口及随机因素干扰下, 瓶颈触发时上游输入亦可能会小于下游输出, 此时应界定ΔSd等于0.因此, 为保证特定时段T内消散路段瓶颈, 单位时间内瓶颈路段上游的驶入总调节量为
| $ \Delta S=\Delta {{S}_{\text{a}}}+{{T}_{\text{max}}}~\{\Delta {{S}_{\text{d}}}, 0\}. $ | (8) |
式中:△S为瓶颈路段上游总调节量, 单位:pcu.
2.2 可控制路段调节量分配模型路段剩余容量是指路段周期最大排队长度[13]之外可容纳的排队车辆数.假设路段i最大排队长度估算值为Ui, 其路段剩余容量为
| $ {{F}_{i}}=\frac{\beta {{L}_{i}}-{{U}_{i}}}{{{h}_{s}}}. $ | (5) |
式中:Li为路段i实际长度, 单位:m;hs为最小车头间距, 单位:m;β为路段安全排队系数, 默认取值0.5.
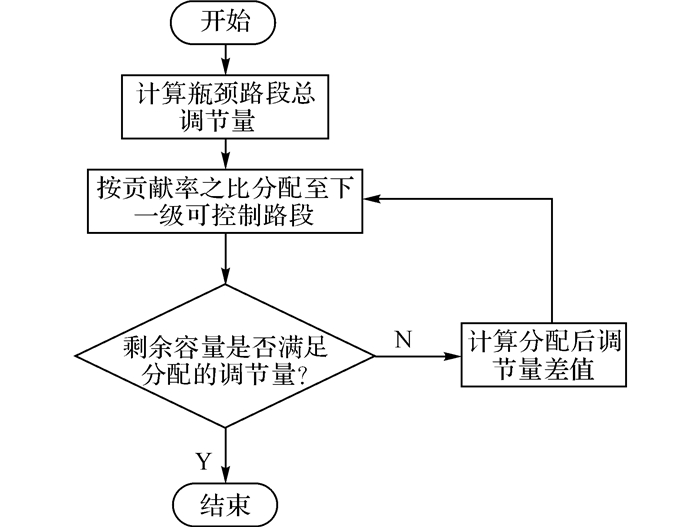
可控制路段分配流量总调节量的核心思路是基于OD数据, 对于每一级可控制路段按瓶颈贡献率的之比分配上一级剩余的调节量.具体模型算法流程如图 3所示.
|
图 3 可控制路段调节量分配流程 Fig. 3 Vehicle allocation process of controlled route |
从一级可控制路段开始, 各可控制路段按贡献率的比例分配驶入流量总调节量.当分配的调节量大于路段剩余容量时, 应将调节量与剩余容量的差值作为下一级分配的总调节量, 继续上一个步骤, 直至边界节点.
2.3 控制路段绿信比调节量假设可控制路段i的车流方向含有φ条车道, 且每条车道的饱和流率均为Qi, 瓶颈触发后分配给该路段的调节量为ΔSi, 则车流所对应相位的绿信比压缩量为
| $ \Delta {{\lambda }_{i}}=\frac{\Delta {{S}_{i}}}{\varphi {{Q}_{i}}}. $ | (9) |
式中:Δλi为可控制路段i对应车流方向相位的绿信比调节量.
3 仿真验证本文基于实际路网数据, 采用VISSIM仿真软件对比分析相同路网及交通条件下新方法对区域交通流运行效率的影响.
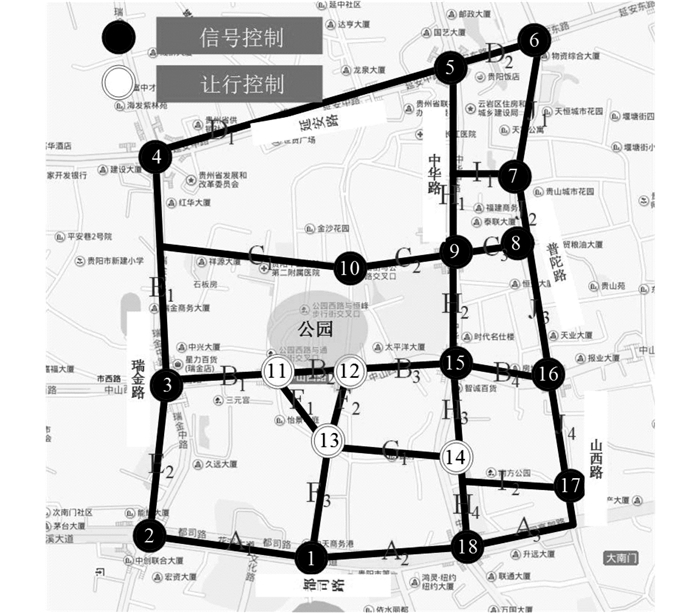
3.1 仿真建立本文选取贵阳市某一拥堵区域为测试区域如图 4所示, 南北长约1.1 m, 东西长约1.2 m, 区域内共包含14个信号控制交叉口.该瓶颈区域内, 都司高架桥在路段A1→A2→A3的上方, 其余道路多为城市主干道和次干道, 其单向路段车道数范围为2~3条.整个测试区域内的高峰路网交通负荷较大, 其中的一中桥交叉口(即18号交叉口)的西进口道经常发生排队溢出现象.
|
图 4 测试区域 Fig. 4 Test area |
根据视频数据提取OD数据并筛选关键路径和可控制路段;利用线圈检测设备统计小时流量, 并计算各车流路径的瓶颈贡献率.由于地形和交通组织的限制, 分析出本区域瓶颈路段的上流限流关键路径仅有一条, 为路径E1→E2→A1→A2, 其中可控制路段为E1, E2, A1和A2.
18号交叉口的西进口路段, 即A2的西进口路段长度为360 m.基于德国PTV集团研发的微观交通仿真软件VISSIM(交通仿真器), 首先建立了测试区域路网仿真模型, 其中关键的控制交叉口信号控制方案如表 1所示, Ti为初始周期, t为初始绿灯时间, 单位:s.通过文献[3]中的瓶颈识别技术, 即利用瓶颈检测器的滚动时间占有率, 确定了瓶颈检测器触发与消散阈值;结合本文的瓶颈控制方法, 通过文献[14]中, 集成VISSIM、Excel VBA和MATLAB的仿真技术, 其中VISSIM和Excel VBA采用COM数据通讯接口集成, Excel与MATLAB之间采用Excel Link扩展接口进行集成[14].仿真对瓶颈检测器滚动时间占有率阈值采用0.6, 触发即进行瓶颈控制, 进行方案计算及下发.仿真评价采用VISSIM自带的评价系统.
| 表 1 可控制交叉口原控制方案 Table 1 Controlled Intersection control program |
为全面评价本文提出的多点联动瓶颈控制方法对瓶颈路段以及整个区域交通流运行效率的影响, 本文采取宏观与中观结合的方式对其进行评价:针对瓶颈路段, 选用瓶颈路段最大排队长度与平均排队长度作为指标;针对整个区域, 评价指标选择为区域中车均延误与车均停车次数.
3.3 结果分析为了对比分析瓶颈控制方案实施前后的控制效果, 本文在相同的仿真条件下, 依据文献[9]优化一套信号控制方案, 并将其称之为原始控制, 其结果显示:仿真时间第1 024 s触发区域瓶颈控制.设置理想消散时间为700 s, 利用触发之前的10 min线圈数据统计瓶颈路段的上游驶入流率以及下游驶离流率, 并根据2.2节的模型计算出实际控制的路段为E2, A1和A2, 优化得到瓶颈控制中各个节点的配时参数.
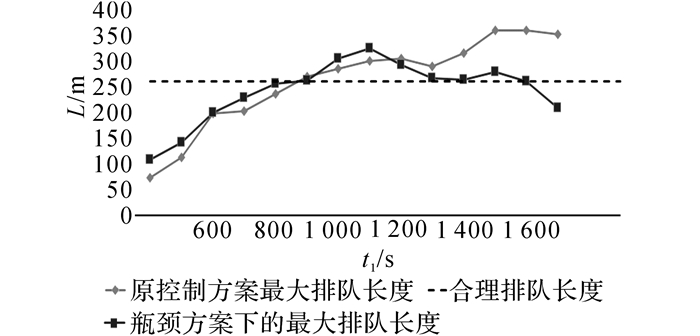
如图 5所示是在2种方案下, 瓶颈路段最大排队长度的变化图.图中L为排队长度,t1为仿真时间, 由于交通流的不可重复性, 仿真软件只能采用2次独立的情况进行对比, 每次仿真的排队长度会有所不同.从图中可以看出, 在瓶颈控制触发以前, 2个方案排队长度相差不大;瓶颈方案在第1 024 s实行瓶颈控制后, 瓶颈路段的排队长度得到了有效控制, 保持在合理排队长度内.
|
图 5 最大排队长度 Fig. 5 The maximum queue length |
整个仿真时段内的具体评价指标对比情况如表 2所示, Lmax为瓶颈路段最大排队长度, Lave为瓶颈路段平均排队长度, D为区域车均延误时间, S为区域车均停车次数.从表中可以看出, 在关键指标(最大排队长度和平均排队长度)上, 瓶颈控制方案情况明显优于常规控制方案.从图 5中可以看出, 在瓶颈控制结束时, 瓶颈路段的排队长度已经下降到合理区间范围内, 然而常规控制方案下的最大排队长度仍然在增长, 极易引发上游路口锁死.瓶颈控制时间内排队逐步消散而非快速消散, 实际上对上游以及整个区域的影响较小.从宏观区域角度上看, 由于防止瓶颈路段的排队溢出情况的发生, 整个区域的延误与停车次数相比常规控制方案都得到了较好的改善, 与实际观察经验相符.
| 表 2 评价指标 Table 2 Evaluation |
本文依靠视频检测设备所能获取的OD等信息以及线圈检测设备所能获取的流量数据, 通过关键路径的筛选定位上游可控制路段, 从区域优化的层面利用负荷度均分的思想提出了一种基于OD信息的瓶颈控制方法, 该方法可以克服传统线圈检测器无法精确定位瓶颈需求来源的缺陷, 实现调节车辆在上游可控制路段上的均衡分配, 从根源上防止拥堵的转移, 保障区域交通流的运行效率.
| [1] | CARLOS F. DAGANZO. Urban gridlock: Macroscopic modeling and mitigation approaches[J]. Transportation Research Part B: Methodological, 2007, 41(1): 49–62. DOI:10.1016/j.trb.2006.03.001 |
| [2] | JAN-DIRK S S A, MICHAEL G H B. Multi-objective signal control of urban junctions-Framework and a London case study[J]. Transportation Research Part C: Emerging Technologies, 2008, 16(4): 454–470. DOI:10.1016/j.trc.2007.09.004 |
| [3] | MA Dong-Fang, WANG Dian-Hai, SUN Feng, et al. Method of spillover identification in urban street networks using loop detector outputs[J]. Journal of Central South University, 2013, 20(2): 572–578. DOI:10.1007/s11771-013-1520-0 |
| [4] |
朱森来, 程琳, 许项东. 基于储备容量的交通网络潜在瓶颈路段识别[J].
系统工程理论与实践, 2014(6): 1572–1577.
ZHU Sen-lai, CHENG Lin, XU Xiang-dong. Identifying bottleneck links in transportation networks based on reserve capacity[J]. Systems Engineering Theory and Practice, 2014(6): 1572–1577. DOI:10.12011/1000-6788(2014)6-1572 |
| [5] |
赵莹莹. 瓶颈交叉口信号控制方法研究[D]. 长春: 吉林大学交通学院, 2011.
ZHAO Ying-ying. Research on signal control method of bottleneck intersection[D]. Changchun: College of Transportation, Jilin University, 2011. |
| [6] |
马东方. 面向瓶颈路段的城市交通信号控制动态优化方法[D]. 长春: 吉林大学交通学院, 2012.
MA Dong-fang. Optimization for traffic signal setting considering the influence of bottleneck in urban street networks[D]. Changchun: College of Transportation, Jilin University, 2012. |
| [7] |
徐洪峰, 耿现彩, 何龙. 单进口轮流放行方式的四路环形交叉口交通信号控制方法[J].
吉林大学学报:工学版, 2016, 44(4): 953–962.
XU Hong-feng, GENG Xian-cai, HE Long. Signal timing plan for fully signalized four-leg roundabouts with single-approach-entering operation[J]. Journal of Jilin University :Engineering and Technology of Jilin Edition, 2016, 44(4): 953–962. |
| [8] | SUN Wei-li, WANG Yun-peng, YU Gui-zhen, et al. Quasi-optimal feedback control for a system of oversaturated intersections[J]. Transportation Research Part C: Emerging Technologies, 2015, 57: 224–240. DOI:10.1016/j.trc.2015.06.018 |
| [9] | SUN Wei-li, WANG Yun-peng, YU Gui-zhen, et al. Quasi-optimal feedback control for an isolated intersection under oversaturation[J]. Transportation Research Part C: Emerging Technologies, 2016, 67: 109–130. DOI:10.1016/j.trc.2015.12.016 |
| [10] | SUN Wei-li, WU Xin-kai, WA NG, Yun-peng, et al. A continuous-flow-intersection-lite design and traffic control for oversaturated bottleneck intersections[J]. Transportation Research Part C: Emerging Technologies, 2015, 56: 18–33. DOI:10.1016/j.trc.2015.03.011 |
| [11] | MEHD K E, WU Xin-kai, VICTOR L K. Controller design for gating traffic control in presence of time-delay in urban road networks[J]. Transportation Research Part C: Emerging Technologies, 2015, 59: 308–322. DOI:10.1016/j.trc.2015.04.031 |
| [12] |
张晓利. 基于车牌识别的交通小区递归划分的OD调查方法与实例分析[C]//第十届中国智能交通年会优秀论文集. 无锡: 中国学术期刊电子出版社, 2015: 13.
ZHANG Xiao-li. A new method of origin-destination survey using license plate recognition by recursive traffic zone division[C]// The 10th China Intelligent Transportation Annual Conference. Wuxi: China Academic Journal Electronic Publishing House, 2015: 13. |
| [13] | GURCAN COMERT. Queue length estimation from probe vehicles at isolated intersections: Estimators for primary parameters[J]. European Journal of Operational Research, 2016, 252(2): 502–521. DOI:10.1016/j.ejor.2016.01.040 |
| [14] |
卢守峰, 韦钦平, 沈文, 等. 集成VISSIM_ExcelVBA和MATLAB的仿真平台研究[J].
交通运输系统工程与信息, 2012, 12(4): 43–48.
LU Shou-feng, WEI Qin-ping, SHEN Wen, et al. Integrated simulation platform of vissim, Excel VBA, MATLAB[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(4): 43–48. |



