2. 国网浙江省电力公司 经济技术研院, 浙江 杭州310000;
3. 国网河南省电力公司 电力科学研究院, 河南 郑州 450052
2. State Grid Zhejiang Economic Research Institute, Hangzhou 310000, China;
3. Electric Power Research Institute of State Grid Hunan Electric Power Company, Zhengzhou400052 China
输电线路风偏容易造成跳闸从而影响线路运行的安全与稳定.由于输电线路跳闸重合的成功率较低, 因此风偏一旦发生, 线路停运的概率很大.仅2005年台风海棠就造成浙江温州地区110~500 kV的各类型线路风偏跳闸共计50多次.多次事故的调查显示[1], 转角塔跳线风偏所引起的故障在所有风偏事故中占有较大的比重.2006年的某次强风作用使得浙江电网共计25条线路跳闸, 而其中12条线路是由于跳线风偏对塔身放电所造成的.已有的研究[1-3]表明跳线发生风偏跳闸的主要原因包括:未考虑微地形下复杂气候条件导致设计校核风速过低;施工中未严格控制跳线长度从而造成跳线过于松弛而在大风作用下出现大幅摆荡.尽管关于输电导线的风偏特性已经有了不少的研究[4-6], 但是对跳线风致运动特点的考察却并不多见.与普通导线相比, 跳线具有长度短、质量轻、更松弛等特点, 因而在风荷载作用下更加容易产生较大的位移响应.此外, 跳线两端与相邻两跨导线耦合连接的特点也使得其风偏运动必然会受到其余各跨导线运动的影响.
由此可见, 有关跳线的风偏特性仍然存在许多有待研究的问题, 研究输电线路转角塔跳线体系在微地形环境下的风偏情况并建立一套关于跳线风偏的有效计算方法对保障输电线路安全具有重要意义.本文将以某条实际线路跳线(普通软跳线)为对象开展风偏分析方法及其在2种地貌下风偏特性比较的研究.
1 跳线风偏的计算方法 1.1 跳线风偏计算理论现行设计中跳线风偏角的常见估算方法是基于静力单摆模型得到的, 具体计算公式如下:
| $ \theta = {\text{arctan}}\;\;\;\;\;((0.5{P_j} + {P_t})/(0.5{G_j} + {G_t})). $ | (1) |
式中:Pj、Pt分别为跳线绝缘子串和跳线装置作用于绝缘子的风荷载, Gj、Gt分别为绝缘子串和跳线装置的重力.虽然静力单摆模型应用简便, 但由于没有考虑到多档导线之间的相互牵扯作用而往往过大的估计了实际的风偏角[6].
除了传统的静力分析方法, 另一种更为精确的方法是基于有限元模型的动力时程分析方法.由于输电线路体系为典型的风敏感非线性结构体系, 其所具有的大跨度、小阻尼、高柔性的特点使之在风荷载作用下将产生显著的速度响应, 因此在风偏计算中应当考虑跳线与来流相对运动的影响.忽略沿导线和跳线方向的作用力, 其具体运动方程如下:
| $ \mathit{\boldsymbol{M\ddot Y}} + \mathit{\boldsymbol{C\dot Y}} + \mathit{\boldsymbol{KY}} = \mathit{\boldsymbol{F}}. $ | (2) |
式中:M、C和K分别为结构的质量、阻尼和考虑几何非线性的刚度矩阵;F=[Fy, Fz]T为外部作用荷载, Y=[Yy, Yz]T为结构的位移响应.其中第i个节点的荷载可以表示为
| $ {F_{iy}} = \frac{1}{2}\rho {C_D}{A_i}V_{_i}^2{\text{cos}}\theta, $ | (3) |
| $ {F_{iz}} = \frac{1}{2}\rho {C_D}{A_i}V_{_i}^2{\text{sin}}\theta - {G_i}. $ | (4) |
式中:ρ为空气密度, CD和Ai分别为导线的阻力系数和迎风面积, Gi为作用在第i节点的集中重力, θ为合风速与水平向的夹角, Vi为水平和竖向的合风速(相对速度), 可以表示为
| $ {V_i} = \sqrt {{{({U_i} - {{\dot Y}_{iy}})}^2} + {{({W_i} - {{\dot Y}_{iz}})}^2}} . $ | (5) |
式中:Ui和Wi分别为导线第i个节点处来流的水平和竖向风速,
| $ {F_{iy}} = \frac{1}{2}\rho {C_D}{A_i}{\text{cos}}\theta [(U_{_i}^2 + W_{_i}^2)-{\text{ }}2({U_i}{{\dot Y}_{iy}} + {W_i}{{\dot Y}_{iz}})], $ | (6) |
| $ {F_{iz}} = \frac{1}{2}\rho {C_D}{A_i}{\text{sin}}\theta [(U_{_i}^2 + W_{_i}^2)-2({U_i}{{\dot Y}_{iy}} + {W_i}{{\dot Y}_{iz}})] - {G_i}. $ | (7) |
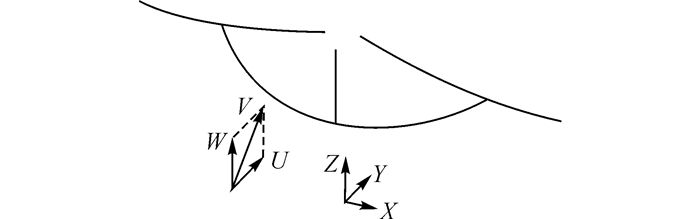
|
图 1 风速和跳线位移方向示意图 Fig. 1 Direction of wind velocity and jumper wire displacement |
式(6) 和(7) 中:风速平方和项对应为脉动风荷载, 风速与跳线运动速度的乘积之和项可以称为考虑跳线相对运动后的气动阻尼.
1.2 计算模型与直线塔悬挂绝缘子运动特性不同的是, 转角塔跳线绝缘子在风荷载作用下的风偏发展情况不仅与跳线串本身的位移响应密切相关, 还将受到跳线两端各跨导线运动的显著影响.因此, 采用简单的静力学单摆模型来近似计算跳线绝缘子串的风偏角将可能带来显著的估计误差.为了反映跳线的实际风偏运动特性, 建立考虑多跨导线影响的转角塔跳线风偏计算模型就显得尤为必要.
为了综合考察多跨导线运动对转角塔跳线风偏发展的影响情况, 对某条实际线路中的转角塔跳线建立了3种不同计算模型:1) 全线路模型, 即包含了11塔10档的整条线路计算模型(如图 2所示, 线路转角约30°).尽管该模型能够准确反映跳线的实际风偏运动状态, 但需消耗大量的计算资源和时间;2)“2+2”简化模型, 对T3号转角塔左右各2跨总计5塔4档线路及相邻耐张段之间的跳线体系进行建模(如图 3所示)并将T5号塔与导线连接位置设为固定约束, 该模型考虑了转角塔左右各2跨导线运动对跳线风偏的影响, 相比全线路模型有明显的简化;3) 局部模型, 该模型仅建立转角塔处的跳线和绝缘子串模型并将其两端节点自由度全部约束(如图 4所示).

|
图 2 全输电线路模型 Fig. 2 Whole transmission line model |
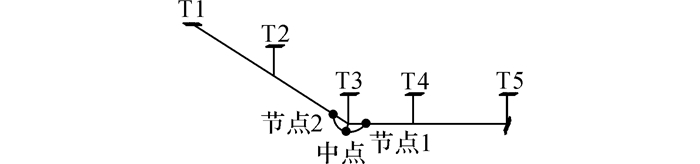
|
图 3 考虑跳线两边各两跨塔的“2+2”模型 Fig. 3 "2+2" model considering two towers on both sides of jumper wire |
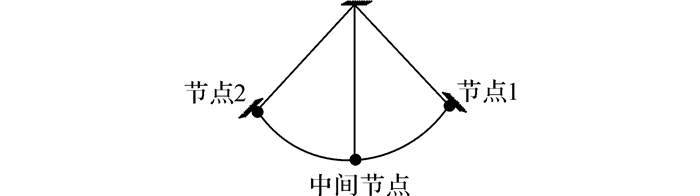
|
图 4 仅考虑跳线的局部模型 Fig. 4 Local model only considering jumper wire |
对1.2节模型分别采用ANSYS有限元软件进行建模和分析.在建模过程中, 考虑到导线运动的一致性, 采用等效单导线模型来模拟实际的四分裂导线.由于导线及耐张段绝缘子均以受张拉力为主, 故使用考虑初始应变的Link10单元来模拟;跳线处导线初始应变过小找形困难, 需要考虑导线刚度等综合因素, 故本文采用Beam188单元进行模拟;直线塔及跳线处悬式复合绝缘子主要承受拉力, 采用Link8单元来模拟.绝缘子串一端铰接于导线相应位置, 另一端约束平动位移但不约束转动.采用Mass单元模拟跳线相应位置处间隔棒的质量.跳线端部节点与多跨导线相应位置的节点采用耦合三维平动位移并约束转角位移的方式来模拟实际的连接.转角塔跳线的有限元模型见图 5.表 1给出我国规范B类地貌(10 m高度水平风速U10= 23 m/s)大气边界层来流风场下各简化跳线计算模型风偏位移与全线路模型计算结果的比值.其中X向为沿跳线方向, Y向为水平垂直跳线平面的方向, Z向为竖直方向(参见图 1).

|
图 5 跳线有限元模型 Fig. 5 Finite element model of jumper wire |
| 表 1 不同模型跳线节点位移的有限元计算结果比较 Table 1 Comparisons of calculated node displacements of jumper wires between different models |
由表 1可知:“2+2”模型与全线路模型的风偏计算结果比较接近, 而跳线两端固定的局部模型计算结果相比其他2个工况明显偏小.这就说明各跨导线的整体运动对跳线风偏的贡献显著, 这一点由某计算时刻跳线风偏运动状态(见图 6) 也可说明.由此可见, 忽略跳线两端导线运动作用而计算得到的跳线风偏位移是偏于不安全的, 而采用“2+2”简化模型能够在保证跳线风偏计算精度的基础上提高计算效率.

|
图 6 跳线风偏运动示意图 Fig. 6 Wind-induced jumper wire swing |
考虑到输电线路在实际情况中可能会经过或者跨越山脉, 深入了解微地形下的风场特性对保障输电线路抗风安全性显得尤为必要.为此, 本文对某山脉在垂直来流情况下的风场特性进行了风洞试验.
2.1 微地形风场风洞试验本文的微地形风洞试验在浙江大学ZD-1风洞内完成, 试验照片见图 7.试验模型为经典的余弦型山体[7-8], 并考虑一定的山脉长度.山体原型的高度和底面直径分别为100 m和300 m, 山脉长度为300 m, 试验模型缩尺比为1:500.模型采用ABS塑料板制作而成, 并在山体表面铺合成纤维来模拟实际山体的粗糙度.模型测点布置如图 8所示.每个测点测试若干个典型高度位置.各高度均指离开山体表面的距离.

|
图 7 风洞试验照片 Fig. 7 Photo of wind tunnel test |
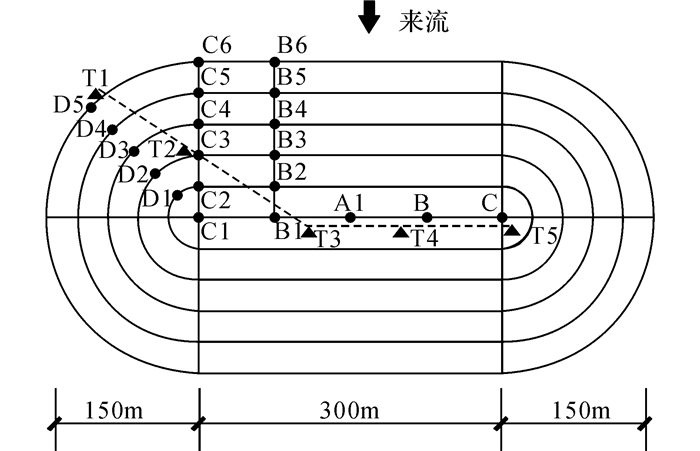
|
图 8 试验模型及测点布置示意图 Fig. 8 Sketch of test model and measuring point layouts |
试验流场的风剖面接近我国规范[9]规定的B类地貌, 湍流度剖面接近ESDU(85020)[10]的标准.风洞试验的风场模拟结果如图 9所示, 其中I为湍流度, H为离地高度, U0为来流不同高度水平风速, UH为梯度风高度处风速.

|
图 9 模拟的试验风场 Fig. 9 Simulated experimental wind field |
微地形下风场的三维脉动风速采用澳大利亚湍流仪(Turbulence Flow Instruments, TFI)公司的眼镜蛇湍流风速测量仪(Series 100 Cobra Probe)进行测试.眼镜蛇三维脉动风速探头是4孔压力探头, 可用于测量三维风速和静态压力, 测量频率高达2 000 Hz, 测试风向角为± 45 °范围.该探头的风速测量精度通常在0.5 m/s, 倾角和偏角精度为1.0 °.本次试验设定的脉动风速采样频率为1 250 Hz, 采样时间约为30 s.试验中对山体不同位置测点的风速特性进行了测试, 来流方向为垂直山脊方向(见图 8).
2.2 微地形风场特性由于山体的存在, 来流经过山体时过流断面减小.根据流体的连续性方程, 过流面积减少将会增大气流在山顶部位的流速, 故加速效应显著.图 10给出了山顶3个典型测点(A1、B1和C1) 在不同离地高度(10、20、30、40、50、100和150 m)上的水平风速U与来流相同离地高度上的水平风速(U0)之比.从该图可以发现, 风速的加速效应在高度较低处最为明显, 10 m处的风速比均超过了1.5.然而, 随着高度的增加风速比会逐渐减少并趋近于1, 这就说明地形对于风速的影响随着高度增加而减弱.
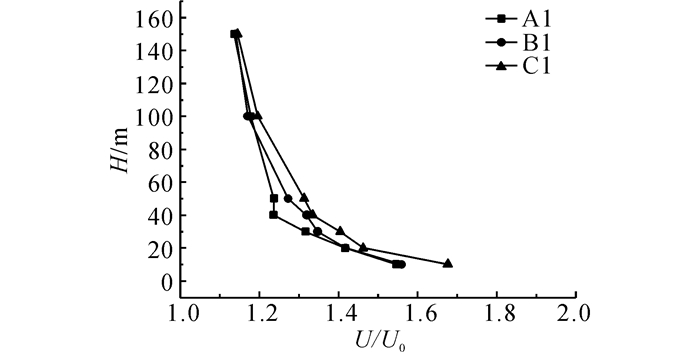
|
图 10 A1~C1不同高度水平风速与来流水平风速比 Fig. 10 Ratios of horizontal wind velocities at different heights of A1-C1 to those of incoming flow |
试验过程还发现:来流风在受到山体阻挡后沿斜坡爬升, 会产生明显的竖向风速分量.如图 11所示为各测点在不同高度处上升气流所产生的无量纲竖向风速W.图中W10为山脊线中点A1在10 m高度处的竖向风速.由图 11可知山脊位置的竖向风速会沿着高度降低并且从山脊中间向两侧逐渐减少.
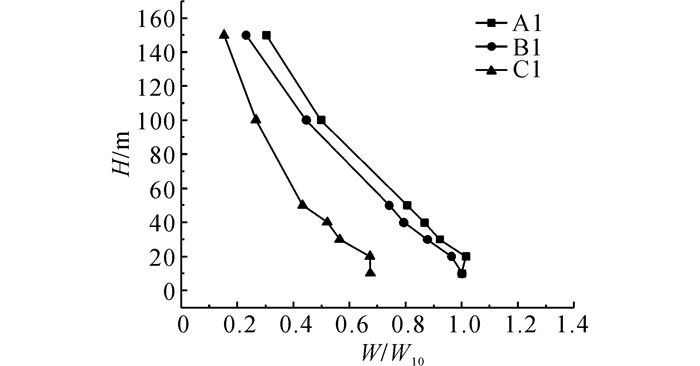
|
图 11 A1~C1不同高度的无量纲竖向风速 Fig. 11 No-dimensional vertical wind velocities at different heights of A1-C1 |
为了解竖向风速相对水平风速的大小, 图 12绘出了山顶各个高度竖向风速与来流相同离地高度的水平风速的比值.在30 m高度以下区域竖向风速占了较大比重, 其中10 m高度处的山脊边缘和中部分别达到了来流水平风速的25%和35%, 因此对于该高度区域范围内的导线和跳线进行风偏分析时应当要考虑竖向风荷载的作用.而当高度增加到100 m以上时, 竖向风速比基本降到15%及以下, 其对输电线路的影响迅速衰减.
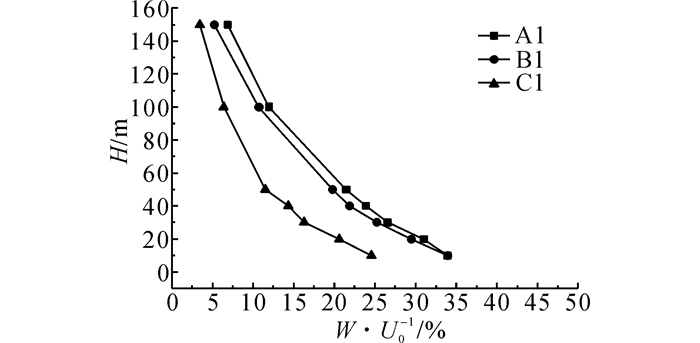
|
图 12 A1~C1不同高度竖向风速与来流水平风速比 Fig. 12 Ratios of vertical wind velocities at different heights of A1-C1 to horizontal wind velocities of incoming flow |
相比平均风荷载, 脉动风对跳线的极值风偏响应有更为重要的意义.反映风速脉动的一个重要指标就是湍流度.为了研究山脊处的脉动风特性, 图 13给出了沿山脊线不同位置处的水平和竖向风的湍流度.X为山脊上距C1点的水平距离,由图 13可以看出, 不同试验高度的水平风速湍流度基本处在11%~12%之间, 相比相同高度处来流湍流度(见图 9) 有所减弱, 且在山脊边缘部位有突变.而由于山体阻挡而产生的竖向风速脉动相比水平向要小, 湍流度绝大部分处在7%~9%之间.为了方便应用, 设计中对该类山脉山脊处的水平和竖向湍流度可分别近似取11.5%和8%.
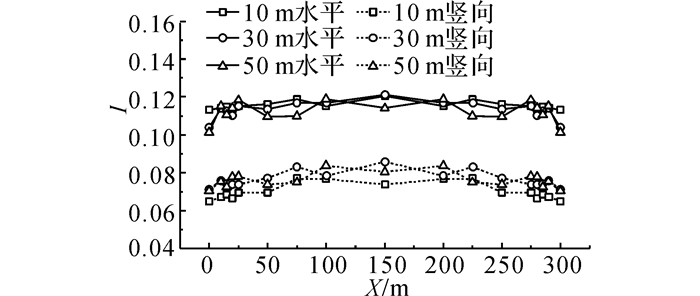
|
图 13 不同高度水平和竖向湍流度沿山脊分布 Fig. 13 Horizontal and vertical turbulence intensities at different heights of hill ridge |
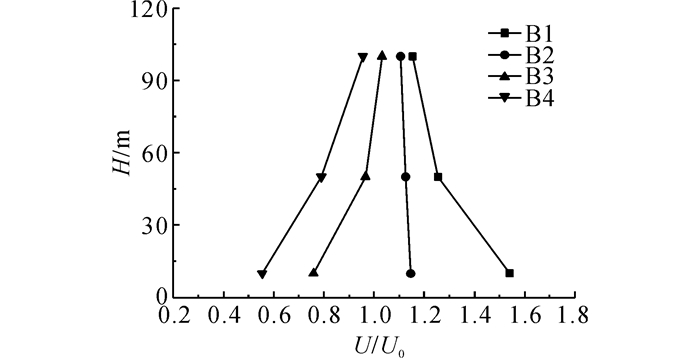
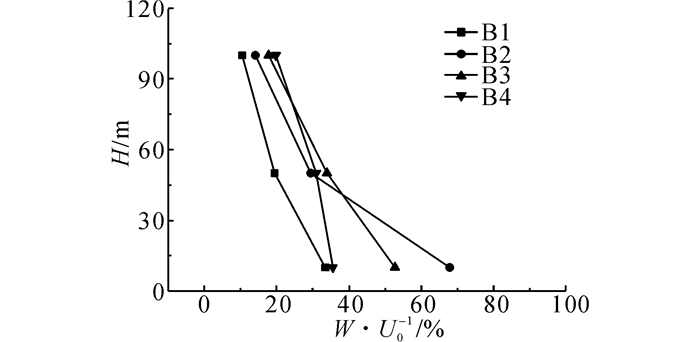
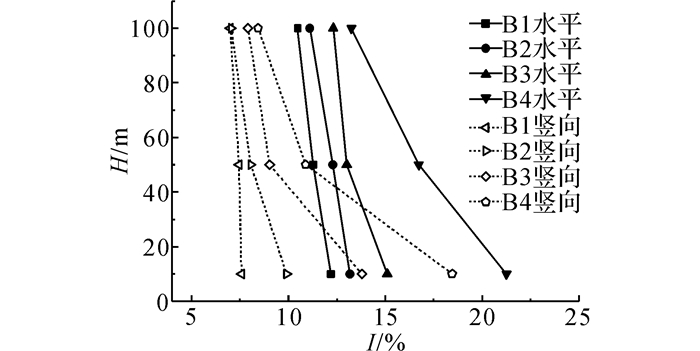
图 14~16给出了测点B1-B4在3个典型离地高度(10、50和100 m)的水平、竖向风速比(均指与相同离地高度来流水平风速的比值)以及湍流度取值情况.由图 14可知:在迎风坡, 水平风速比从坡脚(B4) 到坡顶(B1) 逐渐增加, 接近山顶时风速比超过1.不同位置风速比剖面变化趋势也有所不同.远离山顶位置(B3、B4), 水平风速比剖面形状接近来流风剖面, 即风速比随着离地高度的增加而增加.而在靠近山顶部位(B1、B2), 风速比的剖面形式恰好相反.图 15显示:竖向风速比在山腰位置处比山顶要大, 而且在50 m高度以下山腰部位达到水平风速的30%以上.随着测点离地高度增加, 竖向风速比剖面整体呈下降趋势.微地形下迎风坡无论是水平还是竖向湍流度均是越靠近山顶越小, 且相同位置处竖向湍流度要小于水平向, 这一点由图 16可以说明.
|
图 14 B1-B4不同高度水平风速与来流水平风速比 Fig. 14 Ratios of horizontal velocities at different heights of B1-B4 to those of incoming flow |
|
图 15 B1-B4不同高度竖向风速与来流水平风速比 Fig. 15 Ratios of vertical wind velocities at different heights of B1-B4 to horizontal wind velocities of incoming flow |
|
图 16 B1-B4不同高度水平和竖向湍流度 Fig. 16 Horizontal and vertical turbulence intensities at different heights of B1-B4 |
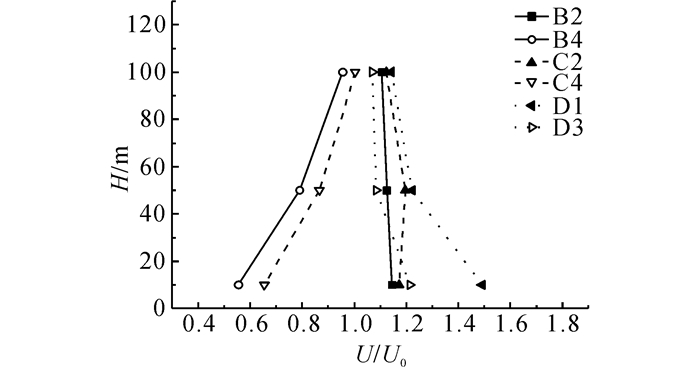
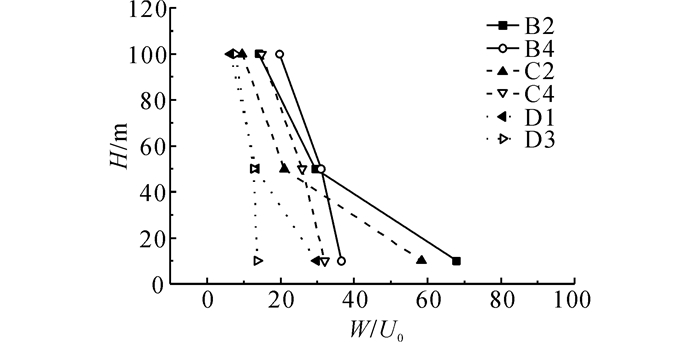
如图 17~18所示分别比较了不同水平位置(B、C、D)处山坡的水平和竖向风速比.图 17表明:水平风速比由B到D逐渐增加, 这是因为山体阻挡使得来流在其两侧产生绕流, 由流量守恒原理可知, 山体两侧的空气流速会增加.与水平风速分布不同的是, 竖向风速比则由山体中间(B)向两侧(D)逐渐降低, 如图 18所示.
|
图 17 山坡不同位置水平风速与来流水平风速比 Fig. 17 Ratios of horizontal velocities on different locations of hillside to those of incoming flow |
|
图 18 山坡不同位置竖向风速与来流水平风速比 Fig. 18 Ratios of vertical wind velocities on different locations of hillside to horizontal wind velocities of incoming flow |
由1.3节分析可知, “2+2”简化模型已经能够较好地反映跳线的实际风偏情况, 故这里以该模型为基础开展输电线路的跳线风偏特性研究.为了比较不同地形对跳线风偏运动的影响, 分别对平坦地貌和微地形地貌下的跳线风致响应进行了有限元动态时程分析.微地形地貌下输电线路的布置情况可参见图 8.具体分析工况包括:1) 对平坦地貌仅考虑了水平(垂直导线方向)风荷载的作用(记为工况1), 2) 对微地形地貌分别考虑了水平风作用(记为工况2) 以及水平和竖向风共同作用(记为工况3) 这2种情况.在进行跳线的有限元动力时程分析之前需要先获得各节点的脉动风速.目前脉动风速的模拟方法主要有:谱表示法和线性滤波法.三维脉动风速的模拟常采用谱表示法中的基于互谱密度矩阵的特征正交分解方法[11-12], 该方法能同时考虑各点的空间和点相关性.模拟中风谱采用经典的Karman谱[13], 其公式如下:
| $ S_{_{ii}}^{^{uu}}\left( \omega \right)=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\frac{4{{\sigma }^{2}}_{u}{{L}_{u}}/\bar{\varphi }}{{{\{1+70.8{{[\omega {{L}_{u}}/(2\text{ }\!\!\pi\!\!\text{ }\bar{\varphi })]}^{2}}\}}^{5/6}}}. $ | (8) |
| $ \begin{align} & SS_{_{ii}}^{\varepsilon \varepsilon }\left( \omega \right)=\frac{4{{\sigma }^{2}}_{\varepsilon }{{L}_{\varepsilon }}/\bar{\varphi }\{1+755.2{{[\omega {{L}_{\varepsilon }}/(2\text{ }\!\!\pi\!\!\text{ }\bar{\varphi })]}^{2}}\}}{2\text{ }\!\!\pi\!\!\text{ }{{\{1+283.2{{[\omega {{L}_{\varepsilon }}/(2\text{ }\!\!\pi\!\!\text{ }\bar{\varphi })]}^{2}}\}}^{11/6}}} \\ & \varepsilon =w,v. \\ \end{align} $ | (9) |
式中:i=1, 2, …, N, N为模拟点数, φ为平均风速, ω为频率, σε2(ε=u, w, v)为3个方向脉动风速的方差, Lε(ε=u, w, v)为3个方向湍流积分尺度.
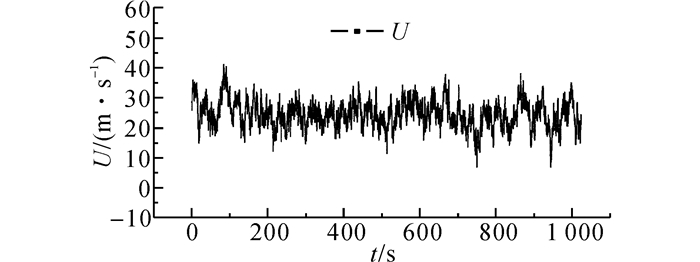
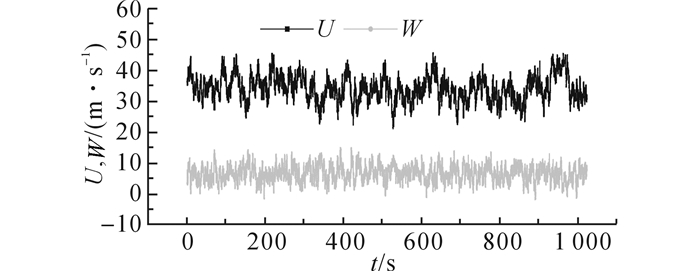
在脉动风速模拟时:对于平坦地貌, 水平平均风速剖面采用我国荷载规范B类地貌剖面, 基本风速取为23 m/s, 湍流度取风洞试验来流湍流度, 湍流积分尺度根据文献[11]中经验公式计算得到.对于微地形地貌, 先根据风洞试验测得的测点风速比插值得到输电线路位置的风速比, 然后由来流水平平均风速计算得到塔线位置的水平和竖向平均风速.同样导线位置的湍流度也可根据风洞试验结果插值得到.而湍流积分尺度则通过试验风速谱与Karman谱的拟合得到.本次模拟中脉动风采样频率为32 Hz, 模拟时长为1 024 s, 平坦地貌和微地形地貌下跳线中部附近某节点的模拟风速时程分别如图 19和20所示.
|
图 19 平坦B类地貌下模拟的水平风速时程 Fig. 19 Simulated time histories of horizontal wind velocity under terrain category B |
|
图 20 微地形下模拟的水平和竖向风速时程 Fig. 20 Simulated time histories of horizontal and vertical wind velocity under hilly terrain |
将模拟到的脉动风荷载输入ANSYS有限元软件可以对跳线风偏进行时程分析.在跳线风偏计算过程中阻力系数CD取1.1, 导线固有阻尼比取0.5%, 单根导线直径为26.8 mm.研究表明[14]不考虑气动阻尼的影响将会过高地估计导线风偏的共振效应从而使得到极值风偏角偏大.因此, 本文在计算中根据式(5) 来考虑导线与来流的相对运动以此反映周边流体对导线结构的附加阻碍作用.
表 2给出了不同地貌下跳线各节点在3个方向上的平均和极值风偏角.其中, 极值风偏角按照下式计算:
| $ \hat \theta = \bar \theta + g\cdot\tilde \theta . $ | (10) |
| 表 2 不同地貌下跳线节点风偏角度计算结果 Table 2 Calculation results of node swing angles of jumper wires under different terrains |
式中:θ和θ分别为风偏角的均值和均方根值, g为峰值因子, 可以根据Davenport[15]提出峰值因子公式进行估算:
| $ g = \sqrt {2{\text{ln}}v{\text{ }}T} + 0.577{\text{ }}2/\sqrt {2{\text{ln}}vT} . $ | (11) |
式中:T为风荷载时程的时距, υ表示随机过程的平均零穿越率.
由表 2可知, 尽管跳线两端节点的风偏角要小于跨中节点, 但其风偏量仍不可忽略, 这也就说明相邻跨导线运动对跳线风偏的影响不可忽略.在平坦B类地貌下, 跳线风偏分析通常仅考虑水平垂直导线方向的风荷载作用且不考虑上升气流的影响.因此, 在表 2的3种计算工况中平坦地貌下跳线的风偏角度最小.而在微地形地貌下, 由于水平风在山脊处存在加速效应, 故跳线风偏角在微地形工况2下比平坦地貌有明显增加.由于实际微地形情况下, 有竖向上升气流的存在需要同时考虑水平和竖向风荷载的作用, 此时跳线风偏角度会进一步增大(见表 2).这可能也是山区地貌下跳线容易发生风偏跳闸的重要原因之一.综上所述, 设计中若不考虑微地形的风速加速效应以及竖向风荷载的作用将会低估跳线的实际风偏角从而使输电线路在强风作用下存在风偏跳闸的风险.
4 结论以某条实际输电线路为对象对跳线风偏特性进行了有限元建模分析, 提出了合理的跳线计算模型, 同时对微地形下的风场特性进行了风洞试验, 并在此基础上比较研究了平坦和微地形地貌下跳线风偏的差异性.主要结论如下:
(1) 通过对不同档距的输电线路进行建模分析发现:转角塔跳线的风偏运动受到相邻两边导线运动的影响十分显著.本文所提出的“2+2”简化模型, 即考虑转角塔左右各2档导线运动影响的计算模型能较好地反映实际线路中跳线的风偏运动状态.而仅考虑跳线本身的局部模型则会低估跳线的实际风偏发展情况.
(2) 在微地形情况下, 当来流垂直山脉走向时, 气流在山脊处有明显的加速效应, 建议提高该处拟架设的输电线路的设计风速, 例如, 在10 m高度设计风速可以增加到1.5倍.山脊处上升气流显著, 最高可达到来流水平风速的35%, 因此在设计中应该适当考虑竖向风荷载的作用.山脊不同位置处风速也有所差别, 越靠近山脊中部竖向风速越高.湍流度相比来流则有所减弱.在本文风场条件下, 山脊处的水平和竖向湍流度可分别近似取11.5%和8%.
(3) 在迎风山坡, 水平风速比由坡脚到坡顶呈增长趋势, 而竖向风速则在山腰位置处更大.越靠近山顶, 湍流度越小, 竖向湍流度值整体小于水平值.
(4) 不同水平位置的测点比较表明:山体两侧的水平风加速比要大于中间位置, 而竖向风速则是山体的中部大于两侧.
(5) 微地形下跳线的风偏角度明显要高于平坦地貌的情况.当有竖向风荷载共同作用时跳线的风偏角相比水平风作用将有进一步的增大.因此, 在进行微地形下输电线路跳线的设计验算时建议考虑竖向风荷载的共同作用.
| [1] |
龚坚刚. 浙江电网跳线风偏跳闸的分析与措施[J].
华东电力, 2007, 35(5): 112–113.
GONG Jian-gang. Line trips in Zhejiang Power Grid due to windage yaw of jumper wires and relevant countermeasures[J]. East China Electric Power, 2007, 35(5): 112–113. |
| [2] |
田靖, 唐雷. "干"字型耐张塔跳线风偏放电分析及防范措施[J].
湖北电力, 2011, 35(6): 24–25.
TIAN Jing, TANG Lei. Analysis of discharge between jumper and tension tower with "JG" shape due to wind deviation and preventive measure[J]. Hubei Electric Power, 2011, 35(6): 24–25. |
| [3] |
弓建新, 秦润生, 贾雷亮, 等. 220 kV输电线路JG1型塔中相跳线风偏问题的探讨[J].
山西电力技术, 2001, 2: 24–25.
GONG Jian-xin, QIN Run-sheng, JIA Lei-liang, et al. Discussion on wind deflection of mid phrase jumper-line JG1 tower on 220 kV power line[J]. Shanxi Electric Power, 2001, 2: 24–25. DOI:10.3969/j.issn.1671-0320.2001.01.010 |
| [4] |
严波, 林雪松, 罗伟, 等. 绝缘子串风偏角风荷载调整系数的研究[J].
工程力学, 2010, 27(1): 221–227.
YAN Bo, LIN Xue-song, LUO Wei, et al. Research on dynamic wind load factors for windage yaw angle of suspension insulator strings[J]. Engineering Mechanics, 2010, 27(1): 221–227. |
| [5] |
李黎, 肖林海, 罗先国, 等. 特高压绝缘子串的风偏计算方法[J].
高电压技术, 2013, 39(12): 2924–2932.
LI Li, XIAO Lin-hai, LUO Xian-guo, et al. Windage yaw calculation method of UHV insulator strings[J]. High Voltage Engineering, 2013, 39(12): 2924–2932. DOI:10.3969/j.issn.1003-6520.2013.12.013 |
| [6] |
楼文娟, 杨悦, 卢明, 等. 连续多跨输电线路动态风偏特征及计算模型研究[J].
电力建设, 2015, 36(2): 1–8.
LOU Wen-juan, YANG Yue, LU Ming, et al. Conductor swinging dynamic characteristic and calculation method of continuous multi-span transmission line[J]. Electric Power Construction, 2015, 36(2): 1–8. |
| [7] |
孙毅, 李正良, 黄汉杰, 等. 山地风场平均及脉动风速特性试验研究[J].
空气动力学学报, 2011, 29(5): 593–599.
SUN Yi, LI Zheng-liang, HUANG Han-jie, et al. Experimental research on mean and fluctuating wind velocity in hilly terrain wind field[J]. Acta Aero dynamica Sinica, 2011, 29(5): 593–599. |
| [8] |
姚旦. 山丘地形风场特性及对输电塔的风荷载作用研究[D]. 杭州: 浙江大学, 2014.
YAO Dan. Research on characteristics of wind field on hilly terrain and its wind load effect on lattice transmission towers[D]. Hangzhou: Zhejiang University, 2014. |
| [9] |
GB 50009-2012. 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.
GB 50009-2012. Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012. |
| [10] | ESDU 85020. Characteristics of atmospheric turbulence near the ground Part Ⅱ: single point data for strong winds (neutral atmosphere) Engineering Science Data Unit[S], London, 2001. |
| [11] |
罗俊杰, 韩大建. 大跨度结构三维随机脉动风场的模拟方法[J].
振动与冲击, 2008, 27(3): 87–91.
LUO Jun-jie, HAN Da-jian. Simulation method for 3-D stochastic wind field around long-span structures[J]. Journal of Vibration and Shock, 2008, 27(3): 87–91. |
| [12] |
胡亮. 基于特征正交分解的桥梁风场随机模拟[D]. 武汉: 华中科技大学, 2007.
HU Liang. Simulation of stochastic wind fields on long-span bridges based on proper orthogonal decomposition[D]. Wuhan: Huazhong University of Science & Technology, 2007. |
| [13] | KARMAN T V. Progress in the statistical theory of turbulence[J]. Proeedings of the National Academy of Sciences of the United States of America, 1948, 34(11): 530–539. DOI:10.1073/pnas.34.11.530 |
| [14] |
楼文娟, 杨悦, 吕中宾, 等. 考虑气动阻尼效应的输电线路风偏动态分析方法[J].
振动与冲击, 2015, 34(6): 24–29.
LOU Wen-juang, YANG Yue, LV Zhong-bin, et al. Windage yaw dynamic analysis methods for transmission lines considering aerodynamic damping effect[J]. Journal of Vibration and Shock, 2015, 34(6): 24–29. |
| [15] | DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Proceedings of the Institution of Civil Engineering, 1964, 28(2): 187–196. DOI:10.1680/iicep.1964.10112 |


