大跨空间结构多用于体育场馆、交通建筑、会展中心等大型公共建筑, 这类结构的重要性不言而喻, 一旦破坏或失效会给社会生产和人民生命安全带来重大损失, 同时也会造成较坏的社会影响[1-2].然而, 近年来随着人类生产活动的逐年递增, 全球自然环境及大气环境受到极大影响, 进而导致全球气候的持续恶化, 灾害天气频繁发生.我国地处北太平洋西岸, 东南沿海地区每年遭受台风侵袭, 台风带来的狂风、暴雨以及风暴潮使人民财产安全受到严重威胁.如2004年台风“云娜”登陆浙江时近中心最大风速达到了45 m/s, 全省有36个测站雨量超过300 mm, 共吹倒房屋达6.43万间, 受灾人口共1 299余万人[3];2006年8号超强台风“桑美”登陆时最大风力达到17级, 造成数千人遇难, 直接经济损失达数百亿[4].因此研究空间结构在台风作用下的动力失效具有重要意义.
弦支网壳结构是综合了网壳结构和张拉整体结构的新型复合空间结构体系, 具有造型美观、质量轻巧、受力合理、施工步骤简单等优点[5], 已有的关于弦支网壳的研究主要集中在预应力设计[6-7]、结构静力性能[8-9]、施工成型[10-11]等方面, 对动力性能研究一般只涉及基本动力性能.有关结构在台风作用下动力失效的研究未见报道.本文对杭州和舟山地区台风风场下弦支网壳结构动力响应进行了数值模拟, 提出了台风作用下弦支网壳结构动力失效判定准则, 并通过算例分析讨论了该准则的合理性和适用性.
1 结构动力分析理论结构在荷载作用下的动力学基本方程为
| $ \mathit{\boldsymbol{M\ddot{u}}}+\mathit{\boldsymbol{C\dot{u}}}+\mathit{\boldsymbol{Ku}}=\mathit{\boldsymbol{F}}. $ | (1) |
式中:M为质量矩阵, C为阻尼矩阵, K为刚度矩阵,
| $ \mathit{\boldsymbol{C}}=\delta \mathit{\boldsymbol{M}}+\beta \mathit{\boldsymbol{K}}. $ | (2) |
式中:δ为质量阻尼系数, β为刚度阻尼系数, 2个阻尼系数可通过振型阻尼比计算得到
| $ \delta =\frac{2{{\omega }_{i}}{{\omega }_{j}}({{\xi }_{i}}{{\omega }_{j}}-{{\xi }_{j}}{{\omega }_{i}})}{{{\omega }^{2}}_{j}-{{\omega }^{2}}_{i}}, \beta =\frac{2({{\xi }_{j}}{{\omega }_{j}}-{{\xi }_{i}}{{\omega }_{i}})}{{{\omega }^{2}}_{j}-{{\omega }^{2}}_{i}}. $ | (3) |
式中:ωi和ωj分别为结构的第i和j阶固有频率;ξi和ξj为相对应的第i和j振型的阻尼比, 由试验确定.一般可取i=1, j=2, 对于钢结构, 阻尼比通常取为0.02.
2 台风作用下弦支网壳结构动力分析 2.1 计算模型和自振特性如图 1所示, 该凯威特2型弦支网壳结构跨度为40 m, 矢高5 m, 结构支承在离地15 m高的刚性支座上, 支承条件为铰支.内、外2圈撑杆高度分别为4.5和5.5 m, 内、外圈环索分别施加50和100 MPa的预应力, 各杆件截面信息如表 1所示.表中S为面积, 结构材料为Q235钢, 采用双线性弹塑性模型, 屈服强度值为235 MPa, 弹性模量为210 GPa, 切线模量为6 100 MPa, 泊松比为0.3.采用ANSYS建模, 上部网壳杆件采用beam188单元模拟, 撑杆用link8单元模拟, 索用link10单元模拟.屋面恒载为0.3 kN/m2, 除风荷载外不考虑其他活荷载.

|
图 1 弦支网壳几何模型 Fig. 1 Geometric model of suspendome |
| 表 1 弦支网壳杆件尺寸 Table 1 Member's section of suspendome |
结构前6阶自振频率如表 2所示, 表中f0为自振频率, 对应的振型图如图 2所示.由表可知, 弦支网壳频率比较密集, 由于结构的对称性, 第2、3阶以及第5、6阶频率相同.由式(3) 可得, 该结构的质量阻尼系数和刚度阻尼系数分别为0.274 3和1.5×10-3.
| 表 2 弦支网壳前6阶自振频率 Table 2 First six natural vibration frequencies of suspendome |

|
图 2 弦支网壳振型图 Fig. 2 Vibration models of suspendome |
用指数率描述台风的平均风剖面, 台风平均风剖面风速公式如式(4) 所示, 本算例模拟的位置为杭州, 以中国台风网实测台风资料为原始数据, 对台风各个关键参数进行概率统计, 得到各个关键参数的概率分布模型.进行随机抽样, 数值模拟10 000组台风, 代入Yan等台风模型计算[12], 与杭州地区实测台风最大风速对比, 选取误差最小时的“等效地面粗糙度”, 可得杭州市气象站台风风剖面指数为0.148.
| $ {{v}_{z}}={{v}_{\text{ref}}}{{\left( \frac{z}{{{z}_{\text{ref}}}} \right)}^{\alpha }}. $ | (4) |
式中:vz为z高度处的风速,z为测点的高度, vref和zref分别为参考点的风速和高度, α是风剖面指数.
本文模拟的脉动风速时仅考虑顺风向, 选用的风速谱为Von Karman谱[13], 如式(5) 所示:
| $ {S_v}\left( {z,\omega } \right) = \frac{{24{u^2}_*(l\omega /{v_z})}}{{\omega {{[1 + 70.8{{(l\omega /{v_z})}^2}]}^{5/6}}}}. $ | (5) |
式中:Sv(z, ω)为Von Karman谱, l为湍流积分尺度, l=100(z/30)1/2, ω为圆频率, u*为地表剪切风速.
采用谐波合成法[14], 用MATLAB编程得到弦支网壳表面各节点的风速时程, 杭州地区台风风场下弦支网壳顶点处脉动风速时程曲线如图 3所示, 图中t为时间, v为瞬时脉动风速;模拟的风速功率谱曲线和Von Karman谱的对比图如图 4所示, f为频率, Ps为脉动功率谱.

|
图 3 杭州台风风场下顶部节点脉动风速时程曲线 Fig. 3 Fluctuating wind speed time history curve of top node in typhoon field of Hangzhou |

|
图 4 杭州台风风场下顶部节点脉动风速功率谱 Fig. 4 Fluctuating wind spectrum of top node in typhoon field of Hangzhou |
依据文献[15], 得到舟山定海气象站台风风剖面指数为0.132, 同样采用谐波合成法, 得到舟山地区台风风场弦支网壳顶点处脉动风速时程曲线如图 5所示, 模拟的功率谱曲线和Von Karman谱的对比如图 6所示.

|
图 5 舟山台风风场下顶部节点脉动风速时程曲线 Fig. 5 Fluctuating wind speed time history curve of top node in typhoon field of Zhoushan |

|
图 6 舟山台风风场下顶部节点脉动风速功率谱 Fig. 6 Fluctuating wind spectrum of top node in typhoon field of Zhoushan |
根据风压和风速之间的转换公式(6), 可得到弦支网壳表面风压时程.
| $ w\left( z, t \right)=\frac{1}{2}\rho {{v}^{2}}\left( z, t \right). $ | (6) |
式中:w(z, t)为t时刻z高度处的瞬时风压, ρ为空气密度, v(z, t)为t时刻z高度处的瞬时风速.
2.3 杭州和舟山地区算例选取20 s杭州地区台风的风速时程, 利用ANSYS瞬态分析模块对台风作用下弦支网壳结构进行动力时程分析.结构内圈环索的应力时程曲线如图 7所示, 图中σ为索中mises应力.在台风作用时程内, 环索先发生卸载, 应力急剧下降, 后维持在一定的水平上, 并呈现动态稳定.由ANSYS结果文件可知, 在风荷载作用结束时, 结构仍处于弹性工作状态.第20 s时的位移云图如图 8所示, 图中uz为节点位移,最大位移为0.033 m, 与撑杆连接处的网壳节点位移显著大于其他节点的位移.

|
图 7 杭州台风风场下内圈环索应力时程曲线 Fig. 7 Stress time history curve of inner hoop cable in typhoon field of Hangzhou |

|
图 8 杭州台风风场下结构位移云图 Fig. 8 Displacement nephogram of structure in typhoon field of Hangzhou |
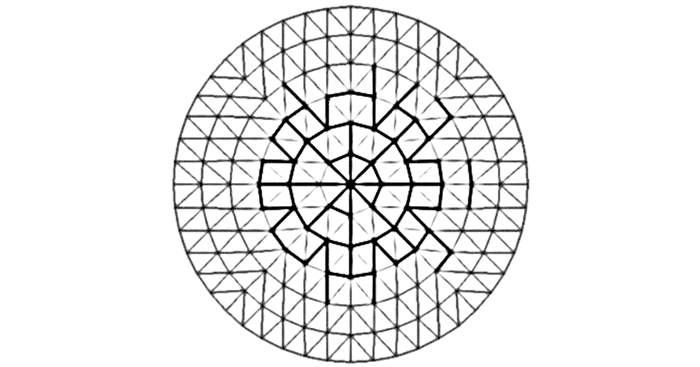
选取20 s舟山地区台风的风速时程, 利用ANSYS瞬态分析模块对台风作用下弦支网壳结构进行动力时程分析.内圈环索应力时程曲线和位移最大节点的位移时程曲线分别如图 9和10所示, 在台风作用下, 环索发生卸载, 与杭州相比, 舟山地区风荷载较大, 部分杆件进入塑性, 导致结构刚度减小, 位移增大, 进一步加速环索卸载, 在第8.7 s时, 环索第1次发生松弛, 节点位移发生突变, 达到最大值, 由于风的脉动性, 松弛的索单元又因几何形状的改变重新获得内力参与受力, 形成动态平衡状态.台风作用结束时结构位移云图如图 11所示, 与杭州地区相同, 位移最大节点为与内圈撑杆相连处节点, 最大位移为0.139 m.塑性杆件分布图如图 12所示, 粗实线表示进入塑性状态的杆件, 从图中可以看出, 塑性杆件主要集中在与内圈撑杆相连的节点附近, 并向四周扩散, 且大体上关于主径向杆呈对称分布.

|
图 9 舟山台风风场下内圈环索应力时程曲线 Fig. 9 Stress time history curve of inner hoop cable in typhoon field of Zhoushan |

|
图 10 舟山台风风场下位移最大节点位移时程曲线 Fig. 10 Maximum nodal displacement time history curve in typhoon field of Zhoushan |

|
图 11 舟山台风风场下结构位移云图 Fig. 11 Displacement nephogram of structure in typhoon field of Zhoushan |
|
图 12 舟山台风风场下塑性杆件分布图 Fig. 12 Distribution of plastic members in typhoon field of Zhoushan |
综合杭州和舟山地区的算例, 在台风作用下, 风荷载在弦支网壳表面形成负压, 结构位移与重力方向相反, 弦支网壳结构下部环索发生卸载, 通过撑杆对上部网壳节点产生反向作用力, 导致与撑杆连接处网壳节点附件杆件受力大于其他区域的杆件, 且该处节点位移要大于其他节点, 该区域是结构易破坏的区域.若风荷载过大, 下部环索会发生松弛, 弦支体系失去作用.
3 台风作用下弦支网壳失效判定准则弦支网壳结构是风敏感结构, 在台风作用下易发生动力失效.最大节点位移、塑性杆件比例和索是否松弛能直观反映弦支网壳结构在台风作用下的动力效应, 但目前对台风作用下弦支网壳动力失效的研究较少.结构动力失效方面的研究主要针对地震作用下网壳的破坏展开, 范峰等[16]依据网壳最大节点位移、不同屈服程度杆件比例、节点位移时程曲线等指标, 取不同的权重, 建立了评价矩阵, 对网壳在地震作用下的失效模式及准则进行判定;杜文风等[17]从能量和变形2方面考虑, 将最大变形和塑性积累耗能线性组合, 提出动力破坏指数;陈东等[18]将最大节点位移作为主要指标, 塑性杆件比例作为辅助指标, 讨论了双层凯威特型网壳在地震作用下损失的评估方法, 并对其破坏等级进行划分, 建立了响应的分界指标.
参考结构在地震作用下动力失效相关研究, 以及上节中弦支网壳在台风作用下的动力响应研究, 本文从以下3个方面对台风作用下弦支网壳结构的动力失效进行判定:1) 由于脉动风的空间相关性, 弦支网壳各节点呈现出各自的脉动特性, 杆件发生剧烈无规则振动, 较大的节点位移会引起屋面材料的翘曲或凹陷, 进而造成屋面材料的破坏, 甚至脱落, 因此在台风作用下, 结构节点位移的限制较为严格;2) 在台风作用下, 风场在与弦支网壳交汇处发生流动分离, 在局部形成分离泡区域, 发生强烈的湍流运动, 形成负压区, 结构受到风吸力作用, 此时杆件内力以拉力为主, 当杆件内部塑性发展较为严重时, 认为弦支网壳已达到破坏极限, 不能满足正常使用功能;3) 在风吸力作用下, 弦支网壳下部索会出现卸载情况, 导致拉力减小, 随着台风荷载增大, 索最终会发生松弛, 从而退出工作, 造成安全隐患.因此, 对于弦支网壳结构, 若发生索松弛, 则可认为结构失效.
由此, 将最大节点位移、塑性杆件比例及索是否松弛作为指标, 对台风作用下弦支网壳结构动力破坏程度进行划分, 提出动力失效判定准则, 具体分界指标如表 3所示, 表中umax为结构最大位移, L为结构跨度, p为塑性杆件比例.
| 表 3 台风作用下弦支网壳结构动力失效判定准则 Table 3 Criteria of dynamical failure of suspendomes under typhoon load |
依据该判定准则, 对上述杭州和舟山地区2个算例进行破坏等级判定如下.
对于杭州地区, 如表 4所示, 结构节点位移很小, 是跨度的1/1 212, 杆件全部处于弹性状态, 下部环索未发生松弛, 结构处于正常工作状态, 破坏等级由最大节点位移和塑性杆件比例控制, 依据判定准则, 可认为结构完好.
| 表 4 杭州台风风场下结构响应指标统计 Table 4 Response indices of dome in typhoon field of Hangzhou |
对于舟山地区, 节点位移较大, 达到跨度的1/288, 有18%的杆件进入塑性状态, 结构变形严重, 屋面材料会发生撕裂, 且环索出现松弛, 不承受荷载, 在脉动风作用下, 易发生晃动, 引起安全隐患, 如表 5所示, 弦支网壳的破坏等级由节点最大位移控制, 依据判定准则, 可认为结构发生中等程度破坏.
| 表 5 舟山台风风场下结构响应指标统计 Table 5 Response indices of dome in typhoon field of Zhoushan |
本文研究了弦支网壳在台风作用下的动力响应, 以最大节点位移、塑性杆件比例和索是否松弛作为指标, 提出台风作用下弦支网壳结构动力失效判定准则.得到如下结论:
(1) 模态分析表明, 弦支网壳频率较为密集, 且由于对称性, 会出现多对相同频率.
(2) 在台风荷载作用下, 弦支网壳位移与重力方向相反, 环索会发生卸载, 上部网壳与撑杆连接处的节点位移最大, 此节点周围杆件受力较大, 易发生破坏.当风荷载过大时, 会引起环索松弛, 弦支体系失去作用.
(3) 最大节点位移、塑性杆件比例和索是否松弛能直观反映弦支网壳结构在台风作用下的动力效应, 以这3个指标作为划分依据的动力失效判定准则是合理、可行的.
| [1] |
董石麟, 罗尧治, 赵阳. 大跨度空间结构的工程实践与学科发展[J].
空间结构, 2005, 11(4): 3–10.
DONG Shi-lin, LUO Yao-zhi, ZHAO Yang. Practical application and research advances of long-span space structures[J]. Spatial Structures, 2005, 11(4): 3–10. |
| [2] | 钱若军, 杨联萍. 索杆张力结构的分析设计施工[M]. 南京: 东南大学出版社, 2003: 5-21. |
| [3] |
薛根元, 俞善贤, 何风翩, 等. 云娜台风灾害特点与浙江省台风灾害初步研究[J].
自然灾害学报, 2006, 15(4): 39–47.
XUE Gen-yuan, YU Shan-xian, HE Feng-pian, et al. Damage characteristics of Typhoon Rananim and primary research on typhoon disasters in Zhejiang Province[J]. Journal of Natural Disasters, 2006, 15(4): 39–47. |
| [4] |
杨波, 林祥, 刘青明, 等. "桑美"超强台风风暴潮增水特征分析[J].
河海大学学报:自然科学版, 2013, 41(4): 348–353.
YANG Bo, LIN Xiang, LIU Qing-ming, et al. Feature analysis of super storm surge due to Typhoon Saomai[J]. Journal of Hohai University: Natural Sciences, 2013, 41(4): 348–353. |
| [5] |
董石麟. 空间结构的发展历史、创新、形式分类与实践应用[J].
空间结构, 2009, 15(3): 22–43.
DONG Shi-lin. The development history, innovation, classification and practical application of spatial structures[J]. Spatial Structures, 2009, 15(3): 22–43. |
| [6] |
刘树堂. 弦支穹顶结构参数优化设计研究[J].
深圳大学学报:理工版, 2013, 30(6): 643–64.
LIU Shu-tang. Study on parametric optimization design of suspendome structure[J]. Journal of Shenzhen University Science and Engineering, 2013, 30(6): 643–64. |
| [7] |
石开荣, 郭正兴, 罗斌. 椭圆形弦支穹顶结构的预应力确定方法研究[J].
土木工程学报, 2010, 43(9): 88–99.
SHI Kai-rong, GUO Zheng-xing, LUO Bin. Method for determining the prestress of elliptical suspendome structures[J]. China Civil Engineering Journal, 2010, 43(9): 88–99. |
| [8] |
陈志华, 冯振昌, 秦亚丽, 等. 弦支穹顶静力性能的理论分析及实物加载试验[J].
天津大学学报, 2006, 39(8): 944–950.
CHEN Zhi-hua, FENG Zhen-chang, QIN Ya-li, et al. Theoretical analysis and actual experimental research static characteristics of suspendome structure[J]. Journal of Tianjin University, 2006, 39(8): 944–950. |
| [9] |
冯玉龙, 周臻, 孟少平, 等. 新型误差可调弦支穹顶模型加载试验研究[J].
工程力学, 2012, 31(10): 100–107.
FENG Yu-long, ZHOU Zhen, MENG Shao-ping. Model loading experimental research on new error-adjustable suspen-dome structures[J]. Engineering Mechanics, 2012, 31(10): 100–107. |
| [10] |
李志强, 张志宏, 袁行飞, 等. 济南奥体中心弦支穹顶结构施工张拉分析[J].
空间结构, 2008, 14(4): 14–20.
LI Zhi-qiang, ZHANG Zhi-hong, YUAN Xing-fei. Construction analysis of the suspen-dome for the Gymnasium of Ji Nan Olympic Sports Center[J]. Spatial Structures, 2008, 14(4): 14–20. |
| [11] |
刘慧娟, 杨绿峰, 罗永峰. 基于双控法弦支穹顶伺服施工过程非线性分析[J].
华中科技大学学报:自然科学版, 2012, 40(3): 89–93.
LIU Hui-juan, YANG Lv-feng, LUO Yong-feng. Geometrically nonlinear analysis of servo-control construction for large-span suspen-domes using double control method[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2012, 40(3): 89–93. |
| [12] | YAN M, MASAHIRO M, KAZUKI H. An analytical model for simulation of the wind field in a typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 56(2/3): 291–310. |
| [13] |
肖仪清, 孙建超, 李秋胜. 台风湍流积分尺度与脉动风速谱-基于实测数据的分析[J].
自然灾害学报, 2006, 15(5): 45–53.
Xiao Yi-qing, SUN Jian-chao, LI Qing-sheng. Turbulence integral scale and fluctuation wind speed spectrum of typhoon: an analysis based on field measurements[J]. Journal of Natural Disasters, 2006, 15(5): 45–53. |
| [14] | 何艳丽. 空间结构风工程[M]. 上海: 上海交通大学出版社, 2012: 60-62. |
| [15] |
王璐璐. 台风作用下跨海斜拉桥的失效机理[D]. 杭州: 浙江大学, 2014: 20-27.
WANG Lu-lu. Failure mechanism of sea-crossing cable-stayed bridge under typhoon wind field[D]. hangzhou: Zhejiang University, 2014: 20-27. |
| [16] |
范峰, 支旭东, 沈世钊. 大跨度网壳结构强震失效机理研究[J].
建筑结构学报, 2010, 31(6): 153–159.
FAN Feng, ZHI Xu-dong, SHEN Shi-zhao. Failure mechanism of large span reticulated shells subjected to severe earthquakes[J]. Journal of Building Structures, 2010, 31(6): 153–159. |
| [17] |
杜文风, 高博青, 董石麟. 单层球面网壳结构动力强度破坏的双控准则[J].
浙江大学学报:工学版, 2007, 41(11): 1916–1926.
DU Wen-feng, GAO Bo-qing, DONG Shi-lin. Double-control criterion of dynamical strength failure for single layer latticed shells[J]. Journal of Zhejiang University :Engineering Science, 2007, 41(11): 1916–1926. |
| [18] |
陈东, 王修信, 徐赵东. 双层球面网壳动力失效分析及地震损失评估[J].
地震工程与工程振动, 2012, 21(1): 36–42.
CHEN Dong, WANG Xiu-xin, XU Zhao-dong. Dynamic failure of double-layer spherical reticulated shell and estimate of seismic losses[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 21(1): 36–42. |



