2. 浙江大学 建筑工程学院 岩土工程研究所, 浙江 杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
土质防污隔离墙(简称“隔离墙”)是一种经济有效的地下水土污染防控技术, 广泛应用于固体废弃物填埋场和工业污染场地[1-2].根据墙体材料, 隔离墙的类型主要有土-膨润土隔离墙、塑性混凝土隔离墙、水泥-膨润土隔离墙等.其中, 多种隔离墙(如土-膨润土隔离墙和塑性混凝土隔离墙)施工中的沟槽开挖过程一般采用膨润土泥浆护壁, 以防止沟槽失稳坍塌.《水利水电工程混凝土防渗墙施工技术规范SL 174-96》规定, 膨润土泥浆新制浆液性能要满足浓度大于4.5%、密度小于1.1 g/cm3、漏斗黏度为30~90 s、塑性黏度小于20 mPa·s, 10 min静切力为1.4~10.0 N/m2, pH值为9.5~12.0.
在膨润土泥浆护壁时, 需控制泥浆液面高于地下水位面, 沟槽内外的水压力差造成泥浆中的自由水渗透进入周围地基土中.若沟槽周围地基土颗粒较细、孔隙较小, 泥浆中水化的膨润土颗粒在沟槽壁上逐渐聚集形成膨润土泥饼(简称“泥饼”);若地基土颗粒较粗, 泥浆中水化的膨润土颗粒进入到土体孔隙中, 在被泥浆渗透的区域形成泥饼[3-5].膨润土泥饼渗透性一般低于隔离墙墙体材料, 对隔离墙整体防渗性能有较大影响.评价隔离墙现场渗透性时应考虑泥饼的作用[6-7].然而, 目前隔离墙的防渗和防污性能研究通常仅考虑墙体材料的作用, 未考虑泥饼的贡献.
国内对膨润土泥饼的研究主要集中在混凝土地下连续墙[8-9]、泥水盾构[10-11]、钻孔灌注桩[12-13]和石油钻井[14-15]等工程中, 研究泥浆渗透及泥饼存在情况下泥浆静液压力的护壁作用, 目前, 泥饼渗透性对成墙后隔离墙整体渗透性影响的研究未见报道.有国外学者[16-19]采用美国石油协会(American Petroleum Institute, API)压滤试验测定泥饼渗透系数, 该方法原用于石油钻井行业测定钻井液滤失量(衡量钻井液质量的重要指标), 由于石油钻井深度大、液柱压力高, API压滤试验中所采用的压滤压力为690 kPa.国外学者研究隔离墙泥饼渗透性时借鉴了API压滤试验, 采用的压滤压力范围为69~690 kPa, Chung等[16]测得3种膨润土泥饼的渗透系数范围分别为3.65×10-11~3.51×10-10 m/s、1.51×10-11~1.34×10-10 m/s和8.16×10-12~5.56×10-11 m/s, Nguyen等[17]得到的膨润土泥饼渗透系数范围为2.15×10-11~2.88×10-10 m/s.在隔离墙沟槽施工时, 地下水位面高的工况沟槽容易失稳, 为控制沟槽稳定性, 泥浆液面通常控制在地下水位面以上1~2 m.此时泥浆液面与地下水位面之间的压力差(即形成泥饼的渗透压力差)小于30 kPa, 显著小于国外学者在泥饼压滤试验中采用的压力值.可见, 国外学者采用的压滤压力过大, 获得的泥饼渗透系数可能过小, 从而造成过大估计泥饼的防渗作用.
本文采用压滤压力为20~80 kPa测定膨润土泥饼渗透系数, 并与国外学者在69~690 kPa压力下得到的泥饼渗透系数以及常见隔离墙墙体材料渗透系数进行比较;进一步分析了泥饼渗透系数、泥饼厚度和墙体材料渗透系数对隔离墙渗透性的影响.
1 试验材料隔离墙建造过程中要求膨润土具备良好的水化性能和膨胀性能, 而不同膨润土矿出产的膨润土性能差别较大.本文首先根据《膨润土膨胀指数试验方法JC/T 2059-2011》测试了美国怀俄明、山东潍坊、吉林刘房子、新疆夏子街和安徽繁昌这5种不同产地膨润土的膨胀指数, 分别为59.0、15.8、14.0、11.5和8.4 mL/2g.可见, 美国怀俄明膨润土的膨胀指数远大于其他几种膨润土, 因此, 本文选择怀俄明膨润土作为试验材料.
怀俄明膨润土的土性参数如表 1所示.根据《土工试验方法标准GB/T 50123-1999》的测试方法, 测得了该膨润土的土粒比重ds=2.65, 液限wL=332.0%, 塑限wP=25.2%, 塑性指数IP=306.8.采用X射线衍射(XRD)法测得了该膨润土的蒙脱石质量分数w1=71.4%, 显著高于我国出产的大部分膨润土(50%左右[20]).采用《气体吸附BET法测定固态物质比表面积GB/T 19587-2004》中的气相色谱法测得了该膨润土的比表面积S=80.2 m2/g, 是一般国产天然膨润土比表面积(20 m2/g左右[21])的4倍左右.
| 表 1 怀俄明膨润土特性 Table 1 Properties of Wyoming bentonite |
根据《膨润土GB/T 20973-2007》中阳离子交换量及交换性阳离子含量试验方法测得了怀俄明膨润土阳离子交换量指标, 阳离子交换量值为764.9 mmol/kg, K+交换量值为0.3 mmol/kg, Na+交换量值为474.0 mmol/kg, Ca2+交换量值为128.2 mmol/kg, Mg2+交换量值为54.2 mmol/kg, 可交换金属离子总量为656.6 mmol/kg.
本文根据泥浆比重值和漏斗黏度值确定膨润土掺量.采用ANY-1型泥浆比重计和黏度计分别测试不同膨润土掺量泥浆的比重和漏斗黏度后, 发现膨润土掺量为6%的泥浆符合规范及工程要求, 其比重为1.05, 漏斗黏度值为25.3 s, 故选用膨润土掺量为6%泥浆进行下述压滤试验.
2 泥饼渗透性试验 2.1 试验仪器和试验方法为了研究膨润土泥饼渗透性, 参考规范ASTM-D5891(2002) 和API-RP 13B-1(1990), 采用RCLF-1A型中压滤失仪进行压滤试验(如图 1所示).RCLF-1A型中压滤失仪主要由泥浆杯、减压阀、压力表和支架组成, 其中泥浆杯由不锈钢杯体、顶盖、杯底、滤网和密封垫等组成, 顶盖由压紧螺杆与仪器支架相连接, 仪器的过滤面积为45.60±0.60 cm2.

|
图 1 压滤试验 Fig. 1 Fluid loss test |
泥浆压滤试验的主要试验步骤如下:1) 称取120.0 g烘干的膨润土, 分多次加入到1 880.0 g自来水中, 此过程中用电动搅拌器搅拌均匀, 制成掺量为6%的膨润土泥浆, 将泥浆静置24 h使膨润土充分水化, 制得的泥浆可供4组不同压滤压力的试验使用;2) 试验前, 用电动搅拌器搅拌膨润土泥浆5 min, 称量350 ml泥浆装入API泥浆杯, 旋紧顶盖, 滴水管下放置量程为5 mL、精度为0.1 mL的量筒;3) 接通压缩气压, 调节减压阀至所需压力值进行压滤试验, 定时记录滤出自由水体积, 前1 h中每15 min记录一次, 之后每30 min记录一次;4) 试验结束, 用注射器抽取泥浆杯中剩余泥浆, 拆除泥浆杯, 去除泥饼表面浮浆, 得到膨润土泥饼(如图 2所示);5) 用天平和玻璃皿称量湿泥饼质量, 将泥饼放入烘箱烘干测定含水率w.

|
图 2 压滤试验得到的膨润土泥饼 Fig. 2 Bentonite filter cake formed in fluid loss test |
本文首先进行预试验, 压滤压力p0均为20 kPa, 进行试验时长分别为3、6和9 h的3组压滤试验, 验证本试验方法的可重复性及选取合适的压滤时长.接着进行20、40、60和80 kPa压力下的4组压滤试验, 压滤时长均为3 h.测定的泥饼含水率w和计算得到的泥饼平均孔隙比e如表 2所示.随着压滤压力增大, 泥饼含水率降低, 孔隙比减小.可见, 压滤压力对泥饼含水率和孔隙比存在一定影响.
| 表 2 压滤试验数据 Table 2 Data of fluid loss test |
由达西定律可得到基本渗透方程:
| $ \frac{\text{d}V}{\text{d}t}=\frac{{{k}_{\text{c}}}}{{{\gamma }_{\text{w}}}}\frac{{{p}_{0}}}{{{b}_{c}}}A. $ | (1) |
式中:V为压滤体积(m3), t为压滤时间(s), kc为泥饼渗透系数(m/s), γw为水重度(kN/m3), bc为泥饼厚度(m), A为压滤面积(m2).
Chung等[16-17]认为压滤过程中由于固体颗粒的沉积, 泥饼不断增厚, 泥饼厚度变化的同时伴随着流速和应力的变化.当进行等压压滤时, 泥饼被认为不可压缩, 泥饼的密度或孔隙比保持不变.因此, 悬液压滤体积与泥饼增量体积呈线性比例关系, 该比例系数可以用来计算泥饼厚度:
| $ {{b}_{\text{c}}}=\beta \frac{V}{A}. $ | (2) |
式中:β为比例系数, 可由压滤系统内的液体质量守恒和固体质量守恒得到
| $ \beta = \frac{{{C_{\rm{m}}}{\rho _{\rm{w}}}\left( {1 + e} \right)}}{{\left( {1 - {C_{\rm{m}}}} \right){\rho _{\rm{s}}} - {C_{\rm{m}}}e{\rho _{\rm{w}}}}}. $ | (3) |
式中:Cm为泥浆中固相含量(%), ρw为自来水密度(g/cm3), ρs为膨润土泥饼干密度(g/cm3).
将式(2) 代入式(1), 积分后可得到
| $ t=\frac{\beta {{\gamma }_{w}}}{2{{A}^{2}}{{k}_{\text{c}}}{{p}_{0}}}{{V}^{2}}.即\frac{{{p}_{0}}t}{V}=\frac{\beta {{\gamma }_{\text{w}}}}{2{{A}^{2}}{{k}_{\text{c}}}}V. $ | (4) |
Chung等[17-18, 22]经过理论分析得到, 当泥饼厚度增加时, 泥饼中有效应力大小沿厚度不同, 但有效应力沿x/bc的分布模式相同, 即泥饼中的平均有效应力不随泥饼厚度变化, 故泥饼的平均孔隙比和平均渗透系数不随泥饼厚度变化.式(4) 中, p0t/V为因变量, V为自变量, 两者为线性关系, βγw/(2A2kc)为比例系数.在同一压滤压力下, 比例系数βγw/(2A2kc)为定值, 且β、γw和A均为常数, 泥饼平均渗透系数kc为定值.
因此, 泥饼渗透系数计算公式可以写成
| $ {{k}_{\text{c}}}=\frac{\beta {{\gamma }_{\text{w}}}}{2{{A}^{2}}}\frac{V}{{{p}_{0}}t/V}. $ | (5) |
当p0=20、40、60和80 kPa条件下的压滤试验获得滤失量V与时间t的关系如图 3所示.从图中可见, 随时间增加, 滤失量增加速度逐渐减小, 压力值对滤失量的影响逐渐增大(各条线同一横坐标对应的纵坐标差值随时间逐渐增大).这是由于泥饼厚度增加时, 泥饼平均渗透系数不变[16-17], 但水分渗透距离增大, 水分通过泥饼的时间增加.

|
图 3 各级压力下滤失量与时间关系 Fig. 3 Relationship between filtrate volume and time at different pressure |
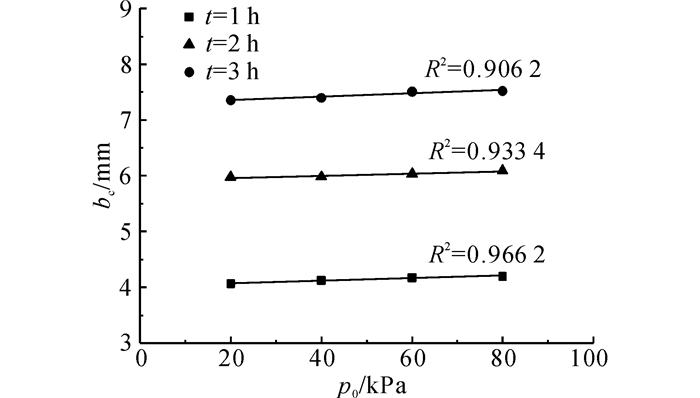
由式(2) 可知同一压滤压力条件下泥饼厚度与泥浆滤失量有关, 即压滤时间不同形成泥饼厚度不同.如图 4所示为压滤时间分别为1、2和3 h所对应的泥饼厚度与压滤压力关系.从图中可见, 泥饼厚度随压滤时间增加而增大, 随时间增加泥饼厚度增大速度呈减小趋势, 这是由于滤失量增加速度逐渐减小;对于同一压滤时间, 泥饼厚度随压滤压力增大而增大, 但压力大小不同导致的泥饼厚度差别较小, 例如, 当t=2 h, p0=20和80 kPa时所对应的bc分别为5.97和6.09 mm.
|
图 4 不同压滤时间下泥饼厚度与压滤压力关系 Fig. 4 Relationship between cake thickness and pressure at different time |
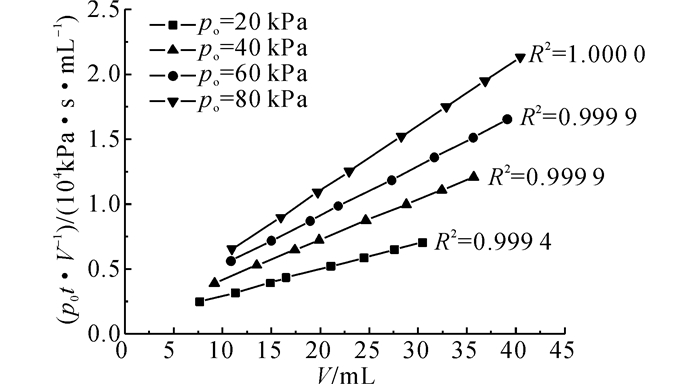
将试验数据根据式(4) 按V为横坐标、p0t/V为纵坐标整理(如图 5所示), 图中数据点进行线性拟合可得到直线斜率βγw/(2A2kc), 进而计算得到了泥饼渗透系数kc.
|
图 5 不同压滤压力下p0t/V与滤失量关系 Fig. 5 Relationship between p0t/V and filtrate volume at different pressure |
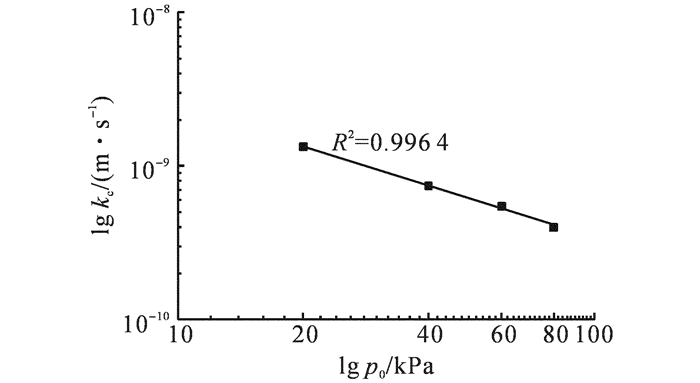
各组压滤压力下泥饼的渗透系数值如图 6所示.当p0=20~80 kPa时, 6%膨润土泥浆形成泥饼的渗透系数kc的变化范围为4.0×10-10~1.3×10-9 m/s, 随压滤压力增大, 形成泥饼渗透系数呈减小趋势, 其中, 当p0=20、40、60和80 kPa时对应的泥饼渗透系数分别为1.3×10-9、7.4×10-10、5.5×10-10和4.0×10-10 m/s.
|
图 6 不同压滤压力下泥饼的渗透系数 Fig. 6 Hydraulic conductivity of filter cake at different pressure |
与Nguyen等[17]在69~690 kPa压力范围下得到的泥饼渗透系数相比, 本文测得的泥饼渗透系数大了1~2个数量级.除了试验采用膨润土种类不同导致的差异, 更多是由于Nguyen等[17]国外学者采用的API试验压滤压力较大, 显著大于沟槽中泥浆液面与地下水位面之间的压力差, 造成泥饼中平均有效应力较大及平均孔隙比较小, 导致了泥饼的平均渗透系数较小.
不同隔离墙的墙体材料渗透性有较大差别, 塑性混凝土墙和水泥-膨润土墙约为10-8 m/s数量级, 土-膨润土墙通常为10-9 m/s数量级, 本文测得的泥饼渗透系数比塑性混凝土墙和水泥-膨润土墙的墙体材料渗透系数小1~2个数量级, 与土-膨润土墙的墙体材料渗透系数接近.
如图 6所示, lgkc与lgp0之间的关系呈线性, 两者之间的关系可表达为
| $ {{k}_{\text{c}}}={{k}_{0}}{{p}_{0}}^{-\alpha }. $ | (6) |
式中:k0为单位压力下的渗透系数(m/s), 参数α为lgkc-lgp0图上的斜率.本文试验获得的k0和α分别为2.0×10-8 m/s和0.86.
3 泥饼对墙体渗透性的影响隔离墙的整体渗透性受到泥饼和墙体回填材料的影响, 两者对墙体渗透性的贡献与材料渗透系数和厚度有关.防污隔离墙的底部通常位于不透水层(渗透系数小于1×10-9 m/s的土层中)内, 截断地下水的渗流通道, 地下水渗流场可简化为一维水平向渗流, 并假定隔离墙两侧均有完整泥饼, 根据达西定律可得到
| $ q=ki=k\frac{\Delta h}{2{{b}_{\text{c}}}+{{b}_{\text{b}}}}={{k}_{\text{c}}}\frac{\Delta {{h}_{\text{c}}}}{2{{b}_{\text{c}}}}={{k}_{\text{b}}}\frac{\Delta {{h}_{\text{b}}}}{{{b}_{\text{b}}}}. $ | (7) |
式中:q为单位横断面上流量(m/s), i为水力梯度, k为隔离墙渗透系数(m/s), Δh为墙体两侧总体水压力差(m), bb为墙体材料厚度(m), Δhc为作用在泥饼上的水压力差(m), kb为墙体材料渗透系数(m/s), Δhb为作用在墙体材料上的水压力差(m).Δh、Δhc与Δhb之间有如下关系:
| $ \Delta h=\Delta {{h}_{\text{c}}}+\Delta {{h}_{\text{b}}}. $ | (8) |
将式(8) 代入式(7) 可得
| $ k=\frac{{{k}_{\text{b}}}{{k}_{\text{c}}}\left( 2{{b}_{\text{c}}}+{{b}_{\text{b}}} \right)}{2{{b}_{\text{c}}}{{k}_{\text{b}}}+{{b}_{\text{b}}}{{k}_{\text{c}}}}. $ | (9) |
由于墙体材料厚度bb一般远大于泥饼厚度bc, 式(9) 可简化为
| $ k={{{b}_{\text{b}}}}/{\left( \frac{{{b}_{\text{b}}}}{{{k}_{\text{b}}}}+\frac{2{{b}_{\text{c}}}}{{{k}_{\text{c}}}} \right)}\;. $ | (10) |
根据式(10) 进行隔离墙渗透系数k影响因素分析, 考虑典型墙体材料厚度bb(0.9 m)、泥饼渗透系数kc(1.0×10-10~1.0×10-9 m/s)和泥饼厚度bc(4~200 mm).
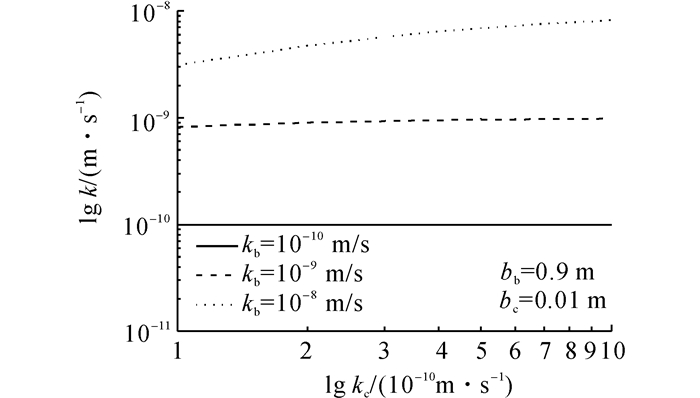
如图 7所示为不同墙体材料渗透系数kb情况下隔离墙渗透系数k与泥饼渗透系数kc关系.从图中可见, 当墙体材料厚度bb和泥饼厚度bc一定时, 隔离墙渗透系数随泥饼渗透系数的增大而增大.墙体材料渗透系数越大, 泥饼渗透系数变化对隔离墙渗透系数的影响越大, 例如, 当bb=0.9 m、bc=0.01 m、kb=1.0×10-9 m/s时, kc从1.0×10-10 m/s增加到1.0×10-9 m/s, 对应的k从8.2×10-10 m/s增加到9.8×10-10 m/s, 增加了19.5%;当kb=1.0×10-8 m/s时, kc从1.0×10-10 m/s增加到1.0×10-9 m/s, 对应的k从3.1×10-9 m/s增加到8.2×10-9 m/s, 增加了164.5%.
|
图 7 不同墙体材料渗透系数情况下隔离墙渗透系数与泥饼渗透系数关系 Fig. 7 Relationship between permeability of cutoff wall and permeability of filter cake at different backfill permeability |
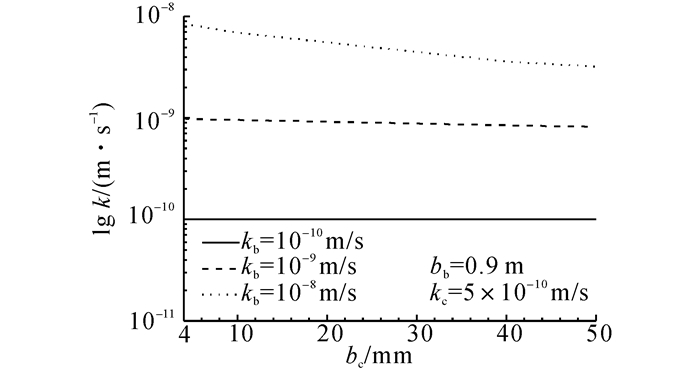
如图 8所示为不同墙体材料渗透系数情况下隔离墙渗透系数与泥饼厚度关系.从图中可见, 当墙体材料厚度和泥饼渗透系数一定时, 隔离墙渗透系数随泥饼厚度的增大而减小.墙体材料渗透系数越大, 泥饼厚度变化对隔离墙渗透系数的影响越大, 例如, 当bb=0.9 m、kc=5.0×10-10 m/s、kb=1.0×10-9 m/s时, bc从4 mm增加到50 mm, 对应的k从9.8×10-10 m/s减小到8.2×10-10 m/s, 减小了16.3%;当kb=1.0×10-8 m/s时, bc从4 mm增加到50 mm, 对应的k从8.5×10-9 m/s减小到3.1×10-9 m/s, 减小了63.5%.
|
图 8 不同墙体材料渗透系数情况下隔离墙渗透系数与泥饼厚度关系 Fig. 8 Relationship between permeability of cutoff wall and thickness of filter cake at different backfill permeability |
由隔离墙渗透系数与泥饼渗透系数及泥饼厚度关系分析可得到, 墙体材料渗透系数越大, 泥饼渗透系数或泥饼厚度的变化对隔离墙渗透系数的影响越大.
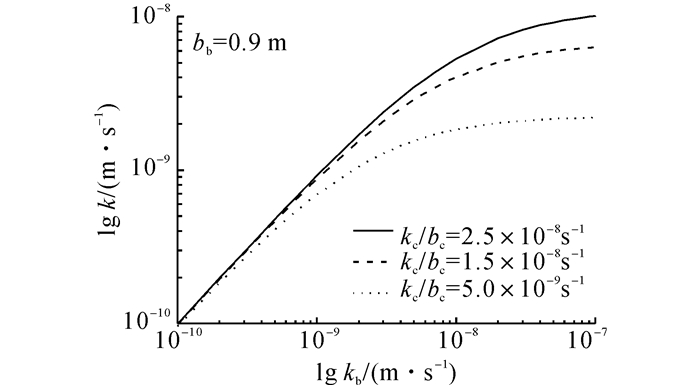
如图 9所示为3个不同泥饼渗透系数与泥饼厚度比值kc/bc所对应的隔离墙渗透系数与墙体材料渗透系数关系.从图中可见, 当墙体材料渗透系数小于等于1.0×10-9 m/s时, 各条线同一横坐标对应的纵坐标值差值较小, 隔离墙渗透系数主要受墙体材料渗透系数控制, 受kc/bc值影响较小, 例如, 当bb=0.9 m、kb=1.0×10-9 m/s时, 泥饼参数kc/bc值为2.5×10-8 s-1、1.5×10-8 s-1和5.0×10-9 s-1时所对应的k分别为9.2×10-10、8.7×10-10和6.9×10-10 m/s.当kb大于等于1.0×10-7 m/s时, 各条线同一横坐标对应的纵坐标值差值逐渐增大, 隔离墙渗透系数逐渐受泥饼参数控制, 例如, 当bb=0.9 m、kb=1.0×10-7 m/s时, 泥饼参数kc/bc值为2.5×10-8、1.5×10-8和5.0×10-9 s-1所对应的k分别为1.0×10-8、6.3×10-9和2.2×10-9 m/s.
|
图 9 不同泥饼参数情况下隔离墙渗透系数与墙体材料渗透系数关系 Fig. 9 Relationship between permeability of cutoff wall and permeability of backfill at different cake parameter |
当墙体材料厚度和泥饼参数kc/bc值一定时, 随着墙体材料渗透系数增大, 隔离墙渗透系数呈增大趋势, 但墙体材料渗透系数增大到1.0×10-7 m/s以上时, 隔离墙渗透系数趋于稳定不再增大, 即隔离墙渗透系数有一极限值, 这是由于墙体材料渗透系数大于等于1.0×10-7 m/s时, 隔离墙渗透系数主要由泥饼渗透系数和厚度决定.
4 结论本文根据实际工程泥浆沟槽中形成泥饼的渗透压力差范围(通常小于30 kPa), 采用API压滤试验方法, 测得压力为20~80 kPa工况下膨润土泥饼的渗透系数为4.0×10-10~1.3×10-9 m/s, 比外国学者在69~690 kPa压力下得到的泥饼渗透系数大1~2个数量级, 主要是由于国外学者采用的API试验压滤压力较大, 显著大于沟槽中泥浆液面与地下水位面之间的压力差, 造成泥饼中平均有效应力较大及平均孔隙比较小, 导致了泥饼的平均渗透系数较小;本文测得的泥饼渗透系数比塑性混凝土墙和水泥-膨润土墙的墙体材料渗透系数小1~2个数量级, 与土-膨润土墙的墙体材料渗透系数接近.
将得到的泥饼渗透系数应用于分析隔离墙整体渗透性, 分析了泥饼渗透系数、泥饼厚度和墙体材料渗透系数对隔离墙渗透性的影响, 主要获得以下结论.
(1) 墙体材料渗透系数较小(kb≤1.0×10-9 m/s)时, 隔离墙渗透性主要受墙体材料渗透系数控制;当墙体材料渗透系数较大(kb≥1.0×10-7 m/s)时, 隔离墙渗透性主要受泥饼参数控制.
(2) 当墙体材料厚度和泥饼参数kc/bc值一定时, 隔离墙渗透系数随墙体材料渗透系数的增大而增大, 但由于存在厚度小且渗透性低的泥饼, 隔离墙渗透系数会趋近于一极限值.
| [1] |
陈云敏. 环境土工基本理论及工程应用[J].
岩土工程学报, 2014, 36(1): 1–46.
CHEN Yun-min. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1–46. DOI:10.11779/CJGE201401001 |
| [2] |
张文杰, 陈云敏, 詹良通. 垃圾填埋场渗滤液穿过垂直防渗帷幕的渗漏分析[J].
环境科学学报, 2008, 28(5): 925–929.
ZHANG Wen-jie, CHEN Yun-min, ZHANG Liang-tong. Transport of leachate through vertical curtain grouting in landfills[J]. Acta Scientiae Circumstantiae, 2008, 28(5): 925–929. |
| [3] | FILZ G M, BOYER R D, DAVIDSON R R. Bentonite-water slurry rheology and cutoff wall trench stability[J]. Geotechnical Special Publication, 1997, 71: 139–153. |
| [4] | HENRY L B, FILZ G M, DAVIDSON R R. Formation and properties of bentonite filter cakes[J]. Geotechnical Special Publication, 1998, 78: 69–88. |
| [5] | SOROUSH A, SOROUSH M. Parameters affecting the thickness of bentonite cake in cutoff wall construction: case study and physical modeling[J]. Canadian Geotechnical Journal, 2005, 42(2): 646–654. DOI:10.1139/t04-090 |
| [6] | NGUYEN T B, LEE C, CHOI H. Slug test analysis in vertical cutoff walls with consideration of filter cake[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(8): 785–797. |
| [7] | NGUYEN T B, LEE C, KIM S, et al. Modification of the bouwer and rice method to a cutoff wall with a filter cake[J]. Ground Water, 2010, 48(6): 898–902. DOI:10.1111/gwat.2010.48.issue-6 |
| [8] |
游朝阳. 广州同和地铁站地下连续墙设计与施工关键技术[D]. 广州: 华南理工大学, 2009.
YOU Chao-yang. Key techniques of diaphram wall design and construction at Tonghe metro station in Guangzhou[D]. Guangzhou: South China University of Technology, 2009. |
| [9] |
杨勇. 复合钠基膨润土泥浆护壁机理及其工程应用[J].
地下空间与工程学报, 2010, 6(4): 838–844.
YANG Yong. Stability maintaining mechanism of compound sodium-based bentonite slurry and its applicationin practical engineering[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(4): 838–844. |
| [10] |
韩晓瑞, 朱伟, 刘泉维, 等. 泥浆性质对泥水盾构开挖面泥膜形成质量影响[J].
岩土力学, 2008, 29(S1): 288–292.
HAN Xiao-rui, ZHU Wei, LIU Quan-wei, et al. Influence of slurry property on filter cake quality on working face of slurry shield[J]. Rock and Soil Mechanics, 2008, 29(S1): 288–292. |
| [11] |
韦良文. 泥水盾构隧道施工土体稳定性分析与试验研究[D]. 上海: 同济大学, 2007.
WEI Liang-wen. Stability analysis of soil body in slurry shield tunneling and test research[D]. Shanghai: Tongji University, 2007. |
| [12] |
王云岗, 章光, 胡琦. 钻孔灌注桩孔壁稳定性分析[J].
岩石力学与工程学报, 2011, 30(S1): 3281–3287.
WANG Yun-gang, ZHANG Guang, HU Qi. Analysisof stability of bored pile hole-wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S1): 3281–3287. |
| [13] |
时仓艳. 钻孔灌注桩孔壁稳定性分析及后压浆应用研究[D]. 南京: 东南大学, 2006.
SHI Cang-yan. Analyses on stbaility of bored piles and researeh on it by base post-grouting[D]. Nanjing: Southeast University, 2006. |
| [14] |
陈良. 钻井液防塌封堵评价方法及封堵机理研究[D]. 成都: 西南石油大学, 2013.
CHEN Liang. Studies evaluation methods of sealing and sealing mechanism of drilling fluid[D]. Chengdu: Southwest Petroleum University, 2013. |
| [15] |
薛玉志. 超低渗透钻井液作用机理及其应用研究[D]. 青岛: 中国石油大学, 2008.
XUE Yu-zhi. Study on the interaction mechanisms and application of ultra-low permeable drilling fluid[D]. Qingdao: China University Of Petroleum, 2008. |
| [16] | CHUNG J, DANIEL D E. Modied fluid loss test as an improved measure of hydraulic conductivity for bentonite[J]. Geotechnical Testing Journal, 2008, 31(3): 1–9. |
| [17] | NGUYEN T B, LEE C, LIM J, et al. Hydraulic characteristics of bentonite cake fabricated on cutoff walls[J]. Clays and Clay Minerals, 2012, 60(1): 40–51. DOI:10.1346/CCMN.2012.0600104 |
| [18] | MAHDI F M, HOLDICH R G. Laboratory cake ltration testing using constant rate[J]. Chemical Engineering Research and Design, 2013, 91(6): 1145–1154. DOI:10.1016/j.cherd.2012.11.012 |
| [19] | IRITANI E, KATAGIRI N, KANETAKE S. Determination of cake ltration characteristics of dilute suspension of bentonite from various ltration tests[J]. Separation and Purication Technology, 2012, 92: 143–151. DOI:10.1016/j.seppur.2011.05.011 |
| [20] |
刘承帅, 万洪富, 侯梅芳, 等. 我国主要产地膨润土颗粒组成和蒙脱石含量研究[J].
非金属矿, 2005, 28(1): 40–43.
LIU Cheng-shuai, WAN Hong-fu, HOU Mei-fang, et al. Study on particle size distribution and montmorillonite content of bentonite in main deposits[J]. Non-Metallic Mines, 2005, 28(1): 40–43. |
| [21] |
夏新兴, 彭毓秀, 李忠正, 等. 膨润土改性方法的研究[J].
中国造纸, 2003, 22(2): 20–23.
XIA Xin-xing, PENG Yu-xiu, LI Zhong-zheng, et al. Modified method of bentonite[J]. China Pulp and Paper, 2003, 22(2): 20–23. |
| [22] | FOX P J, BAXTER C D P. Consolidation properties of soil slurries form hydraulic consolidation test[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(8): 770–776. DOI:10.1061/(ASCE)1090-0241(1997)123:8(770) |



