2. 浙江大学 宁波理工学院, 浙江 宁波 315100
2. Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China
德国工程师Albert在1829年提出结构疲劳问题以来, 疲劳性能一直是土木工程界关心的热点话题[1].由于结构的疲劳破坏形式常为受拉钢筋的脆性断裂, 破坏前毫无征兆, 往往会造成比较严重的后果[2].相关工程事故也是屡见不鲜, 如美国宾夕法尼亚州的SR1014大桥便是由于疲劳荷载与外界侵蚀环境耦合作用下所导致腐蚀疲劳破坏[3].不少学者对钢筋混凝土结构的疲劳性能展开了研究, 然而受限于传统疲劳试验方法中的不足以及既有损伤指标的灵敏程度有限等问题, 使得结构疲劳损伤的研究进展受到了一定程度的制约, 迫切需要宏观与微观相结合以发展新的疲劳性能研究方法[4].
压磁效应是指铁磁性材料在外荷载作用下内部磁畴结构发生定向转动与排列, 进而引起周围磁场的改变.随着压磁效应的相关检测技术的不断发展, 衍生出磁巴克豪森噪声法、磁声发射法、金属磁记忆等无损检测方法, 应用到缺陷、应力集中、疲劳损伤等各个领域.Vandenbossch等[5]的低周疲劳压磁试验显示压磁信号的变化过程与应变等力学参量一致, 均符合疲劳损伤三阶段的规律, 证实了压磁信号应用在疲劳损伤领域的可行性.Mignogna等[6]的试验显示41.4~275.8 MPa的循环应力下磁感强度的变化幅度为2.0×10-7 T, 这个量级的变化易于被磁力仪捕捉到, 又不易被环境磁场干扰.Guralnick等[7-9]随后对铁磁钢材的疲劳压磁特性进行深入了研究, 证实磁感强度应变滞回曲线能反映比传统的应力应变滞回曲线更多的疲劳损伤相关信息, 且具有较好的敏感性.
钢筋锈蚀是工程结构面临有又一常见灾害[10], 不仅使钢筋的屈服强度和极限强度降低, 还大大影响疲劳性能.曹建安[11]对老化构件中取出的锈蚀钢筋进行试验, 绘制了疲劳曲线方程, 并发现钢筋锈蚀后疲劳极限趋于消失.李士彬等[12]对加速锈蚀钢筋的疲劳试验结果表明随着锈蚀率的上升疲劳寿命按指数规律递减.然而试验过程中仅通过疲劳寿命来反映疲劳性能, 即便通过应变监测也很难准确对疲劳过程中的损伤累积进行把控, 难以根据检测的信息预测疲劳寿命.而基于压磁效应的检测技术则为结构疲劳损伤的评估与寿命预测提供了新的途径.
鉴此, 本文对26根加速锈蚀钢筋进行轴向拉伸疲劳试验, 探索压磁效应对锈蚀钢筋疲劳性能的敏感性, 为压磁技术在疲劳损伤领域的发展与工程应用提供依据.
1 压磁检测原理压磁效应本质上是铁磁性材料在恒定弱磁场下表现出来的力与磁相互关系, 是能量从应力能的形式转移到了磁能的形式.外应力作用下铁磁体磁晶的总自由能表达为[13].
| $ E={{E}_{\text{k}}}+{{E}_{\text{ms}}}+{{E}_{\text{el}}}+{{E}_{\text{ }\!\!\sigma\!\!\text{ }}}. $ | (1) |
式中:E为总自由能, Ek为各向异性能, Ems为磁弹性能, Eel为弹性能, Eσ为应力能.根据能量最小原理[14], 当应力能发生改变时, 材料内部的磁畴结构便会自发产生转向与运动, 以改变磁能的方式使得自由能维持在稳定状态.
基于有效场理论建立的J-A模型[15-17]将铁磁性材料在磁化过程中获得的磁化强度分为可逆磁化部分与不可逆磁化部分.循环荷载作用下剩余磁化强度不断累积, 直至达到饱和磁化强度Man后进入可逆磁化状态.此时单个循环内磁化强度的变化以可逆磁化部分为主.可逆磁化强度与不可逆磁化强度之间的关系可以描述为
| $ M={{M}_{\text{rev}}}+{{M}_{\text{irr}}}. $ | (2) |
| $ {{M}_{\text{rev}}}=c\left( {{M}_{\text{an}}}-{{M}_{\text{irr}}} \right). $ | (3) |
式中:M为磁化强度, Mrev为可逆磁化强度, Mirr为不可逆磁化强度, Man为非滞后磁化强度, c为与磁畴壁的弹性有关的常数.
磁化状态的演变与材料疲劳损伤的累积状态存在相关性, 因而可基于压磁场信息来评判材料的疲劳损伤程度.同时, 钢筋的锈蚀会产生应力集中现象, 影响疲劳性能的同时也会改变磁能累积速率, 可探究锈蚀程度与压磁场信号之间的联系.
2 疲劳试验过程 2.1 加速锈蚀试验钢筋选用情况及实测力学性能见表 1.表中d为公称直径, A为截面面积, σy为屈服强度, σu为极限强度, W为单位重量.
| 表 1 钢筋力学性能 Table 1 Mechanical properties of steel bars |
锈蚀钢筋的获取方法目前主要有老化构件替换法、长期暴露试验法与通电加速锈蚀法.而获取老化构件数量往往有限, 长期暴露试验法周期又太长, 故而本文采用溶液模拟加速通电锈蚀的方法获取锈蚀钢筋, 即可较好地控制预期锈蚀率, 又可与实际锈蚀状况相近.同时为防止试件在疲劳试验中因端部应力集中而断在夹持端, 试件端部采用PVC管与玻璃胶密封进行保护, 中间锈蚀段取为300 mm, 见图 1.

|
图 1 钢筋锈蚀试件 Fig. 1 Specimens of corroded steel bars |
以不锈钢板充当阴极, 钢筋试件作阳极, 进行通电加速锈蚀, 电流密度为0.30 mA/cm2, 根据法拉第定律计算通电时间, 达到预定通电时间后酸洗称重.
2.2 试件加载方法锈蚀钢筋的轴向拉伸疲劳试验在250 kN电液伺服疲劳试验机上进行, 采用引伸计测量应变, APS428D磁通门磁力仪测量试件表面的法向与切向磁信号, 数据接入IMC动态数据采集仪中供后期分析处理.通过屏蔽环将环境磁噪声减小到0.2×10-7 T的量级, 磁探头的提离值取33 mm, 固定位置为试件锈蚀段下1/3处以获得理想的信号, 试件的安装见图 2.

|
图 2 量测装置安装 Fig. 2 Installation of measurement devices |
试验采用应力控制方式, 按正弦波进行加载, 应力水平L取0.5~0.7, 而应力下限恒为0.1, 加载频率取2.0 Hz, 较传统的高频试验更接近实际工程.确定试验力时按照预定的L与静载试验的σu进行计算, 并采用以平均截面积衡量的名义应力, 以剔除锈后平均截面积减小对疲劳性能的影响[18].
2.3 加载参数与疲劳寿命结果疲劳试验结果显示, 采用本文中的加速锈蚀方法, 疲劳断裂位置均处于在试件中部的锈蚀段上, 只有在锈蚀率极低的情况下才可能因试件端部应力集中而断裂在夹持端.试验主要参数与结果见表 2.表中ρ为锈蚀率, Nf为疲劳寿命, D为断裂处至锈蚀段下部的距离.
| 表 2 疲劳试验主要参数及结果 Table 2 Parameters and results of fatigue test |
对试验数据统计回归可得疲劳寿命的S-N曲线, 图 3给出了变形钢筋不同锈蚀程度的S-N曲线.其中,N为任意循环次数,S为应力幅,与未锈蚀钢筋试件相比, 平均截面锈蚀率为3%、6%、10%的Nf分别下降了70%、85%、90%.
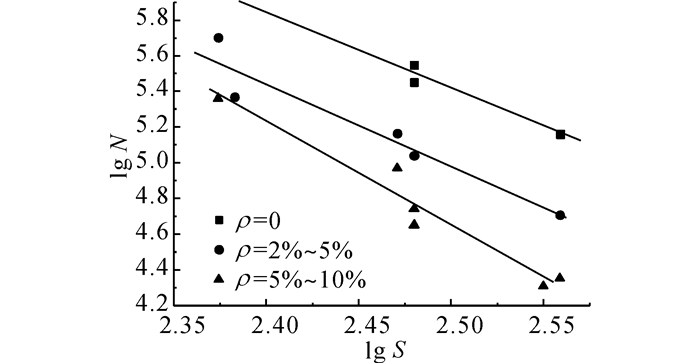
|
图 3 变形钢筋的S-N曲线 Fig. 3 S-N curves of deformed steel bars |
从疲劳试件表面磁感强度值的变化来看, 磁感强度的累积符合疲劳损伤3阶段的变化规律, 即初始阶段的损伤快速增长、稳定阶段的损伤缓慢累积以及破坏阶段的损伤突变剧增.图 4给出了典型的法向残余磁感强度Bn随疲劳循环次数N的变化.

|
图 4 SF14-10法向残余磁感强度变化规律 Fig. 4 Change of normal magnetic field of SF14-10 |
从图 4可知, 磁感强度值的变化与残余应变等传统指标类似, 可反映钢筋疲劳损伤的累积过程, 作为评价损伤的参数.切向磁感强度值Bt的变化规律与Bn类似, 但法向磁信号经屏蔽保护后抗外界干扰能力更强, 下文主要对法向磁信号进行分析.
3.2 磁感强度时变曲线演变就疲劳荷载中的某一个循环过程而言, 应变与荷载的增减是同步的.因此传统的应变时变曲线在整个疲劳损伤过程中除了应变值有所增大外, 形态上并无明显变化, 如图 5所示.图中ε为应变,而磁感强度时变曲线则能反映更多的信息, 图 6给出了疲劳不同阶段法向磁感强度时变曲线Bn(t)形态的变化过程.
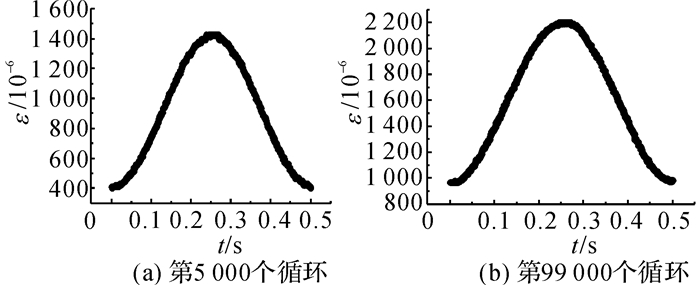
|
图 5 SF14-10不同阶段应变时变曲线 Fig. 5 Time varying curve of strain of SF14-10 |
从图 6中可看到,当应力应变接近峰值时, 磁感强度提前达到极值, 随后略有下降;应力应变从峰值开始下降时, 磁感强度又开始一段升势, 随后才开始下降.磁信号与力学信号并非同步增减.初始阶段与破坏阶段的时变曲线形态较稳定阶段有明显不同, 两极值之间的“波谷”不如稳定阶段明显, 可帮助判断疲劳损伤所处阶段.
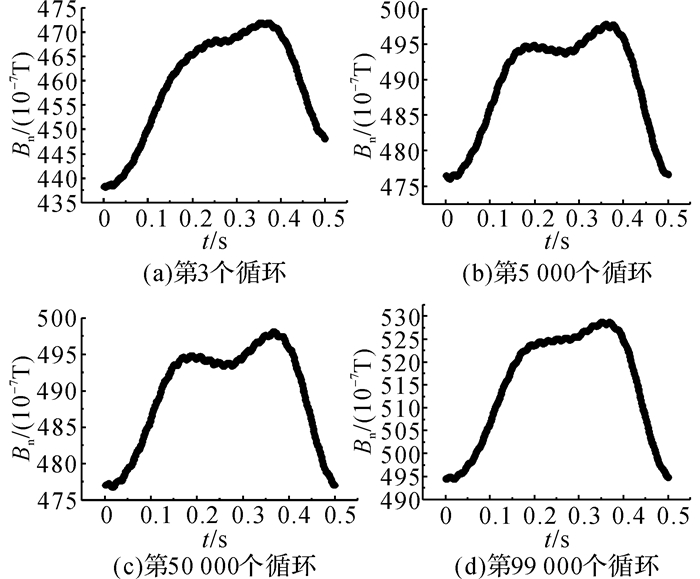
|
图 6 SF14-10不同阶段Bn的时变曲线 Fig. 6 Time varying curve of Bn of SF14-10 |
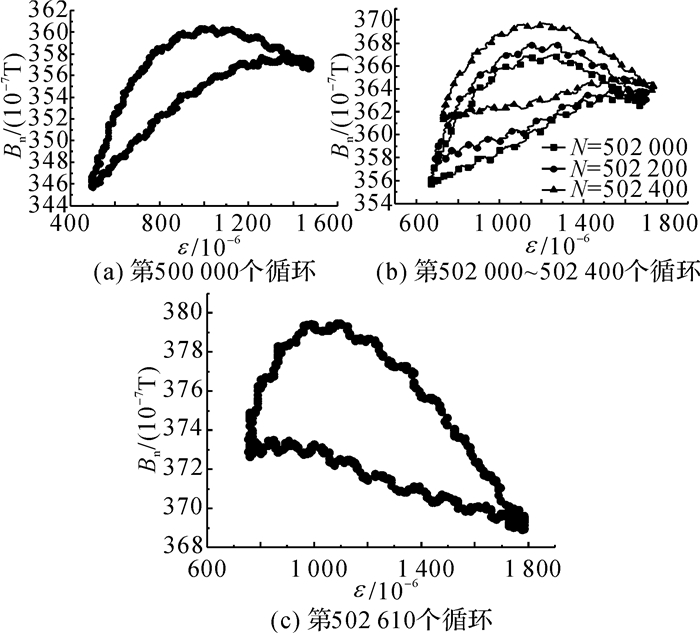
传统的疲劳分析常借助应力(σ)-应变(ε)滞回曲线反映结构的变形特征、刚度退化与能量耗散, 但因疲劳后期形态单调而难以反映更多疲劳损伤相关信息.图 7给出了SF14-10的法向磁感应强度(Bn)-应变(ε)滞回曲线与σ-ε滞回曲线的对比.
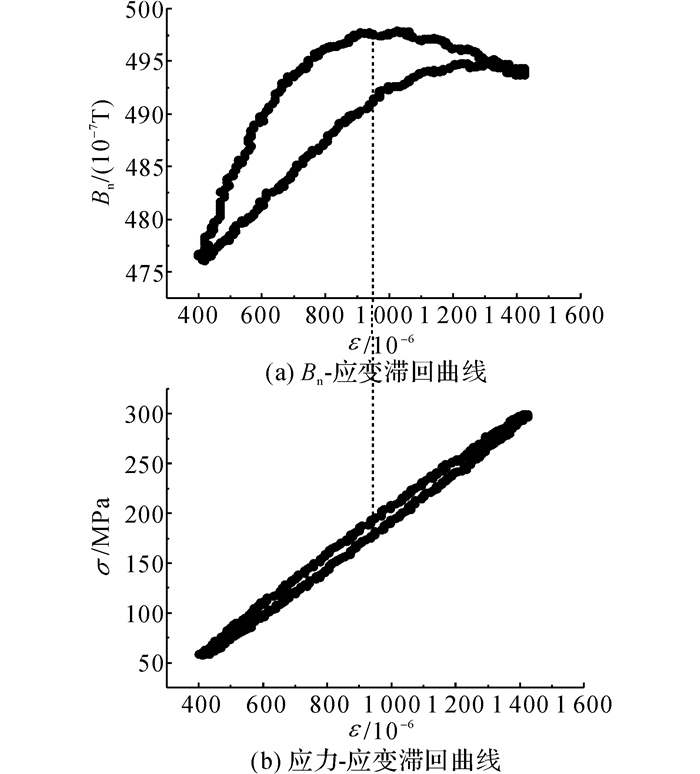
|
图 7 Bn-ε滞回曲线与σ-ε滞回曲线 Fig. 7 Comparison of two hysteresis curves |
由于应力水平并不高, σ-ε滞回曲线较为捏拢, 而Bn-ε滞回曲线的滞回特性更为明显, 形态上两者有很大不同.在临近破坏阶段, Bn-ε滞回曲线发生畸变, 形态上产生明显变化, 在磁感强度-应变坐标系统中从左下角往右上角移动, 可作为疲劳断裂的预警, 见图 8.
|
图 8 SF16-6破坏阶段Bn-ε滞回曲线形态 Fig. 8 Bn-ε curve during fracture stage |
本文采用的疲劳加载方式剔除了锈后平均截面积减小带来的疲劳性能损失, 反映出锈蚀的不均匀性对疲劳寿命的影响.这种不均匀程度往往随着锈蚀率的增大而增大.而传统的应变、位移等指标受限于检测方法与精度, 难以准确识别损伤上的差异.本文试验的结果显示, 压磁磁感强度在单个循环内的振幅较应变与位移能更好地识别锈蚀率的变化.表 3列出了不同锈蚀率下各指标在达到50%疲劳寿命时单个循环内的变化幅度.表中Δs为位移变幅, Δε为应变变化幅度, ΔBn为法向磁场变化幅度.
| 表 3 不同锈蚀率下各指标单个循环内变幅 Table 3 Amplitude of each index under different corrosionrate |
由表 3可知,Bn对锈蚀损伤十分敏感, 锈蚀率ρ的增大会使单个循环内的ΔBn加大;应力幅Δσ越大, 这种增幅就越明显.以HPB300钢筋在0.7应力水平下各指标变幅情况为例, 当ρ从0增大到6.1%, 试验机输出的Δs几乎都为0.70 mm, Δε也均在3.8×10-3 mm上下, ΔBn则从3.31×10-6 T增至9.27×10-6 T, 变化幅度明显.当Δσ与ρ均较大时试件局部进入屈服状态, 磁感强度变幅又会有巨幅提升, 如ρ为8.6%的HRB400钢筋在L为0.7时ΔBn高达1.73×10-5 T, 远远超过其他情形.如图 9所示为应力水平与锈蚀率对磁感强度变幅的影响.

|
图 9 ΔBn与ρ之间的关系 Fig. 9 Relationship of ΔBn and ρ |
综上所述, 钢筋锈蚀后疲劳性能受到大幅影响, 传统的位移、应变等指标受限于测量方法与精度, 不能很好的把握锈蚀情况与相应的疲劳性能, 而基于压磁效应的检测技术, 能够反映出很多与锈蚀、疲劳损伤相关信息, 较传统指标有更好的灵敏度, 为钢筋混凝土结构的无损检测提供了新的思路.
在实际工程的应用中, 要考虑车辆、电线等环境磁噪声干扰, 须通过屏蔽装置的合理设计来保证测量精度.实际构件中的钢筋网在不同受力状态下会产生更为复杂的信号, 探头的合理布置与信号的有效提取将是技术应用中考虑的重点课题, 有待进一步深入研究.
4 结论本文基于压磁效应, 对28根不同锈蚀率的加速锈蚀钢筋进行轴向拉伸疲劳试验, 研究了疲劳损伤过程的压磁信号的演变规律, 探究与锈蚀程度之间的关系, 得到以下结论:
(1) 压磁场信号能够反映众多与材料疲劳损伤相关的信息, 相对传统的损伤指标更为敏感.磁感强度值、磁感强度时变曲线、磁感强度-应变滞回曲线均能很好地呈现材料疲劳损伤3个阶段的变化规律.利用变化的拐点可帮助预测材料疲劳寿命、预警疲劳断裂, 并进行损伤评估.
(2) 单个循环内的钢筋磁感强度变幅随着钢筋锈蚀率的增大而增大, 应力幅越大则增幅越明显, 较传统的位移、应变等检测指标对锈蚀损伤更为敏感.
(3) 钢筋屈服进入塑性阶段后, 单个循环荷载内的磁感强度变化幅值远超未屈服状态下的相应变化幅值.
(4) 基于压磁效应的无损检测方法适用于锈蚀钢筋的疲劳性能检测, 可评价疲劳损伤、预测疲劳寿命、预警疲劳断裂、判断锈蚀程度等等, 具体的应用与分析方法尚需进一步的研究.
| [1] | SURESH S. Fatigue of materials[M]. Cambridge: Cambrige University Press, 1998. |
| [2] | 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002: 1-5. |
| [3] |
孙莉, 刘钊. 2000-2008年美国桥梁倒塌案例分析与启示[J].
世界桥梁, 2009(3): 46–49.
SUN Li, LIU Zhao. Case analysis and lessons drawn from bridge failures in United States from 2000 to 2008[J]. World Bridges, 2009(3): 46–49. |
| [4] |
张功义, 张军, 金伟良, 等. 基于压磁效应的磁性材料力学与疲劳的研究进展[J].
材料导报, 2014, 28(5): 4–10, 24.
ZHANG Gong-yi, ZHANG Jun, JIN Wei-liang, et al. Review of the mechanics and fatigue researches on magnetic materials based on piezomagnetic effect[J]. Materials Review, 2014, 28(5): 4–10, 24. |
| [5] | VANDENBOSSCHE L, DUPR L. Fatigue damage assessment by the continuous examination of the magnetomechanical and mechanical behavior[J]. Journal of Applied Physics, 2009, 105(7): 707. |
| [6] | MIGNOGNA R B, BROWNING V, GUBSER D U, et al. Passive nondestructive evaluation of ferromagnetic materials during deformation using SQUID gradiometers[J]. IEEE Transaction on Applied Superconductivity, 1993, 3(1): 1922–1925. DOI:10.1109/77.233585 |
| [7] | GURALNICK S A, BAO S, ERBER T. Piezomagnetism and fatigue: Ⅱ[J]. Journal of Physics D: Applied Physics, 2008, 41(11): 1–11. |
| [8] | BAO S, JIN W L, GURALNICK S A, et al. Two-parameter characterization of low cycle hysteretic fatigue data[J]. Journal of Zhejiang University: Applied Physics and Engineering, 2010, 11(6): 449–454. DOI:10.1631/jzus.A0900763 |
| [9] | BAO S, ERBER T, GURALNICK S A, et al. Fatigue, magnetic and mechanical hysteresis[J]. Strain, 2011, 47(4): 372–381. DOI:10.1111/str.2011.47.issue-4 |
| [10] |
金伟良, 赵羽习. 混凝土结构耐久性研究的回顾与展望[J].
浙江大学学报:工学版, 2002, 36(4): 371–380, 403.
JIN Wei-liang, ZHAO Yu-xi. State-of-the-art on durability of concrete structures[J]. Journal of Zhejiang University :Engineering Science, 2002, 36(4): 371–380, 403. |
| [11] |
曹建安, 文雨松. 锈蚀钢筋的疲劳试验研究[J].
长沙铁道学院学报, 1998, 16(4): 15–18.
CAO Jian-an, WEN Yu-song. Fatigue experimental study on corrosion reinforcement[J]. Journal of Changsha Railway University, 1998, 16(4): 15–18. |
| [12] |
李士彬, 张伟平, 顾祥林, 等. 加速锈蚀钢筋的疲劳试验研究[J].
铁道学报, 2010, 32(5): 93–97.
LI Shi-bin, ZHANG Wei-ping, GU Xiang-lin, et al. Experimental study on fatigue properties of corrosion-accelerated steel bars[J]. Journal of the China Railway Society, 2010, 32(5): 93–97. |
| [13] |
冷建成. 基于磁记忆技术的铁磁性材料早期损伤诊断方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
LENG J C. Research on early damage diagnosis method of ferromagnetic materials based on magnetic memory testing technique[D]. Harbin: Harbin Institute of technology. |
| [14] | 宛德福, 马兴隆. 磁性物理学[M]. 成都: 电子科技大学出版社, 1994: 185-228. |
| [15] | JILES D C. Theory of the magnetomechanical effect[J]. Journal of Physics D-Applied Physics, 1995, 28(8): 1537–1546. DOI:10.1088/0022-3727/28/8/001 |
| [16] | LI L, JILES D C. Modeling of the magnetomechanical effect: Application of the Rayleigh law to the stress domain[J]. Journal of Applied Physics, 2003, 93(10): 8480–8482. DOI:10.1063/1.1540059 |
| [17] | JILES D C, LI L. A new approach to modeling the magnetomechanical effect[J]. Journal of Applied Physics, 2004, 95(11): 7058–7060. DOI:10.1063/1.1687200 |
| [18] |
张伟平, 李士彬, 顾祥林, 等. 自然锈蚀钢筋的轴向拉伸疲劳试验[J].
中国公路学报, 2009, 22(2): 53–58.
ZHANG Wei-ping, LI Shi-bin, GU Xiang-lin, et al. Experiment on axial tensile fatigue of naturally corroded steel bar[J]. China Journal of Highway and Transport, 2009, 22(2): 53–58. |


